Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Уравнение прямой симметричной данной относительно плоскости
|
|||
|
Здравствуйте, проверьте пожалуйста мое решение, а то какие-то не очень хорошие ответы получились (на мой взгляд).
|
||
| Вернуться к началу |
|
||
|
Alexandr1337 |
Заголовок сообщения: Re: Уравнение прямой симметричной данной относительно плоскости
|
|
vvvv писал(а): Наверное, все-таки правильно так. См.картинку. Спасибо, все пересчитал получился такой ответ.
|
|
| Вернуться к началу |
|
|
dr Watson |
Заголовок сообщения: Re: Уравнение прямой симметричной данной относительно плоскости
|
|
Alexandr1337 писал(а): vvvv писал(а): Спасибо, все пересчитал получился такой ответ. Это правильный ответ. Сумма отнормированных направляющих векторов исходной прямой и симметричной либо параллельна плоскости либо ей перпендикулярна в зависимости от выбора направления.
|
|
| Вернуться к началу |
|
| За это сообщение пользователю dr Watson “Спасибо” сказали: Alexandr1337 |
|
|
dr Watson |
Заголовок сообщения: Re: Уравнение прямой симметричной данной относительно плоскости
|
|
Ошибка была в последней строчке – направляющий вектор получался вычитанием координат точки [math]A[/math] вместо [math]B.[/math] Тут я расслабился и не посмотрел наверху координаты точки [math]B.[/math] Мог бы и обратить (если бы решение было целиком перед глазами) – ведь прямая получилась перпендикулярная плоскости (!!!), ну кто бы мог подумать?
|
|
| Вернуться к началу |
|
| За это сообщение пользователю dr Watson “Спасибо” сказали: Alexandr1337 |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти точку, симметричную данной относительно прямой
в форуме Аналитическая геометрия и Векторная алгебра |
jeenkaaa |
1 |
1325 |
30 май 2013, 13:50 |
|
Найти точку симметричную данной относительно плоскости
в форуме Аналитическая геометрия и Векторная алгебра |
RETU |
17 |
2728 |
24 апр 2018, 14:09 |
|
Построение плоскости перпендикулярной данной прямой
в форуме Геометрия |
Butsilova |
3 |
1592 |
25 май 2016, 17:50 |
|
Построение прямой перпендикулярной данной плоскости
в форуме Геометрия |
Butsilova |
2 |
505 |
26 май 2016, 10:01 |
|
Уравнение плоскости параллельной данной
в форуме Аналитическая геометрия и Векторная алгебра |
Vozart |
2 |
166 |
13 янв 2021, 23:11 |
|
Построение точки, симметричной другой точке отн-но плоскости
в форуме Аналитическая геометрия и Векторная алгебра |
ZOlga |
5 |
642 |
24 дек 2013, 15:03 |
|
Уравнение прямой на плоскости
в форуме Информатика и Компьютерные науки |
AnnaGerasimova |
1 |
1472 |
12 окт 2013, 18:52 |
|
Уравнение прямой и плоскости
в форуме Аналитическая геометрия и Векторная алгебра |
leha93 |
1 |
520 |
22 дек 2014, 19:51 |
|
Найти уравнение прямой на плоскости
в форуме Аналитическая геометрия и Векторная алгебра |
Ali_is |
1 |
487 |
20 дек 2016, 06:35 |
|
Уравнение сферы,плоскости и прямой
в форуме Аналитическая геометрия и Векторная алгебра |
Olga1975 |
1 |
854 |
05 окт 2015, 21:45 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
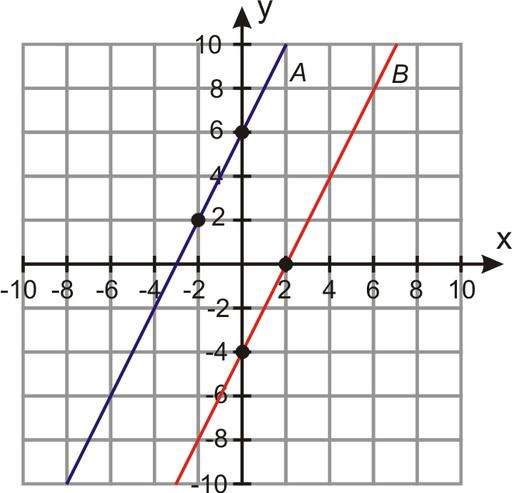
Задача 27867 4.2.78) Составить уравнение прямой.
Условие
![]()
4.2.78) Составить уравнение прямой, симметричной прямой x+2y-6 = 0 относительно точки А(4; 2).
Решение
![]()
1 способ
Прямая, симметричная данной, параллельна данной.
Значит ее уравнение имеет вид
x+2y- d=0
Чтобы найти d подставим координаты точки, принадлежащей этой прямой, например точки Е.
Для этого выберем точку F(2;2), принадлежащую данной прямой и найдем координаты точки Е симметричной относительно А
Е(6;2)
6+2*2-d=0
d=10
2 способ
Составим уравнение прямой, перпендикулярной данной и проходящей через точку А
vector_(данной прямой)=(1;2)
vector_(перпендикулярной прямой)=(2;-1)
Скалярное произведение этих векторов равно 0, векторы ортогональны.
2х-у+с=0
Чтобы найти c подставляем координаты точки А
2*4-2=с
с=-6
2х — у — 6 = 0
Найдем расстояние от точки А до данной прямой
d=|4+2*2-6|/sqrt(1+2^2)=2/sqrt(5)
Составим уравнение окружности с центром в точке А и радиусом R=2/sqrt(5).
Эта окружность касается данной прямой и второй прямой, параллельной данной и находящейся на расстоянии 2/sqrt(5) от точки.
(x-4)^2+(y-2)^2=4/5
(x-4)^2+(2x-6-2)^2=4/5
(x-4)^2=4/25
x-4=2/5 или х-4=-2/5
х=4,4 или х=3,6 — абсцисса точки М
у=2х-6=2*4,4-6=2,8
N(4,4; 2,8)
Прямая, параллельная данной имеет вид
х + 2y — d = 0
Чтобы найти d подставим координаты точки N
4,4+2*2,8 — d=0
О т в е т. х+2y -10 =0 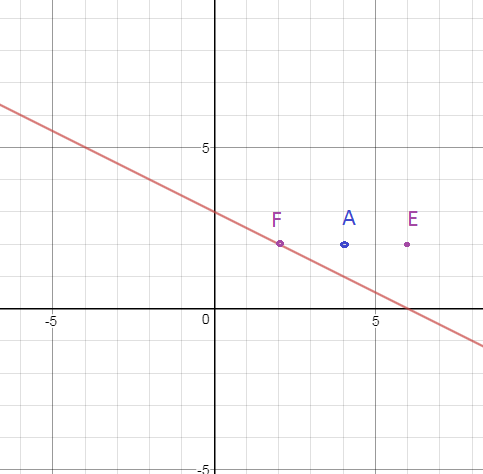
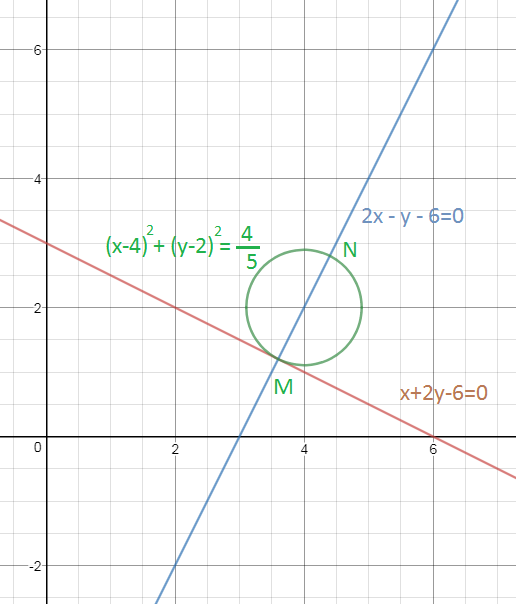
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класс
Урок №5. Метод преобразований решения задач
Перечень вопросов, рассматриваемых в теме:
- симметрия относительно произвольной плоскости;
- понятие «метод движений» в пространстве.
Глоссарий по теме
Метод геометрических преобразований
Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.
Метод параллельного переноса
Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.
Применение симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой точки/оси/плоскости.
Идея метода поворота состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.
Шарыгин И.Ф., Геометрия. 10–11 кл.: учеб. для общеобразоват. учреждений /– М.: Дрофа, 2009. – 235,: ил., ISBN 978–5–358–05346–5, сс. 178-196. Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. учреждений– М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Метод геометрических преобразований
Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.
1.1. Метод параллельного переноса.
Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.
Этим путём иногда удаётся облегчить проведение анализа. Метод параллельного переноса применяют главным образом для объединения разрозненных частей фигур, когда часто построение фигуры становится затруднительным только от того, что части этой фигуры слишком удалены друг от друга, и потому трудно ввести в чертёж данные. В этих случаях какую-нибудь часть искомой фигуры переносят параллельно самой себе на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условий задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большое количество данных.
1.2. Метод симметрии.
Применение осевой симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой оси. При удачном выборе оси и преобразуемой фигуры решение задачи может значительно облегчиться, а в некоторых случаях симметрия непосредственно даёт искомые точки.
Метод симметрии заключается в следующем. Предполагают задачу решённой и одну из данных точек (прямую или окружность) отражают в какой-нибудь известной оси; иногда эта ось проходит через известную точку. Тогда полученную симметричную точку (прямую или окружность) подчиняют тем же условиям, которым должна была удовлетворять заменённая точка (прямая или окружность). После этого получится новая задача, которую решают способами, уже нам известными. Обыкновенно, с решением этой новой задачи предложенная задача уже будет решена сама собой, и только в редких случаях придётся ещё переходить к первоначальным условиям задачи. Таким образом, метод симметрии приводит решение предложенной задачи к решению новой задачи.
1.3. Метод поворота.
Поворотом также пользуются как методом решения геометрических задач на построение. Идея метода вращения состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.
2. Решение задач методом преобразований
2.1. Симметрия относительно произвольной плоскости
Постановка задачи. Найти координаты точки  , симметричной точке
, симметричной точке  , относительно плоскости Ax + By + Cz + D = 0.
, относительно плоскости Ax + By + Cz + D = 0.
1. Находим уравнение прямой, которая перпендикулярна данной плоскости и проходит через точку  . Так как прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е.
. Так как прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е.  .
.
Поэтому уравнение прямой будет: 
2. Находим точку  пересечения прямой
пересечения прямой  и плоскости Ax + By + Cz + D = 0.
и плоскости Ax + By + Cz + D = 0.
Для этого обозначим  и выразим x, y, z:
и выразим x, y, z:
 .
.
Подставим x, y, z в уравнение плоскости:
 найдем значение t.
найдем значение t.
Затем найдем x, y, z. Найденные координаты будут являться координатами точки  .
.
3. Точка  является серединой отрезка
является серединой отрезка  , где точка
, где точка  является точкой симметричной точке
является точкой симметричной точке  , поэтому
, поэтому
 ,
,  ,
,  .
.
Задача 1. Найти точку M’, симметричную точке M относительно плоскости.
M(1, 1, 1), x + 4y + 3z + 5 = 0.
Уравнение прямой, которая проходит через точку M перпендикулярно заданной плоскости будет:
 .
.
Найдем точку пересечения прямой и плоскости.
 ,
,
 ,
,
(1 + t) + 4(1 + 4t) + 3(1 + 3t) + 5 = 0,
Откуда  – точка пересечения прямой и плоскости.
– точка пересечения прямой и плоскости.  является серединой отрезка MM’, поэтому
является серединой отрезка MM’, поэтому
 ,
, 
 ,
, 
 ,
, 
Даны плоскость α: x + 2y – z – 2 = 0 и две точки А(1, -2, -3) и В (-1, -1, -2). Найдите на этой плоскости точку С такую, чтобы ломаная АСВ имела наименьшую длину.
Данная плоскость пересекает оси координат в точках
Две заданные точки лежат по одну сторону от данной плоскости.
Если бы две точки лежали по разные стороны от плоскости α, то очевидно, искомой точкой С была бы точка пересечения отрезка, концами которого являются данные точки, с плоскостью α, а ломаная выродилась бы в отрезок.
Сведем нашу задачу к описанной ситуации.
Для этого найдем точку, симметричную любой из заданных относительно данной плоскости α.
Например, точке А.
Используя решение задачи 1, получим следующую последовательность действий.
Уравнение прямой, которая проходит через точку А перпендикулярно заданной плоскости будет:
 .
.
Найдем точку пересечения полученной прямой и плоскости α.
 .
.
 .
.
(1 + t) + 2(2t – 2) — (-t– 2) – 2 = 0
Откуда точка пересечения прямой, перпендикулярной плоскости α и проходящей через точку А, с плоскость α  . Точка пересечения прямой и плоскости.
. Точка пересечения прямой и плоскости.  является серединой отрезка АА’, поэтому
является серединой отрезка АА’, поэтому
 ,
, 
 ,
, 
 ,
, 
Теперь найдем точку пересечения отрезка A’B с плоскостью α.
Прямая A’B имеет направляющий вектор  .
.
Уравнение прямой A’B:
 .
.
Найдем точку пересечения полученной прямой и плоскости α.
 .
.
 .
.
 .
.
Таким образом, координаты искомой точки  .
.
Ответ:  .
.
Примеры и разбор решения заданий тренировочного модуля
1. Напишите уравнение образа плоскости 2x + 5y – z – 5 = 0 при симметрии относительно плоскости Oxz.
Найдем координаты двух точек плоскости 2x + 5y – z – 5 = 0, лежащих в плоскости Oxz. Для этого найдем точки плоскости, принадлежащие осям координат.
OX: z = y = 0, x = 2,5 A(2,5; 0; 0)
OZ: x = y = 0, z = -5 B(0; 0; -5).
Эти точки принадлежат и образу плоскости 2x + 3y – z – 5 = 0 при симметрии относительно плоскости Oxz.
Теперь найдем точку данной плоскости, принадлежащую оси ординат.
OY: z = x = 0, y = 2,5 С(0; 1; 0).
Точка, симметричная точке С относительно плоскости Oxz, имеет координаты С'(0; -1; 0).
Теперь напишем уравнение плоскости через три полученные точки.
4.1.8. Примеры решения задач по теме «Уравнение прямой на плоскости»
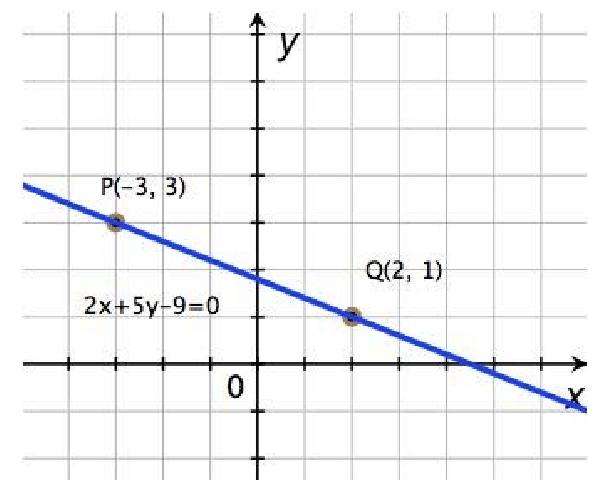
Даны уравнения двух сторон параллелограмма: 2Х + У + 3 = 0 и 2Х – 5У + 9 = 0 и уравнение одной из его диагоналей: 2Х – у — 3 = 0. Найти координаты вершин этого параллелограмма.
Выясните, уравнения каких сторон даны в условии задачи: параллельных или
Смежных, и как расположена данная диагональ по отношению к данным сторонам.

Выясним, уравнения каких сторон даны в условии задачи: параллельных или

Следовательно, прямые пересекаются, то есть даны уравнения смежных сторон параллелограмма.
Условие параллельности прямых
 .
.
Пусть даны уравнения сторон АВ и AD. Тогда координаты точки А будут решением системы уравнений:

Теперь определим, уравнение какой диагонали: АС или BD – нам известно. Если это диагональ АС, то на ней лежит точка А, следовательно, координаты этой точки должны удовлетворять уравнению диагонали. Проверим:

Значит, точка А не лежит на данной прямой, то есть дано уравнение диагонали BD.
Тогда вершина В лежит на прямых АВ и BD, значит, ее координаты найдем из системы:

Система уравнений для определения координат точки D составлена из уравнений прямых AD И BD:

Остается найти координаты точки С. Составим уравнения прямых ВС и DC.
Поскольку ВС параллельна AD, их угловые коэффициенты равны. Найдем угловой коэффициент прямой AD:

Тогда ВС можно задать уравнением

Найдем координаты точки С, решив систему из двух полученных уравнений:

Найти точку, симметричную точке А(2; 1) относительно прямой, проходящей через точки В(-1; 7) и С(1; 8).
Представьте себе, что вам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:
1) провести прямую ВС;
2) провести через точку А прямую, перпендикулярную ВС;
3) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.

Представим себе, что нам нужно Построить искомую точку на плоскости. Последовательность действий при этом можно задать так:
4) провести прямую ВС;
5) провести через точку А прямую, перпендикулярную ВС;
6) найти точку О пересечения этих прямых и отложить на прямой АО по другую сторону прямой ВС отрезок ОА1 = АО.
Тогда точка А1 будет симметричной точке А относительно прямой ВС.
Теперь заменим каждое из действий составлением уравнений и вычислением координат точек.
1) Найдем уравнение прямой ВС в виде:

2) Найдем угловой коэффициент прямой ВС:

Прямая АО Перпендикулярна прямой ВС, поэтому

Составим уравнение прямой АО:

3) Найдем координаты точки О как решение системы:

4) Точка О – середина отрезка АА1, поэтому

Найти угол между прямыми L1: 3Х – у + 5 = 0 и L2: 2Х + У – 7 = 0.
Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда

Где K1 и K2 – угловые коэффициенты прямых L1 и L2.

Если J – угол между прямыми L1 и L2, то J = A2 — A1, где A2 и A1 – углы, образованные прямыми L1 и L2 с положительной полуосью Ох. Тогда

Где K1 и K2 – угловые коэффициенты прямых L1 и L2. Найдем K1 и K2: для L1
Y = 3X + 5, K1 = 3; для второй: Y = -2X + 7, K2 = -2. Следовательно,

Для прямых А1х + В1У + С1 = 0 И А2Х + В2У + С2 = 0
 .
.
Определить, лежит ли точка М(2; 3) внутри или вне треугольника, стороны которого заданы уравнениями 4Х – у – 7 = 0, Х + 3У – 31 = 0, Х + 5У – 7 = 0.
Если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне, а если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника.

Пусть первое уравнение задает сторону АВ, второе – ВС, третье – АС. Найдем координаты точек А, В и С:

Для ответа на вопрос задачи отметим, что:
1) если точка М расположена внутри треугольника АВС, то ее отклонение δ от каждой стороны треугольника имеет тот же знак, что и для вершины, не лежащей на этой стороне (т. е. точка М расположена относительно каждой стороны треугольника в одной полуплоскости с третьей вершиной);
2) если точка М лежит вне треугольника, то по крайней мере с одной из вершин она окажется в разных полуплоскостях относительно стороны треугольника (на рисунке: точки М1 и В расположены по разные стороны от прямой АС).
Составим нормальные уравнения сторон треугольника АВС:

Вычислим соответствующие отклонения:
1) для точек М и А относительно прямой ВС:

2) для точек М и В относительно прямой АС:

3) для точек М и С относительно прямой АВ:

Итак, точки М И С лежат по разные стороны от прямой АВ. Следовательно, точка М расположена вне треугольника АВС.
Ответ: Точка М расположена вне треугольника АВС.
Для треугольника АВС с вершинами А(-3; -1), В(1; 5), С(7; 3) составить уравнения медианы и высоты, выходящих из вершины В.
Составьте уравнение медианы как прямой, проходящей через точки В и М – середину стороны АС, а высоты – как прямой, проходящей через точку В и перпендикулярной стороне АС.

1) Медиана ВМ проходит через точку В и точку М – середину отрезка АС. Найдем координаты точки М:

Тогда уравнение медианы можно записать в виде:

2) Высота ВН перпендикулярна стороне АС. Составим уравнение АС:

Ответ: медиана ВМ: 4Х + У – 9 = 0; высота ВН: 5Х + 2У – 15 = 0.
Определить, при каком значении А прямая
Параллельна оси ординат. Написать уравнение прямой.
Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0
Если прямая параллельна оси ординат, то в уравнении Ах + Ву + С = 0
В = 0, С ≠ 0. Из условия В = 0 получаем: А2 – 1 = 0, А = ± 1.
При А = 1 С = 2 + 7 – 9 = 0 – второе условие не выполняется (получившаяся при этом прямая -4Х = 0 не параллельна оси Оу, а совпадает с ней).
При А = -1 получим: -6Х – 14 = 0, 3Х + 7 = 0.
Составить уравнения всех прямых, проходящих через точку М(2; 3) и отсекающих от координатного угла треугольник площадью 12.
Составьте уравнение искомой прямой «в отрезках»:

Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда

Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках».

Составим уравнение искомой прямой «в отрезках»:

Где |A| и |B| — длины отрезков, отсекаемых прямой на координатных осях. Тогда

Откуда |Ab| = 24. Кроме того, координаты точки М(2; 3) должны удовлетворять уравнению «в отрезках». Таким образом, для А и B можно составить систему уравнений:



Следовательно, условию задачи удовлетворяют три прямые:
источники:
http://resh.edu.ru/subject/lesson/5731/conspect/
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/4-1-8-primery-resheniia-zadach-po-teme-uravnenie-priamoi-na-ploskosti
Параметрическое уравнение прямой. Параметрическое уравнение прямой в пространстве
Прямая вместе с точкой являются важными элементами геометрии, с помощью которых строятся многие фигуры в пространстве и на плоскости. В данной статье подробно рассматривается параметрическое уравнение прямой, а также его связь с другими типами уравнений для этого геометрического элемента.
Прямая и уравнения для ее описания
Прямая в геометрии представляет собой совокупность точек, которые соединяют произвольные две точки пространства отрезком с наименьшей длиной. Этот отрезок является частью прямой. Любые другие кривые, соединяющие зафиксированные две точки в пространстве, будут иметь большую длину, поэтому прямыми не являются.
 Вам будет интересно: Нейтральная лексика – это. Определение, понятие, значение и примеры
Вам будет интересно: Нейтральная лексика – это. Определение, понятие, значение и примеры
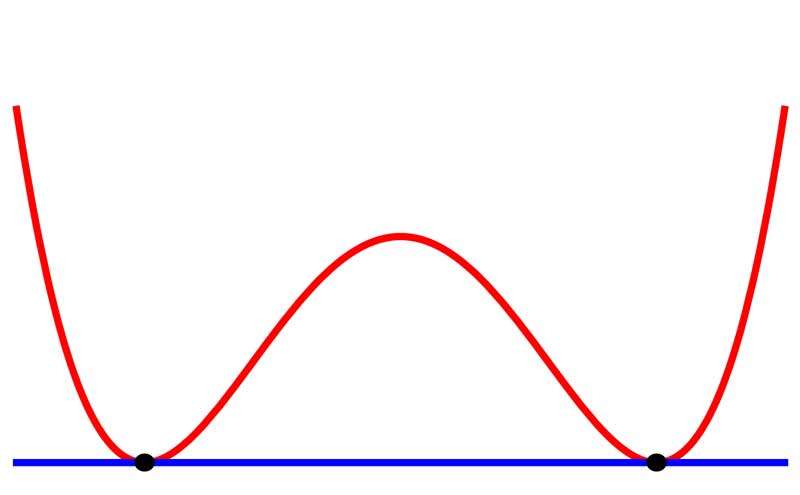
На рисунке выше показаны две черные точки. Синяя линия, соединяющая их, является прямой, а красная – кривой. Очевидно, что длина красной линии между черными точками больше, чем синей.
Существуют несколько видов уравнений прямой, с помощью которых можно описать прямую в трехмерном пространстве или в двумерном. Ниже приведены названия этих уравнений:
- векторное;
- параметрическое;
- в отрезках;
- симметричное или каноническое;
- общего типа.
 Вам будет интересно: А. Пушкин “Песнь о вещем Олеге”: жанр и идея
Вам будет интересно: А. Пушкин “Песнь о вещем Олеге”: жанр и идея
В данной статье рассмотрим параметрическое уравнение прямой, однако выведем его из векторного. Также покажем связь параметрического и симметричного или канонического уравнений.
Уравнение векторное
Понятно, что все приведенные типы уравнений для рассматриваемого геометрического элемента связаны между собой. Тем не менее векторное уравнение является базовым для всех них, поскольку оно непосредственно следует из определения прямой. Рассмотрим, как оно вводится в геометрию.
Допустим, дана точка в пространстве P(x0; y0; z0). Известно, что эта точка принадлежит прямой. Сколько прямых можно провести через нее? Бесконечное множество. Поэтому для того, чтобы можно было провести единственную прямую, необходимо задать направление последней. Направление, как известно, определяется вектором. Обозначим его v¯(a; b; c), где символы в скобках – это его координаты. Для каждой точки Q(x; y; z), которая находится на рассматриваемой прямой, можно записать равенство:
(x; y; z) = (x0; y0; z0) + α × (a; b; c)
Здесь символ α является параметром, принимающим абсолютно любое действительное значение (умножение вектора на число может изменить только его модуль или направление на противоположное). Это равенство называется векторным уравнением для прямой в трехмерном пространстве. Изменяя параметр α, мы получаем все точки (x; y; z), которые образуют эту прямую.
 Вам будет интересно: Тайны “Аненербе”: история, артефакты, архивы
Вам будет интересно: Тайны “Аненербе”: история, артефакты, архивы
Стоящий в уравнении вектор v¯(a; b; c) называется направляющим. Прямая не имеет конкретного направления, а ее длина является бесконечной. Эти факты означают, что любой вектор, полученный из v¯ с помощью умножения на действительное число, также будет направляющим для прямой.
Что касается точки P(x0; y0; z0), то вместо нее в уравнение можно подставить произвольную точку, которая лежит на прямой, и последняя при этом не изменится.
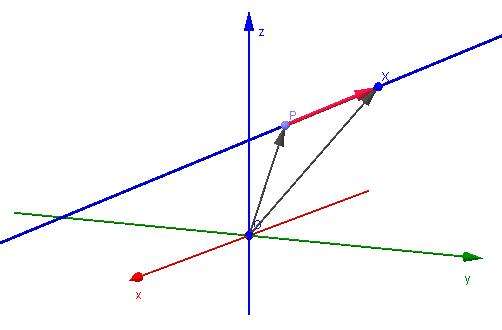
Рисунок выше демонстрирует прямую (синяя линия), которая задана в пространстве через направляющий вектор (красный направленный отрезок).
Не представляет никакого труда получить подобное равенство для двумерного случая. Используя аналогичные рассуждения приходим к выражению:
(x; y) = (x0; y0) + α × (a; b)
Видим, что оно полностью такое же, как и предыдущее, только используются две координаты вместо трех для задания точек и векторов.
Уравнение параметрическое
Сначала получим в пространстве параметрическое уравнение прямой. Выше, когда записывалось векторное равенство, уже упоминалось о параметре, который в нем присутствует. Чтобы получить параметрическое уравнение, достаточно раскрыть векторное. Получаем:
Совокупность этих трех линейных равенств, в каждом из которых имеется одна переменная координата и параметр α, принято называть параметрическим уравнением прямой в пространстве. По сути, мы не сделали ничего нового, а просто явно записали смысл соответствующего векторного выражения. Отметим лишь один момент: число α, хотя и является произвольным, но оно для всех трех равенств одинаковое. Например, если α = -1,5 для 1-го равенства, то такое же его значение следует подставить во второе и в третье равенства при определении координат точки.
Параметрическое уравнение прямой на плоскости подобно таковому для пространственного случая. Оно записывается в виде:
Таким образом, чтобы составить параметрическое уравнение прямой, следует записать в явном виде векторное уравнение для нее.
Получение уравнения канонического
Как выше было отмечено, все уравнения, задающие прямую в пространстве и на плоскости, получаются одно из другого. Покажем, как получить из параметрического уравнения прямой каноническое. Для пространственного случая имеем:
Выразим параметр в каждом равенстве:
Поскольку левые части являются одинаковыми, тогда правые части равенств тоже равны друг другу:
(x – x0) / a = (y – y0) / b = (z – z0) / c
Это и есть каноническое уравнение для прямой в пространстве. Значение знаменателя в каждом выражении является соответствующей координатой направляющего вектора. Значения в числителе, которые вычитаются из каждой переменной, представляют собой координаты точки, принадлежащей этой прямой.
Соответствующее уравнение для случая на плоскости примет вид:
(x – x0) / a = (y – y0) / b
Дальше в статье решим несколько задач, используя полученные знания.
Уравнение прямой через 2 точки
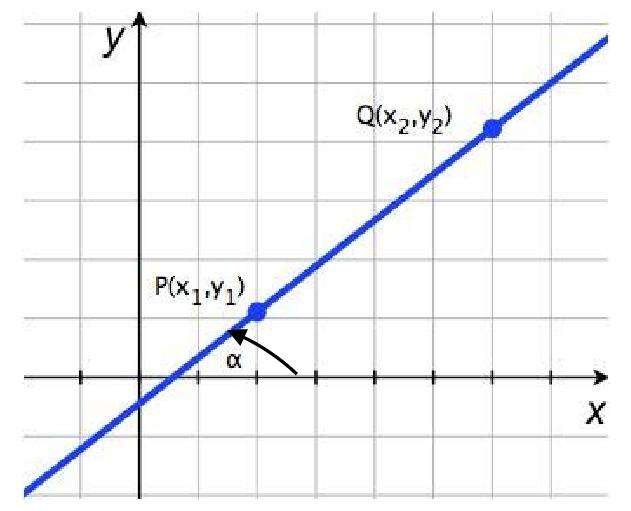
Известно, что две фиксированные точки как на плоскости, так и в пространстве однозначно задают прямую. Предположим, что заданы две следующие точки на плоскости:
Как составить уравнение прямой через них? Для начала следует определить направляющий вектор. Его координаты имеют следующие значения:
PQ¯(x2 – x1; y2 – y1)
Теперь можно записать уравнение в любом из трех видов, которые были рассмотрены в пунктах выше. Например, параметрическое уравнение прямой принимает вид:
x = x1 + α × (x2 – x1);
y = y1 + α × (y2 – y1)
В канонической форме можно переписать его так:
(x – x1 ) / (x2 – x1) = (y – y1) / (y2 – y1)
Видно, что в каноническое уравнение входят координаты обеих точек, причем в числителе можно менять эти точки. Так, последнее уравнение можно переписать следующим образом:
(x – x2) / (x2 – x1) = (y – y2) / (y2 – y1)
Все записанные выражения называются уравнениями прямой через 2 точки.
Задача с тремя точками
Даны координаты следующих трех точек:
Необходимо определить, лежат эти точки на одной прямой или нет.
Решать эту задачу следует так: сначала составить уравнение прямой для любых двух точек, а затем подставить в него координаты третьей и проверить, удовлетворяют ли они полученному равенству.
Составляем уравнение через M и N в параметрической форме. Для этого применим полученную в пункте выше формулу, которую обобщим на трехмерный случай. Имеем:
Теперь подставим в эти выражения координаты точки K и найдем значение параметра альфа, который им соответствует. Получаем:
1 = 5 + α × (-3) => α = 4/3;
-1 = 3 + α × (-1) => α = 4;
-5 = -1 + α × 1 => α = -4
Мы выяснили, что все три равенства будут справедливы, если каждое из них примет отличающееся от других значение параметра α. Последний факт противоречит условию параметрического уравнения прямой, в котором α должны быть равны для всех уравнений. Это означает, что точка K прямой MN не принадлежит, а значит, все три точки на одной прямой не лежат.
Задача на параллельность прямых
Даны два уравнения прямых в параметрическом виде. Они представлены ниже:
Необходимо определить, являются ли прямые параллельными. Проще всего определить параллельность двух прямых с использованием координат направляющих векторов. Обращаясь к общей формуле параметрического уравнения в двумерном пространстве, получаем, что направляющие вектора каждой прямой будут иметь координаты:
Два вектора являются параллельными, если один из них можно получить путем умножения другого на некоторое число. Разделим попарно координаты векторов, получим:
Это означает что:
Направляющие вектора v2¯ и v1¯ параллельны, значит, прямые в условии задачи тоже являются параллельными.
Проверим, не являются ли они одной и той же прямой. Для этого нужно подставить координаты любой точки в уравнение для другой. Возьмем точку (-1; 3), подставим ее в уравнение для второй прямой:
-1 = 2 – 6 × λ => λ = 1/2;
3 = 4 – 3,6 × λ => λ ≈ 0,28
То есть прямые являются разными.
Задача на перпендикулярность прямых
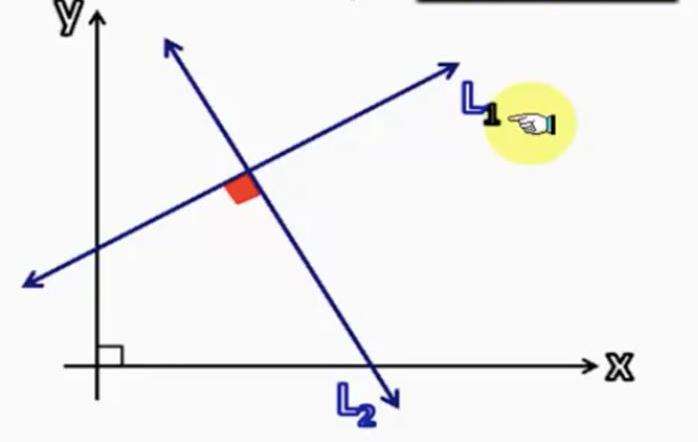
Даны уравнения двух прямых:
Перпендикулярны ли эти прямые?
Две прямые будут перпендикулярны, если скалярное произведение их направляющих векторов равно нулю. Выпишем эти вектора:
Найдем их скалярное произведение:
(v1¯ × v2¯) = 2 × 6 + 3 × (-4) = 12 – 12 = 0
Таким образом, мы выяснили, что рассмотренные прямые перпендикулярны. Они изображены на рисунке выше.
Задача 27867 4.2.78) Составить уравнение прямой.
Условие
![]()
4.2.78) Составить уравнение прямой, симметричной прямой x+2y-6 = 0 относительно точки А(4; 2).
Решение
![]()
1 способ
Прямая, симметричная данной, параллельна данной.
Значит ее уравнение имеет вид
x+2y- d=0
Чтобы найти d подставим координаты точки, принадлежащей этой прямой, например точки Е.
Для этого выберем точку F(2;2), принадлежащую данной прямой и найдем координаты точки Е симметричной относительно А
Е(6;2)
6+2*2-d=0
d=10
2 способ
Составим уравнение прямой, перпендикулярной данной и проходящей через точку А
vector_(данной прямой)=(1;2)
vector_(перпендикулярной прямой)=(2;-1)
Скалярное произведение этих векторов равно 0, векторы ортогональны.
2х-у+с=0
Чтобы найти c подставляем координаты точки А
2*4-2=с
с=-6
2х – у – 6 = 0
Найдем расстояние от точки А до данной прямой
d=|4+2*2-6|/sqrt(1+2^2)=2/sqrt(5)
Составим уравнение окружности с центром в точке А и радиусом R=2/sqrt(5).
Эта окружность касается данной прямой и второй прямой, параллельной данной и находящейся на расстоянии 2/sqrt(5) от точки.
(x-4)^2+(y-2)^2=4/5
(x-4)^2+(2x-6-2)^2=4/5
(x-4)^2=4/25
x-4=2/5 или х-4=-2/5
х=4,4 или х=3,6 – абсцисса точки М
у=2х-6=2*4,4-6=2,8
N(4,4; 2,8)
Прямая, параллельная данной имеет вид
х + 2y – d = 0
Чтобы найти d подставим координаты точки N
4,4+2*2,8 – d=0
О т в е т. х+2y -10 =0 
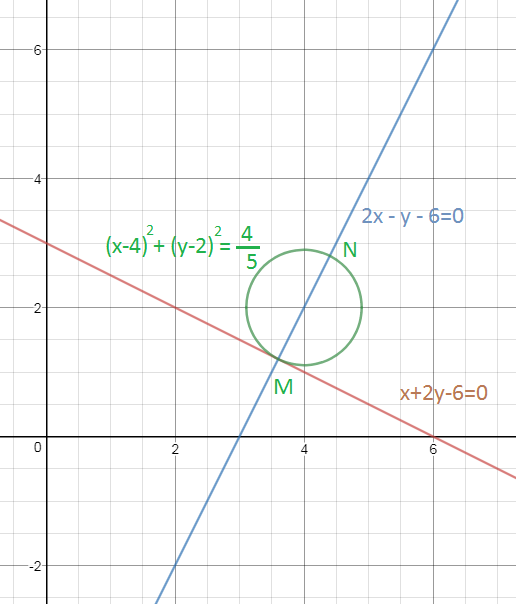
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класс
Урок №5. Метод преобразований решения задач
Перечень вопросов, рассматриваемых в теме:
- симметрия относительно произвольной плоскости;
- понятие «метод движений» в пространстве.
Глоссарий по теме
Метод геометрических преобразований
Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.
Метод параллельного переноса
Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.
Применение симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой точки/оси/плоскости.
Идея метода поворота состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255, сс. 121-126.
Шарыгин И.Ф., Геометрия. 10–11 кл.: учеб. для общеобразоват. учреждений /– М.: Дрофа, 2009. – 235,: ил., ISBN 978–5–358–05346–5, сс. 178-196. Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. учреждений– М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Метод геометрических преобразований
Сущность метода геометрических преобразований при решении геометрических задач заключается в привлечении того или иного геометрического преобразования, опираясь на свойства которого, задача может быть решена.
1.1. Метод параллельного переноса.
Сущность этого метода состоит в том, что наряду с данными и искомыми фигурами рассматриваются некоторые другие фигуры, которые получаются из данных или искомых фигур или их частей путём переноса на некоторый вектор.
Этим путём иногда удаётся облегчить проведение анализа. Метод параллельного переноса применяют главным образом для объединения разрозненных частей фигур, когда часто построение фигуры становится затруднительным только от того, что части этой фигуры слишком удалены друг от друга, и потому трудно ввести в чертёж данные. В этих случаях какую-нибудь часть искомой фигуры переносят параллельно самой себе на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условий задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большое количество данных.
1.2. Метод симметрии.
Применение осевой симметрии к решению задач на построение называют методом симметрии. Метод симметрии состоит в том, что наряду с данными и искомыми фигурами рассматриваются также фигуры, симметричные некоторым из них относительно некоторой оси. При удачном выборе оси и преобразуемой фигуры решение задачи может значительно облегчиться, а в некоторых случаях симметрия непосредственно даёт искомые точки.
Метод симметрии заключается в следующем. Предполагают задачу решённой и одну из данных точек (прямую или окружность) отражают в какой-нибудь известной оси; иногда эта ось проходит через известную точку. Тогда полученную симметричную точку (прямую или окружность) подчиняют тем же условиям, которым должна была удовлетворять заменённая точка (прямая или окружность). После этого получится новая задача, которую решают способами, уже нам известными. Обыкновенно, с решением этой новой задачи предложенная задача уже будет решена сама собой, и только в редких случаях придётся ещё переходить к первоначальным условиям задачи. Таким образом, метод симметрии приводит решение предложенной задачи к решению новой задачи.
1.3. Метод поворота.
Поворотом также пользуются как методом решения геометрических задач на построение. Идея метода вращения состоит в том, чтобы повернуть какую-либо данную или искомую фигуру около целесообразно избранного центра/оси на соответствующий угол так, чтобы облегчить проведение анализа задачи или даже непосредственно прийти к решению.
2. Решение задач методом преобразований
2.1. Симметрия относительно произвольной плоскости
Постановка задачи. Найти координаты точки , симметричной точке , относительно плоскости Ax + By + Cz + D = 0.
1. Находим уравнение прямой, которая перпендикулярна данной плоскости и проходит через точку . Так как прямая перпендикулярна заданной плоскости, то в качестве ее направляющего вектора можно взять вектор нормали плоскости, т.е. .
Поэтому уравнение прямой будет:
2. Находим точку пересечения прямой и плоскости Ax + By + Cz + D = 0.
Для этого обозначим и выразим x, y, z:
.
Подставим x, y, z в уравнение плоскости:
найдем значение t.
Затем найдем x, y, z. Найденные координаты будут являться координатами точки .
3. Точка является серединой отрезка , где точка является точкой симметричной точке , поэтому
, , .
Задача 1. Найти точку M’, симметричную точке M относительно плоскости.
M(1, 1, 1), x + 4y + 3z + 5 = 0.
Уравнение прямой, которая проходит через точку M перпендикулярно заданной плоскости будет:
.
Найдем точку пересечения прямой и плоскости.
,
,
(1 + t) + 4(1 + 4t) + 3(1 + 3t) + 5 = 0,
Откуда – точка пересечения прямой и плоскости. является серединой отрезка MM’, поэтому
,
,
,
Даны плоскость α: x + 2y – z – 2 = 0 и две точки А(1, -2, -3) и В (-1, -1, -2). Найдите на этой плоскости точку С такую, чтобы ломаная АСВ имела наименьшую длину.
Данная плоскость пересекает оси координат в точках
Две заданные точки лежат по одну сторону от данной плоскости.
Если бы две точки лежали по разные стороны от плоскости α, то очевидно, искомой точкой С была бы точка пересечения отрезка, концами которого являются данные точки, с плоскостью α, а ломаная выродилась бы в отрезок.
Сведем нашу задачу к описанной ситуации.
Для этого найдем точку, симметричную любой из заданных относительно данной плоскости α.
Например, точке А.
Используя решение задачи 1, получим следующую последовательность действий.
Уравнение прямой, которая проходит через точку А перпендикулярно заданной плоскости будет:
.
Найдем точку пересечения полученной прямой и плоскости α.
.
.
(1 + t) + 2(2t – 2) – (-t– 2) – 2 = 0
Откуда точка пересечения прямой, перпендикулярной плоскости α и проходящей через точку А, с плоскость α . Точка пересечения прямой и плоскости. является серединой отрезка АА’, поэтому
,
,
,
Теперь найдем точку пересечения отрезка A’B с плоскостью α.
Прямая A’B имеет направляющий вектор .
Уравнение прямой A’B:
.
Найдем точку пересечения полученной прямой и плоскости α.
.
.
.
Таким образом, координаты искомой точки .
Ответ: .
Примеры и разбор решения заданий тренировочного модуля
1. Напишите уравнение образа плоскости 2x + 5y – z – 5 = 0 при симметрии относительно плоскости Oxz.
Найдем координаты двух точек плоскости 2x + 5y – z – 5 = 0, лежащих в плоскости Oxz. Для этого найдем точки плоскости, принадлежащие осям координат.
OX: z = y = 0, x = 2,5 A(2,5; 0; 0)
OZ: x = y = 0, z = -5 B(0; 0; -5).
Эти точки принадлежат и образу плоскости 2x + 3y – z – 5 = 0 при симметрии относительно плоскости Oxz.
Теперь найдем точку данной плоскости, принадлежащую оси ординат.
OY: z = x = 0, y = 2,5 С(0; 1; 0).
Точка, симметричная точке С относительно плоскости Oxz, имеет координаты С'(0; -1; 0).
Теперь напишем уравнение плоскости через три полученные точки.
[spoiler title=”источники:”]
http://reshimvse.com/zadacha.php?id=27867
http://resh.edu.ru/subject/lesson/5731/conspect/
[/spoiler]
|
5 / 5 / 0 Регистрация: 27.09.2020 Сообщений: 103 |
||
|
1 |
||
Составить уравнение прямой, симметричной прямой относительно плоскости20.10.2020, 17:06. Показов 7910. Ответов 15
Добрый день! Помогите, пожалуйста, с решением задачи. Дано: составить уравнение прямой, симметричной прямой (x-2)/3=(y+1)/1=(z-2)/4 относительно плоскости 5x-y+z-4=0 Вложения, ожидающие проверки
0 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
20.10.2020, 18:48 |
2 |
|
окончательно запуталась Не видно вашего решения. Мне кажется проще всего так. Одна точка А – точка пересечения заданных прямой и плоскости, другая точка В – точка симметричная точке (2,-1,2) относительно нашей плоскости. Находите А и В и проводите через них прямую АВ. Эта прямая – искомая.
1 |
|
3968 / 2948 / 893 Регистрация: 19.11.2012 Сообщений: 6,061 |
|
|
20.10.2020, 18:50 |
3 |
|
как решается данное задание Было уже здесь
0 |
|
Любитель математики 1476 / 987 / 282 Регистрация: 27.01.2014 Сообщений: 3,275 |
|
|
20.10.2020, 18:51 |
4 |
|
Предлагаю воспользоваться тем, что прямая полностью определяется двумя своими точками.
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
20.10.2020, 20:21 |
5 |
|
Решение. (На искомой прямой, найденная точка, заменена на точку с целыми координатами, также принадлежащая искомой прямой) Миниатюры
1 |
|
5 / 5 / 0 Регистрация: 27.09.2020 Сообщений: 103 |
|
|
20.10.2020, 22:58 [ТС] |
6 |
|
Спасибо! Завтра пересчитаю, поскольку с ответом не сошлось) в ответе (x+5)/-11=(y-2)/7=(z-4)/8 Добавлено через 2 минуты Добавлено через 49 минут
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
20.10.2020, 23:13 |
7 |
|
Проверил. Оба уравнения верные. Прямая содержит обе точки (6;-5;-4) а также (-5;2;4).
0 |
|
5 / 5 / 0 Регистрация: 27.09.2020 Сообщений: 103 |
|
|
20.10.2020, 23:18 [ТС] |
8 |
|
Nacuott, спасибо большое! Осталось мне понять, как Вы выбираете точки в числителе?
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
20.10.2020, 23:32 |
9 |
|
В числителе можно записать координаты любой точки симметричной точке на заданной прямой относительно заданной плоскости.(смысл предложения понятен?). Так вот, заданная прямая содержит точку с координатами (2;-1;2). Через эту точку
0 |
|
5 / 5 / 0 Регистрация: 27.09.2020 Сообщений: 103 |
|
|
20.10.2020, 23:38 [ТС] |
10 |
|
Нет, если честно, то непонятно, но я попробую проделать все, что Вы описали, чтобы понять) спасибо большое!!
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
20.10.2020, 23:38 |
11 |
|
А что неясно?
0 |
|
5 / 5 / 0 Регистрация: 27.09.2020 Сообщений: 103 |
|
|
21.10.2020, 00:14 [ТС] |
12 |
|
Nacuott, непонятны расчёты, как получить эти числа в числителе. Потому как я решала точно также, дошла до координат точки С, но сломалась на дробных значениях и не сообразила как получить данные для числителя( Вы пишите, что в числитель можно ставить любые точки, симметричные заданным. Но у нас ведь точки а и с симметричны, если я, конечно, окончательно не запуталась. Значит мы можем в числитель брать координаты А?
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
21.10.2020, 00:22 |
13 |
|
Но у нас ведь точки а и с симметричны, если я, конечно, окончательно не запуталась. Значит мы можем в числитель брать координаты А Ну, как же мы можем? Эти точки находятся по разные стороны плоскости.
0 |
|
5 / 5 / 0 Регистрация: 27.09.2020 Сообщений: 103 |
|
|
21.10.2020, 00:40 [ТС] |
14 |
|
Nacuott, спасибо!
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,783 Записей в блоге: 12 |
|
|
21.10.2020, 23:34 |
15 |
|
Кстати, вот точки с целочисленными координатами, которые могут быть испльзованы при составлении уравнения искомой прямой т.к. все они принадлежат этой прямой. Миниатюры
0 |
|
5 / 5 / 0 Регистрация: 27.09.2020 Сообщений: 103 |
|
|
22.10.2020, 00:33 [ТС] |
16 |
|
Nacuott, спасибо огромное!!! Буду завтра разбираться.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
22.10.2020, 00:33 |
|
Помогаю со студенческими работами здесь Составить уравнение плоскости, проходящей через точку, параллельной прямой и перпендикулярной к плоскости
а)Прямой А4М,… Составить уравнение плоскости, перпендикулярной прямой Составить каноническое уравнение прямой, перпендикулярной плоскости Составить уравнение прямой используя её данные о расположении относительно объектов Составить канонические, параметрические или обшие уравнения… Составить уравнение прямой линии, проходящей через точку и параллельной прямой Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 16 |
§ 1. Уравнения прямой на плоскости
Напомним,
что прямая
![]() на плоскости
на плоскости![]() может быть задана следующими уравнениями
может быть задана следующими уравнениями
(см. рис. 1):
общим:
![]() (1)
(1)
Здесь
![]() –нормальный
–нормальный
вектор прямой
(т.е. любой ненулевой вектор, перпендикулярный
этой прямой).
![]() и
и![]() – любые действительные числа, за
– любые действительные числа, за
исключением случая![]()

Рис.1.
Если
прямая проходит через точку
![]() и имеет нормальный вектор
и имеет нормальный вектор![]() то её уравнение может быть записано в
то её уравнение может быть записано в
виде
![]() (2)
(2)
Уравнение
(2) равносильно векторному уравнению
![]() где
где![]()
каноническим:
![]() (3)
(3)
Здесь
![]() –направляющий
–направляющий
вектор
прямой, т.е. любой ненулевой вектор,
коллинеарный этой прямой.
![]() и
и![]() – любые действительные числа, за
– любые действительные числа, за
исключением случая![]() Отметим, что в уравнении (3)формально
Отметим, что в уравнении (3)формально
допускается 0 в знаменателе.
Это не означает, конечно, что допустимо
деление на 0: формулу (3) следует считать
эквивалентом равенства
![]() в котором никакого деления на 0 нет.
в котором никакого деления на 0 нет.
Приведём примеры: уравнение![]() определяет прямую
определяет прямую![]() параллельную оси
параллельную оси![]() уравнение оси
уравнение оси![]() имеет вид
имеет вид![]()
параметрическим:

![]() (4)
(4)
Число
![]() называетсяпараметром.
называетсяпараметром.
Система уравнений (4) равносильна
векторному уравнению
![]() (см. рис. 2).
(см. рис. 2).

Рис.2.
Параметр
![]() имеет прозрачныйгеометрический
имеет прозрачныйгеометрический
смысл: модуль
числа
![]() означает, сколько векторов
означает, сколько векторов![]() “укладывается” на векторе
“укладывается” на векторе![]() а знак обозначает расположение точки
а знак обозначает расположение точки![]() на прямой
на прямой![]() при
при![]() точка
точка![]() находится с той стороны, куда направлен
находится с той стороны, куда направлен
вектор![]() а при
а при![]() – в противоположной стороне.
– в противоположной стороне.
с
угловым коэффициентом
(см. рис. 3):
![]() (5)
(5)

Рис.3.
Здесь
![]() – угловой коэффициент, т.е.
– угловой коэффициент, т.е.![]() где
где![]() – угол наклона прямой
– угол наклона прямой![]() к оси
к оси![]() Уравнением (5) может быть задана любая
Уравнением (5) может быть задана любая
прямая, не коллинеарная оси![]()
“в
отрезках”
(см. рис. 4):
![]() (6)
(6)

Рис.4.
Здесь
![]() – отрезки, отсекаемые прямой
– отрезки, отсекаемые прямой![]() от осей координат. При этом допускается,
от осей координат. При этом допускается,
что![]() или
или![]() Уравнением (6) может быть задана любая
Уравнением (6) может быть задана любая
прямая, за исключением прямых, коллинеарных
какой-либо из осей координат, а также
прямых, проходящих через начало координат.
Замечание.
Уравнения (1)-(6) задают прямые не только
в прямоугольной, но и в произвольной
косоугольной
системе координат. При этом вектор
![]() будет по-прежнему направляющим вектором
будет по-прежнему направляющим вектором
прямой (т.е. вектором, коллинеарным этой
прямой). Однако, вектор![]() в уравнениях (1), (2) может уже не быть
в уравнениях (1), (2) может уже не быть
перпендикулярным данной прямой. “Угловой
коэффициент”![]() в уравнении (5) может не равняться тангенсу
в уравнении (5) может не равняться тангенсу
угла между прямой и осью абсцисс. Наконец,
числа![]() и
и![]() в уравнении (6) в косоугольной системе
в уравнении (6) в косоугольной системе
координат будут не истинными длинами
отсекаемых на осях отрезков, аотносительными
длинами
(если
![]() и
и![]() – базисные векторы, то на оси
– базисные векторы, то на оси![]() отрезки следует измерять “в векторах
отрезки следует измерять “в векторах![]() ”,
”,
а на оси![]() – “в векторах
– “в векторах![]() ”).
”).
Задача
1. Написать
каноническое, параметрическое и общее
уравнение прямой, проходящей через
точки
![]() и
и![]()
Решение.
Направляющим вектором прямой
![]() можно считать вектор
можно считать вектор![]() В качестве точки
В качестве точки![]() можно взять
можно взять![]() или
или![]() Пусть, например,
Пусть, например,![]() Тогда по формуле (3) получим:
Тогда по формуле (3) получим:
![]() (7)
(7)
Это
каноническое уравнение прямой
![]() Приравняем эти дроби к числу
Приравняем эти дроби к числу![]() получим:
получим:![]() откуда
откуда
Это
параметрическое уравнение прямой
![]() Из равенства (7) имеем:
Из равенства (7) имеем:![]() т.е.
т.е.![]()
Это
общее уравнение прямой
![]()
Задача
2. Дана прямая
![]() Составить уравнение прямой
Составить уравнение прямой![]() проходящей через точку
проходящей через точку![]() и параллельной прямой
и параллельной прямой![]() а также прямой
а также прямой![]() проходящей через точку
проходящей через точку![]() и перпендикулярной прямой
и перпендикулярной прямой![]()
Решение.
(см. рис. 5)

Рис.5.
Из
уравнения прямой
![]() находим ее нормальный вектор:
находим ее нормальный вектор:![]() Взяв
Взяв![]() запишем равенство (2):
запишем равенство (2):![]() т.е.
т.е.![]() Это уравнение прямой
Это уравнение прямой![]()
Заметим,
что вектор
![]() является направляющим вектором прямой
является направляющим вектором прямой![]() а значит, можно записать уравнение этой
а значит, можно записать уравнение этой
прямой согласно равенству (3). Мы получим:![]() откуда
откуда![]() или
или![]() Это уравнение прямой
Это уравнение прямой![]()
Задача
3. Найти угол
между прямыми
![]() и
и![]()
Решение.
Найдём нормальные векторы этих прямых:
![]()
![]() Угол
Угол![]() между прямыми равен углу между их
между прямыми равен углу между их
нормальными векторами. Следовательно,
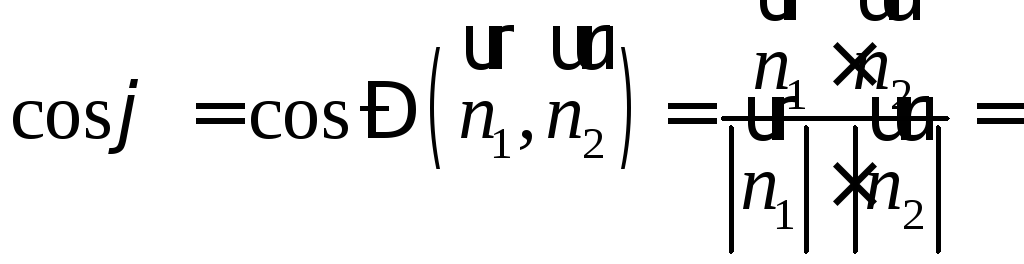
![]()
Отсюда
![]() обычно под углом между прямыми берут
обычно под углом между прямыми берут
острый угол, образованный этими прямыми.
Поэтому мы можем считать, что угол равен![]()
Задача
4. Составить
уравнение прямой, симметричной прямой
![]() относительно:
относительно:
а)
начала координат; б) оси абсцисс; в)
точки
![]()
Решение.
а) Симметрия относительно начала
координат переводит точку
![]() в точку
в точку![]() Поэтому уравнение симметричной прямой
Поэтому уравнение симметричной прямой
мы получим, заменяя![]() на
на![]() и
и![]() на
на![]() Таким образом, искомое уравнение будет
Таким образом, искомое уравнение будет
таково:![]() или
или![]()
б)
Симметрия относительно оси абсцисс
задается формулами
![]()
![]() Отсюда получаем:
Отсюда получаем:![]()
в)
(см. рис. 6)

Рис.6.
Возьмём
какую-нибудь точку прямой
![]() например,
например,![]() (для этого достаточно подобрать числа
(для этого достаточно подобрать числа![]() удовлетворяющие уравнению
удовлетворяющие уравнению![]() ).
).
Пусть![]() – точка, симметричная точке
– точка, симметричная точке![]() относительно точки
относительно точки![]() Тогда
Тогда![]() и
и![]() Следовательно,
Следовательно,![]() Отсюда получаем уравнение прямой
Отсюда получаем уравнение прямой![]() т.е.
т.е.![]()
Замечание.
Решение задачи 4(в) может быть упрощено,
если использовать формулу симметрии
плоскости относительно точки (см. раздел
«Геометрические преобразования»).
Задача
5. Спроектировать
току
![]() на прямую
на прямую![]()
Решение.
(см. рис. 7)

Рис.7.
Обозначим
через
![]() прямую
прямую
![]()
Уравнение этой прямой можно переписать
в виде
![]() Найдём нормальный вектор прямой
Найдём нормальный вектор прямой![]() Этот вектор может быть принят в качестве
Этот вектор может быть принят в качестве
направляющего вектора прямой![]() Запишем параметрические уравнения
Запишем параметрические уравнения
прямой![]()
![]()
![]() (8)
(8)
Теперь
найдем координаты точки
![]() пересечения прямых
пересечения прямых![]() и
и![]() подставив формулы (8) в уравнение прямой
подставив формулы (8) в уравнение прямой![]() получим:
получим:![]() Отсюда
Отсюда![]() Подставим теперь это значение
Подставим теперь это значение![]() в (8), получим:
в (8), получим:![]()
![]() Таким образом,
Таким образом,![]() Точка
Точка![]() – это и есть проекция точки
– это и есть проекция точки![]() на прямую
на прямую![]()
Задача
6. Составить
уравнение высоты
![]() медианы
медианы![]() и биссектрисы
и биссектрисы![]() треугольника
треугольника![]() если
если![]()
![]()
![]()
Решение.
(см. рис. 8).

Рис.8.
Имеем:
![]() Вектор
Вектор![]() является нормальным вектором прямой
является нормальным вектором прямой![]() т.е.
т.е.![]() В качестве точки
В качестве точки![]() прямой
прямой![]() возьмём точку
возьмём точку![]() Запишем теперь уравнение высоты
Запишем теперь уравнение высоты![]()
![]() т.е.
т.е.![]()
Далее,
направляющим вектором прямой
![]() может служить вектор
может служить вектор![]() Если направляющий вектор умножить на
Если направляющий вектор умножить на
2, то он по-прежнему останется направляющим
вектором. Поэтому возьмём![]() Отсюда получаем уравнение прямой
Отсюда получаем уравнение прямой![]()
![]() или
или![]()
Составим
теперь уравнение биссектрисы
![]() Найдём длины векторов
Найдём длины векторов![]() и
и![]()
![]()
![]() Векторы
Векторы![]() и
и![]() имеют одинаковую длину, поэтому вектор
имеют одинаковую длину, поэтому вектор![]() направлен по биссектрисе угла
направлен по биссектрисе угла![]() а значит, является направляющим вектором
а значит, является направляющим вектором
прямой![]() Вычисляем:
Вычисляем:![]() Запишем каноническое уравнение прямой
Запишем каноническое уравнение прямой![]()
![]() отсюда получаем:
отсюда получаем:![]()
Замечание.
Если
![]() и
и![]() – векторы, то вектор
– векторы, то вектор – вектор, направленный по биссектрисе
– вектор, направленный по биссектрисе
угла, образованного векторами![]() и
и![]() а вектор
а вектор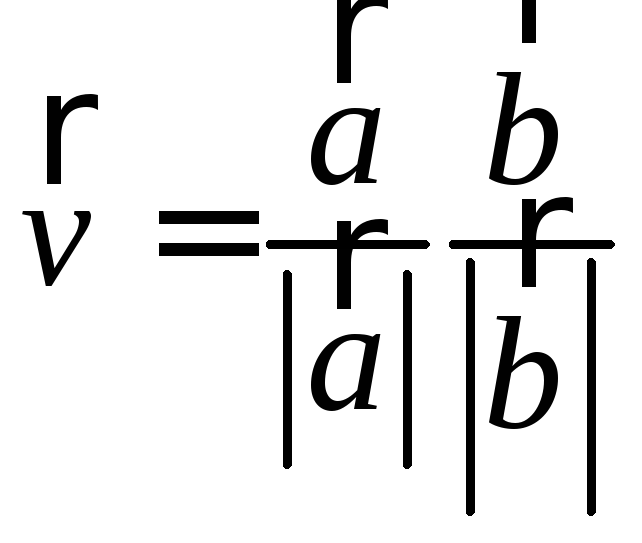 – по биссектрисе смежного угла (см. рис.
– по биссектрисе смежного угла (см. рис.
9).
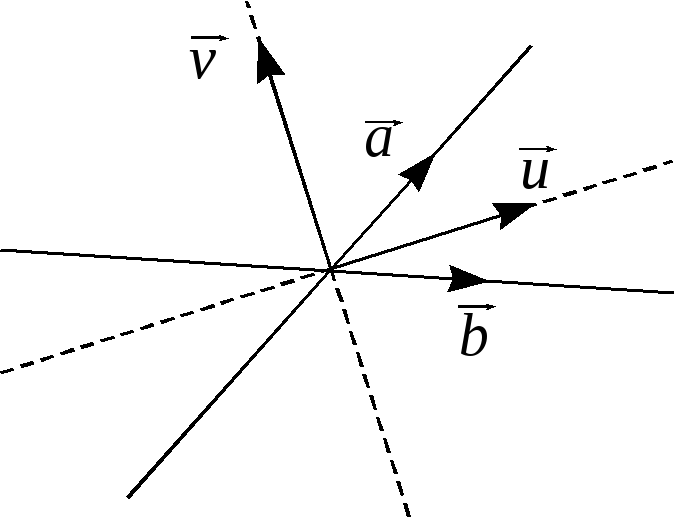
Рис.9.
Если
![]() то
то![]() а
а![]()
Задача
7. Даны
уравнения двух сторон параллелограмма:
![]()
![]() и координаты его центра:
и координаты его центра:![]() Составить уравнения двух других сторон
Составить уравнения двух других сторон
и уравнения диагоналей.
Решение
(см. рис. 10).

Рис.10.
Обозначим
вершины параллелограмма буквами
![]() а его центр буквой
а его центр буквой![]() Можно считать, что даны уравнения сторон
Можно считать, что даны уравнения сторон![]() и
и![]() Найдём вершину
Найдём вершину![]() решив систему
решив систему

Прибавим
к первому уравнению удвоенное второе,
получим:
![]() откуда
откуда![]() Далее,
Далее,![]() Следовательно,
Следовательно,![]() Затем вычисляем:
Затем вычисляем:![]()
![]()
Отсюда
![]() Через точку
Через точку![]() проводим прямую, параллельную
проводим прямую, параллельную![]() получаем
получаем![]()
![]()
![]() Аналогично получаем уравнение
Аналогично получаем уравнение![]()
![]() т.е.
т.е.![]() Теперь найдём точку
Теперь найдём точку![]()

Отсюда
![]()
![]() т.е.
т.е.![]()
Осталось
получить уравнения диагоналей
![]() и
и![]() Имеем:
Имеем:![]() Взяв
Взяв![]()
![]() получим уравнение
получим уравнение![]()
![]() а значит,
а значит,![]() Аналогично получим уравнение
Аналогично получим уравнение![]()
![]()
![]() откуда получаем:
откуда получаем:![]() т.е.
т.е.![]()
Задача
8. Даны
координаты одной из вершин треугольника:
![]() и уравнения двух его медиан:
и уравнения двух его медиан:![]()
![]() Найти координаты двух других вершин
Найти координаты двух других вершин
треугольника.
Решение..
Так как точка
![]() не удовлетворяет уравнениям данных
не удовлетворяет уравнениям данных
прямых, то можно считать, что![]() – это вершина
– это вершина![]() а данные прямые – медианы, выходящие
а данные прямые – медианы, выходящие
из вершин![]() и
и![]() соответственно (см. рис. 11).
соответственно (см. рис. 11).

Рис.11.
Обозначим
данные прямые через
![]() и
и![]() Возьмём какую-нибудь точку на прямой
Возьмём какую-нибудь точку на прямой![]()
![]() Пусть
Пусть![]() – точка, симметричная точке
– точка, симметричная точке![]() относительно
относительно![]() Тогда
Тогда
![]()
Следовательно,
![]() Через точку
Через точку![]() проводим прямую
проводим прямую![]()
![]() т.е.
т.е.![]() Точку
Точку![]() найдём, пересекая прямые
найдём, пересекая прямые![]() и
и![]()

Получаем:
![]()
Аналогично
находим точку
![]() А именно, возьмём точку на прямой
А именно, возьмём точку на прямой![]()
![]() Пусть
Пусть![]() – точка, симметричная точке
– точка, симметричная точке![]() относительно
относительно![]() Тогда
Тогда![]() Уравнение прямой
Уравнение прямой![]() параллельной
параллельной![]() и проходящей через
и проходящей через![]()
![]() Точку
Точку![]() находим из системы
находим из системы
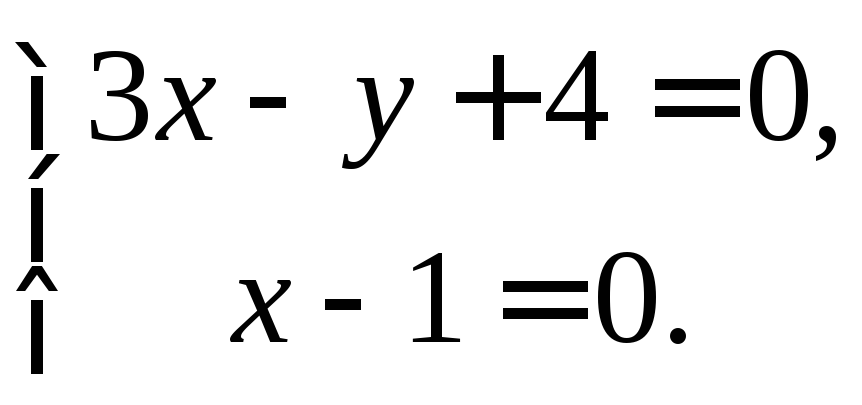
Отсюда
![]()
Задача
9. Через точку
![]() провести прямую, пересекающую положительные
провести прямую, пересекающую положительные
части осей координат и образующую с
осями координат треугольник наименьшей
площади.
Решение
(см. рис. 12).

Рис.12.
Пусть
![]() – искомая прямая и
– искомая прямая и![]() – отрезки, отсекаемые прямой
– отрезки, отсекаемые прямой![]() от осей координат. Тогда
от осей координат. Тогда![]() Запишем уравнение прямой
Запишем уравнение прямой![]() “в отрезках” (см. формулу (6)):
“в отрезках” (см. формулу (6)):![]() Так как
Так как![]() то
то![]() Отсюда
Отсюда Найдём площадь треугольника
Найдём площадь треугольника![]()
![]() Найдём наименьшее значение функции
Найдём наименьшее значение функции![]() на множестве
на множестве![]() Для этого вычислим производную:
Для этого вычислим производную:![]() Очевидно,
Очевидно,![]() при
при![]() Составим таблицу:
Составим таблицу:
-

2


–
0



4

Из
таблицы видно, что функция
![]() имеет в точке
имеет в точке![]() минимум, равный
минимум, равный![]() При
При![]() получаем:
получаем:![]() а значит, уравнение прямой
а значит, уравнение прямой![]() таково:
таково:![]() или
или![]()
Соседние файлы в папке СРС
- #
- #
- #
- #
- #
- #
- #
- #






 – это я над собой смеюсь.
– это я над собой смеюсь. 

 Составить уравнение прямой, перпендикулярной плоскости
Составить уравнение прямой, перпендикулярной плоскости