- Учебники
- 2 класс
- Математика 👍
- Рудницкая
- №3
авторы: Рудницкая, Юдачева.
издательство: “Просвещение”
Раздел:
- Угол. Прямой угол
ГДЗ рабочая тетрадь по математике №2 2 класс Рудницкая. Угол. Прямой угол. Номер №3
- Предыдущее
- Следующее
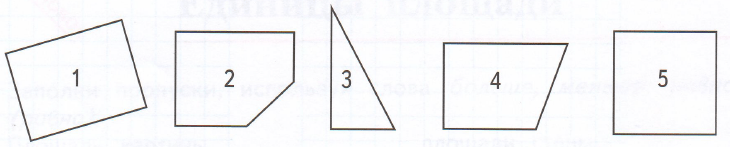
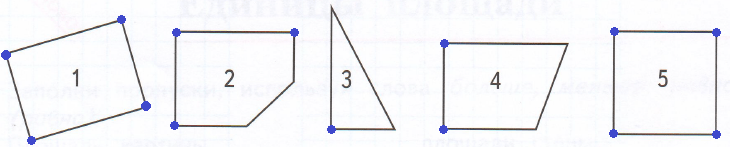
Найди прямые углы многоугольников и отметь точками вершины этих углов.
Выпиши номера многоугольников, имеющих:
один прямой угол _
два прямых угла _
три прямых угла _
четыре прямых угла _
reshalka.com
ГДЗ рабочая тетрадь по математике №2 2 класс Рудницкая. Угол. Прямой угол. Номер №3
Решение
Выпиши номера многоугольников, имеющих:
один прямой угол 3
два прямых угла 4
три прямых угла 2
четыре прямых угла 1, 5
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Тип урока: объяснение нового
материала.
Место урока в структуре по теме: данная тема
изучается в разделе “Табличное сложение
однозначных чисел с переходом через десяток”.
Цель урока: Познакомить учащихся с понятием
“прямой угол” и научить применять полученные
знания на практике.
Задачи урока:
1. Образовательные:
- Познакомить учащихся с понятием “прямой угол”;
- Сформировать практические навыки определения
прямого угла при помощи треугольника и без него; - Продолжить работу по совершенствованию навыка
устного счёта в пределах 100;
2. Развивающие:
- Развитие логического мышления, внимания,
памяти, пространственного воображения; - Развитие творческих умений и навыков по теме
для успешного выполнения заданий; - Развитие культуры речи и эмоций учащихся.
3. Воспитательные:
- В целях решения задач нравственного воспитания
содействовать воспитанию гуманности и
коллективизма, наблюдательности и
любознательности, развитию познавательной
активности, формированию навыков
самостоятельной работы; - В целях решения задач эстетического воспитания
содействовать развитию у учащихся чувства
прекрасного.
ХОД УРОКА
I. Организационный момент.
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте
Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.
– Ребята, сегодня мы опять отправимся в
путешествие по королевству Геометрия.
3. Устный счёт.
2 слайд
– У ворот нас встречают король Точка и его дочь
– принцесса Прямая. Прежде чем король и
принцесса познакомят нас с жителями своего
королевства, они хотят вас испытать.
II. Устный счет.
(Слайд 3)
1) Игра “Гусеница-растеряша”.
– Гусеница растеряла числа, посмотрите на
оставшиеся, разгадайте по какому правилу можно
продолжить ряд чисел. (Дети называют правило: это
чётные числа; каждое последующее число на 2
больше предыдущего).
– Какие же числа растеряла гусеница? (2,4,6,8,10,12,14,16)
(Слайд 4)
2) Игра “Математический баскетбол”.
Баскетбол – командная спортивная игра,
цель которой забросить руками мяч в подвешенную
корзину.
– Любой из вас забьёт гол, если правильно решит
пример. (Дети по цепочке решают примеры). 30 + 7 25 + 5 32
– 12 66 + 4 80 – 7 28 – 10 45 – 45 53 + 7 59 – 9 90 + 9
Слайд 5
Задание на логику
– Сколько пятачков у 15 поросят? (15)
– Когда гусь стоит на двух ногах, то весит 4 кг.
Сколько будет весить гусь, когда встанет на одну
ногу?
6 слайд
– Вы прошли все испытания. Король и принцесса
очень довольны вами и готовы познакомить вас с
жителями королевства “Геометрия”!
(По щелчку створки ворот открываются.)
(Слайд 7)
– Ребята, перед вами жители королевства
“Геометрия”.
– Посмотрите на фигуры в каждой рамке. Какая из
них лишняя? Почему?
(Учащиеся называют лишние фигуры, обосновывают
свой выбор).
– Разделите все оставшиеся фигуры на две группы.
Как это можно сделать? (Оставшиеся фигуры можно
разделить на две группы: линии и многоугольники.)
– Назовите виды линий и многоугольников,
известные вам. (Линии: прямая, ломаная, кривая.
Многоугольники: квадрат, трапеция,
прямоугольник, четырёхугольник, пятиугольник,
шестиугольник, многоугольник).
IV. Работа над новым материалом.
(Слайд 8)
1) – Тему урока вам подскажет кроссворд.
Кроссворд “Геометрический”.
1) Часть прямой, у которой есть начало, но нет
конца. (Луч).
2) Геометрическая фигура, не имеющая углов.
(Круг).
3) Самая маленькая геометрическая фигура.
(Точка).
4) Геометрическая фигура, имеющая форму
вытянутого круга. (Овал).
– Тема нашего урока спряталась по вертикали.
Найдите её. (Угол). (щелчок вылетают
геометрические фигуры).
– Сформулируйте пожалуйста тему нашего урока.
– Ребята, а зачем мы будем изучать углы?
– Как Вы думаете, вам эти знания пригодятся?
(Ответы детей)
– Углы окружают нас и в повседневной жизни.
Приведите свои примеры, где можно найти углы
вокруг нас.
– Ребята, а может, кто-то знает, что такое угол?
(выслушиваются мнения детей)
Правильность нашей формулировки, мы проверим
чуть позже.
– Люди, каких профессий чаще всего встречаются с
углами? (конструктор, инженер, дизайнер,
строитель, архитектор, моряк, астроном,
архитектор, портной и т.д.)
Слайд 9.
Посмотрите на рисунки: уголок соединительный
для труб и уголок канцелярский для бумаг;
угольник плотника и угольник чертёжный; угловой
стол и угловой диван.
– Ребята, а сейчас Король и Принцесса предлагают
немного поиграть.
Слайд 10.
Игра “Им угол имя подарил”.
– Угол важная фигура. Многим фигурам он помог
дать имя. Назовите фигуры.
– Что общего в названиях фигур? (что они имеют
угольник – общая часть)
– Почему первая часть слов везде разная? (потому
что углов разное количество)
Физминутка 11-16 слайды
Открываем тетради, записываем 18 января,
классная работа. (слайд 17)
Слайд 18.
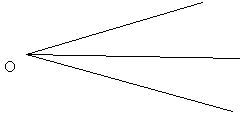
– Ребята, а теперь от красных полей отступите
одну клеточку и поставьте точку О. От этой точки
проведите два луча.
На доске заранее нарисовать точку О (4-5). Вызвать
4-5 детей, чтобы они провели лучи на доске.
– Что за фигуры у нас получилась? (угол)
– Посмотрите, какие разные эти углы.
– Ребята, а теперь соберите правило из слов.
Работа в парах.
(Вывод: угол – это геометрическая фигура,
образованная двумя разными лучами
с общим началом).
– Ребята, а теперь посмотрите на фигуру, которую
нарисовала я.
– Это угол, или нет.
(Дети говорят – нет, еще раз возвращаемся к
правилу, после этого делаем вывод о том, что это
тоже угол – развернутый)
Слайд 19. (вывод по углу)
Плакат на доске
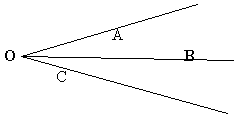
Точка О – вершина угла. Угол можно назвать
одной буквой, записанной около его вершины. Угол
О. Но может быть несколько углов, имеющих одну
вершину. Как быть тогда? (На листе чертеж таких
углов)
Ответы детей.
– В таких случаях если называть разные углы
одной буквой, то будет непонятно, о каком угле
идёт речь. Что этого не произошло, на каждой
стороне угла можно отметить по одной точке,
поставить около неё букву и обозначить угол
тремя буквами, при этом всегда в середине
записывают букву, обозначающую вершину угла.
Угол АОВ. Лучи АО и ОВ – стороны угла.
Плакат на доске
Слайд 20.
– Ребята, у вас на столах лежат разные виды
углов. Найдите пожалуйста одинаковые виды углов.
– Как будете искать? (Ответы детей)
Один человек на моих моделях ищет одинаковые
углы.
– Ребята, смотрите, номера 6 и 7 совпали
полностью, а 1 и 5 – нет. № 5 больше.
– Какой можно сделать вывод? После ответа детей
появляется слайд.
ВЫВОД: слайд 21
- Равные углы при наложении совпадают
- Если один угол наложить на другой и они
совпадут, то эти углы равны
Слайд 22.
Изготовление модели прямого угла.
Слайд 23
Не всегда удобно определять прямой угол на
глаз. Для этого используют линейку-угольник.
– Каким цветом выделен угол больше прямого?
(Голубым).
– Меньше прямого? (Зелёным).
– Какой же угол из трёх предложенных прямой?
– Почему вы так решили? (Вершина и стороны угла
совпали с прямым углом на линейке-угольнике).
– Как же определить вид угла?
ВЫВОД:
- Чтобы определить вид угла, надо совместить его
вершину и сторону соответственно с вершиной и
стороной прямого угла на угольнике.
Слайд 24
– Каждый из углов имеет своё название. Острый
угол – это угол, который меньше прямого. Тупой
угол – это угол, который больше прямого.
(На доске появляются таблички с названием
углов)
– Какой угол мы будем считать главным?
Мама мой взяла листок,
И загнула уголок,
Угол вот такой у взрослых
Называется ПРЯМЫМ.
Если угол уже – ОСТРЫМ,
Если шире, то – ТУПЫМ.
Слайд 25.
– Ребята, а всегда возможно наложить углы?
– Нет. (Если начерчены в тетради…)
– Для этого существует транспортир, с помощью
которого измеряют углы. Углы измеряют в градусах.
Посмотрите на виды транспортиров.
Слайд 26.
Очень часто углы мы можем наблюдать на часах.
Углы образуют часовые стрелки.
Работа по учебнику.
Задание: Используя модель прямого
угла, найди прямые углы и выпиши их номера. (Дети
выполняют задание самостоятельно, затем один
ученик называет свой вариант ответа, все
проверяют работу).
– С помощью угольника удобно не только
определять прямые углы, но главное – строить их.
Построим прямой угол, каждый сам назовёт его
одной или тремя буквами.
Слайд 27-29 (Учитель на доске, а дети в тетрадях
строят прямой угол. Выполняется взаимопроверка в
парах).
Я ОСТРЫЙ – начертить хочу,
Сейчас возьму и начерчу.
Веду из точки две прямых,
Как будто два луча,
И видим ОСТРЫЙ УГОЛ мы,
как остриё меча.А для УГЛА ТУПОГО
Всё повторяем снова:
Из точки две прямых ведём,
Но их пошире разведём.
На чертёж мой посмотри,
Он, как ножницы внутри,
Если их за два кольца
Мы раздвинем до конца.
Практическая работа по закреплению изученного.
На партах у вас проволока. Сделайте из нее
прямой угол и проверьте с помощью угольника,
затем сделайте острый и тупой.
7. Итог урока.
– Расскажите мне по схеме о том, что вам дал
сегодняшний урок математики?
8. Домашнее задание.
Математика, 2 класс
Урок № 33. Угол. Виды углов: прямой, острый, тупой
Перечень вопросов, рассматриваемых в теме:
– Какие бывают углы?
– Как распознавать углы?
Глоссарий по теме:
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Острый угол – это угол, который меньше прямого.
Тупой угол – это угол, который больше прямого.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
- Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 5-е изд. – М.: Просвещение, 2014. – с.8-9.
- Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.3.
- Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.16.
Теоретический материал для самостоятельного изучения
Рассмотрите фигуры и выберите лишнюю.
Лишняя фигура под номером 2. Она образована незамкнутой линией.
Она называется угол.
Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.
Посмотрите на рисунки: по-разному открытый веер, образует разные углы.
У каждого угла есть две стороны и вершина. Углы бывают прямые, острые и тупые. Углы определить можно помощью чертежного угольника.
Прямой угол определяем с помощью чертежного угольника.
Угол, который меньше прямого угла называется острым углом.
Угол, который больше прямого угла называется тупым углом.
Посмотрите, как из обычного листа бумаги можно сделать модель прямого угла. Моделью можно воспользоваться, если у вас нет чертежного угольника. Возьмите лист бумаги и перегните его 2 раза, как показано на рисунках 1 и 2. И получите модель прямого угла.
Разверните лист. Линии сгиба образовали 4 прямых угла.
Чтобы определить, какой угол начерчен, на него накладывают угольник или модель прямого угла.
Вывод: Углы могут быть прямыми и непрямыми. Чтобы определить прямой угол или нет, нужно взять особый инструмент – угольник. Если, приложив угольник к углу, вершиной к вершине, стороны совпадут, то угол – прямой. Не совпадут – непрямой. Непрямые углы делятся на: тупые и острые. Угол, величина которого меньше величины прямого – острый, а, если величина угла больше величины прямого – тупой.
Тренировочные задания.
1.Посмотрите на крыши домов и домиков. Какие углы ты видишь на рисунке? Соотнесите вид угла с изображением домика.
Правильные ответы:
2. Выберите цифры, в записи которых присутствуют только прямые углы.
Правильные ответы:
Слайд № 1
Тема урока: Прямой угол
Цель: познакомить учащихся с понятием «угол», сформировать представление о видах угла: «прямой, тупой, острый»
Задачи:
Образовательные:
- систематизировать и расширить представления детей о геометрических фигурах;
- формировать познавательный интерес к математике.
Развивающие:
- развить познавательные процессы (особенно, внимание, восприятие, мышление);
- развить эмоциональную сферу;
- развить коммуникативные умения
- развить мыслительные процессы (анализ, синтез, классификация и другие).
Воспитательные:
- воспитать умение слушать;
Оборудование: чертежный треугольник, модель прямого угла, фигуры многоугольников, лист бумаги для каждого ученика.
Ход урока:
- Организационный момент
Слайд № 2
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку «5».
- Устный счёт
Слайд № 3 (по щелчку на каждый этап работы)
– Заполните таблицу.
|
Уменьшаемое |
70 |
42 |
80 |
98 |
|
|
Вычитаемое |
4 |
6 |
12 |
||
|
Разность |
20 |
10 |
41 |
- Что неизвестно в первом столбике? Как находили?
- Что неизвестно во втором столбике? Как находили? (Чтобы найти уменьшаемое, нужно к вычитаемое прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.)
– Решение задач
Слайд № 4 (по щелчку на каждый этап работы)
В саду росли 2 березы, 4 яблони, 5 вишен. Сколько всего фруктовых деревьев росло в саду?
Сестре 9 лет, брату 3 года. На сколько сестра будет старше брата через 5 лет?
– Геометрическое задание
На слайде:
- Разделите все фигуры на две группы. (В первую группу фигуры 1, 3, 5; во вторую – фигуры 2, 4.)
- Что общего между фигурами каждой группы? (I группа – есть углы; II группа – нет углов.)
- Работа над новым материалом
- Сегодня на уроке мы поговорим об углах. Все ли углы в фигурах первой группы одинаковы? (Нет.)
Слайд № 5
На слайде:
- Какие бывают углы?
- Сейчас каждый из вас сделает из листа бумаги, который лежит на парте, модель прямого угла. Как это сделать подскажет учебник. Открываем учебник на с. 8.
Слайд № 6 (по щелчку на каждый этап работы)
- Согните лист, как на рисунке 1. Согните еще раз, как на рисунке 2. Получилась модель прямого угла.
Слайд № 7 (по щелчку)
- Покажите стороны прямого угла и вершину.
Дети показывают.
- Моделью прямого угла является также прямой угол чертежного треугольника. Найдите на нем с помощью своей модели прямой угол.
Слайд № 8 (по щелчку)
- Прямой угол на чертежном треугольнике – это модель прямого угла. Теперь разверните лист бумаги, из которого вы сделали модель прямого угла. Сколько прямых углов образовали линии сгиба? ( Четыре прямых угла.)
Слайд № 9-10 (по щелчку)
- Рассмотрите чертежный треугольник. Вы уже убедились, что у него один угол прямой. С помощью модели прямого угла узнайте, будут ли прямыми остальные углы этого треугольника.
- Какие у вас получились углы? (Меньше прямого.)
Слайд № 11 (по щелчку)
- Физкультминутка
Слайд № 12
|
Солнце глянуло в окно, Время отдохнуть пришло. Надо всем нам дружно встать. Раз присесть, достать до пятки. И плечами покачать. |
А затем, как на зарядке, Прямо и красиво встать. Руки вытянуть пошире И на месте поскакать. На носок, потом на пятку. Физкультминутка, как зарядка! |
- Закрепление
1. На слайде появляются разнообразные углы:
Слайд № 13
- Какие углы вы видите? (Ответы детей.)
- У вас есть карточки с изображением этих же углов. Найдите среди них прямые углы. Назовите номера.
- А сейчас проверьте ваши предположения с помощью модели прямого угла.
Слайд № 14
2. На слайде появляются фигуры:
- Какие фигуры вы видите? (Ответы детей.)
- У вас есть карточки с изображением этих же фигур. Найдите прямые углы у этих фигур. Назовите номера.
- А сейчас проверьте ваши предположения с помощью модели прямого угла.
- Повторение пройденного
Слайд № 15 (по щелчку)
- Составьте задачу по выражениям:
- + 7, 12-8.
При составлении задач по выражениям со знаком «минус» не забывать о задачах на разностное сравнение.
- А сейчас более сложное задание. Составьте задачу по выражению № 4, с. 8.
Решение примеров: № 2, с. 8.
- На какие две группы можно разделить все примеры? (I группа примеры на сложение, II группа – на вычитание.)
- Решите эти примеры по группам, и составьте еще по одному примеру в каждую группы.
- Задание на смекалку
Слайд № 16
Вдоль каждой стороны квадратной клумбы надо рассадить 10 кустов роз, так, чтобы у каждой стороны было поровну. Как это сделать?
Слайд № 17
- Итоги урока.
Слайд № 18
– Что нового узнали на уроке?
– Чему научились на уроке?
Домашнее задание: с.8 № 3, 5.
М
– Ох, и устали же мы сегодня. Целый день перетаскивали из угла в угол наш
волшебный говорящий буфет.
Помните,
как выглядит план наших парадных залов? Мы хотели поставить буфет в один из
углов золотого зала. Но, сколько не пытались это сделать, у нас толком ничего
не получилось. Если мы приставляли его к одной стене, то между буфетом и другой
стеной оставалось пространство. Тогда мы попытались поставить буфет в зелёный
зал. Там он вообще не входил ни в один из углов.
–
Мы так устали. И теперь просто не представляем, что же нам делать, куда можно
поставить наш волшебный буфет.
–
Плюс, слышишь, наш компьютер включился. Наверное, сейчас нам по скайпу будет звонить
царица Математика.
–
Ах, мои дорогие Плюс и Минус! Очень обидно, что прежде чем двигать по всему
замку буфет, вы не познакомились с темой «Виды углов». Придётся
сегодня мне объяснить вам эту тему.
Итак,
сегодня мы поговорим о видах углов – прямых, острых и тупых
углах.
–
Какие странные названия – прямой, острый, тупой.
–
Что же такое угол? Если мы поставим точку, а от этой точки проведём прямую, у
нас получится прямая, ограниченная с одной стороны точкой. Такая линия
называется луч. А если из этой же точки мы проведём ещё один луч, то у
нас получится угол. При этом точка, из которой были проведены лучи,
называется вершиной угла, а сами лучи в этом случае называются стороны
угла.
Посмотрите,
какие разнообразные углы можно построить:
Среди
них вы можете увидеть и острые, и прямые, и тупые углы.
–
А как же мы отличим, какие из углов острые, какие – прямые, а какие – тупые?
–
Начнём мы с прямого угла. Посмотрите на этот лист бумаги. Сейчас мы перегнём
его вдвое, потом ещё раз вдвое. Только сгибать надо аккуратно. Так, чтобы линии
сгиба совместились и не выглядывали одна из-под другой. Наш лист сложен в 4
раза. И вот получился угол. Такой угол, который образуется аккуратным сгибанием
листа в четыре раза, называется прямым углом.
А
сейчас развернём лист бумаги:
Видите,
на нём видны линии сгиба. И у нас видны уже четыре угла с одной общей вершиной.
А ещё есть специальная линейка–треугольник. У неё один угол
прямой и два острых. Сейчас мы положим такую линейку на наш лист бумаги так,
чтобы вершины прямого угла линейки и углов на бумаге совместились. А теперь
попытаемся совместить стороны. Получилось?
–
Да, стороны прямого угла треугольника точно легли на стороны прямого угла на
бумаге.
–
Теперь так же положим линейку и на остальные три угла. Как видите, и здесь совмещаются
стороны. Значит точно, все эти углы одинаковые. Все они – прямые.
–
С прямыми углами понятно. А что же это за углы – острые и тупые.
–
Я хочу вам показать один угол. Видите, он такой острый, что его вершиной даже
можно слегка уколоться.
А
теперь посмотрите, угол развернулся, раскрылся. Его вершиной уже вряд ли можно
уколоться. Теперь угол стал тупым:
А
теперь давайте вернёмся к тем углам, которые мы нарисовали. Сейчас на первый
угол кладём линейку.
Вершина
линейки совмещается с вершиной угла. Одна из сторон линейки совместилась со
стороной угла, а вот вторая спряталась под треугольником. Значит, угол раскрыт
меньше, чем прямой угол треугольника. Такие углы, которые раскрыты меньше
прямого угла, называются острыми углами.
Посмотрите
на следующий угол. Он раскрыт значительно шире первого, но, когда мы
прикладываем к нему линейку:
Видно,
что одна из сторон опять спряталась под линейку. Значит, этот угол тоже острый.
Переходим
к следующему углу:
Его
вершина и стороны точно совместились с вершиной и сторонами прямого угла
линейки. Как вы думаете, какой это угол?
–
Конечно, прямой!
–
Совершенно верно. Этот угол прямой. А вот этот?
–
Наверное, острый. Видите, как он наклонился.
–
А если приложить линейку? Ну что, какой угол?
–
Я ошибся… Этот угол тоже прямой………….
–
Ну что же, продолжим. Рассмотрим следующий угол:
Посмотрите,
между второй стороной линейки и стороной нарисованного угла как будто ещё один
уголок появился. Значит, этот угол раскрыт немного шире, чем прямой. Такие углы,
которые раскрыты больше прямого угла, называются тупыми углами.
–
Ну, а если посмотреть на последний угол, то здесь даже без линейки-треугольника
понятно, что он тупой.
–
Да, это очень хорошо видно. Но мы всё-таки приложим линейку и к нему:
Сейчас
очень хорошо видно, что этот угол раскрыт намного шире прямого. Конечно, он –
тупой.
Ну
что, Плюс и Минус, вы поняли, какие бывают углы?
–
Да, поняли. А если присмотреться, то в обычных комнатах все углы – прямые.
–
А еще прямые углы у учебников и тетрадей.
–
У школьных парт и столов.
–
И у нашего волшебного буфета тоже все углы прямые.
–
Значит, поставить его можно только туда, где стены образуют прямой угол.
Посмотрите ещё раз внимательно на план парадных залов.
Ну,
где вы можете найти прямой угол?
–
По-моему, в золотом зале все углы тупые, в зелёном – все острые. А вот прямой….
–
Мне кажется, я вижу два прямых угла в синем зале. Но, всё-таки, проверю-ка я
это при помощи линейки:
Урра!
Получилось! В синем зале- 2 прямых угла. Вот если бы мы сначала поработали с
планом парадных залов, не пришлось бы волшебный буфет таскать по всему дворцу.
–
Ну, а теперь повторите, пожалуйста, чему вы сегодня научились.
–
Угол образуется двумя лучами, которые выходят из одной точки.
–
Прямой угол можно получить аккуратным сгибанием листа бумаги вчетверо.
Но лучше воспользоваться специальной линейкой-треугольником.
–
Углы, которые раскрыты меньше прямого угла, называются острыми углами.
–
Углы, которые раскрыты больше прямого угла, называются тупыми углами.
–
Хорошо, урок вы усвоили. А теперь за работу – поставьте волшебный буфет туда,
куда его можно поставить – в синий зал.
До
свидания.
–
До свидания, царица. Спасибо за урок!
–
До свидания, ребята. Нам пора за работу.