К простейшим геометрическим фигурам на плоскости относят точку и прямую. Точки обозначают прописными буквами латинского алфавита:  . Прямые обозначают или строчными буквами латинского алфавита
. Прямые обозначают или строчными буквами латинского алфавита  или двумя прописными буквами:
или двумя прописными буквами:  и т. д.
и т. д.
Например, на рисунке 8.1 изображена прямая  и прямая
и прямая  . Точка
. Точка 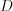 принадлежит прямой
принадлежит прямой  , точка
, точка  не принадлежит данным прямым.
не принадлежит данным прямым.
Часть прямой линии, ограниченную с одной стороны и неограниченную с другой, называют полупрямой или лучом.
Например, на рисунке 8.2 изображены лучи  и
и 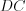 .
.
Полупрямые прямой  , на которые она разбивается любой точкой прямой, называют дополнительными.
, на которые она разбивается любой точкой прямой, называют дополнительными.
Например, на рисунке 8.2 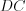 и
и  – пара дополнительных полупрямых.
– пара дополнительных полупрямых.
Часть прямой линии, ограниченную двумя точками, называют отрезком. Отрезки называют равными, если их концы совпадают при наложении одного отрезка на другой.
Например, на рисунке 8.3 изображен отрезок 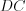 .
.
Линию, состоящую из нескольких отрезков, не лежащих на одной прямой (конец предыдущего отрезка совпадает с началом следующего), называют ломаной линией. Отрезки, из которых состоит ломаная линия, называют ее звеньями.
Например, на рисунке 8.4 изображена ломаная  , состоящая из четырех звеньев:
, состоящая из четырех звеньев:  и
и  .
.
Ломаная называется замкнутой, если ее концы совпадают.
Например, На рисунках 8.5 и 8.6 изображены замкнутые ломаные.

Чтобы найти длину ломаной, необходимо найти сумму длин ее звеньев. Длина отрезка, соединяющего концы ломаной, короче ее длины.
Например, если  мм,
мм,  мм,
мм,  мм,
мм,  мм, то длина ломаной
мм, то длина ломаной  будет равна 84 мм.
будет равна 84 мм.
Углом называют фигуру, образованную двумя лучами, исходящими из одной точки (рис. 8.7). Эту точку называют вершиной угла (точка  ), а лучи – сторонами угла (лучи
), а лучи – сторонами угла (лучи  и
и  ).
).
Угол можно обозначать тремя прописными буквами так, чтобы буква, обозначающая вершину угла, стояла между двумя другими буквами или одной прописной буквой, обозначающей вершину угла. Например, на рисунке 8.7 изображен угол  (угол
(угол  ).
).

Биссектрисой угла называют луч, который выходит из вершины угла и делит этот угол на два равных угла. Каждая точка биссектрисы угла равноудалена от сторон этого угла.
Например, на рисунке 8.8 луч 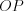 – биссектриса угла
– биссектриса угла  , следовательно, углы
, следовательно, углы  и
и  равны, а точка
равны, а точка  равноудалена от сторон угла.
равноудалена от сторон угла.
Угол называют развернутым, если его стороны являются дополнительными прямыми одной прямой. На рисунке 8.9 угол  – развернутый.
– развернутый.
Основной единицей измерения углов считают угол в 1 градус. Угол в один градус – это угол, равный  части развернутого угла. Развернутый угол равен
части развернутого угла. Развернутый угол равен  . Наряду с градусной мерой угла употребляется и радианная мера: n рад =
. Наряду с градусной мерой угла употребляется и радианная мера: n рад =  , а
, а  рад.
рад.
Например:
1) 5 рад =  ; 2)
; 2)  рад =
рад =  рад.
рад.
Два угла называют смежными, если у них одна сторона общая, а две другие стороны этих углов являются дополнительными полупрямыми. Сумма смежных углов равна  .
.
Например, так как углы  и
и  являются смежными (рис. 8.10) и
являются смежными (рис. 8.10) и  , то
, то  .
.

Острым углом называют угол, градусная мера которого меньше  .
.
Например, на рисунке 8.10 угол 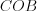 – острый.
– острый.
Тупым углом называют угол, градусная мера которого больше  , но меньше
, но меньше  .
.
Например, на рисунке 8.10 угол  – тупой.
– тупой.
Прямым углом называют угол, градусная мера которого равна  .
.
Например, на рисунке 8.11 угол  – прямой.
– прямой.
Прямые, которые пересекаются под прямым углом, называют взаимно перпендикулярными.
Например, на рисунке 8.12 прямые  и
и  взаимно перпендикулярные. Записывают:
взаимно перпендикулярные. Записывают:  .
.
Две прямые, которые принадлежат одной плоскости и не имеют общих точек, называют параллельными.
Например, на рисунке 8.12 прямая  параллельна прямой
параллельна прямой  . Записывают:
. Записывают:  .
.
Прямую, которая пересекает данную прямую и не перпендикулярна к ней, называют наклонной. Точку пересечения наклонной к прямой с этой прямой называют основанием наклонной.
Например, на рисунке 8.12 прямая  – наклонная к прямой
– наклонная к прямой  (и к
(и к  ). Точка
). Точка  – основание наклонной
– основание наклонной  к прямой
к прямой  .
.
Через точку, не принадлежащую прямой, можно провести единственную прямую, перпендикулярную этой прямой, и бесчисленное множество прямых, которые пересекают эту прямую и образуют с ней непрямые углы.
Например, на рисунке 8.13 через точку  проведены наклонные
проведены наклонные  и
и  к прямой
к прямой  .
.

Из точки, не принадлежащей прямой, можно провести к этой прямой только один перпендикуляр. Точку пересечения перпендикуляра к прямой с этой прямой называют основанием перпендикуляра.
Например, на рисунке 8.14 из точки  к прямой
к прямой  проведен перпендикуляр
проведен перпендикуляр . Точка
. Точка  – основание этого перпендикуляра.
– основание этого перпендикуляра.
Отрезок, соединяющий основания наклонной и перпендикуляра, проведенных из одной точки к прямой, называют проекцией отрезка наклонной на эту прямую.
Расстоянием от точки до прямой называют длину перпендикуляра от данной точки до его основания на данной прямой.
Например, на рисунке 8.15 отрезок  – проекция отрезка наклонной
– проекция отрезка наклонной  к прямой
к прямой  . Расстояние от точки
. Расстояние от точки  до прямой
до прямой  равно длине отрезка
равно длине отрезка  .
.
Серединным перпендикуляром к отрезку называют перпендикуляр, проведенный через середину этого отрезка.
Каждая точка серединного перпендикуляра к отрезку, равноудалена от концов этого отрезка.
Например, на рисунке 8.16  и
и  так как
так как  – серединный перпендикуляр к отрезку
– серединный перпендикуляр к отрезку  .
.
В результате пересечения двух прямых получаем две пары вертикальных углов. Два угла называют вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого. Вертикальные углы равны.
Например, на рисунке 8.17 углы  и
и  , а также углы
, а также углы  и
и 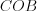 – пары вертикальных углов, причем
– пары вертикальных углов, причем  и
и  .
.

Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Например, на рисунке 8.18 через точки  и
и  прямой
прямой  проведены параллельные прямые
проведены параллельные прямые  и
и  . Так как
. Так как  , то
, то  .
.
Если две прямые  и
и  (рис. 8.19) пересечь третьей прямой
(рис. 8.19) пересечь третьей прямой  (секущей), то получим:
(секущей), то получим:
1) внутренние односторонние углы: 3 и 5, 4 и 6;
2) внутренние накрест лежащие углы: 3 и 6, 4 и 5;
3) соответственные углы: 1 и 5, 2 и 6, 3 и 7, 4 и 8.

Если две параллельные прямые  и
и  (рис. 8.20) пересечь третьей прямой
(рис. 8.20) пересечь третьей прямой  , то:
, то:
1) накрест лежащие углы будут равны ( 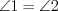 и
и  );
);
2) сумма внутренних односторонних углов будет равна  (
(  и
и  );
);
3) соответственные углы будут равны (например,  ).
).
Признаки параллельности прямых:
1) если прямая с параллельна прямым  и
и  , то прямые
, то прямые  и
и  параллельны;
параллельны;
2) если внутренние накрест лежащие углы прямых  и
и  с секущей
с секущей  равны, или сумма внутренних односторонних углов равна
равны, или сумма внутренних односторонних углов равна  , или соответственные углы равны, то прямые
, или соответственные углы равны, то прямые  и
и  параллельны.
параллельны.
- Учебники
- 4 класс
- Математика 👍
- Моро
- №322

авторы: Моро, Бантова, Бельтюкова.
издательство: Просвещение 2016 год
Раздел:
- ЧАСТЬ 2
- Числа, которые больше 1000
- Деление на двузначное и трехзначное число
- страница 72
Математика 4 класс Моро. Часть 2. Деление на двузначное и трехзначное число. Номер №322
- Предыдущее
- Следующее
Выпиши названия прямых, острых и тупых углов ломаной.


reshalka.com
Математика 4 класс Моро. Часть 2. Деление на двузначное и трехзначное число. Номер №322
Решение
Прямые углы: EMO.
Острые углы: EKD, KDC, DCB, CBA.
Тупые углы: MEK.
- Предыдущее
- Следующее
![]()
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
- Ломаная линия — что это
- Обозначение ломаной линии
- Из чего состоит ломаная линия
- Признак замкнутости
- Как измерить длину ломаной линии
- Чем ломаная линия отличается от прямой
- Примеры ломаных линий в быту
Ломаная линия — определение
Одним из наиболее простых и понятных геометрических терминов считают прямую линию. Есть в математике похожая фигура, но с некоторыми характерными чертами. Давайте попробуем разобраться, что такое ломаная линия и каковы её особенности.
Ломаная линия — математическая фигура, включающая в себя несколько отрезков, которые меняют направление.
Если выражаться более чётко, то это черта, которая не является прямой по всей длине, но может не иметь изгибов на отдельном отрезке.

Таким образом, фигура в обязательном порядке отвечает нескольким признакам:
- состоит из отрезков, которые являются её звеньями;
- конец каждого звена является началом следующего (кроме последнего);
- находящиеся рядом отрезки не могут располагаться на прямой, то есть угол между ними не равен 180 градусам.
Обозначение ломаной линии
Чтобы отметить ломаную линию на чертеже вам необходимо указать наименования точек стыка, в которых она меняет направление, латинскими буквами.
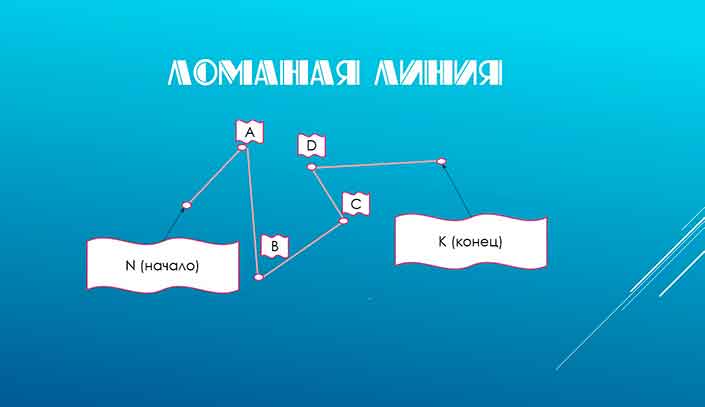
Из чего состоит ломаная линия
Как вы уже успели заметить, на рисунках присутствуют звенья — отрезки, составляющие ломаную линию. А вот начальные и конечные точки этих составных частей — вершины. На картинке вершины ломаной ABCD — позиции A, B, C, D.

Признак замкнутости ломаной линии
Классификация ломаных линий прежде всего осуществляется по свойству замыкания.
Замкнутая ломаная линия — фигура, у которой конечная позиция совпадает с начальной. Иначе говоря, когда она заканчивается в том же месте, где начиналась.
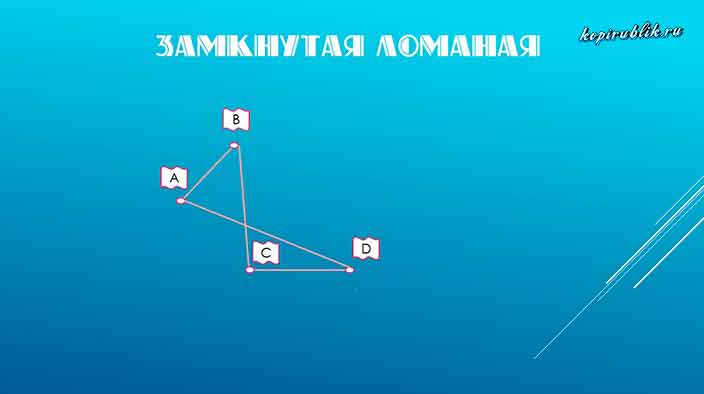
Яркие представители — треугольник и квадрат, а также остальные виды многоугольников:
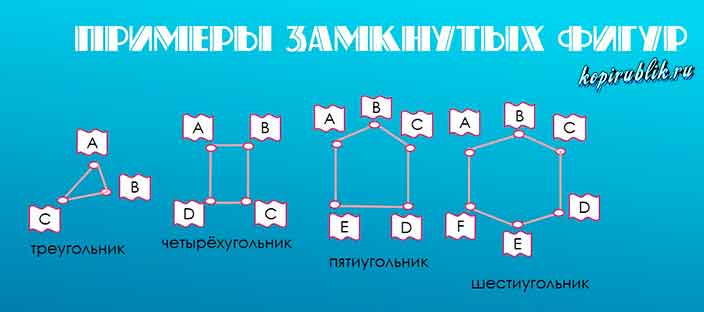
Незамкнутая ломаная линия — фигура, которая приходит в позицию, отличающуюся от начальной.
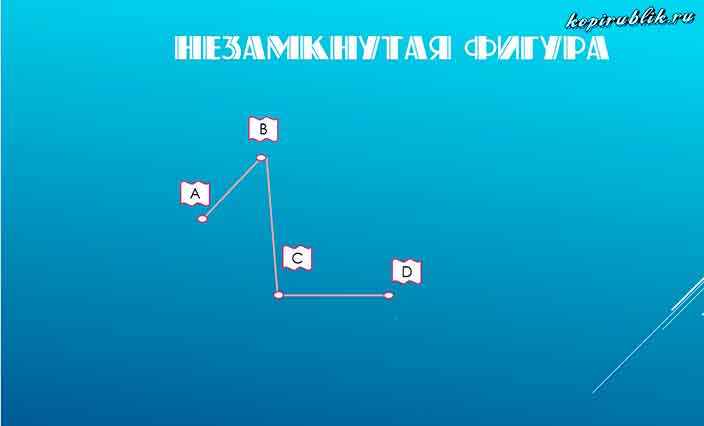
Время от времени, у учащихся возникает вопрос: «Как определить, замкнутая фигура или нет?». Ответ будет весьма прост:»Когда число отрезков равно количеству вершин — она замкнутая, а при наблюдающемся неравенстве — незамкнутая».
В качестве дополнительного вида рассматривают понятие самопересекающаяся ломаная линия — та, которая скрещивается на пути своего следования. Для данного термина не имеет значения сколько раз произошло пересечение.
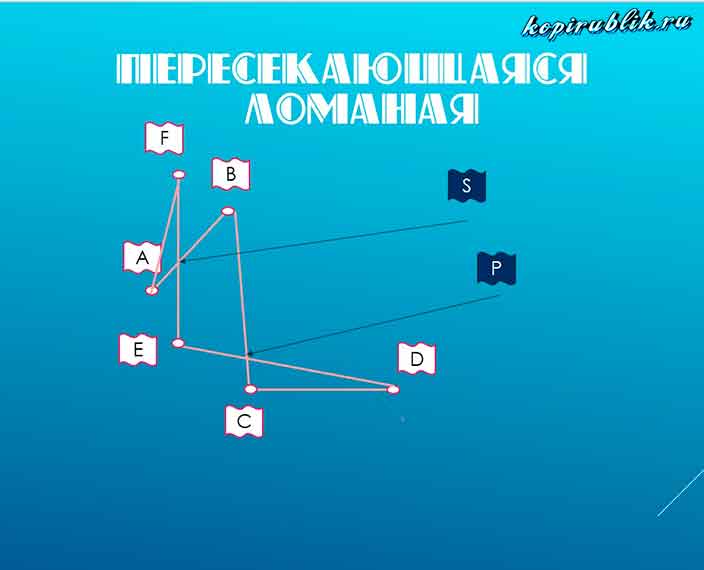
На рисунке отмечены точки пересечения — S, P, а также вершины — A,B,C,D,E,F.
Иногда люди спрашивают — «Могут ли вершины являться точками пересечения?». Чтобы найти ответ, обратите внимание на рисунок с пересекающейся и одновременно замыкающейся — ломаной линией:

Изображение отличается от предыдущего: отрезок EB перемещён, поэтому вершина A приобрела статус точки пересечения.
Как измерить длину ломаной линии
Ломаная линия, имеющая начало и конец, имеет распространённую стандартную характеристику — длину. Имея цель сделать замер её длины, необходимо суммировать длины всех её составных частей — отрезков.
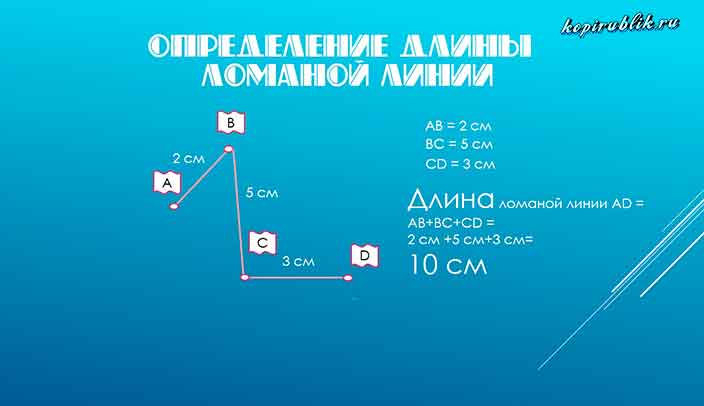
Чем ломаная линия отличается от прямой
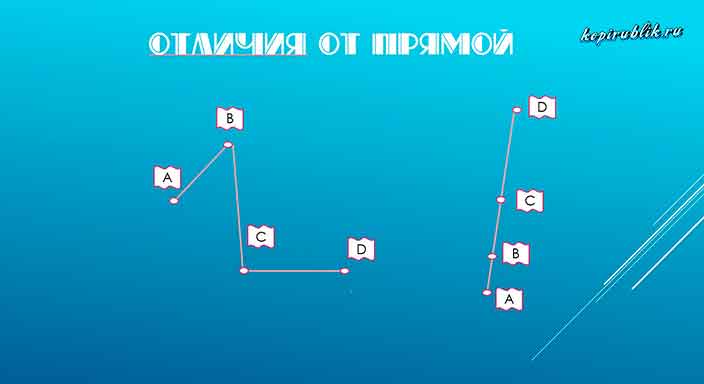
При взгляде на рисунок очевидно: уникальный признак ломаной линии — отсутствие углов, равных 180 градусам. В остальном, фигуры одинаковые и обладают схожими свойствами, например, длиной.
Примеры ломаных линий в быту
В целях наилучшего усвоения теории, разумно на практике ознакомиться с примерами ломаных линий из жизни.
Ломаная линия— график фондового рынка. Так как отрезки графика очень маленькие, поэтому может показаться, что это кривая, но при ближайшем рассмотрении оказывается, что это не так.
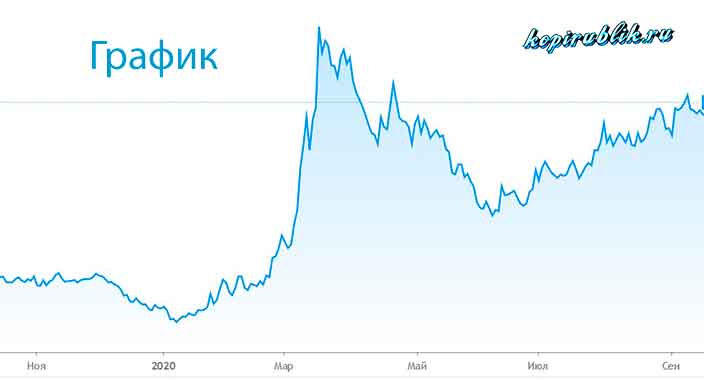
Фасад дома при переводе на «язык геометрии» выглядит как замкнутая ломаная линия.

Пирамиды древнего Египта обладали формой треугольника — одной из самых популярных ломаных линий.

Также рекомендуем прочитать:
Ломаная
Ломаная линия – это геометрическая фигура, состоящая из отрезков,
последовательно соединенных своими концами.
Вершины ломаной – это точки, в
которых соединяются отрезки, образующие ломаную.
Звенья ломаной – это отрезки
ломаной.
Длина ломаной – сумма длин ее звеньев.

3 см + 2 см + 2 см = 7 см
Ответ: длина ломаной 7 см .
Угол. Виды
углов

Ломаная
Ломаная линия – это геометрическая фигура, состоящая из отрезков,
последовательно соединенных своими концами.
Вершины ломаной – это точки, в
которых соединяются отрезки, образующие ломаную.
Звенья ломаной – это отрезки
ломаной.
Длина ломаной – сумма длин ее звеньев.

3 см + 2 см + 2 см = 7 см
Ответ: длина ломаной 7 см .
Угол. Виды
углов

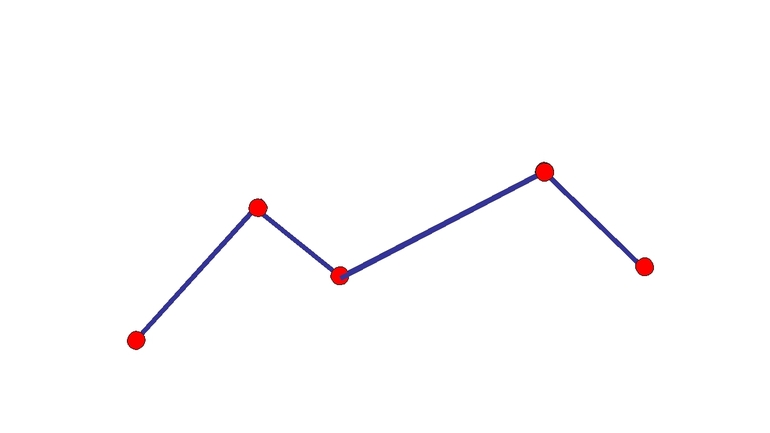
Краткое описание
Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.
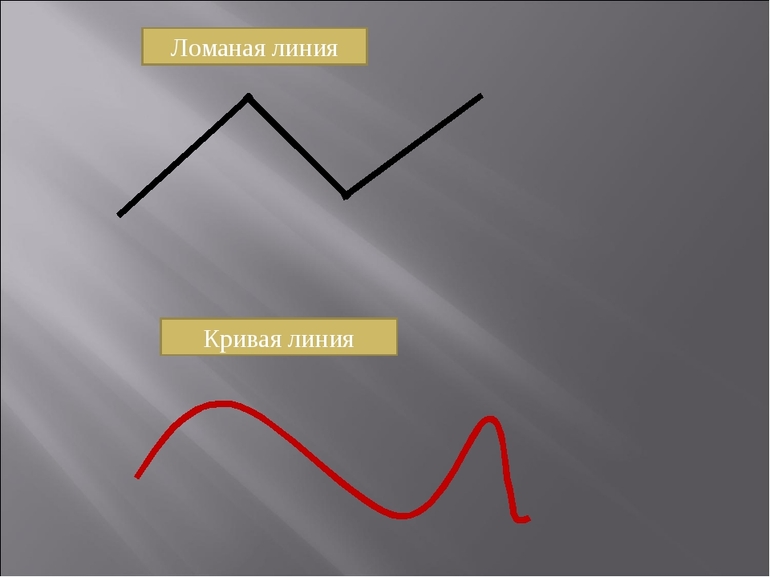
Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.
В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.
Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.
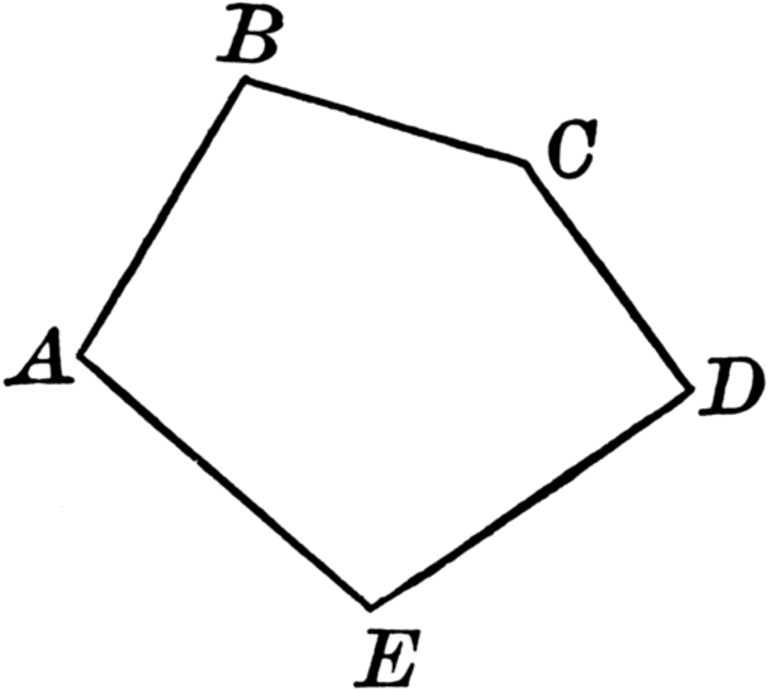
Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.
Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.
Некоторые математические примеры касаются изогнутой линии с самопересечениями (пятиконечная звезда). К этой категории также можно отнести зигзаг, в котором каждый второй отрезок параллелен другому, а последние формируют одинаковый угол.
Математическое определение
Ломанной принято называть ту геометрическую фигуру, которая состоит из обычных отрезков (R1, R2, R3 и R4, Rn-1 Rn). Вершинами изогнутой принято называть точки R1…Rn, а вот все остальные отрезки — это неотъемлемые звенья. Если для любого w действует формула {1, 2, n — 2}, а отрезки не расположены на одной прямой, то такая ломанная будет называться невырожденной. В противном случае придётся иметь дело с вырожденным примером.
Для лучшего усвоения этой темы следует рассмотреть несколько примеров. Изогнутая может иметь самопересечение, но это возможно только в том случае, если минимум два отрезка обладают общей точкой (за исключением вершины).
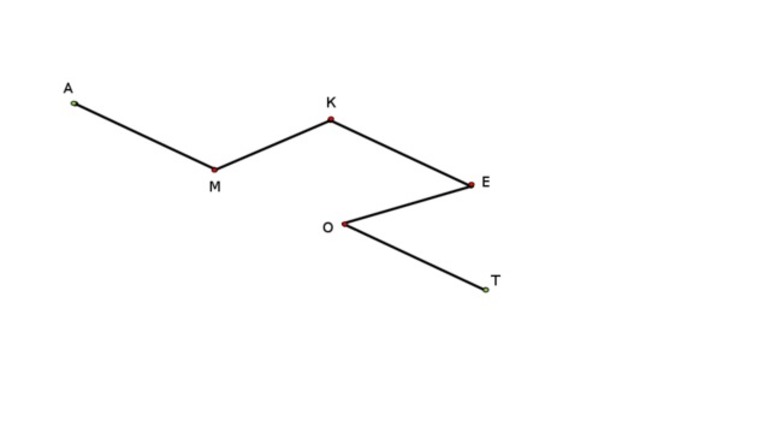
В математике часто можно встретить фигуру, которая является обычной ломаной линией. В этом случае практикуется применение следующей записи: R1R2R3R4R5R6. Если ученику предстоит разобраться со всеми нюансами построения замкнутой ломаной из трёх звеньев и более, тогда ему понадобятся вспомогательные отрезки (к примеру: R1, R2, а также Rn -1 Rn, которые не должны лежать на одной прямой).
Замкнутую плоскую ломаную линию принято называть многоугольником. Если рассматривать многогранники, то все стороны фигуры будут называться рёбрами. Учителя России предпочитают создавать краткосрочное планирование по этой теме, так как в этом случае можно донести больше полезной информации до учеников.
Гораздо проще разобраться с изгибами зигзага, так как они используются в швейном деле, в распространённом декоративном оформлении предметов обихода в качестве орнамента. Стоит отметить, что изогнутая линия нашла широкое применение в различных отраслях:
- Архитектура. Изогнутые линии позволяют сооружать интересные номера.
- Картография (тщательное проектирование маршрутов и подробное схематическое изображение всех улиц).
- Химическая отрасль (различные соединения и своеобразные молекулярные структуры).
- Востребованный дизайн ландшафтов (утончённое оформление, расположение дорожек).
- Медицина (мониторы для наблюдения за сердечным ритмом).
- Метод освоения каллиграфических навыков в китайском языке.
Изучение этой темы в математике является обязательным, так как от этого зависит качество усвоения материала учеником.
Основные разновидности ломаных
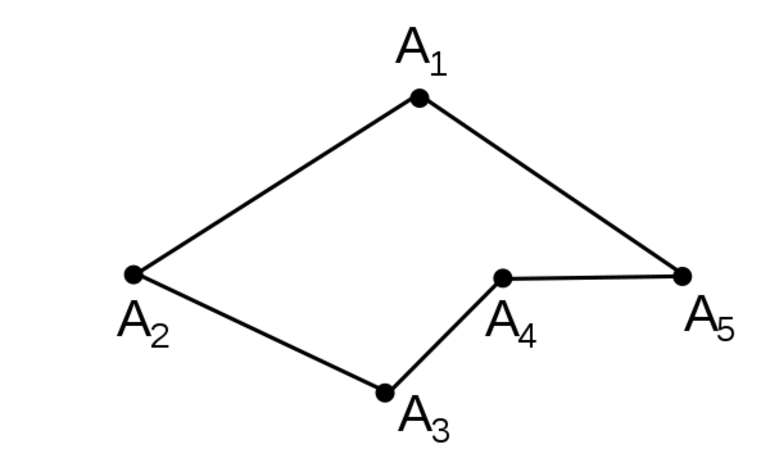
Геометрическая фигура может быть построена совершенно по любому из действующих методов. Специалисты выделяют замкнутую, а также незамкнутую ломанную. Повышенное внимание уделяют самопересекающимся, непересекающимся линиям. Классическая замкнутая ломаная является многоугольником. В математике самопересекающейся принято называть ту линию, отрезки которой имеют минимум одно пересечение. По своей структуре ломаная может быть весьма разнообразной, из-за чего нужно внимательно относиться ко всем аспектам.
В начальных классах школы принято рассматривать следующий пример: ломаная включает в себя сразу пять звеньев либо сторон: ZX, XC, CV, VB, BN. Та точка, где неизбежно соединяются два звена, называется вершиной. В этом случае имеется сразу четыре вершины: X, С, V, B.
Повышенное внимание нужно уделить изучению звена ломаной. Звеньями эксперты привыкли называть стороны либо отрезки, из которых образована линия. Всего одно такое звено может быть рассмотрено только в качестве отрезка. А вот для построения ломаной необходимо задействовать как минимум два звена. Вершины — это классические точки, которые представляют собой концы одних отрезков ломаной. Обозначить точки можно только латинскими буквами.
Пример замкнутой, а также традиционной незамкнутой ломаной линии, которую часто можно встретить в геометрии и алгебре:
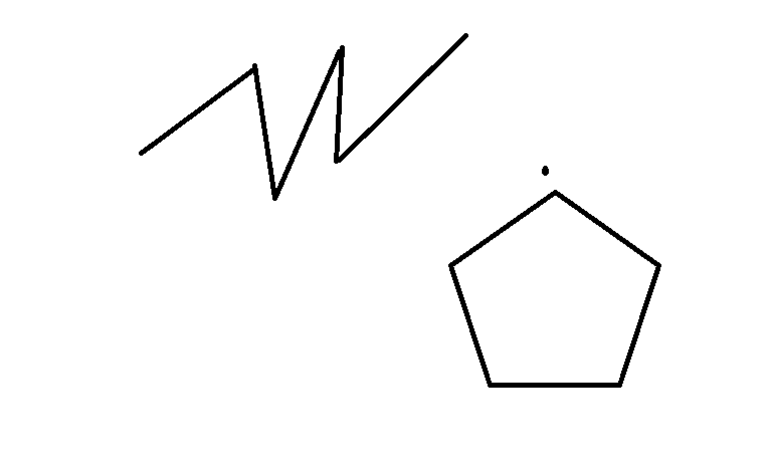
Если необходимо определить точную длину ломаной, то для этого следует поочерёдно сложить все известные данные задействованных звеньев (ZX + XC + CV + VB + BN).
Базовые понятия
Чтобы гарантировано освоить все правила, которые касаются использования изогнутой линии в математике, необходимо разобраться со звеньями. Существует ряд нюансов, которые можно сопоставить с элементарной геометрической конструкцией. Линию формируют отдельные отрезки, которые в математике называются звеньями. Если все концы ломаной соединяются в одной точке, то такая фигура будет называться замкнутой.
Все задействованные звенья могут обладать взаимными пересечениями. Вершинами специалисты привыкли называть точки соединения отрезков. О многоугольнике можно говорить только в том случае, если звенья не пересекаются между собой. Звено обозначают сразу двумя латинскими буквами. Каждая вершина изогнутой линии может обозначаться только одной буквой. Только тщательное изучение всех правил и нюансов позволит правильно решать математические задачи.
Особенности построения многоугольников
В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.
Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.
Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.
Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:
- Элементарные разносторонние. В этом случае каждая следующая сторона отличается своей длиной.
- Равносторонние. Абсолютно все стороны обладают идентичной длиной.
- Специфические остроугольные. Сформированные углы имеют острую форму.
- Универсальные равнобедренные. Сразу две стороны из трёх существующих обладают одинаковой длиной.
- Тупоугольные. Фигура обладает одним тупым углом.
- Традиционные прямоугольные. Нарисованная фигура должна иметь минимум один прямой угол.
Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.
Ключевые нюансы
Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.
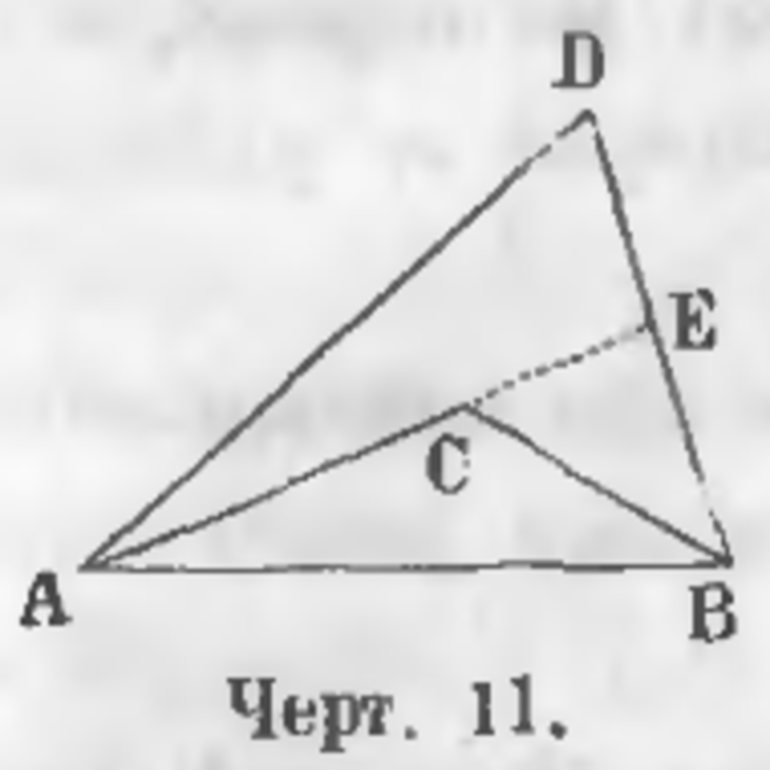
По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.
Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:
- SW+ WE + ET > SF + FT.
- WE + ET = WT.
Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.
Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.
Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.

