Подробно о генераторах случайных и псевдослучайных чисел
Время на прочтение
11 мин
Количество просмотров 292K
На Хабре и в сети часто начали появляться статьи, посвященные уязвимостям генераторов случайных чисел. Данная тема крайне обширна и является одной из основных в криптографии. Под катом находится описание случайных чисел от A до Z. Статья является результатом свободного перевода цикла статей из одного западного блога и личных дополнений автора. Основная цель — получить feedback и поделиться знаниями.

Введение
Генераторы случайных чисел — ключевая часть веб-безопасности. Небольшой список применений:
- Генераторы сессий (PHPSESSID)
- Генерация текста для капчи
- Шифрование
- Генерация соли для хранения паролей в необратимом виде
- Генератор паролей
- Порядок раздачи карт в интернет казино
Как отличить случайную последовательность чисел от неслучайной?
Пусть есть последовательность чисел: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9. Является ли она случайной? Есть строгое определение для случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Но оно не помогает ответить на наш вопрос, так как нам не хватает информации для ответа. Теперь скажем, что данные числа получились набором одной из верхних строк клавиатуры. «Конечно не случайная» — воскликните Вы и тут же назовете следующие число и будете абсолютно правы. Последовательность будет случайной только если между символами, нету зависимости. Например, если бы данные символы появились в результате вытягивания бочонков в лото, то последовательность была бы случайной.
Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.
Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)
Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.
Уязвимости ГПСЧ
- Предсказуемая зависимость между числами.
- Предсказуемое начальное значение генератора.
- Малая длина периода генерируемой последовательности случайных чисел, после которой генератор зацикливается.
Линейный конгруэнтный ГПСЧ (LCPRNG)
Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
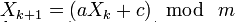
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.
Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].
Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений

Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.
Предсказание результатов линейно-конгруэнтного метода
Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.
public static int a = 45;
public static int c = 21;
public static int m = 67;
public static int seed = 2;
public static int getRand() {
seed = (a * seed + c) % m;
return seed;
}
public static void main(String[] args) {
for(int i=0; i<30; i++)
System.out.println(getRand());
}
Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.
Взлом встроенного генератора случайных чисел в Java
Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы
private static final long multiplier = 0x5DEECE66DL; // 25214903917
private static final long addend = 0xBL; // 11
private static final long mask = (1L << 48) - 1; // 281474976710655 = 2^48 – 1
Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)
protected int next(int bits) {
long oldseed, nextseed;
AtomicLong seed = this.seed;
do {
oldseed = seed.get();
nextseed = (oldseed * multiplier + addend) & mask;
} while (!seed.compareAndSet(oldseed, nextseed));
return (int)(nextseed >>> (48 - bits));
}
Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).
Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:
((x1*multiplier + addend) & mask) << 16
до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так
import java.lang.reflect.Field;
import java.util.Random;
import java.util.concurrent.atomic.AtomicLong;
public class PasswordCracking {
public static final long multiplier = 0x5DEECE66DL;
public static final long addend = 0xBL;
public static final long mask = (1L << 48) - 1;
public static void main(String[] args) {
Random random = new Random();
long v1 = random.nextInt();
long v2 = random.nextInt();
long v3 = random.nextInt();
long v4 = random.nextInt();
System.out.println("v1=" + v1 + "nv2=" + v2 + "nv3=" + v3 + "nv4=" + v4);
// brute-force seed
for (int i = 0; i < 65536; i++) {
long seed = (((long) v1) << 16) + i;
int nextInt = (int)(((seed * multiplier + addend) & mask) >>> 16);
if (nextInt == v2) {
System.out.println("Seed found: " + seed);
Random crackingRandom = new Random();
try {
/* set the seed for Random to be convinced that we have found the
right seed because constructor Random (long seed) uses the
private static long initialScramble (long seed) {
return (seed ^ multiplier) & mask;
}
for simplicity will use Reflection */
Field privateSeedField = Random.class.getDeclaredField("seed");
privateSeedField.setAccessible(true);
AtomicLong crackingSeed = (AtomicLong)privateSeedField.get(crackingRandom);
crackingSeed.set(seed);
}catch(Exception e) {
System.out.println(e.toString());
System.exit(1);
}
long cv1 = crackingRandom.nextInt();
long cv2 = crackingRandom.nextInt();
long cv3 = crackingRandom.nextInt();
long cv4 = crackingRandom.nextInt();
System.out.println("Set fiend seed and generate random numbers");
System.out.println("cv1=" + cv1 + "ncv2=" + cv2 + "ncv3=" + cv3 + "ncv4=" + cv4);
break;
}
}
}
}
Вывод данной программы будет примерно таким:
v1 = -1184958941
v2 = 274285127
v3 = -1566774765
v4 = 30466408
Seed found: -77657469128792
Set fiend seed and generate random numbers
cv1 = 274285127
cv2 = -1566774765
cv3 = 30466408
cv4 = -803980434
Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.
public static long getPreviousSeed(long prevSeed) {
long seed = prevSeed;
// reverse the addend from the seed
seed -= addend; // reverse the addend
long result = 0;
// iterate through the seeds bits
for (int i = 0; i < 48; i++) {
long mask = 1L << i;
// find the next bit
long bit = seed & mask;
// add it to the result
result |= bit;
if (bit == mask) {
// if the bit was 1, subtract its effects from the seed
seed -= multiplier << i;
}
}
System.out.println("Previous seed: " + result);
return result;
}
И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));
И всё, мы успешно взломали ГПСЧ в Java.
Взлом ГПСЧ Mersenne twister в PHP
Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.
Содержимое файла /ext/standard/basic_functions.h
#define MT_N (624)
/* rand.c */
php_uint32 state[MT_N+1]; /* state vector + 1 extra to not violate ANSI C */
php_uint32 *next; /* next random value is computed from here */
int left; /* can *next++ this many times before reloading */
unsigned int rand_seed; /* Seed for rand(), in ts version */
zend_bool rand_is_seeded; /* Whether rand() has been seeded */
zend_bool mt_rand_is_seeded; /* Whether mt_rand() has been seeded */
Содержимое файла /ext/standard/rand.c:
#define N MT_N /* length of state vector */
#define M (397) /* a period parameter */
#define hiBit(u) ((u) & 0x80000000U) /* mask all but highest bit of u */
#define loBit(u) ((u) & 0x00000001U) /* mask all but lowest bit of u */
#define loBits(u) ((u) & 0x7FFFFFFFU) /* mask the highest bit of u */
#define mixBits(u, v) (hiBit(u)|loBits(v)) /* move hi bit of u to hi bit of v */
#define twist(m,u,v) (m ^ (mixBits(u,v)>>1) ^ ((php_uint32)(-(php_int32)(loBit(u))) & 0x9908b0dfU))
/* {{{ php_mt_reload
*/
static inline void php_mt_reload(TSRMLS_D)
{
/* Generate N new values in state
Made clearer and faster by Matthew Bellew (matthew.bellew@home.com) */
register php_uint32 *state = BG(state);
register php_uint32 *p = state;
register int i;
for (i = N - M; i--; ++p)
*p = twist(p[M], p[0], p[1]);
for (i = M; --i; ++p)
*p = twist(p[M-N], p[0], p[1]);
*p = twist(p[M-N], p[0], state[0]);
BG(left) = N;
BG(next) = state;
}
/* }}} */
/* {{{ php_mt_initialize
*/
static inline void php_mt_initialize(php_uint32 seed, php_uint32 *state)
{
/* Initialize generator state with seed
See Knuth TAOCP Vol 2, 3rd Ed, p.106 for multiplier.
In previous versions, most significant bits (MSBs) of the seed affect
only MSBs of the state array. Modified 9 Jan 2002 by Makoto Matsumoto. */
register php_uint32 *s = state;
register php_uint32 *r = state;
register int i = 1;
*s++ = seed & 0xffffffffU;
for( ; i < N; ++i ) {
*s++ = ( 1812433253U * ( *r ^ (*r >> 30) ) + i ) & 0xffffffffU;
r++;
}
}
/* }}} */
/* {{{ php_mt_srand
*/
PHPAPI void php_mt_srand(php_uint32 seed TSRMLS_DC)
{
/* Seed the generator with a simple uint32 */
php_mt_initialize(seed, BG(state));
php_mt_reload(TSRMLS_C);
/* Seed only once */
BG(mt_rand_is_seeded) = 1;
}
/* }}} */
/* {{{ php_mt_rand
*/
PHPAPI php_uint32 php_mt_rand(TSRMLS_D)
{
/* Pull a 32-bit integer from the generator state
Every other access function simply transforms the numbers extracted here */
register php_uint32 s1;
if (BG(left) == 0) {
php_mt_reload(TSRMLS_C);
}
--BG(left);
s1 = *BG(next)++;
s1 ^= (s1 >> 11);
s1 ^= (s1 << 7) & 0x9d2c5680U;
s1 ^= (s1 << 15) & 0xefc60000U;
return ( s1 ^ (s1 >> 18) );
}
Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:
10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor
public static long unBitshiftRightXor(long value, long shift) {
// we part of the value we are up to (with a width of shift bits)
long i = 0;
// we accumulate the result here
long result = 0;
// iterate until we've done the full 32 bits
while (i * shift < 32) {
// create a mask for this part
long partMask = (-1 << (32 - shift)) >>> (shift * i);
// obtain the part
long part = value & partMask;
// unapply the xor from the next part of the integer
value ^= part >>> shift;
// add the part to the result
result |= part;
i++;
}
return result;
}
public static long unBitshiftLeftXor(long value, long shift, long mask) {
// we part of the value we are up to (with a width of shift bits)
long i = 0;
// we accumulate the result here
long result = 0;
// iterate until we've done the full 32 bits
while (i * shift < 32) {
// create a mask for this part
long partMask = (-1 >>> (32 - shift)) << (shift * i);
// obtain the part
long part = value & partMask;
// unapply the xor from the next part of the integer
value ^= (part << shift) & mask;
// add the part to the result
result |= part;
i++;
}
return result;
}
Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так
long value = output;
value = unBitshiftRightXor(value, 18);
value = unBitshiftLeftXor(value, 15, 0xefc60000);
value = unBitshiftLeftXor(value, 7, 0x9d2c5680);
value = unBitshiftRightXor(value, 11);
Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.
Область для взлома
Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.
Задание распределения для генератора псевдослучайных чисел
Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.
Треугольное распределение
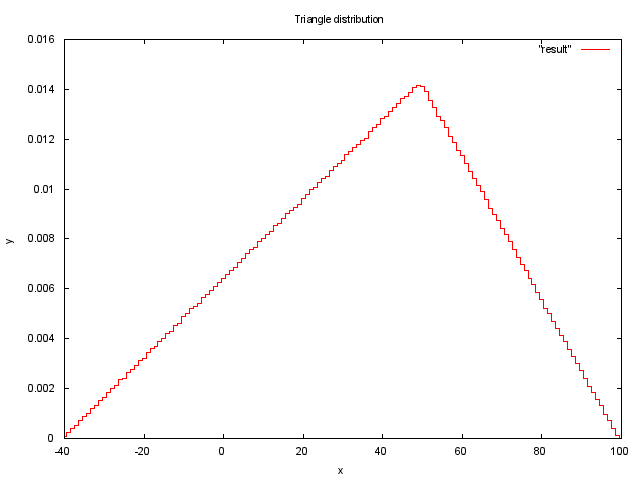
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.
double triangular(double a, double b, double c) {
double U = rand() / (double) RAND_MAX;
double F = (c - a) / (b - a);
if (U <= F)
return a + sqrt(U * (b - a) * (c - a));
else
return b - sqrt((1 - U) * (b - a) * (b - c));
}
В данном случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для параметров a = -40, b = 100, c = 50 график 10000000 измерений будет выглядеть так
Экспоненциальное распределение
Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно заметить, что выражение под знаком логарифма в последней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).
Тесты ГПСЧ
Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.
Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.
В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.
Известные взломы генераторов случайных чисел
- Ранние версии протокола шифрования SSL компании Netscape, c малой энтропией [11]
- Уязвимость PHP сессий habrahabr.ru/company/pt/blog/149746
- CryptGenRandom компании Microsoft [12]
- Многие онлайн казино не раз становились объектом атаки через уязвимости в ГПСЧ
Список литературы
[1] Дональд Кнут, Искусство программирования (Том 2. Получисленные алгоритмы)
[2] Брюс Шнайер, Прикладная криптография(Глава 16)
[4] www.staff.uni-mainz.de/pommeren/Kryptologie/Bitstrom/2_Analyse/LCGcrack.html
[5] www.staff.uni-mainz.de/pommeren/Kryptologie99/English.html
[6] en.wikipedia.org/wiki/Mersenne_twister
[7] en.wikipedia.org/wiki/Triangular_distribution
[8] ru.wikipedia.org/wiki/Линейный_конгруэнтный_метод
[9] zaic101.ru/files/728/using_linear_congruential_generators_for_cryptographic_purposes.pdf
[10] www.cacert.at/random
[11] www.cs.berkeley.edu/~daw/papers/ddj-netscape.html
[12] www.computerworld.com/s/article/9048438/Microsoft_confirms_that_XP_contains_random_number_generator_bug
[13] Описан интересный пример генерации через md5 raz0r.name/articles/magiya-sluchajnyx-chisel-chast-2/comment-page-1
Оригинал
jazzy.id.au/default/2010/09/20/cracking_random_number_generators_part_1.html
jazzy.id.au/default/2010/09/21/cracking_random_number_generators_part_2.html
jazzy.id.au/default/2010/09/22/cracking_random_number_generators_part_3.html
jazzy.id.au/default/2010/09/25/cracking_random_number_generators_part_4.html
Для работы проектов iXBT.com нужны файлы cookie и сервисы аналитики.
Продолжая посещать сайты проектов вы соглашаетесь с нашей
Политикой в отношении файлов cookie
Подбрасывая монетку, можно быть уверенным, что шансы выпадения орла и решки одинаковы. Но можно зайти на сайт с генерацией рандомных чисел или скачать приложение на телефон, в котором будет возможность имитировать бросок монетки. Однако будет ли в таком случае результат действительно случайным, или же программа подберет число/результат, который заранее был известен?
В большинстве случаев результат не будет действительно случайным, он будет получен алгоритмом, выдающим последовательность чисел близкую к случайной. Подобных алгоритмов очень много, и все они используют различные формулы, однако они все зацикливаются и могут выдать ограниченное количество цепочек “случайных” чисел.

Хорошим и простым примером будет один из самых ранних алгоритмов для генерации псевдослучайных чисел. Например, трехзначное число возводится в квадрат, затем из середины квадрата числа берётся трехзначное число, которое и становится результатом. А производя подобные вычисления несколько раз подряд, получается цепочка псевдослучайных чисел. Выглядит это так: допустим начальное значение 111, в таком случае 111² = 12321, получаем результат 232, после чего повторяем процедуру — 232² = 53824 и результатом становится 382. Чтобы подбор чисел не был постоянно одинаковым, важно чтобы начальное значение было разным при запуске алгоритма. Так, например, программы могут брать начальное значение исходя из даты и времени, когда был запущен алгоритм/приложение.
Большинство игр, приложений и сайтов используют именно генераторы псевдослучайных чисел, поскольку это значительно проще в реализации, а результат может быть получен мгновенно и без подключения к сети. Однако предсказуемость подобного генератора совершенно не подходит для использования его в целях шифрования данных. Тут на помощь приходит генератор истинно случайных чисел.
Простейшим истинным генератором случайных чисел является игральный кубик. Однако создать большой массив данных кидая кубик едва ли получится, а чтобы узнать результат даже одного броска, требуется время. Поэтому современные генераторы случайных чисел используют данные, полученные измерением различных физических процессов. Например, используют шум в электрических цепях, атмосферный шум, космическое излучение, колебания электромагнитного поля вакуума или шум радиоактивного распада атомов. Полученные данные являются абсолютно случайными и никак не могут быть предсказаны.

Недостатком подобноных генераторов является относительно медленная скорость выдачи результата, все же передача данных занимает больше времени, чем получение результата путем расчета по алгоритму. Однако уверенность в получении случайного числа важна во многих сферах. Но несмотря на сложность генераторов случайных чисел ими может воспользоваться каждый. Есть большое количество сайтов предоставляющих такую возможность (обычно, если сайт использует генератор истинно случайных чисел, то об этом есть информация).
Сейчас на главной
Новости
Публикации

OPPO
Enco
Free3
— успешное продолжение популярной линейки с привнесением новых фишек: 12,4-мм излучатели
из бамбукового волокна, Bluetooth 5.3, пространственный звук (собственная…

Выбор электроники, используемой
во время занятий спортом, широк и разнообразен. Представленные модели есть на
любой вкус и кошелек. Есть бренды, уже зарекомендовавшие себя как по
функционалу, так…

То, о чем говорили в 2020 году, стало реальностью: Октябрьскую радиобашню в Москве сносят. Несколько дней назад проезжала мимо по МЦК, увидела в окне кочерыжку, выскочила из поезда и догуляла до…

Нравится оно кому-то или нет, но биометрическая
система оплаты проезда в московском транспорте продолжает распространяться на
всё новые маршруты. В частности, с сегодняшнего дня (то есть…

Порядок в салоне авто, особенно в водительской зоне, будет не только эстетически приятен во время поездки, но и позволит значительно повысить комфорт и даже безопасность за рулем. Например,…

Polaris PVCS 7090 — новый флагман швейцарской компании. Пылесос стоит ожидаемо дорого (от 20 до 24 тыс. руб.), но при этом предлагает огромный комплект аксессуаров — в этот…
Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно дискретному равномерному).
Современная информатика широко использует псевдослучайные числа в самых разных приложениях — от метода Монте-Карло и имитационного моделирования до криптографии. При этом от качества используемых ГПСЧ напрямую зависит качество получаемых результатов. Это обстоятельство подчёркивает известный афоризм математика ORNL Роберта Кавью (англ.) (рус.: «генерация случайных чисел слишком важна, чтобы оставлять её на волю случая».
Источники случайных чисел[править | править код]
Источники настоящих случайных чисел найти крайне трудно. Физические шумы[1], такие, как детекторы событий ионизирующей радиации, дробовой шум в резисторе или космическое излучение[2], могут быть такими источниками. Однако применяются такие устройства в приложениях сетевой безопасности редко. Сложности также вызывают грубые атаки на подобные устройства.
У физических источников случайных чисел существует ряд недостатков:
- Время и трудозатраты при установке и настройке по сравнению с программными ГПСЧ;
- Дороговизна;
- Генерация случайных чисел происходит медленнее, чем при программной реализации ГПСЧ;
- Невозможность воспроизведения ранее сгенерированной последовательности случайных чисел.[3]
В то же время случайные числа, получаемые из физического источника, могут использоваться в качестве порождающего элемента (англ. seed) для программных ГПСЧ. Такие комбинированные генераторы применяются в криптографии, лотереях, игровых автоматах.[3]
Качественные требования, предъявляемые к ГПСЧ[править | править код]
Ранние подходы к формированию ПСЧ[править | править код]
Джон фон Нейман считал неприемлемым использование физических генераторов случайных чисел в вычислительной технике, так как при возникновении необходимости проверки вычислений повтор предыдущих действий требовал бы воспроизведение случайного числа, в то время как генерация нового случайного числа недопустима. Предварительная запись и хранение сгенерированных случайных чисел предполагало бы возможность их считывания. Механизм считывания данных являлся одним из самых слабых звеньев вычислительных машин 1940-х годов. Джон фон Нейман привёл следующий метод «середины квадрата» (англ. middle-square method)[4] получения десятизначных псевдослучайных чисел:
- Десятизначное число возводится в квадрат, затем из середины квадрата числа берётся десятизначное число, которое снова возводится в квадрат, и так далее.
Например, для 4-значных чисел, начиная с 1234, получаем 



В 1951 году Д. Г. Лемер предложил линейный конгруэнтный метод,[5] суть которого заключается в задании последовательности целых чисел рекурсивной формулой 





Детерминированные ГПСЧ[править | править код]
Алгоритм[править | править код]
Большинство детерминированных ГПСЧ соответствуют структуре, предложенной П. Лекуером [1] в 1994 году: 






















Наиболее распространены линейный конгруэнтный метод, метод Фибоначчи с запаздываниями, регистр сдвига с линейной обратной связью, регистр сдвига с обобщённой обратной связью.
Из современных ГПСЧ широкое распространение также получил «вихрь Мерсенна», предложенный в 1997 году Мацумото и Нисимурой. Его достоинствами являются колоссальный период (219937−1), равномерное распределение в 623 измерениях (линейный конгруэнтный метод даёт более или менее равномерное распределение максимум в 5 измерениях), быстрая генерация случайных чисел (в 2-3 раза быстрее, чем стандартные ГПСЧ, использующие линейный конгруэнтный метод). Однако существуют алгоритмы, распознающие последовательность, порождаемую вихрем Мерсенна, как неслучайную.
Генератор псевдослучайных чисел включён в состав многих современных процессоров, например, RdRand входит в набор инструкций IA-32.[6]
Разновидностью ГПСЧ являются ГПСБ (PRBG) — генераторы псевдо-случайных бит, а также различных поточных шифров.
Список генераторов псевдослучайных чисел[править | править код]
Ниже приведен список генераторов, которые исторически отметились в области изучения процесса генерации псевдослучайных чисел, либо благодаря своей исторической значимости, либо благодаря тому, что были инновационной моделью для своих эпох. Более того, несмотря на то, что это ГПСЧ, некоторые из них могут быть применимы в области криптографии.
| Алгоритм | Авторы | Ссылки | Описание | |
|---|---|---|---|---|
| Mid-Square | Джон Фон Нейман | 1946 | [7] | ГПСЧ, который считается низкокачественным, но имеет большое историческое значение, поскольку является одним из первых алгоритмов. |
| Lehmer генератор / Линейный конгруэнтный метод | D. H. Lehmer | 1951 | [8] | Также известен как метод мультипликативных линейных конгруэнций и имеет большое влияние в этой области исследований. Он также известен как линейный конгруэнтный метод, основа которого со временем усовершенствовалась. |
| Генератор Фибоначчи с запаздыванием | G. J. Mitchell; D. P. Moore | 1958 | [9] | Очень влиятельный алгоритм в области изучения процессов генерации случайных чисел, вдохновивший других последующих великих авторов, таких как G. Marsaglia создатель теста на качество случайных чисел под названием “Diehard”, например. |
| Регистр сдвига с линейной обратной связью (LFSR) / Генератор Tausworthe | R. C. Tausworthe | 1965 | [10] | Генератор, конструкция которого повлияла на многие другие последующие ГПСЧ. Поэтому очень исторически важен. Также известен как генератор Таusworthe. |
| Wichmann & Hill генератор | B. A. Wichmann; D. I. Hill | 1982 | [11] | Комбинация из трех небольших LCG, подходящих для 16-битных процессоров. Широко используется во многих программах, например, он использовался в Excel 2003 и некоторых более поздних версиях для функции RAND в Excel и был генератором по умолчанию в языке Python до версии 2.2. |
| Rule 30 | Вольфрам, Стивен | 1983 | [12] | Генератор на основе клеточных автоматов. |
| Генератор Blum-Blum-Shub | Блюм, Мануэль; L. Blum; M. Shub | 1986 | [13] | Считается одним из самых безопасных генераторов с криптографической точки зрения, в основном благодаря внедрению в его формулу исследований и концепций, взятых из теории чисел. За этот алгоритм Блюм, Мануэль был удостоен премии Алана Тьюринга 1995 года. |
| Park-Miller генератор | S. K. Park; K. W. Miller | 1988 | [14] | Конкретная реализация генератора Лемера, широко используемая, поскольку она включена в C++ в виде функции minstd_rand0, начиная с C++11. |
| ACORN | R. S. Wikramaratna | 1989 | [15] | Его название происходит от английского акронима ACORN, который расшифровывается как ″Аддитивное конгруэнтное случайное число″. |
| MIXMAX | G. K. Savvidy; N. G. Ter-Arutyunyan-Savvidy | 1991 | [16] | Это генератор, принадлежащий к классу матричных конгруэнтных линейных генераторов, обобщение метода линейных конгруэнций. Логика семейства генераторов MIXMAX основана на результатах эргодической теории и классической механики. |
| Add-with-carry | G. Marsaglia | 1991 | [17] | Модификация генераторов Фибоначчи с запаздыванием. |
| Subtract-with-borrow | G. Marsaglia; A. Zaman | 1991 | [17] | Алгоритм, полученный на основе генераторов Фибоначчи с запаздыванием. |
| ISAAC | R. J. Jenkins Jr. | 1993 | [18] | Генератор криптографически защищенных криптографических данных (CSPRNG), разработанный Робертом Дж. Дженкинсом. |
| Вихрь Мерсенна (Mersenne Twister, MT | M. Matsumoto; T. Nishimura | 1996 | [19] | Это, вероятно, самый известный генератор в этом списке, в основном потому, что это алгоритм, реализованный в функции RAND языков программирования Python и R, в дополнение к его сильному присутствию в электронных играх, таких как Pro Evolution Soccer (PES). |
| Xorshift | G. Marsaglia | 2003 | [20] | Это очень быстрый подтип генераторов LFSR. Марсалья также предложил в качестве улучшения генератор xorwow, в котором выход генератора xorshift суммируется с последовательностью Вейля. Генератор xorwow является генератором по умолчанию в библиотеке CURAND интерфейса прикладного программирования nVidia CUDA для графических процессоров. |
| Алгоритм Fortuna | Шнайер, Брюс; Нильс Фергюсон | 2003 | [21] | Алгоритм считается криптографически безопасным. CSPRNG, хорошо известный тем, что был внедрен в системы и продукты Apple. |
| Well equidistributed long-period linear (WELL) | F. Panneton; P. L’Ecuyer; M. Matsumoto | 2006 | [22] | Алгоритм, известный как дополнение к Mersenne Twister (MT), намеренно стремящийся скрыть его слабые стороны. |
| Усовершенствованная система рандомизации (ARS) | J. Salmon; M. Moraes; R. Dror; D. Shaw | 2011 | [23] | Упрощенная версия блочного шифра AES, обеспечивающая очень высокую производительность на системе, поддерживающей AES-NI. |
| Threefry | J. Salmon, M. Moraes, R. Dror and D. Shaw | 2011 | [23] | Упрощенная версия блочного шифра Threefish, подходящая для реализации на GPU. |
| Philox (Филокс) | J. Salmon, M. Moraes, R. Dror and D. Shaw | 2011 | [23] | Упрощение и модификация блочного шифра Threefish с добавлением S-box. |
| Пермутированный конгруэнциальный генератор (PCG) | M. E. O’Neill | 2014 | [24] | Модель, полученная с помощью линейного конгруэнтного метода. |
| Генератор битов случайного цикла (RCB) | R. Cookman | 2016 | [25] | RCB описывается как генератор битовых шаблонов, созданный для преодоления некоторых недостатков Вихрь Мерсенна (MT) и ограничения короткого периода/длины бита генераторов сдвигов/модулей. |
| Middle Square Weyl Sequence RNG | B. Widynski | 2017 | [26] | Разновидность оригинального метода средних квадратов Джона фон Неймана. |
| Xoroshiro128+ | D. Blackman; S. Vigna | 2018 | [27] | Модификация генератора Xorshift Г. Марсальи, одного из самых быстрых генераторов на современных 64-битных процессорах. Родственными генераторами являются xoroshiro128**, xoshiro256+ и xoshiro256***. |
| 64-bit MELG (MELG-64) | S. Harase; T. Kimoto | 2018 | [28] | Реализация 64-битных линейных генераторов F2 с первичным периодом Мерсенна. |
| Squares RNG | B. Widynski | 2020 | [29] | Основанная на счетчике версия Middle Square Weyl Sequence RNG. По конструкции похож на Philox, но работает значительно быстрее. |
| Itamaracá (Ita) | D. H. Pereira | 2021 | [30] | Известен как первый алгоритм PRNG, основанный на функции абсолютного значения. Itamaracá также является простой и быстрой моделью, которая генерирует апериодические последовательности случайных чисел. |
Одноразовый блокнот[править | править код]
Альтернативным решением является создание набора из большого количества случайных чисел и опубликование его в некотором словаре, называемом «одноразовым блокнотом». Тем не менее, и такие наборы обеспечивают очень ограниченный источник чисел по сравнению с тем количеством, которое требуется приложениям сетевой безопасности. Хотя данные наборы действительно обеспечивают статистическую случайность, они недостаточно безопасны, так как злоумышленник может получить копию словаря.
Недостатки ГПСЧ[править | править код]
Никакой детерминированный алгоритм не может генерировать полностью случайные числа, он может только аппроксимировать некоторые их свойства. Как сказал Джон фон Нейман, «всякий, кто питает слабость к арифметическим методам получения случайных чисел, грешен вне всяких сомнений».
Любой ГПСЧ с ограниченными ресурсами рано или поздно зацикливается — начинает повторять одну и ту же последовательность чисел. Длина циклов ГПСЧ зависит от самого генератора и составляет около 


Большинство простых арифметических генераторов хотя и обладают большой скоростью, но страдают от многих серьёзных недостатков:
- Слишком короткий период/периоды.
- Последовательные значения не являются независимыми.
- Некоторые биты «менее случайны», чем другие.
- Неравномерное одномерное распределение.
- Обратимость.
В частности, алгоритм RANDU, десятилетиями использовавшийся на мейнфреймах, оказался очень плохим[32][33], что вызвало сомнения в достоверности результатов многих исследований, использовавших этот алгоритм.
ГПСЧ с источником энтропии или ГСЧ[править | править код]
Наравне с существующей необходимостью генерировать легко воспроизводимые последовательности случайных чисел, также существует необходимость генерировать совершенно непредсказуемые или попросту абсолютно случайные числа. Такие генераторы называются генераторами случайных чисел (ГСЧ — англ. random number generator, RNG). Так как такие генераторы чаще всего применяются для генерации уникальных симметричных и асимметричных ключей для шифрования, они чаще всего строятся из комбинации криптостойкого ГПСЧ и внешнего источника энтропии (и именно такую комбинацию теперь и принято понимать под ГСЧ).
Почти все крупные производители микрочипов поставляют аппаратные ГСЧ с различными источниками энтропии, используя различные методы для их очистки от неизбежной предсказуемости. Однако на данный момент скорость сбора случайных чисел всеми существующими микрочипами (несколько тысяч бит в секунду) не соответствует быстродействию современных процессоров.
В современных исследованиях осуществляются попытки использования измерения физических свойств объектов (например, температуры) или даже квантовых флуктуаций вакуума в качестве источника энтропии для ГСЧ.[34]
В персональных компьютерах авторы программных ГСЧ используют гораздо более быстрые источники энтропии, такие, как шум звуковой карты или счётчик тактов процессора. Сбор энтропии являлся наиболее уязвимым местом ГСЧ. Эта проблема до сих пор полностью не разрешена во многих устройствах (например, смарт-картах), которые таким образом остаются уязвимыми.[35] Многие ГСЧ используют традиционные испытанные, хотя и медленные, методы сбора энтропии вроде измерения реакции пользователя (движение мыши и т. п.), как, например, в PGP и Yarrow[36], или взаимодействия между потоками, как, например, в Java SecureRandom.
Пример простейшего ГСЧ с источником энтропии[править | править код]
Если в качестве источника энтропии использовать текущее время, то для получения целого числа от 0 до N достаточно вычислить остаток от деления текущего времени в миллисекундах на число N+1. Недостатком этого ГСЧ является то, что в течение одной миллисекунды он выдаёт одно и то же число.
Примеры ГСЧ и источников энтропии[править | править код]
| Источник энтропии | ГПСЧ | Достоинства | Недостатки | |
|---|---|---|---|---|
| /dev/random в UNIX/Linux | Счётчик тактов процессора, однако собирается только во время аппаратных прерываний | РСЛОС, с хешированием выхода через SHA-1 | Есть во всех Unix, надёжный источник энтропии | Очень долго «нагревается», может надолго «застревать», либо работает как ГПСЧ (/dev/urandom) |
| Yarrow от Брюса Шнайера[36] | Традиционные методы | AES-256 и SHA-1 маленького внутреннего состояния | Гибкий криптостойкий дизайн | Медленный |
| Microsoft CryptoAPI | Текущее время, размер жёсткого диска, размер свободной памяти, номер процесса и NETBIOS-имя компьютера | MD5-хеш внутреннего состояния размером в 128 бит | Встроен в Windows, не «застревает» | Сильно зависит от используемого криптопровайдера (CSP). |
| Java SecureRandom | Взаимодействие между потоками | SHA-1-хеш внутреннего состояния (1024 бит) | Большое внутреннее состояние | Медленный сбор энтропии |
| RdRand от intel[37] | Шумы токов | Построение ПСЧ на основе «случайного» битового считывания значений от токов[37] | Очень быстр, не «застревает» | Оригинальная разработка, свойства приведены только по утверждению разработчиков. |
ГПСЧ в криптографии[править | править код]
Одним из критериев того, что ГПСЧ криптографически стойкий, является невозможность отличить выходные значения ГПСЧ от независимой равномерно распределенной на промежутке 



























Криптографические приложения используют для генерации случайных чисел детерминированные алгоритмы, следовательно, генерируют последовательность чисел, которая теоретически не может быть статистически случайной. В то же время, если выбрать хороший алгоритм, полученная численная последовательность — псевдослучайных чисел — будет проходить большинство тестов на случайность. Одной из характеристик такой последовательности является большой период повторения.[3]
Примерами известных криптостойких ГПСЧ являются RC4[31], ISAAC[38], SEAL[39], SNOW[40], совсем медленный теоретический алгоритм Блюм — Блюма — Шуба[31], а также счётчики с криптографическими хеш-функциями или криптостойкими блочными шифрами вместо функции вывода[31].
Также к криптографически стойким шифрам относятся генераторы с несколькими регистрами сдвига, генераторы с нелинейными преобразованиями, мажоритарные генераторы шифрования A5/x.[31]
Примеры криптостойких ГПСЧ[править | править код]
Циклическое шифрование[править | править код]
Происходит шифрование случайных чисел генератора с помощью различных секретных ключей 


- В момент инициализации генерируется секретный ключ
и константа
.
должен быть случайным и используется только для данного генератора.
- На каждой стадии происходит следующее:
Псевдослучайная последовательность, полученная по данной схеме, имеет полный период: каждое выходное значение 







ANSI X9.17[править | править код]
ГПСЧ из стандарта ANSI X9.17 используется во многих приложениях финансовой безопасности и PGP. В основе этого ГПСЧ лежит тройной DES. Генератор ANSI X9.17 состоит из следующих частей:
- В момент инициализации генерируется секретный ключ
. Он должен быть случайным и используется только для данного генератора.
- На каждой стадии происходит следующее:
Входными случайными значениями являются 







Аппаратные ГПСЧ[править | править код]
Кроме устаревших, хорошо известных РСЛОС-генераторов, широко применявшихся в качестве аппаратных ГПСЧ в XX веке, очень мало известно о современных аппаратных ГПСЧ, так как большинство из них разработано для военных целей или запатентованы и держатся в секрете. Аппаратно реализуемые РСЛОС-генераторы Toyocrypt и LILI-128, были взломаны с помощью алгебраических атак[43][44].
В настоящее время известно о применении аппаратных ГПСЧ, реализуемых на основе маломощных шумов в электросхемах.[45]
Применение ГПСЧ в лотереях[править | править код]
Генератор случайных номеров для лотерей — аппаратно-программный комплекс, применяющийся в розыгрышах, в которых необходимо угадывать комбинацию из определенного количества чисел. Любое из возможных чисел имеет одинаковую вероятность появления.
Попытки создать генератор случайных чисел относятся к 3500 году до н. э. и связаны с древнеегипетской настольной игрой Сенет. В Сенете два игрока играют за две стороны. Ходы определяются с помощью 4 плоских палочек, что и может считаться генератором случайных чисел того времени. Бросают все четыре палочки сразу. Подсчёт очков происходит следующим образом: 1 палочка упала белой стороной вверх — 1 очко и дополнительный бросок; 2 — 2 очка; 3 — 3 очка, 4 — 4 и дополнительный бросок. Одна из сторон палочки чёрная и, если все четыре палочки падали чёрной стороной вверх — это максимальный результат — 5 очков и дополнительный бросок.
Известный генератор случайных чисел ERNIE применялся на протяжении многих лет для определения выигрышных номеров британской лотереи.
Основные требования к программному обеспечению и оборудованию, используемому для проведения розыгрышей в Российской Федерации, устанавливаются Федеральным законом от 11.11.2003 № 138-ФЗ «О лотереях»:
- Технические характеристики лотерейного оборудования должны обеспечивать случайность распределения выигрышей при розыгрыше призового фонда тиражных лотерей.
- Не должны использоваться процедуры, реализующие алгоритмы, которые позволяли бы предопределять результат розыгрыша призового фонда до начала такого розыгрыша.
- Лотерейное оборудование, используемое при проведении тиражной лотереи, должно обеспечивать защиту информации от утраты, хищения, искажения, несанкционированных действий по её уничтожению, модификации, копированию и иных подобных действий и несанкционированного доступа по сети передачи данных.[46]
В российских государственных лотереях («Гослото „5 из 36“», «Гослото „6 из 36“», «Гослото „6 из 45“», «Гослото „7 из 49“», «Гослото „4 из 20“», «Спортлото „6 из 49“»)[47] для определения победителей используются самозаряжающиеся лототроны. Трансляция розыгрышей ведется в прямом эфире.[48]
В российских государственных лотереях («Рапидо», «Кено-Спортлото», «Топ-3», «12/24», «Всё по сто») для определения победителей используется генератор случайных чисел — аппаратно-программный комплекс, сертифицированный АНО «МИЦ» и отвечающий рекомендациям ФГУП ВНИИМС. Аппарат формирует непрерывный поток случайных шумов, которые преобразуются в числа. В заданный момент времени из потока выхватываются текущие значения, которые и являются выигрышной лотерейной комбинацией.[49]
В 2015 году бывшему директору по безопасности US Multi-State Lottery Association после выигрыша в 16.5 млн долларов, имевшему доступ к программному обеспечению, используемому при розыгрышах лотерей, было предъявлено обвинение в использовании специальных алгоритмов, позволяющих определять выигрышную комбинацию лотереи в течение нескольких дней в году.[50]
См. также[править | править код]
- Случайное простое число
- Регистр сдвига с обратной связью по переносу
- Тестирование псевдослучайных последовательностей
- Тест на следующий бит
- Генератор Макларена — Марсальи
- РСЛОС
- Аппаратный генератор случайных чисел
- Криптографически стойкий генератор псевдослучайных чисел
- Источник энтропии
- Алгоритм Зиккурат
- Псевдослучайная функция Наора — Рейнгольда
- Экстрактор случайности
Примечания[править | править код]
- ↑ N.G. Bardis, A.P. Markovskyi, N. Doukas, N. V. Karadimas. True Random Number Generation Based on Environmental Noise Measurements for Military Applications // Proceedings of the 8th WSEAS International Conference on SIGNAL PROCESSING, ROBOTICS and AUTOMATION. — 2009. — С. 68—73. — ISBN 978-960-474-054-3. — ISSN 1790-5117. Архивировано 30 августа 2017 года.
- ↑ Random.org. Дата обращения: 19 ноября 2017. Архивировано 24 февраля 2011 года.
- ↑ 1 2 3 4 5 6 L’Ecuyer, Pierre. Random Number Generation // Springer Handbooks of Computational Statistics : Глава. — 2007. — С. 93—137. — doi:10.1002/9780470172445.ch4. Архивировано 1 декабря 2017 года.
- ↑ Von Neumann, John. Various techniques used in connection with random digits // National Bureau of Standards Applied Mathematics Series. — 1951. — № 12. — С. 36—38. Архивировано 6 ноября 2020 года.
- ↑ Lehmer, D.H. Mathematical Methods in Large-Scale Computing Units // Ann, Comput Lab. Harvard Univ.. — 1951. — Vol. 26. — С. 141—146. (недоступная ссылка)
- ↑ Intel Digital Random Number Generator (DRNG): Software Implementation Guide, Revision 1.1 (PDF). Intel Corporation (7 августа 2012). Дата обращения: 25 ноября 2012. Архивировано 18 мая 2013 года.
- ↑ National Bureau of Standards. Annual report 1951 National Bureau of Standards.
- ↑ J. H. Curtiss. A Symposium of Large Scale Digital Calculating Machinery // Mathematical Tables and Other Aids to Computation. — 1947-04. — Т. 2, вып. 18. — С. 229. — doi:10.2307/2002294. Архивировано 11 мая 2022 года.
- ↑ J. W. Wrench. Table errata: The art of computer programming, Vol. 2: Seminumerical algorithms (Addison-Wesley, Reading, Mass., 1969) by Donald E. Knuth (англ.) // Mathematics of Computation. — 1970. — Vol. 24, iss. 110. — P. 504. — ISSN 1088-6842 0025-5718, 1088-6842. — doi:10.1090/S0025-5718-1970-0400642-2.
- ↑ Robert C. Tausworthe. Random numbers generated by linear recurrence modulo two (англ.) // Mathematics of Computation. — 1965. — Vol. 19, iss. 90. — P. 201–209. — ISSN 1088-6842 0025-5718, 1088-6842. — doi:10.1090/S0025-5718-1965-0184406-1.
- ↑ B. A. Wichmann, I. D. Hill. Algorithm AS 183: An Efficient and Portable Pseudo-Random Number Generator // Journal of the Royal Statistical Society. Series C (Applied Statistics). — 1982. — Т. 31, вып. 2. — С. 188–190. — ISSN 0035-9254. — doi:10.2307/2347988. Архивировано 11 мая 2022 года.
- ↑ Stephen Wolfram. Statistical mechanics of cellular automata // Reviews of Modern Physics. — 1983-07-01. — Т. 55, вып. 3. — С. 601–644. — doi:10.1103/RevModPhys.55.601.
- ↑ L. Blum, M. Blum, M. Shub. A Simple Unpredictable Pseudo-Random Number Generator // SIAM Journal on Computing. — 1986-05-01. — Т. 15, вып. 2. — С. 364–383. — ISSN 0097-5397. — doi:10.1137/0215025. Архивировано 27 апреля 2022 года.
- ↑ S. K. Park, K. W. Miller. Random number generators: good ones are hard to find // Communications of the ACM. — 1988-10-01. — Т. 31, вып. 10. — С. 1192–1201. — ISSN 0001-0782. — doi:10.1145/63039.63042.
- ↑ R.S. Wikramaratna. ACORN—A new method for generating sequences of uniformly distributed Pseudo-random Numbers // Journal of Computational Physics. — 1989-07. — Т. 83, вып. 1. — С. 16–31. — ISSN 0021-9991. — doi:10.1016/0021-9991(89)90221-0.
- ↑ G. K Savvidy, N. G Ter-Arutyunyan-Savvidy. On the Monte Carlo simulation of physical systems (англ.) // Journal of Computational Physics. — 1991-12-01. — Vol. 97, iss. 2. — P. 566–572. — ISSN 0021-9991. — doi:10.1016/0021-9991(91)90015-D. Архивировано 11 мая 2022 года.
- ↑ 1 2 George Marsaglia, Arif Zaman. A New Class of Random Number Generators // The Annals of Applied Probability. — 1991-08. — Т. 1, вып. 3. — С. 462–480. — ISSN 2168-8737 1050-5164, 2168-8737. — doi:10.1214/aoap/1177005878. Архивировано 19 апреля 2022 года.
- ↑ ISAAC, a fast cryptographic random number generator. www.burtleburtle.net. Дата обращения: 17 мая 2022.
- ↑ Makoto Matsumoto, Takuji Nishimura. Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator // ACM Transactions on Modeling and Computer Simulation. — 1998-01-01. — Т. 8, вып. 1. — С. 3–30. — ISSN 1049-3301. — doi:10.1145/272991.272995.
- ↑ George Marsaglia. Xorshift RNGs (англ.) // Journal of Statistical Software. — 2003-07-04. — Vol. 8. — P. 1–6. — ISSN 1548-7660. — doi:10.18637/jss.v008.i14.
- ↑ Источники книг — Википедия. ru.wikipedia.org. Дата обращения: 17 мая 2022. Архивировано 24 апреля 2022 года.
- ↑ François Panneton, Pierre L’Ecuyer, Makoto Matsumoto. Improved long-period generators based on linear recurrences modulo 2 // ACM Transactions on Mathematical Software. — 2006-03-01. — Т. 32, вып. 1. — С. 1–16. — ISSN 0098-3500. — doi:10.1145/1132973.1132974.
- ↑ 1 2 3 John K. Salmon, Mark A. Moraes, Ron O. Dror, David E. Shaw. Parallel random numbers: as easy as 1, 2, 3 // Proceedings of 2011 International Conference for High Performance Computing, Networking, Storage and Analysis. — New York, NY, USA: Association for Computing Machinery, 2011-11-12. — С. 1–12. — ISBN 978-1-4503-0771-0. — doi:10.1145/2063384.2063405.
- ↑ B.G. Sileshi, C. Ferrer, J. Oliver. Accelerating hardware Gaussian random number generation using Ziggurat and CORDIC algorithms // 2014 IEEE SENSORS. — 2014-11. — С. 2122–2125. — doi:10.1109/ICSENS.2014.6985457. Архивировано 17 мая 2022 года.
- ↑ Random Bit Generator // SpringerReference. — Berlin/Heidelberg: Springer-Verlag.
- ↑ Bernard Widynski. Middle-Square Weyl Sequence RNG // arXiv:1704.00358 [cs]. — 2022-03-20. Архивировано 17 мая 2022 года.
- ↑ David Blackman, Sebastiano Vigna. Scrambled Linear Pseudorandom Number Generators // arXiv:1805.01407 [cs]. — 2022-03-28. Архивировано 11 мая 2022 года.
- ↑ Shin Harase, Takamitsu Kimoto. Implementing 64-bit Maximally Equidistributed F2-Linear Generators with Mersenne Prime Period // ACM Transactions on Mathematical Software. — 2018-01-03. — Т. 44, вып. 3. — С. 30:1–30:11. — ISSN 0098-3500. — doi:10.1145/3159444.
- ↑ Bernard Widynski. Squares: A Fast Counter-Based RNG // arXiv:2004.06278 [cs]. — 2022-03-13. Архивировано 11 мая 2022 года.
- ↑ Daniel Henrique Pereira. Itamaracá: A Novel Simple Way to Generate Pseudo-random Numbers (англ.). — 2022-01-25. — doi:10.33774/coe-2022-zsw6t. Архивировано 27 апреля 2022 года.
- ↑ 1 2 3 4 5 Габидулин Э. М., Кшевецкий А. С., Колыбельников А. И., Владимиров С. М. Защита информации. Учебное пособие. — С. 100—113. Архивная копия от 24 ноября 2020 на Wayback Machine
- ↑ Дональд Кнут. Глава 3.3. Спектральный критерий // Искусство программирования. Указ. соч. — С. 129—130.
- ↑ William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. — 2nd ed. — Cambridge University Press, 1992. — P. 277. — ISBN 0-521-43108-5.
- ↑ Из квантового вакуума получили случайные числа. Дата обращения: 18 апреля 2012. Архивировано 19 апреля 2012 года.
- ↑ Jovan Dj. Goli ́c. Cryptanalytic Attacks on MIFARE Classic Protocol // Topics in Cryptology – CT-RSA 2013. — Springer, Berlin, Heidelberg, 2013. — № 7779. — С. 239—259. — doi:10.1007/978-3-642-36095-4_16.
- ↑ 1 2 Yarrow. Дата обращения: 10 сентября 2004. Архивировано 8 ноября 2012 года.
- ↑ 1 2 Intel DRNG Software Implementation Guide. Intel. Дата обращения: 8 декабря 2017. Архивировано 21 апреля 2016 года.
- ↑ J.-P. Aumasson. On the pseudo-random generator ISAAC // Cryptology ePrint Archive. — 2006. Архивировано 8 сентября 2016 года.
- ↑ H. Chen, K. Laine, R. Player. [https://eprint.iacr.org/2017/224.pdf Simple Encrypted Arithmetic Library – SEAL
v2.1] // Cryptology ePrint Archive. — 2017. Архивировано 10 июля 2017 года. - ↑ A. Kircanski and A. M. Youssef. [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.301.2615&rep=rep1&type=pdf On the Sliding Property of SNOW 3G and
SNOW 2.0] // Information Security, IET. — 2010. — № 5(4). — С. 199—206. Архивировано 16 декабря 2017 года. - ↑ Лапонина О. Р. Алгоритмы симметричного шифрования. НОУ ИНТУИТ. Дата обращения: 8 декабря 2017. Архивировано 9 декабря 2017 года.
- ↑ Kelsey J., Schneier B., Wagner D., Hall C. Cryptanalytic Attacks on Pseudorandom Number Generators // Fast Software Encryption. FSE 1998. Lecture Notes in Computer Science. — Springer, Berlin, Heidelberg, 1998. — Vol. 1372. — doi:10.1007/3-540-69710-1_12. Архивировано 7 декабря 2017 года.
- ↑ N. T. Courtois. Higher Order Correlation Attacks, XL Algorithm and Cryptanalysis of Toyocrypt // Cryptology ePrint Archive. — 2002. Архивировано 29 марта 2017 года.
- ↑ Ed Dawson, Andrew Clark, J Golic, W Millan, L Penna. The LILI-128 Keystream Generator. — 2000-12-13. Архивировано 16 декабря 2017 года.
- ↑ C. S. Petrie, J. A. Connelly. A noise-based IC random number generator for applications in cryptography // IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. — May 2000. — Vol. 47, № 5. — С. 615–621. — ISSN 1057-7122. — doi:10.1109/81.847868.
- ↑ Статья 12.1. Требования к лотерейному оборудованию и лотерейным терминалам. Дата обращения: 6 декабря 2017. Архивировано 6 декабря 2017 года.
- ↑ Ответы на вопросы о «Столото». Сто Лото. Дата обращения: 6 декабря 2017. Архивировано 6 декабря 2017 года.
- ↑ Трансляции розыгрышей государственных лотерей. Сто Лото. Дата обращения: 6 декабря 2017. Архивировано 6 декабря 2017 года.
- ↑ Генератор случайных чисел. Сто Лото. Дата обращения: 6 декабря 2017. Архивировано 6 декабря 2017 года.
- ↑ Man hacked random-number generator to rig lotteries, investigators say, The Guardian. Архивировано 23 декабря 2017 года. Дата обращения: 6 декабря 2017.
Литература[править | править код]
- Дональд Э. Кнут. Глава 3. Случайные числа // Искусство программирования = The Art of Computer Programming. — 3-е изд. — М.: Вильямс, 2000. — Т. 2. Получисленные алгоритмы. — 832 с. — 7000 экз. — ISBN 5-8459-0081-6 (рус.) ISBN 0-201-89684-2 (англ.).
- Кельтон В., Лоу А. Имитационное моделирование. Классика CS. — 3-е изд.. — СПб.: Питер, 2004. — С. 465, 466. — 487 с. — ISBN 0070592926. — ISBN 5-94723-981-7.
- L’Ecuyer, Pierre. Random Number Generation // Springer Handbooks of Computational Statistics : Глава. — 2007. — С. 93—137. — doi:10.1002/9780470172445.ch4.
Ссылки[править | править код]
- В. А. Успенский. Четыре алгоритмических лица случайности. — МЦНМО, 2006. — 48 с. — ISBN 978-5-94057-485-9.
- Юрий Лифшиц. Лекция 9: Псевдослучайные генераторы // Современные задачи криптографии. — Курс лекций.
- Л. Бараш. Алгоритм AKS проверки чисел на простоту и поиск констант генераторов псевдослучайных чисел // Безопасность информационных технологий. — 2005. — № 2. — С. 27—38. Архивировано 18 октября 2014 года.
- Жельников В. Псевдослучайные последовательности чисел // Криптография от папируса до компьютера. — М.: ABF, 1996. — 335 с. — ISBN 5-87484-054-0.
- Cryptographic Random Numbers (англ.)
- Theory and Practice of Random Number Generation (англ.)
- Zvi Gutterman, Benny Pinkas, Tzachy Reinman. Analysis of the Linux Random Number Generator (англ.)
- A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications (англ.) NIST SP 800-22
Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.
В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.
Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.
Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.
Создание случайных чисел из семени
Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.
Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.
Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.
R(Input) -> Output
Начнём с того, что R – это простая функция, которая всего лишь прибавляет единицу.
R(x) = x + 1
Если значение нашего семени 1, то R создаст ряд 1, 2, 3, 4, … Выглядит совсем не случайно, но мы дойдём до этого. Пусть теперь R добавляет константу вместо 1.
R(x) = x + c
Если с равняется, например, 7, то мы получим ряд 1, 8, 15, 22, … Всё ещё не то. Очевидно, что мы упускаем то, что числа не должны только увеличиваться, они должны быть разбросаны по какому-то диапазону. Нам нужно, чтобы наша последовательность возвращалась в начало – круг из чисел!
Числовой круг
Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.
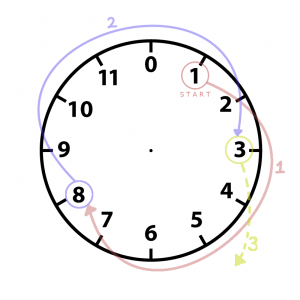
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.
Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.
Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.
R(x) = (x + c) % m
На этом этапе вы можете заметить, что некоторые числа не подходят для c. Если c = 4, и мы начали с 1, наша последовательность была бы 1, 5, 9, 1, 5, 9, 1, 5, 9, … что нам конечно же не подходит, потому что эта последовательность абсолютно не случайная. Становится понятно, что числа, которые мы выбираем для длины цикла и длины прыжка должны быть связаны особым образом.
Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.
До сих пор мы делали “прыжки” за счёт добавления, но что если использовать умножение? Умножим х на константу a.
R(x) = (ax + c) % m
Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:
- (а – 1) должно делиться на все простые множители m
- (а – 1) должно делиться на 4, если m делится на 4
Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.
Выбор семени
Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.
Еще один способ – это получать семя из нового источника каждый раз при запуске программы, как в системных часах. Это пригодится в случае, когда нужно общее рандомное число, как в программе с бросанием кубика.
Конечный результат
Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:
x(n) = (a * x(n - 1) + c) % m
Где начальное значение х – это семя, а – множитель, с – константа, m – оператор остатка от деления.
То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.
В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.
Заключительные замечания
Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.
Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.
На этом всё, спасибо что прочитали!
Оригинал статьи
Источник: Nuances of Programming
Что общего у любителей проходить видеоигры на скорость, азартных игроков и криптографов? Они зависят от случайных чисел. От перетасовки музыки до шифрования интернета, случайные числа — важнейшая часть современной жизни. И мы, как правило, полагаемся на компьютеры, которые генерируют их.
Это заставляет задуматься: как именно компьютеры это делают? Скорее всего, вы когда-либо использовали генератор случайных чисел. Языки программирования очень упрощают это действие. Например, в Ruby достаточно вызвать rand.
На первый взгляд, создание случайных чисел может показаться простым. В конце концов, числа на компьютере — это набор единиц и нулей. Компьютеру просто нужно случайным образом выбрать 1 или 0 и повторить это столько раз, сколько необходимо.
Человеку не составит труда сделать это:
100101011010010110001101
Вот, готово.
Примечание: ведутся споры о том, может ли человек демонстрировать по-настоящему случайное поведение. Но это выходит за рамки данной статьи.
Тем не менее, все еще остается вопрос: как компьютер случайно выбирает между нулем и единицей? Ответ оказывается довольно сложным. Он коренится в таких темах, как рекурсивные алгоритмы, компьютерное оборудование и немного — теория хаоса.
Если это звучит для вас интересно, тогда погрузимся глубже.
Как компьютеры генерируют случайные числа?
Простой ответ на этот вопрос заключается в том, что они не могут. По крайней мере, не сами по себе.
Люди создали компьютеры, чтобы они были тем, чем не являемся мы, — полностью логическими машинами. Случайность не в их природе. В конце концов, вы же не хотите, чтобы сервер спонтанно решил не следовать логике приложения.
По своей сути компьютеры — простые машины, которые принимают данные и выдают их обратно. Чтобы компьютеры могли генерировать случайные числа, им нужен внешний источник случайности. И этот источник будет варьироваться в зависимости от того, каким генератором случайных чисел вы решите воспользоваться.
Вероятно, последнее предложение вызвало несколько растерянных взглядов. Что подразумевается под “своего рода генератором случайных чисел”? Разве они не все одинаковы?
Не совсем. Существует два основных типа генераторов случайных чисел.
Примечание: далее названия генераторов случайных чисел будут использоваться в сокращении.
Генератор псевдослучайных чисел (ГПСЧ)
Наиболее распространенный тип — генератор псевдослучайных чисел. Он называется псевдослучайным, потому что не создает “по-настоящему” случайных чисел.
Согласно Википедии:
“ГПСЧ — это алгоритмы, которые могут автоматически создавать длинные ряды чисел с хорошими случайными свойствами, но в конечном итоге последовательность повторяется”.
Несмотря на то, что ГПСЧ следуют определенной схеме, эта схема не прослеживается людьми. Поэтому они “достаточно хороши” для большинства случаев, к примеру для видеоигр.
Генераторам псевдослучайных чисел для работы необходимы две составляющие:
- алгоритм генерации случайных чисел;
- семя.
Первоначально в качестве алгоритмов ГПСЧ применялись линейные конгруэнтные генераторы. Это рекурсивные алгоритмы, которые генерируют следующую величину на основе предыдущей. Вот почему этим алгоритмам требуется “семя” (seed) или начальное значение. О семени можно думать как о фрагменте случайности.
Однако со временем на смену линейным конгруэнтным генераторам пришел вихрь Мерсенна, и он по сей день остается самым популярным алгоритмом ГПСЧ.
Хотя псевдослучайные числа на самом деле не случайные, есть множество причин ими пользоваться. Во-первых, они быстры и дешевы в создании. Кроме того, поскольку ГПСЧ — всего лишь алгоритмы, их можно протестировать и убедиться, что они всегда будут работать правильно.
Вот почему в большинстве, если не во всех, языках программирования случайные числа по умолчанию генерируются именно через ГПСЧ.
Но у генерации псевдослучайных чисел есть и свои недостатки. ГСПЧ работают, потому что случайны для неподготовленного глаза. Однако, если бы вы знали начальное значение для определенной последовательности ГПСЧ, то могли бы предсказать, какие числа будут следующими.
Этой уязвимостью часто пользуются любители ускоренного прохождения видеоигр — они называют это манипулированием ГСЧ. Они заставляют игру работать предсказуемо, чтобы пройти ее как можно быстрее. К счастью, если семя видеоигры будет скомпрометировано, ничего особенного не случится. В этом нет ни вреда, ни зла.
Но бывают случаи, когда предсказание случайных чисел имеет гораздо большее значение. Например, создание ключей безопасности.
Если злоумышленник выяснит исходное значение, используемое для создания ключей RSA в сертификатах TLS, он потенциально может расшифровать сетевой трафик. Это означает, что он сможет получать пароли и другую личную информацию, передаваемую через интернет.
В таких ситуациях нужен более безопасный способ получения случайных чисел.
Генератор истинно случайных чисел (ГИСЧ)
Как вы можете догадаться, истинно случайные числа непредсказуемы и не следуют шаблону.
Но как компьютер может достичь этого? Как было указано ранее, компьютерам требуется внешний источник случайности. В случае ГПСЧ, это было семя. В случае ГИСЧ, это энтропия.
Теория хаоса и термодинамика выходят далеко за рамки данной статьи. Достаточно сказать, что энтропия — это чистый нефильтрованный хаос. И лучший источник этого хаоса — сам компьютер.
Компьютер не может функционировать случайным образом, но составляющие его части — могут. Компьютер — это сложная система со множеством движущихся частей и изменчивостью. Тепловой шум, фотоэффект и другие квантовые явления происходят постоянно.
Компьютерное оборудование — не единственный источник энтропии. Также можно использовать движения мыши и клавиатуры пользователя.
Но хаос был бы бесполезен, если бы его нельзя было обуздать. К счастью, инженеры-аппаратчики придумали, как это сделать. Посредством сложной схемы аппаратных микросхем и компонентов, компьютеры могут преобразовывать этот физический шум в цифровые нули и единицы.
Один из наиболее очевидных вариантов применения ГИСЧ — цифровые азартные игры. Бросание костей, перетасовка карт и вращение колеса рулетки — все это зависит от того, чтобы быть неопределимым. Хотя он часто используется при опросах общественного мнения, призыве на военную службу и отборе присяжных, а также там, где случайность используется как метод справедливости.
В действительности сферы применения ГИСЧ довольно ограничены, поскольку у них есть свой набор недостатков. Во-первых, они медлительны. Хотя это варьируется, ГИСЧ может выдавать только небольшое количество бит в секунду.
Кроме того, ГИСЧ не всегда надежны. Компьютерам требуется достаточное количество энтропии для производства истинно случайных чисел. Но суть случайности в том, что она возникает случайным образом. Простаивающий или новый сервер не сможет генерировать числа настолько же качественно, как активный.
Эта ненадежность создает угрозу безопасности при использовании ГИСЧ для создания криптографических ключей. В 2012 году в исследовательской работе под названием Ron was Wrong, Whit is Right обнаружилось, что тысячи SSL-ключей небезопасны. Хотя основная причина неизвестна, обычно считается, что это результат ошибочной генерации случайных чисел.
Криптографически стойкий генератор псевдослучайных чисел (КСГПЧ)
Из-за недостатков ГИСЧ и ГПСЧ криптографы разработали гибридный подход, называемый криптографически защищенной генерацией псевдослучайных чисел. Этот метод направлен на обеспечение скорости ГПСЧ с гарантией безопасности ГИСЧ.
КСГПЧ прост в теории. В нем применяется высококачественный источник энтропии для получения начального значения, которое дальше вводится в алгоритм, а тот затем выдает безопасные случайные числа.
Проще говоря, он задействует ГИСЧ при создании начального значения для ГПСЧ. Если все сделано правильно, КСГПЧ гарантирует, что начальное значение действительно случайное, и ГПСЧ не может быть скомпрометирован или изменен.
Пример этому — /dev/random в системах Unix и Linux.
Несмотря на преимущества КСГПЧ, здесь, как и везде в технологической отрасли, нельзя гарантировать полную безопасность.
Завершающие мысли
Многие разработчики программного обеспечения не понимают сложности, связанной с генерацией случайных чисел. Это свидетельствует в пользу архитекторов, которые создали существующую систему. От инженеров-аппаратчиков, которые разрабатывали чипы для преобразования шума в данные, до разработчиков ядра и языков программирования, которые преобразовали эти данные в простые для использования API.
Возможно, в следующий раз, когда вы будете играть в видеоигру, слушать музыку в случайном порядке или просто генерировать произвольное число у себя в коде, вы лучше станете понимать волшебство, которое происходит под капотом.
Читайте также:
Читайте нас в Telegram, VK
Перевод статьи Sunny Beatteay: Generating Random Numbers Is a Lot Harder Than You Think





