Загрузить PDF
Загрузить PDF
В двумерном пространстве две прямые пересекаются только в одной точке,[1]
задаваемой координатами (х,y). Так как обе прямые проходят через точку их пересечения, то координаты (х,y) должны удовлетворять обоим уравнениям, которые описывают эти прямые. Воспользовавшись некоторыми дополнительными навыками, вы сможете находить точки пересечения парабол и других квадратичных кривых.
-

1
Запишите уравнение каждой прямой, обособив переменную «у» на левой стороне уравнения. Другие члены уравнения должны размещаться на правой стороне уравнения. Возможно, данное вам уравнение вместо «у» будет содержать переменную f(x) или g(x); в этом случае обособьте такую переменную. Для обособления переменной выполните соответствующие математические операции на обеих сторонах уравнения.
-

2
Приравняйте выражения, расположенные с правой стороны каждого уравнения. Наша задача — найти точку пересечения обеих прямых, то есть точку, координаты (х,у) которой удовлетворяют обоим уравнениям. Так как на левой стороне каждого уравнения находится переменная «у», то выражения, расположенные с правой стороны каждого уравнения, можно приравнять. Запишите новое уравнение.
-

3
Найдите значение переменной «х». Новое уравнение содержит только одну переменную «х». Для нахождения «х» обособьте эту переменную на левой стороне уравнения, выполнив соответствующие математические операции на обеих сторонах уравнения. Вы должны получить уравнение вида х = __ (если это невозможно, перейдите в конец этого раздела).
-

4
Используйте найденное значение переменной «х» для вычисления значения переменной «у». Для этого подставьте найденное значение «х» в уравнение (любое) прямой.
-

5
Проверьте ответ. Для этого подставьте значение «х» в другое уравнение прямой и найдите значение «у». Если вы получите разные значение «у», проверьте правильность ваших вычислений.
-

6
Запишите координаты (х,у). Вычислив значения «х» и «у», вы нашли координаты точки пересечения двух прямых. Запишите координаты точки пересечения в виде (х,у).
-

7
Вычисления в особых случаях. В некоторых случаях значение переменной «х» найти нельзя. Но это не значит, что вы допустили ошибку. Особый случай имеет место при выполнении одного из следующих условий:
Реклама
-

1
Определение квадратичной функции. В квадратичной функции одна или несколько переменных имеют вторую степень (но не выше), например,
или
. Графиками квадратичных функций являются кривые, которые могут не пересекаться или пересекаться в одной или двух точках. В этом разделе мы расскажем вам, как найти точку или точки пересечения квадратичных кривых.
- Если уравнение включает выражение в скобках, раскройте их, чтобы удостовериться, что функция является квадратичной. Например, функция
является квадратичной, так как, раскрыв скобки, вы получите
- Функция, описывающая окружность, включает как
, так и
.[2]
[3]
Если у вас возникли проблемы при решении задач с такой функцией, перейдите в раздел «Советы».
- Если уравнение включает выражение в скобках, раскройте их, чтобы удостовериться, что функция является квадратичной. Например, функция
-

2
Перепишите каждое уравнение, обособив переменную «у» на левой стороне уравнения. Другие члены уравнения должны размещаться на правой стороне уравнения.
-

3
Приравняйте выражения, расположенные с правой стороны каждого уравнения. Так как на левой стороне каждого уравнения находится переменная «у», то выражения, расположенные с правой стороны каждого уравнения, можно приравнять.
-

4
Перенесите все члены полученного уравнения на его левую сторону, а на правой стороне запишите 0. Для этого выполните базовые математические операции. Это позволит вам решить полученное уравнение.
-

5
-

6
Не забудьте про вторую точку пересечения двух графиков. В спешке можно забыть про вторую точку пересечения. Вот как найти координаты «х» двух точек пересечения:
-

7
Графики пересекаются в одной точке или вообще не пересекаются. Такие ситуации имеют место при соблюдении следующих условий:
-

8
Подставьте найденное значение переменной «х» в уравнение (любое) кривой. Так вы найдете значение переменной «у». Если у вас есть два значения переменной «х», проделайте описанный процесс с обоими значениями «х».
-

9
Запишите координаты точки пересечения в виде (х,у). Вычислив значения «х» и «у», вы нашли координаты точки пересечения двух графиков. Если вы определили по два значения «х» и «у», запишите две пары координат, не перепутав соответствующие значения «х» и «у».
Реклама
Советы
- Функция, описывающая окружность, включает как
, так и
. Для нахождения точки (точек) пересечения окружности и прямой вычислите «х», используя линейное уравнение.[4]
Затем подставьте найденное значение «х» в функцию, описывающую окружность, и вы получите простое квадратное уравнение, которое может не иметь решения или иметь одно или два решения. - Окружность и кривая (квадратичная или иная) могут не пересекаться или пересекаться в одной, двух, трех, четырех точках. В этом случае необходимо найти значение x2 (а не «х»), а затем подставить его во вторую функцию. Вычислив «у», вы получите одно или два решения или вообще не получите решений. Теперь подставьте найденное значение «у» в одну из двух функций и найдите значение «х». В этом случае вы получите одно или два решения или вообще не получите решений.
Реклама
Об этой статье
Эту страницу просматривали 94 600 раз.
Была ли эта статья полезной?
Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.
Точка пересечения двух прямых – определение
Необходимо дать определение точкам пересечения двух прямых.
Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.
Определение точки пересечения прямых звучит так:
Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.
Рассмотрим на рисунке, приведенном ниже.
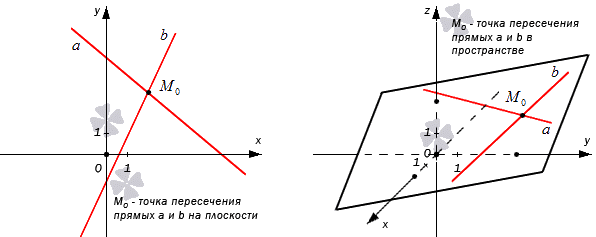
Нахождение координат точки пересечения двух прямых на плоскости
Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.
Если на плоскости имеется система координат Оху, то задаются две прямые a и b. Прямой a соответствует общее уравнение вида A1x+B1y+C1=0, для прямой b – A2x+B2y+C2=0. Тогда M0(x0, y0) является некоторой точкой плоскости необходимо выявить , будет ли точка М0 являться точкой пересечения этих прямых.
Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A1x+B1y+C1=0 и A2x+B2y+C2=0. Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M0(x0, y0) считается их точкой пересечения.
Даны две пересекающиеся прямые 5x-2y-16=0 и 2x-5y-19=0. Будет ли точка М0 с координатами (2,-3) являться точкой пересечения.
Решение
Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что
5·2-2·(-3)-16=0⇔0=02·2-5·(-3)-19=0⇔0=0
Оба равенства верные, значит М0 (2, -3) является точкой пересечения заданных прямых.
Изобразим данное решение на координатной прямой рисунка, приведенного ниже.
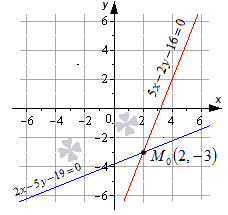
Ответ: заданная точка с координатами (2,-3) будет являться точкой пересечения заданных прямых.
Пересекутся ли прямые 5x+3y-1=0 и 7x-2y+11=0 в точке M0 (2, -3)?
Решение
Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что
5·2+3·(-3)-1=0⇔0=07·2-2·(-3)+11=0⇔31=0
Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7x-2y+11=0. Отсюда имеем, что точка М0 не точка пересечения прямых.
Чертеж наглядно показывает, что М0 – это не точка пересечения прямых. Они имеют общую точку с координатами (-1,2).
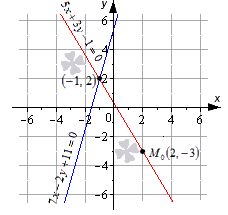
Ответ: точка с координатами (2,-3) не является точкой пересечения заданных прямых.
Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.
Задаются две пересекающиеся прямые a и b уравнениями вида A1x+B1y+C1=0 и A2x+B2y+C2=0, расположенных в Оху. При обозначении точки пересечения М0 получим, что следует продолжить поиск координат по уравнениям A1x+B1y+C1=0 и A2x+B2y+C2=0.
Из определения очевидно, что М0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A1x+B1y+C1=0 и A2x+B2y+C2=0. Иными словами это и есть решение полученной системы A1x+B1y+C1=0A2x+B2y+C2=0.
Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.
Заданы две прямые x-9y+14=0 и 5x-2y-16=0 на плоскости. необходимо найти их пересечение.
Решение
Данные по условию уравнения необходимо собрать в систему, после чего получим x-9y+14=05x-2y-16=0. Чтобы решить его, разрешается первое уравнение относительно x, подставляется выражение во второе:
x-9y+14=05x-2y-16=0⇔x=9y-145x-2y-16=0⇔⇔x=9y-145·9y-14-2y-16=0⇔x=9y-1443y-86=0⇔⇔x=9y-14y=2⇔x=9·2-14y=2⇔x=4y=2
Получившиеся числа являются координатами, которые необходимо было найти.
Ответ: M0 (4, 2) является точкой пересечения прямых x-9y+14=0 и 5x-2y-16=0.
Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.
Определить координаты точек пересечения прямых x-5=y-4-3 и x=4+9·λy=2+λ, λ∈R.
Решение
Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x=4+9·λy=2+λ, λ∈R преобразуется таким образом:
x=4+9·λy=2+λ⇔λ=x-49λ=y-21⇔x-49=y-21⇔⇔1·(x-4)=9·(y-2)⇔x-9y+14=0
После чего беремся за уравнение канонического вида x-5=y-4-3 и преобразуем. Получаем, что
x-5=y-4-3⇔-3·x=-5·y-4⇔3x-5y+20=0
Отсюда имеем, что координаты – это точка пересечения
x-9y+14=03x-5y+20=0⇔x-9y=-143x-5y=-20
Применим метод Крамера для нахождения координат:
∆=1-93-5=1·(-5)-(-9)·3=22∆x=-14-9-20-5=-14·(-5)-(-9)·(-20)=-110⇒x=∆x∆=-11022=-5∆y=1-143-20=1·(-20)-(-14)·3=22⇒y=∆y∆=2222=1
Ответ: M0 (-5, 1).
Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x=x1+ax·λy=y1+ay·λ, λ∈R. Тогда вместо значения x подставляется x=x1+ax·λ и y=y1+ay·λ, где получим λ=λ0, соответствующее точке пересечения, имеющей координаты x1+ax·λ0, y1+ay·λ0.
Определить координаты точки пересечения прямой x=4+9·λy=2+λ, λ∈R и x-5=y-4-3.
Решение
Необходимо выполнить подстановку в x-5=y-4-3 выражением x=4+9·λ, y=2+λ, тогда получим:
4+9·λ-5=2+λ-4-3
При решении получаем, что λ=-1. Отсюда следует, что имеется точка пересечения между прямыми x=4+9·λy=2+λ, λ∈R и x-5=y-4-3. Для вычисления координат необходимо подставить выражение λ=-1 в параметрическое уравнение. Тогда получаем, что x=4+9·(-1)y=2+(-1)⇔x=-5y=1.
Ответ: M0 (-5, 1).
Для полного понимания темы, необходимо знать некоторые нюансы.
Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A1x+B1y+ C1=0A2x+B2+C2=0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.
Даны прямые x3+y-4=1 и y=43x-4. Определить, имеют ли они общую точку.
Решение
Упрощая заданные уравнения, получаем 13x-14y-1=0 и 43x-y-4=0.
Следует собрать уравнения в систему для последующего решения:
13x-14y-1=013x-y-4=0⇔13x-14y=143x-y=4
Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x3+y-4=1 и y=43x-4 определяют одну и ту же прямую. Поэтому нет точек пересечения.
Ответ: заданные уравнения определяют одну и ту же прямую.
Найти координаты точки пересекающихся прямых 2x+(2-3)y+7=0 и 23+2x-7y-1=0.
Решение
По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:
2x+(2-3)y+7=02(3+2)x-7y-1=0⇔2x+(2-3)y=-72(3+2)x-7y=1⇔⇔2x+2-3y=-72(3+2)x-7y+(2x+(2-3)y)·(-(3+2))=1+-7·(-(3+2))⇔⇔2x+(2-3)y=-70=22-72
Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.
Второй способ решения.
Для начала нужно определить наличие пересечения прямых.
n1→=(2, 2-3) является нормальным вектором прямой 2x+(2-3)y+7=0, тогда вектор n2→=(2(3+2), -7 – нормальный вектор для прямой 23+2x-7y-1=0.
Необходимо выполнить проверку коллинеарности векторов n1→=(2, 2-3) и n2→=(2(3+2), -7). Получим равенство вида 22(3+2)=2-3-7. Оно верное, потому как 223+2-2-3-7=7+2-3(3+2)7(3+2)=7-77(3+2)=0. Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.
Ответ: точек пересечения нет, прямые параллельны.
Найти координаты пересечения заданных прямых 2x-1=0 и y=54x-2.
Решение
Для решения составляем систему уравнений. Получаем
2x-1=054x-y-2=0⇔2x=154x-y=2
Найдем определитель основной матрицы. Для этого 2054-1=2·(-1)-0·54=-2. Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:
2x=154x-y=2⇔x=1245x-y=2⇔x=1254·12-y=2⇔x=12y=-118
Получили, что точка пересечения заданных прямых имеет координаты M0(12, -118).
Ответ: M0(12, -118).
Нахождения координат точки пересечения двух прямых в пространстве
Таким же образом находятся точки пересечения прямых пространства.
Когда заданы прямые a и b в координатной плоскости Охуz уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A1x+B1y+C1z+D1=0A2x+B2y+C2z+D1=0 а прямая b – A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0.
Когда точка М0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:
A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0
Рассмотрим подобные задания на примерах.
Найти координаты точки пересечения заданных прямых x-1=0y+2z+3=0 и 3x+2y+3=04x-2z-4=0
Решение
Составляем систему x-1=0y+2z+3=03x+2y+3=04x-2z-4=0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A=10001232040-2 и расширенную T=1001012-340-24. Определяем ранг матрицы по Гауссу.
Получаем, что
1=1≠0, 1001=1≠0, 100012320=-4≠0, 1001012-3320-340-24=0
Отсюда следует, что ранг расширенной матрицы имеет значение 3. Тогда система уравнений x-1=0y+2z+3=03x+2y+3=04x-27-4=0 в результате дает только одно решение.
Базисный минор имеет определитель 100012320=-4≠0, тогда последнее уравнение не подходит. Получим, что x-1=0y+2z+3=03x+2y+3=04x-2z-4=0⇔x=1y+2z=-33x+2y-3 . Решение системы x=1y+2z=-33x+2y=-3⇔x=1y+2z=-33·1+2y=-3⇔x=1y+2z=-3y=-3⇔⇔x=1-3+2z=-3y=-3⇔x=1z=0y=-3.
Значит, имеем, что точка пересечения x-1=0y+2z+3=0 и 3x+2y+3=04x-2z-4=0 имеет координаты (1, -3, 0).
Ответ: (1, -3, 0).
Система вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0 имеет только одно решение. Значит, прямые a и b пересекаются.
В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.
Поэтому система вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.
Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.
Заданы уравнения прямых x+2y-3z-4=02x-y+5=0 и x-3z=03x-2y+2z-1=0. Найти точку пересечения.
Решение
Для начала составим систему уравнений. Получим, что x+2y-3z-4=02x-y+5=0x-3z=03x-2y+2z-1=0 . решаем ее методом Гаусса:
12-342-10-510-303-221~12-340-56-130-20-40-811-11~~12-340-56-1300-125650075-1595~12-340-56-1300-1256500031110
Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.
Ответ: нет точки пересечения.
Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.
Заданы две прямые x=-3-λy=-3·λz=-2+3·λ, λ∈R и x2=y-30=z5 в Охуz. Найти точку пересечения.
Решение
Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что
x=-3-λy=-3·λz=-2+3·λ⇔λ=x+3-1λ=y-3λ=z+23⇔x+3-1=y-3=z+23⇔⇔x+3-1=y-3x+3-1=z+23⇔3x-y+9=03x+z+11=0x2=y-30=z5⇔y-3=0x2=z5⇔y-3=05x-2z=0
Находим координаты 3x-y+9=03x+z+11=0y-3=05x-2z=0, для этого посчитаем ранги матрицы. Ранг матрицы равен 3, а базисный минор 3-10301010=-3≠0, значит, что из системы необходимо исключить последнее уравнение. Получаем, что
3x-y+9=03x+z+11=0y-3=05x-2z=0⇔3x-y+9=03x+z+11=0y-3=0
Решим систему методом Крамер. Получаем, что x=-2y=3z=-5. Отсюда получаем, что пересечение заданных прямых дает точку с координатами (-2, 3, -5).
Ответ: (-2, 3, -5).

В евклидовой геометрии пересечение двух прямых может быть пустым множеством, точкой или прямой. Различение этих случаев и поиск точки пересечения используется, например, в компьютерной графике, при планировании движения[en] и для обнаружения столкновений.
В трёхмерной евклидовой геометрии, если две прямые не лежат в одной плоскости, они называются скрещивающимися и не имеют точек пересечения. Если прямые находятся в одной плоскости, имеется три возможности. Если они совпадают, они имеют бесконечно много общих точек (а именно, все точки на этих прямых). Если прямые различны, но имеют один и тот же наклон, они параллельны и не имеют общих точек. В противном случае они имеют одну точку пересечения.
В неевклидовой геометрии две прямые могут пересекаться в нескольких точках и число непересекающихся с данной прямой других прямых (параллельных) может быть больше единицы.
Пересечение двух прямых[править | править код]
Необходимым условием пересечения двух прямых является принадлежность их одной плоскости, то есть эти прямые не должны быть скрещивающимися. Выполнение этого условия эквивалентно вырожденности тетраэдра, у которого две вершины лежат на одной прямой, а две другие — на другой (т.е. объём этого тетраэдра равен нулю). Алгебраическую форму этого условия можно посмотреть в статье «Проверка скрещенности».
Если заданы по две точки на каждой прямой[править | править код]
Рассмотрим пересечение двух прямых 







Пересечение 


Определители можно переписать в виде:
Заметим, что точка пересечения относится к бесконечным прямым, а не отрезкам между точками, и она может лежать вне отрезков. Если (вместо решения за один шаг) искать решение в терминах кривых Безье первого порядка, то можно проверить параметры этих кривых 0.0 ≤ t ≤ 1.0 и 0.0 ≤ u ≤ 1.0 (t и u — параметры).
Если две прямые параллельны или совпадают, знаменатель обращается в ноль:
Если прямые очень близки к параллельности (почти параллельны), при вычислении на компьютере могут возникнуть числовые проблемы и распознавание такого условия может потребовать подходящего теста на «неопределённость» для приложения. Более устойчивое и общее решение может быть получено при вращении отрезков таким образом, что один из них станет горизонтальным, а тогда параметрическое решение второй прямой легко получить. При решении необходимо внимательное рассмотрение специальных случаев (параллельность/совпадение прямых, наложение отрезков).
Если заданы уравнения прямых[править | править код]
Координаты 

Предположим, что две прямые имеют уравнения 






.
Мы можем преобразовать это равенство с целью выделения 
,
а тогда
.
Чтобы найти координату y, всё что нам нужно, это подставить значение x в одну из формул прямых, например, в первую:
.
Отсюда получаем точку пересечения прямых
.
Заметим, что при a = b две прямые параллельны. Если при этом c ≠ d, прямые различны и не имеют пересечений, в противном же случае прямые совпадают [2].
Использование однородных координат[править | править код]
При использовании однородных координат точка пересечения двух явно заданных прямых может быть найдена достаточно просто. В 2-мерном пространстве любая точка может быть определена как проекция 3-мерной точки, заданной тройкой 


Предположим, что мы хотим найти пересечение двух бесконечных прямых в 2-мерном пространстве, которые заданы формулами 



Пересечение 

Если 
Пересечение n прямых[править | править код]
Существование и выражение пересечения[править | править код]
В двухмерном пространстве[править | править код]
В двухмерном пространстве прямые числом больше двух почти достоверно не пересекаются в одной точке. Чтобы определить, пересекаются ли они в одной точке, и, если пересекаются, чтобы найти точку пересечения, запишем i-ое уравнение (i = 1, …,n) как 
где i-ая строка n × 2 матрицы A равна 
где 

В трёхмерном пространстве[править | править код]
Представленный выше подход без труда распространяется на трёхмерное пространство. В трёхмерном и более высоких пространствах даже две прямые почти наверняка не пересекаются. Пары непараллельных непересекающихся прямых называются скрещивающимися. Но когда пересечение существует, его можно найти следующим образом.
В трёхмерном пространстве прямая представляется пересечением двух плоскостей, каждая из которых задаётся формулой 
,
где A — матрица 2n × 3, а b — 2n × 1. Как и ранее, единственная точка пересечения существует тогда и только тогда, когда A имеет полный ранг по столбцам, а расширенная матрица [A | b ] таковой не является. Единственная точка пересечения, если существует, задаётся формулой
Ближайшая точка к непересекающимся прямым[править | править код]
В размерностях два и выше можно найти точку, которая является ближайшей к этим двум (или более) прямым в смысле наименьшей суммы квадратов.
В двухмерном пространстве[править | править код]
В случае двухмерного пространства представим прямую i как точку 




,
который является единичным вектором вдоль прямой, повёрнутым на 90º.
Заметим, что расстояние от точки x до прямой 
Следовательно, квадрат расстояния от x до прямой равен
Сумма квадратов расстояний до набора прямых является целевой функцией:
Выражение можно преобразовать:
Чтобы найти минимум, продифференцируем по x и приравняем результат нулю:
Таким образом,
откуда
В трёхмерном пространстве[править | править код]
Хотя в размерностях выше двух нормаль 



превращается в
,
где E — единичная матрица, а тогда
См. также[править | править код]
- Пересечение отрезков
- Расстояние от точки до прямой на плоскости
- Аксиома параллельности Евклида
Примечания[править | править код]
- ↑ Weisstein, Eric W. “Line-Line Intersection.” From MathWorld. A Wolfram Web Resource. Дата обращения: 10 января 2008. Архивировано 10 октября 2007 года.
- ↑ Похожие выкладки можно найти в книге Делоне и Райкова (стр. 202-203)
- ↑ Homogeneous coordinates. robotics.stanford.edu. Дата обращения: 18 августа 2015. Архивировано 23 августа 2015 года.
Литература[править | править код]
- Б. Н. Делоне, Д. А. Райков. Аналитическая геометрия. — М., Л.: ОГИЗ, Государственнон издательство технико-теоретической литературы, 1948. — Т. 1.
Ссылки[править | править код]
- Distance between Lines and Segments with their Closest Point of Approach, applicable to two, three, or more dimensions.
Точка пересечения двух прямых на плоскости
Методы решения. Существует два метода решения плоских задач на определение координат точки пересечения прямых:
- графический
- аналитический
Графический метод решения. Используя уравнения, начертить графики прямых и с помощью линейки найти координаты точки пересечения.
Аналитический метод решения. Необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны между собой)

Пример 1. Найти точку пересечения прямых y = 2x – 1 и y = -3x + 1.
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2x – 1
y = -3x + 1
Вычтем из первого уравнения второе
y – y = 2x – 1 – (-3x + 1)
y = -3x + 1
=>
0 = 5x – 2
y = -3x + 1
Из первого уравнения найдем значение x
5x = 2
y = -3x + 1
=>
x = 25 = 0.4
y = -3x + 1
Подставим значение x во второе уравнение и найдем значение y
x = 0.4
y = -3·(0.4) + 1 = -1.2 + 1 = -0.2
Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)

Пример 2. Найти точку пересечения прямых y = 2x – 1 и x = 2t + 1y = t.
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2x – 1
x = 2t + 1
y = t
В первое уравнение подставим значения x и y из второго и третьего уравнений.
t = 2·(2t + 1) – 1
x = 2t + 1
y = t
=>
t = 4t + 1
x = 2t + 1
y = t
=>
-3t = 1
x = 2t + 1
y = t
=>
t = -13
x = 2t + 1
y = t
Подставим значение t во второе и третье уравнение
t = -13
x = 2·(-13) + 1 = -23 + 1 = 13
y = -13
Ответ. Точка пересечения двух прямых имеет координаты (13, -13)
Пример 3 Найти точку пересечения прямых 2x + 3y = 0 и x – 23 = y4.
Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
2x + 3y = 0
x – 23 = y4
Из второго уравнения выразим y через x
2x + 3y = 0
y = 4·x – 23
Подставим y в первое уравнение
2x + 3·4·x – 23 = 0
y = 4·x – 23
=>
2x + 4·(x – 2) = 0
y = 4·x – 23
=>
2x + 4x – 8 = 0
y = 4·x – 23
=>
6x = 8
y = 4·x – 23
=>
x = 86 = 43
y = 4·x – 23
=>
x = 86 = 43
y = 4·4/3 – 23 = 4·-2/3 3 = -89
Ответ. Точка пересечения двух прямых имеет координаты (43, -89)
Пример 4. Найти точку пересечения прямых y = 2x – 1 и y = 2x + 1.
Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k1 = k2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
y = 2x – 1
y = 2x + 1
Вычтем из первого уравнения второе
y – y = 2x – 1 – (2x + 1)
y = -3x + 1
=>
0 = -2
y = -3x + 1
В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений – отсутствуют точки пересечения прямых (прямые параллельны).
Ответ. Прямые не пересекаются (прямые параллельны).
Пример 5. Проверить является ли точка N(1, 1) точкой пересечения прямых y = x и y = 3x – 2.
Решение: Подставим координаты точки N в уравнения прямых.
1 = 1
1 = 3·1 – 2 = 1
Ответ. Так как оба уравнения превратились в тождества, то точка N – точка пересечения этих прямых.
Точка пересечения двух прямых в пространстве
Метод решения. Для определение координат точки пересечения прямых в пространстве, необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)
Пример 6. Найти точку пересечения прямых x – 1 = y – 1 = z – 1 и x – 3-2 = 2 – y = z.
Решение: Составим систему уравнений
x – 1 = a
y – 1 = a
z – 1 = a
x – 3-2 = b
2 – y = b
z = b
=>
x = a + 1
y = a + 1
z = a + 1
x – 3-2 = b
2 – y = b
z = b
=>
Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = a + 1
y = a + 1
z = a + 1
a + 1 – 3-2 = b
2 – (a + 1) = b
a + 1 = b
=>
x = a + 1
y = a + 1
z = a + 1
a – 2-2 = b
1 – a = b
a + 1 = b
К шестому уравнению добавим пятое уравнение
x = a + 1
y = a + 1
z = a + 1
a – 2-2 = b
1 – a = b
a + 1 + (1 – a) = b + b
=>
x = a + 1
y = a + 1
z = a + 1
a – 2-2 = b
1 – a = b
b = 1
Подставим значение b в четвертое и пятое уравнения
x = a + 1
y = a + 1
z = a + 1
a – 2-2 = 1
1 – a = 1
b = 1
=>
x = a + 1
y = a + 1
z = a + 1
a – 2 = -2
a = 0
b = 1
=>
x = a + 1
y = a + 1
z = a + 1
a = 0
a = 0
b = 1
=>
x = 0 + 1 = 1
y = 0 + 1 = 1
z = 0 + 1 = 1
a = 0
a = 0
b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Замечание. Если уравнения прямых заданы параметрически, и в обоих уравнениях параметр задан одной и той же буквой, то при составлении системы в одном из уравнений необходимо заменить букву отвечающую за параметр.
Пример 7. Найти точку пересечения прямых
x = 2t – 3
y = t
z = –t + 2
и
x = t + 1
y = 3t – 2
z = 3
.
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
x = 2t – 3
y = t
z = –t + 2
x = a + 1
y = 3a – 2
z = 3
Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = 2t – 3
y = t
z = –t + 2
2t – 3 = a + 1
t = 3a – 2
–t + 2 = 3
=>
x = 2t – 3
y = t
z = –t + 2
2t = a + 4
t = 3a – 2
t = -1
=>
Подставим значение t из шестого уравнения в остальные уравнения
x = 2·(-1) – 3
y = (-1)
z = -(-1) + 2
2·(-1) = a + 4
-1 = 3a – 2
t = -1
=>
x = -5
y = -1
z = 3
a = -6
a = 13
t = -1
Ответ. Так как -6 ≠ 13, то прямые не пересекаются.
Координаты точки пересечения двух прямых – примеры нахождения
Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.
Точка пересечения двух прямых – определение
Необходимо дать определение точкам пересечения двух прямых.
Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.
Определение точки пересечения прямых звучит так:
Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.
Рассмотрим на рисунке, приведенном ниже.

Нахождение координат точки пересечения двух прямых на плоскости
Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.
Если на плоскости имеется система координат О х у , то задаются две прямые a и b . Прямой a соответствует общее уравнение вида A 1 x + B 1 y + C 1 = 0 , для прямой b – A 2 x + B 2 y + C 2 = 0 . Тогда M 0 ( x 0 , y 0 ) является некоторой точкой плоскости необходимо выявить , будет ли точка М 0 являться точкой пересечения этих прямых.
Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M 0 ( x 0 , y 0 ) считается их точкой пересечения.
Даны две пересекающиеся прямые 5 x – 2 y – 16 = 0 и 2 x – 5 y – 19 = 0 . Будет ли точка М 0 с координатами ( 2 , – 3 ) являться точкой пересечения.
Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что
5 · 2 – 2 · ( – 3 ) – 16 = 0 ⇔ 0 = 0 2 · 2 – 5 · ( – 3 ) – 19 = 0 ⇔ 0 = 0
Оба равенства верные, значит М 0 ( 2 , – 3 ) является точкой пересечения заданных прямых.
Изобразим данное решение на координатной прямой рисунка, приведенного ниже.

Ответ: заданная точка с координатами ( 2 , – 3 ) будет являться точкой пересечения заданных прямых.
Пересекутся ли прямые 5 x + 3 y – 1 = 0 и 7 x – 2 y + 11 = 0 в точке M 0 ( 2 , – 3 ) ?
Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что
5 · 2 + 3 · ( – 3 ) – 1 = 0 ⇔ 0 = 0 7 · 2 – 2 · ( – 3 ) + 11 = 0 ⇔ 31 = 0
Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7 x – 2 y + 11 = 0 . Отсюда имеем, что точка М 0 не точка пересечения прямых.
Чертеж наглядно показывает, что М 0 – это не точка пересечения прямых. Они имеют общую точку с координатами ( – 1 , 2 ) .

Ответ: точка с координатами ( 2 , – 3 ) не является точкой пересечения заданных прямых.
Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.
Задаются две пересекающиеся прямые a и b уравнениями вида A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 , расположенных в О х у . При обозначении точки пересечения М 0 получим, что следует продолжить поиск координат по уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .
Из определения очевидно, что М 0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Иными словами это и есть решение полученной системы A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 .
Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.
Заданы две прямые x – 9 y + 14 = 0 и 5 x – 2 y – 16 = 0 на плоскости. необходимо найти их пересечение.
Данные по условию уравнения необходимо собрать в систему, после чего получим x – 9 y + 14 = 0 5 x – 2 y – 16 = 0 . Чтобы решить его, разрешается первое уравнение относительно x , подставляется выражение во второе:
x – 9 y + 14 = 0 5 x – 2 y – 16 = 0 ⇔ x = 9 y – 14 5 x – 2 y – 16 = 0 ⇔ ⇔ x = 9 y – 14 5 · 9 y – 14 – 2 y – 16 = 0 ⇔ x = 9 y – 14 43 y – 86 = 0 ⇔ ⇔ x = 9 y – 14 y = 2 ⇔ x = 9 · 2 – 14 y = 2 ⇔ x = 4 y = 2
Получившиеся числа являются координатами, которые необходимо было найти.
Ответ: M 0 ( 4 , 2 ) является точкой пересечения прямых x – 9 y + 14 = 0 и 5 x – 2 y – 16 = 0 .
Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.
Определить координаты точек пересечения прямых x – 5 = y – 4 – 3 и x = 4 + 9 · λ y = 2 + λ , λ ∈ R .
Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x = 4 + 9 · λ y = 2 + λ , λ ∈ R преобразуется таким образом:
x = 4 + 9 · λ y = 2 + λ ⇔ λ = x – 4 9 λ = y – 2 1 ⇔ x – 4 9 = y – 2 1 ⇔ ⇔ 1 · ( x – 4 ) = 9 · ( y – 2 ) ⇔ x – 9 y + 14 = 0
После чего беремся за уравнение канонического вида x – 5 = y – 4 – 3 и преобразуем. Получаем, что
x – 5 = y – 4 – 3 ⇔ – 3 · x = – 5 · y – 4 ⇔ 3 x – 5 y + 20 = 0
Отсюда имеем, что координаты – это точка пересечения
x – 9 y + 14 = 0 3 x – 5 y + 20 = 0 ⇔ x – 9 y = – 14 3 x – 5 y = – 20
Применим метод Крамера для нахождения координат:
∆ = 1 – 9 3 – 5 = 1 · ( – 5 ) – ( – 9 ) · 3 = 22 ∆ x = – 14 – 9 – 20 – 5 = – 14 · ( – 5 ) – ( – 9 ) · ( – 20 ) = – 110 ⇒ x = ∆ x ∆ = – 110 22 = – 5 ∆ y = 1 – 14 3 – 20 = 1 · ( – 20 ) – ( – 14 ) · 3 = 22 ⇒ y = ∆ y ∆ = 22 22 = 1
Ответ: M 0 ( – 5 , 1 ) .
Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x = x 1 + a x · λ y = y 1 + a y · λ , λ ∈ R . Тогда вместо значения x подставляется x = x 1 + a x · λ и y = y 1 + a y · λ , где получим λ = λ 0 , соответствующее точке пересечения, имеющей координаты x 1 + a x · λ 0 , y 1 + a y · λ 0 .
Определить координаты точки пересечения прямой x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x – 5 = y – 4 – 3 .
Необходимо выполнить подстановку в x – 5 = y – 4 – 3 выражением x = 4 + 9 · λ , y = 2 + λ , тогда получим:
4 + 9 · λ – 5 = 2 + λ – 4 – 3
При решении получаем, что λ = – 1 . Отсюда следует, что имеется точка пересечения между прямыми x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x – 5 = y – 4 – 3 . Для вычисления координат необходимо подставить выражение λ = – 1 в параметрическое уравнение. Тогда получаем, что x = 4 + 9 · ( – 1 ) y = 2 + ( – 1 ) ⇔ x = – 5 y = 1 .
Ответ: M 0 ( – 5 , 1 ) .
Для полного понимания темы, необходимо знать некоторые нюансы.
Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.
Даны прямые x 3 + y – 4 = 1 и y = 4 3 x – 4 . Определить, имеют ли они общую точку.
Упрощая заданные уравнения, получаем 1 3 x – 1 4 y – 1 = 0 и 4 3 x – y – 4 = 0 .
Следует собрать уравнения в систему для последующего решения:
1 3 x – 1 4 y – 1 = 0 1 3 x – y – 4 = 0 ⇔ 1 3 x – 1 4 y = 1 4 3 x – y = 4
Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x 3 + y – 4 = 1 и y = 4 3 x – 4 определяют одну и ту же прямую. Поэтому нет точек пересечения.
Ответ: заданные уравнения определяют одну и ту же прямую.
Найти координаты точки пересекающихся прямых 2 x + ( 2 – 3 ) y + 7 = 0 и 2 3 + 2 x – 7 y – 1 = 0 .
По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:
2 x + ( 2 – 3 ) y + 7 = 0 2 ( 3 + 2 ) x – 7 y – 1 = 0 ⇔ 2 x + ( 2 – 3 ) y = – 7 2 ( 3 + 2 ) x – 7 y = 1 ⇔ ⇔ 2 x + 2 – 3 y = – 7 2 ( 3 + 2 ) x – 7 y + ( 2 x + ( 2 – 3 ) y ) · ( – ( 3 + 2 ) ) = 1 + – 7 · ( – ( 3 + 2 ) ) ⇔ ⇔ 2 x + ( 2 – 3 ) y = – 7 0 = 22 – 7 2
Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.
Второй способ решения.
Для начала нужно определить наличие пересечения прямых.
n 1 → = ( 2 , 2 – 3 ) является нормальным вектором прямой 2 x + ( 2 – 3 ) y + 7 = 0 , тогда вектор n 2 → = ( 2 ( 3 + 2 ) , – 7 – нормальный вектор для прямой 2 3 + 2 x – 7 y – 1 = 0 .
Необходимо выполнить проверку коллинеарности векторов n 1 → = ( 2 , 2 – 3 ) и n 2 → = ( 2 ( 3 + 2 ) , – 7 ) . Получим равенство вида 2 2 ( 3 + 2 ) = 2 – 3 – 7 . Оно верное, потому как 2 2 3 + 2 – 2 – 3 – 7 = 7 + 2 – 3 ( 3 + 2 ) 7 ( 3 + 2 ) = 7 – 7 7 ( 3 + 2 ) = 0 . Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.
Ответ: точек пересечения нет, прямые параллельны.
Найти координаты пересечения заданных прямых 2 x – 1 = 0 и y = 5 4 x – 2 .
Для решения составляем систему уравнений. Получаем
2 x – 1 = 0 5 4 x – y – 2 = 0 ⇔ 2 x = 1 5 4 x – y = 2
Найдем определитель основной матрицы. Для этого 2 0 5 4 – 1 = 2 · ( – 1 ) – 0 · 5 4 = – 2 . Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:
2 x = 1 5 4 x – y = 2 ⇔ x = 1 2 4 5 x – y = 2 ⇔ x = 1 2 5 4 · 1 2 – y = 2 ⇔ x = 1 2 y = – 11 8
Получили, что точка пересечения заданных прямых имеет координаты M 0 ( 1 2 , – 11 8 ) .
Ответ: M 0 ( 1 2 , – 11 8 ) .
Нахождения координат точки пересечения двух прямых в пространстве
Таким же образом находятся точки пересечения прямых пространства.
Когда заданы прямые a и b в координатной плоскости О х у z уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 1 = 0 а прямая b – A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 .
Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0
Рассмотрим подобные задания на примерах.
Найти координаты точки пересечения заданных прямых x – 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0
Составляем систему x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A = 1 0 0 0 1 2 3 2 0 4 0 – 2 и расширенную T = 1 0 0 1 0 1 2 – 3 4 0 – 2 4 . Определяем ранг матрицы по Гауссу.
1 = 1 ≠ 0 , 1 0 0 1 = 1 ≠ 0 , 1 0 0 0 1 2 3 2 0 = – 4 ≠ 0 , 1 0 0 1 0 1 2 – 3 3 2 0 – 3 4 0 – 2 4 = 0
Отсюда следует, что ранг расширенной матрицы имеет значение 3 . Тогда система уравнений x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 27 – 4 = 0 в результате дает только одно решение.
Базисный минор имеет определитель 1 0 0 0 1 2 3 2 0 = – 4 ≠ 0 , тогда последнее уравнение не подходит. Получим, что x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 ⇔ x = 1 y + 2 z = – 3 3 x + 2 y – 3 . Решение системы x = 1 y + 2 z = – 3 3 x + 2 y = – 3 ⇔ x = 1 y + 2 z = – 3 3 · 1 + 2 y = – 3 ⇔ x = 1 y + 2 z = – 3 y = – 3 ⇔ ⇔ x = 1 – 3 + 2 z = – 3 y = – 3 ⇔ x = 1 z = 0 y = – 3 .
Значит, имеем, что точка пересечения x – 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 имеет координаты ( 1 , – 3 , 0 ) .
Ответ: ( 1 , – 3 , 0 ) .
Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.
В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.
Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.
Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.
Заданы уравнения прямых x + 2 y – 3 z – 4 = 0 2 x – y + 5 = 0 и x – 3 z = 0 3 x – 2 y + 2 z – 1 = 0 . Найти точку пересечения.
Для начала составим систему уравнений. Получим, что x + 2 y – 3 z – 4 = 0 2 x – y + 5 = 0 x – 3 z = 0 3 x – 2 y + 2 z – 1 = 0 . решаем ее методом Гаусса:
1 2 – 3 4 2 – 1 0 – 5 1 0 – 3 0 3 – 2 2 1
1 2 – 3 4 0 – 5 6 – 13 0 – 2 0 – 4 0 – 8 11 – 11
1 2 – 3 4 0 – 5 6 – 13 0 0 – 12 5 6 5 0 0 7 5 – 159 5
1 2 – 3 4 0 – 5 6 – 13 0 0 – 12 5 6 5 0 0 0 311 10
Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.
Ответ: нет точки пересечения.
Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.
Заданы две прямые x = – 3 – λ y = – 3 · λ z = – 2 + 3 · λ , λ ∈ R и x 2 = y – 3 0 = z 5 в О х у z . Найти точку пересечения.
Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что
x = – 3 – λ y = – 3 · λ z = – 2 + 3 · λ ⇔ λ = x + 3 – 1 λ = y – 3 λ = z + 2 3 ⇔ x + 3 – 1 = y – 3 = z + 2 3 ⇔ ⇔ x + 3 – 1 = y – 3 x + 3 – 1 = z + 2 3 ⇔ 3 x – y + 9 = 0 3 x + z + 11 = 0 x 2 = y – 3 0 = z 5 ⇔ y – 3 = 0 x 2 = z 5 ⇔ y – 3 = 0 5 x – 2 z = 0
Находим координаты 3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0 5 x – 2 z = 0 , для этого посчитаем ранги матрицы. Ранг матрицы равен 3 , а базисный минор 3 – 1 0 3 0 1 0 1 0 = – 3 ≠ 0 , значит, что из системы необходимо исключить последнее уравнение. Получаем, что
3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0 5 x – 2 z = 0 ⇔ 3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0
Решим систему методом Крамер. Получаем, что x = – 2 y = 3 z = – 5 . Отсюда получаем, что пересечение заданных прямых дает точку с координатами ( – 2 , 3 , – 5 ) .
Пересечение прямых. Точка пересечения двух прямых
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Точка пересечения двух прямых на плоскости
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны между собой)

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2 x – 1 y = -3 x + 1
Вычтем из первого уравнения второе
y – y = 2 x – 1 – (-3 x + 1) y = -3 x + 1 => 0 = 5 x – 2 y = -3 x + 1
Из первого уравнения найдем значение x
5 x = 2 y = -3 x + 1 => x = 2 5 = 0.4 y = -3 x + 1
Подставим значение x во второе уравнение и найдем значение y
x = 0.4 y = -3·(0.4) + 1 = -1.2 + 1 = -0.2
Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
y = 2 x – 1 x = 2 t + 1 y = t
В первое уравнение подставим значения x и y из второго и третьего уравнений.
t = 2·(2 t + 1) – 1 x = 2 t + 1 y = t => t = 4 t + 1 x = 2 t + 1 y = t =>
-3 t = 1 x = 2 t + 1 y = t => t = – 1 3 x = 2 t + 1 y = t
Подставим значение t во второе и третье уравнение
t = – 1 3 x = 2·(- 1 3 ) + 1 = – 2 3 + 1 = 1 3 y = – 1 3
Ответ. Точка пересечения двух прямых имеет координаты ( 1 3 , – 1 3 )

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:
2 x + 3 y = 0 x – 2 3 = y 4
Из второго уравнения выразим y через x
2 x + 3 y = 0 y = 4· x – 2 3
Подставим y в первое уравнение
2 x + 3·4· x – 2 3 = 0 y = 4· x – 2 3 => 2 x + 4·( x – 2) = 0 y = 4· x – 2 3 =>
2 x + 4 x – 8 = 0 y = 4· x – 2 3 => 6 x = 8 y = 4· x – 2 3 =>
x = 8 6 = 4 3 y = 4· x – 2 3 => x = 8 6 = 4 3 y = 4· 4/3 – 2 3 = 4· -2/3 3 = – 8 9
Ответ. Точка пересечения двух прямых имеет координаты ( 4 3 , – 8 9 )

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k 1 = k 2 = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.
Решим также эту задачу используя систему уравнений:
y = 2 x – 1 y = 2 x + 1
Вычтем из первого уравнения второе
y – y = 2 x – 1 – (2 x + 1) y = -3 x + 1 => 0 = -2 y = -3 x + 1
В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений – отсутствуют точки пересечения прямых (прямые параллельны).
Ответ. Прямые не пересекаются (прямые параллельны).

Решение: Подставим координаты точки N в уравнения прямых.
Ответ. Так как оба уравнения превратились в тождества, то точка N – точка пересечения этих прямых.
Точка пересечения двух прямых в пространстве
Если система уравнений:
- имеет единственное решение, то прямые пересекаются;
- имеет бесконечное множество решений, то прямые совпадают;
- не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)
Решение: Составим систему уравнений
x – 1 = a y – 1 = a z – 1 = a x – 3 -2 = b 2 – y = b z = b => x = a + 1 y = a + 1 z = a + 1 x – 3 -2 = b 2 – y = b z = b =>
Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = a + 1 y = a + 1 z = a + 1 a + 1 – 3 -2 = b 2 – ( a + 1) = b a + 1 = b => x = a + 1 y = a + 1 z = a + 1 a – 2 -2 = b 1 – a = b a + 1 = b
К шестому уравнению добавим пятое уравнение
x = a + 1 y = a + 1 z = a + 1 a – 2 -2 = b 1 – a = b a + 1 + (1 – a ) = b + b => x = a + 1 y = a + 1 z = a + 1 a – 2 -2 = b 1 – a = b b = 1
Подставим значение b в четвертое и пятое уравнения
x = a + 1 y = a + 1 z = a + 1 a – 2 -2 = 1 1 – a = 1 b = 1 => x = a + 1 y = a + 1 z = a + 1 a – 2 = -2 a = 0 b = 1 =>
x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1
Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).
Решение: Составим систему уравнений заменив во втором уравнении параметр t на a
x = 2 t – 3 y = t z = – t + 2 x = a + 1 y = 3 a – 2 z = 3
Подставим значения x , y , z из 1, 2, 3 уравнений в 4, 5, 6 уравнения
x = 2 t – 3 y = t z = – t + 2 2 t – 3 = a + 1 t = 3 a – 2 – t + 2 = 3 => x = 2 t – 3 y = t z = – t + 2 2 t = a + 4 t = 3 a – 2 t = -1 =>
Подставим значение t из шестого уравнения в остальные уравнения
x = 2·(-1) – 3 y = (-1) z = -(-1) + 2 2·(-1) = a + 4 -1 = 3 a – 2 t = -1 => x = -5 y = -1 z = 3 a = -6 a = 1 3 t = -1
Ответ. Так как -6 ≠ 1 3 , то прямые не пересекаются.
Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых (“канонический” или “параметрический” ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
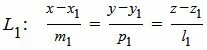 , , |
(1) |
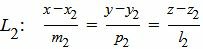 , , |
(2) |
Найти точку пересечения прямых L1 и L2 (Рис.1).
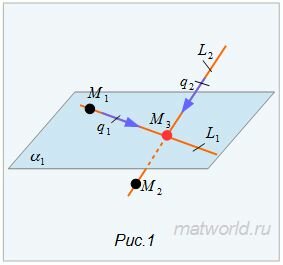
Запишем уравнение (1) в виде системы двух линейных уравнений:
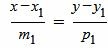 , , |
(3) |
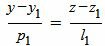 |
(4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
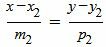 , , |
(7) |
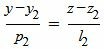 |
(8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
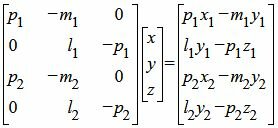 |
(11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
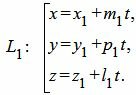 |
(12) |
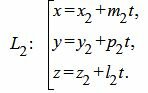 |
(13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
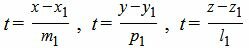 |
(14) |
Так как левые части уравнений (14) равны, то можем записать:
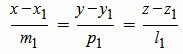 |
(15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
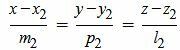 |
(16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
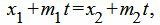 |
(17) |
 |
(18) |
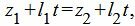 |
(19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 |
(20) |
 |
(21) |
Представим уравнение (20) в виде двух уравнений:
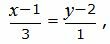 |
(22) |
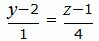 |
(23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
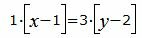
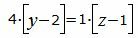
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
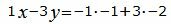
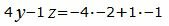
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
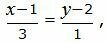 |
(26) |
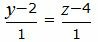 |
(27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
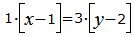
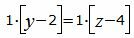
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
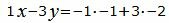
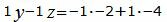
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
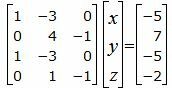 |
(30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
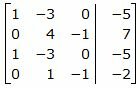
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
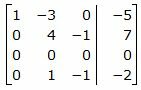
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:

Сделаем перестановку строк 3 и 4.
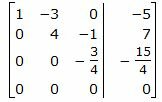
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
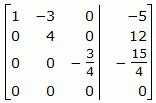
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
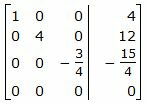
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
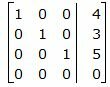
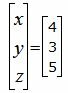
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 |
(31) |
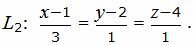 |
(32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
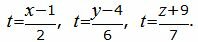
Из равентсв выше получим каноническое уравнение прямой:
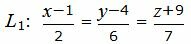 |
(33) |
Представим уравнение (33) в виде двух уравнений:
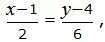 |
(34) |
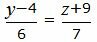 |
(35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):

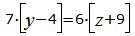
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

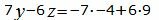
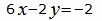 |
(36) |
 . . |
(37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
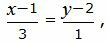 |
(38) |
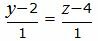 |
(39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
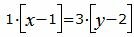
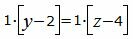
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
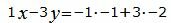
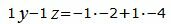
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
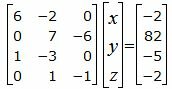 |
(42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:

Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
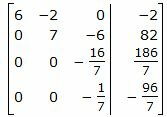
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
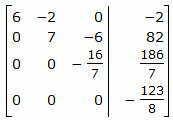
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
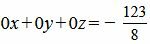 |
(43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=<2,6,7>, а прямая L2 имеет направляющий вектор q2=<3,1,1>. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/library/analytic_geometry/lines_intersection/
http://matworld.ru/analytic-geometry/tochka-peresechenija-prjamyh-3d.php
[/spoiler]















