На прошлых уроках мы познакомились с определением механического движения, узнали, каким бывает движение, изучили его свойства и характеристики. Теперь нам известны формулы для расчета скорости при равномерном движении ($upsilon = frac{S}{t}$) и средней скорости при неравномерном ($upsilon_{ср} = frac{S}{t}$).
На данном уроке мы посмотрим на эти формулы с другой стороны — научимся использовать их для расчета пути и времени движения, а также рассмотрим графики скорости и пути для равномерного движения.
Формулы для расчета пути и времени движения при равномерном движении тела
Скорость тела при равномерном движении вычисляется по формуле $upsilon = frac{S}{t}$. Отсюда, если мы знаем скорость и время, то можем найти пройденный путь:
$S = upsilon t$.
Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время его движения.
Выразим время:
$t = frac{S}{upsilon}$.
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле:
$upsilon_{ср} = frac{S}{t}$.
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$large S = upsilon_{ср} t$.
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$t = frac{s}{upsilon_{ср}}$.
График скорости равномерного движения
Так как скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Если динозавр начнет двигаться к дому, то его скорость будет положительной, так как направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, так как направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Из графика видно, что скорости с течением времени не изменяется – они постоянны в любой выбранный момент времени. Если мы посмотрим на график положительной скорости, то увидим, что $upsilon = 6 frac{м}{с}$, на график отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 space с$.
$S = upsilon t = 6 frac{м}{с} cdot space 4 c = 24 space м$.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 space с$, $S = 2 space м$. Тогда,
$upsilon = frac{S}{t} = frac{2 space м}{1 space с} = 2 frac{м}{с}$.
Задачи
Задача №1
Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 space м}{3600 space с} approx 33 frac{м}{с}$.
Дано:
$upsilon = 120 frac{км}{ч}$
$t = 3 space c$
СИ:
$upsilon = 33 frac{м}{с}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t$,
$S = 33 frac{м}{с} cdot 3 с approx 100 space м$
Ответ: $S = 100 space м$.
Задача №2
Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$,
$900 space км = 900 space 000 м$.
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$S = 900 space км$
CИ:
$upsilon_{ср} = 11 frac{м}{с}$
$S = 900 space 000 space м$
$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}}$,
$t = frac{900 space 000 space м}{11 frac{м}{с}} approx 82 space 000 space с$.
Переведем время в часы:
$1 space ч = 60 space мин = 60 cdot 60 space c = 3600 space c$.
Тогда:
$t = frac{82 space 000 space c}{3600 space c} approx 23 space ч$.
Ответ: $t = 23 space ч$.
Больше задач на расчет пути и времени движения с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Пользуясь таблицей 1 из прошлого урока, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за $5 space с$.
Дано:
$upsilon_1 = 22 frac{м}{с}$
$upsilon_2 = 20 frac{м}{с}$
$upsilon_3 = 8000 frac{м}{с}$
$t = 5 space с$
$S_1 — ?$
$S_2 — ?$
$S_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь, пройденный страусом:
$S_1 = upsilon_1 t$,
$S_1 = 22 frac{м}{с} cdot 5 space с = 110 space м$.
Путь, пройденный автомобилем:
$S_2 = upsilon_2 t$,
$S_2 = 20 frac{м}{с} cdot 5 space с = 100 space м$.
Путь, пройденный искусственным спутником Земли:
$S_3 = upsilon_3 t$,
$S_3 = 8000 frac{м}{с} cdot 5 space с = 40 space 000 space м = 40 space км$.
Ответ: $S_1 = 110 space м$, $S_2 = 100 space м$, $S_3 = 40 space км$.
Упражнение №2
На велосипеде можно без особого напряжения ехать со скоростью $3 frac{м}{с}$. На какое расстояние можно уехать за $1.5 space ч$?
Дано:
$t = 1.5 space ч$
$upsilon = 3 frac{м}{с}$
СИ:
$t = 5400 space с$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем путь, который можно проехать на велосипеде с указанной скоростью:
$S = upsilon t$,
$S = 3 frac{м}{с} cdot 5400 space с = 16 space 200 space м = 16.2 space км$.
Ответ: $S = 16.2 space км$.
Упражнение №3
На рисунке 4 показан график зависимости пути равномерного движения тела от времени ($S$ — ось пройденного пути, $t$ — ось времени). По этому графику найдите, чему равен путь, пройденный телом за $2 space ч$. Затем рассчитайте скорость тела.
Определим из графика путь, пройденный телом за $2 space ч$. Этому времени на графике соответствует значение пути, равное $200 space км$. Запишем условие задачи и решим ее.
Дано:
$S = 200 space км$
$t = 2 space ч$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитываем по формуле:
$upsilon = frac{S}{t}$.
$upsilon = frac{200 space км}{2 space ч} = 100 frac{км}{ч}$.
Ответ: $upsilon = 100 frac{км}{ч}$.
Упражнение №4
График зависимости скорости равномерного движения тела от времени представлен на рисунке 5. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за $2 space ч$, $4 space ч$.
Из графика видно, что скорость тела равна $8 frac{м}{с}$. Этот график представляет собой прямую, параллельную оси времени, потому что движение равномерное, и скорость тела не изменяется с течением времени. Запишем условие задачи и решим ее.
Дано:
$t_1 = 2 space ч$
$t_2 = 4 space ч$
$upsilon = 8 frac{м}{с}$
СИ:
$t_1 = 7200 space с$
$t_2 = 14 space 400 space с$
$S_1 — ?$
$S_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь рассчитаем по формуле: $S = upsilon t$.
За $2 space ч$ тело пройдет путь:
$S_1 = upsilon t_1$,
$S_1 = 8 frac{м}{с} cdot 7200 space с = 57 space 600 space м = 57.6 space км$.
За $4 space ч$ тело пройдет путь:
$S_2 = upsilon t_2$,
$S_2 = 8 frac{м}{с} cdot 14 space 400 space с = 115 space 200 space м = 115.2 space км$.
Ответ: $S_1 = 57.6 space км$, $S_2 = 115.2 space км$.
Упражнения №5
По графикам зависимости путей от времени (рисунок 6) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?
Для того, чтобы рассчитать скорость тела, нам нужно знать путь и время, за которое этот путь был пройден. Возьмем эти значения для двух тел из их графиков. Первое тело (I) проходит путь, равный $4 space м$, за $2 space с$. Второе тело (II) проходит путь, равный $4 space м$, за $4 space с$. Запишем условие задачи и решим ее.
Дано:
$S = 4 space м$
$t_1 = 2 space с$
$t_2 = 4 space с$
$upsilon_1 — ?$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость первого тела:
$upsilon_1 = frac{S}{t_1}$,
$upsilon_1 = frac{4 space м}{2 space с} = 2 frac{м}{с}$.
Рассчитаем скорость второго тела:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{4 space м}{4 space с} = 1 frac{м}{с}$.
Получается, что скорость первого тела больше скорости второго.
Ответ: $upsilon_1 = 2 frac{м}{с}$, $upsilon_2 = 1 frac{м}{с}$, $upsilon_1 > upsilon_2$.
1. Нахождение пути по графику зависимости скорости от времени
Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени.
Начнем с самого простого случая – равномерного движения. На рисунке 6.1 изображен график зависимости v(t) – скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении скорость постоянна.
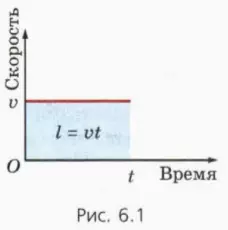
Фигура, заключенная под этим графиком, – прямоугольник (он закрашен на рисунке). Его площадь численно равна произведению скорости v на время движения t. С другой стороны, произведение vt равно пути l, пройденному телом. Итак, при равномерном движении
путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени.
Покажем теперь, что этим замечательным свойством обладает и неравномерное движение.
Пусть, например, график зависимости скорости от времени имеет вид кривой, изображенной на рисунке 6.2.
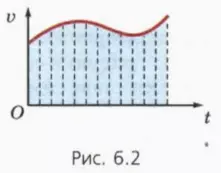
Разобьем мысленно все время движения на столь малые промежутки, чтобы в течение каждого из них движение тела можно было считать практически равномерным (это разбиение показано штриховыми линиями на рисунке 6.2).
Тогда путь, пройденный за каждый такой промежуток, численно равен площади фигуры под соответствующим ком графика. Поэтому и весь путь равен площади фигур заключенной под всем графиком. (Использованный нами прием лежит в основе интегрального исчисления, основы которого вы будете изучать в курсе «Начала математического анализа».)
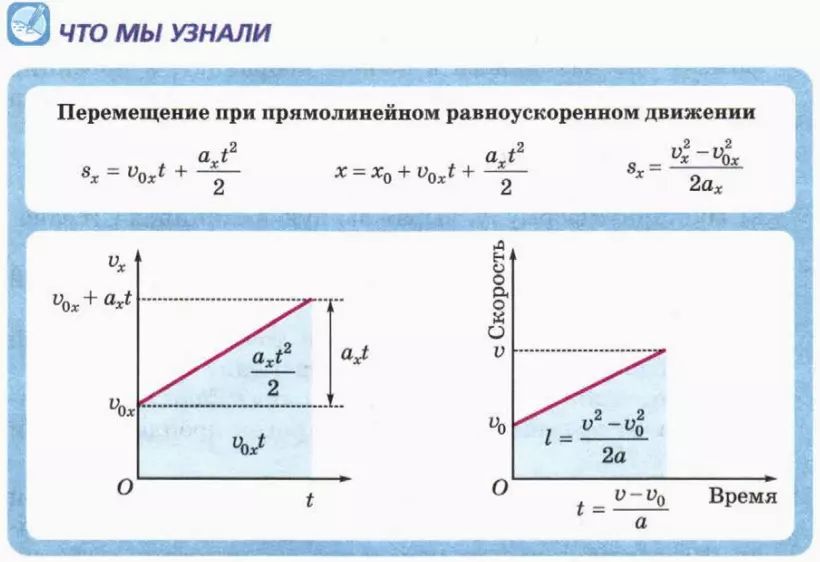
2. Путь и перемещение при прямолинейном равноускоренном движении
Применим теперь описанный выше способ нахождения пути к прямолинейному равноускоренному движению.
Начальная скорость тела равна нулю
Направим ось x в сторону ускорения тела. Тогда ax = a, vx = v. Следовательно,
v = at. (1)
На рисунке 6.3 изображен график зависимости v(t).
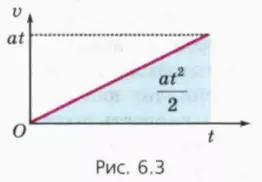
? 1. Используя рисунок 6.3, докажите, что при прямолинейном равноускоренном движении без начальной скорости путь l выражается через модуль ускорения a и время движения t формулой
l = at2/2. (2)
Главный вывод:
при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату времени движения.
Этим равноускоренное движение существенно отличается от равномерного.
На рисунке 6.4 приведены графики зависимости пути от времени для двух тел, одно из которых движется равномерно, а другое – равноускоренно без начальной скорости.
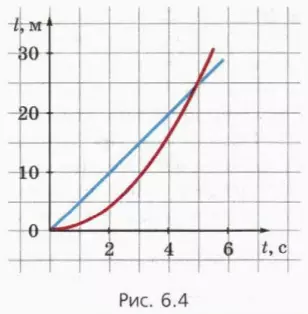
? 2. Рассмотрите рисунок 6.4 и ответьте на вопросы.
а) Каким цветом изображен график для тела, движущегося равноускоренно?
б) Чему равно ускорение этого тела?
в) Чему равны скорости тел в тот момент, когда они прошли одинаковый путь?
г) В какой момент времени скорости тел равны?
? 3. Тронувшись с места, автомобиль за первые 4 с проехал расстояние 20 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какое расстояние проедет автомобиль:
а) за 8 с? б) за 16 с? в) за 2 с?
Найдем теперь зависимость проекции перемещения sx от времени. В данном случае проекция ускорения на ось x положительна, поэтому sx = l, ax = a. Таким образом, из формулы (2) следует:
sx = axt2/2. (3)
Формулы (2) и (3) очень похожи, что приводит порой к ошибкам при решении простых задач. Дело в том, что значение проекции перемещения может быть отрицательным. Так будет, если ось x направлена противоположно перемещению: тогда sx < 0. А путь отрицательным быть не может!
? 4. На рисунке 6.5 изображены графики зависимости от времени пути и проекции перемещения для некоторого тела. Какой цвет у графика проекции перемещения?
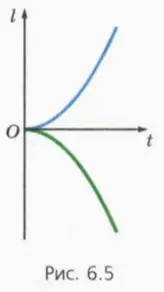
Начальная скорость тела не равна нулю
Напомним, что в таком случае зависимость проекции скорости от времени выражается формулой
vx = v0x + axt, (4)
где v0x – проекция начальной скорости на ось x.
Мы рассмотрим далее случай, когда v0x > 0, ax > 0. В этом случае снова можно воспользоваться тем, что путь численно равен площади фигуры под графиком зависимости скорости от времени. (Другие комбинации знаков проекции начальной скорости и ускорения рассмотрите самостоятельно: в результате получится та же общая формула (5).
На рисунке 6.6 изображен график зависимости vx(t) при v0x > 0, ax > 0.
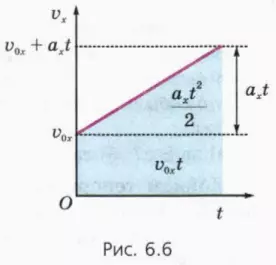
? 5. Используя рисунок 6.6, докажите, что при прямолинейном равноускоренном движении с начальной скоростью проекция перемещения
sx = v0x + axt2/2. (5)
Эта формула позволяет найти зависимость координаты x тела от времени. Напомним (см. формулу (6), § 2), что координата x тела связана с проекцией его перемещения sx соотношением
sx = x – x0,
где x0 — начальная координата тела. Следовательно,
x = x0 + sx, (6)
Из формул (5), (6) получаем:
x = x0 + v0xt + axt2/2. (7)
6. Зависимость координаты от времени для некоторого тела, движущегося вдоль оси x, выражается в единицах СИ формулой x = 6 – 5t + t2.
а) Чему равна начальная координата тела?
б) Чему равна проекция начальной скорости на ось x?
в) Чему равна проекция ускорения на ось x?
г) Начертите график зависимости координаты x от времени.
д) Начертите график зависимости проекции скорости от времени.
е) В какой момент скорость тела равна нулю?
ж) Вернется ли тело в начальную точку? Если да, то в какой момент (моменты) времени?
з) Пройдет ли тело через начало координат? Если да, то в какой момент (моменты) времени?
и) Начертите график зависимости проекции перемещения от времени.
к) Начертите график зависимости пути от времени.
3. Соотношение между путем и скоростью
При решении задач часто используют соотношения между путем, ускорением и скоростью (начальной v0, конечной v или ими обеими). Выведем эти соотношения. Начнем с движения без начальной скорости. Из формулы (1) получаем для времени движения:
t = v/a. (8)
Подставим это выражение в формулу (2) для пути:
l = at2/2 = a/2(v/a)2 = v2/2a. (9)
Главный вывод:
при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату конечной скорости.
? 7. Тронувшись с места, автомобиль набрал скорость 10 м/с на пути 40 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какой путь от начала движения проехал автомобиль, когда его скорость была равна: а) 20 м/с? б) 40 м/с? в) 5 м/с?
Соотношение (9) можно получить также, вспомнив, что путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени (рис. 6.7).
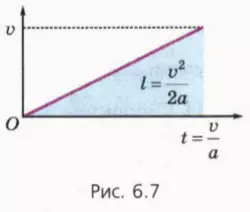
Это соображение поможет вам легко справиться со следующим заданием.
? 8. Используя рисунок 6.8, докажите, что при торможении с постоянным ускорением тело проходит до полной остановки путь lт = v02/2a, где v0 – начальная скорость тела, a – модуль ускорения.
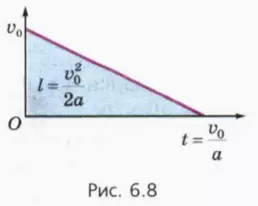
В случае торможения транспортного средства (автомобиль, поезд) путь, пройденный до полной остановки, называют тормозным путём. Обратите внимание: тормозной путь при начальной скорости v0 и путь, пройденный при разгоне с места до скорости v0 с тем же по модулю ускорением a, одинаковы.
? 9. При экстренном торможении на сухом асфальте ускорение автомобиля равно по модулю 5 м/с2. Чему равен тормозной путь автомобиля при начальной скорости: а) 60 км/ч (максимальная разрешенная скорость в городе); б) 120 км/ч? Найдите тормозной путь при указанных скоростях во время гололеда, когда модуль ускорения равен 2 м/с2. Сравните найденные вами значения тормозного пути с длиной классной комнаты.
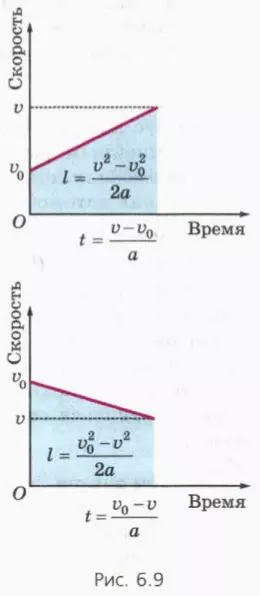
? 10. Используя рисунок 6.9 и формулу, выражающую площадь трапеции через ее высоту и полусумму оснований, докажите, что при прямолинейном равноускоренном движении:
а) l = (v2 – v02)/2a, если скорость тела увеличивается;
б) l = (v02 – v2)/2a, если скорость тела уменьшается.
? 11. Докажите, что проекции перемещения, начальной и конечной скорости, а также ускорения связаны соотношением
sx = (vx2 – v0x2)/2ax (10)
? 12. Автомобиль на пути 200 м разогнался от скорости 10 м/с до 30 м/с.
а) С каким ускорением двигался автомобиль?
б) За какое время автомобиль проехал указанный путь?
в) Чему равна средняя скорость автомобиля?
Лютый опыт
Дополнительные вопросы и задания
13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон – с постоянным ускорением до полной остановки.
а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.
б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?
14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин – равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.
а) Начертите схематически график зависимости проекции скорости электрички от времени.
б) Используя этот график, найдите расстояние между станциями.
в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором – тормозила? Какова была бы при этом ее максимальная скорость?
15. Тело движется равноускоренно вдоль оси x. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.
а) Чему равна проекция ускорения тела?
б) Постройте график зависимости vx(t).
в) Напишите формулу, выражающую в единицах СИ зависимость x(t).
г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?
д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?
е) Вернется ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?
16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени t1 и t2 после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.
а) Направьте ось x вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика v0 и модуль ускорения шарика a.
б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t1 и t2 составьте систему двух уравнений с двумя неизвестными v0 и a.
в) Решив эту систему уравнений, выразите v0 и a через b, t1 и t2.
г) Выразите весь пройденный шариком путь l через b, t1 и t2.
д) Найдите числовые значения v0, a и l при b = 30 см, t1 = 1с, t2 = 2 с.
е) Постройте графики зависимости vx(t), sx(t), l(t).
ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.
- Прямолинейное равномерное движение на координатной прямой
- Уравнение прямолинейного равномерного движения
- Удобная система отсчета для решения задачи о прямолинейном движении
- График движения x=x(t)
- Как найти уравнение движения по графику движения?
- График скорости vx=vx(t)
- Как найти путь и перемещение по графику скорости?
- Задачи
п.1. Прямолинейное равномерное движение на координатной прямой
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin{gather*} x=x_0+s=x_0+vt\ x=20+10t end{gather*}

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin{gather*} x=x_0-st=x_0-vt\ x=20-10t end{gather*} Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Основная задача механики – уметь определять положение тела в пространстве в любой момент времени.
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
Назовем проекцией вектора скорости (overrightarrow{x}) на параллельную ему ось координат OX величину (v_x=pm|overrightarrow{v}|=pm v).
Знак проекции определяется следующим правилом:
- если направление вектора (overrightarrow{v}) совпадает с направлением оси OX, то (v_x=vgt 0)
- если направление вектора (overrightarrow{v}) противоположно направлению оси OX, то (v_x=-vlt 0)
В любой момент времени t координата тела x(t) при прямолинейном равномерном движении описывается уравнением: $$ x(t)=x_0+v_x t $$ где (x_0) – координата в начальный момент времени, (v_x) – проекция вектора скорости движения.
Проекция перемещения (overrightarrow{r}) на параллельную ему ось координат OX в любой момент времени t определяется формулой: $$ triangle x=x(t)-x_0 $$ Знак (triangle x) указывает на направление совершенного перемещения:
- если (triangle xgt 0), перемещение (overrightarrow{r}) произошло в направлении оси OX;
- если (triangle xlt 0), перемещение (overrightarrow{r}) произошло противоположно направлению оси OX.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Прямолинейное движение описывается с помощью координатной прямой, параллельной направлению движения тела.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
В осях (t) и (x) график (x(t)=x_0+v_x t) является прямой.
Эта прямая:
- возрастает, если (v_xgt 0)
- убывает, если (v_xlt 0)
- постоянна (параллельна оси (t)), если (v_x= 0)
 |
Построим графики зависимости координаты от времени для нашего примера:
x=20+10t – машина движется вправо (в направлении оси OX) |
п.5. Как найти уравнение движения по графику движения?

Шаг 1. Выбрать на прямой любые две точки (A(t_1,x_1)) и (B(t_2,x_2)).
Шаг 2. Найти проекцию скорости как отношение: $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{triangle x}{triangle t} $$ Шаг 3. Найти начальную координату по одной из формул: $$ x_0=x_1-v_x t_1 text{или} x_0=x_2-v_x t_2 $$ Шаг 4. Записать найденное уравнение движения: $$ x(t)=x_0+v_x t $$
п.6. График скорости vx=vx(t)
В осях (t) и (x) график (v_x(t)=v_x=const) является прямой, параллельной оси (t).
Эта прямая:
- расположена над осью (t), если (v_xgt 0)
- расположена под осью (t), если (v_xlt 0)
- совпадает с осью (t), если (v_x=0)
Для рассмотренного примера:
Внимание!
В отличие от алгебры, в физике масштабы на осях, как правило, разные.
Поэтому обязательно нужно:
1) указывать обозначения и единицы измерения физических величин, которым соответствуют оси графика;
2) подбирать масштабы так, чтобы с графиком было удобно работать.
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости: 
На графике скорости путь, пройденный за промежуток времени (triangle t=t_2-t_1) равен площади прямоугольника, длина которого равна (triangle t), а ширина (triangle |v_x|): $$ s=|v_x|triangle t $$
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
На графике скорости проекция перемещения на ось OX за промежуток времени (triangle t=t_2-t_1) равна площади (v_xtriangle t), с учетом знака: $$ triangle x=v_xtriangle t $$
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin{gather*} x_1=x(5)=8cdot 5=40 text{(м)}\ x_2=x(10)=8cdot 10=80 text{(м)} end{gather*}
б) Скорость (v_x=8) м/с – постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text{(м)} $$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac{x_2-x_1}{t_2-t_1}=frac{56-38}{2-1}=18 (text{тыс.км/ч}) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text{тыс.км/ч}) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text{тыс.км}) $$
г) Переведем скорость в км/с: $$ 18000frac{text{км}}{text{ч}}=frac{18000 text{км}}{1 text{ч}}=frac{18000 text{км}}{3600 text{c}}=5 text{км/c} $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
Физика
Тема 2: Кинематика
Урок 8: Графический способ нахождения пути и перемещения
- Видео
- Тренажер
- Теория
Заметили ошибку?
Графический способ нахождения пути и перемещения
При равномерном движении, проекция перемещения на ось х (S x) вычисляется как S x=v x t.
Если мы на графике изобразим зависимость скорости v xот времени, то получим прямую линию, параллельную оси t . Тогда S xна графике – это площадь прямоугольника

Если тело движется против оси х, то проекция скорости vнаправлена против оси х и v x будет отрицательной. Тогда

S x=−vx t.
При неравномерном движении, мы разбиваем проекцию перемещения на маленькие участки, где на каждом участке, скорость практически не менялась и движение равномерно

Сложив площади всех маленьких участков (где площадь каждого участка S x=v x t ¿, мы получим общую площадь под графиком, т. е. проекцию перемещения на ось t .

Задача 1
Электропоезд, отходящий от станции, в течение 0,5 мин двигался с ускорением 0,8 м/с2. Определите путь, который он прошёл за это время, и скорость в конце пути.
Дано

Решение

Задача 2
Тело движется прямолинейно вдоль оси ОХ (рис 8). График зависимости скорости V x от времени представлен на рисунке 7. По данному графику определите перемещение и путь, пройденные телом за время t = 6 с.

Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.
Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. Уравнение, которое описывает это движение, было выведено Галилеем в (XVI) веке. Необходимо помнить, что при прямолинейном равномерном или неравномерном движении модуль перемещения совпадает по своему значению с пройденным путём. Формула выглядит следующим образом:
, где (а) — это ускорение.
Сравним графики равномерного и равноускоренного движения.
Графики прямолинейного равномерного движения
Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость (a(t)) — прямая линия, которая лежит на оси времени.
Зависимость скорости от времени. Скорость со временем не изменяется, график (v(t)) — прямая линия, параллельная оси времени.
Правило определения пути по графику (v(t)): численное значение перемещения (пути) — это площадь прямоугольника под графиком скорости.
Зависимость пути от времени. График (s(t)) — наклонная линия.

Рис. (1). График зависимости скорости от времени при равномерном прямолинейном движении

Рис. (2). График зависимости пути от времени при равномерном прямолинейном движении
Графики равноускоренного движения
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график (a(t)) — прямая линия, параллельная оси времени.
Зависимость скорости от времени. Скорость изменяется согласно линейной зависимости.
Зависимость пути от времени. При равноускоренном движении путь изменяется согласно квадратной зависимости:
s=v0t+at22
. В координатах зависимость имеет вид:
x=x0+v0xt+axt22
.
Графиком является ветка параболы.

Рис. (3). График зависимости пути от времени при равноускоренном движении
Источники:
Рис. 1. График зависимости скорости от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 2. График зависимости пути от времени при равномерном прямолинейном движении. © ЯКласс.
Рис. 3. График зависимости пути от времени при равноускоренном движении. © ЯКласс.
