Как найти путь по течению формула

Через уравнение.

S – пройденный путь, растояние, которое прошла, например, лодка. (км)

t – время, за которое она прошла расстояние S. (часов, минут)

V – собственная её скорость (км/ч, м/ч)

Такие задачи решаются далее: если известны: (под формулы подставляем числа)

t и V, то перемножаем – t * V, получаем S.

t и S, то расстояние делим время – S : t, получаем V

S и V, также – S : V, получаем t

Также если в задаче указана V (её ищем)

по течению, то V собственная + V по течению

против течения, то V собств. – V прот. теч.

Тогда формулы звучат так: если известны:

t и V, то t * (V с. +/- V) = S

t и S, то S : t = V с. +/- V

V и S, то S : (V c. +/- V) = t

Теперь ещё раз:

V c. – собственная скорость

V c. + V – скорость + скорость по теч.

V c. – V – скорость + скорость прот. теч.

Ну так чтоли… Плохой из меня учитель(((

Привет! У тех, кто готовится к ОГЭ, возникает много вопросов по поводу задач на движение из второй части. И один из возможных вариантов таких задач – это задача про лодку, которая плывёт по течению и против течения. Сегодня разберем конкретный пример такой задачи:

Моторная лодка прошла 45 км против течения реки и вернулась в пункт отправления. При этом на обратный путь она затратила на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.

• Шаг № 1

Давайте для начала разберемся в самой ситуации. У каждой моторной лодки есть двигатель (мотор), который приводит её в движение. Если лодка плывёт, например, по пруду со стоячей водой, то она двигается только благодаря мотору. Скорость лодки в данном случае называется собственная скорость лодки. Её ничего не подгоняет и ничего не тормозит. Именно скорость лодки в неподвижной (стоячей) воде (то есть её собственную скорость) и просят найти авторы задания. То, что нужно найти, в задачах обозначается за «Х».

Итак, собственная скорость лодки = Х.

Лодка будет плыть с собственной скоростью только в неподвижной воде. Если переместить её на реку, то мы столкнёмся с таким явлением, как течение. В реке вода не стоит на месте: она движется в определённую сторону. Скорость течения реки в нашем задании = 3 км/ч.

Что же произойдёт, если лодка будет плыть по течению? Во-первых, её будет приводить в движение мотор. А во-вторых, ее будет подгонять течение. Логично, что по течению лодка будет двигаться быстрее, чем в стоячей воде.

Но как же найти скорость лодки по течению? Очень просто! Она равна сумме собственной скорости лодки и скорости течения реки.

Так как скорость течения нам известна по условию, а собственную скорость лодки мы уже обозначили за «Х», то нам лишь осталось подставить в формулу наши значения. То есть в нашем случае вычислить скорость лодки по течению можно так:

Vпо течению = Vсобственная + Vтечения

Vпо течению = Х + 3 км/ч.

А если лодка будет плыть против течения? В этом случае течение будет её не подгонять, а тормозить. Ведь вода движется в одну сторону, а лодка – в противоположную.

Значит теперь скорость будет меньше, чем в стоячей воде. Найти её можно так: вычесть из собственной скорости лодки скорость течения реки:

Вычислим скорость против течения для нашего случая:

Vпротив течения = Vсобственная – Vтечения

Vпротив течения = Х – 3 км/ч.

Отлично! Перед тем, как перейти к дальнейшим действиям, вспомним формулы для задач на движение:

• Шаг №2

Теперь давайте оформим таблицу, в которую занесем все наши данные. Так мы точно не запутаемся!

Для начала заполним столбик «Расстояние». Для пути против течения оно равно 45 км. Сказано, что лодка вернулась назад. В этом случае на обратном пути по течению она проплыла ровно столько же!

Со скоростями мы уже разобрались. Скорость по течению = Х + 3 км/ч, а против течения = Х – 3 км/ч.

Теперь разберемся со временем. Напомню, что оно вычисляется по формуле: расстояние поделить на скорость. Расстояния у нас есть, скорости тоже, и записать время нам ничего не мешает!

Отлично, все данные записаны, теперь переходим к основному решению!

• Шаг №3

Обратимся к условию ещё раз. Сказано, что на обратный путь по течению лодка затратила на 2 часа меньше, чем на путь против течения. Так что теперь работаем со временем.

Давайте обозначим время движения против течения за t1, а время движения по течению t2. Если на обратный путь было затрачено на 2 часа меньше, то путь «туда» на 2 часа больше.

Из вышесказанного делаем вывод, что t1 > t2 на 2 часа. Это значит, что если из t1 вычесть t2, то получится 2.

t1 – t2 = 2

А теперь подставим в наше выражение t1 – t2 = 2 вместо t1 и t2 наши значения из таблицы. Тогда мы получим замечательное уравнение, которое и поможет нам прийти к ответу.

• Шаг №4

Мы получили дробно-рациональное уравнение. Это значит, что неизвестный «Х» стоит в знаменателе.

И первый шаг в решении подобных уравнений – это запись ОДЗ (области допустимых значений). ОДЗ показывает, каким числом «Х» может быть, а каким – нет.

«Х» стоит в знаменателе, а основное, что мы знаем про знаменатель – это то, что он не может быть равен нулю, потому что на ноль делить нельзя. Запишем знаменатели наших дробей и отметим, что они не равны нулю:

1) Х – 3 ≠ 0

2) Х + 3 ≠ 0

Продолжаем работать с этой записью, как с уравнением:

1) Х ≠ 3

2) Х ≠ – 3

Значит, ОДЗ: Х ≠ ±3. “Х” также должен быть больше нуля, так как скорость (а за “Х” мы обозначили именно её) не может быть отрицательной.

Итог шага №4: ОДЗ: Х ≠ ±3; Х > 0

• Шаг №5

Продолжаем работу с уравнением. Мы разобрались с ОДЗ, а значит, можем с чистой совестью избавиться от знаменателя. Для этого умножим обе части уравнения на наименьший общий знаменатель.

Наименьший общий знаменатель (НОЗ) – это наименьшее число, которое делится на все знаменатели рассматриваемых дробей. В нашем случае это (Х – 3) (Х + 3). Он делится и на (Х – 3), и на (Х + 3). Вперед!

Чтобы лучше разобраться в сложных числовых махинациях, обратимся к подробной записи:

Обратите внимание, что дроби слева сокращаются, таким образом исчезает знаменатель.

Итак, вот что у нас получается:

45(х + 3) – 45(х – 3) = 2(х – 3)(х + 3)

Обратим внимание на скобки (х – 3)(х + 3). Они представляют собой разложенную разность квадратов. Вспомним эту формулу:

Скобки (х – 3)(х + 3) соответствуют части (a + b)(a – b) в формуле. Чтобы свернуть её обратно, нам нужно записать квадрат первого числа(Х^2), поставить знак минус, а затем записать квадрат второго числа (3^2 = 9).

45(х + 3) – 45(х – 3) = 2(х^2 – 9)

Предлагаю перенести все элементы в одну сторону. Напомню, что при переходе в противоположную сторону элемент должен поменять знак. То есть если справа мы видим 2(х^2 – 9), то перенести влево должны
– 2(х^2 – 9). При этом справа ничего не остаётся, поэтому ставим ноль. Приступим!

45(х + 3) – 45(х – 3) – 2(х^2 – 9) = 0

Теперь давайте раскроем скобки и приведем подобные слагаемые.

45(х + 3) – 45(х – 3) – 2(х^2 – 9) = 0

45х + 135 – 45х + 135 – 2х^2 + 18 = 0

Слагаемые 45х и – 45х в сумме дают ноль, поэтому их можно больше не записывать. Они «взаимоуничтожаются»

288 – 2х^2 = 0

Теперь перенесем все числовые значения вправо, а буквенные оставим слева, а затем продолжим решение:

– 2х^2 = – 288

x^2 = – 288/- 2

х^2 = 144

х = ±√144 = ±12.

Мы получили два корня. Корень – 12 нам не подходит, так как он отрицательный, а выше мы писали, что х > 0. А вот корень 12 удовлетворяет всем условиям, он нам подходит. Так как за “Х” мы обозначили собственную скорость лодки, которую и требуется найти в задании, то, решив это уравнение, мы получили ответ!

Ответ: 12 км/ч.

А вот решение без лишних пояснений:

Надеюсь, все было максимально понятно:)

До новых встреч!!

§ 1  Методика решения задач на движение по течению и против течения

Из всех текстовых задач на движение особое место занимают задачи на движение по течению и против течения реки. Для успешного их решения необходимо различать 4 вида движения: течение реки, собственное движение, движение по течению и движение против течения реки.

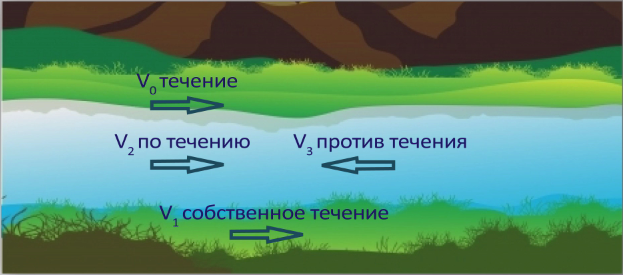
Вид движения «течение реки» встречается в тех задачах, в которых рассматриваются движения немеханизированных объектов, например, движение плота. Такой вид движения возможен только по течению и скорость движущегося объекта всегда совпадает со скоростью течения реки.

Собственное движение характерно для механизированных объектов в стоячей воде, например, катер движется по озеру.

Движение по течению и движение против течения реки формируется из двух видов движения – собственного и течения реки.

При движении по течению направления течения реки и движения объекта совпадают, поэтому скорость перемещения тела при этом виде движения равна сумме собственной скорости тела и скорости течения

vсобств + vтечения.

При движении против течения течение реки препятствует движению объекта, поэтому скорость перемещения тела при этом виде движения равна разности собственной скорости тела и скорости течения

vсобств– vтечения.

Полезно знать, что сумма скоростей по течению и против течения реки равна удвоенной собственной скорости

vпо теч + vпротив теч = 2vсобств,

а разность этих скоростей равна удвоенной скорости течения реки

vпо теч – vпротив теч = 2vтечения.

Часто упрощает решение задач на движение понимание взаимной обратной зависимости скорости и времени движения: чем больше время, тем меньше скорость движения, и, наоборот, чем больше скорость движения, тем меньше времени тратится на прохождение пути.

В качестве неизвестных в таких текстовых задачах удобно выбирать расстояние и скорости движущихся тел, если они не заданы. В задачах, где в условии не представлены единицы длины, принято весь путь брать за единицу длины, а часть этого пути выражают долей всего пути без наименования.

В текстовых задачах на движение, связанных с течением реки, при проведении смысловой проверки полезно знать, что моторная лодка имеет собственную скорость12 – 40 км/ч, скорость течения реки изменяется в пределах 1 – 4км/ч, а скорость лодки на вёслах составляет примерно 3 – 8км/ч.

Рассмотрим приёмы решения текстовых задач на движение по течению и против течения на примерах решения следующих задач.

§ 2  Примеры решения задач на движение по течению и против течения

Задача 1.От пристани А до пристани В моторная лодка по течению реки проходит за 6 часов, а возвращается за 10 часов. За сколько часов пройдёт расстояние от А до В плот?

РЕШЕНИЕ.Решим задачу арифметическим способом.

Мы знаем, что расстояние определяется по формуле S = vt, где v– скорость лодки, t– время движения лодки, выраженное в часах. В задаче не используются единицы длины, значит, расстояние от А до В обозначим за единицу 1.

По условию задачи моторная лодка по течению реки проходит за 6 часов, значит, скорость по течению реки равна 1 : 6.

Моторная лодка возвращается за 10 часов, значит, расстояние АВ против течения реки лодка проходит за 10 часов, следовательно, её скорость при таком движении равна одной десятой. Для того, чтобы найти время движения плота на дистанции АВ, надо найти скорость плота, которая совпадает со скоростью течения реки. Известно, что удвоенная скорость течения реки равна разности скоростей по течению и против течения, то есть 

2vтечения = vпо теч – vпротив теч.

Вычислив разность скоростей по течению и против течения реки, имеем

Таким образом, решив уравнение

получаем, что скорость течения реки

Получили, что за 1 час плот проплывёт одну тридцатую всего пути от пункта А до пункта В.

Чтобы найти время движения плота, надо путь 1 единицу разделить на скорость его движения.

Получили, что плот пройдёт расстояние от А до В за 30часов.

Ответ: 30 часов.

А теперь рассмотрим алгебраический способ решения данной задачи. введём переменные пусть х км/ч – собственная скорость моторной лодки, у км/ч – скорость течения реки.

Cоставим таблицу данных с введёнными переменными.

Обозначим в столбцах таблицы элементы движения:

v– скорость, выраженная в км/ч,

t– время, выраженное в часах,

S– расстояние, выраженное в км.

В строках – виды движения: собственное движение, течение, движение по течению, движение против течения. Заметим, что движение течения и движение плота – это идентичные виды движения. Заполним таблицу согласно условий задачи.

В собственном виде движения мы ввели скорость движения лодки х км/ч, внесём её в соответствующую ячейку таблицы, в ячейках t и S поставим прочерк, так как эти данные не используются в данной задаче. В движении плота мы ввели скорость течения реки у км/ч, внесём в таблицу, а ячейки t и S заполним позже.

В движении по течению реки выразим скорость v суммой скоростей лодки и течения, то есть х + у км/ч, время t по условию задачи равно 6ч, значит, можем выразить расстояние от пункта А до пункта В. Оно равно 6(х + у)км.

В движении против течения реки выразим скорость vразностью скоростей лодки и течения, то есть х – у км/ч, время t по условию задачи равно 10ч, значит, можем выразить расстояние от пункта А до пункта В. Оно равно 10(х – у)км.

В движениях по течению и против течения реки расстояния равны между собой, значит, можем составить уравнение 6(х + у) = 10(х – у).

Дополним строку движения плота: расстояние S будет равно расстоянию движения по течению или против течения, значит, можем вписать выражение 6(х + у) км или 10(х – у) км.

Теперь можем выразить время движения плота

Или

Из уравнения 6(х + у) = 10(х – у) выразим одну переменную через другую, например, переменную х через у.

Имеем, 6х + 6у = 10х – 10у.

Отсюда получаем 4х = 16у, следовательно, х = 4у.

Подставим 4у вместо х в одно из выражений времени движения плота, имеем

Мы ответили на главный вопрос задачи: за 30 часов плот пройдёт расстояние от А до В.

Решим эту же задачу графическим способом.

Зададим координатную плоскость: по горизонтальной оси абсцисс будем отмечать время движения, по вертикальной оси ординат отметим расстояние АВ. По течению реки лодка прошла 6 часов, значит, изобразим движение лодки синим отрезком АС с концами в точках А(0; 0) и С(6; АВ).

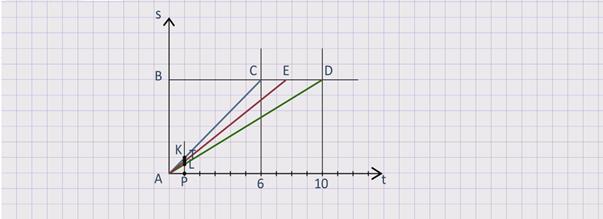
Против течения реки лодка прошла 10 часов, значит, изобразим движение лодки зелёным отрезком АD с концами в точках A(0; 0) и D(10; АВ). Рассмотрим на синей и зелёной линиях точки с абсциссой 1 и отметим их точками K и L соответственно. Точку на оси абсцисс с абсциссой 1 обозначим буквой Р. Таким образом, отрезок РК моделирует скорость движения лодки по течению, PL моделирует скорость движения лодки против течения.

Так как собственная скорость лодки есть среднее арифметическое между скоростями по течению и против течения реки, то линия собственного движения будет расположена между синей и зелёной линиями и будет являться медианой треугольника, образованного этими линиями и прямой х = 1. Обозначим середину отрезка КL точкой Т. Отрезок РТ моделирует собственную скорость движения лодки, Чтобы ответить на главный вопрос задачи, надо расстояние АВ поделить на скорость течения реки. Эта скорость моделируется на графикеравными отрезками КТ и ТL. Отрезки будут равны, так как они отражают разность скоростей по течению и собственной или разность скоростей собственной и против течения.

Отметим красным цветом отрезок АЕ с концами в точке А(0;0) и точке Е – точкой пересечения луча АЕ с прямой у = АВ, лежащий на отрезке АТ. Таким образом, время движения плота равно отношению длины отрезка АВ к длине отрезка КТ или АВ к длине отрезка TL, то есть

Чтобы найти длину отрезка KТ, надо найти полуразность скоростей по течению и против течения реки, а значит, полуразность длин отрезков РК и РL, то есть (РК – PL) : 2.

Так как АВ = 6РК = 10PL, то PL = 0,6PK. Имеем,

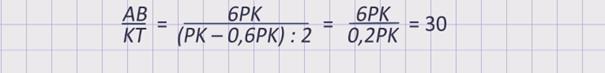
Получили, что плот пройдёт расстояние АВ за 30 часов.

Таким образом, на этом занятии мы решили одну и ту же задачу тремя различными способами и увидели, что ответ на главный вопрос задачи не зависит от способа её решения. Во всех трёх случаях мы получили один и тот же ответ.

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.