Как найти путь при движении по окружности

1.Равномерное
движение по окружности

2.Угловая скорость
вращательного движения.

3.Период вращения.

4.Частота вращения.

5.Связь линейной
скорости с угловой.

6.Центростремительное
ускорение.

7.Равнопеременное
движение по окружности.

8.Угловое ускорение
в равнопеременном движении по окружности.

9.Тангенциальное
ускорение.

10.Закон равноускоренного
движения по окружности.

11. Средняя угловая
скорость в равноускоренном движении
по окружности.

12.Формулы,
устанавливающие связь между угловой
скоростью, угловым ускорением и углом
поворота в равноускоренном движении
по окружности.

1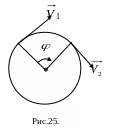
.Равномерное
движение по окружности
– движение, при котором материальная
точка за равные интервалы времени
проходит равные отрезки дуги окружности,
т.е. точка движется по окружности с
постоянной по модулю скоростью. В этом
случае скорость равна отношению дуги
окружности, пройденной точкой ко времени
движения, т.е.

и называется
линейной скоростью движения по окружности.

Как и в криволинейном
движении вектор скорости направлен по
касательной к окружности в направлении
движения (Рис.25).

2. Угловая
скорость в равномерном движении по
окружности
– отношение угла поворота радиуса ко
времени поворота:

В равномерном
движении по окружности угловая скорость
постоянна. В системе СИ угловая скорость
измеряется в(рад/c).
Один радиан – рад это центральный угол,
стягивающий дугу окружности длиной
равной радиусу. Полный угол содержит

радиан, т.е. за один оборот радиус
поворачивается на угол

радиан.

3. Период
вращения –
интервал времени Т, в течении которого
материальная точка совершает один
полный оборот. В системе СИ период
измеряется в секундах.

4. Частота
вращения –
число оборотов

,
совершаемых за одну секунду. В системе
СИ частота измеряется в герцах ( 1Гц =
1
)
. Один герц – частота, при которой за
одну секунду совершается один оборот.
Легко сообразить, что

Если за время t
точка совершает n
оборотов по окружности то

.

Зная период и
частоту вращения, угловую скорость
можно вычислять по формуле:

или

5 Связь
линейной скорости с угловой.
Длина дуги окружности равна

где
центральный
угол, выраженный в радианах, стягивающий
дугу

радиус
окружности. Теперь линейную скорость
запишем в виде

,
где

.

Ч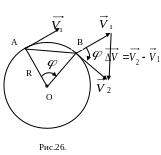
асто
бывает удобно использовать формулы:

или

Угловую скорость часто называют
циклической частотой, а частоту

линейной
частотой.

6. Центростремительное
ускорение.
В равномерном движении по окружности
модуль скорости остаётся неизменным

,
а направление её непрерывно меняется
(Рис.26). Это значит, что тело, движущееся
равномерно по окружности, испытывает
ускорение, которое направлено к центру
и называется центростремительным
ускорением.

Пусть за промежуток
времени

прошло путь равный дуге окружности

.
Перенесём вектор

,
оставляя его параллельным самому себе,
так чтобы его начало совпало с началом
вектора

в точке В. Модуль изменения скорости
равен

,
а модуль центростремительного ускорения
равен

На Рис.26 треугольники
АОВ и ДВС равнобедренные и углы при
вершинах О и В равны, как углы с взаимно
перпендикулярными сторонами АО
и
ОВ

Это значит, что треугольники АОВ и ДВС
подобные. Следовательно

Если

то
есть интервал времени

принимает сколь угодно малые значения,
то дугу

можно
приближенно считать равной хорде АВ,
т.е.

.
Поэтому можем записать

Учитывая,
что ВД=
,
ОА=R
получим

Умножая обе части последнего равенства
на

,
получим

и далее выражение для модуля
центростремительного ускорения в
равномерном движении по окружности:

.
Учитывая,
что

получим две часто применяемые формулы:

,

.

Итак, в равномерном
движении по окружности центростремительное
ускорение постоянно по модулю.

Легко сообразить,
что в пределе при

,
угол

.
Это значит, что углы при основании ДС
треугольника ДВС стремятся значению

,
а вектор изменения скорости
становится
перпендикулярным к вектору скорости

,
т.е. направлен по радиусу к центру
окружности.

7. Равнопеременное
движение по окружности
– движение по окружности, при котором
за равные интервалы времени угловая
скорость изменяется на одну и ту же
величину.

8. Угловое
ускорение в равнопеременном движении
по окружности
– отношение изменения угловой скорости
к интервалу времени

,
в течении которого это изменение
произошло, т.е.

где

начальное
значение угловой скорости,

конечное
значение угловой скорости,

угловое ускорение, в системе СИ измеряется
в

.
Из последнего равенства получим формулы
для вычисления угловой скорости

и

,
если

.

Умножая обе части
этих равенств на

и учитывая, что

–
тангенциальное ускорение, т.е. ускорение,
направленное по касательной к окружности
, получим формулы для вычисления линейной
скорости:

и

,
если

9. Тангенциальное
ускорение
численно равно изменению скорости в
единицу времени и направлено вдоль
касательной к окружности. Если

>0,

>0,
то движение равноускоренное. Если

<0
и

<0
– движение.

10. Закон
равноускоренного движения по окружности.
Путь, пройденный по окружности за время

в равноускоренном движении, вычисляется
по формуле:

Подставляя сюда

,

сокращая на

,
получим закон равноускоренного движения
по окружности:

,
или

,
если

Если же движение равнозамедленное, т.е.

<0,
то

1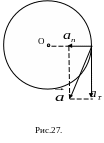
1.Полное
ускорение в равноускоренном движении
по окружности.
В равноускоренном движении по окружности
центростремительное ускорение с
течением времени возрастает, т.к.
благодаря тангенциальному ускорению
возрастает линейная скорость. Очень
часто центростремительное ускорение
называют нормальным и обозначают как

.
Так как

полное ускорение в данный момент
определяют по теореме Пифагора

(Рис.27).

12. Средняя
угловая скорость в равноускоренном
движении по окружности.
Средняя линейная скорость в равноускоренном
движении по окружности равна

.
Подставляя сюда

и сокращая на

получим

Если

,
то

.

12. Формулы,
устанавливающие связь между угловой
скоростью, угловым
ускорением
и углом поворота в равноускоренном
движении по окружности.

Подставляя в
формулу

величины

,

,
,

и сокращая на

,
получим

Если

,
то

и далее

,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности

Наряду с движением вдоль прямой в школьной физике рассматривают движение по окружности. Для него, по аналогии с прямолинейным движением, вводятся понятия пройденного пути, скорости движения и ускорения.

В физике выделяют несколько видов движения тел. Движение по окружности – это один из случаев движения вдоль кривой линии — криволинейного движения.

Сравним понятия пройденного пути, скорости и ускорения для прямолинейного движения и движения по окружности.

Угловой путь

Для начала, вспомним, что линейное перемещение – это разница между конечным и начальным положением точки на оси (рис. 1).

Рассмотрим теперь колесо (рис. 2). На горизонтальной линии, проходящей через диаметр колеса, справа отметим красную точку, от которой мы начнем отсчитывать углы. Условимся считать, что возле этой точки находится нулевой угол.

На ободе колеса выберем точку, например — ниппель. Сначала ниппель находился в точке 1. Точка 1 сдвинута на угол (gamma_<1>) относительно начала отсчета.

Будем вращать колесо в направлении, обозначенном синей стрелкой. Повернем колесо на некоторый угол, так, чтобы к концу движения ниппель переместился в точку, обозначенную цифрой 2 на рисунке. Эта точка смещена на угол (gamma_<2>) по отношению к началу отсчета.

По аналогии с поступательным движением, угловой путь, который прошел ниппель — это разница (разность) угловых положений точек 1 и 2.

(varphi left( text<рад>right)) – угловой путь измеряется в радианах.

Угловой путь – это угол, на который повернулся ниппель, по отношению к его начальному положению.

Угловая скорость — куда она направлена

Если тело двигалось равномерно (с неизменной скоростью), то линейную скорость можно определить по формуле

(v left( frac<text<м>> right)) — линейная скорость – это путь, деленный на время, поэтому она имеет размерность метров деленных на секунду.

Аналогично линейному случаю, если угловой путь поделить на время движения, получим угловую скорость.

(omega left( frac<text<рад>> right)) – угловая скорость – это угловой путь, деленный на время, поэтому она имеет размерность радиан деленных на секунду.

Угловая скорость ( omega ), так же, как и линейная скорость, является вектором. Но в отличии от линейной скорости его направление можно определить по правилу буравчика (правого винта).

Примечание: Направление вектора угловой скорости ( vec <omega>) можно определить по правилу буравчика (правого винта)!

На рисунке 3 окружность располагается в горизонтальной плоскости, а вектор ( vec<omega >) направлен вдоль вертикальной оси вращения. Направление вращения указано синей стрелкой.

При движении по окружности вектор линейной скорости (vec) изменяет свое направление. Но в каждой точке окружности вектор (vec) направлен по касательной к окружности, т. е. перпендикулярно радиусу.

Примечание: Касательная и радиус перпендикулярны, это известно из геометрии.

Если точка начнет вращаться в противоположную сторону, то векторы линейной и угловой скорости развернутся противоположно направлениям, указанным на рисунке 3.

Связь между линейной и угловой скоростью

Угловая и линейная скорость связаны математически. Линейная скорость – это векторное произведение вектора угловой скорости и вектора радиуса окружности.

Примечание: Радиус окружности – это вектор, он направлен от центра окружности к ее внешней границе.

Скалярный вид записи связи скоростей:

(omega left( frac<text<рад>> right)) – угловая скорость;

(v left( frac<text<м>> right)) — линейная скорость;

(R left( text<м>right)) – радиус окружности.

Частота и период

Вращательное движение описывают с помощью таких характеристик, как частота и период.

Период обращения – это время одного полного оборота. В системе СИ период измеряют в секундах.

( T left(c right)) – время, за которое тело совершило полный оборот – период. Время – это скалярная величина.

Частота отвечает на вопрос: «Сколько полных оборотов совершило тело за одну секунду?».

( displaystyle nuleft( frac<1> right)) – частота оборотов, скаляр.

Вместо записи ( displaystyle left( frac<1> right)) иногда используют (displaystyle left( c^ <-1>right)), или ( left( text <Гц>right)) – Герц. Это фамилия Генриха Герца, знаменитого физика.

[displaystyle 1 text <Гц>= frac<1> = c^ <-1>]

Частота и период связаны обратной пропорциональностью:

Количество оборотов

Двигаясь по окружности достаточное время, тело может пройти не один оборот. Зная угловой путь (varphi ) мы можем вычислить количество N оборотов.

( N ) – количество оборотов, скаляр. Обороты считают поштучно.

Связь между угловой скоростью и частотой

Разделим обе части уравнения на время t, в течение которого тело вращалось

Левая часть уравнения – это угловая скорость.

А дробь в правой части – это частота

Таким образом, мы получили связь между угловой скоростью и частотой

Примечание: Решая задачи на равноускоренное движение по окружности, удобно переходить от частоты к угловой скорости. Тогда можно будет применять аналогию с формулами для равноускоренного движения по прямой.

Репетитор
по физике

Задачи на движение по окружности .

(T) – период обращения ( время за которое тело совершает 1 оборот )

(N)-количество оборотов за все время

(n) – частота обращения
частота обращения это количество оборотов за 1 секунду
( n=dfrac<1> )

(l=2 pi R )-формула нахождения длины окружности
(S=vt ) – формула связывающая путь,скорость и время
длина и путь это одно и то же ( (S=l) )
(2 pi R=vt )
(2 pi R=vT )

(v) скорость
(T) период
(R) радиус
(piapprox 3,14)

1. Тело при движении по окружности совершает (N=10) оборотов за время (t=1 c). Найти период обращения тела
Показать ответ Показать решение Видеорешение

[spoiler title=”источники:”]

Движение по окружности

http://kornev-school.ru/f9_circular_motion.html

[/spoiler]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 ноября 2016 года; проверки требуют 5 правок.

О разновидности перекрёстков: см. Круговой перекрёсток.

В физике кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является окружностью, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение.

Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма.

Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.

Формулы для равномерного кругового движения[править | править код]

Рис. 1: Взаимосвязи векторов равномерного кругового движения; вектор Ω, представляющий вращение, перпендикулярен к плоскости орбиты.

Для движения по кругу радиуса R длина окружности будет C = 2π R. Если период вращения есть T, то угловая скорость вращения ω будет равна:

$omega ={frac {2pi }{T}} .$

Скорость движения объекта равна

$v,={frac {2pi R}{T}}=omega R$

Угол поворота θ за время t равен:

${displaystyle theta =2pi {frac {t}{T}}=omega t}$

Ускорение, вызванное изменением направления скорости, можно найти, если заметить, что скорость совершает полное изменение направления за то же самое время T, за которое объект делает один оборот. Тогда вектор скорости проходит путь длиной 2π v каждые T секунд, или:

$a,={frac {2pi v}{T}}=omega ^{2} R ,$

и направлено радиально к центру.

Взаимосвязи векторов показаны на рис. 1. Ось вращения изображена вектором Ω, перпендикулярно плоскости орбиты и имеет величину ω = dθ / dt. Направление вектора Ω выбрано в соответствии с правилом правой руки. По этому соглашению скорость это векторное произведение вида:

{mathbf {v}}={boldsymbol Omega }times {mathbf r} ,

и есть вектор, перпендикулярный как Ω так и r ( t ), направленный по касательной к орбите и имеющий величину ω R. Аналогично, ускорение определяется как:

{mathbf {a}}={boldsymbol Omega }times {mathbf v} ,

Оно представляет собой вектор, перпендикулярный как Ω так и v ( t ), имеющий величину ω |v| = ω² R и направление строго противоположно к r ( t ).

Постоянная скорость[править | править код]

В простейшем случае скорость, масса и радиус являются постоянными.

Рассмотрим тело массой один килограмм, движущееся по кругу радиуса один метр с угловой скоростью один радиан в секунду.

Теперь рассмотрим тело массы , движущееся по кругу радиуса с угловой скоростью

Переменная скорость[править | править код]

В круговом движении полную силу, приложенную к объекту, можно разложить на две составляющие: центростремительную, удерживающую тело на круговой орбите (т. е. меняющую направление вектора скорости), и тангенциальную, направленную по касательной к окружности и вызывающую изменение длины вектора скорости (т. е. меняющую скорость вращения тела по орбите). Величина центростремительной составляющей зависит от мгновенной скорости.

Для примера, когда камень привязан к концу верёвки, то он подвергается воздействию некоторой силы, которую мы можем разложить на радиальную и боковую составляющие. Радиальная направлена к центру (вовнутрь) окружности и вызвана тем, что веревка сопротивляется удлинению. А боковая составляющая определяет будет вращение камня ускоряться или замедляться.

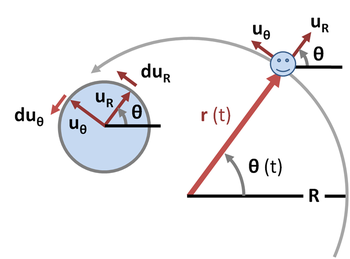
Описание кругового движения в полярных координатах[править | править код]

Траектория кругового движения тела может быть описана в полярной системе координат значениями фиксированного расстояние R от центра орбиты, являющейся точкой отсчёта, и угла ориентации θ (t) от некоторого фиксированного направления (рис. 2). Вектор перемещения является радиальным вектором от полюса до текущего положения:

${vec r}=R{hat u}_{R}(t) ,$

где ${hat u}_{R}(t)$ — единичный вектор, параллельный радиусу в момент t и направленный от полюса. Удобно также ввести единичный вектор, ортогональный к ${hat u}_{R}$ , который назовём ${hat u}_{theta }$ . Обычно его ориентация выбирается по направлению движения вдоль орбиты.

Скорость является производной перемещения по времени:

${vec v}={frac {d}{dt}}{vec r}(t)={frac {dR}{dt}}{hat u}_{R}+R{frac {d{hat u}_{R}}{dt}} .$

Поскольку радиус окружности является константой, радиальная составляющая скорости равна нулю. Единичный вектор ${hat u}_{R}$ имеет инвариантное по времени значение, так что при изменении времени его конец всегда лежит на окружности единичного радиуса, а угол θ такой же, как у . Если произошло малое приращение угла dθ за время dt, тогда ${hat u}_{R}$ описывает дугу единичной окружности со значением dθ (см. единичную окружность слева на рис. 2). Следовательно:

${frac {d{hat u}_{R}}{dt}}={frac {dtheta }{dt}}{hat u}_{theta } ,$

где направление изменения должно быть перпендикулярно к ${hat u}_{R}$ (или, другими словами, вдоль ${hat u}_{theta }$ ), поскольку любое изменение d ${hat u}_{R}$ в направлении ${hat u}_{R}$ будет изменять величину ${hat u}_{R}$ . Знак положительный, потому что увеличение dθ влияет на объект и ${hat u}_{R}$ передвигается в направлении ${hat u}_{theta }$ .
Следовательно, скорость становится:

${vec v}={frac {d}{dt}}{vec r}(t)=R{frac {d{hat u}_{R}}{dt}}=R{frac {dtheta }{dt}}{hat u}_{theta } =Romega {hat u}_{theta } .$

Ускорение тела также можно разложить на радиальную и тангенциальную составляющие. Ускорение есть производная скорости по времени:

${vec a}={frac {d}{dt}}{vec v}={frac {d}{dt}}left(R omega {hat u}_{theta } right) .$

$=Rleft({frac {domega }{dt}} {hat u}_{theta }+omega {frac {d{hat u}_{theta }}{dt}}right) .$

Производная по времени от ${hat u}_{theta }$ находится таким же путём, как и для ${hat u}_{R}$ . Опять же, ${hat u}_{theta }$ есть единичный вектор, и его конец расположен на единичной окружности, а угол равен π/2 + θ. Следовательно, приращение угла dθ вектора перемещает ${hat u}_{theta }$ по дуге на величину dθ, и поскольку ${hat u}_{theta }$ перпендикулярен к ${hat u}_{R}$ , мы имеем:

${frac {d{hat u}_{theta }}{dt}}=-{frac {dtheta }{dt}}{hat u}_{R}=-omega {hat u}_{R} ,$

где отрицательный знак необходим, чтобы сохранить ${hat u}_{theta }$ перпендикулярным к ${hat u}_{R}$ . (Иначе угол между ${hat u}_{theta }$ и ${hat u}_{R}$ будет уменьшаться с увеличением dθ, см. единичную окружность слева на рис. 2). Следовательно, ускорение равно:

${vec a}=Rleft({frac {domega }{dt}} {hat u}_{theta }+omega {frac {d{hat u}_{theta }}{dt}}right)$

$=R{frac {domega }{dt}} {hat u}_{theta }-omega ^{2}R {hat u}_{R} .$

Центростремительное ускорение — это радиальная составляющая, направленная по радиусу вовнутрь:

${vec a}_{R}=-omega ^{2}R{hat u}_{R} ,$

тогда как тангенциальная составляющая изменяет значение скорости:

${vec a}_{{theta }}=R{frac {domega }{dt}} {hat u}_{theta }={frac {dRomega }{dt}} {hat u}_{theta }={frac {d|{vec v}|}{dt}} {hat u}_{theta } .$

Описание кругового движения в комплексных числах[править | править код]

Круговое движение можно описать с использованием комплексных чисел. Пусть — ось вещественных чисел, а — ось мнимых чисел. Тогда положение тела может быть задано в виде комплексного “вектора” :

$z=x+iy=R(cos theta +isin theta )=Re^{{itheta }} ,$

где есть мнимая единица, и

есть угол комплексного вектора по отношению к вещественной оси как функция времени t.
Поскольку радиус есть константа:

где точка означает дифференциал по времени.
В этих обозначениях скорость имеет вид :

${displaystyle v={dot {z}}=R{frac {d}{dt}}left(itheta right)e^{itheta }=iR{dot {theta }}e^{itheta }=iomega cdot Re^{itheta }=iomega z}$

а ускорение:

$a={dot v}=i{dot omega }z+iomega {dot z}=(i{dot omega }-omega ^{2})z$

$=left(i{dot omega }-omega ^{2}right)Re^{{itheta }}$

$=-omega ^{2}Re^{{itheta }}+{dot omega }e^{{i{frac {pi }{2}}}}Re^{{itheta }} .$

Первое слагаемое направлено против вектора перемещения, а второе — перпендикулярно ему, как и в предыдущих результатах.

Ссылки[править | править код]

BIGS animation (англ.) Круговое движение
Circular Motion (англ.) – глава из онлайн-учебника

См. также[править | править код]

Момент импульса
Уравнения движения
Математический маятник
Центростремительная сила
Сила инерции

Источник

Угловой путь

[ S = x – x_{0} ]

Рис. 1. Линейное перемещение равно разности между конечным и начальным положениями точки на оси

Рис. 2. Точка из положения 1 сместилась в положение 2, пройдя угловой путь

На ободе колеса выберем точку, например — ниппель. Сначала ниппель находился в точке 1. Точка 1 сдвинута на угол (gamma_{1}) относительно начала отсчета.

Будем вращать колесо в направлении, обозначенном синей стрелкой. Повернем колесо на некоторый угол, так, чтобы к концу движения ниппель переместился в точку, обозначенную цифрой 2 на рисунке. Эта точка смещена на угол (gamma_{2}) по отношению к началу отсчета.

[large boxed{ varphi = gamma_{2} — gamma_{1} }]

(varphi left( text{рад}right)) – угловой путь измеряется в радианах.

Угловой путь – это угол, на который повернулся ниппель, по отношению к его начальному положению.

Угловая скорость — куда она направлена

Если тело двигалось равномерно (с неизменной скоростью), то линейную скорость можно определить по формуле

[v = frac{S}{t} ]

(v left( frac{text{м}}{c} right)) — линейная скорость – это путь, деленный на время, поэтому она имеет размерность метров деленных на секунду.

Аналогично линейному случаю, если угловой путь поделить на время движения, получим угловую скорость.

[ large boxed{ omega = frac{varphi}{t} } ]

(omega left( frac{text{рад}}{c} right)) – угловая скорость – это угловой путь, деленный на время, поэтому она имеет размерность радиан деленных на секунду.

Примечание: Направление вектора угловой скорости ( vec{omega} ) можно определить по правилу буравчика (правого винта)!

На рисунке 3 окружность располагается в горизонтальной плоскости, а вектор ( vec{omega }) направлен вдоль вертикальной оси вращения. Направление вращения указано синей стрелкой.

Рис. 3. Линейная и угловая скорости точки, вращающейся по окружности. Угловая скорость направлена по правилу правого винта вдоль оси вращения

При движении по окружности вектор линейной скорости (vec{v}) изменяет свое направление. Но в каждой точке окружности вектор (vec{v}) направлен по касательной к окружности, т. е. перпендикулярно радиусу.

Примечание: Касательная и радиус перпендикулярны, это известно из геометрии.

Связь между линейной и угловой скоростью

Примечание: Радиус окружности – это вектор, он направлен от центра окружности к ее внешней границе.

Векторный вид:

[large boxed{ left[vec{omega}, vec{R} right] = vec{v} }]

Скалярный вид записи связи скоростей:

[ large boxed{ omega cdot R = v }]

(omega left( frac{text{рад}}{c} right)) – угловая скорость;

(v left( frac{text{м}}{c} right)) — линейная скорость;

(R left( text{м}right)) – радиус окружности.

Частота и период

Вращательное движение описывают с помощью таких характеристик, как частота и период.

Период обращения – это время одного полного оборота. В системе СИ период измеряют в секундах.

( T left(c right)) – время, за которое тело совершило полный оборот – период. Время – это скалярная величина.

Частота отвечает на вопрос: «Сколько полных оборотов совершило тело за одну секунду?».

( displaystyle nuleft( frac{1}{c} right)) – частота оборотов, скаляр.

Вместо записи ( displaystyle left( frac{1}{c} right)) иногда используют (displaystyle left( c^{-1} right)), или ( left( text{Гц} right)) – Герц. Это фамилия Генриха Герца, знаменитого физика.

[displaystyle 1 text{Гц} = frac{1}{c} = c^{-1} ]

Частота и период связаны обратной пропорциональностью:

[ large boxed{ T = frac{1}{nu} } ]

Количество оборотов

[large boxed{ varphi = 2 pi cdot N }]

( N ) – количество оборотов, скаляр. Обороты считают поштучно.

Связь между угловой скоростью и частотой

Разделим обе части уравнения на время t, в течение которого тело вращалось

[ frac{varphi }{t} = 2 pi cdot frac{N}{t} ]

Левая часть уравнения – это угловая скорость.

[ large boxed{ frac{varphi }{t} = omega }]

А дробь в правой части – это частота

[ large boxed{ frac{N}{t} = nu }]

Таким образом, мы получили связь между угловой скоростью и частотой

[ large boxed{ left|vec{omega} right|= 2 pi cdot nu } ]

Источник

Задачи на движение по окружности .

( T=dfrac{t}{N} )

(T) – период обращения ( время за которое тело совершает 1 оборот )

(N)-количество оборотов за все время

(n) – частота обращения

частота обращения это количество оборотов за 1 секунду

( n=dfrac{1}{T} )

(l=2 pi R )-формула нахождения длины окружности
(S=vt ) – формула связывающая путь,скорость и время
длина и путь это одно и то же ( (S=l) )

(2 pi R=vt )
(2 pi R=vT )

(v=dfrac{2 pi R}{T} )

(v) скорость
(T) период
(R) радиус
(piapprox 3,14)

1. Тело при движении по окружности совершает (N=10) оборотов за время (t=1 c).
Найти период обращения тела
Показать ответ
Показать решение
Видеорешение

2. Тело при движении по окружности совершает (N=10) оборотов за время (t=50 c).
Найти период обращения тела
Показать ответ
Показать решение
Видеорешение

3. Тело при движении по окружности совершает (N=2000) оборотов за время (t=60 c).
Найти период обращения тела
Показать ответ
Показать решение
Видеорешение

4. Период обращения тела при движении по окружности равен (0,2 с).
Найти частоту обращения.

Показать ответ
Показать решение
Видеорешение

5. Период обращения тела при движении по окружности равен (8 с).
Найти частоту обращения.

Показать ответ
Показать решение
Видеорешение

6. Частота обращения тела при движении по окружности равна (100 Гц).
Найти период обращения.

Показать ответ
Показать решение
Видеорешение

7. Лопасть вентилятора совершает (N=2000) оборотов за время (t=50 c).
Каждая точка лопасти вентилятора движется по окружности.
Найти частоту обращения лопасти вентилятора (n).
Показать ответ
Показать решение
Видеорешение

9. При вращении винта вертолета каждая точка винта движется по окружности.
Найти линейную скорость (v) крайних точек винта вертолета,
если полный оборот совершается за 0,05 с, а радиус винта (R=5 м ).

Показать ответ
Показать решение
Видеорешение

10. Найти линейную скорость (v) крайних точек лопасти ветрогенератора,
если полный оборот совершается за 0,5 с, а радиус лопасти (R=1 м ).

Показать ответ
Показать решение
Видеорешение

11. Лопасть вентилятора совершает (N=2000) оборотов за время (t=157 c).
Каждая точка лопасти вентилятора движется по окружности.Радиус лопасти (R=0,2 м ).
Найти линейную скорость крайних точек лопасти вентилятора (v).
Показать ответ
Показать решение
Видеорешение

12.
Найти линейную скорость крайней точки минутной стрелки кремлевских курантов,
если ее длина составляет 3,27 метра.
Принять ( pi=3,14 . )

Дать ответ в сантиметрах в секунду, округлить до десятых.

Показать ответ
Показать решение
Видеорешение

Источник

I. Механика

Тестирование онлайн

Угловая скорость

Период и частота

Линейная скорость

Центростремительное ускорение

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

Движение по окружности

Угловой путь

Угловая скорость — куда она направлена

Связь между линейной и угловой скоростью

Частота и период

Количество оборотов

Связь между угловой скоростью и частотой