Как найти путь при вращательном движении

Содержание:

Вращательное движение тела:

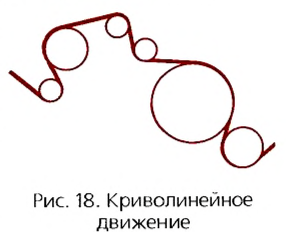
До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18).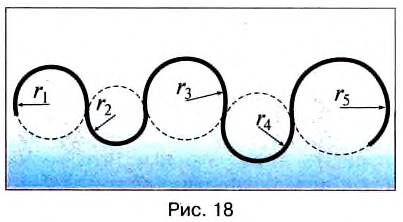

Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.

Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.

Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги

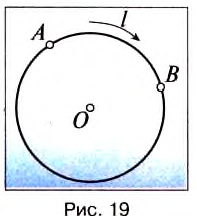
где 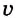— скорость движения тела по окружности; 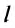— пройденный телом путь (длина дуги);  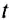— время движения тела.

Направление скорости проще всего определить на опыте.

Опыт:

К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).

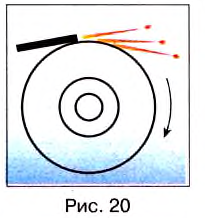
Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.

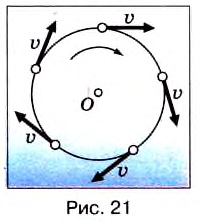
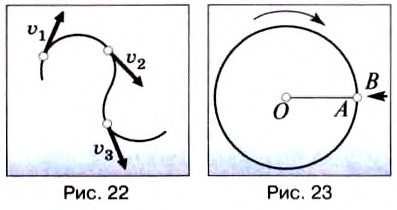
Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22). 

Опыт:

Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.

Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.

Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.

Период обращения – это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.

Обозначается период обращения большой латинской буквой Т.

Если за время материальная точка при равномерном движении по окружности совершает N оборотов, то период обращения определяется формулой:

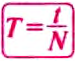
Единицей периода обращения в СИ является одна секунда (1 с).

Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.

Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности

Обозначается частота обращения малой латинской буквой .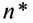

* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой 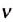(ню).

Если за время материальная точка совершила N оборотов, то, чтобы определить частоту обращения 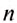, нужно N поделить на , т. е.:
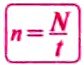 а так как = ТN , то .
Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.

Единицей частоты обращения в СИ является единица, разделённая на секунду 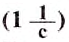.  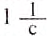это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду 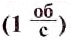, часто применяют также единицу один оборот в минуту .

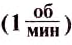Движение точки по окружности

Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.

Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.

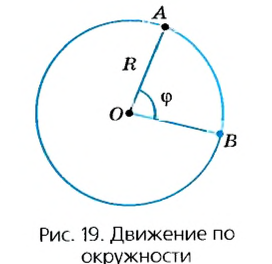
Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время 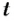переходит из точки А в точку В. При этом отрезок OA поворачивается на угол – угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:

где 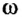(греческая буква «омега») – угловая скорость; (греческая буква «фи») – угловое перемещение.

Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки – длина дуги окружности АВ – равна длине радиуса R.

Единицей угловой скорости является радиан в секунду (рад/с).

1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.

При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).

Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.

Период вращения (Т) – это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:

где t — время вращения, N — количество выполненных оборотов.

Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):

где N — количество совершенных оборотов за время t .

Частота вращения измеряется в оборотах за секунду (об/с).

Частота вращения  определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.

Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой 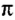(«пи»).

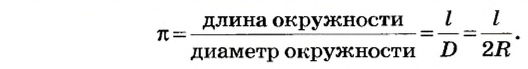
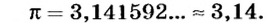
Таким образом, длина окружности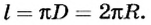

За один оборот материальная точка осуществляет угловое перемещение 2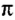 рад.

Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь 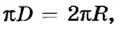 то линейная скорость равномерного движения точки по окружност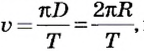и или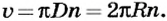

Вращение твердого тела

Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.

Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.

В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?

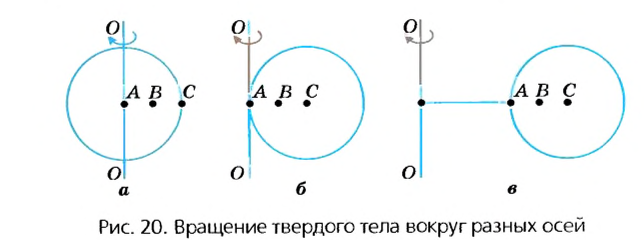
Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.

Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния – чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение всех точек одинаково. Следовательно, и угловая скорость 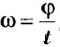 для всех точек данного тела также будет одинаковой.

Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т – время одного полного вращения; вращательная частота (частота вращения) 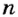— количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.

Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.

Динамика вращательного движения

При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.

Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:

По третьему закону Ньютона:

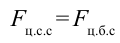
и при вращении появляется также центробежная сила.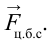 
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.

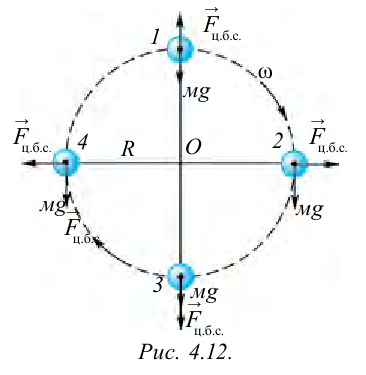
На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом 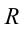. В точке 1, из-за того что центробежная сила 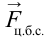направлена противоположно силе тяжести 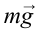, вес тела уменьшается:

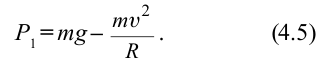
В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:

Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения. 
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.

• Заказать решение задач по физике

Пример

При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки 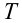. Скорость тела в точке 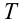равна 30 м/с.
Дано:

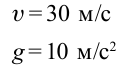
Найти:

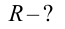
Решение:

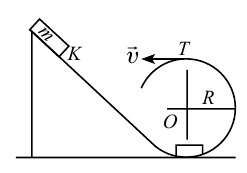
Чтобы тело не упало из точки 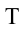должно  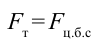выполняться следующее условие: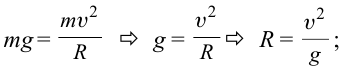 

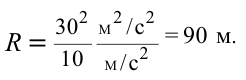
Ответ: 90 м.

Кинематика вращательного движения

При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.

Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.

Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.

Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота 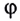(рис. 25)

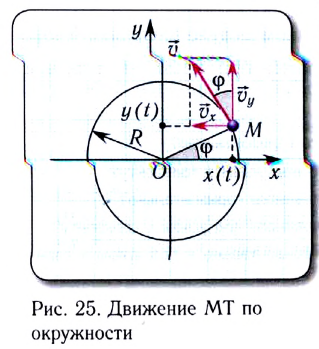
радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:

По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению

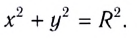
Скорость 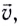с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).

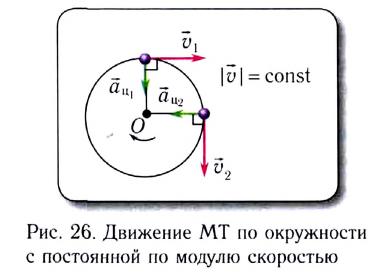
Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения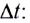

Модуль угловой скорости 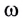— это отношение угла поворота 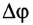к промежутку времени 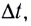за который этот поворот произошел:

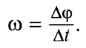
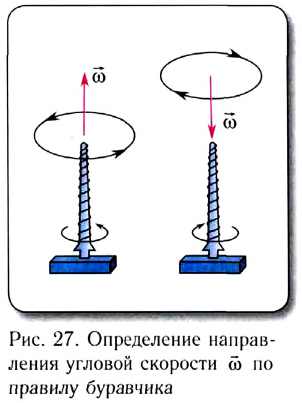
Угловая скорость 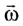 со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).

Единица угловой скорости в СИ — радиан в секунду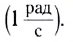

При движении по окружности с постоянной по модулю скоростью v угловая скорость 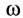является величиной постоянной и ее модуль равен отношению угла поворота 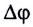к промежутку времени 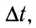за который этот поворот произошел:

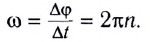
Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:

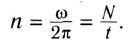
Единица частоты вращения в СИ — секунда в минус первой степени 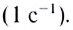Время совершения одного оборота называется периодом вращения Т.

Следовательно, 

В СИ период измеряется в секундах (1с).

При совершении полного оборота 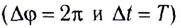период определяется по формуле    

Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле

Проекции скорости 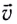(см. рис. 25) с течением времени изменяются по закону

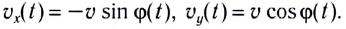
Модуль угловой скорости определяется соотношением

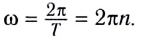
Следовательно, соотношение между модулями линейной и угловой скорости имеет вид

Поскольку 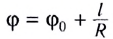(докажите самостоятельно), где 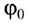— угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид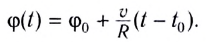

При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным 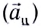или нормальным 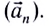Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости 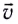с течением  (см. рис. 26). Его модуль определяется формулой

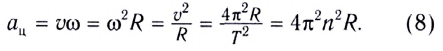
Нормальное ускорение 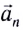в любой момент времени перпендикулярно скорости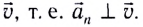

Как и при прямолинейном равноускоренном движении, ускорение 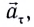называемое тангенциальным (касательным), совпадает с направлением скорости 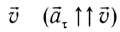или направлено противоположно ей 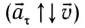и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение 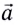можно представить в виде векторной суммы нормального ускорения 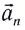и тангенциального ускорения 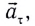направленного по касательной к окружности в данной точке (рис. 28):

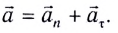
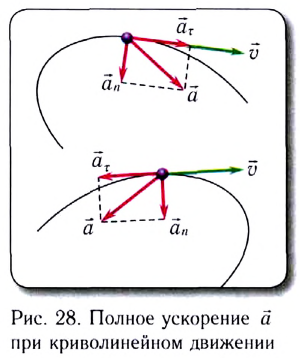
Полное ускорение 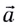всегда направлено в сторону вогнутости траектории (см. рис. 28).

Модуль полного ускорения находится по теореме Пифагора:

где 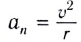 – нормальное ускорение, с которым точка двигалась бы по дуге
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.

Вращательное движение твердого тела – движение, при котором все точки объекта описывают траекторию в виде окружности. 

Распространенный случай в физике – вокруг покоящейся оси (рис. 1).

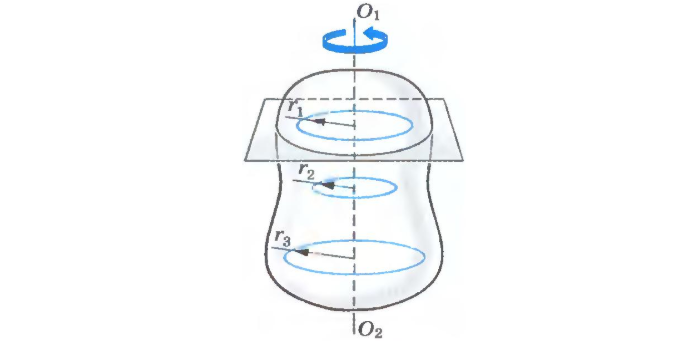
Рис. 1 Вращение твердого тела вокруг оси

Линия, соединяющая неподвижные точки, читается осью вращения. Кинематика перемещения в целом аналогична поступательной. Только путь измеряется не в метрах, а в радианах или градусах. 

Последние связаны между собой следующей формулой:

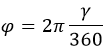
где:

• ϕ – угол в радианах (рад);

• γ – угол в градусах (°).

Закон и уравнение вращательного движения твердого тела

Законы движения также схожи. Для равноускоренного движения:

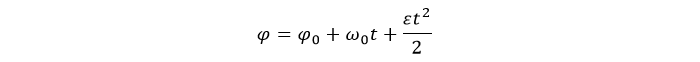
где:

• ϕ₀ – начальный угол (рад);

• ω₀ – начальная угловая скорость (рад/с);

• t – время (с);

• ε – угловое ускорение (рад/с²).

Под положительным понимают перемещение против часовой стрелки.

Угловая скорость

В обычной жизни вращение оценивается в оборотах за единицу времени. За минуту чаще всего. Для расчетов такие характеристики неудобны. Поэтому определяется так:

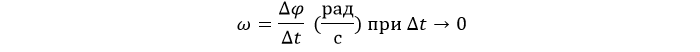
Скорость в оборотах ν легко связать с угловой:

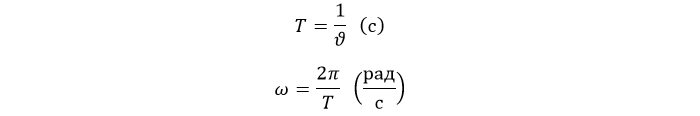
где:

ν – скорость в оборотах (1/с).

Используется еще одна важная величина – период вращения T. За это время предмет совершает полный поворот:

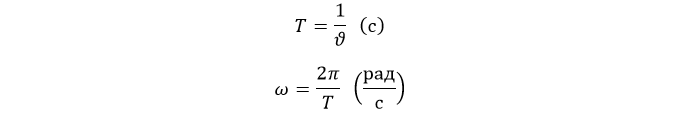
Угловое ускорение

Это величина:

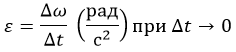
В уравнении движения был показан частный случай равноускоренного перемещения. Но это не всегда так. Также ε может принимать отрицательные значения в случае замедления.

Линейные величины

При малых величинах пройденный путь (см. рис. 2) будет равен:

где r – расстояние до центра вращения (м).

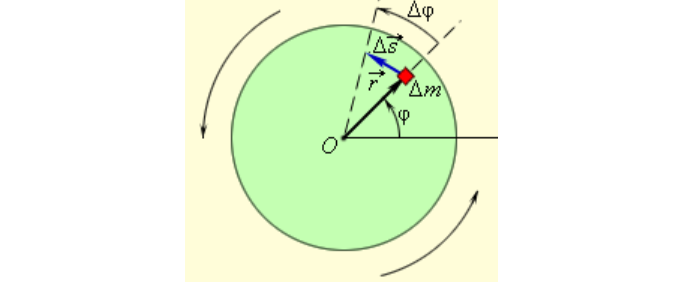
Рис. 2 Перемещение

Откуда следует линейная скорость:

Вектор, перпендикулярный отрезку, r. То есть расположенный на касательной к окружности вращения.

И, соответственно, ускорение:

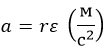
Кроме того, передвижение по кривой линии невозможно без центростремительного ускорения:

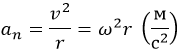
Возвратно-вращательное движение

Общий случай раскачивания маятника. Анализ подобных противоположных телодвижений пары объектов порождает некоторые парадоксы.

Возникают странные и дико звучащие названия вроде «безопорного движителя». Выводы в конечном итоге противоречат законам механики Ньютона.

Приверженцы таких рассуждений существуют и доводы имеют право на жизнь. Не все общепринятые взгляды безупречны. Евклидова геометрия тому пример. Теория довольно запутана, и здесь мы ее рассматривать не будем.

С учетом масс

Представив себе, что тело состоит из незначительных масс m_i, получим любопытные результаты. Кинетическая энергия выразится так:

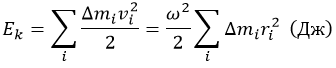
Джоуль (Дж) – единица энергии и работы в системе СИ.

Моментом инерции относительно выбранной оси называется:

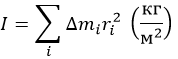
или в соответствующей интегральной форме.

Тогда энергия выразится следующим образом:

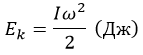
То есть имеется некий аналог массы. Но последняя является неизменной присущей объекту величиной. Момент же инерции зависит от местонахождения оси.

В реальных условиях распространен случай вращения вокруг оси, включающей центр масс. Найдем его для системы, указанной на рис. 3.

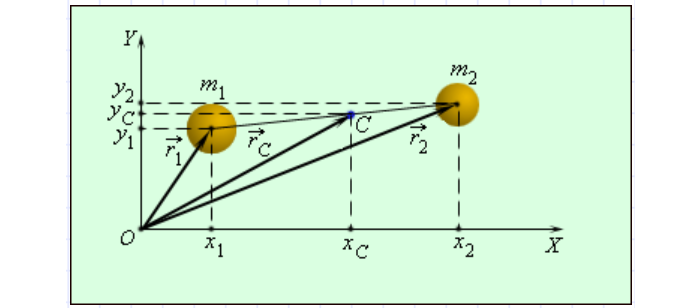
Рис. 3 Определение центра масс.

Определится по формулам:

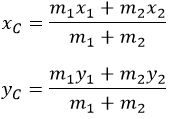
Вектор, направленный из начала координат в центр масс, в общем случае выразится следующим образом:

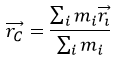
Можно перевести в интегральную форму. В присутствии гравитации – заодно и центр тяжести.

Можно сказать, что общее движение предмета включает поступательное и вращательное. Пример – качение чего-то округлого (рис. 4). При этом все перемещение точек можно исчерпывающе изобразить на рисунке. В таком варианте движение называется плоским. 

Полная кинетическая энергия равна:

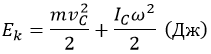
где:

• m – масса объекта;

• I_C – момент инерции относительно оси, включающей центр масс.

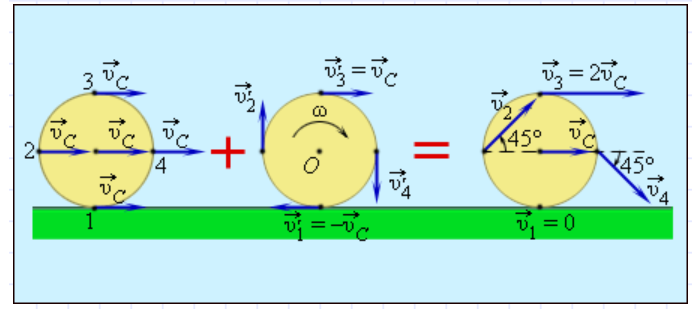
Рис. 4 Качение колеса

Частные случаи вращательного движения

Рассмотрим несколько:

1. Равномерное (рис. 5), с постоянной скоростью, с нулевым ускорением. 

Выражается уравнением: φ = φ₀ + ωt

Рис. 5 При ε = 0.

2. Равноускоренное. Рассмотрено ранее. Но все же уместны некоторые пояснения (рис. 6).

Рис. 6 ε = const.

3. Вокруг неподвижной оси. Наиболее распространенный в рассмотрении вариант. Как для реальных нужд, так и в теории.

4. Возвратно-вращательное. В математическом выражении напоминает колебания. При подробном рассмотрении вызывает неудобные вопросы.

Заключение

Для разработчиков оборудования тема отнюдь не праздная. Рассматриваются задачи по передаче силового момента (в частности в ременных механизмах). Разбирается механика работы подшипников, гироскопов.

В артиллерии снаряды стабилизируются вращением. Да и расчеты их на прочность связаны со сложным напряженным состоянием в связи с раскручиванием в стволе.

Орбиты планет имеют отношение к рассматриваемой кинематике.

На самом деле все сферы использования данной темы невозможно перечислить, это действительно нужный раздел.

>

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности

Наряду с движением вдоль прямой в школьной физике рассматривают движение по окружности. Для него, по аналогии с прямолинейным движением, вводятся понятия пройденного пути, скорости движения и ускорения.

В физике выделяют несколько видов движения тел. Движение по окружности – это один из случаев движения вдоль кривой линии — криволинейного движения.

Сравним понятия пройденного пути, скорости и ускорения для прямолинейного движения и движения по окружности.

Угловой путь

Для начала, вспомним, что линейное перемещение – это разница между конечным и начальным положением точки на оси (рис. 1).

Рассмотрим теперь колесо (рис. 2). На горизонтальной линии, проходящей через диаметр колеса, справа отметим красную точку, от которой мы начнем отсчитывать углы. Условимся считать, что возле этой точки находится нулевой угол.

На ободе колеса выберем точку, например — ниппель. Сначала ниппель находился в точке 1. Точка 1 сдвинута на угол (gamma_<1>) относительно начала отсчета.

Будем вращать колесо в направлении, обозначенном синей стрелкой. Повернем колесо на некоторый угол, так, чтобы к концу движения ниппель переместился в точку, обозначенную цифрой 2 на рисунке. Эта точка смещена на угол (gamma_<2>) по отношению к началу отсчета.

По аналогии с поступательным движением, угловой путь, который прошел ниппель — это разница (разность) угловых положений точек 1 и 2.

(varphi left( text<рад>right)) – угловой путь измеряется в радианах.

Угловой путь – это угол, на который повернулся ниппель, по отношению к его начальному положению.

Угловая скорость — куда она направлена

Если тело двигалось равномерно (с неизменной скоростью), то линейную скорость можно определить по формуле

(v left( frac<text<м>> right)) — линейная скорость – это путь, деленный на время, поэтому она имеет размерность метров деленных на секунду.

Аналогично линейному случаю, если угловой путь поделить на время движения, получим угловую скорость.

(omega left( frac<text<рад>> right)) – угловая скорость – это угловой путь, деленный на время, поэтому она имеет размерность радиан деленных на секунду.

Угловая скорость ( omega ), так же, как и линейная скорость, является вектором. Но в отличии от линейной скорости его направление можно определить по правилу буравчика (правого винта).

Примечание: Направление вектора угловой скорости ( vec <omega>) можно определить по правилу буравчика (правого винта)!

На рисунке 3 окружность располагается в горизонтальной плоскости, а вектор ( vec<omega >) направлен вдоль вертикальной оси вращения. Направление вращения указано синей стрелкой.

При движении по окружности вектор линейной скорости (vec) изменяет свое направление. Но в каждой точке окружности вектор (vec) направлен по касательной к окружности, т. е. перпендикулярно радиусу.

Примечание: Касательная и радиус перпендикулярны, это известно из геометрии.

Если точка начнет вращаться в противоположную сторону, то векторы линейной и угловой скорости развернутся противоположно направлениям, указанным на рисунке 3.

Связь между линейной и угловой скоростью

Угловая и линейная скорость связаны математически. Линейная скорость – это векторное произведение вектора угловой скорости и вектора радиуса окружности.

Примечание: Радиус окружности – это вектор, он направлен от центра окружности к ее внешней границе.

Скалярный вид записи связи скоростей:

(omega left( frac<text<рад>> right)) – угловая скорость;

(v left( frac<text<м>> right)) — линейная скорость;

(R left( text<м>right)) – радиус окружности.

Частота и период

Вращательное движение описывают с помощью таких характеристик, как частота и период.

Период обращения – это время одного полного оборота. В системе СИ период измеряют в секундах.

( T left(c right)) – время, за которое тело совершило полный оборот – период. Время – это скалярная величина.

Частота отвечает на вопрос: «Сколько полных оборотов совершило тело за одну секунду?».

( displaystyle nuleft( frac<1> right)) – частота оборотов, скаляр.

Вместо записи ( displaystyle left( frac<1> right)) иногда используют (displaystyle left( c^ <-1>right)), или ( left( text <Гц>right)) – Герц. Это фамилия Генриха Герца, знаменитого физика.

[displaystyle 1 text <Гц>= frac<1> = c^ <-1>]

Частота и период связаны обратной пропорциональностью:

Количество оборотов

Двигаясь по окружности достаточное время, тело может пройти не один оборот. Зная угловой путь (varphi ) мы можем вычислить количество N оборотов.

( N ) – количество оборотов, скаляр. Обороты считают поштучно.

Связь между угловой скоростью и частотой

Разделим обе части уравнения на время t, в течение которого тело вращалось

Левая часть уравнения – это угловая скорость.

А дробь в правой части – это частота

Таким образом, мы получили связь между угловой скоростью и частотой

Примечание: Решая задачи на равноускоренное движение по окружности, удобно переходить от частоты к угловой скорости. Тогда можно будет применять аналогию с формулами для равноускоренного движения по прямой.

Как найти путь при движении по окружности

Репетитор
по физике

Задачи на движение по окружности .

(T) – период обращения ( время за которое тело совершает 1 оборот )

(N)-количество оборотов за все время

(n) – частота обращения
частота обращения это количество оборотов за 1 секунду
( n=dfrac<1> )

(l=2 pi R )-формула нахождения длины окружности
(S=vt ) – формула связывающая путь,скорость и время
длина и путь это одно и то же ( (S=l) )
(2 pi R=vt )
(2 pi R=vT )

(v) скорость
(T) период
(R) радиус
(piapprox 3,14)

1. Тело при движении по окружности совершает (N=10) оборотов за время (t=1 c). Найти период обращения тела
Показать ответ Показать решение Видеорешение

[spoiler title=”источники:”]

http://kornev-school.ru/f9_circular_motion.html

[/spoiler]

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 ноября 2021 года; проверки требуют 2 правки.

Враща́тельное движе́ние — вид механического движения. При вращательном движении материальная точка описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым.

Основной закон динамики вращательного движения[править | править код]

Производная по времени от момента количества движения механической системы относительно неподвижной инерциальной системы отсчёта точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе.

Характеристики вращения тела[править | править код]

Кинематические характеристики[править | править код]

Вращение характеризуется углом , измеряющимся в градусах или радианах, угловой скоростью (измеряется в рад/с) и угловым ускорением (единица измерения — рад/с²).

При равномерном вращении ( — период вращения),

• Частота вращения — число оборотов в единицу времени.

• Линейная скорость точки, находящейся на расстоянии от оси вращения

• Угловая скорость вращения тела — аксиальный вектор (псевдовектор).

Динамические характеристики[править | править код]

Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:

В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы

• Момент инерции — физическая величина, мера инертности тела во вращательном движении. Характеризует распределение масс в теле. Различают осевой и центробежный момент инерции. Осевой момент инерции определяется равенством:

где  — масса,  — расстояние от -й точки до оси^[1].

См. также[править | править код]

• Поступательное движение
• Плоскопараллельное движение
• Сложное движение
• Сферическое движение

Примечания[править | править код]

Ссылки[править | править код]

• Бобылёв Д. К. Ось, в математике, механике и физике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Вращение твердого тела. Открытая Физика 2.6. Часть I. «ФИЗИКОН». Дата обращения: 23 января 2015.
• Джанибеков демонстрирует пример вращения абсолютно жесткого тела, закрученного вокруг оси, не совпадающей с осью наименьшего или наибольшего момента инерции
• Вращение твёрдых тел в невесомости вокруг разных осей
• Б. Яворский А. Детлаф, Физика, М.: Дрофа, 1998.

Вращательным
движением твердого тела вокруг
неподвижной оси называется движение,
при котором все точки тела движут­ся
по окруж­ности, центры которых лежат
на од­ной прямой, называемой осью
вра­щения. Ось вращения перпен­дику­ляр­на
плоскостям, в ко­торых лежат эти
окружности. Она может проходить сквозь
тело или лежать за его пре­де­ла­ми.
Если ось вращения проходит сквозь тело,
то те точки тела, которые лежат на этой
оси, во время движения тела остаются в
покое.

При
вращательном движении абсолютно твердого
тела нельзя поль­­зоваться моделью
материальной точ­ки, ибо разные точки
тела движутся по окружностям разного
радиуса, т.е. их пути и скорости различны
(рис. 1.4). В силу этой же причины враще­ние
твердого тела (как целого) не может быть
охарак­те­ри­зо­ва­но линей­ным
переме­щением и линей­ной ско­ростью,
как это было сделано в посту­пательном
дви­жении. Вместе с тем, нетрудно
заметить, что радиусы-век­то­ры,
соеди­ня­ющие все точки твер­дого
тела с центрами описы­ва­е­мых
ими окруж­ностей, пово­ра­чи­­ва­ются
за один и тот же про­ме­жу­ток
времени

на одинаковый угол

(см. рис. 1.4). Следовательно, все точки
абсо­лют­но твердого тела во
вращательном движении проходят одинаковые
уг­ло­вые пути и имеют одинаковые
угло­вую скорость и уг­ловое
ускорение. Поэтому в качестве кинематических
характеристик вра­ща­тельного
движе­ния тела должны быть выбраны
век­тор углового пере­мещения,
угловая скорость и угловое ускорение.

При
малых поворотах тела угол поворота
можно рассматривать как векторную
величину ,
численно равную модулю d,
и направленную вдоль оси вращения ОО^/
так, чтобы из конца вектора поворот тела
был виден против часовой стрелки (правило
буравчика) (см. рис. 1.5).

Угловой
скоростью тела называют вектор
,
численно равный первой производной от
угла поворота

по
времени и направленный вдоль оси вращения
по правилу буравчика, т.е. так же, как
вектор угла поворота.

.
(1.23)

Угловая
скорость характеризует направление и
быстроту вращения тела как целого вокруг
оси. Если

=
const, то движение тела называют равномерным
вращением вокруг неподвижной оси.

Скорость

произвольной
точки М
тела, вращающегося с угловой скоростью
,
называют линейной скоростью этой точки.
За время dt
точка
М
проходит по дуге окружности радиуса R
путь ds
= vdt
=Rd
так, что

.
(1.24)

Из
рис. 1.5 видно, что вектор

направлен
перпендикулярно и к

и к радиусу-вектору

в ту же сторону, что и векторное
произведение
.
Так как векторы

и

взаимно перпендикулярны, то ||
= R
=

v.

Следовательно,

.
(1.25)

Так
как в случае вращения тела вокруг
неподвижной оси за начало координат,
из которого проводят радиусы-векторы

,
можно
выбрать любую точку оси вращения, то
выражение (1.25) можно переписать в виде:

.
(1.26)

Для
характеристики неравномерного вращения
тела вводится понятие углового ускорения.

Угловым
ускорением называют вектор
,
характеризующий быстроту изменения
угловой скорости со временем и численно
равный первой производной угловой
скорости по времени:

.
(1.27)

В
случае вращения тела вокруг неподвижной
оси изме­нение вектора

обусловлено только изменением его
чис­лен­ного значения. При этом
вектор


направлен
вдоль оси вращения (рис. 1.6): в ту же
сторону, что и
,
при
уско­рен­­ном вращении ()
и в про­тиво­полож­ную сторону 
при за­мед­лен­ном вращении ().

Наряду
с понятием угловой ско­рости пользуются
понятиями периода и частоты вращения.

Периодом
вращения Т
называют промежуток време­ни, в течение
которого тело со­вершает один полный
оборот, т.е. поворачивается на угол 2
.

Частотой
вращения n
называют
число оборотов, совершаемых телом за
одну секунду.

Связь
между ,
T
и n
имеет вид

.
(1.28)

Угол
поворота в системе СИ измеряется в
радианах (рад), угловая скорость 
в радианах в секунду (рад/с), угловое
ускорение 
в радианах в секунду в квадрате (рад/с²).

Выразим
тангенциальное и нормальное ускорение
произвольной точки тела, вращающегося
вокруг неподвижной оси, через угловую
скорость и угловое ускорение тела:

,
(1.29)

.
(1.30)

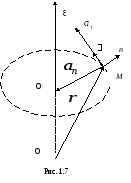
Из
рис. 1.7 и уравнения (1.29) следует, что
вектор

равен векторному произведению вектора
углового ускорения

на
радиус-вектор
,
соединяющий произвольную точку на оси
вращения с точкой М:

.
(1.31)

Вектор

нормального ускорения направлен к оси
вращения, т. е. в противо­по­ложную
сторону от
:

.
(1.32)

В
табл. 1.1, 1.2 сопоставляются характеристики
и законы поступательного и вращательного
движения материальной точки. Аналитическое
и графическое описа­ния этих двух
видов движений аналогичные. Кроме того,
в таблицах приводятся формулы, связывающие
характеристики поступательного и
вращатель­ного движений материальной
точки. В табл. 1.3 даны единицы измерения
кинематических характерис­тик
поступательного и вращательного
движений.

Таблица
1.1

Сопоставление
характеристик

поступательного
и вращательного движения материальной
точки.

поступательное движение	характеристики	вращательное движение
Путь s Скорость v = ds/dt Тангенциальное ускорение а = dv/dt Нормальное ускорение аn = v2/R Полное ускорение	s = R  v = R  а = R  аn=  R	Угловой путь  Угловая скорость  = d/dt Угловое ускорение  = d/dt

Таблица
1.2

Виды
движения (уравнения и графики)

Поступательное движение	Вращательное движение
Равномерное
;;.	;;.
Окончание табл. 1.2
Поступательное движение	Вращательное движение
Равнопеременное
; ;	; ;
t
Неравномерное

Таблица
1.3

Единицы
измерения и кинематические характеристики

поступательного
и вращательного движений

Наименова-ние харак­те­ристики	Обозначение и определяющее уравнение	Название единицы измерения	Сокращенное обозначение единицы измерения
Длина	l	метр (основная ед.)	м
Время	t	cекунда(основная ед.)	с
Скорость	v = dl/d t	метр в секунду	м/с
Ускорение	a = dv/dt	метр в секунду в квадрате	м/с2
Плоский угол		радиан	рад
Угловая скорость	 = /t	радиан в секунду	рад/с
Угловое ускорение	 = /t	радиан в секунду в квадрате	рад/с2
Частота		секунда в минус первой степени	с-1

ВОПРОСЫ
ДЛЯ САМОКОНТРОЛЯ

1.
Какое движение называется механическим?

2.
Что понимают под системой отсчета? Для
чего нужны систе­мы отсчета?

3.
Какое движение называется поступательным?

4.
Что называется материальной точкой?

5.
Что понимают под траекторией движения?
На какие виды делится механическое
движение по характеру траектории?

6.
Что такое путь? Скалярная или векторная
это величина?

7.
Что такое вектор перемещения?

8.
Что отражает уравнение (задан ли вид
траектории): а)
;
б) r
= =r(t);
в)

9.
Что такое скорость механического
движения?

10.
Что называется: а) средней скоростью
механического движения; б) мгновенной
скоростью механического движения?

11.
Как записать мгновенную скорость
переменного движения: а) векторным
способом; б) координатным способом
(величина и направление)?

12.
Как направлена скорость криволинейного
движения точки?

13.
Как по графику скорости найти путь?

14.
Что характеризует ускорение поступательного
движения? Чем опре­де­ля­ются
величина и направление ускорения?

15.
Какое ускорение называется: а) средним;
б) мгновенным?

16.
Как направлен вектор ускорения по
отношению: а) к траектории движения (в
некоторой точке); б) к вектору скорости,
в) к равнодействующей силе?

17.
Как записать ускорение поступательного
движения: а) векторным способом; б)
координатным способом?

18.
Что характеризует: а) касательная
составляющая ускорения, б) нормальная
составляющая ускорения?

19.
Каковы величина и направление: а)
касательной составляющей ускорения;
б) нормальной составляющей ускорения?

20.
Может ли точка, двигающаяся по кривой,
обладать: а) танген­ци­аль­ным
ускорением, равным нулю, б) нормальным
ускорением, равным нулю?

21.
Может ли полное ускорение точки,
двигающейся по кривой, быть направленным
в сторону: а) вогнутости траектории; б)
выпуклости траектории?

22.
Каковы величина и направление полного
ускорения тела, брошенного под углом к
горизонту?

23.
Каков характер движения тела, брошенного:
а) в вертикальном напра­в­ле­нии;
б) в горизонтальном направлении; в) под
углом к горизонту?

24.
Написать зависимость скорости от времени
для тела, бро­шенного: а) в вертикальном
направлении; б) в горизонтальном
направлении; в) под углом к горизонту?

25.
Какое движение называется вращательным?

26.
Что называется абсолютно твердым телом?

27.
Чем определяется положение вращающегося
тела в прост­ранстве?

28.
Что называется угловой скоростью?
Скалярная или вектор­ная это величина?

29.
Как могут быть представлены: а) средняя
угловая скорость; б) мгно­вен­ная
угловая скорость?

30.
Какое вращение называется: а) равномерным;
б) равнопеременным; в) пе­­ременным?

31.
Что называется угловым ускорением?

32.
Как выражаются среднее и мгновенное
угловые ускорения при любом переменном
вращении тела?

33.
Как могут быть представлены при
равнопеременном вращении: угол поворота
в функции времени, угловая скорость,
угловое ускорение?

34.
Как строятся векторы: а) угловой скорости;
б) углового ускорения?

35.
Как связаны: а) путь, пройденный какой-либо
точкой вращающегося тела; б) ее линейная
скорость; в) тангенциальное ускорение;
г) нормальное ускорение; д) полное
ускорение с соответствующими угловыми
характеристиками?

36.
В каких единицах в СИ измеряются: а)
линейный путь; б) угловой путь; в) линейная
скорость; г) угловая скорость; д) линейное
ускорение; е) угловое ускорение?

37.
Какой формулой выражается связь угловой
скорости и числа оборотов вала в единицу
времени?

38.
Какой формулой выражается связь угловой
скорости с пе­риодом вращения?

Соседние файлы в папке Физика

• #
• #
• #
• #
• #