Известна работа и сила , как найти путь s.
На этой странице вы найдете ответ на вопрос Известна работа и сила , как найти путь s?. Вопрос
соответствует категории Физика и уровню подготовки учащихся 5 – 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно
ознакомиться с вариантами ответов других посетителей страницы или обсудить с
ними интересующую тему. Здесь также можно воспользоваться «умным поиском»,
который покажет аналогичные вопросы в этой категории. Если ни один из
предложенных ответов не подходит, попробуйте самостоятельно сформулировать
вопрос иначе, нажав кнопку вверху страницы.
Содержание:
- § 1 Механическая работа
- § 2 Решение задач на определение механической работы
- § 3 Краткий итог урока
§ 1 Механическая работа
В этом уроке мы рассмотрим новую физическую величину – механическую работу, изучим условия совершения механической работы и единицы ее измерения.
Мы в жизни часто используем слово «работа». Программист сидит за
компьютером – это его работа, работают станок, холодильник, телевизор, работает строитель, работает инженер. Словом «работа» мы выражаем всякое полезное действие человека или устройства. В физике термин «работа» имеет несколько иной смысл. Рассмотрим примеры.
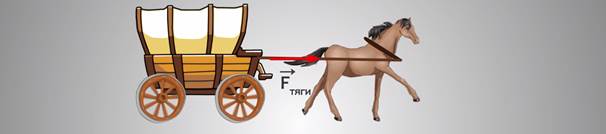
Лошадь тянет телегу, действуя на нее с некоторой силой – силой тяги, которую обозначим Fтяги. Телега движется по направлению силы тяги лошади. Говорят, что сила тяги совершает механическую работу по перемещению телеги.
Механическая работа (или работа силы над телом) – это скалярная физическая величина, равная произведению модуля силы на путь, пройденный телом вдоль направления этой силы.
Механическая работа обозначается строчной буквой «А». По определению формула работы запишется так:

В честь английского ученого Джеймса Джоуля единица измерения работы получила название Джоуль.
За 1 Джоуль принята работа, совершаемая силой 1 Ньютон на пути, равном 1 метру: 1 Дж = 1 Н · м.
Кратные единицы измерения:
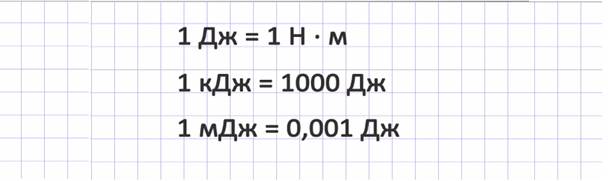
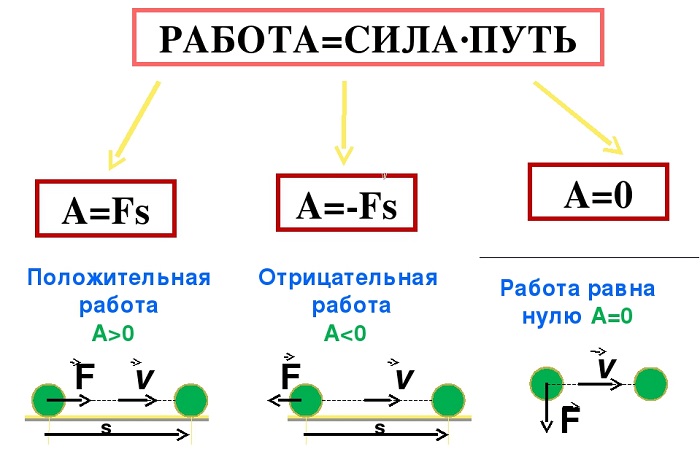
В зависимости от направления действующей силы механическая работа может быть положительной и отрицательной.
Если направление силы совпадает с направлением движения тела, то работу силы считают положительной.
Например, лошадь тянет телегу (см. рис.) и совершает положительную работу:

камень падает (см. рис.) – сила тяжести совершает положительную работу:

выстрелили из лука (см. рис.) – сила упругости натянутой тетивы совершает положительную работу:

Если направление силы противоположно направлению движения тела, то работу силы считают отрицательной.
Например, сила трения скольжения совершает отрицательную работу, так как она направлена противоположно движению и тормозит движение тела:
А = – Fтрения · s.

Если направление силы перпендикулярно направлению движения тела, то работа этой силы равна нулю.
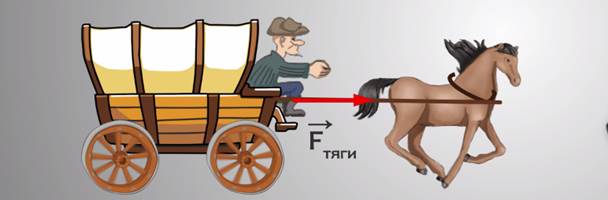
Например, сила давления человека, сидящего на телеге (см. рис.), перпендикулярна направлению движения телеги, телега под действием этой силы не перемещается, и поэтому работа силы давления равна нулю.
Если тело под действием силы не движется, то работа также равна нулю.
На гирю, подвешенную к нити, действует сила тяжести, но гиря не движется, значит, работа силы тяжести равна нулю (рис. 2).
Работа равна нулю и в том случае, если тело движется по инерции, то есть на него не действуют силы. Тогда в формуле работы А = F· sсила равна нулю, следовательно, работа равна нулю.
Итак, механическая работа совершается только в том случае, если на тело действует сила, и тело под действием этой силы движется.
§ 2 Решение задач на определение механической работы
Рассмотрим решение задач на определение механической работы.
Задача 1. Буксирный катер тянет баржу с одного причала на другой, действуя с силой 5000 Н. Расстояние между причалами составляет 1000 м. Вычислить работу, совершаемую катером.
Запишем условие задачи: нам известна сила F = 5000 Н. Известно расстояние, на которое перемещается баржа: s =1000 м. Требуется найти работу.
Решение задач на вычисление механической работы будем проводить по определенной схеме.
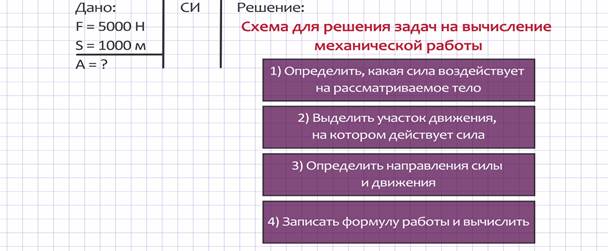
1)Определим, какая сила воздействует на рассматриваемое тело. В этой задаче катер действует с силой 5000 Н на баржу, следовательно, работу совершает сила тяги катера.
2)Выделим участок движения, на котором действует сила: баржа перемещается от одного причала до другого на 1000 м.
3)Определим направления силы и движения: баржа движется в сторону действующей силы тяги, значит, работа, совершаемая силой тяги, положительная.
4) Запишем формулу работы и вычислим:
А = Fтяги · s = 5000 Н · 1000 м = 5000000 Н·м = 5000000 Дж = 5000 кДж.

Задача 2. Хоккеист ударил по шайбе с силой 100 Н. Шайба, пройдя по льду путь 20 м, влетела в ворота противника. Найти механическую работу, совершенную хоккеистом.
Условие задачи: сила F = 100 Н, путь s = 20 м. Найти работу А.
Рассмотрим решение по схеме.
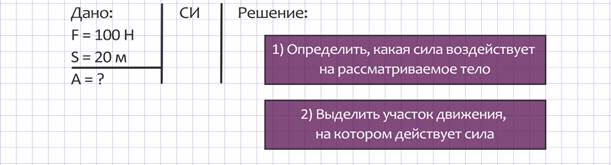
1. Определим, какая сила воздействует на рассматриваемое тело: хоккеист ударил по шайбе с силой 100 Н.
2. Выделим участок движения, на котором действует сила: сила хоккеиста действует только на том участке, где лежала шайба в момент удара, дальше сила удара не действует, шайба движется по инерции.
Так как путь, пройденный шайбой в момент удара, равен нулю, то мы можем сделать вывод, что работа, совершенная силой удара, равна нулю.

Итак, при решении задач на расчет механической работы нужно установить, какая сила совершает работу, какой путь проходит тело под действием этой силы, определить направление действующей силы и направление движения.
§ 3 Краткий итог урока
Механическая работ – это скалярная физическая величина, равная произведению модуля силы на путь, пройденный телом вдоль направления этой силы.
Формула для вычисления работы: А = F · s
Единица измерения работы: 1 Дж = 1 Н · м
Механическая работа положительна, если направление силы совпадает с направлением движения.
Работа отрицательна, если направление силы противоположно направлению движения.
Работа равна нулю, если направление силы перпендикулярно направлению движения, или если тело движется по инерции, или перемещение тела под действием силы равно нулю.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
Основные цели урока:
Сформировать представление о величине «производительность», выявить зависимость между величинами: объемом выполненной работы (А), производительностью (V) и временем (t), сформировать способность к построению формулы работы А=v×t.
Формировать умение находить по формуле работы v и t и использовать формулу работы для решения задач.
Тренировать способность детей к решению задач на все изученные виды зависимости между величинами.
Закрепить алгоритм умножения многозначного числа на трехзначное.
Развивать самостоятельность, умения преодолевать трудности в учении, используя проблемные ситуации, разноуровневые задания, самостоятельные упражнения.
Развивать мыслительные операции, внимание, речь, коммуникативные способности, прививать интерес к математике.
Ход урока
I. ЭМОЦИОНАЛЬНЫЙ НАСТРОЙ НА ПРЕДСТОЯЩУЮ ДЕЯТЕЛЬНОСТЬ
I. Организационный момент.
Урок я хочу начать словами французского философа Ж.Ж. Руссо (1712-1778гг.): “Вы – талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…”
–Я желаю вам уже сегодня на уроке убедиться в этих словах, ведь вас ждёт открытие новых знаний при решении задач..
II. АКТУАЛИЗАЦИЯ ЗНАНИЙ УЧАЩИХСЯ
1. Устный счет
– Вот песочные часы, песок высыпается в нижнюю часть за 1 минуту.
– Сколько заданий вы выполните за 1 минуту. (1 ученик выполняет у доски)
У 640-560х0=
М 240:60х100=
Ф 3х(180-90)-70=
А (940-720)х4=
Л 1000:5х4=
Р 400:50х40=
О (320-80)х1=
Самопроверка. Самооценивание.
Критерии выставления оценок:
«5» – без ошибок
«4» – 1 ошибка
«3» – 3-4 ошибки
«2» – 5 и более ошибок
– Что интересного заметили в ответах? (Все числа трехзначные, круглые, кратные 2,4,5,8,10).
– Расположите ответы в порядке возрастания.Ф О Р М У Л А
200
240
320
400
630
800
880
– Что мы называем формулой? По словарю (Формулой мы называем равенство, которое помогает нам установить зависимость между величинами).
2. Повторение известных формул.
Работа в группах
Восстановите формулы.
Слайды
Ученики крепят под названиями таблички с восстановленными формулами.
Проверка. (Чтобы найти …, надо …)
– По какому правилу можно получить 2 последние формулы? (По правилу нахождения неизвестного множителя).
– Для чего вам нужны формулы? (Для решения задач).
– Как вы думаете, какое теперь задание я вам предложу? (Решение задач).
3. Решение задач
На листочках даны задачи трех уровней каждому ученику.
– Прочитать задания, выбрать уровень сложности, записать только решение.1 уровень
Избушка на курьих ножках за 8 часов пробежала 72 км. С какой скоростью бегает избушка?
Кощей Бессмертный проехал на Змее Горыныче 180 км. Сколько часов они были в пути, если средняя скорость Змея Горыныча 90 км/ч?
Иван-царевич шёл тропинками нехожеными 6 часов со скоростью 6 км/ч. Какова длина тех тропинок?
2 уровень
Ковер-самолет летит со скоростью 200 км/ч. Какое расстояние он пролетит за а часов?
Ступа Бабы Яги пролетела x км за y часов. Какова скорость ступы Бабы Яги?
Иван-царевич за 3 часа проехал на волшебном коне d км. За сколько времени он преодолеет расстояние t, если скорость останется прежней?
3 уровень
Водяной плывет d км за 4 часа, а Баба Яга на метле это же расстояние пролетает за 2 часа. На сколько километров в час скорость Бабы Яги больше?
Жар-птице нужно пролететь х км. Она уже пролетела а часов со скоростью b км/ч. Сколько ей осталось пролететь?
Средняя скорость полета Финиста-ясного сокола b м/с, Жар-птицы – с м/с. На сколько метров больше пролетит Финист-ясный сокол, чем Жар-птица, за 20 секунд?
Самопроверка.
Сравните свое решение с правильным (слайд 1).1 уровень
72:8=9 км/ч
180:90=2 ч
6×6=36 км 2 уровень
200:а = (км)
x:y = км/ч
t: (d:3) = км 3 уровень
d:2-d:4= (км/ч)
x-b×a= (км)
b×20-c×20= (км) или (b-c) × 20 = (км)
– Если вы решали задания 1 уровня, и все решили без ошибок, запишите себе три балла. Задания 2 уровня соответствуют 4 баллам. 5 баллов ставит себе тот, кто решил задания 3 уровня и не допустил ни одной ошибки.
– Что общего в задачах, которые вы решали? (Задачи на движение).
– Какой формулой вы воспользовались, когда решали задачи? (Формулой пути).
– Как найти путь? (S=v×t)
– Как из этой формулы можно получить ещё две? (Находим неизвестный множитель: V= s÷t; t=s÷t).
III. ПОСТАНОВКА ПРОБЛЕМЫ
– А сейчас я вам предложу «вкусную задачу». Мама одной ученицы приготовила для вас эту задачу. Видеоролик включается (слайд 2): «На масленицу я вам напекла гору вкусных блинов. Я их выпекала в несколько приемов. В начале, я выпекала 3 блина в минуту. Сколько блинов приготовила я, работая 20 минут».
– Подберите формулу к задаче.
– Чем эта задача отличается от тех, которые мы решали. (Задачи были с известными величинами: стороны и площадь; время, скорость и путь; стоимость, количество и цена. А в этой задаче не все величины знакомы, знаем только время).
– Почему возникли затруднения? (Новые величины, нет формул).
IV. ОТКРЫТИЕ ДЕТЬМИ НОВОГО ЗНАНИЯ
Как же назвать эту формулу?
– Что нужно найти в задаче? (Сколько всего блинов испекла мама, т.е. её работу).
Эта формула называется «ФОРМУЛА РАБОТЫ».
– О каких величинах ещё идет речь? (Выпекала 3 блина в минуту, т.е. скорость работы).
– Скорость работы называют «ПРОИЗВОДИТЕЛЬНОСТЬЮ». Обозначим эту величину буквой «V».
– Что еще известно в задаче? (Время работы).
– О какой величине идет речь? (О времени).
– Какой буквой обозначается эта величина? («t»).
– Что нужно узнать в задаче? (Количество всех блинов, т.е. какую работу выполнила мама)
– Как найти количество блинов, которые испекла мама за 20 минут, если известно, что за 1 минуту мама выпекает 3 блина. (Надо 3 блина умножить на 20 минут: 3×20=60 блинов испекла мама).
– Записать в тетрадь решение.
– Какую величину находим? (Работу).
– Как находили? (Производительность работы умножили на время).
– Запишите формулу зависимости этих величин.A = V×t
– Все ли формулы открыты? (Нет).
– Чтобы их открыть, нужно отдохнуть.
Физпауза
– Выведите две другие формулы.
– По какому правилу можно получить? (По правилу нахождения неизвестного множителя)
– Какую величину будете находить? (Время)t = A÷V
– Чтобы найти время нужно работу разделить на производительность труда.
– Запишите эту формулу в тетради и на доске.
– Какая величина еще неизвестна? (Производительность труда)
– А что такое производительность труда? (Это работа, выполненная за единицу времени).
– Как найти производительность? V= A÷t
– Все ли формулы открыты? (Да)
– Как можно проверить правильность ваших выводов? (Можно посмотреть в учебнике). Работа с учебником (с.43).
– Сравните выведенные вами формулы.
– Прочтите формулировки.
– Как найти работу?
– Время работы?
– Как называется работа, выполненная за единицу времени? (Производительность труда).
– А теперь мы вернемся к практической работе, которую выполняли в начале урока. Сколько заданий вы выполнили за одну минуту? Это наша производительность.
– Одинаковым ли было количество заданий у каждого из вас? (Нет, одни выполнили больше заданий, другие – меньше).
– Что можно сказать о производительности труда наших учеников? (Она разная. Это зависело от того, кто сразу начал работу, кто отвлекался, кто хорошо знает таблицу умножения,..).
А если бы вы решали 10 минут, сколько всего таких заданий вы бы выполнили? Какие задачи теперь сможете решать (Задачи на работу).

V. ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ ВО ВНЕШНЕЙ РЕЧИ
– Откройте учебник на стр. 44, №1.
– Какое задание надо выполнить? (Объяснить смысл предложений)
а) Вася каждый час съедает 3 мороженых. А сколько мороженых Вася съест за 2 часа? (3×2=6 мороженых)
– Какую величину находили? (Работу).
б) Оля за одну минуту лепит 2 штуки пельменей. Дополните условие и поставьте вопрос к задаче.
№2. Какое задание будете выполнять? (Решать задачу).
– Прочтите задачу.
– Анализ задачи. Один из учащихся анализирует условие задачи.
– Какие величины известны? Что надо найти?
V= 8 дет/ч
A= V×t
– Найдите работу, выполненную мастером за 6 часов, 7 часов. (Учащиеся работают в парах)
– Найдите работу за 9 часов и за время t самостоятельно.
Заполненная таблица вывешивается на доску.
VI. САМОСТОЯТЕЛЬНАЯ РАБОТА С САМОПРОВЕРКОЙ ПО ЭТАЛОНУ
По данным таблицы составьте задачи и решите их.
1 вариант – с.44, №4а; 2 вариант – с.44, № 4б.
Проверьте по эталону (слайд 3)?
– Какой формулой пользовались? Как решали? Правильность оцените с помощью знаков «+» или «-». У кого все верно? Молодцы!
VII. ВКЛЮЧЕНИЕ В СИСТЕМУ ЗНАНИЙ И ПОВТОРЕНИЕ
Где сможем применить полученное знание? (При решении задач)
№5, стр. 44. Двое учащихся работают на закрытой части доски, остальные – в тетрадях. Фронтально проводится проверка правильности выполнения задания.
– Чем пользовались? (Алгоритм решения задач, формулой работы, алгоритмом умножения многозначных чисел).
– Кто допустил ошибки? Проанализируйте их. Запишите ответ задачи. Можно ли по этой записи определить число автомобилей, которые выпускает завод:
за 5 дней (1040 м)
за 6 дней (1248 м)
за 60 дней (12480 м)
за 300 дней (62400 м).
– Можно ли, не вычисляя, сказать, на сколько второе произведение больше первого? (208×365 < 208×366 на 208).
VII. РЕФЛЕКСИЯ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ НА УРОКЕ
– Какие цели ставили на уроке? (Установить, какие величины описывают процесс выполнения работы, ввести обозначения этих величин и установить взаимосвязь между ними, т.е. построить формулу работы).
– Что явилось итогом работы? (Формулы).
– Достигли вы этой цели? Докажите.
– Заполните эталон. (слайд 4)
Формула…….(работы) A = V×…10010
(Производительность) – это работа, выполненная за единицу времени.V= … : t
t=A : …
– Если затрудняетесь, где можно найти ответ? (В учебнике).
– Вы сами сделали открытие и ряд изученных формул пополнился.
Проанализируйте свою работу. (Внимательно слушал, смотрел, сделал открытие, все получилось – доволен собой/ не доволен).
Оцените свою работу на полях тетради – нарисуйте лицо человечка.
– Благодарю вас за активную работу на уроке.
Урок я хочу закончить пословицей о труде.
Всегда помните: «Всякое умение трудом дается».
VIII. ДОМАШНЕЕ ЗАДАНИЕ
Презентация (слайд 5).
На слайде представлены данные о ежегодном выпуске автомобилей на российских заводах. Почему заводы выпускают разное количество машин? От чего это зависит? (От опыта работы, возраста, модернизации, от производительности труда, оборудования). Придумайте задачи на нахождение производительности, времени, работы, используя данные из таблицы.
Найти пословицы и поговорки о работе.
Решить №6, стр. 45.
Рефлексия: Слайд № 10
дети оценивают свои знания и умения при помощи цветных сигнальных карточек.
(красная) Я могу
(желтая) Я сомневаюсь, надо ещё поработать.
(зеленая) Мне многое непонятно.
Общая самооценка.
Чтобы вы хотели пожелать себе и своим товарищам на следующий урок?
Поблагодарите друг друга за помощь, поддержку на уроке. (Выставление оценок.)
Вы были внимательны!
Вы успели сделать все!
Вы м о л о д ц ы!
Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.
Что такое работа в физике – определение и формула
Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию.
В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:
A = F * S
В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:
A = F * S * cosA
В чем измеряется работа
Физические единицы, в которых выражается механическая работа, – Джоули.

Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах.
Работа силы трения
При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной.
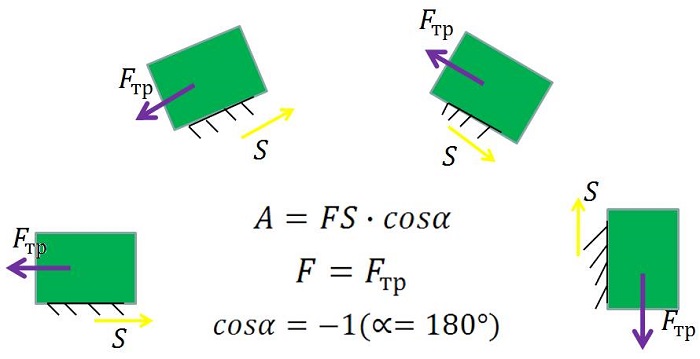
Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.
Положительная и отрицательная работа
Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости.
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей.
Полезная или затраченная работа
У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле.
Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:
КПД = А полезная / А затраченная,
и выражается в процентах. КПД всегда меньше 100.

Мощность
Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:
Р = A / t
В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.
Однако при равномерном движении можно использовать и другую формулу:
Р = F * v
Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.
Примеры решения задач
Рассмотрим несколько простых задач на нахождение механической работы.

Задача 1
Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.
Решение:
Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.
При помощи простой математики найдем числовой ответ:
A = 50 м * 10 кг * 10 Н/кг;
A = 5000 Дж.
Ответ: 5000 Дж.
Впрочем, не всегда речь идет о силе тяжести.
Задача 2
Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.
Решение:
Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.
Далее при помощи элементарных вычислений рассчитаем ответ:
A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.
Ответ: 0,4 Дж.
Но во всех задачах по данной теме траектория движения тела прямая.
Задача 3
Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.
Решение:
В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.
Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.
Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).
В таком случае:
F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.
Ответ: 5308 Н.
В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.
Задача 4
Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.
Решение:
На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы.
Запишем условие в более наглядном виде.
Дано:
m = 2500 кг;
F = 10000 H;
t = 10 с;
КПД = 30%;
угол A = 1500 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);
V – ?
Выведение формулы:
Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).
A1 = mg;
A2 = P * t / КПД.
То есть mg = P * t / КПД.
Шаг 2. P = F * V * cosA.
Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.
V = (m * g * КПД) / (F * t * cosA).
Числовое решение:
V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);
V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);
V = 7500 / 50000;
V = 0,15 м/с.
Ответ: 0,15 м/с.
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
