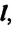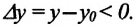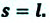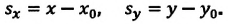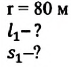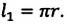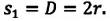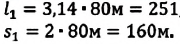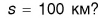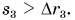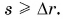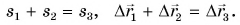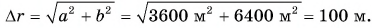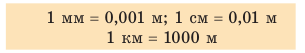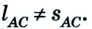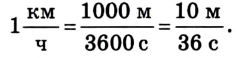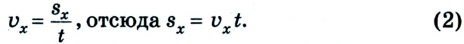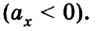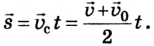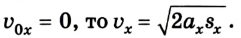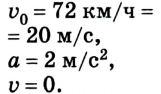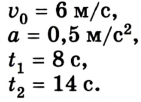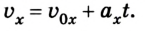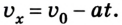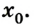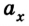Как мы изучали перемещение. Есть два типа смещения; горизонтальное смещение и вертикальное смещение. В этой статье мы обсудим, что такое горизонтальное смещение и как его найти.
Когда объект выстреливается по диагонали вблизи поверхности земли, он движется с постоянной скоростью по извилистому маршруту, ведущему к центру земли. Горизонтальное движение выстрела – это название, данное этому типу движения объекта, где выстрел относится к маршруту частицы.
Когда объект движется вдоль оси X, смещение в направлении х является горизонтальным смещение. Горизонтальное смещение, вызванное скоростью выстрела объекта, рассчитывается по формуле
ΔX=v0Xt
Где ΔX — горизонтальное смещение.
v0 скорость объекта
t время полета
Движение называется вертикальным движением снаряда, когда частица движется с постоянной скоростью, когда частица движется поперек оси y.
Как найти горизонтальное перемещение снаряда?
Горизонтальное смещение объекта, выпущенного в направлении x, можно рассчитать, если известны начальная скорость и время полета объекта.
Если в приведенную формулу подставить соответствующие значения начальной скорости и времени полета;
ΔX=v0Xt
Формула горизонтального смещения
ΔX=v0Xt
Где ΔX — горизонтальное смещение.
v0 скорость объекта
t время полета
Как рассчитать полное горизонтальное смещение ?
Нам нужно знать конечную и начальную скорость обстреливаемого объекта, чтобы найти полное горизонтальное перемещение.
Мы можем рассчитать полное горизонтальное смещение, используя время полета, начальную и конечную скорость объекта, который выстреливается в направлении x, и помещая эти значения в данную формулу:
s=ut+(1/2)в2
Расстояние и перемещение
Мы вообще думаем расстояние и смещение как одно и то же количество, но оба эти понятия используются для разных значений. Давайте подробнее рассмотрим разницу между расстоянием и смещением.
Расстояние
Мы можем определить расстояние как площадь, покрываемую элементом, независимо от его начального или конечного положения.
«Расстояние — это общий путь или маршрут, по которому следует какой-либо объект».
Водоизмещение
Стрелка используется для указания направления некоторого объекта от начальной точки до конечной точки. Например, местоположение объекта меняется, когда он перемещается из положения А в положение В. Различие между расстоянием и перемещением.
«Смещение — это кратчайшая или минимальная длина между начальными координатами и конечными координатами объекта».
Различие между расстоянием и смещением
| Нет. | Расстояние | Водоизмещение |
| 1. | Вся длина маршрута, пройденного объектом, называется расстоянием. | Смещение — это наименьшее расстояние между начальной и конечной координатами объекта. |
| 2. | Обозначается буквой «д». | Обозначается буквой «с». |
| 3. | Он просто содержит величину, а не направление. | Он содержит величину, а также направление. |
| 4. | В конце концов, это скалярная величина. | Это переменная с вектором. |
| 5. | Расстояние можно использовать для получения некоторых основных данных о маршруте объекта из одного места в другое. | Поскольку мы знаем, что смещение касается только координат начальной и конечной точек, поэтому оно не может предоставить данные о маршруте, по которому объект следовал от начальной точки до конца.. |
| 6. | Скорость*время | Скорость*время |
| 7. | Для расстояния возможны только положительные значения. | Смещение может быть отрицательным, нулевым или положительным. |
| 8. | Он не представлен стрелкой. | Смещение представлено b стрелкой, указывающей направление. |
| 9. | Расстояние можно рассчитать по непрямолинейному пути. | Для измерения смещения требуется прямолинейный путь. |
Проблемы
Проблема 1
Измерьте величину горизонтального смещения объекта при движении снаряда с постоянной скоростью 30 м/с и периодом полета 60 секунд.
Решения
Данный;
Скорость объекта = 30 м/с
Время полета = 60 с
Мы можем рассчитать горизонтальное смещение, подставив заданные значения в формулу смещения.
Дана формула для горизонтального смещения движения снаряда
ΔX=v0Xt
ΔХ=30*60=1800м
Проблема 2
Найти горизонтальное перемещение тела, которое выстрелили со скоростью 15 м/с в течение 30 с.
Решения
Данный;
Скорость частицы = 15 м/с
Время полета =30с
Мы можем рассчитать горизонтальное смещение, подставив заданные значения в формулу смещения.
Дана формула для горизонтального смещения при движении снаряда.
ΔX=v0Xt
ΔХ=15*30=450м
Проблема 3
Найти полное перемещение тела, выпущенного со скоростью 30 м/с. Через 60 секунд полета этот объект ударяется о землю со скоростью 30 м/с.
Решения
Данный;
Начальная скорость объекта = 15 м/с
Конечная скорость объекта = 30 м/с
Время полета = 60 секунд
Мы можем рассчитать общее горизонтальное смещение, подставив заданные значения в формулу полного смещения.
Формула для полного горизонтального смещения:
Часто задаваемые вопросы | Часто задаваемые вопросы
Q. Чему равно полное горизонтальное смещение снаряда?
Досягаемость снаряда представляет собой горизонтальное смещение снаряда и определяется предварительной скоростью объекта. Если снаряд выпущен с той же начальной скоростью, но с двух дополнительных углов проекции, его дальность будет равна.
Q. Является ли горизонтальное перемещение снаряда постоянным?
Когда горизонтальная длина, пройденная пулей за секунду, остается неизменной: пуля движется со скоростью 20 метров в секунду, поскольку горизонтальное ускорение отсутствует. В результате горизонтальное смещение составляет 10 метров за одну секунду, 20 метров за две секунды, 30 метров за три секунды. , и так далее.
Q. Как называется горизонтальное смещение снаряда?
Досягаемость снаряда — это горизонтальное смещение снаряда, определяемое начальной скоростью объекта.
Содержание:
Путь и перемещение:
Вы знаете, что любой вид движения совершается по определенной траектории.
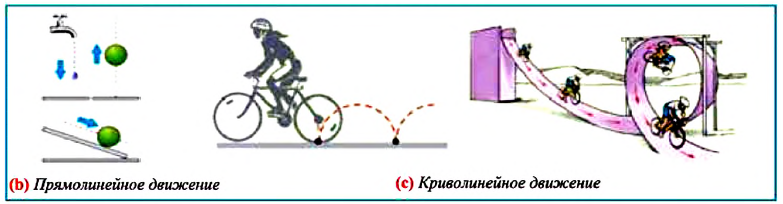
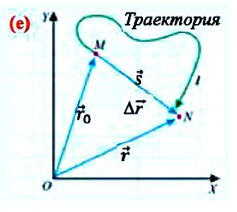
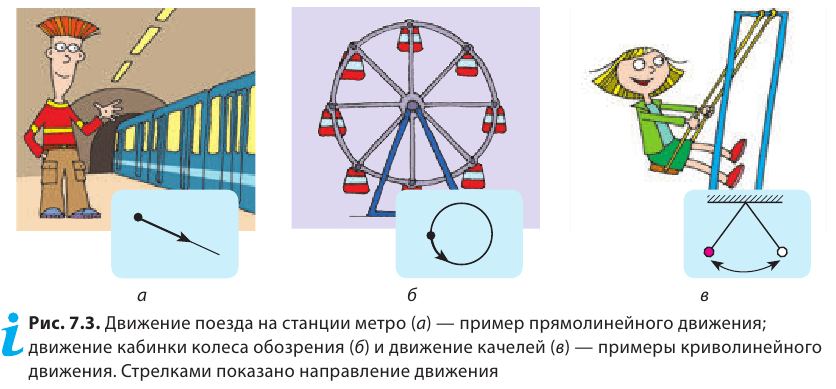
Траектория – это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.
Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, – криволинейным (с).
Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой
Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.
Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком 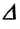
Изменение координат материальной точки во время движения
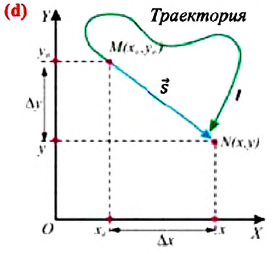
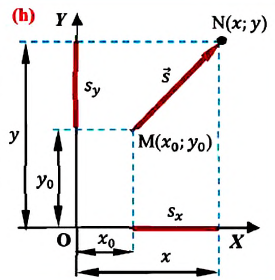
Изменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается 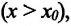
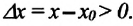
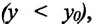
Изменение радиус-вектора материальной точки во время движения
На следующем рисунке представлены радиус-векторы 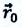
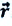
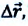
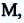
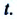

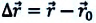
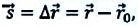
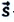
Перемещение – это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением. Перемещение — векторная величина.
Векторная величина – это величина, определяемая, кроме числового значения (модуля), также и направлением.
К вектору перемещения, как векторной величине, можно применить известные действия над векторами – сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.
Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.
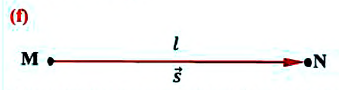
Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).
Материальная точка прошла расстояние 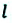
Материальная точка прошла расстояние 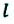
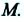
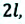
Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение 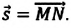
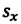
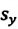
Одинаковы ли путь и перемещение
Задача:
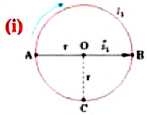
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).
Дано:
Решение:
Пройденный путь 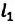
Модуль перемещения же равен диаметру окружности:
Вычисление:
Что такое путь и перемещение
Автобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путь
Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.
Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.
Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.
А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
Обозначим перемещение символом 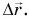
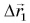
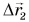
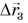
Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.
Можно ли сравнивать путь S, пройденный телом, с его перемещением 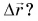
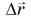
Сравнивать путь S можно с модулем перемещения 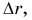
В рассматриваемом примере путь, пройденный автобусом за два часа, 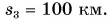
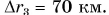
Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.
Следовательно, путь всегда не меньше модуля перемещения:
Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:
Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.
Равен ли при этом модуль 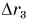
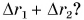
Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.
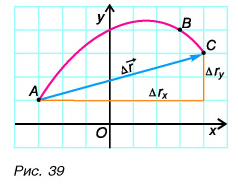
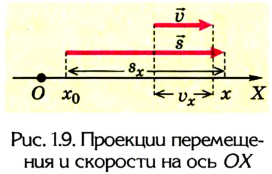
При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора 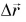
Главные выводы:
- Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Путь — положительная скалярная величина.
- Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
- Путь не меньше модуля перемещения тела за то же время.
- Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.
Пример:
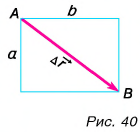
Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.
Решение
Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:
Путь конькобежца:
Путь пешехода:
Ответ:
- Заказать решение задач по физике
Траектория движения
Возьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис. 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.
Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.
Так, в безоблачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел (рис. 7.3).
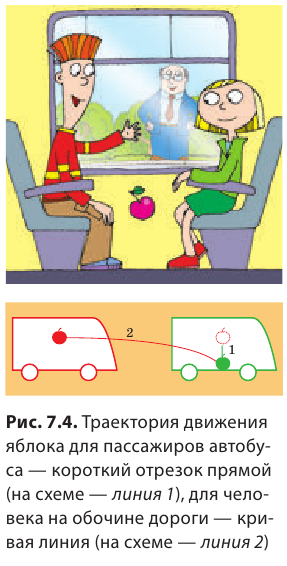
Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.
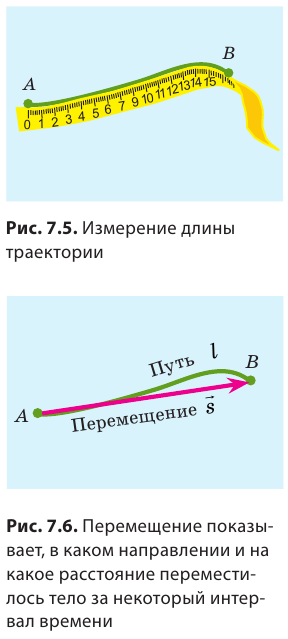
Чем путь отличается от перемещения
Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):
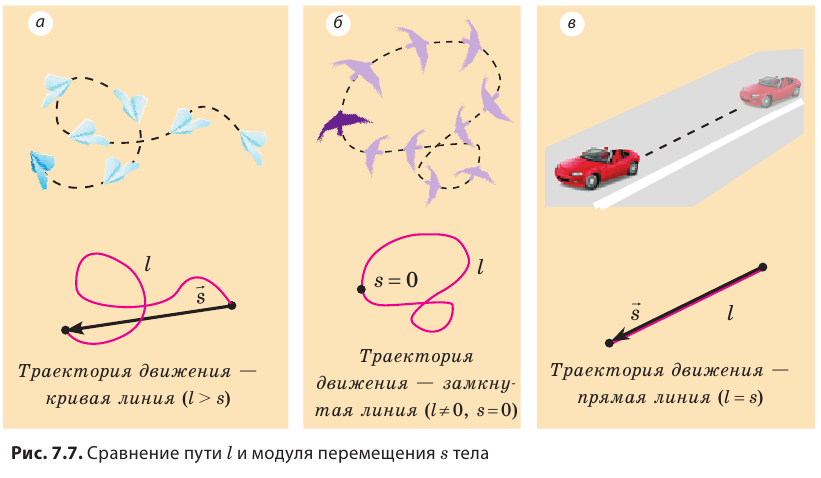
Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом 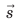
Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).
Итоги:
Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение 
Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Прямолинейное равноускоренное движение
- Сложение скоростей
- Физический и математический маятники
- Пружинные и математические маятники
- Скалярные и векторные величины и действия над ними
- Проекция вектора на ось
Путь и перемещение, теория и онлайн калькуляторы
Путь и перемещение
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь – длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь – это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
[Delta s=left|x_2-x_1right|left(1right),]
где $x_1$ – координата начального положения тела; $x_2$ – конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
[Delta s=vt left(2right),]
где $t$ – время движения тела.
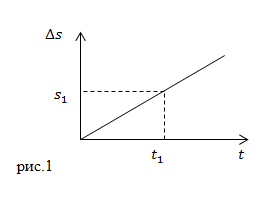
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку ${Delta s}_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
[Delta overline{r}=overline{r }left(t+Delta tright)-overline{r }left(tright)left(3right).]
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки – это перемещение ($Delta overline{r}$).
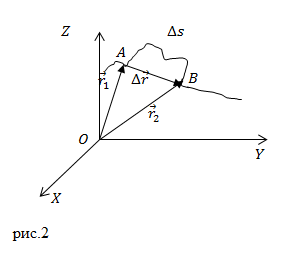
В декартовой системе координат радиус-вектор точки представляют в виде:
[overline{r }left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(4right),]
где $overline{i}$, $overline{j}$,$ overline{k}$ – единичные орты осей X,Y,Z. Тогда $Delta overline{r}$ равен:
[Delta overline{r}=left[xleft(t+Delta tright)-xleft(tright)right]overline{i}+left[yleft(t+?tright)-yleft(tright)right]overline{j}+left[zleft(t+?tright)-zleft(tright)right]overline{k}left(5right).]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overline{r}right|=Delta s left(6right).]
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overline{r}right|$ или просто $Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
[Delta overline{r}=Delta {overline{r}}_1+Delta {overline{r}}_2+dots left(7right).]
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
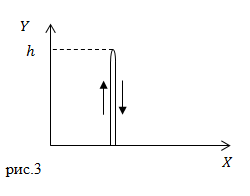
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь – длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
[Delta s=2h.]
Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
[Delta r=0.]
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Пример 2
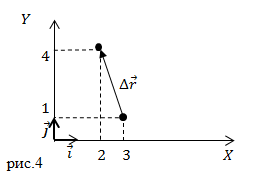
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
Радиус – вектор начальной точки запишем как:
[{overline{r }}_0left(tright)=x_0left(tright)overline{i}+y_0left(tright)overline{j}=3overline{i}+1overline{j}left(2.1right).]
Радиус – вектор конечной точки имеет вид:
[overline{r}left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}=2overline{i}+4overline{j}left(2.2right).]
Вектор перемещения представим как:
[Delta overline{r}=left[xleft(tright)-x_0left(tright)right]overline{i}+left[уleft(tright)-у_0left(tright)right]overline{j}=left[2-3right]+left[1-4right]overline{j}=-1overline{i}+3overline{j}(2.3).]
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Читать дальше: равнодействующая всех сил.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание
- Химическое равновесие
- Практические аспекты ОУ. Напряжение смещения, ток смещения, дрейф
- Напряжение смещения
- Ток смещения
- Резюме
- Дрейф
- Резюме
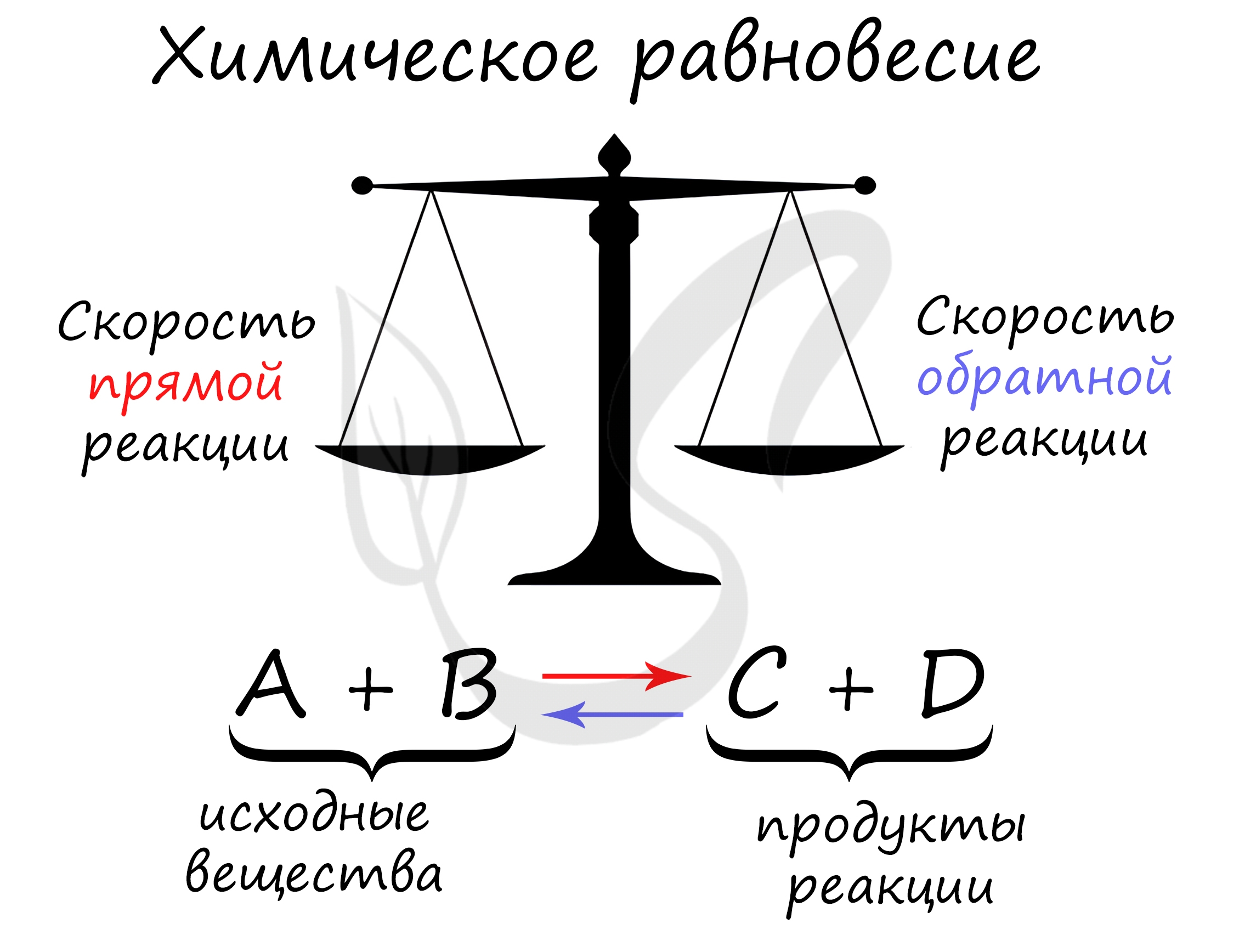
Химическое равновесие
Химическое равновесие — состояние химической системы, при котором скорость прямой реакции равна скорости обратной.
В большом количестве заданий, которые мне довелось увидеть, я ни один раз видел, как коверкают это определение. Например, в заданиях верно-неверно предлагают похожий вариант, однако говорят о «равенстве концентраций исходных веществ и продуктов» — это грубая ошибка. Химическое равновесие — равенство скоростей.
Принцип Ле Шателье
В 1884 году французским химиком Анри Ле Шателье был предложен принцип, согласно которому, если на систему, находящуюся в состоянии равновесия, оказать внешнее воздействие (изменить температуру, давление, концентрацию), то система будет стремиться компенсировать внешнее воздействие.
Это принцип обоснован термодинамически и доказан. Однако в такой абстрактной формулировке его сложно применить для решения конкретных задач по химическому равновесию. В этой статье я покажу конкретные примеры и обозначу алгоритм действия, чтобы вы могли успешно справляться с заданиями.
Влияние изменения концентрации на химическое равновесие
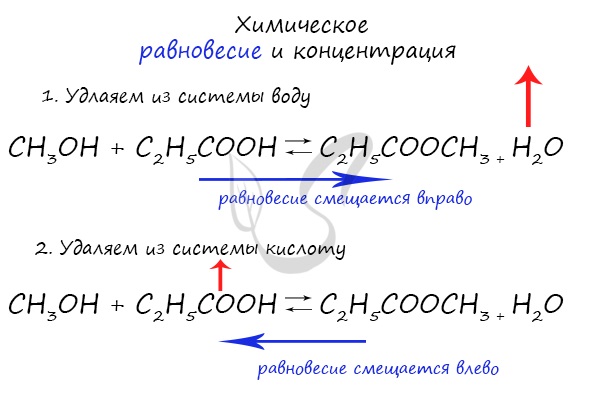
При увеличении концентрации какого-либо компонента химической реакции, система будет стремиться восстановить равновесие: равновесие будет смещаться в сторону расходования добавленного компонента.
Объясню проще: если вы увеличиваете концентрацию вещества, которое находится в левой части, равновесие сместится в правую сторону. Если добавляете вещество из левой части (продуктов реакции) — смещается в сторону исходных веществ. Посмотрите на пример ниже.
Если мы попытаемся удалить какое-либо вещество из системы (уменьшить его концентрацию), то система будет стремиться заполнить «пустое» место, которые мы создали. Наглядно демонстрирую на примере:
Можно подвести итог полученным знаниям таким образом: «Куда добавляем — оттуда смещается, откуда берем — туда смещается». Воспользуйтесь этой или придумайте свое правило для запоминания этой закономерности 😉
Изменения давления и химическое равновесие
Если речь в задании идет об изменении давления, то первое, что нужно сделать, это посчитать количество газов в уравнении слева и справа. Твердые вещества и жидкости считать не нужно. Например:
В приведенном уравнении количество молекул газа в левой части — 1, в правой — 2.
Запомните правило: «При увеличении давления равновесие смещается в сторону меньших газов, при уменьшении давления — в сторону больших газов». Для нашей системы правило действует таким образом:
В случае, если слева и справа количество молекул газа одинаково, например, в реакции:
Слева — 2 газа, и справа — 2. В такой реакции увеличение или уменьшение давления не повлияет на химическое равновесие.
Изменение температуры и химическое равновесие
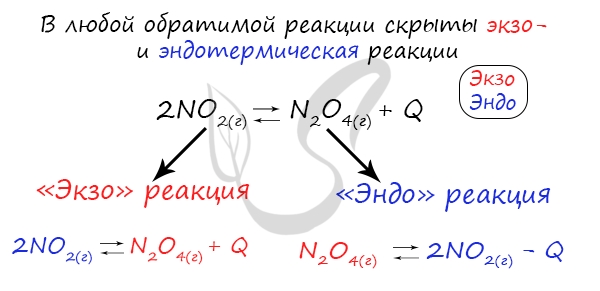
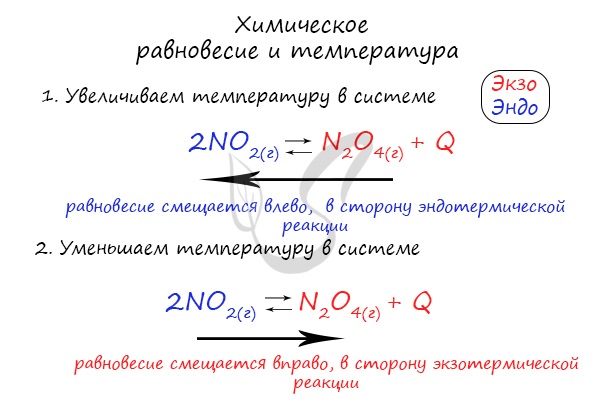
Если в задании увеличивают или уменьшают температуру, то первое, что вы должны оценить: экзотермическая это реакция или эндотермическая.
Следуйте следующему правилу: «При увеличении температуры равновесие смещается в сторону эндотермической реакции, при уменьшении — в сторону экзотермической реакции». У любой обратимой реакции есть экзо- и эндотермические части:
Поэтому данное правило универсально и применимо для всех реакций. Для примера разберем следующие задачи:
Чтобы не осталось белых пятен, возьмем экзотермическую реакцию и повторим с ней подобный эксперимент.
Катализатор и ингибитор
Действие катализатора и ингибитора соответственно касается только ускорения и замедления химической реакции. Они никоим образом не влияют на равновесие.
Константа равновесия
Константой равновесия называют отношения скоростей прямой и обратной реакции. Для реакции типа aA + bB = cC + dD константа равновесия будет записана следующим образом:
Решим задачу. Дана реакция: 2NO + Cl2 ⇄ 2NOCl . Вычислите константу равновесия, если равновесные концентрации веществ для данной реакции: c(NO) = 1.8 моль/л , c(Cl2) = 1.2 моль/л , c(NOCl) = 0.8 моль/л.
Константу равновесия для данной задачи можно представить в виде 1.64 * 10 -1 .
© Беллевич Юрий Сергеевич 2018-2021
Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение (в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования, обратитесь, пожалуйста, к Беллевичу Юрию.
Источник
Практические аспекты ОУ. Напряжение смещения, ток смещения, дрейф
У реальных операционных усилителей по сравнению с «идеальной» моделью есть некоторые недостатки. Реальное устройство отличается от идеального дифференциального усилителя. У него может быть смещение как у аналогового измерительного устройства, которое не обнуляется. Входы могут потреблять ток. Характеристики могут дрейфовать с возрастом и температурой. Эти недостатки могут привести к незначительным ошибкам в одних приложениях и недопустимым ошибкам в других приложениях. В некоторых случаях эти ошибки могут быть компенсированы. Иногда требуется более высокое качество и более дорогостоящее устройство.
Напряжение смещения
Другой практической проблемой для производительности операционного усилителя является смещение напряжения. То есть влияние наличия выходного напряжения на величину, отличную от нуля, когда два входных вывода закорочены вместе. Помните, что операционные усилители – это, прежде всего, дифференциальные усилители: они должны усиливать разность напряжений между двумя входными выводами и не более того. Когда разность входных напряжений точно равна нулю, мы (в идеале) ожидаем, что на выходе будет точно нулевое напряжение. Однако в реальном мире это случается редко. Даже если рассматриваемый операционный усилитель имеет нулевой коэффициент усиления синфазного сигнала (бесконечный CMRR), выходное напряжение может быть не равным нулю, когда оба входа закорочены вместе. Это отклонение называется смещением выходного уровня операционного усилителя.
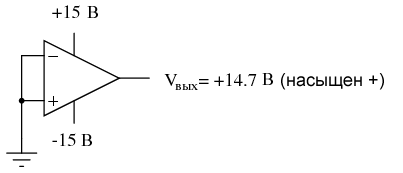
Идеальный операционный усилитель выдает ровно ноль вольт, когда оба входа закорочены вместе и соединены с землей. Тем не менее, большинство стандартных операционных усилителей будут сдвигать свое выходное напряжение в сторону уровня насыщения, либо отрицательного, либо положительного. В приведенном выше примере выходное напряжение насыщается при значении положительных 14,7 вольт, чуть меньше, чем +V (+15 вольт) из-за предела положительного насыщения этого конкретного операционного усилителя. Поскольку смещение приводит выходное напряжение к точке полного насыщения, нельзя сказать, какое смещение напряжения присутствует на выходе. Если раздельный источник питания +V/-V был достаточно высокого напряжения, кто знает, может быть, выходное напряжение составляло бы несколько сотен вольт из-за влияния смещения!
По этой причине напряжение смещения обычно выражается через эквивалентную величину дифференциального входного напряжения, создающего этот эффект. Другими словами, мы предполагаем, что операционный усилитель является идеальным (без смещения вовсе), и небольшое напряжение прикладывается последовательно с одним из входов, чтобы заставить выходное напряжение в ту или иную сторону отойти от нуля. Поскольку дифференциальные коэффициенты усиления операционных усилителей настолько велики, значение «входного напряжения смещения» необязательно должно учитывать то, что мы видим с закороченными входами:

Напряжение смещения будет приводить к небольшим ошибкам в любой схеме на операционных усилителях. Итак, как мы компенсируем его? В отличие от синфазного коэффициента усиления, производители обычно предусматривают средства устранения смещения в корпусных операционных усилителях. Обычно два дополнительных вывода на корпусе операционного усилителя зарезервированы для подключения внешнего «подстроечного» потенциометра. Эти выводы обозначаются как смещение нуля и используются следующим обобщенным образом:
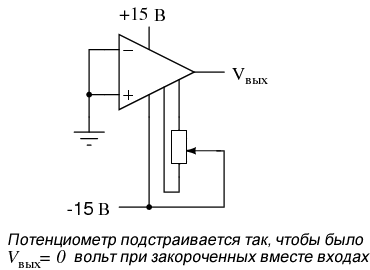
На одиночных операционных усилителях, таких как 741 и 3130, выводы смещения нуля – это выводы 1 и 5 на 8-выводном DIP корпусе. Другие модели операционных усилителей могут использовать другие выводы для смещения нуля и/или потребовать немного отличающиеся схемы подключения подстроечного потенциометра. Некоторые операционные усилители вообще не предоставляют выводов смещения нуля! Подробности смотрите в технических описаниях от производителей.
Ток смещения
Входы операционного усилителя имеют чрезвычайно высокие импедансы. То есть входные токи, поступающие или выходящие из двух входных сигнальных выводов операционного усилителя, чрезвычайно малы. Для большинства целей анализа схем на операционном усилителе мы относимся к ним так, как будто их вообще нет. Мы анализируем схему, как если бы ток, входящий или выходящий из входных выводов, был равен абсолютному нулю.
Однако эта идиллическая картина не совсем верна. Операционные усилители, особенно операционные усилители с биполярными транзисторами на входах, должны пропускать некоторый ток через свои входные выводы, чтобы их внутренние схемы были правильно смещены. Эти токи, логично, называются токами смещения. При определенных условиях токи смещения операционного усилителя могут вызывать проблемы. Следующая схема иллюстрирует одно из этих проблемных условий:
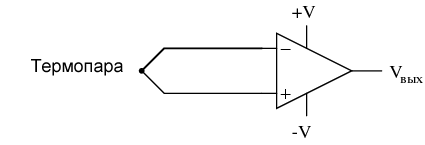
На первый взгляд мы не видим никаких явных проблем с этой схемой. Термопара, создающая небольшое напряжение, пропорциональное температуре (на самом деле, напряжение пропорционально разнице температур между измерительным переходом и «опорным» переходом, сформированным при соединении проводов сплава термопары с медными проводами, ведущими к операционному усилителю), управляет операционным усилителем либо в положительную, либо в отрицательную сторону. Другими словами, это своего рода схема компаратора, сравнивающая температуру между переходом на конце термопары и опорным переходом (около операционного усилителя). Проблема заключается в следующем: проводная петля, образованная термопарой, не обеспечивает путь для обоих входных токов смещения, поскольку оба тока пытаются идти одним и тем же путем (либо в операционный усилитель, либо из него).
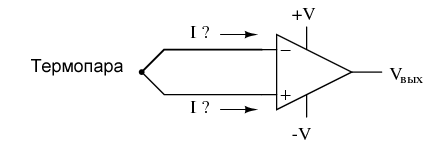
Чтобы эта схема работала должным образом, мы должны соединить с землей один из входных проводов, таким образом обеспечивая путь к (или из) точке земли для обоих токов:
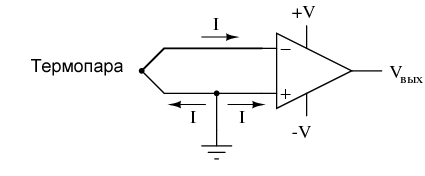
Эта проблема необязательно очевидна, но очень реальна!
Входные токи смещения могут вызвать проблемы другим способом: нежелательные падения напряжения на сопротивлениях схемы. Возьмем для примера следующую схему:
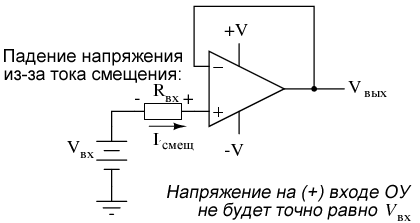
Мы ожидаем, что схема повторителя напряжения, такая как приведенная выше, точно воспроизводит на выходе входное напряжение. Но что насчет сопротивления последовательно с источником входного напряжения? Если есть какой-либо ток смещения через неинвертирующий (+) вход, он вызовет некоторое падение напряжения на Rвх, таким образом, напряжение на неинвертирующем входе будет не соответствовать фактическому значению Vвх. Токи смещения обычно находятся в диапазоне микроамперов, поэтому падение напряжения на Rвх будет не очень большим. Одним из примеров приложения, где входное сопротивление (Rвх) может быть очень большим, является то, которое имеет электроды pH-пробника, где один электрод содержит ионно-проницаемый стеклянный барьер (очень плохой проводник с сопротивлением в миллионы ом).
Если бы мы на самом деле строили схему на операционном усилителе для измерения напряжения на pH электроде, мы бы, вероятно, захотели использовать операционный усилитель с входами на полевых (FET или MOSFET, IGFET) транзисторах, вместо операционного усилителя с входами на биполярных транзисторах (для уменьшения входного тока смещения). Но даже тогда, могут оставаться небольшие токи смещения, которые могут вызывать ошибки измерений, поэтому мы должны найти какой-то способ уменьшить их с помощью хорошего проектирования.
Один из способов сделать это основан на предположении, что два входных тока смещения будут одинаковыми. В действительности, они часто близки к тому, чтобы быть одинаковыми, разница между ними называется током входного смещения. Если они одинаковы, тогда мы должны иметь возможность убрать влияние падения напряжения на входном сопротивлении, вставив сопротивление равной величины последовательно с другим входом, например:
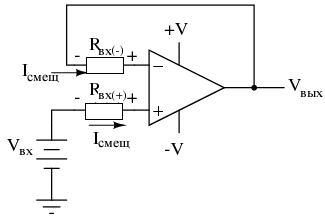
При добавлении в схему дополнительного сопротивления выходное напряжение будет ближе к Vвх, чем раньше, даже если есть некоторое смещение между этими двумя входными токами.
И для схемы инвертирующего усилителя, и для схемы неинвертирующего усилителя компенсирующий резистор помещается последовательно с неинвертирующим (+) входом, чтобы компенсировать падения напряжения в цепи делителя из-за тока смещения.


В любом случае значение компенсирующего резистора определяется путем вычисления параллельного сопротивления R1 и R2. Почему значение равно параллельному эквиваленту R1 и R2? При использовании теоремы суперпозиции для определения того, насколько большое падение напряжения будет создаваться током смещения инвертирующего (-) входа, мы рассматриваем ток смещения, как если бы он исходил от источника тока внутри ОУ и закорачивал все источники напряжения (Vвх и Vвых). Это дает два параллельных пути для тока смещения (через R1 и через R2, оба на землю). Мы хотим дублировать эффект тока смещения на неинвертирующем (+) входе, поэтому значение резистора, которое мы выбираем для вставки последовательно с этим входом, должно быть равно R1 параллельно с R2.
Связанная с этим проблема, которую иногда испытывают учащиеся при изучении построения схем на операционных усилителях, вызвана отсутствием соединения источника питания с общей землей. Для правильной работы ОУ необходимо, чтобы какой-либо вывод источника питания постоянного напряжения был общим с точкой «земли» входного сигнала(ов). Это обеспечивает полный путь для токов смещения, тока(ов) обратной связи, а также для (выходного) тока нагрузки. Возьмем для примера следующую схему, показывающую источник питания, правильно соединенный с землей:
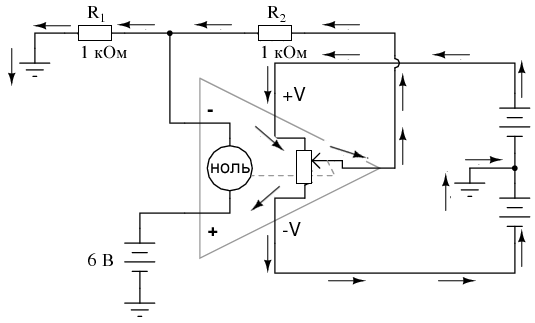
Здесь стрелки обозначают путь протекания токов через батареи источника питания, как для питания внутренних схем операционного усилителя («потенциометр» внутри него, который управляет выходным напряжением), так и для питания петли обратной связи из резисторов R1 и R2. Предположим, что точка земли этого «раздельного» источника питания постоянного напряжения была удалена. Эффект от этого будет огромен:
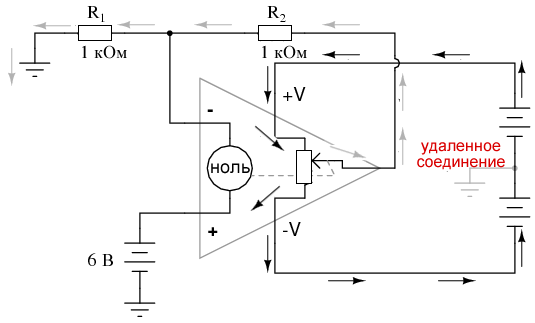
Соединение источника питания с землей обязательно для работы схемы!
Никакие электроны не могут протекать в или из выходного вывода операционного усилителя, потому что путь к источнику питания заканчивается «тупиком». Таким образом, никакие электроны не протекают ни через точку земли слева от R1, ни через петлю обратной связи. Это фактически делает операционный усилитель бесполезным: он не может ни поддерживать ток через петлю обратной связи, ни через соединенную с землей нагрузку, поскольку нет никакого соединения какой-либо точки источника питания с землей.
Токи смещения также останавливаются, поскольку они полагаются на путь к источнику питания и обратно к входному источнику через землю. На следующем рисунке показаны токи смещения (только), когда они проходят через входные выводы операционного усилителя, через выводы баз входных транзисторов и, в конечном счете, через вывод(ы) источника питания и обратно на землю.
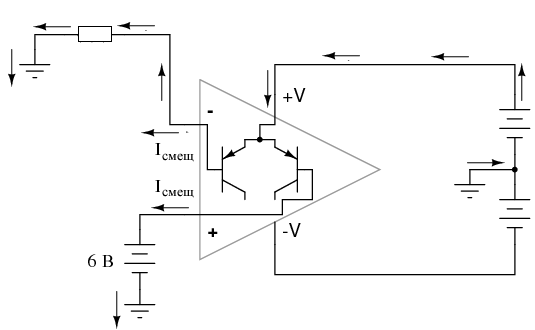
Пути протекания токов смещения показаны через источник питания
Без опорной точки земли на источнике питания токи смещения не будут иметь полного пути в схеме, и они будут остановлены. Поскольку биполярные транзисторы являются устройствами, управляемыми током, это также делает бесполезным входной каскад операционного усилителя, так как оба входных транзистора будут вынуждены уйти в режим отсечки из-за полного отсутствия тока базы.
Резюме
- Входы операционного усилителя обычно проводят очень малые токи, называемые токами смещения, и необходимые для правильного смещения первого транзисторного усилительного каскада в схеме операционного усилителя. Токи смещения не большие по величине (в диапазоне микроампер), но достаточно большие, чтобы вызывать проблемы в некоторых приложениях.
- Токи смещения на обоих входах должны иметь пути для протекания к одной из «шин» источника питания или к земле. Недостаточно просто обеспечить проводящий путь от одного входа к другому.
- Чтобы устранить любые напряжения смещения, вызванные током смещения, протекающим через сопротивления, просто добавьте эквивалентное сопротивление последовательно с другим входом операционного усилителя (так называемое компенсирующее сопротивление). Эта корректирующая мера основана на предположении, что два входных тока смещения будут равны.
- Любое неравенство между токами смещения в операционном усилителе составляет то, что называется током входного смещения.
- Для правильной работы операционного усилителя важно, чтобы на каком-либо выводе источника питания была опорная точка земли, чтобы сформировать полные пути для токов смещения, тока обратной связи и тока нагрузки.
Дрейф
Будучи полупроводниковыми устройствами, операционные усилители подвергаются незначительным изменениям в поведении при изменениях рабочей температуры. Любые изменения в производительности ОУ, связанные с температурой, относятся к категории дрейфа операционного усилителя. Параметры дрейфа могут быть указаны для токов смещения, напряжения смещения и т.п.. Для более подробной информации смотрите техническое описание на конкретный операционный усилитель от производителя.
Чтобы свести дрейф операционного усилителя к минимуму, мы можем выбрать операционный усилитель, имеющий минимальный дрейф, и/или мы можем сделать всё возможное, чтобы поддерживать рабочую температуру как можно более стабильной. Последнее действие может включать в себя обеспечение некоторой формы управления температурой для внутренней части оборудования, в которой размещается операционный усилитель(и). Это не так странно, как может показаться на первый взгляд. Известно, что, например, в стандартных лабораторных опорных генераторах точного напряжения иногда используются «печи» (термостаты) для поддержания чувствительных компонентов (таких как стабилитроны) при постоянной температуре. Если требуется высокая точность при обычных факторах стоимости и гибкости, это может быть вариант, на который стоит обратить внимание.
Резюме
Операционные усилители, будучи полупроводниковыми устройствами, подвержены изменениям температуры. Любые изменения в производительности усилителя, возникающие в результате изменения температуры, известны как дрейф. Дрейф лучше всего минимизировать с помощью управления температурой окружающей среды.
Источник
Кинематика в физике – основные понятия, формулы и определения с примерами
Содержание:
Основная задача механики – описание движения тел, т. е. выяснение закона (уравнения) их движения. Как отмечал А. Эйнштейн, наиболее фундаментальная проблема, остававшаяся нерешенной на протяжении тысячелетий, – это проблема движения. Собственно, учение о движении стало наукой лишь со времен Галилео Галилея и Исаака Ньютона.
Кинематика, изучает конкретные механические та их взаимодействия с другими телами. Она фактически объединяет простейшие пространственно-временные зависимости, в частности изменение координат тела со временем (как функцию времени).
Поэтому кинематику часто называют геометрией движения.
Кинематика изучает механические движения тел без учета их взаимодействия с другими телами.
Кинематика
Физика изучает разнообразные явления и процессы, происходящие вокруг нас. Как вам известно, в зависимости от их природы различают механические, тепловые, электрические, магнитные, световые и другие физические явления. Раздел физики, который объясняет движение и взаимодействие тел, называется механикой.
Слово «механика» впервые ввел Аристотель. Оно означает «машина».
Механика – одна из древнейших наук. Ее возникновение и развитие связано с практическими потребностями человека. Первые труды по механике, в которых рассматривались свойства простых механизмов и машин, появились еще в Древней Греции. Весомый вклад в ее становление сделали такие корифеи науки, как Аристотель (IV в. до н. э.), Архимед (III в. до н. э.), Леонардо да Винчи (XV в.), Галилео Галилей (XVII в.) и др. В завершенном виде как классическая теория она получила обоснование в работе Исаака Ньютона «Математические начала натуральной философии» (1687 г.). Современная механика, в основе которой лежит теория относительности, создана в начале XX в. Альбертом Эйнштейном.
Основная задача механики состоит в том, чтобы на основании параметров движения тела: координат, пройденного пути, перемещения, угла поворота, скорости, силы и т. д. – найти закон или уравнение, которое описывает это движение.
Основная задача механики состоит в том, чтобы найти уравнение движения тела с помощью параметров, описывающих это движение.
Т. е. если мы при помощи этих физических величин сможем установить положение тела в любой момент времени, то основная задача механики считается решенной. В зависимости от способов ее решения в механике выделяют три раздела: кинематика, динамика и статика.
Кинематика изучает, как движется тело, не вникая в причины, вызывающие именно такое движение. Поэтому кинематические уравнения состоят лишь из пространственных характеристик механического движения: пройденного пути, изменения координат тела, скорости и т. д. В них нет сил, изменяющих это движение.
В переводе с греческого слово кинематика» (kinematos) означает движение.
Механическое движение и траектория движения
Чаще всего в обыденной жизни мы наблюдаем явление, которое называется механическим движением. Например, автомобиль едет по дороге, в небе «плывут» тучи, ребенок катается на качелях, Луна вращается вокруг Земли и т. д. Во всех этих случаях происходит изменение положения одного тела или его частей относительно других. Чтобы убедиться в этом, необходимо выбрать тело отсчета, относительно которого можно фиксировать положение движущегося тела в любой момент времени. Тело отсчета выбирают произвольно. В приведенных примерах это может быть столб или дерево возле дороги, дом, поверхность Земли и т. д.
Для того чтобы описать движение тела, необходимо точно знать его местоположение в пространстве в произвольный момент времени, т. е. уметь определять изменение положения тела в пространстве относительно других тел с течением времени. Как известно, легче всего это можно сделать с помощью системы координат. Например, зафиксировать «адрес» тела как определенное его положение в пространстве, измерив расстояния или углы в некоторой системе координат.
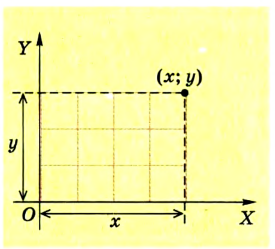
Например, в географии положение тела на земной поверхности задается двумя числами на пересечении меридиана и параллели, которые называются географической долготой и широтой. В математике «адрес» точки чаще всего определяют ее координатами, в частности в прямоугольной (декартовой) системе координат на плоскости – это расстояния х и у (рис. 1.1).
Взаимные изменения положения тела или его частей в пространстве с течением времени называются механическим движением.
Систему координат, как правило, связывают с телом отсчета. В данном случае движущееся тело характеризуется изменением положения в пространстве относительно тела отсчета, т. е. изменением его координат с течением времени.
Математически это можно записать в таком виде: х = x(t); у = y(t).
Для того чтобы определить такое изменение в любой момент времени, с телом отсчета и системой координат необходимо связать средство измерения времени, к примеру секундомер или хронометр. Тогда тело отсчета, связанную с ним систему координат и секундомер как единое целое называют системой отсчета.
Как известно, реальные физические тела имеют форму и объем. Поэтому однозначно задать их положение в пространстве не всегда представляется возможным, поскольку различные их части имеют разные координаты. Однако эту проблему можно упростить, если не брать во внимание размеры тела. Такое возможно лишь при определенных условиях.
Чтобы выяснить их, рассмотрим движение автомобиля. На значительных расстояниях, например на шоссе между Киевом и Харьковом, размерами автомобиля можно пренебречь, поскольку они значительно меньше расстояния между этими городами. Поэтому нет необходимости рассматривать особенности движения каждой части кузова автомобиля – достаточно его представить как движение точки.
Таким образом, для упрощения описания движения тел, когда их размерами при определенных условиях можно пренебречь, применяют понятие материальной точки. Это условное тело, не имеющее размеров, которое определяет положение реального тела в пространстве при помощи координат такой, материальной точки. Ее геометрический образ – невесомая точка, не имеющая размеров. В случае поступательного движения, при котором все точки тела движутся одинаково, любое тело можно считать материальной точкой.
Материальная точка – это физическая модель, при помощи которой представляют реальное тело, пренебрегая его размерами.
Часто кроме движущихся предметов мы наблюдаем тела, пребывающие в состоянии покоя. Однако абсолютно неподвижных тел в природе не существует.
Рассмотрим такой пример. В вагоне на столе стоит бутылка с водой (рис. 1.2). Во время движения поезда разные наблюдатели – пассажир в купе и провожающий на перроне – оценят ее состояние движения по-разному. Для сидящего пассажира она неподвижна, поскольку расстояние от него до бутылки не изменяется. Для провожающего на перроне 16 она движется, потому что изменяет свое положение с течением времени в системе отсчета, связанной с перроном.
Следовательно, состояние покоя является относительным, равно как и состояние движения, поскольку зависит от выбранной системы отсчета. Поэтому в дальнейшем при рассмотрении движения тела мы в первую очередь будем определяться с выбором системы отсчета, потому что от этого нередко зависит сложность уравнений, описывающих данное движение. Правильный выбор системы отсчета ведет к упрощению уравнений движения.
Состояние покоя и состояние движения тела относительны, поскольку зависят от выбора системы отсчета.
Рассмотрим движущееся тело, последовательно фиксируя его положение в определенные моменты времени. Если теперь соединить все точки, в которых побывало тело во время своего движения, то получим мнимую линию, которая называется траекторией движения. Траектория движения может быть видимой (след от самолета на небосклоне, линия от карандаша или ручки при записи в тетради) и невидимой (полет птички, движение теннисного мяча и т. д.).
По форме траектории механическое движение бывает прямолинейным и криволинейным (рис. 1.3).
Положение броуновской частички через определенные промежутки времени.
Рис. 1.3. Различные формы траектории
Траектория прямолинейного движения – прямая линия. Например, падение тела с определенной высоты или движение шарика по наклонному желобу. Во время криволинейного движения тело перемещается по произвольной кривой. Часто реальное движение тел является комбинацией прямолинейного и криволинейного движений. Например, комбинированным есть движение автобуса по маршруту: на разных участках траектория его движения может быть и прямолинейной, и криволинейной.
Поскольку движение тел происходит в определенных системах отсчета, то и траектория рассматривается относительно них. Ведь она отображает во времени последовательные положения тела в некоторой системе отсчета. Поэтому она будет отличаться формой в различных системах отсчета, т. е. траектории движения также относительны. Например, все точки колеса велосипеда относительно его оси описывают окружность, однако в системе отсчета, связанной с землей, эта линия более сложная (рис. 1.4).
Рис. 1.4. Траектория движения точки обода колеса велосипеда
Путь и перемещение
Зная траекторию движения, можно определить путь, пройденный телом: для этого необходимо измерить длину траектории между начальной и конечной точками движения.
Путь – это длина траектории, которую проходит тело или материальная точка за определенный интервал времени. Он обозначается латинской буквой l. Данная физическая величина является скалярной и характеризуется лишь значением длины траектории движения.
В Международной системе единиц (СИ) путь измеряется в метрах (м). На практике используют также другие единицы пути – километр (км), сантиметр (см) и др.
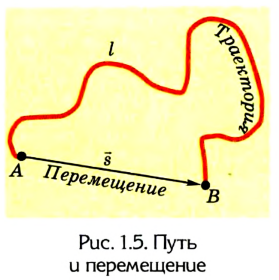
Часто, для того чтобы более полно охарактеризовать движение тела и найти его новое положение, кроме пройденного пути (длины траектории), необходимо указать также направление, в котором двигалось тело. Например, водителю автомобиля приходится ехать по извилистой дороге (рис. 1.5).
Пройденный путь – это длина дороги I, по которой ехал автомобиль. Водитель же совершил перемещение в пространстве из точки А в точку В, которое можно найти, соединив начальное и конечное положение тела прямой линией, указав при этом направление движения.
Следовательно, направленный отрезок прямой, соединяющий начальное положение движущегося тела с конечным, называется перемещением. Перемещение – это векторная величина. Оно обозначается латинской буквой 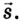
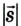
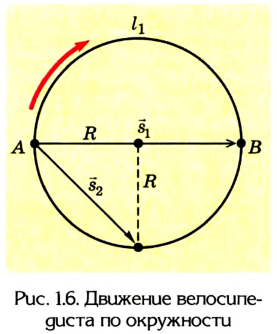
Путь и перемещение могут отличаться своими значениями. Чтобы убедиться в этом, рассмотрим движение велосипедиста по окружности радиуса R= 100 м (рис. 1.6).
Допустим велосипедист стартует в точке А. Проехав половину окружности, он окажется в точке В. Пройденный им путь равен дуге 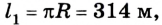
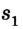
В момент времени, когда велосипедист проедет 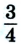
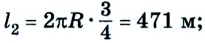
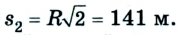
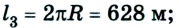
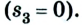
Путь и перемещение имеют также одинаковые значения, когда тело движется прямолинейно лишь в одном направлении.
В рассмотренном нами примере пройденный путь и перемещение разные, отличаются по своему значению. Возникает вопрос: могут ли они совпадать, быть одинаковыми? Можно легко убедиться в том, что такое возможно, если, во-первых, траектория движения будет прямой, во-вторых, движение происходит в одну сторону. Как подтверждение этого, рассмотрим — такой пример.
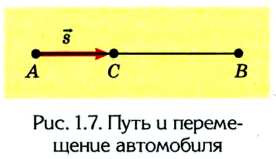
Допустим, что автомобиль движется прямолинейно по шоссе из пункта А в пункт В, а затем возвращается в пункт С. Расстояние между пунктами 2 км и 4 км соответственно, все они размещены на одной прямой (рис. 1.7).
Двигаясь из пункта А в пункт В, автомобиль проходит путь 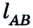
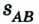
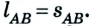
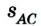
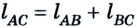
Следовательно, пройденный путь и перемещение по своему значению одинаковы лишь в том случае, если тело движется по прямой и не изменяет направление движения.
Равномерное прямолинейное движение
Простейшим видом механического движения является равномерное прямолинейное движение. Это такое движение, при котором тело, двигаясь по прямой, за любые одинаковые интервалы времени совершает одинаковые перемещения. Его траектория – прямая линия. Поэтому его можно описать переменой одной из координат, например х = x(t), если координатная ось совпадает с направлением движения.
Пусть тело в начальный момент движения имеет координату 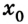
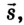
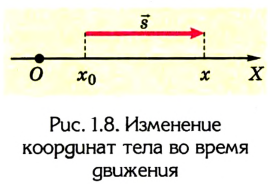
Как известно, в СИ скорость
измеряется в метрах за секунду (м/с). 1 м/с – это скорость такого равномерного прямолинейного движения, при которой тело за 1 с совершает перемещение 1 м. На практике используют также другие единицы скорости, например километр в час:
Поскольку перемещение 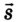
При равномерном движении значение скорости остается постоянным, поскольку за любые равные интервалы времени совершаются равные перемещения.
Как известно, основной задачей механики является определение положения тела в пространстве в произвольный момент времени. Следовательно, чтобы ее решить, надо найти координаты тела либо их изменение во времени: х – x(t). В механике такое уравнение называется уравнением движения. При решении задач с использованием уравнения движения векторные величины, характеризующие движение тела, записывают в проекциях на соответствующую ось. Следовательно, из формулы (1) получаем:
Из рисунков 1.8 и 1.9 понятно, что 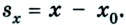
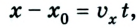

Уравнения равномерного прямолинейного движения:
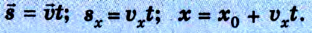
Рассмотрим теперь различные случаи равномерного прямолинейного движения (рис. 1.10).
Из рисунка следует, что если направление движения тела совпадает с направлением координатной оси, то 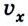
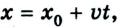
Если же направление движения тела противоположно направлению координатной оси, то 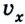
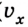
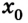
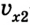
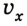
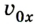
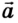
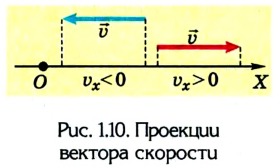
Если скорость тела со временем уменьшается 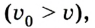
В данном случае в соответствии с выбранным направлением координатной оси ОХ проекция ускорения будет отрицательной
Вместе с тем знак проекции ускорения не определяет характер движения – оно ускоряющееся или замедляющееся, в зависимости от выбора системы отсчета. В этом легко убедиться, если рассмотреть случай, когда оба тела движутся в противоположных направлениях. Тогда одно из тел имеет положительную проекцию ускорения 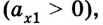
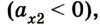
Из формул (1) и (2) можно получить кинематическое уравнение скорости для равноускоренного движения:

или в проекциях на ось ОХ:
Выведем теперь кинематическое уравнение перемещения для равноускоренного движения. Учтем, что скорость во время такого движения постоянно изменяется, например сначала она равна 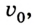
Подставив в данную формулу уравнение (3) и произведя некоторые преобразования, получим: 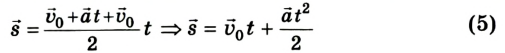
или в проекциях на ось ОХ: 
Если начальная скорость тела равна 0 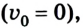

или в проекциях на ось ОХ: 
Для прямолинейного движения, учитывая, что 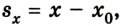
или для случая, когда 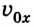

Следует помнить, что в ходе решения задач необходимо учитывать знаки проекций в соответствующих уравнениях.
При определении проекции перемещения не всегда известно время, в течение которого происходило движение. Тогда можно воспользоваться иным уравнением. Чтобы его получить, подставим в кинематическое уравнение 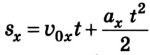
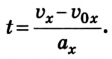

Отсюда 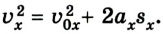
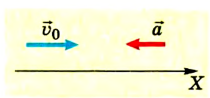
Задача №5
Водитель начинает тормозить в тот момент, когда спидометр автомобиля фиксирует скорость 72 км/ч. Через какое время автомобиль остановится, если он двигался с ускорением 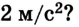
Дано:
По условию задачи спидометр показывает начальную скорость автомобиля 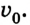
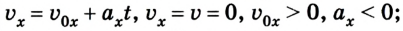
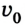
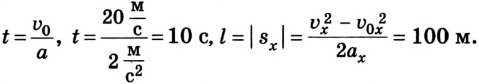
Ответ: автомобиль остановился через 10 с, проехав 100 м.
Задача №6
Шарик толкнули по наклонному желобу вверх со скоростью 6 м/с. Шарик движется с ускорением 0,5 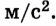
Дано:
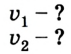
Решение
Направим ось ОХ вдоль желоба (см. рис.).
Учитывая знаки проекций скорости и ускорения, имеем
Отсюда уравнение для 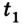
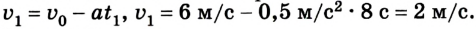
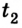
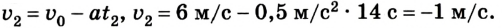
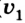
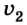
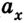
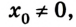
Если 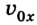
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Перемещение и путь при равноускоренном прямолинейном движении
теория по физике 🧲 кинематика
Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.
При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:
Пример №1. По графику определить перемещение тела в момент времени t=3 с.
Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:
Извлекаем из графика необходимые данные:
- Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
- Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).
Подставляем известные данные в формулу:
Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.
Варианты записи формулы перемещения
Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:
В итоге получается формула:
Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».
Если начальная скорость равна 0 (v0 = 0), эта формула принимает
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:
Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.
Перемещение при разгоне и торможении тела
Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:
Этап торможения
Время торможения равно разности полного времени движения и времени второго этапа:
Когда тело тормозит, через некоторое время t1оно останавливается. Поэтому скорость в момент времени t1 равна 0:
При торможении перемещение s1 равно:
Этап разгона
Время разгона равно разности полного времени движения и времени первого этапа:
Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t2 равна:
При разгоне перемещение s2 равно:
При этом модуль перемещения в течение всего времени движения равен:
Полный путь (обозначим его l), пройденный телом за оба этапа, равен:
Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.
В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:
Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:
Подставляем выраженные величины в формулу:
Перемещение в n-ную секунду прямолинейного равноускоренного движения
Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:
За первую секунду тело переместится на расстояние, равное:
За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:
За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:
Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:
Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:
Формула перемещения за n-ную секунду
Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.
Подставляем известные данные в формулу и получаем:
Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:
где t — время одного промежутка, а n — порядковый номер этого промежутка.
Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.
Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.
Подставляем известные данные в формулу:
Проекция и график перемещения
Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:
График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:
Определение направления знака проекции ускорения по графику его перемещения:
- Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
- Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.
Пример №6. Определить ускорение тела по графику его перемещения.
Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:
Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:
График пути
График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.
В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:
- 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
- 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.
Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.
При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:
Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x ( t ) = x 0 + v 0 t + a t 2 2 . .
Теперь мы можем выделить кинематические характеристики движения тела:
Перемещение тела определяется формулой:
s = v 0 t + a t 2 2 . .
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2
Кинетическая энергия тела определяется формулой:
Скорость при прямолинейном равноускоренном движении равна:
v = v 0 + a t = 5 − 6 t
Поэтому кинетическая энергия тела равна:
E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2
Следовательно, правильная последовательность цифр в ответе будет: 34.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
pазбирался: Алиса Никитина | обсудить разбор | оценить
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Охарактеризовать движение тела на различных участках графика.
- Выделить участки движения, над которыми нужно работать по условию задачи.
- Записать исходные данные.
- Записать формулу определения искомой величины.
- Произвести вычисления.
Решение
Весь график можно поделить на 3 участка:
- От t1 = 0 c до t2 = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
- От t1 = 10 c до t2 = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
- От t1 = 30 c до t2 = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
- От t1 = 20 c до t2 = 30 с — с равномерным движением.
- От t1 = 30 c до t2 = 50 с — с равнозамедленным движением.
- Для первого участка. Начальный момент времени t1 = 20 c. Конечный момент времени t2 = 30 с. Скорость (определяем по графику) — 10 м/с.
- Для второго участка. Начальный момент времени t1 = 30 c. Конечный момент времени t2 = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Механическое движение
О чем эта статья:
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
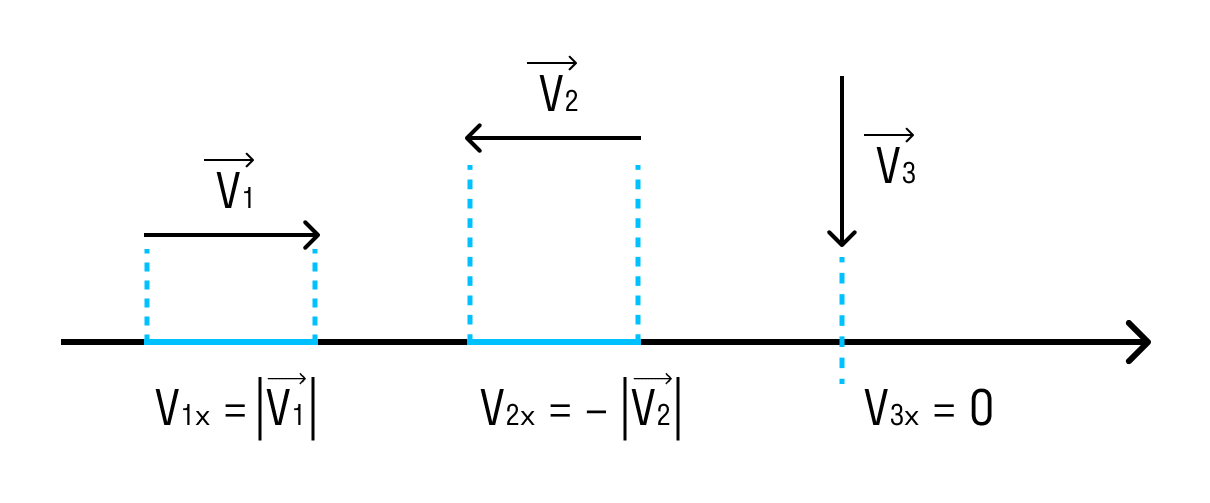
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с]
— перемещение [м]
— время [с]
Средняя путевая скорость
V ср.путевая = S/t
V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]
Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!
Уравнение движения
Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v
Уравнение движения при движении против оси
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
vx — скорость тела в данный момент времени [м/с]
t — момент времени [с]
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.
Уравнение движения и формула конечной скорости
Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.
Уравнение движения для равноускоренного движения
x(t) — искомая координата в момент времени t [м]
x0 — начальная координата [м]
v0x — начальная скорость тела в [м/с]
t — время [с]
ax — ускорение [м/с 2 ]
Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:
Формула конечной скорости
— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]
Задача
Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.
Решение:
Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:
Так как автобус двигался с места, . Значит
Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.
3 минуты = 3/60 часа = 1/20 часа = 0,05 часа
Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x0 + v0xt + axt 2 /2
Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:
Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.
Подставим циферки:
км
Ответ: через полчаса координата автобуса будет равна 150 км.
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
[spoiler title=”источники:”]
http://skysmart.ru/articles/physics/mehanicheskoe-dvizhenie
[/spoiler]