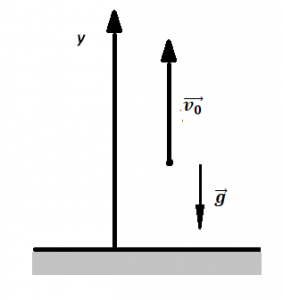
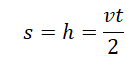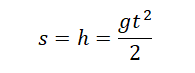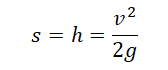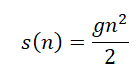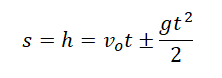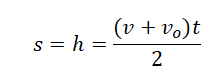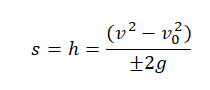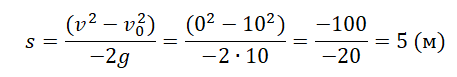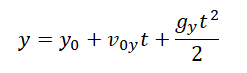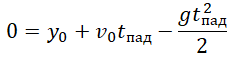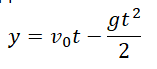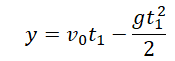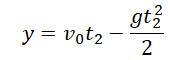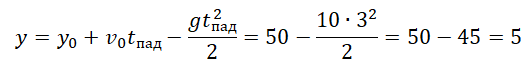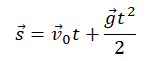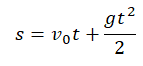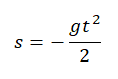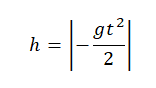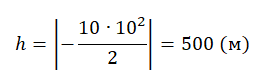Что такое свободное падение? Это падение тел на Землю при отсутствии сопротивления воздуха. Иначе говоря – падение в пустоте. Конечно, отсутствие сопротивления воздуха – это вакуум, который нельзя встретить на Земле в нормальных условиях. Поэтому мы не будем брать силу сопротивления воздуха во внимание, считая ее настолько малой, что ей можно пренебречь.
Ускорение свободного падения
Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.
Ускорение свободного падения – ускорение, с которым все тела падают на Землю.
Ускорение свободного падения приблизительно равно 9,81 мс2 и обозначается буквой g. Иногда, когда точность принципиально не важна, ускорение свободного падения округляют до 10 мс2.
Земля – не идеальный шар, и в различных точках земной поверхности, в зависимости от координат и высоты над уровнем моря, значение g варьируется. Так, самое большое ускорение свободного падения – на полюсах (≈9,83 мс2), а самое малое – на экваторе (≈9,78 мс2).
Свободное падение тела
Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.
Свободное падение – прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.
h=v0+gt22.
Так как начальна скорость равна нулю, перепишем:
h=gt22.
Отсюда находится выражение для времени падения тела с высоты h:
t=2hg.
Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:
v=2hg·g=2hg.
Движение тела, брошенного вертикально вверх
Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.
Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:
v=v0-gt.
Подставив v=0, найдем время подъема тела на максимальную высоту:
t=v0g.
Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.
Максимальная высота подъема тела, брошенного вертикально:
h=v022g.
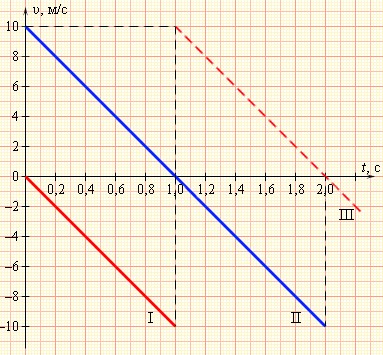
Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.
Первый график – это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.
Второй график – движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.
Движение тела, брошенного под углом к горизонту
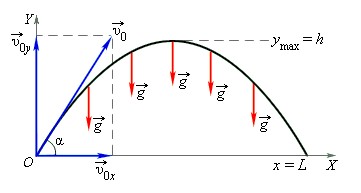
С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.
Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения – v0y. Движение вдоль оси OX – равномерное и прямолинейное, с начальной скоростью v0x.
Условия для движения вдоль оси ОХ:
x0=0; v0x=v0cosα; ax=0.
Условия для движения вдоль оси OY:
y0=0; v0y=v0sinα; ay=-g.
Приведем формулы для движения тела, брошенного под углом к горизонту.
Время полета тела:
t=2v0sinαg.
Дальность полета тела:
L=v02sin2αg.
Максимальная дальность полета достигается при угле α=45°.
Lmax=v02g.
Максимальная высота подъема:
h=v02sin2α2g.
Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука – баллистика.
Свободное падение
Свободное падение представляет собой частный случай равномерно ускоренного движения без начальной скорости. Ускорение этого движения равно ускорению свободного падения, называемого также ускорением силы тяжести.
Для этого движения справедливы формулы:
Если:
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота с которой падает тело,
t — время, в течение которого продолжалось падение,
То, свободное падение описывается следующими формулами:
Расстояние, пройденное телом за время падения, зная конечную скорость
[ h = frac{ut}{2} ]
Расстояние, пройденное телом за время падения, зная ускорение свободного падения
[ h = frac{gt^2}{2} ]
Скорость тела, в конце падения, зная ускорение свободного падения и время
[ u = gt ]
Скорость тела, в конце падения, зная ускорение свободного падения и высоту
[ u = sqrt{2gh} ]
Примечание к статье: Свободное падение
Свободное падение |
стр. 408 |
|---|
Физика
Анонимный вопрос
16 января 2018 · 35,9 K
ОтветитьУточнить
Ирина С.6,1 K
Книги, звери и еда – это хобби навсегда. · 19 янв 2019
Путь, пройденный телом при свободном падении, можно рассчитать по формуле:
S=g*t^2/2, где g – ускорение свободного падения, t – время падения. Подставляя g=10 м/с^2 и t=5 с, получим:
S=10*5^2/2=125 м.
27,5 K
Виталий Черняев
23 ноября 2020
Вообще полная формула S=V0×t+-g×t^2/2 где S-путь, V0-начальная скорость, t-время, g-ускорение свободного падения… Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Свободное падение яблока.
Свобо́дное падéние — равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы. На поверхности Земли (на уровне моря) ускорение свободного падения меняется от 9,832 м/с² на полюсах, до 9,78 м/с² на экваторе.
В частности, парашютист в течение нескольких первых секунд прыжка находится практически в свободном падении.
Свободное падение возможно на поверхность любого тела, обладающего достаточной массой (планеты и их спутники, звёзды, и т. п.).
Во время свободного падения какого-либо объекта этот объект находится в состоянии невесомости (как если бы он находился на борту космического аппарата, движущегося по околоземной орбите). Данное обстоятельство используется, например, при тренировке космонавтов: самолёт с космонавтами набирает большую высоту и пикирует, находясь в течение нескольких десятков секунд в состоянии свободного падения; космонавты и экипаж самолёта при этом испытывают состояние невесомости[1].
Комментарий к определению[править | править код]
Поскольку сила тяжести понимается как сила, действующая вблизи планеты, определению «свободного падения» строго соответствуют движения тела около поверхности Земли или другого крупного астрономического объекта. Важным условием является малость сопротивления среды (или её отсутствие[2]). Примером служит полёт камня, брошенного с поверхности или с некоторой высоты под любым углом (при небольших скоростях сопротивлением воздуха можно пренебречь), причём движение вверх тоже является свободным падением, вопреки интуитивному восприятию. Траектория может иметь форму участка параболы или отрезка прямой.
Очень часто, однако, под «свободным падением» подразумевается только движение тела вертикально вниз и без начальной скорости, у земной поверхности[3]. При этом, в бытовых рассуждениях, сила сопротивления атмосферы иногда трактуется не как искажающий фактор, а как полноценный атрибут такого движения, на равных с силой тяжести.
Изредка «свободное падение» трактуется шире официального определения, а именно допускается движение тела на значительном удалении от планеты. Тогда в определение вписываются, скажем, вращение Луны вокруг Земли или падение тел из космоса. Объект, свободно падающий из бесконечности на планету, достигает её поверхности или верхних слоёв атмосферы со скоростью не ниже второй космической, а траектория представляет собой кусок гиперболы, параболы или прямой; ускорение непостоянно, так как изменения гравитационной силы в пределах изучаемой области существенны.
История[править | править код]
Первые попытки построить количественную теорию свободного падения тяжёлого тела были предприняты учёными Средневековья; в первую очередь следует назвать имена Альберта Саксонского и Николая Орема. Однако они ошибочно утверждали[4][5], что скорость падающего тяжёлого тела растёт пропорционально пройденному пути. Эту ошибку впервые исправил Д. Сото (1545), который сделал правильный вывод о том, что скорость тела растёт пропорционально времени, прошедшему с момента начала падения, и нашёл[6][7] закон зависимости пути от времени при свободном падении (хотя эта зависимость была дана им в завуалированном виде). Чёткая же формулировка закона квадратичной зависимости пути, пройденного падающим телом, от времени принадлежит[8] Г. Галилею (1590) и изложена им в книге «Беседы и математические доказательства двух новых наук»[9]. Сначала Лейбниц, а затем, в 1892—1893 гг. профессор МГУ Н. А. Любимов поставили опыты, демонстрирующие возникновение невесомости при свободном падении[10].
Демонстрация явления[править | править код]
Свободное падение. Вектор силы тяжести направлен вертикально вниз.
При демонстрации явления свободного падения откачивают воздух из длинной трубки, в которую помещают несколько предметов разной массы. Если перевернуть трубку, то тела, независимо от их массы, упадут на дно трубки одновременно.
Если же эти предметы поместить в какую-либо среду, то к действию силы тяжести добавится сила сопротивления, и тогда времена падения данных предметов уже не обязательно будут совпадать, а будут в каждом случае зависеть от формы тела и его плотности.
Количественный анализ[править | править код]
Введём систему координат Oxyz с началом на поверхности Земли и направленной вертикально вверх осью y и рассмотрим свободное падение тела массы m с высоты y0[11], пренебрегая вращением Земли и сопротивлением воздуха. Дифференциальное уравнение движения тела в проекции на ось y имеет[12] вид:
где g — ускорение свободного падения, а точками над величиной обозначается её дифференцирование по времени.
Интегрируя данное дифференциальное уравнение при заданных начальных условиях y = y0 и v = v0 (здесь v — проекция скорости тела на вертикальную ось), находим[13] зависимость переменных y и v от времени t:
В частном случае, когда начальная скорость равна нулю (то есть тело начинает падение, не испытав толчка вверх или вниз), из этих формул видно, что текущая скорость тела пропорциональна времени, прошедшему с момента начала свободного падения, а пройденный телом путь — квадрату времени.
Подчеркнём, что результаты не зависят от значения массы m.
Рекорды свободного падения[править | править код]
В бытовом смысле под свободным падением нередко подразумевают движение в атмосфере Земли, когда на тело не действуют никакие сдерживающие или ускоряющие факторы, кроме силы тяжести и сопротивления воздуха.
Согласно Книге рекордов Гиннесса, мировой рекорд расстояния, преодолённого при свободном падении, составляющий 24 500 м, принадлежит Евгению Андрееву. Последний установил данный рекорд во время парашютного прыжка с высоты 25 457 м, совершённого 1 ноября 1962 года в районе Саратова; тормозной парашют при этом не применялся[14].
16 августа 1960 г. Джозеф Киттингер совершил рекордный прыжок с высоты 31 км с использованием тормозного парашюта.
В 2005 году Луиджи Кани установил мировой рекорд скорости (прыжок в тропосфере), достигнутой в свободном падении — 553 км/ч.
В 2012 году Феликс Баумгартнер установил новый мировой рекорд скорости в свободном падении, развив скорость 1342 километра в час[15].
30 июля 2016 года американский скайдайвер Люк Айкинс установил уникальный рекорд, совершив прыжок без парашюта с высоты 7600 метров на сеть размером 30×30 м с использованием наземных средств для ориентации[16].
См. также[править | править код]
- Перемещение
Примечания[править | править код]
- ↑ Бутенин, Лунц, Меркин, 1985, с. 132—136.
- ↑ Е. И. Бутиков, А. С. Кондратьев. Физика для углублённого изучения, разд. 1 «Механика», стр. 50. М.: Физматлит (2004). — «Свободным падением называют движение в вакууме, когда сопротивление воздуха отсутствует». Дата обращения: 13 февраля 2018. Архивировано 27 января 2018 года.
- ↑ Свободное падение. Справочный портал «Калькулятор». — «Падение тела, обусловленное притяжением Земли, при отсутствии начальной скорости и сопротивления воздуха считают свободным падением». Дата обращения: 13 февраля 2018. Архивировано 16 февраля 2018 года.
- ↑ Моисеев, 1961, с. 100–101.
- ↑ Тюлина, 1979, с. 51.
- ↑ Моисеев, 1961, с. 105.
- ↑ Тюлина, 1979, с. 53—54.
- ↑ Моисеев, 1961, с. 116.
- ↑ Галилео Галилей. День четвёртый. // Математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению. — М.—Л.: ГИТТЛ, 1934.
- ↑ Перельман Я. И. Межпланетные путешествия. Начальные основания звездоплавания. — 6-е изд. — Л.: Прибой. — С. 163. — 5000 экз.
- ↑ Считаем, что тело при своём движении не слишком удаляется от поверхности Земли, так что ускорение свободного падения можно считать постоянным.
- ↑ Бутенин, Лунц, Меркин, 1985, с. 22.
- ↑ Бутенин, Лунц, Меркин, 1985, с. 23, 32.
- ↑ Рекорд ФАИ № 1623 Архивировано 14 июля 2014 года. — на сайте Международной авиационной федерации (ФАИ).
- ↑ World Record Jump | Red Bull Stratos. Дата обращения: 12 сентября 2013. Архивировано 2 октября 2013 года.
- ↑ Бес страховки. Дата обращения: 2 августа 2016. Архивировано 20 августа 2016 года.
Литература[править | править код]
- Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики: Учебник. Т. II. 3-е изд. — М.: Наука, 1985. — 496 с.
- Моисеев Н. Д. Очерки истории развития механики. — М.: Изд-во Моск. ун-та, 1961. — 478 с.
- Тюлина И. А. История и методология механики. — М.: Изд-во Моск. ун-та, 1979. — 282 с.
Свободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
Внимание!
В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Ускорение свободного падения — векторная физическая величина. Вектор ускорения свободного падения всегда направлен вниз к центру Земли. Обозначается как g.
Единица измерения ускорения свободного падения — 1 м/с2.
Модуль ускорения свободного падения — скалярная величина. Обозначается как g. Численно равна 9,8 м/с2. При решении задач это значение округляется до целых: g = 10 м/с2.
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
Скорость
v = gt
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
v = gt = 10∙3 = 30 (м/с).
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Высота падения
Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
Формула определения перемещения тела в n-ную секунду свободного падения:
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.
Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
Два этапа движения тела, брошенного вертикально вверхЭтап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях (v↑↓g).
Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону (v↑↑g).
Формулы для расчета параметров движения тела, брошенного вертикально вверхПеремещение тела, брошенного вертикально вверх, определяется по формуле:
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
Если время движения неизвестно, для определения перемещения используется следующая формула:
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
- Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
- Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
Уравнение скорости при свободном падении:
vy = v0y + gyt
Полезные факты
- В момент падения тела на землю y = 0.
- В момент броска тела от земли y0 = 0.
- Когда тело падает без начальной скорости (свободно) v0 = 0.
- Когда тело достигает наибольшей высоты v = 0.
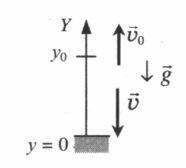
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
План построения чертежа
- Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
- Отмечаются начальная и конечная координаты тела (y и y0).
- Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.
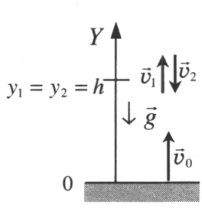
Свободное падение на землю с некоторой высоты
Чертеж:
Уравнение скорости:
–v = v0 – gtпад
Уравнение координаты:
Тело подбросили от земли и поймали на некоторой высоте
Чертеж:
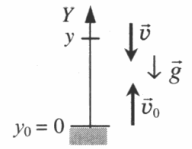
–v = v0 – gt
Уравнение координаты:
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Чертеж:
Интервал времени между моментами прохождения высоты h:
∆t = t2 – t1
Уравнение координаты для первого прохождения h:
Уравнение координаты для второго прохождения h:
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Поэтому:
Через 3 с после падения тело окажется на высоте 5 м.
Задание EF17519
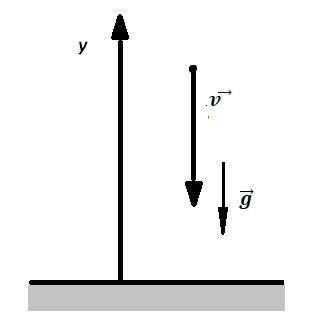
С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17483
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.5k