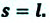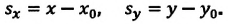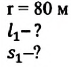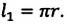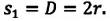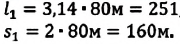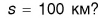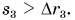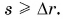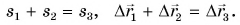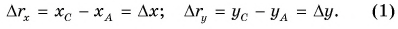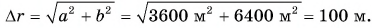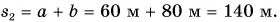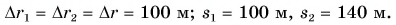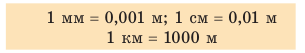Как найти путь тела движущегося не прямо

Как найти путь тела движущегося не прямо

Путь при неравномерном движении.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Сейчас мы будем рассматривать неравномерное движение – то есть движение, при котором абсолютная величина скорости меняется со временем. Оказывается, существует простая геометрическая интерпретация пути, пройденного телом при произвольном движении.
Начнём с равномерного движения. Пусть скорость тела постоянна и равна v. Возьмём два момента времени: начальный момент t_{displaystyle 1} и конечный момент t_{displaystyle 2}. Длительность рассматриваемого промежутка времени равна Delta t= t_{displaystyle 2} - t_{displaystyle 1}.

Очевидно, что за промежуток времени [t_{displaystyle 1},t_{displaystyle 2}] тело проходит путь:

s=v(t_{displaystyle 2}-t_{displaystyle 1})=vDelta t (1)

Давайте построим график зависимости скорости от времени. В данном случае это будет прямая, параллельная оси абсцисс (рис. 1).

Рис. 1. Путь при равномерном движении

Нетрудно видеть, что пройденный путь равен площади прямоугольника, расположенного под графиком скорости. В самом деле, первый множитель v в формуле (1) есть вертикальная сторона этого прямоугольника, а второй множитель Delta t – его горизонтальная сторона.

Теперь нам предстоит обобщить эту геометрическую интерпретацию на случай неравномерного движения.

Пусть скорость тела v зависит от времени, и на рассматриваемом промежутке [t_{displaystyle 1},t_{displaystyle 2}] график скорости выглядит, например, так (рис. 2):

Рис. 2. Неравномерное движение

Дальше мы рассуждаем следующим образом.

1. Разобьём наш промежуток времени [t_{displaystyle 1},t_{displaystyle 2}] на небольшие отрезки величиной Delta t.

2. Предположим, что на каждом таком отрезке [t_{displaystyle i},t_{displaystyle i}+Delta t] тело движется с постоянной скоростью v(t_{displaystyle i}). То есть, плавное изменение скорости заменим ступенчатой аппроксимацией*: в течение каждого небольшого отрезка времени тело движется равномерно, а затем скорость тела мгновенно и cкачком меняется.
На рис. 3 показаны две ступенчатые аппроксимации. Ширина ступенек Delta t на правом рисунке вдвое меньше, чем на левом.

Рис. 3. Ступенчатая аппроксимация

Путь, пройденный за время Delta t равномерного движения – это площадь прямоугольника, расположенного под ступенькой. Поэтому путь, пройденный за всё время такого “ступенчатого” движения – это сумма площадей всех прямоугольников на графике.

3. Теперь устремляем Delta t к нулю. Ясно, что в пределе наша ступенчатая аппроксимация перейдёт в исходный график скорости на рис. 2. Сумма площадей прямоугольников перейдёт в площадь под графиком скорости; следовательно, эта площадь и есть путь, пройденный телом за время от t_{displaystyle 1} до t_{displaystyle 2}. (рис. 4

Рис. 4. Путь при неравномерном движении

В итоге мы приходим к нужному нам обобщению геометрической интерпретации пути, полученной выше для случая равномерного движения.

Аппроксимация – это приближённая замена достаточно сложного объекта более простой моделью, которую удобнее изучать.

Геометрическая интерпретация пути.Путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.

Посмотрим, как работает эта геометрическая интерпретация в важном частном случае равноускоренного движения.

Задача. Тело, имеющее скорость v_{0} в начальный момент t=0, разгоняется с постоянным ускорением a. Найти путь, пройденный телом к моменту времени t.

Решение. Зависимость скорости от времени в данном случае имеет вид:

v=v_{0}+at. (2)

График скорости – прямая, изображённая на рис. 5. Искомый путь есть площадь трапеции, расположенной под графиком скорости.

Рис. 5. Путь при равноускоренном движении

Меньшее основание трапеции равно v_{0}. Большее основание равно v=v_{0}+at. Высота трапеции равна t. Поскольку площадь трапеции есть произведение полусуммы оснований на высоту, имеем:

s=frac{displaystyle v_{0}+displaystyle v}{2}cdot t=frac{displaystyle v_{0}+(v_{0}+at)}{2}cdot t=frac{displaystyle 2v_{0}t+at^{2}}{2}.

Эту формулу можно переписать в более привычном виде:

s=v_{0}t+frac{displaystyle at^{2}}{displaystyle2}.

Она, разумеется, вам хорошо известна из темы “Равноускоренное движение”.

Задача. График скорости тела является полуокружностью диаметра tau (рис. 6). Максимальная скорость тела равна v. Найти путь, пройденный телом за время tau .

Решение. Как вы знаете, площадь круга радиуса R равна pi R^{2}. Но в данной задаче необходимо учесть, что радиусы полуокружности имеют разные размерности: горизонтальный радиус есть время tau /2 , а вертикальный радиус есть скорость v.

Поэтому пройденный путь, вычисляемый как площадь полукруга, равен половине произведения pi на горизонтальный радиус и на вертикальный радиус:

s=frac{1}{2}cdot pi cdot frac{displaystyle tau }{2}cdot v=frac{displaystyle pi vtau }{displaystyle 4}.

Рис. 6. К задаче

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Путь при неравномерном движении.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Неравномерное прямолинейное движение. Средняя скорость

  1. График скорости при неравномерном прямолинейном движении
  2. Как найти путь и перемещение по графику скорости?
  3. Средняя скорость и средняя путевая скорость
  4. Задачи
  5. Лабораторная работа №3. Определение средней скорости движения тела

п.1. График скорости при неравномерном прямолинейном движении

Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.

Движение с переменной скоростью называют неравномерным.

Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.

Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=3 text{км/ч} $$ Построим график скорости для этого случая:
График скорости при неравномерном прямолинейном движении

Графиком скорости (v_x=v_x(t)) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.

п.2. Как найти путь и перемещение по графику скорости?

Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).

В таком случае, путь велосипедиста в нашем примере:
Как найти путь и перемещение по графику скорости begin{gather*} s=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.
Как найти путь и перемещение по графику скорости
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6 text{(км)} $$ Перемещение по оси ОХ: (triangle x=x_{к}-x_0=6 text{(км)}).

Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=-3 text{км/ч} $$ Построим график скорости для этого случая:
Как найти путь и перемещение по графику скорости
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin{gather*} x=v_{x1}cdot triangle t_1+|v_{x2}|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} Как найти путь и перемещение по графику скорости
Если мы учтем знак (v_{x2}) и уберем модуль, то получим величину перемещения по оси ОХ: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+triangle x=0+3=3 text{(км)} $$ Как найти путь и перемещение по графику скорости
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.

Пусть неравномерное прямолинейное движение разбито на (n) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени (triangle t_i) и постоянная скорость (v_{xi}, i=overline{1,n}).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|cdottriangle t_1+|v_{x2}|cdottriangle t_2+…+|v_{xn}|cdottriangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ triangle x=v_{x1}cdottriangle t_1+v_{x2}cdottriangle t_2+…+v_{xn}cdottriangle t_n $$ Конечная координата равна: (x_{к}=x_0+triangle x).

п.3. Средняя скорость и средняя путевая скорость

Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ overrightarrow{v_{cp}}=frac{overrightarrow{r_1}+overrightarrow{r_2}+…+overrightarrow{r_n}}{t_1+t_2+…+t_n}=frac{overrightarrow{r}}{t} $$

Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=frac{s}{t} $$

Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.

В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 61=6 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости равна средней путевой скорости.

А вот для случая, когда велосипедист развернулся и пошел обратно: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 31=3 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости меньше средней путевой скорости.

п.4. Задачи

Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.

a)
Задача 1
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=1 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=2 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text{(м)} end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow{v_{cp}}|=v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|=v_{cp.п}=3 text{(м/с)})

б)
Задача 1
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=-2 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=1 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text{(м)} end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2+v_{x3}cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text{(м)} end{gather*} Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow{v_{cp}}|=frac{triangle x}{t}=frac{13}{7}approx 1,86 text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|approx 1,86 text{(м/с)}; v_{cp.п}=3 text{(м/с)})

Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.

Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:

Скорость, км/ч Время, ч Расстояние, км
1й участок 40 (frac{2d}{40}=frac{d}{20}) (2d)
2й участок 80 (frac{d}{80}) (d)
Сумма – (t=frac{d}{20}+frac{d}{80}) (s=2d+d=3d)

Упростим сумму дробей: $$ t=frac{d}{20}+frac{d}{80}=frac{4d+d}{80}=frac{5d}{80}=frac{d}{16} $$ Получаем: $$ v_{cp}=frac st=frac{3d}{d/16}=3cdot 16=48 text{(км/ч)} $$
Ответ: 48 км/ч

Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.

Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:

Скорость, км/ч Время, ч Расстояние, км
1й участок 90 (frac{s}{2cdot 90}=frac{s}{180}) (frac s2)
2й участок 30 (frac{s}{2cdot 30}=frac{s}{60}) (frac s2)
Сумма – (t=frac{s}{180}+frac{s}{60}) (s)

Упростим сумму дробей: $$ t=frac{s}{180}+frac{s}{60}=frac{s+3s}{180}=frac{4s}{180}=frac{s}{45} $$ Получаем: $$ v_{cp}=frac st=frac{s}{s/45}=45 text{(км/ч)} $$
Ответ: 45 км/ч

Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.

Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:

Скорость, км/ч Время, ч Расстояние, км
1й участок (frac{d}{4t}) (4t) (d)
2й участок (frac{4d}{t}) (t) (4d)
3й участок (frac{45d}{20t}) (20t) (45d)
Сумма – (25t) (50d)

По условию средняя скорость: $$ v_{cp}=frac st=frac{50d}{25t}=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin{gather*} v_1=frac{d}{4t}=frac{16}{4}=4 text{(км/ч)}\ v_2=frac{4d}{t}=4cdot 16=64 text{(км/ч)}\ v_3=frac{9d}{4t}=frac{9}{4}cdot 16=36 text{(км/ч)} end{gather*}
Ответ: 4 км/ч, 64 км/ч и 36 км/ч

Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?

Пусть (v) – скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_{cp}) и сравним ее со скоростью (v).
Если (v_{cp}gt v), то турист выиграл время.
Заполним таблицу:

Скорость, км/ч Время, ч Расстояние, км
1й участок (10v) (frac{s}{2cdot 10v}=frac{s}{20v}) (frac s2)
2й участок (frac{v}{2}) (frac{s}{2cdot v/2}=frac sv) (frac s2)
Сумма – (t=frac{s}{20v}+frac sv) (s)

Упростим сумму дробей: $$ t=frac{s}{20v}+frac sv=frac svleft(frac{1}{20}+1right)=frac{21}{20}cdot frac sv $$ Средняя скорость: $$ v_{cp}=frac{s}{frac{21}{20}cdotfrac sv}=frac{20}{21}vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет

п.5. Лабораторная работа №3. Определение средней скорости движения тела

Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.

Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.

Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=frac{s_1+s_2}{t_1+t_2} $$ где (s_1) и (s_2) – длина первого и второго участка; (t_1) и (t_2) – время движения по каждому из участков.

Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac{triangle}{2}=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см

Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)

Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ triangle v_{cp}=v_{cp}cdot delta_{v_{cp}} $$

Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.

Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с.
Определение средней скорости движения тела
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_{s_1+s_2}=frac{triangle(s_1+s_2)}{s_1+s_2})
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_{t_1+t_2})
7. По результатам измерений и вычислений найдите (v_{cp}, delta_{v_{cp}}) и (triangle v_{cp}).
8. Сделайте выводы о проделанной работе.

Результаты измерений и вычислений

1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac{triangle}{2}=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_{s_1+s_2}=frac{triangle (s_1+s_2)}{s_1+s_2}=frac{1}{320}=0,3125% $$

2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1) с

Время движения по наклонному желобу

№ опыта 1 2 3 4 5 Сумма
(t_1) c 1,5 1,6 1,5 1,4 1,4 7,4
(triangle) c 0,02 0,12 0,02 0,08 0,08 0,32

Найдем среднее время спуска с наклонного желоба: $$ t_1=frac{1,5+1,6+1,5+1,4+1,4}{5}=frac{7,4}{5}=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,02+0,12+0,02+0,08+0,08}{5}=frac{0,32}{5}=0,064 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,064right}=0,1 text{c} $$ Округляем полученное значение времени до десятых. begin{gather*} t_1=(1,5pm 0,1) text{c}\ delta_{t_1}=frac{0,1}{1,5}=frac{1}{15}approx 6,7text{%} end{gather*} Время движения по горизонтальному желобу

№ опыта 1 2 3 4 5 Сумма
(t_2) c 2,3 2,4 2,2 2,2 2,4 11,5
(triangle) c 0 0,1 0,1 0,1 0,1 0,4

Найдем среднее время движения по горизонтали: $$ t_2=frac{2,3+2,4+2,2+2,2+2,4}{5}=frac{11,5}{5}=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0+0,1+0,1+0,1+0,1}{5}=frac{0,4}{5}=0,08 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,08right}=0,1 text{c} $$ Получаем: begin{gather*} t_2=(2,3pm 0,1) text{c}\ delta_{t_2}=frac{0,1}{2,3}=frac{1}{23}approx 4,4text{%} end{gather*}

3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text{(c)} $$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text{(c)} $$ Относительная погрешность суммы: $$ delta_{t_1+t_2}=frac{triangle (t_1+t_2)}{t_1+t_2}=frac{0,2}{3,8}=frac{1}{19}approx 5,3text{%} $$

4) Расчет средней скорости $$ v_{cp}=frac{s_1+s_2}{t_1+t_2}=frac{320}{3,8}approx 84,2 left(frac{text{см}}{text{c}}right) $$ Относительная ошибка частного: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2}=frac{1}{320}+frac{1}{19}approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}cdotdelta_{v_{cp}}=84,2cdot 0,056approx 4,7 left(frac{text{см}}{text{c}}right) $$ Получаем: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}

Выводы
На основании проделанной работы можно сделать следующие выводы.

Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}

Источник

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

На рис. 1.1:

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

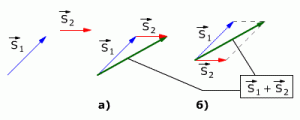
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Проекции вектора перемещения

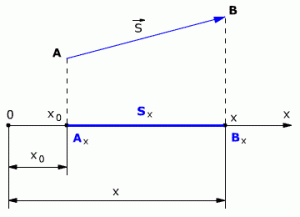
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения  (см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Sx = AxBx

ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор с проекцией вектора на какую-либо ось (например, Sx). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Sx = x – x0

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Sy = y – y0
Sz = z – z0

Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

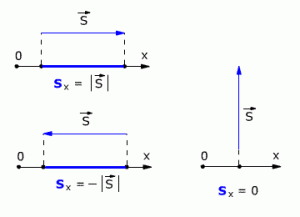
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

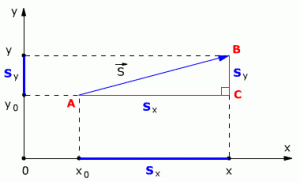
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

Sx = x – x0
Sy = y – y0

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

АС = sx
CB = sy

По теореме Пифагора

S2 = Sx2 + Sy2

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Источник

Пример №1

Допустим, из точки ( displaystyle A) и из точки ( displaystyle B) навстречу друг другу выехали две машины. Скорость одной машины – ( displaystyle 60) км/ч, а скорость ( displaystyle 2) машины – ( displaystyle 40) км/ч. Они встретились через ( displaystyle 1,2) часа.

Какое расстояние между пунктами ( displaystyle A) и ( displaystyle B)?

1 вариант решения

Можно рассуждать так: машины встретились, значит расстояние между городами – это сумма расстояния, которая прошла первая машина, и расстояния, которое прошла вторая.

( displaystyle 60cdot 1,2text{ }=text{ }72) (км) – путь, который проехала первая машина

( displaystyle 40cdot 1,2text{ }=text{ }48) (км) – путь, который проехала вторая машина

( displaystyle 72 + 48 = 120) (км) – расстояние, которое проехали обе машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).

2 вариант решения (более рациональный)

А можно просто воспользоваться очень логичной формулой о сложении скоростей.

Проверим, работает ли она:

( displaystyle 60 + 40 = 100) (км/ч) – скорость сближения машин

( displaystyle 100cdot 1,2text{ }=text{ }120) (км) – расстояние, которые проехали машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).

Оба решения являются верными. Второе просто более рациональное.

Пример №3

Итак, задача:

Из пункта ( displaystyle A) и пункта ( displaystyle B) машины движутся навстречу друг другу со скоростями ( displaystyle 50) км/ч и ( displaystyle 80) км/ч. Расстояние между пунктами – ( displaystyle 195) км.

Через сколько времени машины встретятся?

1 вариант решения

Пусть ( displaystyle x) – время, которое едут машины, тогда путь первой машины – ( displaystyle 50x), а путь второй машины – ( displaystyle 80x).

Их сумма и будет равна расстоянию между пунктами ( A) и ( B) – ( displaystyle 50x+80x=195).

Решим уравнение:

( displaystyle 50x+80x=195)

( displaystyle 130x=195)

( displaystyle x=1,5) (ч) – время, через которое встретились машины.

2 вариант решения (более рациональный)

( displaystyle 50 + 80 = 130) (км/ч) – скорость сближения машин;

( displaystyle 195:130 = 1,5) (ч) – время, которое машины были в пути.

Задача решена.

Пример №4

Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями ( displaystyle 60) км/ч и ( displaystyle 40) км/ч. Через сколько минут они встретятся. Если расстояние между пунктами ( displaystyle 100) км?

2 способа решения:

I способ

Относительная скорость автомобилей ( displaystyle 60+40=100) км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью ( displaystyle 100) км/ч. Так как между автомобилями изначально расстояние ( displaystyle 100) км, время, через которое второй автомобиль проедет мимо первого:

( displaystyle t=frac{100}{100}=1 час=60 минут).

II способ

Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его ( displaystyle t). Тогда первый автомобиль проехал путь ( displaystyle 60t), а второй – ( displaystyle 40t).

В сумме они проехали все ( displaystyle 100) км. Значит,

( displaystyle 60t+40t=100Rightarrow t=1 час=60 минут).

Из пункта ( displaystyle A) в пункт ( displaystyle B), расстояние между которыми ( displaystyle 30) км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на ( displaystyle 65) км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт ( displaystyle B) на ( displaystyle 156) минут позже, чем мотоциклист.

Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт ( displaystyle A), пункт ( displaystyle B), две стрелочки…

В общем рисуй, и сейчас сравним, что у тебя получилось.

Пустовато как-то, правда? Рисуем таблицу.

Как ты помнишь, все задачи на движения состоят из ( displaystyle 3) компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.

Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.

Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?

У тебя получилась вот такая таблица?

Скорость,
км/ч		 Время t,
часов		 Путь S,
км
велосипедист
мотоциклист

Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.

Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен ( displaystyle 30) км. Вносим!

Скорость,
км/ч		 Время t,
часов		 Путь S,
км
велосипедист ( displaystyle 30)
мотоциклист ( displaystyle 30)

Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на ( displaystyle 65) км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…

Возьмем скорость велосипедиста за ( displaystyle x), тогда скорость мотоциклиста будет ( displaystyle x+65)…

Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!

Скорость,
км/ч		 Время t,
часов		 Путь S,
км
велосипедист ( displaystyle x) ( displaystyle 30)
мотоциклист ( displaystyle x+65) ( displaystyle 30)

Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?

Правильно, разделить путь на скорость. Вноси это в таблицу.

Скорость,
км/ч		 Время t,
часов		 Путь S,
км
велосипедист ( displaystyle x) ( displaystyle frac{30}{x}) ( displaystyle 30)
мотоциклист ( displaystyle x+65) ( displaystyle frac{30}{65+x}) ( displaystyle 30)

Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.

Что мы можем на нем отразить?

Молодец. Скорость передвижения мотоциклиста и велосипедиста.

Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.

Какие данные не отражены ни в таблице, ни на рисунке?

Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени – ( displaystyle 156) минут.

Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.

( displaystyle 156) минут / ( displaystyle 60) минут = ( displaystyle 2,6) часа.

И что дальше, спросишь ты? А дальше числовая магия!

Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?

Правильно. Мы можем составить уравнение, основываясь на разнице во времени!

( displaystyle frac{30}{x}-frac{30}{65+x}=2,6)

Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.

Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».

Приводим слагаемые к общему знаменателю:

( displaystyle frac{30cdot left( 65+x right)}{xcdot left( 65+x right)}-frac{30x}{xcdot left( 65+x right)}=2,6)

Раскроем скобки и приведем подобные слагаемые: Уф! Усвоил? Попробуй свои силы на следующей задаче.

( displaystyle frac{1950}{xcdot left( 65+x right)}=2,6)

Из этого уравнения мы получаем следующее:

( displaystyle 2,6cdot xcdot left( 65+x right)=1950)

( displaystyle xcdot left( 65+x right)=frac{1950}{2,6})

( displaystyle xcdot left( 65+x right)=750)

Раскроем скобки и перенесем все в левую часть уравнения:

( displaystyle {{x}^{2}}+65{x}-750=0)

Вуаля! У нас простое квадратное уравнение. Решаем!

( displaystyle {{x}^{2}}+65{x}-750=0)

( displaystyle D={{b}^{2}}-4ac)

( displaystyle D={{65}^{2}}-4cdot 1cdot left( -750 right)=4225+3000=7225)

( displaystyle sqrt{D}=sqrt{7225}=85)

( displaystyle {{x}_{1,2}}=frac{-bpm sqrt{D}}{2a})

( displaystyle {{x}_{1}}=frac{-65+85}{2}=10)

( displaystyle {{x}_{2}}=frac{-65-85}{2}=-75)

Мы получили два варианта ответа. Смотрим, что мы взяли за ( displaystyle x)? Правильно, скорость велосипедиста.

Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь, о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ – ( displaystyle 10) км/ч.

Пример №9

Два велосипедиста одновременно отправились в ( displaystyle 165)-километровый пробег. Первый ехал со скоростью, на ( displaystyle 5) км/ч большей, чем скорость второго, и прибыл к финишу на ( displaystyle 5,5) часов раньше второго.

Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

Напоминаю:

  • Прочитай задачу пару раз – усвой все-все детали. Усвоил?
  • Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
  • Проверь, все ли величины у тебя одинаковой размерности, и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь, какие там графы?).
  • Пока все это пишешь, думай, что взять за ( displaystyle x)? Выбрал? Записывай в таблицу!
  • Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!

Все сделал? Молодец! У меня получилось, что скорость велосипедиста – ( displaystyle 10) км/ч.

Пример №10

Из пункта ( displaystyle A) круговой трассы выехал велосипедист. Через ( displaystyle 40) минут он еще не вернулся в пункт ( displaystyle A) и из пункта ( displaystyle A) следом за ним отправился мотоциклист.

Через ( displaystyle 20) минут после отправления он догнал велосипедиста в первый раз, а еще через ( displaystyle 40) минут после этого догнал его во второй раз.

Найдите скорость велосипедиста, если длина трассы равна ( displaystyle 50) км. Ответ дайте в км/ч.

Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:

Пусть скорость велосипедиста будет ( displaystyle x), а мотоциклиста – ( displaystyle y). До момента первой встречи велосипедист был в пути ( displaystyle 60) минут, а мотоциклист – ( displaystyle 20).

При этом они проехали равные расстояния:

( displaystyle 60x=20y (1))

Между встречами велосипедист проехал расстояние ( displaystyle 40x), а мотоциклист – ( displaystyle 40y).

Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:

(Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.)

Значит,

( displaystyle 40x+50=40y (2))

Полученные уравнения решаем в системе:

( displaystyle left{ begin{array}{l}60x=20y\40x+50=40yend{array} right.Leftrightarrow left{ begin{array}{l}y=3x\4x+5=4yend{array} right.Rightarrow text{4}x+5=12xRightarrow )

( displaystyle Rightarrow x=frac{5}{8}=0,625frac{text{км}}{мин}=0,625cdot 60frac{text{км}}{text{ч}}=37,5frac{text{км}}{text{ч}})

Ответ: ( displaystyle 37,5).

Разобрался? Попробуй решить самостоятельно следующие задачи:

Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.

Скорость течения в озере равна ( displaystyle 0).

Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести.

Это понятно? Логично же.

А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…

Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.

Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.

Разобрался? Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?

Здесь возможно два случая:

1 случай – ты плывешь по течению, и тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.

2 случай – ты плывешь против течения. Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы ( displaystyle 100) метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.

Источник

Содержание:

Путь и перемещение:

Вы знаете, что любой вид движения совершается по определенной траектории.

Траектория – это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.

Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, – криволинейным (с).

Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой Путь и перемещение в физике - формулы и определения с примерами

Путь и перемещение в физике - формулы и определения с примерами

Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.

Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком 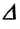Путь и перемещение в физике - формулы и определения с примерами (буква греч. алфавита) перед этой величиной.

Изменение координат материальной точки во время движения

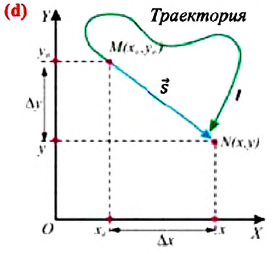
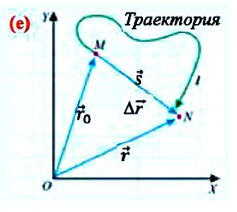
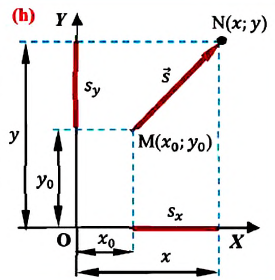
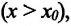
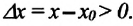
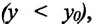
Изменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается Путь и перемещение в физике - формулы и определения с примерами то изменение координаты по этой оси будет положительным: Путь и перемещение в физике - формулы и определения с примерами Координата же муравья по оси У уменьшается Путь и перемещение в физике - формулы и определения с примерами поэтому изменение его координаты по этой оси будет отрицательным: Путь и перемещение в физике - формулы и определения с примерами

Путь и перемещение в физике - формулы и определения с примерами

Изменение радиус-вектора материальной точки во время движения

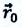
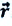
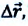
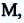
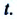
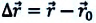
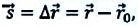
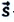
На следующем рисунке представлены радиус-векторы Путь и перемещение в физике - формулы и определения с примерами и Путь и перемещение в физике - формулы и определения с примерами начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор Путь и перемещение в физике - формулы и определения с примерами соединяющий концы этих радиус-векторов Путь и перемещение в физике - формулы и определения с примерами называют перемещением данной материальной точки за промежуток времени Путь и перемещение в физике - формулы и определения с примерами Согласно правилу сложения векторов: Путь и перемещение в физике - формулы и определения с примерами Из последнего выражения получается, Путь и перемещение в физике - формулы и определения с примерами или Путь и перемещение в физике - формулы и определения с примерами где Путь и перемещение в физике - формулы и определения с примерами — перемещение материальной точки.

Путь и перемещение в физике - формулы и определения с примерами

Перемещение – это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением. Перемещение — векторная величина.

Векторная величина – это величина, определяемая, кроме числового значения (модуля), также и направлением.

К вектору перемещения, как векторной величине, можно применить известные действия над векторами – сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.

Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.

Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).

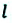
Путь и перемещение в физике - формулы и определения с примерами

Материальная точка прошла расстояние Путь и перемещение в физике - формулы и определения с примерами от точки М до точки N по прямой линии. В этом случае пройденный путь равен модулю перемещения: Путь и перемещение в физике - формулы и определения с примерами

Путь и перемещение в физике - формулы и определения с примерами

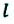
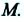
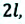
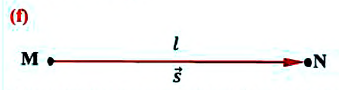
Материальная точка прошла расстояние Путь и перемещение в физике - формулы и определения с примерами от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку Путь и перемещение в физике - формулы и определения с примерами В этом случае материальная точка прошла путь, равный Путь и перемещение в физике - формулы и определения с примерами а модуль перемещения равен нулю:

Путь и перемещение в физике - формулы и определения с примерами

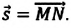
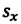
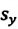
Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение Путь и перемещение в физике - формулы и определения с примерами Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения Путь и перемещение в физике - формулы и определения с примерами и Путь и перемещение в физике - формулы и определения с примерами (h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки: 

Путь и перемещение в физике - формулы и определения с примерами

Путь и перемещение в физике - формулы и определения с примерами

Одинаковы ли путь и перемещение

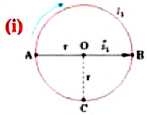
Задача:

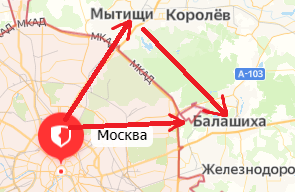
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).

Путь и перемещение в физике - формулы и определения с примерами

Дано:

Путь и перемещение в физике - формулы и определения с примерами

Решение:

Пройденный путь 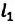Путь и перемещение в физике - формулы и определения с примерами равен длине дуги: Путь и перемещение в физике - формулы и определения с примерами

Модуль перемещения же равен диаметру окружности: Путь и перемещение в физике - формулы и определения с примерами

Вычисление:

Путь и перемещение в физике - формулы и определения с примерами

Что такое путь и перемещение

Путь и перемещение в физике - формулы и определения с примерами

Автобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путьПуть и перемещение в физике - формулы и определения с примерами

Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.

Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.

Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.

А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.

Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).

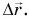
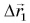
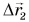
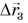
Обозначим перемещение символом Путь и перемещение в физике - формулы и определения с примерами На рисунке 38 вектор Путь и перемещение в физике - формулы и определения с примерами — это перемещение автобуса из Минска в Мытищи, вектор Путь и перемещение в физике - формулы и определения с примерами — из Мытищь в Балашиху, а вектор Путь и перемещение в физике - формулы и определения с примерами — из Минска в Борисов.

Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.

Путь и перемещение в физике - формулы и определения с примерами

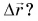
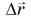
Можно ли сравнивать путь S, пройденный телом, с его перемещением Путь и перемещение в физике - формулы и определения с примерами Нельзя, поскольку путь S — скаляр, а перемещение Путь и перемещение в физике - формулы и определения с примерами — вектор.

Сравнивать путь S можно с модулем перемещения Путь и перемещение в физике - формулы и определения с примерами который является скалярной величиной. Равен ли путь модулю перемещения?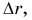

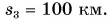
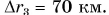
В рассматриваемом примере путь, пройденный автобусом за два часа, Путь и перемещение в физике - формулы и определения с примерами Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см. рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова: Путь и перемещение в физике - формулы и определения с примерами Путь автобуса больше модуля его перемещения: Путь и перемещение в физике - формулы и определения с примерами

Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.

Следовательно, путь всегда не меньше модуля перемещения:

Путь и перемещение в физике - формулы и определения с примерами

Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:

Путь и перемещение в физике - формулы и определения с примерами

Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.

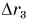
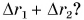
Равен ли при этом модуль Путь и перемещение в физике - формулы и определения с примерами сумме модулей Путь и перемещение в физике - формулы и определения с примерами Ответьте самостоятельно.

Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.

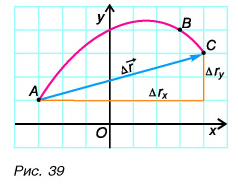
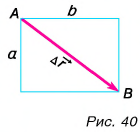
Путь и перемещение в физике - формулы и определения с примерами

При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора 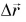Путь и перемещение в физике - формулы и определения с примерами на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:

Путь и перемещение в физике - формулы и определения с примерами

Главные выводы:

  1. Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Путь — положительная скалярная величина.
  2. Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
  3. Путь не меньше модуля перемещения тела за то же время.
  4. Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.

Пример:

Путь и перемещение в физике - формулы и определения с примерамиПуть и перемещение в физике - формулы и определения с примерами
Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.

Решение

Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:

Путь и перемещение в физике - формулы и определения с примерами

Путь конькобежца: Путь и перемещение в физике - формулы и определения с примерами

Путь пешехода: Путь и перемещение в физике - формулы и определения с примерами

Ответ: Путь и перемещение в физике - формулы и определения с примерами

  • Заказать решение задач по физике

Траектория движения

Возьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис. 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.

Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.

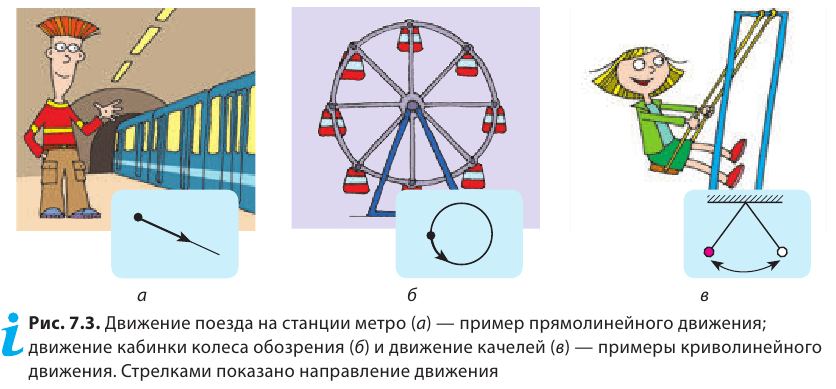
Так, в без­облачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории разли­чают прямолинейное и криволинейное движе­ния тел (рис. 7.3).

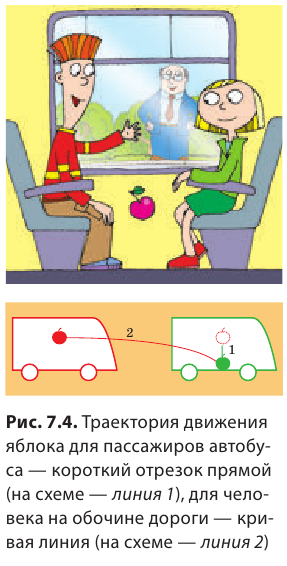
Путь и перемещение в физике - формулы и определения с примерами

Путь и перемещение в физике - формулы и определения с примерами

Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.

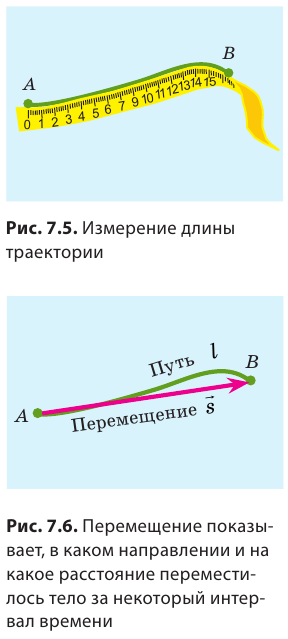
Чем путь отличается от перемещения

Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):

Путь и перемещение в физике - формулы и определения с примерами

Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).

Путь и перемещение в физике - формулы и определения с примерами

Путь и перемещение в физике - формулы и определения с примерами

Путь и перемещение в физике - формулы и определения с примерами

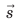
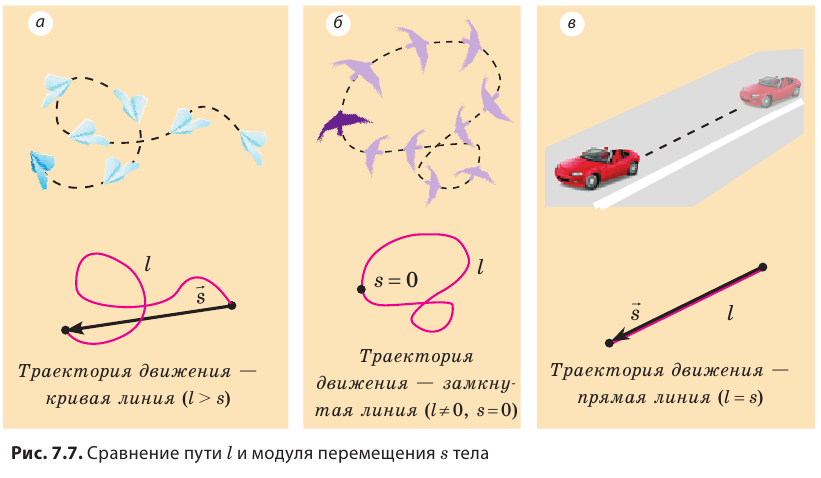
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом Путь и перемещение в физике - формулы и определения с примерами . Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.

Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).

Итоги:

Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение 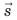Путь и перемещение в физике - формулы и определения с примерами — это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).

Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.

  • Равномерное прямолинейное движение
  • Прямолинейное неравномерное движение 
  • Прямолинейное равноускоренное движение
  • Сложение скоростей
  • Физический и математический маятники
  • Пружинные и математические маятники
  • Скалярные и векторные величины и действия над ними
  • Проекция вектора на ось
Источник

Добавить комментарий