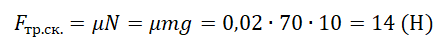Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
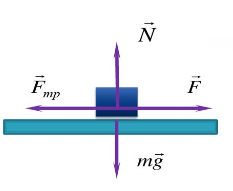
Сила трения скольжения определяется формулой:
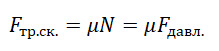
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
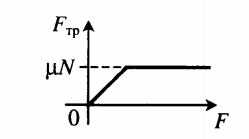
Способы определения вида силы трения, возникающей между телами, и ее модуля:
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
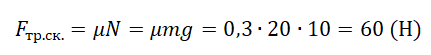
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
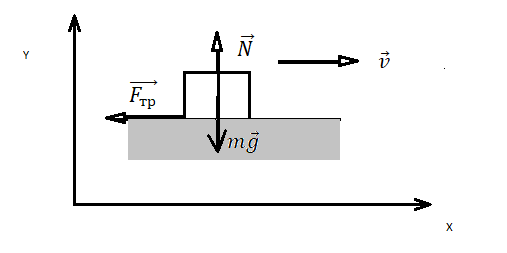
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
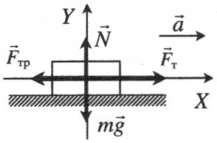
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
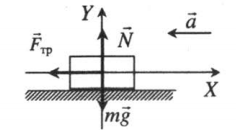
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
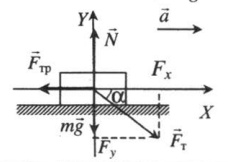 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
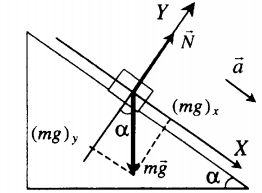
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
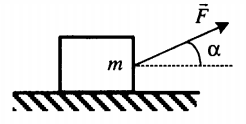
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
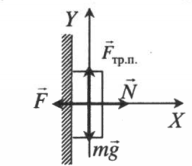 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
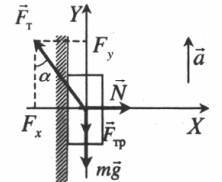 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
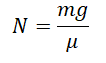
Следовательно:
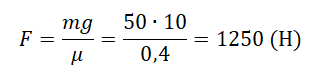
Движение тела по наклонной плоскости
Движение вниз без трения |
|
 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
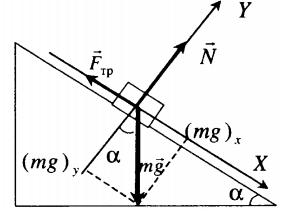 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
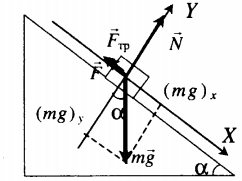 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
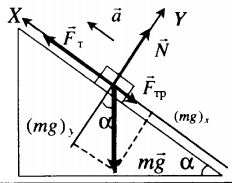 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
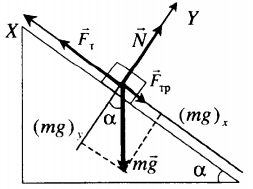 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
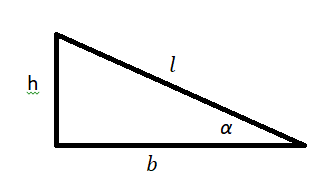
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
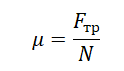
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
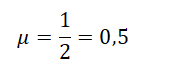
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17513
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
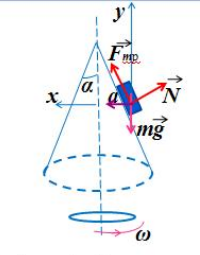
Второй закон Ньютона в векторном виде выглядит следующим образом:
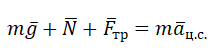
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
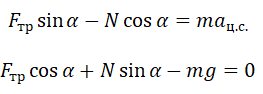
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
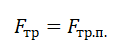
Максимальное значение силы трения равно:
![]()
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
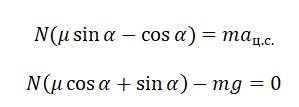
Запишем систему уравнение в следующем виде:
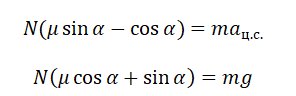
Поделим первое уравнение на второе и получим:
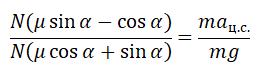
Сделаем сокращения и получим:
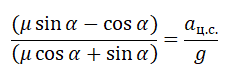
Отсюда центростремительное ускорение равно:
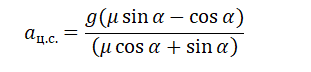
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
![]()
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
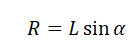
Отсюда центростремительное ускорение равно:
![]()
Выразим искомую величину L:
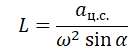
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
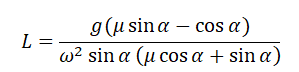
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
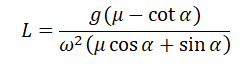
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
Запишем второй закон Ньютона в векторной форме:
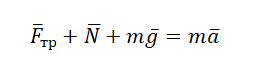
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
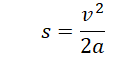
Выразим ускорение через проекцию сил на ось ОХ:
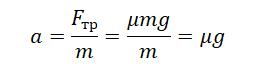
Подставим найденное ускорение в формулу тормозного пути и получим:
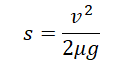
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.4k
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение тела, возникающее вследствие силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ – тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Под действием сила трения $overline{F}_{mp} $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.

Рисунок 1.
Так как сила трения $overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline{F}_{mp} right|$, то:
Но ускорение определяется также формулой:
где $v_{0} $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
«Движение тела под действием силы трения» 👇
Таким образом:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Так как $v=0$, то:
Так как $overline{a}=-frac{left|overline{F}_{mp} right|}{m} $, получим:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
Пример 1
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Найти: $v$-?
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
$l=frac{mv_{0}^{2} }{2overline{left|F_{mp} right|}} $. (1)
Так как $F_{mp} =mu mg$, подставим в формулу (1) и получим:
$l=frac{mv_{0}^{2} }{2mu mg} $. (2)
Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:
$v_{0} =sqrt{2mu gl} =20$м/с
Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.
Пример 2
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.
Найти: $F_{mp} $, $mu $-?
Решение:
Уравнение движения сноубордиста будет иметь вид:
[ma=F_{mp} .]
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
[a=-frac{v_{0} }{t} .]
Тогда:
$F_{mp} =ma=-mfrac{v_{0} }{t} =40H$.
Так как сила трения $overline{F}_{mp} $равна $F_{mp} =mu Bg$, находим коэффициент трения $mu $:
[mu =frac{F_{mp} }{mg} =0,05.]
Ответ: $F_{mp} =40H$, $mu =0,05$.
Пример 3
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Найти: $a$-?
Решение:
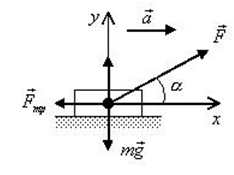
Рисунок 2.
Уравнение движения тела:
[moverline{a}=moverline{g}+overline{N}+overline{F}+overline{F}_{mp} .]
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
[begin{array}{l} {ma=Fcos alpha -F_{mp} } \ {0=-Bg+N+Fsin alpha } end{array}]
Поскольку $F_{mp} =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_{mp} =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
$a=frac{1}{m} [Fcos alpha -mu (mg-Fsin alpha )]approx 7,6м/с^2$
Ответ: $a$=$7,6м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

В этой главе…
- Постигаем гравитацию
- Изучаем влияние наклона плоскости
- Учитываем силы трения
- Измеряем дальность полета под действием силы тяжести
Сила гравитационного притяжения — вот основная тема этой главы. В главе 5 было показано, что для ее преодоления требуется применять силу. В этой главе будет представлены способы влияния гравитационного притяжения и трения на движение объектов по наклонным плоскостям. Кроме того, будет показано, как гравитация влияет на траекторию полета объекта.
Содержание
- Разбираемся с гравитацией
- Движемся по наклонной плоскости
- Вычисляем углы
- Ищем компоненту вектора силы Fg вдоль наклонной плоскости
- Вычисляем скорость вдоль наклонной плоскости
- Разбираемся с ускорением
- Вычисляем углы
- Преодолеваем трение
- Вычисляем силу трения и нормальную силу
- Разбираемся с коэффициентом трения
- Знакомимся со статическим и кинетическим трением
- Изучаем статическое трение
- Поддерживаем движение вопреки трению скольжения
- Тянем груз в гору и боремся с трением
- Вычисляем компоненту силы тяжести
- Определяем силу трения
- Вычисляем путь скольжения холодильника до полной остановки
- Вычисляем ускорение скольжения
- Вычисляем путь скольжения по полу
- Как гравитация влияет на свободное падение объектов
- Стреляем вверх: максимальная высота
- Время подъема ядра
- Общее время полета
- Стреляем под углом
- Разбиваем движение ядра на компоненты
- Определяем максимальную дальность полета ядра
Разбираемся с гравитацией
На поверхности Земли сила гравитационного притяжения ( mathbf{F_g} ) (или сила тяжести) постоянна и равна ( mmathbf{g} ), где ( m ) — это масса объекта, a ( mathbf{g} ) — ускорение свободного падения под действием силы тяжести, равное 9,8 м/с2.
Ускорение — это вектор, а значит, он имеет величину, направление и точку приложения (подробнее об этом см. главу 4). Уравнение ( mathbf{F_g}=mmathbf{g} ) интересно тем, что ускорение свободного падения объекта ( g ) не зависит от массы объекта.
Поскольку ускорение свободного падения не зависит от массы объекта, то более тяжелый объект падает нисколько не быстрее, чем более легкий объект. Сила тяжести сообщает свободно падающим телам одинаковое направленное вниз ускорение ( mathbf{a} ) (на поверхности Земли равное ( mathbf{g} )), независимо от их массы.
Сказанное выше относится к объектам вблизи поверхности Земли, а в главе 7 рассматриваются другие ситуации вдали от Земли (например, на орбите Луны), где сила тяжести и ускорение свободного падения имеют другие значения. Чем дальше вы находитесь от центра Земли, тем меньше сила тяжести и ускорение свободного падения. В примерах этой главы ускорение свободного падения направлено вниз. Но это не значит, что оно влияет только на движение предметов вертикально вниз. Здесь рассматриваются также примеры движения объектов под углом к вертикали.
Движемся по наклонной плоскости
В курсе физики часто упоминаются наклонные плоскости и рассматривается движение объектов по ним. Взгляните на рис. 6.1. На нем показана тележка, которая скатывается по наклонной плоскости. Тележка движется не строго вертикально, а вдоль плоскости, наклоненной под углом ( theta ) к горизонтали.
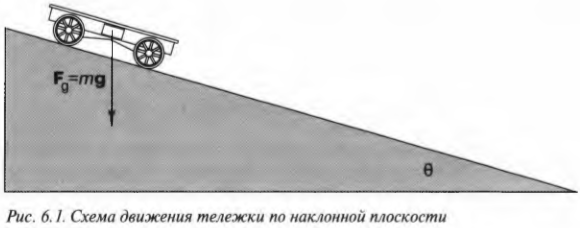
Допустим, что угол ( theta ) = 30°, а длина наклонной плоскости равна 5 метрам. До какой скорости разгонится тележка в конце наклонной плоскости? Сила тяжести сообщит тележке ускорение, но учтите, что вдоль наклонной плоскости ускорение будет отличаться от ускорения свободного падения. Дело в том, что разгон вдоль наклонной плоскости будет выполнять только компонента силы тяжести вдоль этой наклонной плоскости.
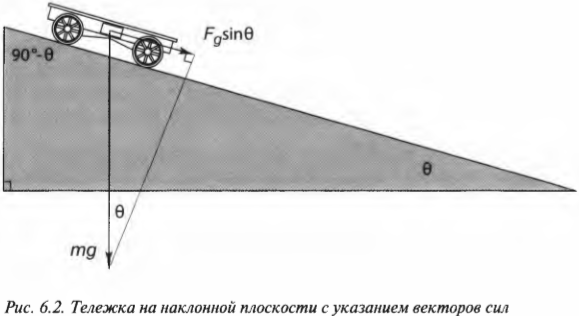
Чему равна компонента силы тяжести, действующей вдоль наклонной плоскости, если на тележку действует направленная вертикально сила тяжести ( mathbf{F_g} )? Взгляните на рис. 6.2, на котором показаны упомянутые выше угол ( theta ) и вектор силы ( mathbf{F_g} ) (подробнее о векторах см. главу 4). Для определения компоненты силы тяжести, действующей вдоль наклонной плоскости, нужно определить угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью. Для этого потребуются элементарные сведения из геометрии (подробности см. в главе 2), а именно то, что сумма углов треугольника равна 180°. Угол между вектором силы ( mathbf{F_g} ) и основанием наклонной плоскости равен 90°, а угол между наклонной плоскостью и ее основанием равен ( theta ). Поэтому, глядя на рис. 6.2 , можно легко определить угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью: 180°-90°-( theta ) или 90°-( theta ).
Вычисляем углы
Преподаватели физики используют особый способ вычисления углов между векторами и наклонными плоскостями. Однако читателям книги можно раскрыть этот “секрет” определения угла ( theta ). Для начала обратите внимание на то, что если ( theta ) стремится к 0°, то угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью стремится к 90°. И наоборот, если ( theta ) стремится к 90°, то угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью стремится к 0°. На основании этого простого наблюдения можно предположить, что угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью равняется 90°-( theta ). Как видите, для определения взаимосвязи между углами бывает полезно попробовать поменять значения некоторых углов от 0° до 90°.
Ищем компоненту вектора силы Fg вдоль наклонной плоскости
Итак, зададимся вопросом: чему равна компонента вектора силы ( mathbf{F_g} ) вдоль наклонной плоскости? Теперь мы знаем, что угол между вектором силы ( mathbf{F_g} ) и наклонной плоскостью равняется 90°-( theta ). Значит, компонента вектора силы вдоль наклонной плоскости ( F_{g,накл} ) равна:
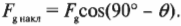
Если вы добросовестно учили тригонометрию, то вам наверняка должно быть известно (а если нет, то обратитесь к главе 2), что:
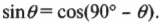
(Часто это знать совсем не обязательно, и может сгодиться предыдущее уравнение.)
Следовательно:

Полученное выражение можно легко проверить следующим образом. Когда ( theta ) стремится к 0°, то значение компоненты силы вдоль наклонной плоскости ( F_{g,накл} ) стремится к 0, поскольку наклонная плоскость стремится к горизонтальному положению. А когда ( theta ) стремится к 90°, то значение компоненты силы вдоль наклонной плоскости ( F_{g,накл} ) стремится к ( F_g ) поскольку наклонная плоскость стремится к вертикальному положению. Итак, если вдоль наклонной плоскости на тележку с массой 800 кг действует сила ( F_gsintheta ), то каким будет ускорение тележки? Это легко определить по известной формуле:
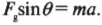
Следовательно:
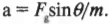
Задача упрощается, если вспомнить, что ( F_g=mg ) и тогда:
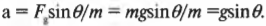
Итак, теперь нам известно, что ускорение тележки вдоль наклонной плоскости равно ( a=gsintheta ). Это соотношение справедливо для любого объекта, ускоряющегося под действием силы тяжести, если не учитывать силы трения.
Вычисляем скорость вдоль наклонной плоскости
Логично было бы поинтересоваться: а какова скорость тележки в конце наклонной плоскости? Для этого нам потребуется следующее уравнение, которое было выведено в главе 3:
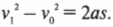
Поскольку начальная скорость ( v_0 ) = 0, а длина наклонной плоскости ( s ) = 5 м, то получим:
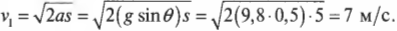
Итак, скорость тележки в конце наклонной плоскости ( v_1 ) = 7 метров в секунду. Хотя это не такая уж и большая скорость для автомобиля, но все же не рекомендуется проводить такие эксперименты в домашних условиях. Имейте в виду, что на самом деле скорость будет несколько ниже, поскольку часть энергии расходуется на вращение колес, движение других частей автомобиля, трение и т.д.
Разбираемся с ускорением
Блиц-вопрос: а какую скорость в конце наклонной плоскости приобретет кубик льда при скольжении без трения? Ответ: он будет иметь такую же скорость, что и тележка в предыдущем примере, т.е. 7 м/с. Ускорение любого объекта, движущегося без трения вдоль наклонной плоскости под углом ( theta ), равно ( gsintheta ). Как видите, имеет значение не масса объекта, а компонента ускорения свободного падения вдоль наклонной плоскости. Если нам известно ускорение движения кубика льда и пройденное расстояние ( s ), то получим значение скорости по известной формуле:
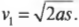
Итак, масса не входит в формулу для определения конечной скорости.
Преодолеваем трение
Трудно представить себе повседневную жизнь без трения. Без трения автомобили не могли бы ездить, люди — ходить, а руки — брать любые предметы. Трение создает проблемы, но без него жизнь была бы просто невозможной.
Трение возникает из-за взаимодействия между поверхностными неровностями. Поверхность состоит из множества микроскопических выступов и впадин. При соединении двух поверхностей эти выступы одной поверхности и впадины другой поверхности сцепляются и препятствуют свободному проскальзыванию.
Допустим, что ваши сбережения хранятся в виде огромного золотого слитка, который показан на рис. 6.3, и некий злоумышленник задумал украсть его, но не может нести такой огромный слиток в руках, а может только тащить его волоком. Этот воришка стремится приложить силу к слитку, чтобы ускорить его и сбежать от преследующей его полиции. Однако благодаря силе трения вор не сможет развить большого ускорения.
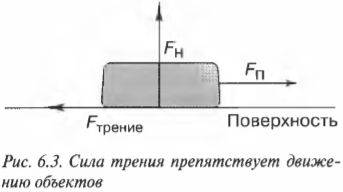
Определим количественно влияние силы трения на движение объектов. Результирующая сила на слиток и создаваемое ею ускорение определяется как разность приложенной силы ( F_п ) и силы трения ( F_{трение} ) вдоль оси X:
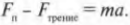
Эта формула выглядит очень просто, но как определить силу трения? Как будет показано ниже, она зависит от нормальной силы.
Вычисляем силу трения и нормальную силу
Сила трения ( F_{трение} ) всегда противодействует приложенной силе, которая вызывает движение. Причем сила трения пропорциональна приложенной силе.
Как показано на рис. 6.3, слиток золота давит на горизонтальную поверхность с силой, равной весу слитка, ( mg ). А поверхность с той же силой действует на слиток. Эту силу называют нормальной силой (или силой нормального давления), ( F_н ).(Нормальной называется компонента силы со стороны поверхности, направленная по нормали к поверхности, т.е. перпендикулярно к поверхности.) Нормальная сила по величине не всегда совпадает с силой тяжести, поскольку нормальная сила всегда перпендикулярна поверхности, по которой движется объект. Иначе говоря, нормальная сила — это сила взаимодействия поверхностей разных объектов, и чем она больше, тем сильнее трение.
В примере на рис. 6.3 слиток скользит вдоль горизонтальной поверхности, поэтому нормальная сила равна весу объекта, т.е. ( F_н=mg ) Итак, у нас есть нормальная сила, которая равна силе давления слитка на горизонтальную поверхность. Для чего она нам нужна? Для определения силы трения.
Разбираемся с коэффициентом трения
Сила трения определяется характеристиками поверхностей соприкасающихся материалов. Как физики теоретически описывают их? Никак. У физиков есть множество общих уравнений, которые предсказывают общее поведение объектов, например ( sum!F=ma ) (см. главу 5). Однако у физиков нет полного теоретического понимания механизмов взаимодействия поверхностей материалов. Поэтому поверхностные характеристики материалов известны, в основном, из опыта.
А из опыта известно, что нормальная сила непосредственно связана с силой трения. Оказывается, что с большой точностью эти две силы пропорциональны друг другу и их можно связать с помощью константы ( mu ) следующим образом:

Согласно этому уравнению, чтобы определить силу трения, нужно умножить нормальную силу на некую постоянную величину, т.е. константу ( mu ). Такая константа называется коэффициентом трения, и именно она характеризует свойства сцепления шероховатостей данных поверхностей.
Величина коэффициента трения находится в диапазоне от 0 до 1. Значение 0 возможно только в идеализированном случае, когда трение отсутствует вообще. А значение 1 соответствует случаю, когда сила трения максимальна и равна нормальной силе. Это значит, что максимальная сила трения для автомобиля не может превышать его веса.
Обратите внимание, что уравнение ( F_{трение}=mu F_н ) не является соотношением между векторами, поскольку эти векторы направлены в разные стороны. Например, на рис. 6.3 они перпендикулярны друг другу. Действительно, нормальная сила ( mathbf{F_н} ) всегда перпендикулярна поверхности, а сила трения ( mathbf{F_{трение}} ) — параллельна. Эти направления определяются их природой: нормальная сила ( mathbf{F_н} ) определяет степень сжатия поверхностей, а сила трения ( mathbf{F_{трение}} ) — степень противодействия скольжению вдоль поверхностей.
Сила трения не зависит от площади соприкосновения двух поверхностей. Это значит, что слиток с той же массой, но вдвое длиннее и вдвое ниже исходного будет испытывать точно такую же силу трения при скольжении по поверхности. При этом увеличивается вдвое площадь соприкосновения, но уменьшается вдвое давление, т.е. величина силы, которая приходится на единицу площади.
Итак, мы получили предварительные сведения и готовы вычислить силу трения? Не так быстро. Оказывается, что коэффициент трения бывает двух типов.
Знакомимся со статическим и кинетическим трением
Два разных коэффициента трения соответствуют двум разным типам трения: статическому трению (или трению покоя) и кинетическому трению (или трению скольжения).
Дело в том, что эти типы трения соответствуют двум разным физическим процессам. Если две поверхности не движутся относительно друг друга, то на микроскопическом уровне они взаимодействуют более интенсивно, и этот случай называется трением покоя. А когда поверхности уже скользят относительно друг друга, то микроскопические неровности не успевают вступить в интенсивное взаимодействие, и этот случай называется трением скольжения. На практике это значит, что для каждого из этих двух типов трения используются свои коэффициенты трения: коэффициент трения покоя ( mu_п ) и коэффициент скольжения ( mu_с ).
Изучаем статическое трение
Трение покоя сильнее трения скольжения, т.е. коэффициент трения покоя ( mu_п ) больше коэффициента трения скольжения ( mu_с ). Это можно упрощенно объяснить следующим образом. В состоянии покоя соприкасающиеся поверхности интенсивно взаимодействуют на микроскопическом уровне, а при скольжении поверхности успевают вступить в интенсивное взаимодействие только на более крупном макроскопическом уровне.
Трение покоя возникает тогда, когда нужно привести в движение покоящийся объект. Именно такую силу трения нужно преодолеть для начала скольжения объекта.
Предположим, что в примере на рис. 6.3 коэффициент трения покоя между слитком и поверхностью равен 0,3, а масса слитка равна 1000 кг (очень приличный слиток). Какую силу должен приложить воришка, чтобы сдвинуть слиток? Из предыдущих разделов нам уже известно, что:
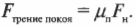
Поскольку поверхность горизонтальна, то нормальная сила направлена противоположно силе тяжести слитка и имеет ту же величину:
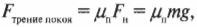
где ( m ) — масса слитка, a ( g ) — ускорение свободного падения, вызванное силой притяжения со стороны Земли. Подставляя численные значения, получим:
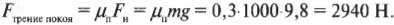
Итак, воришке потребуется приложить силу 2940 Н, чтобы сдвинуть с места неподвижный слиток. Довольно большая сила! А какая сила потребуется ему, чтобы поддерживать скольжение слитка? Для ответа на этот вопрос нужно рассмотреть трение скольжения.
Поддерживаем движение вопреки трению скольжения
Сила трения скольжения, возникающая из-за скольжения двух соприкасающихся поверхностей, не так велика, как сила трения покоя. Но это совсем не значит, что коэффициент трения скольжения можно легко вычислить теоретически, даже если нам известен коэффициент трения покоя. Оба коэффициента трения приходится определять из опыта.
Именно из опыта известно, что трение покоя больше трения скольжения. Представьте себе, что вы разгружаете неподвижный ящик на наклонной плоскости, но он вдруг начинает скользить вниз. Достаточно заблокировать его движение ногой и с большой вероятностью ящик останется в состоянии покоя, если аккуратно убрать ногу. Именно так, в состоянии покоя, проявляется трение покоя, а в процессе движения ящика — трение скольжения.
Пусть слиток на рис. 6.3 имеет массу 1000 кг, а коэффициент трения скольжения ( mu_c ) равен 0,18. Какую силу должен приложить воришка, чтобы сдвинуть с места неподвижный слиток? Для ответа на этот вопрос нужно воспользоваться следующей формулой:
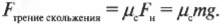
Подставляя численные значения, получим:
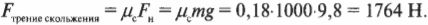
Воришке потребуется приложить силу 1764 Н, чтобы поддерживать скольжение слитка. Не такая уж и маленькая сила, если, конечно, воришке не помогают его верные друзья. Однако это не так уж и легко, и полиция быстро сможет догнать этого воришку. Зная законы физики, полицейские вряд ли захотят прилагать лишние усилия: “Слиток-то мы нашли, а вот домой тащите его сами”.
Тянем груз в гору и боремся с трением
В предыдущих примерах со слитком описывалось трение на горизонтальной поверхности. А как определить силу сопротивления со стороны трения на наклонной плоскости?
Допустим, что, собираясь на рыбалку, вы решили захватить с собой холодильник массой 100 кг. Единственный способ погрузить его в багажник автомобиля — это втащить холодильник по наклонной плоскости, как показано на рис. 6.4. Пусть наклонная плоскость расположена под углом 30°, коэффициент трения покоя равен 0,2, а коэффициент трения скольжения — 0,15. Хорошая новость заключается в том, что вам помогают два друга, а плохая — в том, что каждый из вас способен приложить силу не более 350 Н.
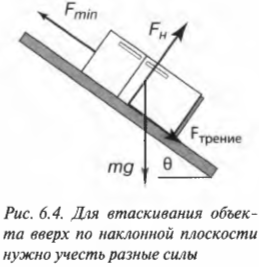
Ваши друзья растеряны? “Не стоит беспокоиться, немного физики — и все будет в порядке”, — можете ответить им вы, доставая калькулятор. Итак, нам нужно вычислить минимальную силу, которую нужно приложить, чтобы втащить холодильник вверх по наклонной плоскости в багажник автомобиля вопреки силе трения и силе тяжести.
Вычисляем компоненту силы тяжести
Для этого нужно внимательно изучить схему на рис. 6.4. Сила тяжести действует на холодильник и направлена вертикально вниз. Сумма углов треугольника, образованного вектором силы тяжести, наклонной плоскостью и ее основанием, равна 180°. Угол между вектором силы тяжести и основанием наклонной плоскости равен 90°, а угол между наклонной плоскостью и ее основанием — ( theta ). Поэтому угол между наклонной плоскостью и вектором силы тяжести равен:
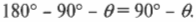
Компонента силы тяжести, действующая вдоль наклонной плоскости, равна:
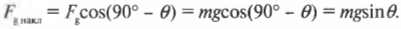
Таким образом, минимальная сила, с которой нужно толкать холодильник вверх по наклонной плоскости, равна сумме силы трения, ( F_{трение} ), и этой компоненты ( F_{g,накл} ), т.е.:
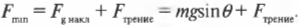
Определяем силу трения
Следующий вопрос: чему равна сила трения, ( F_{трение} )? Какой коэффициент трения нужно использовать для ее определения: покоя или скольжения? Поскольку коэффициент трения покоя больше коэффициента трения скольжения, то для оценки минимально необходимой силы имеет смысл учесть коэффициент трения покоя. Ведь после того как холодильник удастся сдвинуть с места, для скольжения придется прикладывать меньшую силу. Итак, с учетом коэффициента трения покоя, получим для силы трения

Для определения этой силы трения нам потребуется вычислить нормальную силу, ( F_н ) (более подробно эта сила описывается выше в этой главе). Она равна компоненте силы тяжести, которая направлена перпендикулярно (т.е. по нормали, откуда и происходит ее название) к наклонной плоскости. Как мы уже выяснили, угол между наклонной плоскостью и вектором силы тяжести равен 90°-( theta )(рис. 6.5).
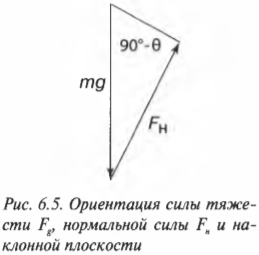
С помощью тригонометрических соотношений (см. главу 2) получим:
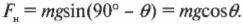
Чтобы проверить справедливость этого выражения, попробуйте устремить угол ( theta ) к нулю, при котором нормальная сила ( F_н ) становится равной ( mg ), что и следовало ожидать. Теперь получаем:
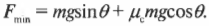
После подстановки численных значений получим:

Итак, три человека должны приложить минимально необходимую силу 660 Н, т.е. по 220 Н каждый, что меньше максимально возможной силы 350 Н. С радостным призывом “Приступим!” вы приступаете к работе, втаскиваете холодильник на самый верх наклонной плоскости. Допустим, что из-за несогласованности действий кто-то из вас перестал прикладывать силу. Как результат, холодильник после непродолжительной остановки неожиданно заскользил вниз, а после достижения основания продолжил движение по полу до полной остановки.
Вычисляем путь скольжения холодильника до полной остановки
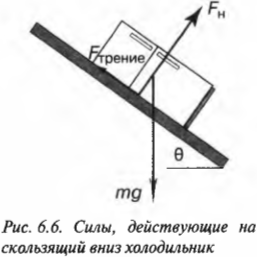
Допустим, что наклонная плоскость и пол имеют одинаковые коэффициенты трения скольжения. Каким будет путь скольжения холодильника до полной остановки? Пусть сначала холодильник скользит из состояния покоя до основания наклонной плоскости длиной 3 м, как показано на рис. 6.6. Во время такого скольжения холодильник разгоняется и вполне может столкнуться с автомобилем на расстоянии 7,5 м. О, Боже! Неужели они столкнутся? Нужно немедленно достать калькулятор и приступить к расчетам.
Вычисляем ускорение скольжения
При скольжении вниз действующие на холодильник силы направлены иначе, чем при скольжении вверх. Теперь вы и ваши друзья уже не прилагают свои силы, а холодильник скользит только под действием компоненты силы тяжести, направленной вдоль наклонной плоскости. А ей противодействует лишь сила трения. Чему же равна результирующая сумма этих сил? Из предыдущих разделов уже известно, что компонента силы тяжести вдоль наклонной плоскости равна:
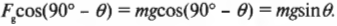
А нормальная сила равна:
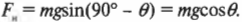
Это значит, что сила трения скольжения равна:
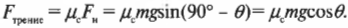
Результирующая сила, которая действует на холодильник в направлении движения и определяет его ускорение, равна:
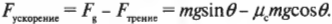
Обратите внимание на то, что сила трения, ( F_{трение} ), имеет отрицательный знак, т.е. она направлена противоположно компоненте силы тяжести вдоль наклонной плоскости, которая приводит в движение холодильник. После подстановки численных значений получим:
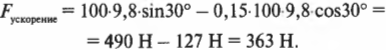
Поскольку масса холодильника равна 100 кг, то он скользит с ускорением 363 Н/100 кг = 3,63 м/с2 вдоль наклонной плоскости длиной 3 м. Для вычисления конечной скорости холодильника, ( v ), в конце наклонной плоскости нужно использовать следующую известную нам формулу:
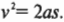
После извлечения квадратного корня и подстановки численных значений получим:
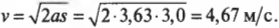
Такой будет скорость холодильника в конце наклонной плоскости.
Вычисляем путь скольжения по полу
Как на основе данных, полученных в предыдущем разделе, определить путь скольжения холодильника по полу? Столкнется ли холодильник с автомобилем?
Итак, нам известно, что холодильник начинает движение по полу со скоростью 4,67 м/с. Вопрос: какое расстояние он пройдет до полной остановки? Теперь в горизонтальном направлении на него действует только сила трения, а компонента силы тяжести по горизонтали равна нулю. Поэтому холодильник постепенно замедляется и рано или поздно остановится. Но уцелеет ли при этом стоящий поодаль автомобиль? Как обычно, сначала вычисляем суммарную силу ( F ), действующую на холодильник в направлении движения и определяющую его ускорение. В данном случае она равна силе трения:
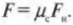
Поскольку холодильник движется вдоль горизонтальной поверхности, то нормальная сила ( F_н ) равна силе тяжести ( F_g ), действующей на холодильник:
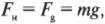
т.е. суммарная сила равна:
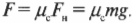
После подстановки численных значений получим:
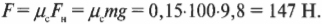
Именно такая сила сопротивления действует на холодильник и… терроризирует всю округу! Итак, насколько длинным будет тормозной путь холодильника? Подставим численные значения и получим:
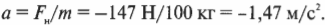
Здесь отрицательный знак обозначает замедление холодильника (см. главу 2).
По формуле:
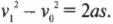
найдем тормозной путь холодильника:
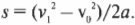
Поскольку конечная скорость ( v_1 ), равна 0, то эта формула упрощается и принимает вид:
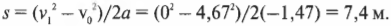
Вот это да! Холодильник проедет расстояние 7,4 м и остановится всего в 10 см от автомобиля, который находится на расстоянии 7,5 м от основания наклонной плоскости. Можно расслабиться и понаблюдать за вашими друзьями, которые охвачены паникой и с ужасом в глазах ожидают столкновения холодильника и автомобиля.
Как гравитация влияет на свободное падение объектов
В главе 7 сила гравитационного притяжения (или сила тяжести) описывается в космическом масштабе, а здесь она рассматривается только вблизи поверхности Земли. В физике часто встречаются задачи с учетом силы тяжести. Этот раздел посвящен тому, как сила тяжести влияет на свободное падение объектов, и его следует рассматривать, как переходный между материалом предыдущей главы и материалом главы 7.
Стреляем вверх: максимальная высота
Зная ускорение свободного падения и начальную скорость объекта, можно легко вычислить дальность его полета. Эти знания могут пригодиться при подготовке праздничных фейерверков!
Предположим невероятное: на день рождения друзья подарили вам пушку, способную разгонять ядро весом 10 кг до начальной скорости 860 м/с. С изумлением рассматривая ее, гости начали спорить: а на какую максимальную высоту эта пушка способна выстрелить? Поскольку вы уже владеете всеми необходимыми знаниями, то можете быстро дать ответ на этот вопрос.
Нам известна начальная скорость ядра, ( v_0 ), и ускорение свободного падения ( g ) под действием силы тяжести. Как определить максимальную высоту подъема ядра? В точке максимального подъема ядра его скорость будет равна нулю, а затем оно начнет обратное движение вниз. Следовательно, для вычисления максимальной высоты подъема ядра, ( s ), можно использовать следующую формулу, в которой конечная скорость ( v_1 ) равна нулю:
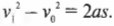
Отсюда получим:
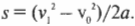
Подставляя численные значения для начальной скорости ( v_0 ) = 860 м/с2, ускорения свободного падения под действием силы тяжести ( g ) = —9,8 м/с2 (минус обозначает направление ускорения, противоположное направлению перемещения), получим:
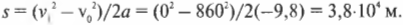
Ого! Ядро улетит на высоту 38 км. Совсем неплохо для пушки, подаренной на день рождения. Интересно, а сколько же времени придется его ждать обратно?
Время подъема ядра
Итак, сколько времени потребуется для того, чтобы ядро поднялось на максимальную высоту? В примере из главы 4, где мяч для игры в гольф падал с вершины обрыва, для вычисления дальности его полета использовалось следующее уравнение:
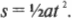
Однако это уравнение представляет собой всего один из многих возможных вариантов поиска ответа на заданный вопрос.
Нам известно, что в точке максимального подъема скорость ядра равна 0. Поэтому для определения времени полета до максимальной высоты можно использовать следующее уравнение:
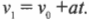
Поскольку ( v_1 ) = 0 и ( a ) = ( -g ), то:
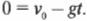
Иначе говоря, получим:
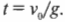
После подстановки численных значений получим:
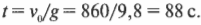
Итак, ядру потребуется 88 с, чтобы достичь максимальной высоты. А каково общее время полета?
Общее время полета
Сколько времени потребуется ядру, чтобы достичь максимальной высоты 38 км и вернуться обратно к пушке, если на подъем ему потребовалось 88 с? Общее время полета вычислить очень просто, поскольку обратный путь вниз симметричен прямому пути вверх. Это значит, что скорость ядра в каждой точке обратного пути вниз равна по величине и имеет противоположное направление по сравнению с прямым путем вверх. Поэтому время падения равно времени подъема и общее время полета равно удвоенному времени подъема:
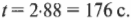
Итак, общее время полета равно 176 с, или 2 минуты и 56 секунд.
Стреляем под углом
В предыдущих разделах пушка стреляла вертикально вверх. Попробуем теперь поразить цель, стреляя ядром из пушки под углом, как показано на рис. 6.7.

Разбиваем движение ядра на компоненты
Как характеризовать движение ядра при стрельбе под углом? Поскольку любое движение всегда можно разбить на компоненты по осям X и Y, а в данном примере сила притяжения действует только вдоль оси Y, то задача упрощается. Разобьем начальную скорость на компоненты (подробнее об этом рассказывается в главе 4):
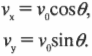
Эти компоненты независимы, а сила притяжения действует только в направлении оси Y. Это значит, что компонента ( v_x ) остается постоянной, а меняется только компонента ( v_y ):
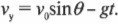
Теперь легко определить координаты ядра в любой момент. Например, координата ядра по оси X выражается формулой:
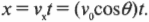
Поскольку сила тяжести влияет на движение ядра по вертикали, то координата ядра по оси Y выражается формулой:
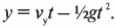
Из предыдущего раздела нам уже известно, что общее время полета ядра по вертикали равно:
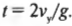
Теперь, зная время, можно легко определить дальность полета ядра по оси X:
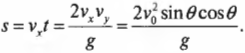
Итак, для вычисления дальности полета ядра по горизонтали нужно знать начальную скорость ядра, ( v_0 ), и угол, ( theta ), под которым сделан выстрел.
Определяем максимальную дальность полета ядра
При каком угле выстрела ( theta ) ядро улетит на максимальное расстояние по горизонтали? Из тригонометрии известно, что ( 2sinthetacostheta=sin2theta ).
Тогда:
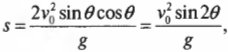
и расстояние ( s ) будет максимальным при максимальном значении ( sin2theta=1 ), т.е. при ( theta ) = 45°.
В таком случае:
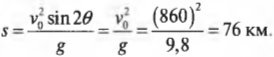
Совсем неплохо для пушки, подаренной на день рождения!
Глава 6. Запрягаемся в упряжку: наклонные плоскости и трение
2.9 (58.38%) 37 votes
Техническая механика
Трение – основные понятия, законы и зависимости
Понятие трения
Как известно, в природе не существует абсолютно гладких и абсолютно твердых тел, поэтому при перемещении одного тела по поверхности другого возникает сопротивление, которое называется трением.
Трение – явление сопротивления относительному перемещению, возникающее между двумя телами в зонах соприкасания поверхностей по касательной к ним.
Трение – явление чрезвычайно распространенное в природе и имеющее большое значение. При этом оно может выполнять и полезные, и вредные функции. На трении основана работа фрикционных и ременных передач, муфт, наклонных транспортеров, прокатных станов, тормозных устройств и т. п.
Трение обеспечивает сцепление тел с земной поверхностью и, следовательно, работу машин, тракторов и другой транспортной самоходной техники. При отсутствии трения мы не могли бы ходить по земле, поскольку наши ноги скользили бы и разъезжались в разные стороны, как у неумелого конькобежца на гладком льду.
Наряду с полезными свойствами, трение является во многих устройствах и механизмах вредным сопротивлением, которое отнимает львиную долю мощности и энергии у машин. Для уменьшения трения в механизмах конструкторам приходится применять различные приемы и способы, чтобы снизить непродуктивные потери энергии.
Трение классифицируют по характеру движения, в результате которого оно возникает. Различают трение покоя, трение скольжения, трение качения и трение качения с проскальзыванием . Очевидно, что последний из перечисленных видов трения является комбинацией трения скольжения и трения качения.
Трением покоя называется трение двух тел при начальном (бесконечно малом) относительном перемещении в момент перехода от состояния покоя к состоянию относительного движения. Это явление можно объяснить шероховатостью поверхностей соприкасающихся тел, а также их деформацией, вызванной взаимным давлением друг на друга.
Кроме того, при таком взаимном давлении (контакте) между телами, на их поверхностях возникают силы молекулярного сцепления. Для того, чтобы начать взаимное перемещение тел, необходимо преодолеть все эти факторы, обуславливающие трение покоя.
Трением движения называется трение двух тел, находящихся в относительном движении. Рассмотрим основные виды трения в зависимости от характера относительного движения тел.
Трение скольжения
Трением скольжения называется трение движения, при котором скорости тел в точке касания различны по значению и (или) направлению.
Трение скольжения, как и трение покоя, обусловлено, прежде всего, шероховатостью и деформацией поверхностей, а также наличием молекулярного сцепления прижатых друг к другу тел. Трение скольжения сопровождается изнашиванием, т. е. отделением или остаточной деформацией материала, а также нагревом трущихся поверхностей тел (остаточной называется деформация, не исчезающая после прекращения действия внешних сил).
Трение характеризуется силой трения.
Сила трения есть сила сопротивления относительному перемещению двух тел при трении.
Рассмотрим тело, лежащее на горизонтальной шероховатой плоскости (см. рисунок 1) .
Сила тяжести G уравновешивается нормальной реакцией плоской поверхности N . Если к телу приложить небольшую движущую силу P , то оно не придет в движение, так как эта сила будет уравновешиваться силой трения Fтр , которая является, таким образом, составляющей реакции опорной плоскости, направленной вдоль плоскости в противоположную перемещению сторону.
Если постепенно увеличивать сдвигающую силу P , то до определенного ее значения тело будет оставаться в покое, а затем придет в движение.
Очевидно, что сила трения в состоянии покоя может изменяться в зависимости от степени микросмещения может изменяться от нуля до какого-то максимального значения F max тр , причем в промежутке между нулем и максимальным значением сила трения Fтр по модулю всегда равна сдвигающей силе P .
Максимальное значение сила трения покоя имеет в момент начала относительного движения. Это значение называется наибольшей силой трения покоя или просто силой трения покоя.
Сила трения всегда направлена в сторону, противоположную направлению относительного движения тела.
В XVIII веке французские ученые Гийом Атонтон (1663-1705) , а затем Шарль Огюстен Кулон (1736-1806) провели фундаментальные исследования в области трения, и на основе их сформулировали три основных закона трения скольжения, которые обычно называют законами Кулона.
1-й закон Кулона
Cила трения не зависит от величины площади трущихся поверхностей.
Первый закон можно объяснить с помощью следующих умозаключений. Если площадь трущихся поверхностей увеличится, то увеличится и количество сцепляющихся неровностей, но уменьшится давление на опорную поверхность, которое обратно пропорционально площади контакта тел. Поэтому сопротивление относительному перемещению останется прежним.
2-й закон Кулона
Максимальная сила трения прямо пропорциональна нормальной составляющей внешних сил, действующих на поверхности тела.
Второй закон Кулона говорит о том, что если увеличится нормальная составляющая внешних сил, действующих на поверхности тела (иначе говоря, увеличится сила нормального давления или реакции), то во столько же раз возрастет максимальная сила трения.
Поскольку зависимость эта прямо пропорциональная, можно выделить коэффициент, характеризующий ее пропорциональность. Этот коэффициент называется коэффициентом трения скольжения , и определяется он, как отношение силы трения Fтр к нормальной составляющей N внешних сил, действующих на поверхности тела. Обозначается коэффициент трения скольжения f .
При наибольшей силе трения покоя коэффициент трения называют коэффициентом сцепления .
В результате второй закон трения скольжения можно сформулировать так: сила трения равна коэффициенту трения скольжения, умноженному на силу нормального давления или реакции.
Очевидно, что коэффициент трения скольжения – величина безразмерная.
Нормальная реакция N опорной поверхности и сила трения Fтр дают равнодействующую R , которая называется полной реакцией опорной поверхности (см. рисунок 2) .
Полная реакция R составляет с нормалью к опорной поверхности некоторый угол. Максимальное значение этого угла (достигает в момент начала относительного движения) называется углом трения и обозначается φ .
Из рисунка 2 очевидно, что
т. е. коэффициент трения скольжения равен тангенсу угла трения.
Если коэффициент трения скольжения одинаков для всех направлений движения, то множество (геометрическое место) полных реакций образует круговой конус, который называется конусом трения (см. рисунок 2) .
Если для разных направлений движения коэффициент трения неодинаков (например, при скольжении по дереву вдоль волокон и поперек волокон), то конус трения будет некруговым (несимметричным).
Свойство конуса трения заключается в том, что для равновесия тела, лежащего на шероховатой поверхности, равнодействующая приложенных к нему активных сил должна проходить внутри конуса трения.
Действительно, если равнодействующую P активных сил, приложенных к телу, разложить на составляющие P2 (движущая сила) и P2 (сила нормального давления) , то
По второму закону трения скольжения
Следовательно, при α будет P1 и движение окажется невозможным.
3-й закон Кулона
Сила трения зависит от материала тел, состояния трущихся поверхностей и рода смазки.
Согласно третьему закону трения скольжения, коэффициент трения скольжения зависит от материалов трущихся тел, качества обработки их поверхности (степени шероховатости), рода и температуры смазки. В зависимости от наличия между сопрягаемыми поверхностями слоя смазки трение подразделяется на два вида: трение без смазочного материала (сухое трение) и трение в условиях смазки.
Коэффициент трения скольжения определяют опытным путем; значения его для различных условий приведены в справочниках. Примеры коэффициентов трения для некоторых материалов приведены ниже.
- Металл по металлу без смазки . 0,15. 0,30
- То же, со смазкой . 0,10. 0,18
- Дерево по дереву без смазки . 0,40. 0,60
- Кожа по чугуну без смазки . 0,30. 0,50
- То же, со смазкой . 0,15
- Сталь по льду . 0,02
Коэффициент трения скольжения при движении обычно меньше, чем при покое, и в первом приближении не зависит от скорости относительного перемещения тел.
Методы решения задач статики при наличии трения остаются такими же, как и при отсутствии его, причем в уравнения равновесия обычно вводят максимальные значения сил трения.
Трение на наклонной поверхности
Рассмотрим тело, лежащее на шероховатой наклонной плоскости, составляющей угол α с горизонтальной плоскостью (см. рисунок 3) .
Разложим силу тяжести тела G на составляющие G1 и G2 , параллельную и перпендикулярную наклонной плоскости. Модули этих составляющих определим, используя тригонометрические зависимости:
Составляющая G1 стремится сдвинуть тело вдоль наклонной плоскости. Полностью или частично эта составляющая уравновешивается силой трения; согласно второму закону трения скольжения, ее максимальное значение равно:
Fтр = fN = fG cosα , где f – коэффициент трения скольжения тела по наклонной плоскости.
Для того, чтобы тело, лежащее на наклонной плоскости, находилось в равновесии, движущая сила G1 должна быть по модулю равна силе трения Fтр ,т. е.
G sinα = fG cosα или tgα = f = tgφ , откуда следует, что α = φ .
Если угол, который наклонная плоскость составляет с горизонтом, будет равен углу трения, то тело, лежащее на наклонной плоскости ,будет под действием собственной силы тяжести либо равномерно скользить вниз, либо находиться в состоянии покоя (что, собственно, одно и то же).
Для того, чтобы тело, лежащее на наклонной плоскости, заведомо не скользило вниз под действием собственной силы тяжести, должно быть соблюдено условие α .
Наклонной плоскостью с переменным углом наклона к горизонту пользуются для экспериментального определения угла трения φ и коэффициента трения f (см. рисунок 4а) .
Определим модуль силы Р , параллельной наклонной плоскости, в случае равномерного перемещения тела вверх по шероховатой наклонной плоскости (см. рисунок 4б) . Спроецируем силы, действующие на тело, на ось x . Составим уравнение равновесия:
ΣX = 0; P – G sinα – Fтр = 0 .
Так как Fтр = fG cosα , то P = G sinα + fG cosα или после преобразований: P = G (tgα + f) .
Определим модуль горизонтальной силы Р , которую надо приложить к телу для равномерного перемещения его вверх по шероховатой наклонной плоскости (см. рисунок 5) .
Применим геометрическое условие равновесия плоской системы сил (размерами тела пренебрегаем) и построим замкнутый силовой многоугольник, соответствующий уравнению равновесия:
G + P + N + Fтр = 0 .
Из треугольника abc имеем: P = Gtg(α + φ) .
Этот случай движения имеет место при взаимном перемещении винта и гайки с прямоугольной резьбой, так как резьбу винта можно рассматривать как наклонную плоскость, угол наклона которой равен углу подъема винтовой линии.
Трение в резьбе, имеющей треугольный или трапецеидальный профиль, подобно трению в клинчатом ползуне. Поэтому рассмотрим клинчатый ползун с углом заострения 2β , нагруженный вертикальной силой Q (см. рисунок 6) . Определим силу P , необходимую для равномерного перемещения ползуна вдоль горизонтальных направляющих, если коэффициент трения скольжения равен f .
Составим два уравнения равновесия ползуна:
ΣX = 0; P – 2Fтр = 0;
ΣY = 0; 2Nsinβ – Q = 0 ,
где Fтр – сила трения на каждой грани ползуна; N – нормальная реакция направляющей.
Решая эту систему уравнений и учитывая, что Fтр = fN , получим:
где f’ = f/sinβ – приведенный коэффициент трения.
Соответствующий этому приведенному коэффициенту угол трения обозначим φ’ и назовем приведенным углом трения , тогда:
Очевидно, что f’> f , следовательно, при прочих равных условиях трение в клинчатом ползуне больше трения на плоскости.
Понятие приведенного коэффициента трения условно, так как он изменяется в зависимости от угла заострения клинчатого ползуна.
По аналогии с движением тела вверх по наклонной плоскости под действием горизонтальной силы для равномерного перемещения клинчатого ползуна по направляющим, наклоненным к горизонту под углом α , нужно приложить горизонтальную силу равную
Трение в крепежной метрической резьбе подобно трению клинчатого ползуна с углом заострения 2β = 120˚ , для трапецеидальной резьбы угол 2β = 150˚ .
С трением связано понятие угла естественного откоса – наибольшим углом между наклонной плоскостью и горизонтом, при котором сыпучее тело удерживает свои частицы на поверхности, без их движения (осыпания) вниз. Угол естественного откоса сыпучего тела равен углу трения между его частицами. Этот угол приходится принимать во внимание, например, при различных земляных работах на уклонах и скатах.
Трение в теоретической механике
Содержание:
Трение:
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения.
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Возникновение силы трения, препятствующей скольжению, иногда называют трением первого рода, а возникновение пары сил, препятствующей качению,— трением второго рода.
Трение скольжения
Пусть на тело действует плоская система активных сил и тело находится в равновесии, соприкасаясь с поверхностью другого тела, являющегося связью для рассматриваемого тела. Если поверхности соприкасающихся тел абсолютно гладкие и тела абсолютно твердые, то реакция поверхности связи направлена по нормали к общей касательной в точке соприкосновения и направление реакции в этом случае не зависит от действующих на тело активных сил. От активных сил зависит только числовое значение силы реакции. В действительности абсолютно гладких поверхностей и абсолютно твердых тел не бывает. Все поверхности тел в той или иной степени шероховаты и все тела деформируемы. В связи с этим и сила реакции 
Если силу реакции 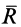
В теоретической механике обычно рассматривается только сухое трение между поверхностями тел, т. е. такое трение, когда между ними нет смазывающего вещества. Для сухого трения надо различать трение скольжения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.
При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила трения вычисляется по формуле
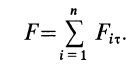
Аналогично, при выбранном направлении нормали нормальная реакция выражается через заданные силы
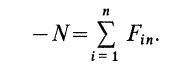
В 1781 г. Кулон установил основные приближенные законы для сухого трения скольжения. В дальнейшем законы Кулона многократно проверялись другими исследователями. Но эти законы подтверждались в случае, когда поверхности тел не вдавливались друг в друга и шероховатость была не очень велика.
Законы Кулона можно установить на приборе, схема которого дана рис. 59. На этом приборе изменяя вес гири, можно изменять нормальное давление 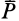 (или равную ему нормальную реакцию
(или равную ему нормальную реакцию 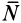 ) между трущимися поверхностями. Изменяя же вес гирь
) между трущимися поверхностями. Изменяя же вес гирь  , можно изменять силу
, можно изменять силу  , которая стремится двигать тело вдоль поверхности другого тела, являющегося связью. Очевидно, что если сила
, которая стремится двигать тело вдоль поверхности другого тела, являющегося связью. Очевидно, что если сила  , то тело находится в равновесии и сила трения
, то тело находится в равновесии и сила трения 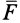 равна нулю.
равна нулю.
Если силу 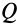 увеличить (при этом тело не скользит по поверхности, а находится в равновесии), то по условию равновесия возникает сила трения
увеличить (при этом тело не скользит по поверхности, а находится в равновесии), то по условию равновесия возникает сила трения 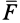 , которая равна, но противоположна активной силе
, которая равна, но противоположна активной силе 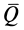 . Нормальная реакция
. Нормальная реакция 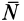 равна нормальному давлению
равна нормальному давлению 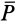 . Увеличивая силу
. Увеличивая силу 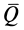 при одном и том же нормальном давлении
при одном и том же нормальном давлении 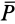 , можно достичь и такого положения, когда ничтожно малое дальнейшее увеличение силы
, можно достичь и такого положения, когда ничтожно малое дальнейшее увеличение силы 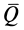 выведет тело из равновесия, заставляя его скользить по поверхности связи. Очевидно, будет достигнуто предельное положение, при котором сила трения станет наибольшей и не сможет уравновешивать силу
выведет тело из равновесия, заставляя его скользить по поверхности связи. Очевидно, будет достигнуто предельное положение, при котором сила трения станет наибольшей и не сможет уравновешивать силу 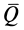 при ее дальнейшем увеличении. Изменяя силу нормального давления
при ее дальнейшем увеличении. Изменяя силу нормального давления 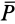 , можно исследовать, как изменяется при этом предельная сила трения
, можно исследовать, как изменяется при этом предельная сила трения 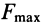 . Можно также исследовать влияние на предельную силу трения площади соприкосновения тел, сохраняя при этом нормальное давление, а также влияние материала тел, характер обработки поверхностей и другие факторы. Такие опыты позволяют проверить законы Кулона для сухого трения скольжения.
. Можно также исследовать влияние на предельную силу трения площади соприкосновения тел, сохраняя при этом нормальное давление, а также влияние материала тел, характер обработки поверхностей и другие факторы. Такие опыты позволяют проверить законы Кулона для сухого трения скольжения.
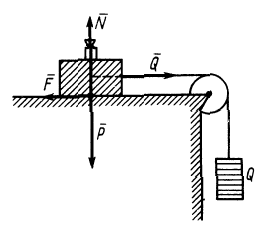
Рис. 59
Трение скольжения:
При решении многих технических вопросов приходится принимать в расчет силы трения. Остановимся на рассмотрении сил трения 1-го рода (скольжения).
Пусть на тело А (рис. 31), лежащее на горизонтальной негладкой плоскости, действует сила Р под углом а к вертикали. Раскладывая силу Р на две составляющие  и
и  замечаем, что сила
замечаем, что сила 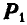 уравновешивается с реакцией плоскости N; вторая же составляющая
уравновешивается с реакцией плоскости N; вторая же составляющая 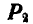 неминуемо должна была бы сообщить телу А движение вправо, но при небольшом угле α тело А находится еще в покое; следовательно, в противоположную сторону силы
неминуемо должна была бы сообщить телу А движение вправо, но при небольшом угле α тело А находится еще в покое; следовательно, в противоположную сторону силы 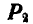 направлено сопротивление, которое обусловлено силой трения F. Увеличивая постепенно угол будет возрастать до некоторого предела. Обозначим через
направлено сопротивление, которое обусловлено силой трения F. Увеличивая постепенно угол будет возрастать до некоторого предела. Обозначим через 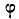 угол, при котором начинается скольжение тела по плоскости. В этом случае сила трения достигает наибольшей величины; определяем ее из Δabc при
угол, при котором начинается скольжение тела по плоскости. В этом случае сила трения достигает наибольшей величины; определяем ее из Δabc при  по формуле:
по формуле:
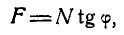
где 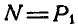 — нормальная реакция плоскости.
— нормальная реакция плоскости.
Угол  называется углом трения, а тангенс этого угла — коэффициентом трения скольжения и обозначается через f; следовательно, вообще:
называется углом трения, а тангенс этого угла — коэффициентом трения скольжения и обозначается через f; следовательно, вообще:
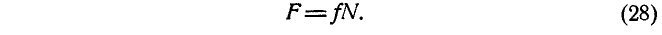
Формула (28) выражает первый закон трения, который формулируется так:
Первый закон трения
1. Сила трения прямо пропорциональна нормальному давлению или реакции связи и направлена в сторону, противоположную относительному перемещению трущихся тел.
Этот закон был установлен опытным путем. Амонтоном-Кулоном и другими исследователями были установлены еще следующие законы:
2. Коэффициент трения зависит от материала и состояния трущихся поверхностей.
3. Коэффициент трения в покое больше коэффициента трения в движении.
4. Коэффициент трения не зависит от величины трущихся поверхностей (можно считать правильным лишь в первом приближении).
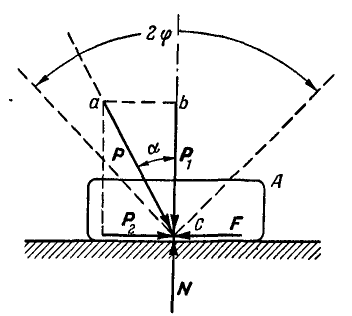
5. Коэффициент трения зависит от скорости движения трущихся поверхностей и с увеличением этой скорости уменьшается, приближаясь к некоторой предельной величине.
Обращаясь к рисунку 31, замечаем, что тело А находится в равновесии, если сила Р проходит внутри конуса с углом при вершине С, равным двойному углу трения 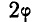 ; такой конус называется конусом трения и играет важную роль при решении задач.
; такой конус называется конусом трения и играет важную роль при решении задач.
Когда тело А находится еще в покое (рис. 31), то по мере увеличения угла 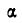 возрастает также и сила
возрастает также и сила 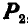 , а сила F уменьшается. Наконец, наступает такой момент, когда при
, а сила F уменьшается. Наконец, наступает такой момент, когда при 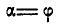 тело находится на грани между покоем и скольжением. В этом случае сила F и коэффициент трения в покое f достигают наибольшего значения. При незначительном увеличении силы
тело находится на грани между покоем и скольжением. В этом случае сила F и коэффициент трения в покое f достигают наибольшего значения. При незначительном увеличении силы 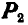 тело А начинает скользить по плоскости, благодаря чему нарушается сцепление между поверхностями соприкасания тела и плоскости. В этом случае сила трения скольжения F коэффициент трения в движении f уменьшаются по величине, приближаясь к некоторой предельной величине с увеличением относительной скорости скольжения. Исключение составляют лишь некоторые’материалы, например при трении кожи о металл в ременных передачах, где с увеличением скорости относительного скольжения коэффициент трения также возрастает.
тело А начинает скользить по плоскости, благодаря чему нарушается сцепление между поверхностями соприкасания тела и плоскости. В этом случае сила трения скольжения F коэффициент трения в движении f уменьшаются по величине, приближаясь к некоторой предельной величине с увеличением относительной скорости скольжения. Исключение составляют лишь некоторые’материалы, например при трении кожи о металл в ременных передачах, где с увеличением скорости относительного скольжения коэффициент трения также возрастает.
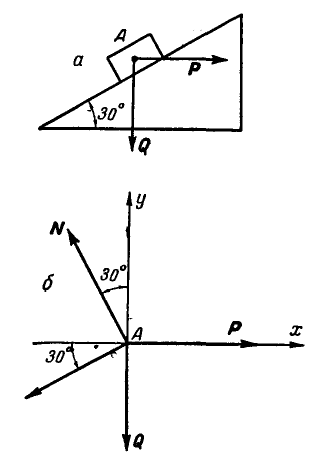
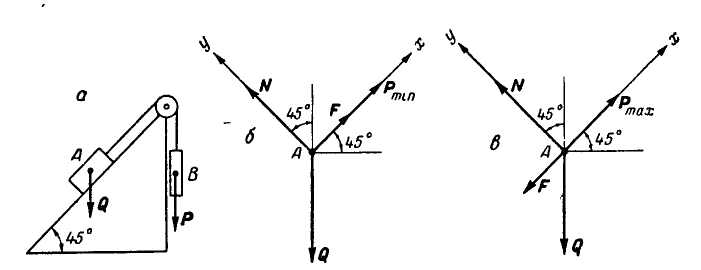
Задача №1
Тело А весом Q=100кГ лежит на шероховатой наклонной плоскости (рис. 32,а). Какую наименьшую горизонтальную силу Р ладо приложить к телу, чтобы оно начало двигаться, если коэффициент трения тела о плоскость f=0,2.
Решение. Рассмотрим равновесие тела А. Помимо горизонтальной силы Р на тело действует сила Q, нормальная реакция N плоскости и сила трения F, направленная параллельно плоскости в обратную сторону движения тела (рис. 32,6).
Составляя уравнения равновесия (27), имеем:
В двух уравнениях имеются три неизвестные величины: Р, N и F. Для получения третьего уравнения по формуле (28) имеем > зависимость:  .
.
Выражая в уравнениях равновесия F через N, получим:
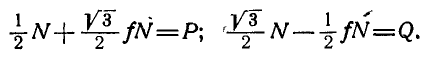
Оторда находим: 
Задача №2
Определить наибольший и наименьший груз Р, при котором груз Q = 10 кГ не будет двигаться (рис» 33, а). Коэффициент трения груза Q о плоскость f=0,2.
Указание: при наименьшем грузе 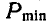 тело А будет стремиться сползти вниз, следовательно сила трения F будет направлена параллельно плоскости вверх (рис. 33, б). При наибольшем грузе
тело А будет стремиться сползти вниз, следовательно сила трения F будет направлена параллельно плоскости вверх (рис. 33, б). При наибольшем грузе  , напротив, тело А стремится двигаться кверху, а потому сила трения F будет направлена параллельно плоскости вниз (рис. 33, в).
, напротив, тело А стремится двигаться кверху, а потому сила трения F будет направлена параллельно плоскости вниз (рис. 33, в).
Составляя для каждого из случаев (рис. 33, б и 33, в) по два уравнения равновесия и принимая во внимание формулу (28), получим:
32
Законы Кулона
1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения тела под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т. е.
2. Максимальная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью он положен на поверхность, широкой или узкой.
3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции), т. е.

где безразмерный коэффициент  называют коэффициентом трения скольжения; он не зависит от нормального давления.
называют коэффициентом трения скольжения; он не зависит от нормального давления.
4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, т. е. от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения скольжения в зависимости от различных условий устанавливается экспериментально. Так, коэффициент трения для кирпича по бетону равен 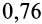 ; для стали по стали —
; для стали по стали — 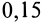 ; для дуба по дубу поперек волокон —
; для дуба по дубу поперек волокон — 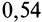 , а для дуба по дубу вдоль волокон —
, а для дуба по дубу вдоль волокон — 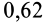 .
.
Опыты показывают, что при скольжении одного тела по поверхности другого с некоторой относительной скоростью возникает сила трения скольжения, равная максимальной, только при этом коэффициент трения скольжения незначительно изменяется в зависимости от скорости скольжения. Для большинства материалов он уменьшается с увеличением скорости скольжения, но для некоторых материалов, наоборот, увеличивается (трение кожи о металл).
В приближенных технических расчетах обычно считают, что коэффициент трения скольжения не зависит от относительной скорости скольжения.
В отличие от сухого трения трение при наличии смазывающего слоя между поверхностями определяется распределением относительной скорости скольжения в этом слое. В этом случае трение происходит не между поверхностями тел, а между слоями смазывающего вещества. Теория трения в смазывающем слое жидкости рассматривается в гидродинамике.
Угол и конус трения
Многие задачи на равновесие тела на шероховатой поверхности, т. е. при наличии силы трения, удобно решать геометрически. Для этой цели введем понятия угла и конуса трения.
Пусть твердое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия, т. е. таком состоянии, когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции (рис. 60). В этом случае полная реакция шероховатой поверхности 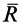 отклонена от нормали общей касательной плоскости трущихся поверхностей на наибольший угол.
отклонена от нормали общей касательной плоскости трущихся поверхностей на наибольший угол.
Этот наибольший угол 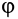 между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции, и направлением нормальной реакции называют углом трения.
между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции, и направлением нормальной реакции называют углом трения.
Угол трения 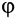 зависит от коэффициента трения, т. е.
зависит от коэффициента трения, т. е.
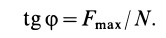
Но по третьему закону Кулона,
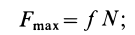

т. е. тангенс угла трения равен коэффициенту трения.
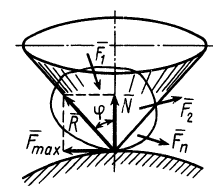
Рис. 60
Конусом трения называют конус, описанный полной реакцией, построенной на максимальной силе трения, вокруг направления нормальной реакции. Его можно получить изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей.
Если коэффициент трения во всех направлениях одинаков, то конус трения круговой. Если не одинаков, то конус трения не круговой, например в случае, когда свойства соприкасающихся поверхностей различны (вследствие определенного направления волокон или в зависимости от направления обработки поверхности тел, если обработка происходит на строгальном станке и т. п.).
Равновесие тела на шероховатой поверхности
При равновесии сил, действующих на твердое тело, находящееся в равновесии на шероховатой поверхности, возникает дополнительно неизвестная сила реакции шероховатой поверхности— сила трения. В случае предельного равновесия сила трения достигает своего максимального значения и по формуле (1) выражается через нормальную реакцию. В общем случае равновесия сила трения находится между нулем и ее максимальным значением. Поэтому соответствующие условия равновесия, в которые входит сила трения после замены ее максимальным значением, становятся неравенствами. После этого неизвестные находят путем совместного решения уравнений и неравенств. Для всех неизвестных или для их части получают решения в виде неравенств.
Некоторые задачи на равновесие с учетом сил трения удобно решать геометрически с помощью конуса трения.
Можно сформулировать условия равновесия тела на шероховатой поверхности используя конус трения. Если активные силы, действующие на тело, приводятся к равнодействующей силе  , то при равновесии тела на шероховатой поверхности равнодействующая активных сил
, то при равновесии тела на шероховатой поверхности равнодействующая активных сил  по аксиоме о равновесии двух сил, приложенных к твердому телу, уравновешивается полной реакцией R шероховатой поверхности (рис. 61). Полная реакция проходит через вершину конуса, а следовательно, через вершину конуса проходит и равнодействующая активных сил.
по аксиоме о равновесии двух сил, приложенных к твердому телу, уравновешивается полной реакцией R шероховатой поверхности (рис. 61). Полная реакция проходит через вершину конуса, а следовательно, через вершину конуса проходит и равнодействующая активных сил.
Очевидно, при изменении равнодействующей активных сил тело находится в равновесии до тех пор, пока составляющая  равнодействующей активных сил, лежащая в общей касательной плоскости соприкасающихся поверхностей не будет превышать наибольшего значения силы трения
равнодействующей активных сил, лежащая в общей касательной плоскости соприкасающихся поверхностей не будет превышать наибольшего значения силы трения  .
.
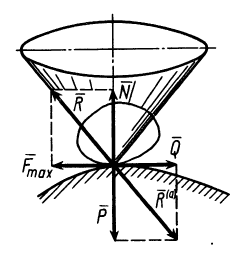
Рис. 61
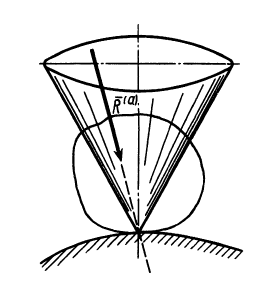
Рис. 62
Предельным положением равновесия тела является случай, когда сила 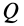 равна силе
равна силе 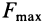 . В этом случае равнодействующая активных сил
. В этом случае равнодействующая активных сил 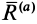 направлена по образующей конуса трения, так как
направлена по образующей конуса трения, так как 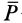 —составляющая равнодействующей активных сил по нормали — уравновешена нормальной реакцией
—составляющая равнодействующей активных сил по нормали — уравновешена нормальной реакцией 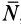 , если только активные силы не отделяют тела от шероховатой поверхности. Поэтому условие равновесия тела на шероховатой поверхности можно сформулировать так: для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину (рис. 62).
, если только активные силы не отделяют тела от шероховатой поверхности. Поэтому условие равновесия тела на шероховатой поверхности можно сформулировать так: для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину (рис. 62).
Тело нельзя вывести из равновесия любой по модулю активной силой, если ее линия действия проходит внутри конуса трения.
Если линия действия равнодействующей активных сил не проходит внутри конуса трения или по его образующей, то тело на шероховатой поверхности не может находиться в равновесии (рис. 63).
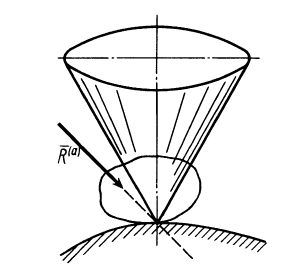
Рис. 63
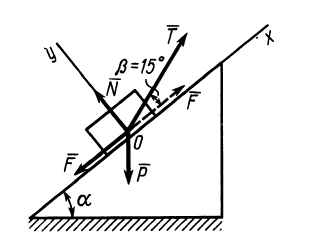
Рис. 64
Пример 1.
Тело, сила тяжести которого  , удерживается в равновесии силой
, удерживается в равновесии силой 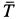 на шероховатой наклонной плоскости, имеющей угол наклона
на шероховатой наклонной плоскости, имеющей угол наклона 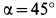 (рис. 64). Коэффициент трения скольжения между телом и плоскостью
(рис. 64). Коэффициент трения скольжения между телом и плоскостью 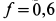 . Сила
. Сила 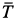 действует на тело под углом
действует на тело под углом 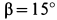 к линии наибольшего ската. Определить значение силы
к линии наибольшего ската. Определить значение силы 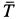 при равновесии тела на шероховатой наклонной плоскости.
при равновесии тела на шероховатой наклонной плоскости.
Решение. К телу приложены силы 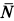 ,
, 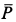 ,
, 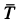 и сила трения
и сила трения 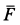 . Возможны два случая предельного равновесия тела и соответственно два предельных значения силы
. Возможны два случая предельного равновесия тела и соответственно два предельных значения силы 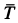 при двух направлениях силы трения по наклонной плоскости вниз и вверх в зависимости от направления возможного скольжения вверх по наклонной плоскости и вниз. Для составления уравнений равновесия целесообразно ввести
при двух направлениях силы трения по наклонной плоскости вниз и вверх в зависимости от направления возможного скольжения вверх по наклонной плоскости и вниз. Для составления уравнений равновесия целесообразно ввести 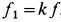 , где
, где 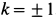 .
.
Составляем условия равновесия в виде суммы проекций сил на координатные оси для обоих предельных случаев. Имеем

По закону Кулона,
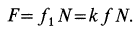
Решая эти уравнения относительно  , получаем
, получаем
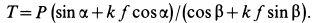
Отсюда при 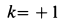
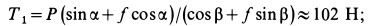
при 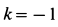
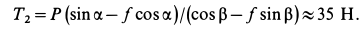
Таким образом, сила 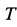 при равновесии тела должна удовлетворять условию
при равновесии тела должна удовлетворять условию  .
.
Пример 2.
Однородный тяжелый стержень  длиной
длиной  опирается концом
опирается концом 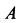 на гладкую вертикальную стену, а другим
на гладкую вертикальную стену, а другим 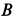 — на шероховатую вертикальную стену (рис.65). Расстояние между стенами
— на шероховатую вертикальную стену (рис.65). Расстояние между стенами 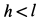 . Определить коэффициент трения стены
. Определить коэффициент трения стены 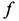 , при котором возможно равновесие стержня.
, при котором возможно равновесие стержня.
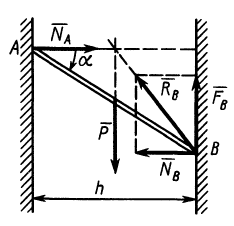
Рис. 65
Решение. Рассмотрим случай, когда точка  расположена выше точки
расположена выше точки  стержня. Равновесие стержня невозможно, если точка
стержня. Равновесие стержня невозможно, если точка  расположена ниже точки
расположена ниже точки 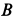 . На стержень действуют сила тяжести
. На стержень действуют сила тяжести 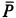 , приложенная посередине стержня нормальная реакция гладкой стены
, приложенная посередине стержня нормальная реакция гладкой стены 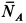 и реакция шероховатой стены
и реакция шероховатой стены 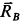 , которую разложим на нормальную реакцию
, которую разложим на нормальную реакцию 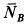 и силу трения
и силу трения 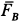 .
.
Составим условия равновесия плоской системы сил:
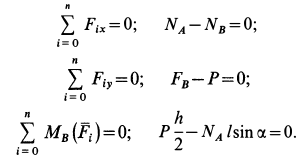
К этим условиям следует добавить неравенство для силы трения
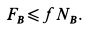
Из уравнений равновесия находим
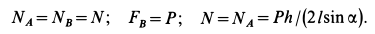
Из геометрических условий задачи имеем
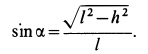
Итак, для силы трения 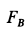 имеем следующие уравнение и неравенство:
имеем следующие уравнение и неравенство:
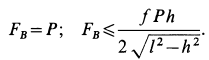
Исключая из них силу трения 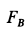 , после сокращения на
, после сокращения на 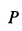 получаем
получаем
Искомое условие для коэффициента трения 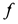 при равновесии стержня принимает вид
при равновесии стержня принимает вид
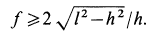
Трение качения
Если рассматриваемое тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте соприкосновения могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса, как, например, у электровозов, вагонов, автомашин, шарики и ролики в шариковых и роликовых подшипниках и т. п.
Пусть цилиндрический каток находится на горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью из-за деформации фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке. Если активные силы приложены симметрично относительно среднего сечения катка, т. е. вызывают одинаковые деформации вдоль всей его образующей, то можно изучать только одно среднее сечение катка. Этот случай рассмотрен ниже.
Активные силы, действующие на катки в виде колес (рис. 66), кроме силы тяжести  обычно состоят из силы
обычно состоят из силы  , приложенной к центру колеса параллельно общей касательной в точке
, приложенной к центру колеса параллельно общей касательной в точке  , и пары сил с моментом
, и пары сил с моментом 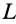 , стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если
, стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если 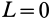 , а
, а 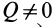 то колесо называют ведомым-, если
то колесо называют ведомым-, если 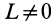 , a
, a 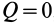 , то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.
, то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.
Если активные силы, действующие на колесо, привести к точке  соприкосновения катка с плоскостью, у которых нет деформации, то в общем случае получим силу и пару сил, стремящиеся заставить каток скользить и катиться. Следует различать чистое качение, когда точка соприкосновения
соприкосновения катка с плоскостью, у которых нет деформации, то в общем случае получим силу и пару сил, стремящиеся заставить каток скользить и катиться. Следует различать чистое качение, когда точка соприкосновения  катка не скользит по неподвижной плоскости, и качение со скольжением, когда наряду с вращением катка есть и скольжение, т. е. точка
катка не скользит по неподвижной плоскости, и качение со скольжением, когда наряду с вращением катка есть и скольжение, т. е. точка  катка движется по плоскости. При чистом скольжении, наоборот, каток движется по плоскости, не имея вращения.
катка движется по плоскости. При чистом скольжении, наоборот, каток движется по плоскости, не имея вращения.
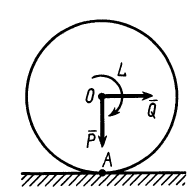
Рис. 66
Рис. 67
Рис. 68
Соприкосновение среднего сечения колеса с неподвижной плоскостью из-за деформации колеса и плоскости происходит по некоторой линии  . По этой линии на колесо действуют распределенные силы реакции (рис. 67). Если привести распределенные силы к точке
. По этой линии на колесо действуют распределенные силы реакции (рис. 67). Если привести распределенные силы к точке 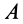 , то в этой точке получим главный вектор
, то в этой точке получим главный вектор 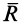 этих распределенных сил с составляющими
этих распределенных сил с составляющими 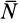 (нормальная реакция) и
(нормальная реакция) и 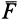 (сила трения скольжения), а также пару сил с моментом
(сила трения скольжения), а также пару сил с моментом 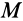 . При симметричном распределении сил по линии
. При симметричном распределении сил по линии  относительно точки
относительно точки  момент
момент  пары сил равен нулю. В этом случае нет активных сил, стремящихся катить каток в каком-либо направлении. _
пары сил равен нулю. В этом случае нет активных сил, стремящихся катить каток в каком-либо направлении. _
Приведем активные силы 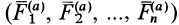 в общем случае к точке
в общем случае к точке  . В этой точке получим главный вектор этих сил
. В этой точке получим главный вектор этих сил  и пару сил, момент которой равен главному моменту
и пару сил, момент которой равен главному моменту  (рис. 68).
(рис. 68).
При равновесии катка, т. е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,
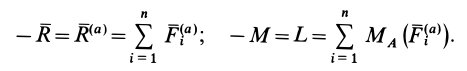
Изменив активные силы, приложенные к катку так, чтобы увеличивался момент  пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению момент
пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению момент  пары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значение
пары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значение  достигается в момент начала качения катка по плоскости.
достигается в момент начала качения катка по плоскости.
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента 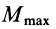 пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции
пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции 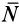 :
:

Коэффициент пропорциональности 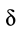 называют коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (3) следует, что
называют коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (3) следует, что 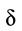 имеет размерность длины.
имеет размерность длины.
3. Коэффициент трения качения 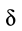 зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости. Для случая качения вагонного колеса по стальному рельсу коэффициент трения качения
зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости. Для случая качения вагонного колеса по стальному рельсу коэффициент трения качения 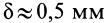 .
.
Законы трения качения, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и плоскости.
Эти законы позволяют не рассматривать деформации катка и плоскости, считая их абсолютно твердыми телами, касающимися в одной точке. В этой точке соприкосновения в среднем сечении катка кроме нормальной реакции и силы трения надо приложить еще и пару сил, препятствующую качению.
Коэффициент трения качения равен длине  , которую вычислим следующим образом. Сложим нормальную реакцию
, которую вычислим следующим образом. Сложим нормальную реакцию 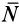 с парой сил, препятствующей качению в момент, когда
с парой сил, препятствующей качению в момент, когда 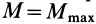 . Получим ту же силу
. Получим ту же силу 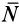 , но сдвинутую параллельно самой себе на расстояние
, но сдвинутую параллельно самой себе на расстояние
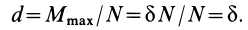
В предельном случае равновесия катка 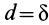 . Эту величину следует отложить в направлении, в котором активные силы стремятся катить каток (рис. 69).
. Эту величину следует отложить в направлении, в котором активные силы стремятся катить каток (рис. 69).
Для того чтобы каток не скользил, необходимо выполнение условия

Для заданных активных сил соответственно
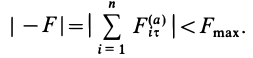
Для того чтобы каток не катился, должно выполняться условие

Для активных сил оно имеет вид
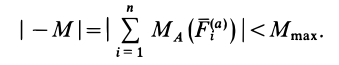
Рис. 69
Рис. 70
Для примера рассмотрим случай ведомого колеса, к которому кроме силы тяжести 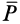 приложена еще горизонтальная активная сила
приложена еще горизонтальная активная сила 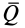 (рис. 70).
(рис. 70).
Если каток находится в равновесии, то из условий равновесия плоской системы сил, приложенных к катку, получаем
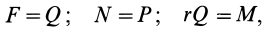
где за моментную точку взята точка  .
.
В случае отсутствия скольжения по формуле (4) с учетом условий равновесия
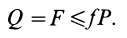
Аналогично, при отсутствии качения по формуле (5) имеем
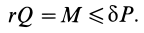
Таким образом, при отсутствии скольжения сила 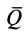 должна удовлетворять условию
должна удовлетворять условию 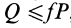 , а при отсутствии качения эта же сила
, а при отсутствии качения эта же сила 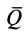 — удовлетворять другому условию:
— удовлетворять другому условию:
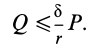
Если 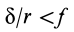 , то, пока
, то, пока 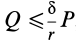 , каток находится в равновесии.
, каток находится в равновесии.
Если 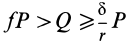 , то каток катится без скольжения (чистое качение). При
, то каток катится без скольжения (чистое качение). При 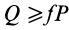 кроме качения появляется еще и скольжение. При
кроме качения появляется еще и скольжение. При 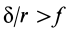 каток находится в равновесии, пока
каток находится в равновесии, пока 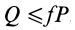 . Если
. Если 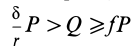 , он скользит не вращаясь (поступательное движение). При
, он скользит не вращаясь (поступательное движение). При 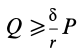 наряду со скольжением возникает качение.
наряду со скольжением возникает качение.
В том случае, если 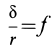 , каток находится в равновесии, пока
, каток находится в равновесии, пока 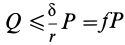 . Если же
. Если же 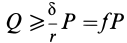 , то он катится со скольжением.
, то он катится со скольжением.
Обычно  и, следовательно, для начала качения катка требуется значительно меньшая сила
и, следовательно, для начала качения катка требуется значительно меньшая сила  , чем для начала его скольжения. Поэтому по мере увеличения силы
, чем для начала его скольжения. Поэтому по мере увеличения силы  каток сначала начинает катиться, а при дальнейшем ее росте к качению добавляется еще и скольжение.
каток сначала начинает катиться, а при дальнейшем ее росте к качению добавляется еще и скольжение.
С точки зрения затраты энергии выгодно заменять скольжение качением. Этим объясняется преимущество шариковых и роликовых подшипников по сравнению с подшипниками скольжения, если даже в них трение и не уменьшается введением смазывающего вещества.
Аналогично трению качения можно рассмотреть и явление возникновения так называемого трения верчения, т.е. случая, когда активные силы стремятся вращать тело, например в форме шара, вокруг нормали к общей касательной поверхности соприкосновения.
В этом случае возникает пара сил, препятствующая верчению, причем наибольший ее момент, возникающий в момент начала верчения, также прямо пропорционален нормальной реакции. Коэффициент пропорциональности, т. е. коэффициент трения верчения, обычно значительно меньше коэффициента трения качения.
Равновесие с учетом сил трения
Задачи, приведенные в этом параграфе, отличаются от предыдущих тем, что в них рассматривается равновесие тел, имеющих, кроме идеальных, еще и реальные связи, т. е. связи с трением.
При свободном опирании тела на поверхность идеальной связи реакция такой связи  (рис. 117, а) направлена перпендикулярно к ее поверхности, т. е. по нормали п к этой поверхности.
(рис. 117, а) направлена перпендикулярно к ее поверхности, т. е. по нормали п к этой поверхности.
Если же тело опирается на поверхность реальной связи (в отличие от идеальных связей реальные связи условимся отмечать двойной штриховкой), то ее реакция  (рис. 117,6)в зависимости от нагрузок, приложенных к телу, отклонится от нормали п к поверхности связи на некоторый угол
(рис. 117,6)в зависимости от нагрузок, приложенных к телу, отклонится от нормали п к поверхности связи на некоторый угол 
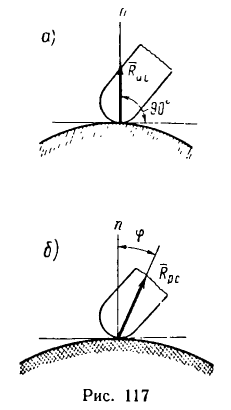
Поясним это общее положение следующим примером.
Наклонный брус (рис. 118, а), вес которого G, опирается в двух
точках А и В соответственно на вертикальную и горизонтальную поверхности идеальных связей. Этот брус не может находиться в равновесии, потому что три силы —вес бруса G и реакции 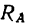 и
и  —расположены так, что не выполняется необходимое условие равновесия трех непараллельных сил; их линии действия не пересекаются в одной точке.
—расположены так, что не выполняется необходимое условие равновесия трех непараллельных сил; их линии действия не пересекаются в одной точке.
Чтобы брус, показанный на рис. 118, а, находился в равновесии, необходимо наложить еще одну связь, например, удержать брус шнуром или упереть в выступ на горизонтальной плоскости (обе возможные связи показаны пунктиром).
Теперь представим, что в точке В брус опирается не на идеально гладкую, а на шероховатую (реальную) поверхность (рис 118, б). В этом случае брус может находиться в равновесии без дополнительной связи (шнура или упорной планки). Значит три силы — вес  и реакции опор
и реакции опор 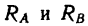 — образуют уравновешенную систему. Равновесие трех сил, действующих на брус, возможно потому, что реакция
— образуют уравновешенную систему. Равновесие трех сил, действующих на брус, возможно потому, что реакция 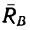 реальной связи отклоняется на некоторый угол
реальной связи отклоняется на некоторый угол 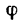 от нормали к поверхности связи и линии действия всех трех сил пересекаются в точке О.
от нормали к поверхности связи и линии действия всех трех сил пересекаются в точке О.
Если реакцию 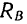 реальной связи разложим на две составляющие, направленные вдоль поверхности и перпендикулярно к ней (это разложение показано на рис. 118, а справа), то получим силу
реальной связи разложим на две составляющие, направленные вдоль поверхности и перпендикулярно к ней (это разложение показано на рис. 118, а справа), то получим силу 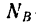 —нормальную составляющую
—нормальную составляющую 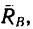 , численно равную нормальному давлению, производимому концом бруса на опору, и силу F—касательную составляющую реакции
, численно равную нормальному давлению, производимому концом бруса на опору, и силу F—касательную составляющую реакции 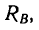 которая называется силой трения.
которая называется силой трения.
При увеличении угла а, характеризующего наклон бруса относительно горизонтальной поверхности, угол 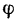 уменьшается, а вместе с ним уменьшается и сила трения, но брус сохраняет равновесие.
уменьшается, а вместе с ним уменьшается и сила трения, но брус сохраняет равновесие.
Если же уменьшать угол а, то угол ф, характеризующий отклонение реакции 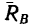 от нормали, увеличивается, а вместе с ним увеличивается и сила трения (рис. 118, в). При некотором наклоне бруса, определенном для данной пары соприкасающихся в точке В тел (например, для деревянного бруса, опирающегося о деревянный пол), брус скользит. Это означает, что сила трения, достигая предельного значения, больше увеличиваться не может. При этом реакция отклоняется также до предельного значения
от нормали, увеличивается, а вместе с ним увеличивается и сила трения (рис. 118, в). При некотором наклоне бруса, определенном для данной пары соприкасающихся в точке В тел (например, для деревянного бруса, опирающегося о деревянный пол), брус скользит. Это означает, что сила трения, достигая предельного значения, больше увеличиваться не может. При этом реакция отклоняется также до предельного значения 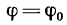 и при дальнейшем уменьшении угла а линия действия реакции
и при дальнейшем уменьшении угла а линия действия реакции  уже не попадает в точку пересечения сил G и
уже не попадает в точку пересечения сил G и 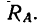
У гол 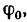 соответствующий
соответствующий 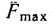 максимальному значению силы трения, называется углом трения. Числовое значение угла трения зависит от материала соприкасающихся тел и от состояния их поверхностей.
максимальному значению силы трения, называется углом трения. Числовое значение угла трения зависит от материала соприкасающихся тел и от состояния их поверхностей.
Для случая предельного равновесия между силой трения и углом трения имеем такую зависимость; 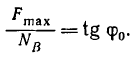
Постоянное для данной пары соприкасающихся тел значение 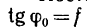 называется коэффициентом трения при покое.
называется коэффициентом трения при покое.
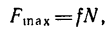
При решении задач необходимо учитывать, что сила трения направлена всегда в сторону, противоположную той, при которой точка может скользить по идеальной поверхности.
Если в число реакций связей, обеспечивающих равновесие тела, входит сила трения, то такое состояние равновесия называется самоторможением. Во всех приведенных ниже задачах рассмотрены различные случаи самоторможения (равновесия при наличии силы трения) и условия, при которых возможно самоторможение.
Задача №3
Тело А массой 8 кг поставлено на шероховатую горизонтальную поверхность стола. К телу привязана нить, перекинутая через блок Б (рис. 119, а). Какой груз Р можно подвязать к концу нити, свешивающейся с блока, чтобы не нарушить равновесия тела А? Коэффициент трения f = 0,4. Трением на блоке пренебречь.
1. Если масса тела А m = 8 кг, то его вес
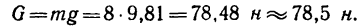
2. Пренебрегая размерами тела, будем считать, что все силы приложены к точке А.
3. Когда тело поставлено на горизонтальную поверхность, то на него действуют только две силы: вес  и противоположно направленная реакция опоры
и противоположно направленная реакция опоры  (рис. 119,6).
(рис. 119,6).
4. Если же приложить некоторую силу 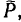 действующую вдоль горизонтальной поверхности, то реакция
действующую вдоль горизонтальной поверхности, то реакция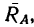 уравновешивающая силы
уравновешивающая силы 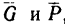 начнет отклоняться от вертикали, но тело А будет находиться в равновесии до тех пор, пока модуль силы Р не превысит максимального значения силы трения F, соответствующей предельному значению угла
начнет отклоняться от вертикали, но тело А будет находиться в равновесии до тех пор, пока модуль силы Р не превысит максимального значения силы трения F, соответствующей предельному значению угла 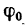 (рис. 119, в).
(рис. 119, в).
5. Разложив реакцию 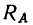 на две составляющие
на две составляющие 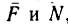 получаем систему четырех сил, приложенных к одной точке (рис. 119, г).
получаем систему четырех сил, приложенных к одной точке (рис. 119, г).
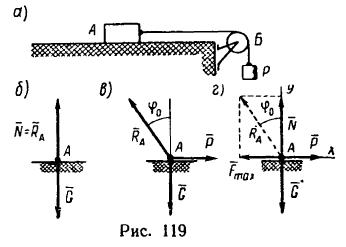
Спроектировав эту систему сил на оси хну, получим два уравнения равновесия:
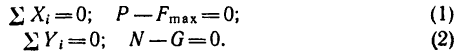
Решаем полученную систему уравнений: 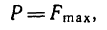
но 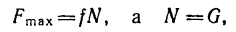
поэтому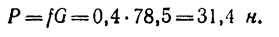
Таким образом, равновесие тела А сохраняется при условии, что к концу нити, перекинутой через блок, подвешен груз, не превышающий по весу 31,4 н.
При этом масса груза Р
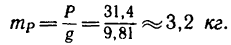
Задача №4
При каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую стену, как показано на рис. 120, а? Вес лестницы G = 120 н.
1. На лестницу действует только одна нагрузка — ее собственный вес, приложенный в точке С посредине длины лестницы АВ.
2. Вес лестницы уравновешен реакцией 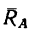 гладкой стены и реакцией шероховатого пола, которую заменим двумя составляющими:
гладкой стены и реакцией шероховатого пола, которую заменим двумя составляющими: 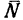 — нормальной составляющей и
— нормальной составляющей и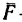 —силой трения (рис. 120,6).
—силой трения (рис. 120,6).
3. Составим три уравнения равновесия:
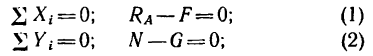
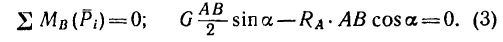
4. Из уравнений (1) и (3) 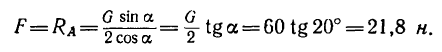
А так как N = G [из уравнения (2)[, то минимальный коэффициент трения, обеспечивающий равновесие лестницы. 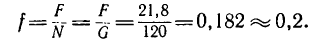
Таким образом, при  0,2 лестница находится в равновесии.
0,2 лестница находится в равновесии.
Задача №5
В месте соприкосновения пола и лестницы в предыдущей задаче коэффициент трения f= 0,4. Сможет ли человек, масса которого 70 кг, подняться по лестнице до самого верха и чтобы лестница при этом не скользила по полу?
1. К силам 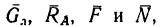 действующим на лестницу и приведенным в предыдущей задаче, необходимо добавить еще одну нагрузку —вес человека
действующим на лестницу и приведенным в предыдущей задаче, необходимо добавить еще одну нагрузку —вес человека  — и приложить его у верхнего конца лестницы (рис. 121).
— и приложить его у верхнего конца лестницы (рис. 121).
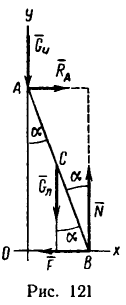
2. Вес человека 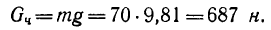
3. Человек сможет подняться до самого верха лестницы лишь в том случае, если горизонтальная составляющая реакции пола (сила 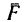 на рис. 121) будет меньше
на рис. 121) будет меньше 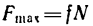 максимального значения силы трения, возможного при данном коэффициенте трения.
максимального значения силы трения, возможного при данном коэффициенте трения.
4. Составим уравнения равновесия:
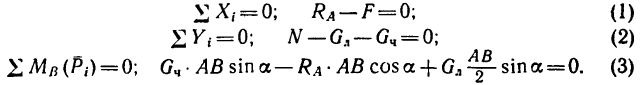
5. Из уравнения (2)
Максимальная сила трения, которая может возникнуть в данном случае
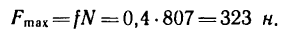
Из уравнений (1) и (3) находим силу F—горизонтальную составляющую реакции пола, которая может обеспечить равновесие лестницы с человеком, стоящим наверху:
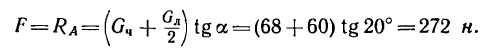
Следовательно, человек сможет подняться по лестнице до самого верха.
Задача №6
При каких значениях угла а, образуемого с гладкой вертикальной стеной, лестница, опирающаяся нижним концом о шероховатый горизонтальный пол, будет находиться в равновесии, если, кроме собственного веса, она ничем не нагружена и известно, что коэффициент трения при соприкосновении лестницы с полом f?
1. Для решения этой задачи воспользуемся рис. 120, б, так как на лестницу действуют те же четыре силы: вес лестницы  реакция гладкой стены
реакция гладкой стены 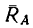 и две составляющие реакции пола —
и две составляющие реакции пола —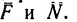
2. Лестница не выйдет из состояния равновесия (не начнет скользить) до тех пор, пока

т. е. пока горизонтальная составляющая реакции пола остается меньше максимальной силы трения, возникающей при опирании лестницы о пол в данном случае.
3. Из уравнений (1) и (3), составленных при решении задачи 90-15, найдено, что

Сопоставляем уравнения (а) и (б):
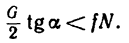
А так как в данном случае G =N, то лестница находится равновесии до тех пор, пока выполняется неравенство

или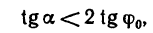
где  — угол трения.
— угол трения.
Следовательно, лестница находится в равновесии до тех пор, пока тангенс угла, образуемого лестницей с вертикальной гладкой стеной, остается меньше удвоенного коэффициента трения между лестницей и полом. Например, при f=0,4
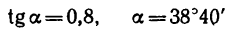
и неравенство (в) соблюдается при значениях углов
Следовательно, при f=0,4 лестница не будет скользить по полу при любом значении угла a от 0 до 38°40′.
Следующую задачу рекомендуется решить самостоятельно.
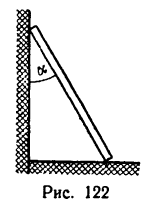
Задача №7
При каких значениях угла a однородная лестница, опирающаяся на шероховатые стену и пол (рис. 122), будет находиться в равновесии? Коэффициенты трения при опирании лестницы о стену и о пол считать одинаковыми и равными f.
Ответ. 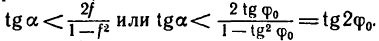
Указание. В данной задаче в системе сил, действующих на лестницу, образуется пять неизвестных: четыре реакции и угол а. Поэтому при решении задачи нужно к трем уравнениям равновесия добавить еще два уравнения, выражающих зависимость сил трения от нормального давления.
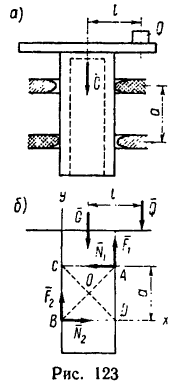
Задача №8
Цилиндр с горизонтальной площадкой наверху (рис. 123, а), находясь в двух кольцевых направляющих, скользит вниз, так как между поверхностью цилиндра и поверхностями направляющих имеется незначительный зазор. Вес цилиндра  На каком наименьшем расстоянии l от оси цилиндра необходимо поместить груз Q, чтобы цилиндр перестал скользить? Коэффициент трения f. Расстояние между направляющими кольцами а.
На каком наименьшем расстоянии l от оси цилиндра необходимо поместить груз Q, чтобы цилиндр перестал скользить? Коэффициент трения f. Расстояние между направляющими кольцами а.
1. На цилиндр в состоянии равновесия действуют две нагрузки: вес  и груз
и груз 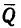 (рис. 123, б).
(рис. 123, б).
2. Груз Q, помещенный на горизонтальную площадку, прижимает цилиндр к верхнему направляющему кольцу в точке А, а к нижнему — в точке В. Благодаря зазору в точках С и D цилиндр не касается направляющих колец. В точках А и В возникают две реакции, которые заменим их составляющими 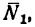
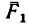 (в точке А) и
(в точке А) и 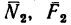 (в точке В).
(в точке В).
3. Образовалось пять неизвестных величин: 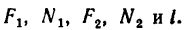
Если спроектировать все силы на ось х, то получим 



также, имея в виду равенство (1а), находим что 
Скоректировав все силы на ось у, получим четвертое уравнение: 
откуда с учетом (За)
Приняв за центр моментов точку О, лежащую на оси цилиндра и на середине расстояния а, составим пятое уравнение — уравнение моментов, в котором d- диаметр цилиндра (d = CA = BD): 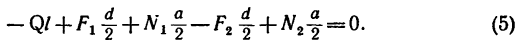
Имея в виду равенства (1а) и (За), уравнение (5) можно упростить так:

Если теперь в уравнение (2) подставить значение 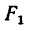 из (4а), то
из (4а), то 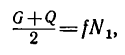
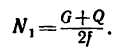
И теперь выражение (5а) принимает окончательный вид: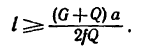
При значениях /, удовлетворяющих полученному неравенству, цилиндр не скользит вниз.
Задача №9
Тело А поставлено на негладкую пластину ВС, которую можно поворачивать около шарнира В. Коэффициент трения f между телом А и пластиной ВС известен. Определить, при каких значениях угла а (рис. 124, а) тело А будет оставаться на пластине в покое? Решение.
1. Представим, что пластина ВС наклонена к горизонту на некоторый угол а (рис. 124, б).
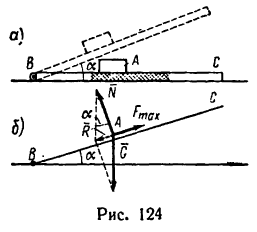
При этом положении пластины на тело А действуют три силы: его собственный вес 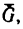 нормальная реакция
нормальная реакция 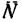 пластины и сила трения
пластины и сила трения  действующая на тело вдоль пластины и которая при некотором положении пластины ВС сможет достичь максимального значения.
действующая на тело вдоль пластины и которая при некотором положении пластины ВС сможет достичь максимального значения.
2. Тело А будет находиться в покое до тех пор, пока равнодействующая сил  направленная вдоль пластины, будет оставаться меньше
направленная вдоль пластины, будет оставаться меньше 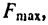 т. е. пока
т. е. пока 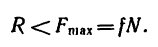
но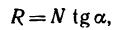
поэтому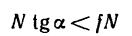
или 
Следовательно, пока тангенс угла наклона пластины к горизонту меньше коэффициента трения, тело А остается в покое.
Это положение выражает так называемое условие самоторможения тела по наклонной плоскости.
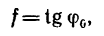
где  — угол трения, неравенство (а) можно представить в виде
— угол трения, неравенство (а) можно представить в виде 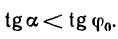
Так как углы  —острые и, следовательно, меньшему тан генсу соответствует меньший угол, последнее неравенство можно заменить равносильным неравенством
—острые и, следовательно, меньшему тан генсу соответствует меньший угол, последнее неравенство можно заменить равносильным неравенством
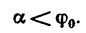
Тело А находится в покое на наклонной плоскости до тех пор, пока угол наклона плоскости меньше угла трения.
Следующую задачу рекомендуется решить самостоятельно.
Равновесие при наличии трения
Постановка Задачи. Конструкция состоит из двух шарнирно соединенных между собой тел. Одна из опор конструкции представляет собой одностороннюю связь и допускает проскальзывание с трением. Коэффициент трения, размеры конструкции и часть внешних нагрузок заданы. Найти пределы изменения одной из внешних нагрузок, действующей на конструкцию в условии равновесия.
1. Задаем направление возможного движения подвижной опоры, скользящей с трением. Прикладываем к этой опоре силу трения, направляя ее в сторону противоположную возможному движению. Предельное значение силы трения связываем с величиной нормальной реакции опоры N по формуле Кулона 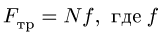 — коэффициент трения, зависящий от свойств контактирующих материалов и заданный в условии задачи.
— коэффициент трения, зависящий от свойств контактирующих материалов и заданный в условии задачи.
2. Решаем задачу о равновесии системы тел. Для этого разбиваем систему на две отдельные части, для которых составляем и решаем уравнения равновесия. Из решения определяем предельное значение нагрузки д.чя заданного направления скольжения опоры.
3. Меняем направление возможного движения системы и направление предельной силы трения. Предыдущий пункт плана выполняем заново и определяем другое предельное значение нагрузки. Два найденных значения нагрузки определяют ту область ее изменения, при которой конструкция находится в равновесии.
Задача №10
Конструкция состоит из двух частей, шарнирно соединенных в точке С (рис. 52). Опора В представляет собой одностороннюю связь и допускает проскальзывание с коэффициентом трения 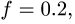 опора А — неподвижный шарнир. К конструкции приложена пара сил с моментом М = 10 кНм, сила Q = 10 кН под углом
опора А — неподвижный шарнир. К конструкции приложена пара сил с моментом М = 10 кНм, сила Q = 10 кН под углом 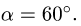
Размеры даны в метрах. Найти продолы изменения нагрузки Р, действующей под углом  на конструкцию, в условии равновесия.
на конструкцию, в условии равновесия. 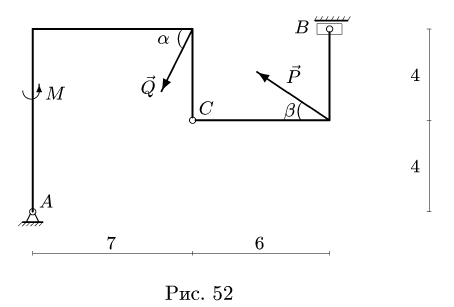
Решение
1. Задаем направление возможного движения подвижной опоры, скользящей с трением Предполагая возможное движение ползуна В влево, силу трения  направим направо (рис. 53). Предельное значение силы трения связываем с нормальной реакцией опоры N по формуле Кулона:
направим направо (рис. 53). Предельное значение силы трения связываем с нормальной реакцией опоры N по формуле Кулона:

где 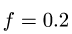 — коэффициент трения.
— коэффициент трения. 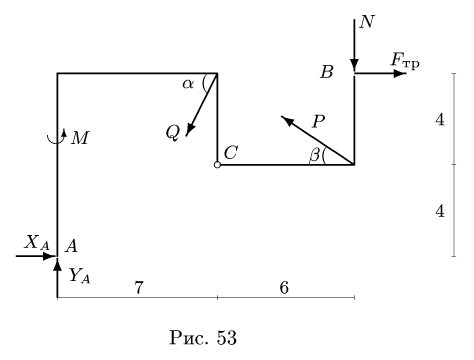
2. Решаем задачу о равновесии системы тел. Для этого систему разбиваем по шарниру С на две отдельные части — АС и СВ. Реакции шарнира С 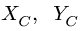 для левой и правой части направлены в противоположные стороны (рис. 54). К точке А прикладываем две составляющие реакции неподвижного шарнира
для левой и правой части направлены в противоположные стороны (рис. 54). К точке А прикладываем две составляющие реакции неподвижного шарнира 
Действие ползуна заменяем нормальной реакцией N, направленной вниз, так как ползун по условию задачи является односторонней связью, и силой трения 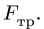 Из множества комбинаций уравнений равновесия (§ 2.4, с. 60) выберем уравнение моментов относительно точки А для всей системы в целом (рис. 53) и сумму моментов относительно С для правой части:
Из множества комбинаций уравнений равновесия (§ 2.4, с. 60) выберем уравнение моментов относительно точки А для всей системы в целом (рис. 53) и сумму моментов относительно С для правой части:
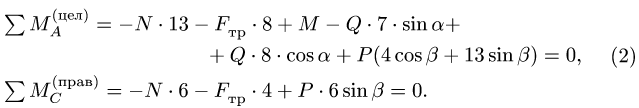
Уравнения (2) вместе с законом Кулона (1) образуют замкнутую систему трех линейных уравнений с тремя неизвестными  Решение системы имеет вид
Решение системы имеет вид
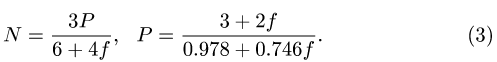
При 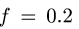 получаем
получаем 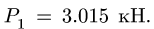 Эта нагрузка для движения влево является предельной.
Эта нагрузка для движения влево является предельной.
3. Меняем направление возможного движения системы и направление предельной силы трения. Пусть ползун В движется вправо. Силу  направим в противоположную сторону. Очевидно, знак момента силы
направим в противоположную сторону. Очевидно, знак момента силы  в уравнениях (2) изменится на противоположный, следовательно, решение для нового направления движения будет отличаться от (3) только знаком при
в уравнениях (2) изменится на противоположный, следовательно, решение для нового направления движения будет отличаться от (3) только знаком при 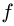 . Формально подставляя в (3)
. Формально подставляя в (3) 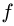 = —0.2, получим
= —0.2, получим  Значения
Значения  являются границами области равновесия.
являются границами области равновесия.
Чтобы убедиться, что равновесие соответствует значениям нагрузки между этими числами, определим Р при 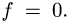 Действительно, из (3) имеем
Действительно, из (3) имеем 
Из выражения (3) для N также следует, что при 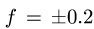 нормальная реакция N > 0, поэтому отрыв ползуна В от поверхности невозможен. Таким образом, рама находится в равновесии при
нормальная реакция N > 0, поэтому отрыв ползуна В от поверхности невозможен. Таким образом, рама находится в равновесии при
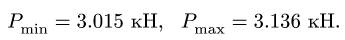
Этим нагрузкам соответствуют следующие значения нормальной реакции: 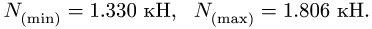
Замечание. Неравенство  не является обязательным.
не является обязательным.
Трение качения
Постановка задачи. Система состоит из двух цилиндров, соединенных стержнем. Цилиндры могут кататься без проскальзывания, один цилиндр без сопротивления, другой — с трением качения. В каких пределах меняется внешний момент, приложенный к одному из цилиндров, в условии равновесия системы?
Трение качения происходит за счет деформации цилиндра и опорной поверхности в месте контакта. В результате реакция опоры смещается в сторону возможного движения на половину длины площадки контакта и создает момент сопротивления. Плечо этого момента принимают за коэффициент трения качения. Таким образом, 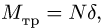 где N— реакция опоры,
где N— реакция опоры, 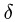 — коэффициент трения качения, имеющий размерность длины. Так в рамках теоретической механики, где изучается твердое тело, для объяснения явления трения качения вводят гипотезу деформируемости. Считают, что область деформаций
— коэффициент трения качения, имеющий размерность длины. Так в рамках теоретической механики, где изучается твердое тело, для объяснения явления трения качения вводят гипотезу деформируемости. Считают, что область деформаций
в теле мала, а глубиной продавливания цилиндра в поверхность (или величиной смятия цилиндра) пренебрегают. Коэффициент трения качения зависит не только от свойств материала цилиндра и поверхности, но и от радиуса цилиндра.
1. Задаем направление возможного движения при достижении условия предельного равновесия. К катящемуся телу (цилиндру, колесу) прикладываем момент трения качения, направляя его в сторону, противоположную возможному движению. Не забываем про силу сцепления в точке контакта, направленную вдоль плоскости.
2. Решаем задачу о равновесии системы тел. Используем метод разбиения системы на отдельные тела. Внешние и внутренние связи заменяем их реакциями. Составляем и решаем уравнения равновесия. Оси координат для уравнения проекций для цилиндрических тел выбираем вдоль нормальной реакции, а уравнение моментов составляем относительно точки касания. Из решения системы уравнений равновесия определяем условие предельного равновесия.
3. Меняем направление возможного движения системы и направление момента трения качения. Решаем задачу заново, определяем второе условие предельного равновесия.
Задача №11
Система состоит из двух цилиндров весом 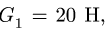 и
и 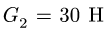 с одинаковыми радиусами R = 50 см, соединенных однородным стержнем веса
с одинаковыми радиусами R = 50 см, соединенных однородным стержнем веса 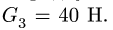 Цилиндры могут кататься без проскальзывания, цилиндр 1 — без сопротивления, а цилиндр 2 — с трением качения.
Цилиндры могут кататься без проскальзывания, цилиндр 1 — без сопротивления, а цилиндр 2 — с трением качения. 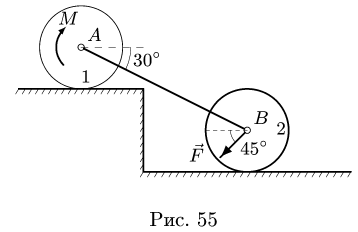
Коэффициент трения качения 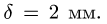 К цилиндру 1 приложена пара с моментом М. К оси цилиндра 2 приложена наклонная сила F = 10 Н (рис. 55). В каких пределах меняется момент М в условии равновесия системы?
К цилиндру 1 приложена пара с моментом М. К оси цилиндра 2 приложена наклонная сила F = 10 Н (рис. 55). В каких пределах меняется момент М в условии равновесия системы?
1. Задаем направление возможного движения при достижении условия предельного равновесия. Пусть за счет достаточно большой, по сравнению с моментом М, силы F произойдет движение системы влево. Тогда момент трения качения, приложенный к цилиндру 2, будет направлен по часовой стрелке (рис. 57). Его величину находим по формуле 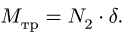
2. Решаем задачу о равновесии системы двух цилиндров и стержня. Разбиваем систему на три тела (рис. 56, 57, 58). Внешние связи заменяем реакциями 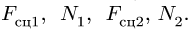
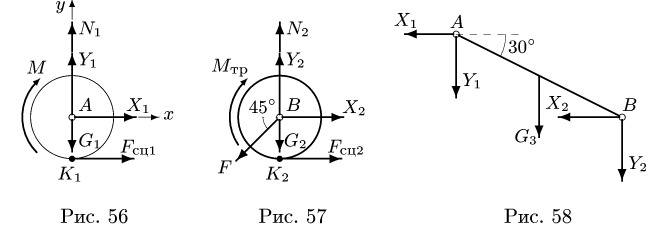
Реакции 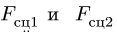 приложены к цилиндрам в точках их касания поверхностей, вызваны силами сцепления (трения) и обеспечивают вращение цилиндров. Реакции внутренних связей —
приложены к цилиндрам в точках их касания поверхностей, вызваны силами сцепления (трения) и обеспечивают вращение цилиндров. Реакции внутренних связей — 
При составлении системы семи уравнений с неизвестными 
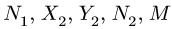 избегаем уравнения, в которые входят неизвестные реакции
избегаем уравнения, в которые входят неизвестные реакции 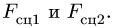
Составляем уравнения равновесия для цилиндра 1 (рис. 56):
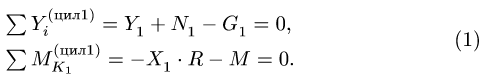
Уравнения равновесия цилиндра 2 (рис. 57) имеют вид
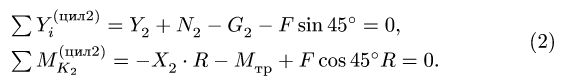
Уравнения равновесия стержня АВ (рис. 58) имеют вид
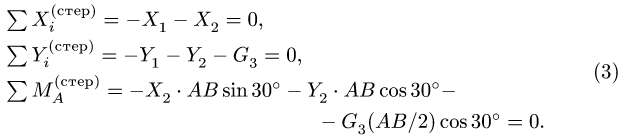
Из решения системы уравнений (1-3) определяем
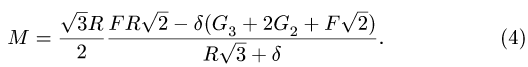
Радиус и коэффициент трения качения переводим в метры R = 0.5 м,  Получаем М — 3.414 Нм. Вычисляем нормальные реакции опор:
Получаем М — 3.414 Нм. Вычисляем нормальные реакции опор:
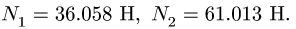
Убеждаемся, что 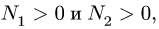 что соответствует наличию опоры. Если реакция опоры равна нулю, то это означает отрыв тела от поверхности, отрицательной реакции опоры
что соответствует наличию опоры. Если реакция опоры равна нулю, то это означает отрыв тела от поверхности, отрицательной реакции опоры  в задаче с односторонней связью не существует (физически не реализуется).
в задаче с односторонней связью не существует (физически не реализуется).
3. Меняем направление возможного движения системы. Пусть за счет действия момента М произойдет движение системы вправо. Момент трения качения направим против часовой стрелки (рис. 59). Составляя уравнения равновесия для новой системы сил, заметим, что отличие от прежней системы проявляется только в знаке 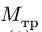 во втором уравнении равновесия (2). Так как
во втором уравнении равновесия (2). Так как 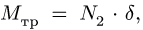 то новое решение для М будет формально отличаться от (4) только знаком у коэффициента трения
то новое решение для М будет формально отличаться от (4) только знаком у коэффициента трения 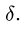 Поэтому, не решая (и даже не составляя) системы уравнений равновесия типа (1-3) для нового направления возможного движения, записываем ответ, изменяя знаки у
Поэтому, не решая (и даже не составляя) системы уравнений равновесия типа (1-3) для нового направления возможного движения, записываем ответ, изменяя знаки у 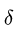 в (4):
в (4):
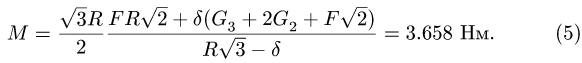
Точно так же находим нормальные реакции опор: 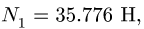
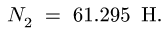 При равновесии системы момент, приложенный к
При равновесии системы момент, приложенный к
цилиндру 1, изменяется в пределах (в Нм) 
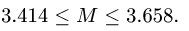
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Пространственная система сил
- Центр тяжести
- Кинематика точки
- Плоское движение твердого тела
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Сила трения
теория по физике 🧲 динамика
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как F тр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: F тр↑↓ v .

Сила трения скольжения определяется формулой:
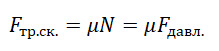
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
Способы определения вида силы трения, возникающей между телами, и ее модуля:
-
Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
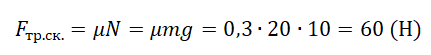
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Описание движения тел с учетом сил трения
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх)

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз)

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Внимание! В случаях, когда сила тяги F т направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?  Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Проекция сил на ось ОУ выглядит так:
Отсюда силы реакции опоры равна:
Подставим ее в формулу для вычисления силы трения и получим:
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Тело поднимается под действием силы тяги, направленной под углом к вертикали

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя. Проекция на ось ОХ:
Отсюда следует, что сила должна быть равна силе реакции опоры. Проекция на ось ОУ:
Перепишем, выразив силу трения через силу реакции опоры:
Отсюда выразим силу реакции опоры: 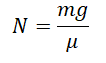 Следовательно:
Следовательно: 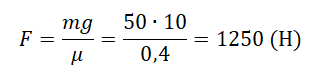
Движение тела по наклонной плоскости
Движение вниз без трения

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Тело покоится на наклонной плоскости

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Тело удерживают на наклонной плоскости

Второй закон Ньютона в векторной форме:
m g + N + F + F тр = m a
Проекция на ось ОХ:
Проекция на ось ОУ:
Равноускоренное движение вверх с учетом силы трения

Второй закон Ньютона в векторной форме:
Проекция на ось ОХ:
Проекция на ось ОУ:
Равномерное движение вверх с учетом силы трения

Второй закон Ньютона в векторной форме:
m g + N + F + F тр = m a
Проекция на ось ОХ:
Проекция на ось ОУ:
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.  Переведем массу в килограммы: 200 г = 0,2 кг. Проекция сил, действующих на тело, на ось ОХ:
Переведем массу в килограммы: 200 г = 0,2 кг. Проекция сил, действующих на тело, на ось ОХ:
Отсюда сила трения равна:
Подставляем известные данные и вычисляем:
Полезная информация 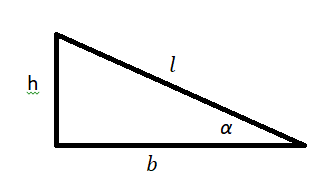
При исследовании зависимости силы трения скольжения F тр от силы нормального давления F д были получены следующие данные:
[spoiler title=”источники:”]
http://www.evkova.org/trenie-v-teoreticheskoj-mehanike
[/spoiler]
Задачи на Движение
под действием силы трения
Тренировочные задания для подготовки к контрольным,
самостоятельным и диагностическим работам по теме
«ЗАДАЧИ на Движение под действием силы трения» + Решения
Модуль силы трения скольжения можно определить по формуле: Fтр = µN, где µ — коэффициент трения, N— модуль силы нормального давления (и силы реакции опоры). Максимальная сила трения покоя: (Fтр)мах = µN. При одинаковых условиях сила трения скольжения намного больше силы трения качения. Вектор силы трения скольжения всегда направлен противоположно вектору скорости тела. Коэффициент трения можно определить по формуле: µ = Fтр/N. Это величина безразмерная.
Если на тело действует только сила трения, то такое тело движется равнозамедленно до остановки. Расстояние, которое тело проходит до остановки, называют тормозным путем. Обозначают буквой l. Время торможения — время, нужное для остановки.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Автомобиль массой 5 т движется с постоянной скоростью по прямой горизонтальной дороге. Коэффициент трения шин о дорогу равен 0,03. Определите силу тяги, развиваемую двигателем.
ОТВЕТ: Fтяги = 1470 Н.
РЕШЕНИЕ:
Задача № 2.
Сани со стальными полозьями перемещают равномерно по льду, прилагая горизонтальное усилие 2 Н. Каков вес саней?
ОТВЕТ: Вес саней 100 Н.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 3.
Деревянный брусок массой 3 кг тянут по горизонтальной деревянной доске с помощью пружины. Коэффициент трения равен 0,3. Найти удлинение пружины, если ее жесткость 10 кН/м.
ОТВЕТ: Удлинение пружины 0,09 см.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 4.
Велосипедист, ехавший со скоростью 36 км/ч, увидел примерно в 10 м от себя препятствие и резко затормозил. Успеет ли велосипедист остановиться до препятствия?
ОТВЕТ: Велосипедист успеет остановиться до препятствия, так как S = 10 м (расстояние до препятствия), а тормозной путь велосипедиста ≈ 7 м. Если скорость движения возрастет вдвое, то тормозной путь увеличится в 4 раза.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 5.
Автомобиль движется со скоростью 10 м/с по гладкой горизонтальной дороге. Пройдя с выключенным мотором расстояние 150 м, автомобиль останавливается. Сколько времени автомобиль двигался с выключенным мотором и каков коэффициент трения при его движении?
ОТВЕТ: t = 30 с; µ = 0,033.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

ЗАДАЧИ на Движение под действием силы трения
Задача № 6.
Лыжник массой 60 кг, имеющий в конце спуска скорость 10 м/с, останавливается через 40 с после окончания спуска. Определить величину силы сопротивления.
ОТВЕТ: Fтp = 15 Н.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 7.
Тело скользит равномерно по наклонной плоскости с углом наклона 30°. Определите коэффициент трения тела о плоскость.
ОТВЕТ: µ ≈ 0,58.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 8.
С какой наибольшей скоростью может ехать мотоциклист по горизонтальной плоскости, описывая дугу радиусом 80 м, если коэффициент трения резины о почву 0,4? На какой угол от вертикального положения он при этом отклоняется?
ОТВЕТ: vмах = 17,7 м/с = 64 км/ч — наибольшая скорость движения; a ≈ 22°.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 9.
Шофер грузовика, едущего со скоростью 72 км/ч, заметил на дороге знак. Сможет ли он, не сбавляя скорости, проехать поворот, если его радиус равен 25 м? Считать коэффициент трения шин о дорогу 0,4.
ОТВЕТ: Шофер должен уменьшить скорость движения, так как радиус окружности, которую опишет грузовик при данной скорости, 100 м, а радиус поворота — 25 м. В противном случае грузовик занесет на обочину дороги.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Дополнительный материал для решения задач



Конспект урока по физике «ЗАДАЧИ на Движение под действием силы трения с решениями». Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам. Выберите дальнейшее действие:
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике