Как найти путь в паскале

Вопрос очень сильно зависит от того, как вы представляете граф.

Например, можно возвести матрицу переходов в квадрат. То есть из матрицы переходов город->город за 1 шаг построить матрицу переходов да 1 и 2 шага. Потом возвести её в квадрат ещё раз, получится матрица переходов за 1…4 шаг. Так будет сделано за log(n) действий и мы увидим перечни городов в которые мы можем попасть из каждого города.

Но у вас задача проще – понять, что такое поиск в глубину. Никогда не копируйте в свои программы чужие алгоритмы на графах, которые вам не понятны.

Если на пальцах, то поиск в глубину – это попытки достичь определённой вершины, имея список уже посещенных вершин. В уже посещенные вершины возвращаться нельзя.
Как бы вы действовали в жизни?
Я бы написал списочек, куда пойти можно. Он может быть:
1. пуст – зашли в тупик, но так и не нашли, путь неправильный, надо вернуться (остановка ветви поиска)
2. в списке оказалась искомая вершина. Мы имеем путь к текущей, текущую и искомую – решение найдено.
3. в нем есть какие-то вершины – идём дальше. Надо добавить себя к списку посещенных вершин и с обновленным списком посещенных перебрать все вершины из доступных к переходу, повторяя алгоритм для каждой из них.

Если конкретный путь не важен, можно поступить интереснее:
Иметь вектор признаков (нет_пути | есть_путь | в_процессе), в который можно попасть из вершины 1. Изначально его заполнить исходящими из 1 с признаком в_процессе, остальные – нет_пути.
Если в этом векторе есть вершина X с признаком в_процессе, то нужно добавить в вектор все исходящие из неё вершины. Добавление обновляет признак нет_пути, заменяя его на в_процессе, признаки есть_путь и в_процессе не изменяются. После этого вершина X меняет признак с в_процессе на есть_путь. Повторять алгоритм пока в векторе либо не останется вершин в_процессе (это будет, когда в вершину n нет пути из 1), либо появится вершина n с признаком отличным от нет_пути.

Алгоритм голландского ученого Эдсгера Дейкстры находит все кратчайшие пути из одной изначально заданной вершины графа до всех остальных. С его помощью, при наличии всей необходимой информации, можно, например, узнать какую последовательность дорог лучше использовать, чтобы добраться из одного города до каждого из многих других, или в какие страны выгодней экспортировать нефть и тому подобное.

Минусом данного метода является невозможность обработки графов, в которых имеются ребра с отрицательным весом, т. е. если, например, некоторая система предусматривает убыточные для Вашей фирмы маршруты, то для работы с ней следует воспользоваться отличным от алгоритма Дейкстры методом.

Для программной реализации алгоритма понадобиться два массива: логический visited – для хранения информации о посещенных вершинах и численный distance, в который будут заноситься найденные кратчайшие пути. Итак, имеется граф G=(V, E). Каждая из вершин входящих во множество V, изначально отмечена как не посещенная, т. е. элементам массива visited присвоено значение false.

Поскольку самые выгодные пути только предстоит найти, в каждый элемент вектора distance записывается такое число, которое заведомо больше любого потенциального пути (обычно это число называют бесконечностью, но в программе используют, например максимальное значение конкретного типа данных). В качестве исходного пункта выбирается вершина s и ей приписывается нулевой путь: distance[s]=0, т. к. нет ребра из s в s (метод не предусматривает петель).

Далее, находятся все соседние вершины (в которые есть ребро из s) [пусть таковыми будут t и u] и поочередно исследуются, а именно вычисляется стоимость маршрута из s поочередно в каждую из них:

• distance[t]=distance[s]+весинцидентного s и t ребра;
• distance[u]=distance[s]+ весинцидентного s и u ребра.

Но вполне вероятно, что в ту или иную вершину из s существует несколько путей, поэтому цену пути в такую вершину в массиве distance придется пересматривать, тогда наибольшее (неоптимальное) значение игнорируется, а наименьшее ставиться в соответствие вершине.

После обработки смежных с s вершин она помечается как посещенная: visited[s]=true, и активной становится та вершина, путь из s в которую минимален. Допустим, путь из s в u короче, чем из s в t, следовательно, вершина u становиться активной и выше описанным образом исследуются ее соседи, за исключением вершины s. Далее, u помечается как пройденная: visited[u]=true, активной становится вершина t, и вся процедура повторяется для нее. Алгоритм Дейкстры продолжается до тех пор, пока все доступные из s вершины не будут исследованы.

Теперь на конкретном графе проследим работу алгоритма, найдем все кратчайшие пути между истоковой и всеми остальными вершинами. Размер (количество ребер) изображенного ниже графа равен 7 (|E|=7), а порядок (количество вершин) – 6 (|V|=6). Это взвешенный граф, каждому из его ребер поставлено в соответствие некоторое числовое значение, поэтому ценность маршрута необязательно определяется числом ребер, лежащих между парой вершин.

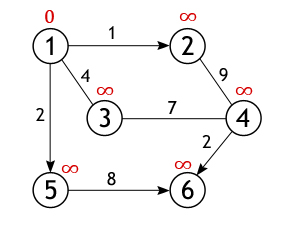
Из всех вершин входящих во множество V выберем одну, ту, от которой необходимо найти кратчайшие пути до остальных доступных вершин. Пусть таковой будет вершина 1. Длина пути до всех вершин, кроме первой, изначально равна бесконечности, а до нее – 0, т. к. граф не имеет петель.

У вершины 1 ровно 3 соседа (вершины 2, 3, 5), и чтобы вычислить длину пути до них нужно сложить вес дуг, лежащих между вершинами: 1 и 2, 1 и 3, 1 и 5 со значением первой вершины (с нулем):

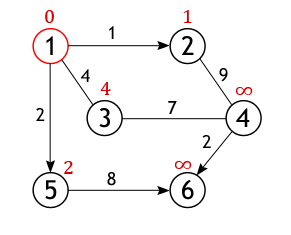
Как уже отмечалось, получившиеся значения присваиваются вершинам, лишь в том случае если они «лучше» (меньше) тех которые значатся на настоящий момент. А так как каждое из трех чисел меньше бесконечности, они становятся новыми величинами, определяющими длину пути из вершины 1 до вершин 2, 3 и 5.

Далее, активная вершина помечается как посещенная, статус «активной» (красный круг) переходит к одной из ее соседок, а именно к вершине 2, поскольку она ближайшая к ранее активной вершине.

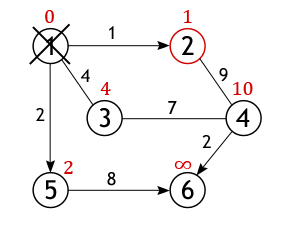
У вершины 2 всего один не рассмотренный сосед (вершина 1 помечена как посещенная), расстояние до которого из нее равно 9, но нам необходимо вычислить длину пути из истоковой вершины, для чего нужно сложить величину приписанную вершине 2 с весом дуги из нее в вершину 4

Условие «краткости» (10<∞) выполняется, следовательно, вершина 4 получает новое значение длины пути.

Вершина 2 перестает быть активной, также как и вершина 1 удаляется из списка не посещённых. Теперь тем же способом исследуются соседи вершины 5, и вычисляется расстояние до них.

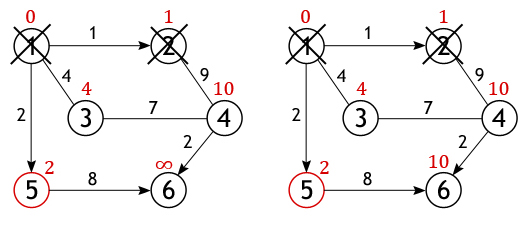
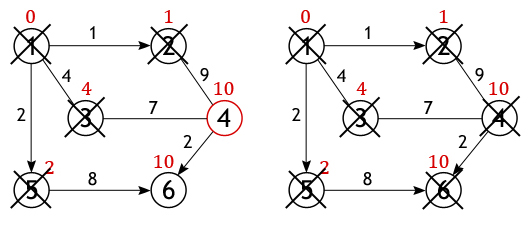
Когда дело доходит до осмотра соседей вершины 3, то тут важно не ошибиться, т. к. вершина 4 уже была исследована и расстояние одного из возможных путей из истока до нее вычислено. Если двигаться в нее через вершину 3, то путь составит 4+7=11, а 11>10, поэтому новое значение игнорируется, старое остается.

Аналогичная ситуация с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно получается только в том случае, если идти через вершину 5.

Когда все вершины графа, либо все те, что доступны из истока, будут помечены как посещенные, тогда работа алгоритма Дейкстры завершится, и все найденные пути будут кратчайшими. Так, например, будет выглядеть список самых оптимальных расстояний лежащих между вершиной 1 и всеми остальными вершинами, рассматриваемого графа:

В программе, находящей ближайшие пути между вершинами посредством метода Дейкстры, граф будет представлен в виде не бинарной матрицы смежности. Вместо единиц в ней будут выставлены веса ребер, функция нулей останется прежней: показывать, между какими вершинами нет ребер или же они есть, но отрицательно направленны.

Код программы на C++:

#include "stdafx.h"
#include <iostream>
using namespace std;
const int V=6;
//алгоритм Дейкстры
void Dijkstra(int GR[V][V], int st)
{
int distance[V], count, index, i, u, m=st+1;
bool visited[V];
for (i=0; i<V; i++)
{
distance[i]=INT_MAX; visited[i]=false;
}
distance[st]=0;
for (count=0; count<V-1; count++)
{
int min=INT_MAX;
for (i=0; i<V; i++)
if (!visited[i] && distance[i]<=min)
{
min=distance[i]; index=i;
}
u=index;
visited[u]=true;
for (i=0; i<V; i++)
if (!visited[i] && GR[u][i] && distance[u]!=INT_MAX &&
distance[u]+GR[u][i]<distance[i])
distance[i]=distance[u]+GR[u][i];
}
cout<<"Стоимость пути из начальной вершины до остальных:tn";
for (i=0; i<V; i++) if (distance[i]!=INT_MAX)
cout<<m<<" > "<<i+1<<" = "<<distance[i]<<endl;
else cout<<m<<" > "<<i+1<<" = "<<"маршрут недоступен"<<endl;
}
//главная функция
void main()
{
setlocale(LC_ALL, "Rus");
int start, GR[V][V]={
{0, 1, 4, 0, 2, 0},
{0, 0, 0, 9, 0, 0},
{4, 0, 0, 7, 0, 0},
{0, 9, 7, 0, 0, 2},
{0, 0, 0, 0, 0, 8},
{0, 0, 0, 0, 0, 0}};
cout<<"Начальная вершина >> "; cin>>start;
Dijkstra(GR, start-1);
system("pause>>void");
}

Код программы на Pascal:

program DijkstraAlgorithm;
uses crt;
const V=6; inf=100000;
type vektor=array[1..V] of integer;
var start: integer;
const GR: array[1..V, 1..V] of integer=(
(0, 1, 4, 0, 2, 0),
(0, 0, 0, 9, 0, 0),
(4, 0, 0, 7, 0, 0),
(0, 9, 7, 0, 0, 2),
(0, 0, 0, 0, 0, 8),
(0, 0, 0, 0, 0, 0));
{алгоритм Дейкстры}
procedure Dijkstra(GR: array[1..V, 1..V] of integer; st: integer);
var count, index, i, u, m, min: integer;
distance: vektor;
visited: array[1..V] of boolean;
begin
m:=st;
for i:=1 to V do
begin
distance[i]:=inf; visited[i]:=false;
end;
distance[st]:=0;
for count:=1 to V-1 do
begin
min:=inf;
for i:=1 to V do
if (not visited[i]) and (distance[i]<=min) then
begin
min:=distance[i]; index:=i;
end;
u:=index;
visited[u]:=true;
for i:=1 to V do
if (not visited[i]) and (GR[u, i]<>0) and (distance[u]<>inf) and
(distance[u]+GR[u, i]<distance[i]) then
distance[i]:=distance[u]+GR[u, i];
end;
write('Стоимость пути из начальной вершины до остальных:'); writeln;
for i:=1 to V do
if distance[i]<>inf then
writeln(m,' > ', i,' = ', distance[i])
else writeln(m,' > ', i,' = ', 'маршрут недоступен');
end;
{основной блок программы}
begin
clrscr;
write('Начальная вершина >> '); read(start);
Dijkstra(GR, start);
end.

{
V - множество вершин графа (vertex)
E - множество рёбер графа
w[i,j] - вес (длина) ребра ij
a - вершина, расстояния от которой ищутся
U - множество посещённых вершин (used)
d[u] - по окончании работы алгоритма равно
       длине кратчайшего пути из a до вершины u (distance)
p[u] - по окончании работы алгоритма содержит кратчайший путь из a в u
       (предшествующий u элемент, previous)
}
program Dijkstra;
 
const
  INFINITY  = MaxInt;
  UNDEFINED = -1;
 
const
  Nmax = 6;
type
  TMatrix = array[0..Nmax - 1, 0..Nmax - 1] of integer;
  TVertexList = array[0..Nmax - 1] of integer;
  TDistance = array[0..Nmax - 1] of integer;
  TUsed = array[0..Nmax - 1] of boolean;
 
  function MinOf(const a: TDistance; const m: TUsed): integer;
  var
    i: integer;
    Imin: integer;
    Min: integer;
  begin
    i := low(a);
    while i <= high(a) do
    begin
      if not m[i] then
      begin
        Imin := i;
        Min  := a[i];
        break;
      end;
      inc(i);
    end;
    for i := Imin + 1 to high(a) do
      if (Min > a[i]) and not m[i] then
      begin
        Imin := i;
        Min  := a[i];
      end;
    MinOf := Imin;
  end;
 
  procedure DijkstrasAlgorithm(const W: TMatrix; a: integer;
  var D: TDistance; var P: TVertexList);
  var
    v: integer;
    U: TUsed;
    i, j: integer;
  begin
    {initialization    
      d[a]:=0; p[a]:=0;
      d[v]:=INFINITY; p[v]:=UNDEFINED; для всех вершин отличных от a
    }
    for v := low(D) to high(D) do
    begin
      if v = a then
      begin
        D[v] := 0;
        P[v] := UNDEFINED;
      end
      else
      begin
        D[v] := INFINITY;
        P[v] := UNDEFINED;
      end;
      U[v] := False;
    end;
    {основной цикл}
    for i := low(D) to high(D) do {пока есть нерассмотренные вершины}
    begin
      v := MinOf(D, U); {берём непосещённую вершину с минимальным d[v]}
      U[v] := True;     {отмечаем её как посещённую}
      for j := low(D) to high(D) do
        if W[v, j] <> INFINITY then
          if D[j] > D[v] + W[v, j] then
          begin
            D[j] := D[v] + W[v, j];
            P[j] := v;
          end;
    end;
  end;
 
  procedure ShowPath(A, B: integer; const P: TVertexList; const D: TDistance);
  var
    Q: TVertexList;
    Len: integer;
    v: integer;
  begin
    Len := 0;
    if D[B] = INFINITY then
      writeln('There is not exist path from ', A, ' to ', B, '.')
    else
    begin
      v := B;
      repeat
        Q[Len] := v;
        Inc(Len);
        v := P[v];
      until v=UNDEFINED;
      write('A path from ', A, ' to ', B, ' is <');
      for v := Len - 1 downto 0 do
        Write(Q[v]: 4);
      writeln('>.');
    end;
  end;
 
var
  W: TMatrix =
  (
    (00, 07, 09, 00, 00, 14),
    (07, 00, 10, 15, 00, 00),
    (09, 10, 00, 11, 00, 02),
    (00, 15, 11, 00, 06, 00),
    (00, 00, 00, 06, 00, 09),
    (14, 00, 02, 00, 09, 00)
  );
var
  i, j: integer;
  P: TVertexList;
  D: TDistance;
  A, B: integer;
begin
  {для упрощения ввода вместо INFINITY в матрице весов W я использовал нули
   Поэтому нужно удалить нули из матрицы весов, заменив их на бесконечность}
  for i := 0 to Nmax - 1 do
    for j := 0 to Nmax - 1 do
      if (i <> j) and (W[i, j] = 0) then
        W[i, j] := INFINITY;
  {Ввод начальной и конечной точек маршрута}
  A := 0;
  B := 4;
  {Обработка графа по алгоритму Дейкстры}
  DijkstrasAlgorithm(W, A, D, P);
  {контрольный вывод значений результирующих массивов}
  write('Distance: ');
  for i := low(D) to high(D) do
    Write(D[i]: 4);
  writeln;
  write('Previous: ');
  for i := low(P) to high(P) do
    Write(P[i]: 4);
  writeln;
  {вывод вершин по кратчайшему пути из A в B}
  ShowPath(A, B, P, D);
end.

Задача коммивояжера (ЗК) является одной из знаменитых задач теории комбинаторики. Она была поставлена в 1934 году, и её, как Великую теорему Ферма пытались решить многие математики. В своей области (оптимизации дискретных задач) ЗК служит своеобразным полигоном, на котором испытываются всё новые методы.

Приведем классическую постановку задачи.Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по разу в неизвестном порядке города 2,3, … ,n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?

Чтобы привести задачу к математическому виду, введём некоторые термины. Итак, города перенумерованы числами jТ=(1,2,3..n). Тур коммивояжера может быть описан циклической перестановкой t=(j₁,j₂,..,jn,j₁), причём все j₁..jn – разные номера; повторяющийся в начале и в конце j₁,показывает, что перестановка зациклена. Расстояния между парами вершин С_ijобразуют матрицу С. Задача состоит в том, чтобы найти такой тур t, чтобы минимизировать функционал

(1)

Относительно математизированной формулировки ЗК необходимо сделать два замечания.

Во-первых, в постановке С_ijозначали расстояния, поэтому они должны быть неотрицательными, т.е. для всех jТ:

С_ij0; C_jj=∞ (2)

(последнее равенство означает запрет на петли в туре),

симметричными, т.е. для всех i,j:

С_ij= С_ji , (3)

и удовлетворять неравенству треугольника, т.е. для всех:

С_ij+ С_jkC_ik . (4)

В математической постановке говорится о произвольной матрице. Сделано это потому, что имеется много прикладных задач, которые описываются основной моделью, но всем условиям (2)-(4) не удовлетворяют. Особенно часто нарушается условие (3) (например, если С_ij – не расстояние, а плата за проезд: часто туда билет стоит одну цену, а обратно – другую). Поэтому различают два варианта ЗК: симметричную задачу, когда условие (3) выполнено, и несимметричную – в противном случае.

Второе замечание касается числа всех возможных туров. В несимметричной ЗК все туры t=(j1,j2,..,jn,j1) и t’=(j1,jn,..,j2,j1) имеют разную длину и должны учитываться оба. Разных туров очевидно (n-1)!.

Зафиксируем на первом и последнем месте в циклической перестановке номер j1, а оставшиеся n-1 номеров переставим всеми (n-1)! возможными способами. В результате получим все несимметричные туры. Симметричных туров имеется в два раз меньше, т.к. каждый засчитан два раза: как t и как t’.

Можно представить, что С состоит только из единиц и нулей. Тогда С можно интерпретировать, как граф, где ребро (i,j) проведено, если Сij=0 и не проведено, если Сij=1. Тогда, если существует тур длины 0, то он пройдёт по циклу, который включает все вершины по одному разу. Такой цикл называется гамильтоновым циклом. Незамкнутый гамильтонов цикл называется гамильтоновой цепью (гамильтоновым путём).

В терминах теории графов симметричную ЗК можно сформулировать так:

Дана полная сеть с n вершинами, длина ребра (i,j)= Сij. Найти гамильтонов цикл минимальной длины.

В несимметричной ЗК вместо “цикл” надо говорить “контур”, а вместо “ребра” ‒ “дуги” или “стрелки”.

Некоторые прикладные задачи формулируются как ЗК, но в них нужно минимизировать длину не гамильтонова цикла, а гамильтоновой цепи. Такие задачи называются незамкнутыми. Некоторые модели сводятся к задаче о нескольких коммивояжерах, но их решать более сложно.

Следующий алгоритм, после алгоритма прямого перебора, ”жадный” алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. “Жадным” этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.

Рис. 1. ‒ Сеть, представляющую узкий ромб, и найденный “жадным” алгоритмом тур

Посмотрим, как поведет себя при решении ЗК жадный алгоритм. Здесь он превратится в стратегию “иди в ближайший (в который еще не входил) город”. Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть на рис. 1, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм “иди вы ближайший город” выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.

В пользу процедуры “иди в ближайший” можно сказать лишь то, что при старте из одного города она не уступит стратегии “иди в дальнейший”.

К идее метода ветвей и границ приходили многие исследователи, но Литтл с соавторами на основе указанного метода разработали удачный алгоритм решения ЗК и тем самым способствовали популяризации подхода. С тех пор метод ветвей и границ был успешно применен ко многим задачам, для решения ЗК было придумано несколько других модификаций метода.

Общая идея метода: нужно разделить огромное число перебираемых вариантов на классы и получить оценки (снизу – в задаче минимизации, сверху – в задаче максимизации) для этих классов, чтобы иметь возможность отбрасывать варианты не по одному, а целыми классами. Трудность состоит в том, чтобы найти такое разделение на классы (ветви) и такие оценки (границы), чтобы процедура была эффективной.

Из рассмотренных методов программно реализуем метод перебора, так как ”жадный” алгоритм, как показано выше, часто приводит к неверному ответу, а метод ветвей и границ достаточно сложен для программирования.

Нахождение кратчайшего пути методом перебора. Классическим примером переборной задачи и служит задача коммивояжера. Пусть дано множество из N городов, расстояния между которыми известны. В каком порядке должен посетить их коммивояжер, заезжая в каждый город лишь один раз, чтобы общий пройденный путь был кратчайшим?

Опишем решение задачи методом перебора или “brute-force enumeration” ‒ “перебор животной силой”, как его называют в англоязычной литературе. Понятно, что полный перебор практически применим только в задачах малого размера. Напомним, что ЗК с N городами требует при полном переборе рассмотрения (N-1)!/2 туров в симметричной задаче и (N-1)! туров в несимметричной, а факториал, как показано в следующей таблице, растет удручающе быстро (табл. 1), однако быстродействие современных ПК позволяет справиться с этой задачей.

Таблица 1

Чтобы проводить полный перебор в ЗК, нужно научиться (разумеется, без повторений) генерировать все перестановки заданного числа m элементов.

Предполагаемыми решениями здесь являются перестановки из N городов. Из них нужно выбрать ту, которая даст наименьшую суммарную длину маршрута.

Первое, что нужно сделать, решая задачу коммивояжера, это организовать генерацию перестановок. Занумеруем города числами от 1 до N. Все перестановки можно получить, выбирая из множества [2..N] один элемент всевозможными способами и присоединяя к нему поочередно перестановки и из оставшихся элементов. Это рекурсивный алгоритм, т.к. для построения перестановок из N элементов он нуждается в перестановках из N-1 элемента. Первый элемент в сгенерированной перестановке всегда 1, т.к. мы предполагаем, что автотранспортное предприятие расположено в нем и отсюда начинается маршрут. Последний элемент в перестановке также 1, потому что маршрут считается замкнутым – транспорт возвращается в город с номером 1. Добавим, что единственная перестановка из одного элемента – это сам элемент.

Реализуем алгоритм в среде Паскаль-ABC. Запрограммируем получение перестановок в виде рекурсивной процедуры.

Расчет проведен для следующей симметричной матрицы С_6х6 расстояний между городами.

Таблица 2

Множество переставляемых элементов сделаем параметром процедуры. Другим параметром будет позиция перестановки, которая заполняется данным вызовом процедуры. Все перестановки будем поочередно строить во внешнем массиве из N целых чисел, за исключением числа 1.

Процедура Comm строит перестановки в массиве А. Перестановка готова, когда S=[]. Процедура дополнена подсчетом длины пути, заданного перестановкой, и выбором самого короткого из них. Для хранения кратчайшего из построенных маршрутов и его длины воспользуемся внешними переменными Аmin и Lmin. Расстояния между городами записаны в двумерном массиве Dist. Листинг программы приведен на рис. 2.

Рис. 2. ‒ Листинг в среде Паскаль-ABC программы нахождения замкнутого маршрута

с минимальной длиной пути

В результате решения по данной программе получен оптимальный замкнутый маршрут (рис. 3) движения коммивояжера: 1→2→6→5→4→3→1, длина пути которого составляет 6+10+7+5+4+4=36 условных единиц.

Рис. 3. ‒ Результаты решения задачи коммивояжера

Оптимальный замкнутый маршрут с минимальной длиной пути можно изобразить в виде следующего графа (рис. 4).

Рис. 4. ‒ Оптимальный замкнутый маршрут с минимальной длиной пути

По подобному алгоритму может быть получен разомкнутый маршрут движения с минимальной длиной пути с заданными начальным и конечным пунктами назначения. Кроме этого под элементами матрицы С понимаются любые затраты (финансовые, временные и т.п.), сумму которых при движении по маршруту необходимо минимизировать.