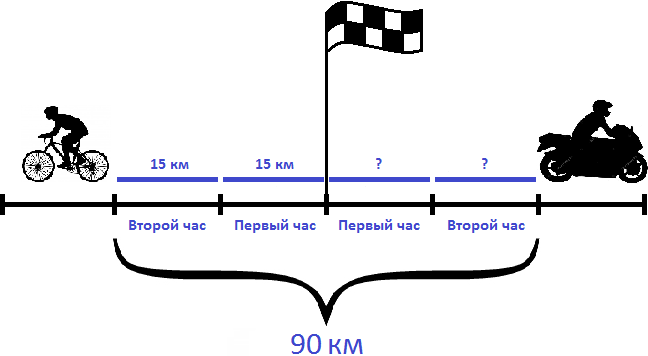
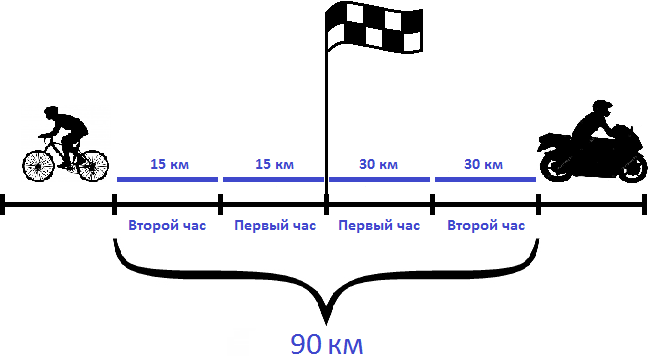
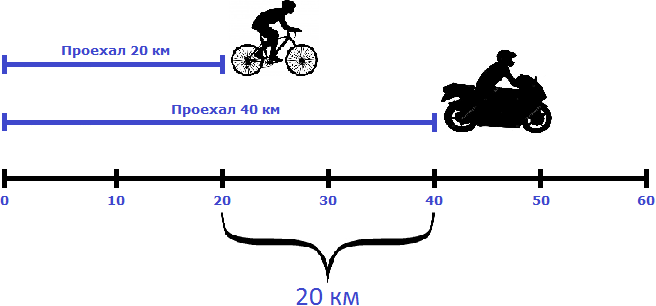
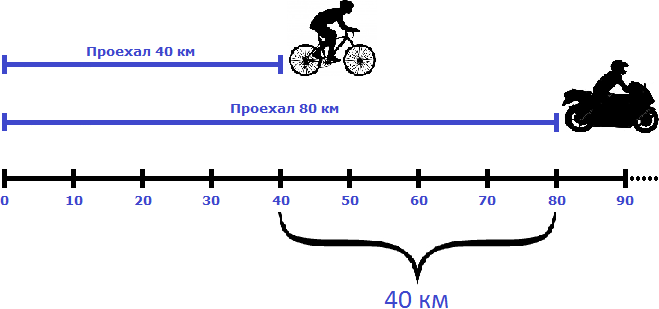
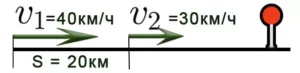
Продолжаем изучать элементарные задачи по математике. Данный урок посвящен задачам на движение.
Задача на нахождение расстояния/скорости/времени
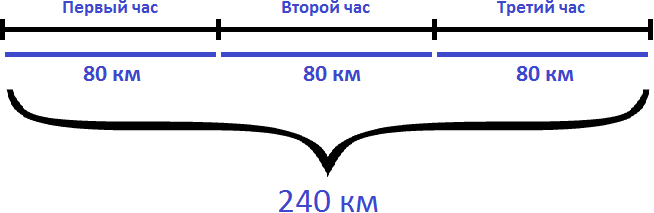
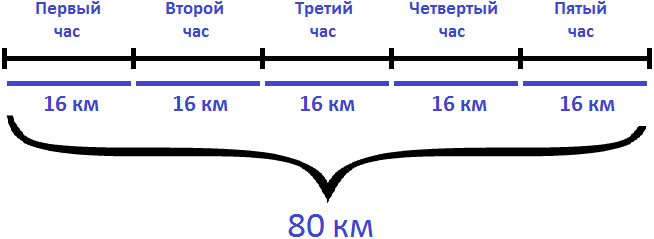
Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?
Решение
Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)
80 × 3 = 240 км
Ответ: за 3 часа автомобиль проедет 240 километров.
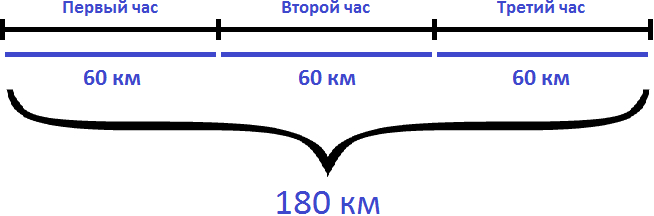
Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?
Решение
Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.
Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:
180 : 3 = 60 км/ч
Ответ: скорость автомобиля составляет 60 км/ч
Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?
Решение
Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)
96 : 2 = 48 км/ч
Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)
72 : 6 = 12 км/ч
Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12
Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.
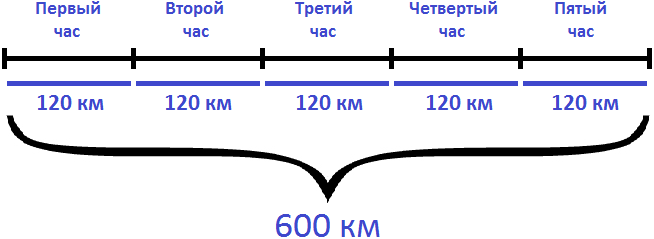
Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Решение
Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения
600 : 120 = 5 часов
Ответ: вертолет был в пути 5 часов.
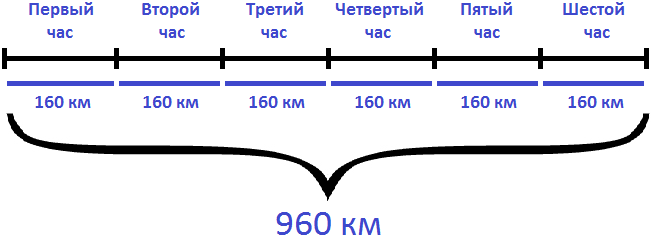
Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?
Решение
Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время
160 × 6 = 960 км
Ответ: за 6 часов вертолет преодолел 960 км.
Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.
Решение
Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9
55 × 9 = 495 км
Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения
723 − 495 = 228 км
Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:
228 : 4 = 57 км/ч
Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч
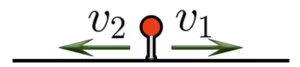
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
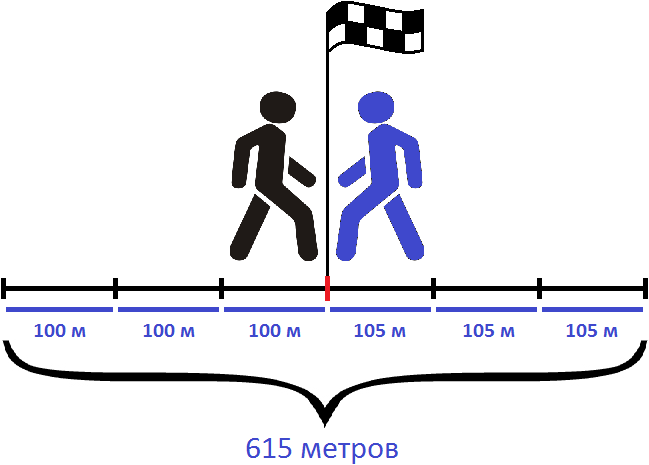
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
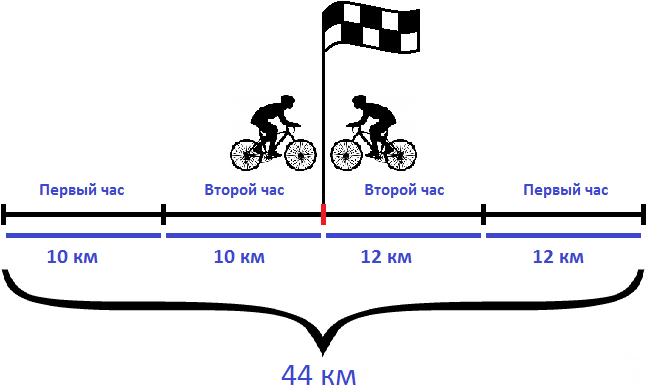
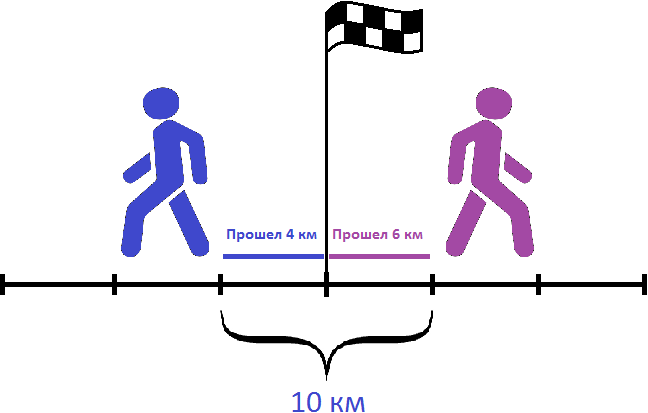
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
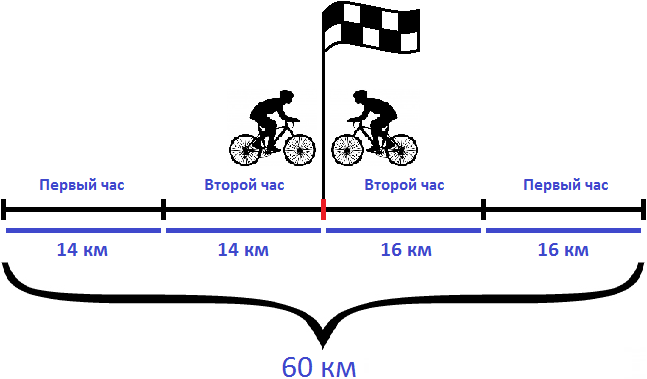
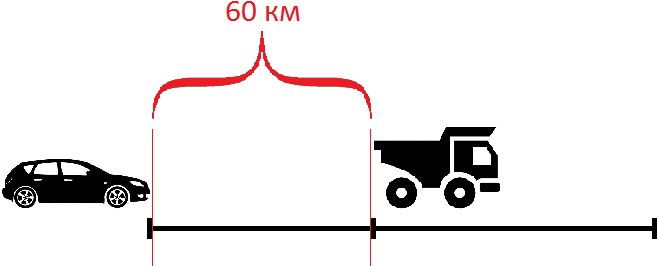
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
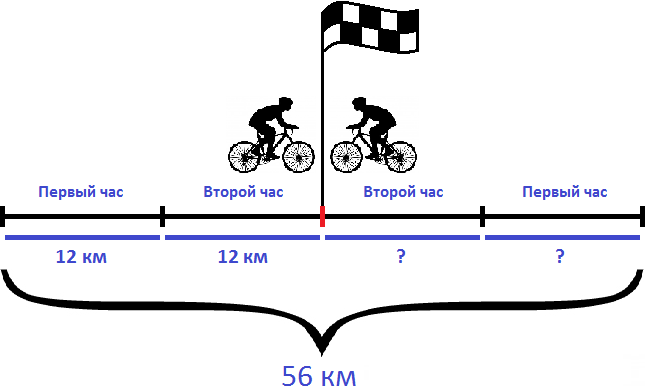
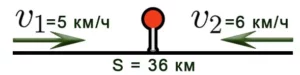
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
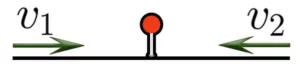
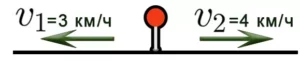
Скорость удаления
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
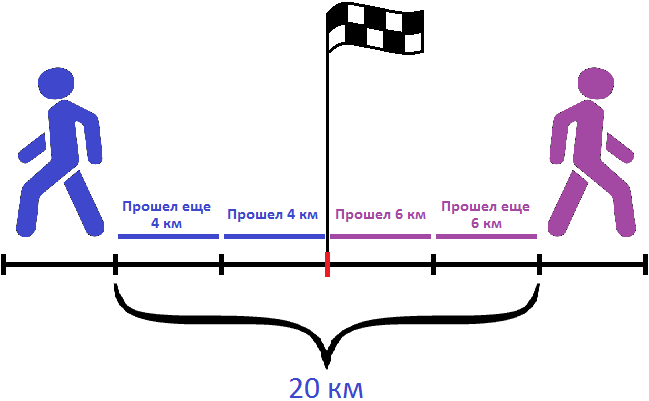
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит
Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.
Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:
Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?
Решение
Определим скорость удаления поездов. Для этого сложим их скорости:
40 + 180 = 220 км/ч
Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2
220 × 2 = 440 км
Ответ: через 2 часа расстояние будет между поездами будет 440 километров.
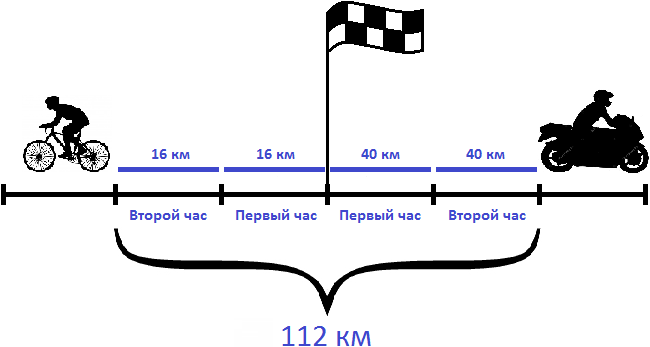
Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
16 км/ч + 40 км/ч = 56 км/ч
Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа
56 × 2 = 112 км
Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.
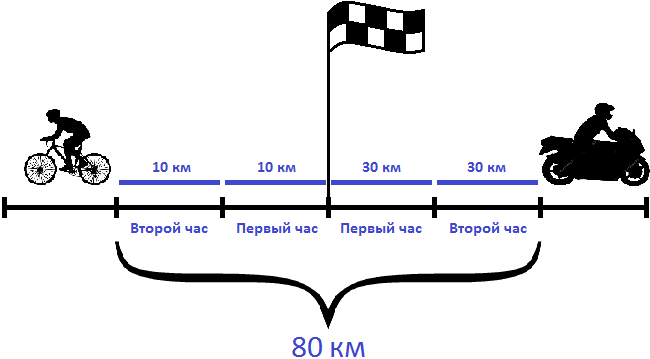
Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Решение
Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:
10 км/ч + 30 км/ч = 40 км/ч
За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км
80 : 40 = 2
Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.
Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста
Решение
Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа
15 × 2 = 30 км
На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.
Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:
90 км − 30 км = 60 км
Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
60 : 2 = 30 км/ч
Значит скорость мотоциклиста составляла 30 км/ч.
Ответ: скорость мотоциклиста составляла 30 км/ч.
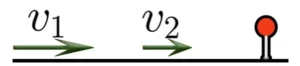
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние
Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час
На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.
В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.
Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20
40 км/ч − 20 км/ч = 20 км/ч
Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?
Решение
Найдем скорость удаления. Для этого из большей скорости вычтем меньшую
120 км/ч − 80 км/ч = 40 км/ч
Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:
40 × 2 = 80 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.
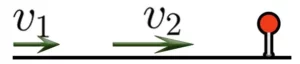
Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.
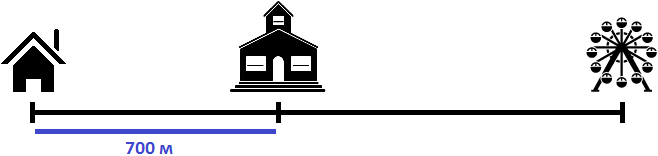
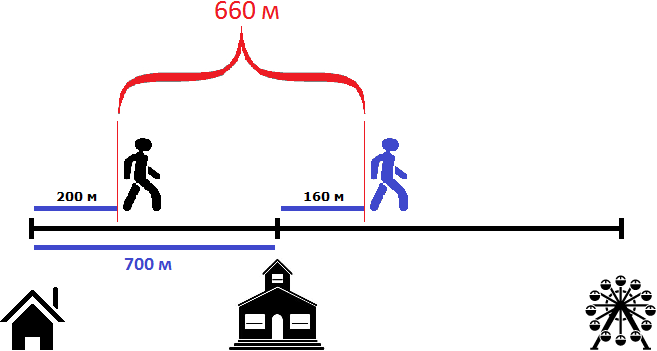
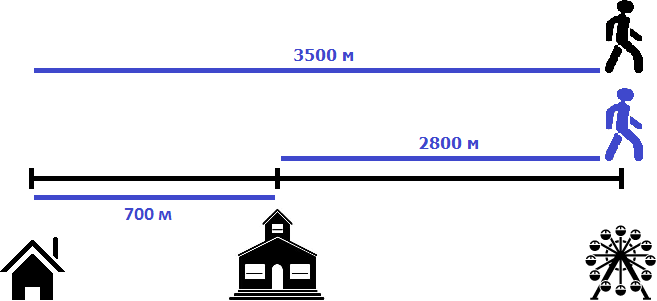
Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров
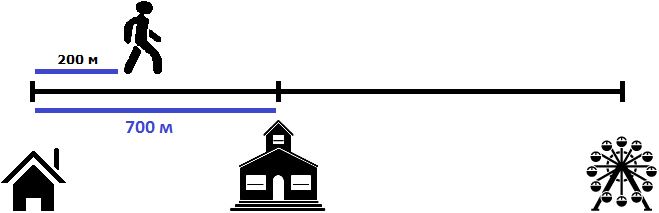
Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?
Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров
100 × 2 = 200 метров
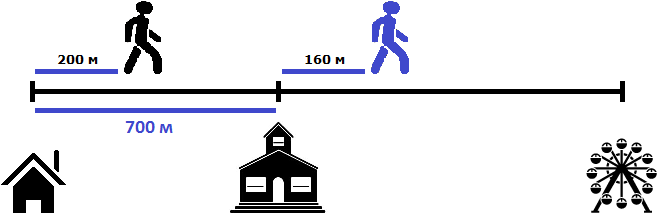
Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров
80 × 2 = 160 метров
Теперь нужно найти расстояние между пешеходами
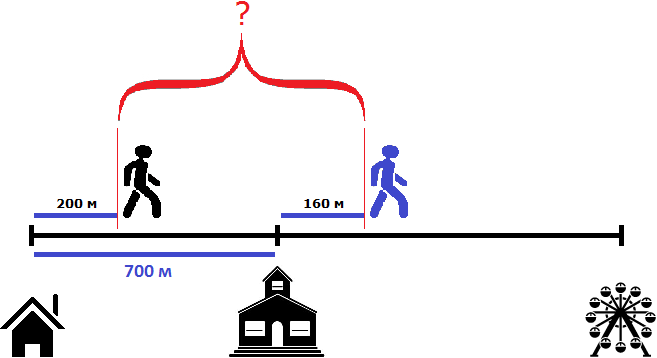
Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)
700 м + 160 м = 860 м
860 м − 200 м = 660 м
Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)
700 м − 200 м = 500 м
500 м + 160 м = 660 м
Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров
Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?
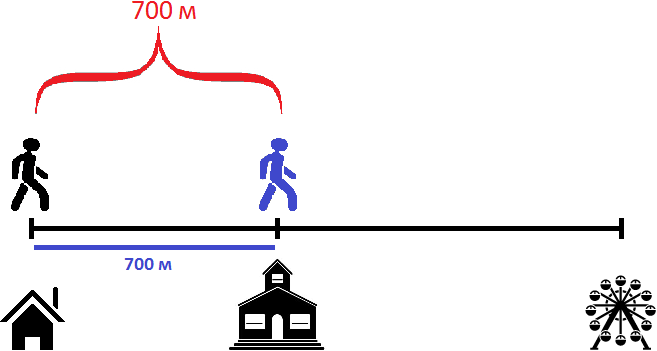
Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение
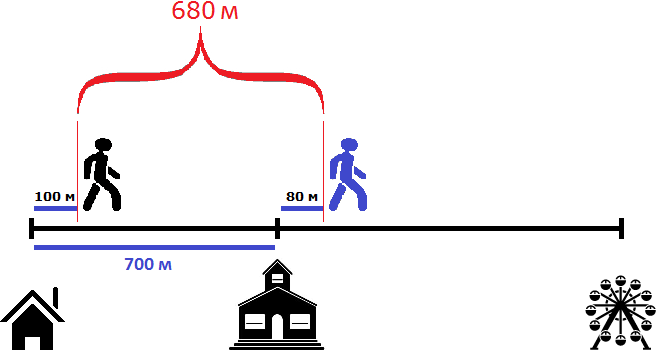
Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:
100 м × 1 = 100 м
80 м × 1 = 80 м
700 м + 80 м − 100 м = 780 м − 100 м = 680 м
Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:
100 м × 2 = 200 м
80 м × 2 = 160 м
700 м + 160 м − 200м = 860 м − 200 м = 660 м
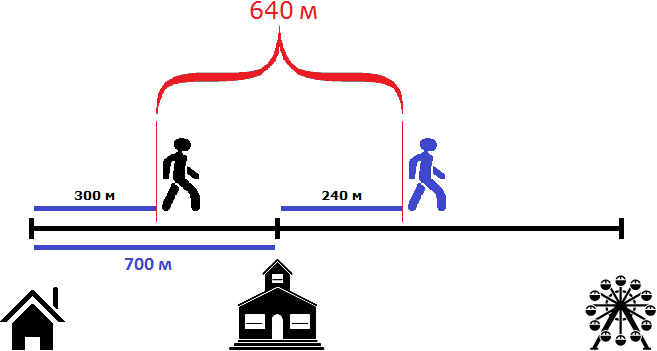
Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:
100 м × 3 = 300 м
80 м × 3 = 240 м
700 м + 240 м − 300м = 940 м − 300 м = 640 м
Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.
Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.
А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго
700 : 20 = 35
Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше
100 × 35 = 3500 м
Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше
80 × 35 = 2800 м
Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м
Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.
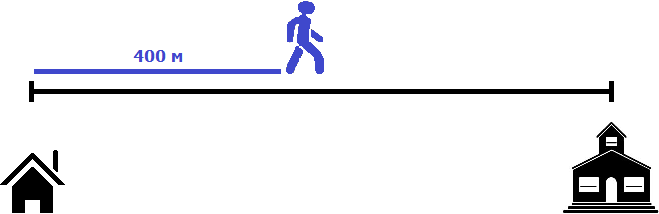
Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?
Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут
80 × 5 = 400 метров
Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.
Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.
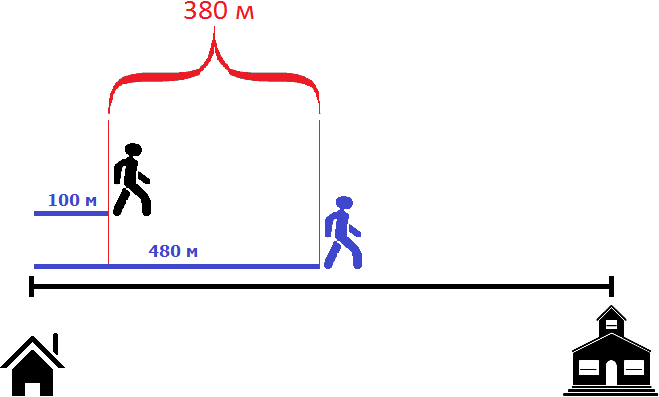
Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров
Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20
400 : 20 = 20
Значит через 20 минут второй пешеход догонит первого.
Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
Решение
Найдем скорость сближения
35 км/ч − 15 км/ч = 20 км/ч
Определим через часов автобус догонит велосипедиста
40 : 20 = 2
Ответ: автобус догонит велосипедиста через 2 часа.
Задача на движение по реке
Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.
Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.
Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.
Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с собственной скоростью.
Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что собственная скорость моторной лодки составляет 40 км/ч.
Как определить скорость судна?
Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч по течению реки, и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)
30 км/ч + 2 км/ч = 32 км/ч
Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.
Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.
Например, если моторная лодка плывет со скоростью 30 км/ч против течения реки, и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)
30 км/ч − 2 км/ч = 28 км/ч
Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.
Задача 1. Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?
Ответ:
Если катер будет двигаться по течения реки, то скорость его движения составит 40 + 3, то есть 43 км/ч.
Если катер будет двигаться против течения реки, то скорость его движения составит 40 − 3, то есть 37 км/ч.
Задача 2. Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?
Решение
Собственная скорость теплохода составляет 23 км/ч. Если теплоход будет двигаться по течению реки, то скорость его движения составит 23 + 3, то есть 26 км/ч. За три часа он пройдет в три раза больше
26 × 3 = 78 км
Если теплоход будет двигаться против течения реки, то скорость его движения составит 23 − 3, то есть 20 км/ч. За три часа он пройдет в три раза больше
20 × 3 = 60 км
Задача 3. Расстояние от пункта А до пункта B лодка преодолела за 3 часа 20 минут, а расстояние от пункта B до А — за 2 часа 50 минут. В каком направлении течет река: от А к В или от В к А, если известно, что скорость яхты не менялась?
Решение
Скорость яхты не менялась. Узнаем на какой путь она затратила больше времени: на путь от А до В или на путь от В до А. Тот путь, который затратил больше времени будет тем путем, течение реки которого шло против яхты
3 часа 20 минут больше, чем 2 часа 50 минут. Это значит, что течение реки снизило скорость яхты и это отразилось на времени пути. 3 часа 20 минут это время, затраченное на путь от от А до В. Значит река течет от пункта B к пункту А
Задача 4. За какое время при движении против течения реки
теплоход пройдет 204 км, если его собственная скорость
15 км/ч, а скорость течения в 5 раз меньше собственной
скорости теплохода?
Решение
Требуется найти время за которое теплоход пройдет 204 километра против течения реки. Собственная скорость теплохода составляет 15 км/ч. Двигается он против течения реки, поэтому нужно определить его скорость при таком движении.
Чтобы определить скорость против течения реки, нужно из собственной скорости теплохода (15 км/ч) вычесть скорость движения реки. В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз
15 : 5 = 3 км/ч
Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода
15 км/ч − 3 км/ч = 12 км/ч
Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров
204 : 12 = 17 ч
Ответ: теплоход пройдет 204 километра за 17 часов
Задача 5. Двигаясь по течению реки, за 6 часов лодка
прошла 102 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)
102 : 6 = 17 км/ч
Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)
17 − 4 = 13 км/ч
Задача 6. Двигаясь против течения реки, за 5 часов лодка
прошла 110 км. Определите собственную скорость лодки,
если скорость течения – 4 км/ч.
Решение
Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)
110 : 5 = 22 км/ч
Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки
22 + 4 = 26 км/ч
Ответ: собственная скорость лодки составляет 26 км/ч
Задача 7. За какое время при движении против течения реки лодка
пройдет 56 км, если скорость течения – 2 км/ч, а её
собственная скорость на 8 км/ч больше скорости течения?
Решение
Найдем собственную скорость лодки. В условии сказано, что она на 8 км/ч больше скорости течения. Поэтому для определения собственной скорости лодки, к скорости течения (2 км/ч) прибавим еще 8 км/ч
2 км/ч + 8 км/ч = 10 км/ч
Лодка движется против течения реки, поэтому из собственной скорости лодки (10 км/ч) вычтем скорость движения реки (2 км/ч)
10 км/ч − 2 км/ч = 8 км/ч
Узнаем за какое время лодка пройдет 56 км. Для этого расстояние (56км) разделим на скорость движения лодки:
56 : 8 = 7 ч
Ответ: при движении против течения реки лодка пройдет 56 км за 7 часов
Задачи для самостоятельного решения
Задача 1. Сколько времени потребуется пешеходу, чтобы пройти 20 км, если скорость его равна 5 км/ч?
Решение
За один час пешеход проходит 5 километров. Чтобы определить за какое время он пройдет 20 км, нужно узнать сколько раз 20 километров содержат по 5 км. Либо воспользоваться правилом нахождения времени: разделить пройденное расстояние на скорость движения
20 : 5 = 4 часа
Задача 2. Из пункта А в пункт В велосипедист ехал 5 часов со скоростью 16 км/ч, а обратно он ехал по тому же пути со скоростью 10 км/ч. Сколько времени потратил велосипедист на обратный путь?
Решение
Определим расстояние от пункта А до пункта В. Для этого умножим скорость с которой ехал велосипедист из пункта А в пункт В (16км/ч) на время движения (5ч)
16 × 5 = 80 км
Определим сколько времени велосипедист затратил на обратный путь. Для этого расстояние (80км) разделим на скорость движения (10км/ч)
80 : 10 = 8 ч
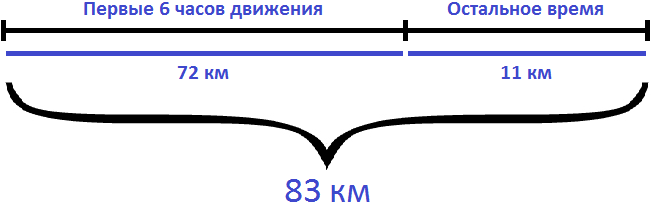
Задача 3. Велосипедист ехал 6 ч с некоторой скоростью. После того как он проехал ещё 11 км с той же скоростью, его путь стал равным 83 км. С какой скоростью ехал велосипедист?
Решение
Определим путь, пройденный велосипедистом за 6 часов. Для этого из 83 км вычтем путь, который он прошел после шести часов движения (11км)
83 − 11 = 72 км
Определим с какой скоростью ехал велосипедист первые 6 часов. Для этого разделим 72 км на 6 часов
72 : 6 = 12 км/ч
Поскольку в условии задаче сказано, что остальные 11 км велосипедист проехал с той же скоростью, что и в первые 6 часов движения, то скорость равная 12 км/ч является ответом к задаче.
Ответ: велосипедист ехал со скоростью 12 км/ч.
Задача 4. Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?
Решение
Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов
72 : 36 = 2 км/ч
Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа
72 : 4 = 18 км/ч
Если против течения реки скорость теплохода составляет 18 км/ч, то собственная его скорость равна 18+2, то есть 20 км/ч. А по течению реки его скорость будет составлять 20+2, то есть 22 км/ч
Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров
110 : 22 = 5 ч
Ответ: по течению реки теплоход проплывет 110 километров за 5 часов.
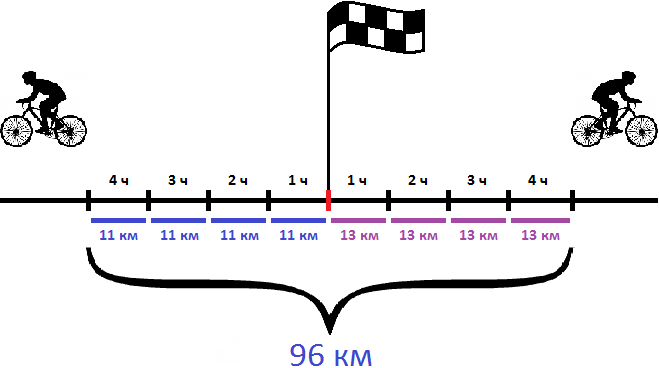
Задача 5. Из одного пункта одновременно в противоположных направлениях выехали два велосипедиста. Один из них ехал со скоростью 11 км/ч, а второй со скоростью 13 км/ч. Какое расстояние будет между ними через 4 часа?
Решение
Найдем скорость удаления велосипедистов
11 + 13 = 24 км
Узнаем какое расстояние будет между ними через 4 часа
24 × 4 = 96 км
Ответ: через 4 часа расстояние между велосипедистами будет 96 км.
Задача 6. От двух пристаней одновременно навстречу друг другу отошли два теплохода, и через 6 часов они встретились. Какое расстояние до встречи прошел каждый теплоход и какое расстояние между пристанями, если один теплоход шел со скоростью 21 км/ч, а другой — со скоростью 24 км/ч?
Решение
Определим расстояние, пройденное первым теплоходом. Для этого умножим его скорость (21 км/ч) на время движения до встречи (6ч)
21 × 6 = 126 км
Определим расстояние, пройденное вторым теплоходом. Для этого умножим его скорость (24 км/ч) на время движения до встречи (6ч)
24 × 6 = 144 км
Определим расстояние между пристанями. Для этого сложим расстояния, пройденные первым и вторым теплоходами
126 км + 144 км = 270 км
Ответ: первый теплоход прошел 126 км, второй — 144 км. Расстояние между пристанями составляет 270 км.
Задача 7. Одновременно из Москвы и Уфы вышли два поезда. Через 16 часов они встретились. Московский поезд шел со скоростью 51 км/ч. С какой скоростью шел поезд, вышедший из Уфы, если расстояние между Москвой и Уфой 1520 км? Какое расстояние было между поездами через 5 часов после их встречи?
Решение
Определим сколько километров до встречи прошел поезд, вышедший из Москвы. Для этого умножим его скорость (51 км/ч) на 16 часов
51 × 16 = 816 км
Узнаем сколько километров до встречи прошел поезд, вышедший из Уфы. Для этого из расстояния между Москвой и Уфой (1520км) вычтем расстояние, пройденное поездом, вышедшим из Москвы
1520 − 816 = 704 км
Определим скорость с которой шел поезд, вышедший из Уфы. Для этого расстояние, пройденное им до встречи, нужно разделить на 16 часов
704 : 16 = 44 км/ч
Определим расстояние, которое будет между поездами через 5 часов после их встречи. Для этого найдем скорость удаления поездов и умножим эту скорость на 5
51 км/ч + 44 км/ч = 95 км/ч
95 × 5 = 475 км.
Ответ: поезд, вышедший из Уфы, шел со скоростью 44 км/ч. Через 5 часов после их встречи поездов расстояние между ними будет составлять 475 км.
Задача 8. Из одного пункта одновременно в противоположных направлениях отправились два автобуса. Скорость одного автобуса 48 км/ч, другого на 6 км/ч больше. Через сколько часов расстояние между автобусами будет равно 510 км?
Решение
Найдем скорость второго автобуса. Она на 6 км/ч больше скорости первого автобуса
48 км/ч + 6 км/ч = 54 км/ч
Найдем скорость удаления автобусов. Для этого сложим их скорости:
48 км/ч + 54 км/ч = 102 км/ч
За час расстояние между автобусами увеличивается на 102 километра. Чтобы узнать через сколько часов расстояние между ними будет 510 км, нужно узнать сколько раз 510 км содержит по 102 км/ч
510 : 102 = 5 ч
Ответ: 510 км между автобусами будет через 5 часов.
Задача 9. Расстояние от Ростова-на-Дону до Москвы 1230 км. Из Москвы и Ростова навстречу друг другу вышли два поезда. Поезд из Москвы идет со скоростью 63 км/ч, а скорость ростовского поезда составляет 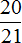
Решение
Найдем скорость ростовского поезда. Она составляет 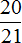
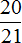
63 : 21 × 20 = 3 × 20 = 60 км/ч
Найдем скорость сближения поездов
63 км/ч + 60 км/ч = 123 км/ч
Определим через сколько часов поезда встретятся
1230 : 123 = 10 ч
Узнаем на каком расстоянии от Ростова встретятся поезда. Для этого достаточно найти расстояние, пройденное ростовским поездом до встречи
60 × 10 = 600 км.
Ответ: поезда встретятся на расстоянии 600 км от Ростова.
Задача 10. От двух пристаней, расстояние между которыми 75 км, навстречу друг другу одновременно отошли две моторные лодки. Одна шла со скоростью 16 км/ч, а скорость другой составляла 75% скорости первой лодки. Какое расстояние будет между лодками через 2 ч?
Решение
Найдем скорость второй лодки. Она составляет 75% скорости первой лодки. Поэтому чтобы найти скорость второй лодки, нужно 75% от 16 км
16 × 0,75 = 12 км/ч
Найдем скорость сближения лодок
16 км/ч + 12 км/ч = 28 км/ч
С каждым часом расстояние между лодками будет уменьшáться на 28 км. Через 2 часа оно уменьшится на 28×2, то есть на 56 км. Чтобы узнать какое будет расстояние между лодками в этот момент, нужно из 75 км вычесть 56 км
75 км − 56 км = 19 км
Ответ: через 2 часа между лодками будет 19 км.
Задача 11. Легковая машина, скорость которой 62 км/ч, догоняет грузовую машину, скорость которой 47 км/ч. Через сколько времени и на каком расстоянии от начала движения легковая автомашина догонит грузовую, если первоначальное расстояние между ними было 60 км?
Решение
Найдем скорость сближения
62 км/ч − 47 км/ч = 15 км/ч
Если первоначально расстояние между машинами было 60 километров, то с каждым часом это расстояние будет уменьшáться на 15 км, и в конце концов легковая машина догонит грузовую. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 60 км содержит по 15 км
60 : 15 = 4 ч
Узнаем на каком расстоянии от начала движения легковая машина догнала грузовую. Для этого умножим скорость легковой машины (62 км/ч) на время её движения до встречи (4ч)
62 × 4 = 248 км
Ответ: легковая машина догонит грузовую через 4 часа. В момент встречи легковая машина будет на расстоянии 248 км от начала движения.
Задача 12. Из одного пункта в одном направлении одновременно выезжали два мотоциклиста. Скорость одного 35 км/ч, а скорость другого составляла 80% скорости первого мотоциклиста. Какое расстояние будет между ними через 5 часов?
Решение
Найдем скорость второго мотоциклиста. Она составляет 80% скорости первого мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно найти 80% от 35 км/ч
35 × 0,80 = 28 км/ч
Первый мотоциклист двигается на 35-28 км/ч быстрее
35 км/ч − 28 км/ч = 7 км/ч
За один час первый мотоциклиста преодолевает на 7 километров больше. С каждым часом она будет приближáться ко второму мотоциклисту на эти 7 километров.
Через 5 часов первый мотоциклист пройдет 35×5, то есть 175 км, а второй мотоциклист пройдет 28×5, то есть 140 км. Определим расстояние, которое между ними. Для этого из 175 км вычтем 140 км
175 − 140 = 35 км
Ответ: через 5 часов расстояние между мотоциклистами будет 35 км.
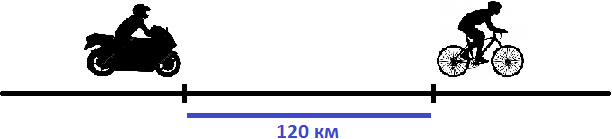
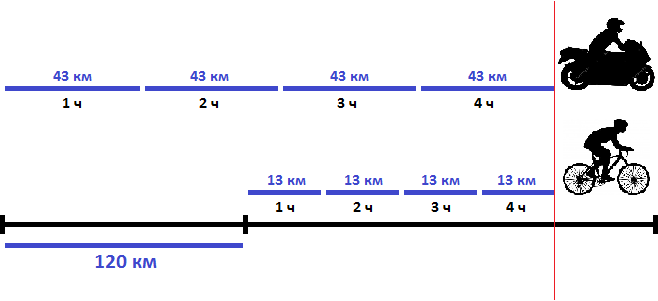
Задача 13. Мотоциклист, скорость которого 43 км/ч, догоняет велосипедиста, скорость которого 13 км/ч. Через сколько часов мотоциклист догонит велосипедиста, если первоначальное расстояние между ними было 120 км?
Решение
Найдем скорость сближения:
43 км/ч − 13 км/ч = 30 км/ч
Если первоначально расстояние между мотоциклистом и велосипедистом было 120 километров, то с каждым часом это расстояние будет уменьшáться на 30 км, и в конце концов мотоциклист догонит велосипедиста. Чтобы узнать через сколько часов это произойдет, нужно определить сколько раз 120 км содержит по 30 км
120 : 30 = 4 ч
Значит через 4 часа мотоциклист догонит велосипедиста
На рисунке представлено движение мотоциклиста и велосипедиста. Видно, что через 4 часа после начала движения они сровнялись.
Ответ: мотоциклист догонит велосипедиста через 4 часа.
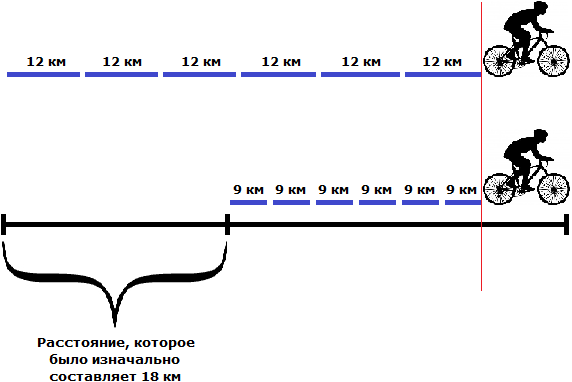
Задача 14. Велосипедист, скорость которого 12 км/ч, догоняет велосипедиста, скорость которого составляет 75 % его скорости. Через 6 часов второй велосипедист догнал велосипедиста, ехавшего первым. Какое расстояние было между велосипедистами первоначально?
Решение
Определим скорость велосипедиста, ехавшего впереди. Для этого найдем 75% от скорости велосипедиста, ехавшего сзади:
12 × 0,75 = 9 км/ч — скорость ехавшего впереди
Узнаем сколько километров проехал каждый велосипедист до того, как второй догнал первого:
12 × 6 = 72 км — проехал ехавший сзади
9 × 6 = 54 км — проехал ехавший впереди
Узнаем какое расстояние было между велосипедистами первоначально. Для этого из расстояния, пройденного вторым велосипедистом (который догонял) вычтем расстояние, пройденное первым велосипедистом (которого догнали)
72 км − 54 км = 18 км
Ответ: между велосипедистами первоначально было 18 км.
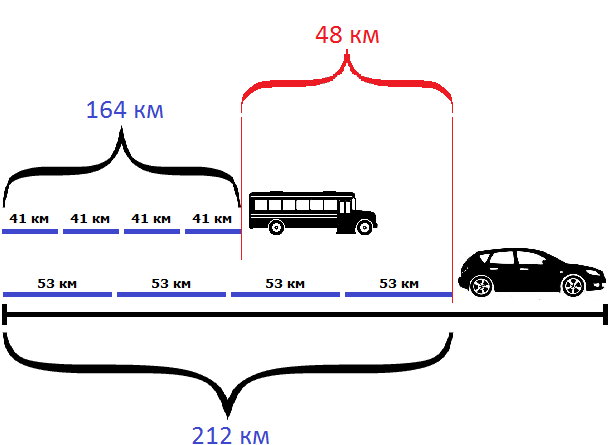
Задача 15. Автомобиль и автобус выехали одновременно из одного пункта в одном направлении. Скорость автомобиля 53 км/ч, скорость автобуса 41 км/ч. Через сколько часов после выезда автомобиль будет впереди автобуса на 48 км?
Решение
Найдем скорость удаления автомобиля от автобуса
53 км/ч − 41 км/ч = 12 км/ч
С каждым часом автомобиль будет удаляться от автобуса на 12 километров. На рисунке показано положение машин после первого часа движения
Видно, что автомобиль впереди автобуса на 12 км.
Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48 километров, нужно определить сколько раз 48 км содержит по 12 км
48 : 12 = 4 ч
Ответ: через 4 часа после выезда автомобиль будет впереди автобуса на 48 километров.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Пример №1
Допустим, из точки ( displaystyle A) и из точки ( displaystyle B) навстречу друг другу выехали две машины. Скорость одной машины – ( displaystyle 60) км/ч, а скорость ( displaystyle 2) машины – ( displaystyle 40) км/ч. Они встретились через ( displaystyle 1,2) часа.
Какое расстояние между пунктами ( displaystyle A) и ( displaystyle B)?
1 вариант решения
Можно рассуждать так: машины встретились, значит расстояние между городами – это сумма расстояния, которая прошла первая машина, и расстояния, которое прошла вторая.
( displaystyle 60cdot 1,2text{ }=text{ }72) (км) – путь, который проехала первая машина
( displaystyle 40cdot 1,2text{ }=text{ }48) (км) – путь, который проехала вторая машина
( displaystyle 72 + 48 = 120) (км) – расстояние, которое проехали обе машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).
2 вариант решения (более рациональный)
А можно просто воспользоваться очень логичной формулой о сложении скоростей.
Проверим, работает ли она:
( displaystyle 60 + 40 = 100) (км/ч) – скорость сближения машин
( displaystyle 100cdot 1,2text{ }=text{ }120) (км) – расстояние, которые проехали машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).
Оба решения являются верными. Второе просто более рациональное.
Пример №3
Итак, задача:
Из пункта ( displaystyle A) и пункта ( displaystyle B) машины движутся навстречу друг другу со скоростями ( displaystyle 50) км/ч и ( displaystyle 80) км/ч. Расстояние между пунктами – ( displaystyle 195) км.
Через сколько времени машины встретятся?
1 вариант решения
Пусть ( displaystyle x) – время, которое едут машины, тогда путь первой машины – ( displaystyle 50x), а путь второй машины – ( displaystyle 80x).
Их сумма и будет равна расстоянию между пунктами ( A) и ( B) – ( displaystyle 50x+80x=195).
Решим уравнение:
( displaystyle 50x+80x=195)
( displaystyle 130x=195)
( displaystyle x=1,5) (ч) – время, через которое встретились машины.
2 вариант решения (более рациональный)
( displaystyle 50 + 80 = 130) (км/ч) – скорость сближения машин;
( displaystyle 195:130 = 1,5) (ч) – время, которое машины были в пути.
Задача решена.
Пример №4
Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями ( displaystyle 60) км/ч и ( displaystyle 40) км/ч. Через сколько минут они встретятся. Если расстояние между пунктами ( displaystyle 100) км?
2 способа решения:
I способ
Относительная скорость автомобилей ( displaystyle 60+40=100) км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью ( displaystyle 100) км/ч. Так как между автомобилями изначально расстояние ( displaystyle 100) км, время, через которое второй автомобиль проедет мимо первого:
( displaystyle t=frac{100}{100}=1 час=60 минут).
II способ
Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его ( displaystyle t). Тогда первый автомобиль проехал путь ( displaystyle 60t), а второй – ( displaystyle 40t).
В сумме они проехали все ( displaystyle 100) км. Значит,
( displaystyle 60t+40t=100Rightarrow t=1 час=60 минут).
Из пункта ( displaystyle A) в пункт ( displaystyle B), расстояние между которыми ( displaystyle 30) км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на ( displaystyle 65) км больше, чем велосипедист.
Определите скорость велосипедиста, если известно, что он прибыл в пункт ( displaystyle B) на ( displaystyle 156) минут позже, чем мотоциклист.
Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт ( displaystyle A), пункт ( displaystyle B), две стрелочки…
В общем рисуй, и сейчас сравним, что у тебя получилось.
Пустовато как-то, правда? Рисуем таблицу.
Как ты помнишь, все задачи на движения состоят из ( displaystyle 3) компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.
Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.
Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?
У тебя получилась вот такая таблица?
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | |||
| мотоциклист |
Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.
Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен ( displaystyle 30) км. Вносим!
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle 30) | ||
| мотоциклист | ( displaystyle 30) |
Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на ( displaystyle 65) км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…
Возьмем скорость велосипедиста за ( displaystyle x), тогда скорость мотоциклиста будет ( displaystyle x+65)…
Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle x) | ( displaystyle 30) | |
| мотоциклист | ( displaystyle x+65) | ( displaystyle 30) |
Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?
Правильно, разделить путь на скорость. Вноси это в таблицу.
| Скорость, км/ч |
Время t, часов |
Путь S, км |
|
| велосипедист | ( displaystyle x) | ( displaystyle frac{30}{x}) | ( displaystyle 30) |
| мотоциклист | ( displaystyle x+65) | ( displaystyle frac{30}{65+x}) | ( displaystyle 30) |
Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.
Что мы можем на нем отразить?
Молодец. Скорость передвижения мотоциклиста и велосипедиста.
Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.
Какие данные не отражены ни в таблице, ни на рисунке?
Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени – ( displaystyle 156) минут.
Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.
( displaystyle 156) минут / ( displaystyle 60) минут = ( displaystyle 2,6) часа.
И что дальше, спросишь ты? А дальше числовая магия!
Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?
Правильно. Мы можем составить уравнение, основываясь на разнице во времени!
( displaystyle frac{30}{x}-frac{30}{65+x}=2,6)
Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.
Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».
Приводим слагаемые к общему знаменателю:
( displaystyle frac{30cdot left( 65+x right)}{xcdot left( 65+x right)}-frac{30x}{xcdot left( 65+x right)}=2,6)
Раскроем скобки и приведем подобные слагаемые: Уф! Усвоил? Попробуй свои силы на следующей задаче.
( displaystyle frac{1950}{xcdot left( 65+x right)}=2,6)
Из этого уравнения мы получаем следующее:
( displaystyle 2,6cdot xcdot left( 65+x right)=1950)
( displaystyle xcdot left( 65+x right)=frac{1950}{2,6})
( displaystyle xcdot left( 65+x right)=750)
Раскроем скобки и перенесем все в левую часть уравнения:
( displaystyle {{x}^{2}}+65{x}-750=0)
Вуаля! У нас простое квадратное уравнение. Решаем!
( displaystyle {{x}^{2}}+65{x}-750=0)
( displaystyle D={{b}^{2}}-4ac)
( displaystyle D={{65}^{2}}-4cdot 1cdot left( -750 right)=4225+3000=7225)
( displaystyle sqrt{D}=sqrt{7225}=85)
( displaystyle {{x}_{1,2}}=frac{-bpm sqrt{D}}{2a})
( displaystyle {{x}_{1}}=frac{-65+85}{2}=10)
( displaystyle {{x}_{2}}=frac{-65-85}{2}=-75)
Мы получили два варианта ответа. Смотрим, что мы взяли за ( displaystyle x)? Правильно, скорость велосипедиста.
Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь, о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ – ( displaystyle 10) км/ч.
Пример №9
Два велосипедиста одновременно отправились в ( displaystyle 165)-километровый пробег. Первый ехал со скоростью, на ( displaystyle 5) км/ч большей, чем скорость второго, и прибыл к финишу на ( displaystyle 5,5) часов раньше второго.
Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Напоминаю:
- Прочитай задачу пару раз – усвой все-все детали. Усвоил?
- Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
- Проверь, все ли величины у тебя одинаковой размерности, и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь, какие там графы?).
- Пока все это пишешь, думай, что взять за ( displaystyle x)? Выбрал? Записывай в таблицу!
- Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!
Все сделал? Молодец! У меня получилось, что скорость велосипедиста – ( displaystyle 10) км/ч.
Пример №10
Из пункта ( displaystyle A) круговой трассы выехал велосипедист. Через ( displaystyle 40) минут он еще не вернулся в пункт ( displaystyle A) и из пункта ( displaystyle A) следом за ним отправился мотоциклист.
Через ( displaystyle 20) минут после отправления он догнал велосипедиста в первый раз, а еще через ( displaystyle 40) минут после этого догнал его во второй раз.
Найдите скорость велосипедиста, если длина трассы равна ( displaystyle 50) км. Ответ дайте в км/ч.
Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:
Пусть скорость велосипедиста будет ( displaystyle x), а мотоциклиста – ( displaystyle y). До момента первой встречи велосипедист был в пути ( displaystyle 60) минут, а мотоциклист – ( displaystyle 20).
При этом они проехали равные расстояния:
( displaystyle 60x=20y (1))
Между встречами велосипедист проехал расстояние ( displaystyle 40x), а мотоциклист – ( displaystyle 40y).
Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:
(Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.)
Значит,
( displaystyle 40x+50=40y (2))
Полученные уравнения решаем в системе:
( displaystyle left{ begin{array}{l}60x=20y\40x+50=40yend{array} right.Leftrightarrow left{ begin{array}{l}y=3x\4x+5=4yend{array} right.Rightarrow text{4}x+5=12xRightarrow )
( displaystyle Rightarrow x=frac{5}{8}=0,625frac{text{км}}{мин}=0,625cdot 60frac{text{км}}{text{ч}}=37,5frac{text{км}}{text{ч}})
Ответ: ( displaystyle 37,5).
Разобрался? Попробуй решить самостоятельно следующие задачи:
Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.
Скорость течения в озере равна ( displaystyle 0).
Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести.
Это понятно? Логично же.
А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…
Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.
Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.
Разобрался? Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?
Здесь возможно два случая:
1 случай – ты плывешь по течению, и тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.
2 случай – ты плывешь против течения. Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы ( displaystyle 100) метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.

где:
- Скорость (V) — расстояние, пройденное за единицу времени.
- Время (t) — время в пути.
- Расстояние (S) — пройденный путь, или расстояние.
Зная эту формулу (для расстояния), вы можете легко вывести из неё формулу для скорости, или времени.
Если вы запомните эту формулу, то сможете решить любую задачу на движение, так как все задачи на движение по прямой — это применение данной формулы к одному или нескольким взаимосвязанным объектам.
Рассмотрим, как решать разные задачи на движение в зависимости от условий и уровня сложности.
Все задачи на движение делятся на следующие типы:
- простые задачи на скорость, время и расстояние;
- задачи на движение в разных направлениях: сближение и удаление;
- задачи на движение в одном направлении: сближение и удаление;
- решение задач на движение по реке.
Решение простых задач на движение: скорость, время и расстояние
В простых задачах на движение, как правило, есть один движущийся объект, для которого нужно найти неизвестную величину: скорость, время или расстояние. В данном случае применяется формула в ее первоначальном виде:
Задача 1. Автомобиль ехал 2ч со скоростью 85 км/ч. Определите расстояние.
Решение: Вычислим путь по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.
Задача 2. Велосипедист проехал 60 км за 5ч. Определите скорость.
Решение: Вычислим скорость велосипедиста по формуле: V = S:t = 60 км : 5 ч = 12 км/ч.
Задача 3. Мотоциклист проехал 30 км со скоростью 15км/ч. Сколько времени он затратил на этот путь?
Решение: Вычислим время движения мотоциклиста по формуле: t = S:V = 30 км : 15 км/ч = 2 ч.
В таких задачах нужно также следить, чтобы были одинаковыми единицы измерения. Например, если расстояние измеряется в километрах, а время — в часах, то скорость буде измеряться в км/час. Но если единицы измерения скорости — метр/час, а время дано в минутах, то в этом случае скорость и время нужно привести к одинаковым единица измерения, иначе ответ будет неверным.
Задача 4. Мотоциклист ехал 30 минут со скоростью 60 км/ч. Какое расстояние он проехал?
Решение: для того, чтобы вычислить расстояние, нужно время и скорость привести к одинаковым единицам измерения. При этом есть 2 способа:
1) Переведем время: 30 минут = 30/60 = 0,5 часа.
Найдем расстояние: 60 км/ч * 0,5 ч = 30 км.
2) Переведем скорость: 60 км/ч = 60км / 1час = 60км / 60 мин = 1км/мин.
Найдем расстояние: 1км/мин*30минут = 30 км.
Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)
При встречном движении расстояние между объектами уменьшается. Объекты приближаются друг к другу со скоростью сближения.
Скорость сближения находится по формуле:
При движении в противоположных направлениях скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью удаления.
Скорость удаления находится по формуле:
При решении подобных задач лучше нарисовать схему движения, чтобы было легче решать.
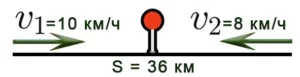
Задача 5. Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого велосипедиста 10 км/ч, второго — 8 км/ч. Через сколько часов они встретятся?
Решение: 1) Найдем скорость сближения: V=10+8 = 18 км/ч.
2) Найдем время: t = S:V = 36 : 18 = 2 ч.
Задача 6. Два пешехода вышли одновременно из одного и того же пункта в противоположных направлениях. Скорость первого пешехода 3км/ч, второго — 4км/ч. Какое расстояние между ними будет через 30 минут?
Решение: 1) Найдем скорость удаления пешеходов: V = 3+4=7 км/час.
2) Переведем в соответствие единицы измерения: t=30 мин = 0,5 ч.
3) Найдем расстояние: S=V × t = 7 × 0,5 = 3,5 км.
Задача 7. Два автобуса выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 300 км. Через 2 часа они встретились. Найдите второго второго автобуса, если первый ехал со скоростью 70 км/ч.
Решение. 1) Нам известно расстояние и скорость, поэтому найдем скорость по формуле: V = S:t = 300:2=150км/ч. Это скорость сближения.
2) Найдем скорость второго автобуса: 150-70 = 80км/ч.
Решение задач на движение в одном направлении: сближение и удаление
Если два объекта движутся в одном направлении и один объект “догоняет” второй, то расстояние между объектами уменьшается.
Скорость сближения при таком движении определяют по формуле:
Если два объекта движутся в одном направлении и один объект “отстает” от второго, то расстояние между объектами увеличивается.
Скорость удаления при таком движении определяют по формуле:
Если объект движется в стоячей воде (озере), то его скорость называют собственной скоростью объекта. То есть, скорость объекта равная собственной скорости объекта.
Заметим, что плот — это тело, у которого собственная скорость равна нулю (V=0). Значит, плот может плыть только по течению и со скоростью течения.
Задача 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль едет со скоростью 40км/ч, второй — со скоростью 30км/ч. Через сколько часов первый автомобиль догонит второй?
Решение. 1) Найдем скорость сближения автомобилей: V=40-30=10км/ч.
2) Зная расстояние (20км) и скорость сближения (10км/ч) найдем время: 20:10=2 часа.
Задача 9. Из одного населенного пункта выехали автомобиль и автобус. скорость автомобиля 70 км/ч, скорость автобуса — 50 км/ч. Какое расстояние будет между ними через 3 часа?
Решение. 1) Найдем скорость удаления : V=70-50=20км/ч.
2) Зная скорость удаления и время, найдем расстояние: S = 20*3 =60 км.
Решение задач на движение по реке
Особенностью задач на движение реке является то, что у объекта появляется дополнительная скорость — скорость течения реки. При этом возможно два варианта:
- по течению реки → скорость увеличивается;
- против течения реки → скорость уменьшается.
Таким образом, в задачах рассматривают 2 скорости:
- Скорость собственная — Vs;
- Скорость течения реки — Vt.
Задача 9. Собственная скорость лодки составляет 12 км/ч. Скорость течения реки равна 3 км/ч. Какое расстояние проплывёт лодка через 3 часа, если она плывёт по течению реки?
Решение. 1) Найдем скорость лодки. Так как она плывет по течению реки, ее скорость увеличивается.
V = Vs+ Vt = 12+3 =15км/ч.
2) Найдем расстояние: S=V×t = 15×3=45км.
Задача 10. Собственная скорость катера составляет 30 км/ч. Скорость течения реки равна 4 км/ч. Какое расстояние преодолеет катер через 4 часа, если он плывёт против течения реки?
Решение. 1) Найдем скорость. Так как катер плывет против течения реки, его скорость уменьшится.
V = Vs- Vt = 30-4 =26 км/ч.
2) Найдем расстояние: S=V×t = 26 * 4 = 104 км.
Задача 10. Скорость лодки равна 10 км/ч. При этом надо успеть проплыть 25 км за 2 часа по течению реки. Какой должна быть скорость течения реки, чтобы успеть в срок?
Решение. 1) Найдем нужную скорость: V=S:t = 25:2=12,5 км/ч.
2) Найдем скорость, которую нужно прибавить до нужно (скорость течения реки): 12,5-10=2,5км/ч.
Задача 11. Уровень ЕГЭ.
Катер прошёл по течению реки 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения.
Решение: Пусть Vt — cкорость течения реки, тогда:
1) В одну сторону: 27+Vt – скорость перемещения катера по течению, S=120км.
2) В обратную сторону: 27-Vt – скорость перемещения катера против течения, S=120км.
Выразим время:
1) В одну сторону: t=S:V = 120:(27+Vt) – время, затраченное катером на перемещение по течению,
2) В обратную сторону: t=S:V = 120:(27-Vt) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то:
120:(27+Vt) +1 = 120:(27-Vt).
Далее решаем уравнение и получаем ответ 3 км/ч.
Больше задач на движение Ваш ребёнок может решить, скачав программы:
Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.
Полезные советы для решения задач на движения
- В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
- Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.
- При решении задач на движение рисуйте картинки. Особенно, когда текст задачи большой и сразу в голове не укладывается. Чаще всего это нужно делать в задачах, где кто-то кого-то догоняет, встречается, или перемещается между пунктами А и В туда и обратно. На картинке сразу видно, какие отрезки пути можно просчитать. Картинка облегчает составление математической модели.
Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.
Скорость, путь и время являются важными характеристиками любого механического движения. Они связаны между собой формулами:
- $upsilon = frac{S}{t}$
- $S = upsilon t$
- $t = frac{S}{upsilon}$
Данные формулы описывают равномерное движение. При неравномерном движении мы говорим о средней скорости: $upsilon_{ср} = frac{S}{t}$.
Чтобы полноценно научиться использовать вышеупомянутые определения и величины, в данном уроке мы рассмотрим решение разнообразных задач. Вы научитесь вычислять скорость, среднюю скорость, время и путь, переводить единицы измерения скорости из одних в другие, узнаете, как использовать графики этих величин.
Задача №1
Выразите в метрах в секунду ($frac{м}{с}$) скорости: $60 frac{км}{ч}$; $90 frac{км}{ч}$; $300 frac{км}{ч}$; $120 frac{м}{мин}$.
Дано:
$upsilon_1 = 60 frac{км}{ч}$
$upsilon_2 = 90 frac{км}{ч}$
$upsilon_3 = 300 frac{км}{ч}$
$upsilon_4 = 120 frac{м}{мин}$
Показать решение и ответ
Скрыть
Решение:
Для перевода скорости в метры в секунду нам нужно:
- перевести километры в метры ($1 space км = 1000 space м$)
- выразить часы или минуты в секундах ($1 space мин = 60 space с$; $1 space ч = 60 space мин = 3600 space с$)
Тогда,
$upsilon_1 = 60 frac{км}{ч} = 60 frac{1000 space м}{3600 space c} = frac{1000 space м}{60 space c} approx 16.7 frac{м}{с}$.
При вычислениях старайтесь увидеть величины, которые можно сократить (как 60 и 3600).
Если мы вычислим множитель $frac{1000 space м}{3600 space c}$, то получим, что $1 frac{км}{ч} = frac{}{3.6} frac{м}{с}$.
Вы можете каждый раз последовательно переводить величины (километры в метры и часы в секунды) или просто разделить скорость, выраженную в километрах в час на $3.6$ и получить скорость в метрах в секунду. Рекомендуется идти первым путем, потому что второй способствует потере точности.
Переведем следующие две скорости в единицы СИ:
$upsilon_2 = 90 frac{км}{ч} = 90 frac{1000 space м}{3600 space c} = 1000 cdot 0.025 frac{м}{с} = 25 frac{м}{с}$,
$upsilon_3 = 300 frac{км}{ч} = 300 frac{1000 space м}{3600 space c} = frac{1000 space м}{12 space c} approx 83.3 frac{м}{с}$.
Теперь переведем скорость, выраженную в метрах в минуту в метры в секунду:
$upsilon_4 = 120 frac{м}{мин} = 120 frac{м}{60 space c} = 2 frac{м}{с}$.
Ответ: $upsilon_1 approx 16.7 frac{м}{с}$; $upsilon_2 = 25 frac{м}{с}$; $upsilon_1 approx 83.3 frac{м}{с}$; $upsilon_4 = 2 frac{м}{с}$.
Задача №2
Пуля, выпущенная из винтовки, долетела до цели, находящейся на расстоянии $1 space км$, за $2.5 space с$. Найдите скорость пули.
Дано:
$S = 1 space км$
$t = 2.5 space с$
СИ:
$S = 1000 space м$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета скорости:
$upsilon = frac{S}{t}$.
Перед вычислениями не забывайте переводить единицы измерения величин в СИ!
Рассчитаем скорость:
$upsilon = frac{1000 space м}{2.5 space с} = 400 frac{м}{с}$.
Ответ: $upsilon = 400 frac{м}{с}$.
Задача №3
Пароход, двигаясь против течения со скоростью $14 frac{км}{ч}$, проходит расстояние между двумя пристанями за $4 space ч$. За какое время он пройдет то же расстояние по течению, если его скорость в этом случае равна $5.6 frac{м}{с}$?
Дано:
$upsilon_1 = 14 frac{км}{ч}$
$t_1 = 4 space ч$
$upsilon_2 = 5.6 frac{м}{с}$
$t_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Найдем расстояние между двумя пристанями:
$S = upsilon_1 t_1$,
$S = 14 frac{км}{ч} cdot 4 space ч = 56 space км = 56 space 000 space м$.
Обратите внимание, что мы изначально не перевели единицы измерения в СИ (километры в час в метры в секунду и часы в секунды), потому что удобнее это сделать после расчета расстояния $S$. Таким образом мы сохраняем более высокую точность вычислений.
Итак, мы знаем расстояние и скорость движения парохода по течению. Теперь мы можем рассчитать время движения парохода по течению:
$t_2 = frac{S}{upsilon_2}$,
$t_2 = frac{56 space 000 space м}{5.6 frac{м}{с}} = 10 space 000 space с$.
Ответ: $t_2 = 10 space 000 space с$.
Задача №4
Автомобиль проехал равномерно участок дороги длиной $3.5 space км$ за $3 space мин$. Нарушил ли правила дорожного движения водитель, если на обочине расположен дорожный знак “скорость не более $50 frac{км}{ч}$”?
Дано:
$S = 3.5 space км$
$t = 3 space мин$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
После того, как мы рассчитаем скорость движения автомобиля, нам нужно будет сравнить ее со скоростным ограничением в $50 frac{км}{ч}$. Для того чтобы это сделать, нужно, чтобы скорость тоже была выражена в километрах в час.
Так как водитель двигался равномерно, рассчитывать скорость его движения мы будем по формуле:
$upsilon = frac{S}{t}$.
Путь $S$ у нас и так выражен в километрах, а время — в минутах. Поэтому, перед рассветом скорости переведем время из минут в часы:
$t = 3 space мин = frac{3}{60} cdot ч = 0.05 space ч$.
Теперь мы можем рассчитать скорость движения автомобиля:
$upsilon = frac{3.5 space км}{0.05 space ч} = 70 frac{км}{ч}$.
Получается, что водитель нарушил правила дорожного движения, ведь $70 frac{км}{ч} > 50 frac{км}{ч}$.
Ответ: нарушил.
Задача №5
Росток бамбука за сутки вырастает на $86.4 space см$. На сколько он вырастает за $1 space мин$?
Дано:
$S = 86.4 space см$
$t = 1 space сут$
$t_1 = 1 space мин$
$S_1 — ?$
Показать решение и ответ
Скрыть
Решение:
Переведем сутки в минуты:
$t = 1 space сут = 24 space ч = 24 cdot 60 space мин = 1440 space мин$.
Рассчитаем скорость роста бамбука, выраженную в сантиметрах в минуту:
$upsilon = frac{86.4 space см}{1440 space мин} = 0.06 frac{см}{мин}$.
Понятие скорости в физике определяет расстояние, которое тело проходит в единицу времени. В нашем случае полученную скорость роста мы можем описать так:
бамбук вырастает на расстояние, равное $0.06 space см$, за $1 space мин$.
Значит,
$S_1 = 0.06 space см = 0.6 space мм$.
Ответ: $S_1 = 0.6 space мм$.
Задача №6
Самолет, летящий со скоростью $300 frac{км}{ч}$, в безветренную погоду пролетел расстояние между аэродромами A и B за $2.2 space ч$. Обратный полет из-за встречного ветра он совершил за $2.5 space ч$. Определите скорость ветра.
Дано:
$upsilon_1 = 300 frac{км}{ч}$
$t_1 = 2.2 space ч$
$t_2 = 2.5 space ч$
$upsilon_в — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала вычислим расстояние между аэродромами, которое пролетает самолет:
$S = upsilon_1 t_1$,
$S = 300 frac{км}{ч} cdot 2.2 space ч = 660 space км$.
Теперь рассчитаем скорость, с которой самолет совершил обратный полет:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{660 space км}{2.5 space ч} = 264 frac{км}{ч}$
Если бы ветра не было, то скорость самолета составила бы $300 frac{км}{ч}$. Но ветер направлен противоположно движению самолеты, вектор его скорости противоположно направлен вектору скорости самолета. Поэтому мы можем записать, что скорость самолета, летящего при встречном ветре, равна разности скорости самолета в безветренной обстановке и скорости ветра:
$upsilon_2 = upsilon_1 — upsilon_в$.
Рассчитаем скорость ветра:
$upsilon_в = upsilon_1 — upsilon_2$,
$upsilon_в = 300 frac{км}{ч} — 264 frac{км}{ч} = 36 frac{км}{ч}$,
или в СИ $upsilon_в = 36 cdot frac{1000 space м}{3600 space с} = 10 frac{м}{с}$.
Ответ: $upsilon_в = 10 frac{м}{с}$.
Определите по графику равномерного движения, изображенному на рисунке 1:
- скорость движения
- путь, пройденный телом в течение $4.5 space с$
- время, в течение которого пройден путь, равный $15 space м$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитывается по формуле:
$upsilon = frac{S}{t}$.
Выберем на графике такую точку, данные которой мы можем точно определить. Например, в момент времени, равный $4 space с$, был пройден путь, равный $16 space м$.
Используя эти данные, рассчитаем скорость:
$upsilon = frac{16 space м}{4 space с} = 4 frac{м}{с}$.
Найдем путь, пройденный телом в течение $4.5 space с$. Если мы взглянем на график, то в этот момент времени тело прошло путь, приблизительно равный $18 space м$. Давайте проверим точность этих данных с помощью вычислений:
$S = upsilon t$,
$S = 4 frac{м}{с} cdot 4.5 space с = 18 space м$.
Используя график, мы не можем точно определить время, в течение которого пройден путь, равный $15 space м$. Поэтому вычислим его:
$t = frac{S}{upsilon}$,
$t = frac{15 space м}{4 frac{м}{с}} = 3.75 space с$.
Ответ: $4 frac{м}{с}$, $18 space м$, $3.75 space с$.
Задача №8
Средняя скорость велосипедиста на всем пути равна $40 frac{км}{ч}$. Первую половину пути он ехал со скоростью $60 frac{км}{ч}$. С какой скоростью велосипедист проехал остаток пути?
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$upsilon_1 = 60 frac{км}{ч}$
$S_1 = S_2 = frac{1}{2}S$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу средней скорости при неравномерном движении:
$upsilon_{ср} = frac{S}{t}$.
Общее время движения $t$ мы можем представить в виде суммы $t_1 + t_2$, где $t_1$ — это время движения на первой половине пути, а $t_2$ — время движения на второй половине пути:
$upsilon_{ср} = frac{S}{t_1 + t_2}$.
Время мы можем выразить через скорость на данном участке пути и пройденный за это время путь:
$t_1 = frac{S_1}{upsilon_1} = frac{frac{1}{2}S}{upsilon_1} = frac{S}{2 upsilon_1}$,
$t_2 = frac{S_2}{upsilon_2} = frac{frac{1}{2}S}{upsilon_2} = frac{S}{2 upsilon_2}$,
$upsilon_{ср} = frac{S}{frac{S}{2 upsilon_1} + frac{S}{2 upsilon_2}} = frac{S}{frac{S(upsilon_1 + upsilon_2)}{2 upsilon_1 upsilon_2}} = frac{2 upsilon_1 upsilon_2}{upsilon_1 + upsilon_2}$.
Теперь выразим отсюда скорость $upsilon_2$, с которой велосипедист двигался вторую половину пути:
$2 upsilon_1 upsilon_2 = upsilon_{ср} upsilon_1 + upsilon_{ср} upsilon_2$,
$2 upsilon_1 upsilon_2 — upsilon_{ср} upsilon_2 = upsilon_{ср} upsilon_1$,
$upsilon_2 cdot (2 upsilon_1 — upsilon_{ср}) = upsilon_{ср} upsilon_1$,
$upsilon_2 = frac{upsilon_{ср} upsilon_1}{2 upsilon_1 — upsilon_{ср}}$.
Рассчитаем эту скорость:
$upsilon_2 = frac{40 frac{км}{ч} cdot 60 frac{км}{ч}}{2 cdot 60 frac{км}{ч} — 40 frac{км}{ч}} = frac{2400 frac{км}{ч}}{80} = 30 frac{км}{ч}$.
Ответ: $upsilon_2 = 30 frac{км}{ч}$.
Задача №9
На рисунке 2 дан график пути движения поезда. Определите скорости движения на участках, изображенных отрезками графика OA, AB и BC. Какой путь пройден поездом в течении $3 space ч$ с начала его движения?
Дано:
$t = 3 space ч$
$upsilon_1 — ?$, $upsilon_2 — ?$, $upsilon_3 — ?$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы определить скорость на каждом участке пути, мы будем выбирать удобную нам точку на графике и проводить вычисления.
Определим скорость движения поезда на участке OA. В момент времени, равный $1 space ч$, пройденный поездом путь составил $40 space км$:
$upsilon_1 = frac{S_1}{t_1}$,
$upsilon_1 = frac{40 space км}{1 space ч} = 40 frac{км}{ч}$.
Участок графика AB параллелен оси времени, пройденный путь не изменяется. Значит скорость здесь равна нулю: $upsilon_2 = 0 frac{км}{ч}$.
Определим скорость движения поезда на участке BC. По наклону прямой графика мы видим, что скорость после остановки изменилась. За время с $2 space ч$ до $3 space ч$, пройденный путь изменился с $60 space км$ до $80 space км$. Значит, за $1 space ч$ поезд прошел путь, равный $20 space км$:
$upsilon_3 = frac{S_3}{t_3}$,
$upsilon_3 = frac{20 space км}{1 space ч} = 20 frac{км}{ч}$.
Теперь нам нужно найти путь, пройденный поездом за $3 space ч$ с момента начала движения. Этот путь будет складываться из трех составляющих на разных участках:
$S = S_1 + S_2 + S_3$.
Путь $S_2$, соответствующий участку AB будет равен нулю, так как на нем скорость движения равна нулю.
Тогда, используя данные графика и рассчитанные значения скоростей, мы можем записать:
$S = S_1 + S_3 = upsilon_1 t_1 + upsilon_3 t_3$,
$S = 40 frac{км}{ч} cdot 1.5 space ч + 20 frac{км}{ч} cdot 1 space ч = 80 space км$.
Ответ: $upsilon_1 = 40 frac{км}{ч}$, $upsilon_2 = 0 frac{км}{ч}$, $upsilon_3 = 20 frac{км}{ч}$, $S = 80 space км$.
Задача №10
От одной и той же станции в одном и том же направлении отправляются два поезда. Скорость первого $30 frac{км}{ч}$, второго $40 frac{км}{ч}$. Второй поезд отправляется через $10 space мин$ после первого. После сорокаминутного движения первый поезд делает пятиминутную остановку, потом продолжает двигаться дальше с прежней скоростью.
Определите графически, когда и на каком расстоянии от станции второй поезд догонит первый. Графическое решение проверьте вычислением.
Дано:
$upsilon_1 = 30 frac{км}{ч}$
$upsilon_2 = 40 frac{км}{ч}$
$t_{01} = 0 space мин$
$t_{02} = 10 space мин$
$t_1 = 40 space мин$
$t_{1о} = 5 space мин$
$t — ?$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала займемся построением графика движения поездов.
По оси $x$ мы будем откладывать время, а по оси $y$ — расстояние. Время оставим в $мин$, а расстояние будем отмечать в $км$.
Построим график движения первого поезда (рисунок 3). Он начинает свое движение в момент времени $t_{01} = 0 space мин$.
Движется он со скоростью $30 frac{км}{ч}$ в течение $t_1 = 40 space мин$. Переведем эту скорость в $frac{км}{мин}$ и вычислим, какое расстояние этот поезд пройдет за указанное время:
$upsilon_1 = 30 frac{км}{ч} = 30 frac{км}{60 space мин} = 0.5 frac{км}{мин}$,
$S_1 = upsilon_1 t_2$,
$S = 0.5 frac{км}{мин} cdot 40 space мин = 20 space км$.
Поставим эту точку на графике и соединим с началом координат.
Далее поезд сделал остановку. Этот участок графика будет параллелен оси времени — значение пройденного пути остается постоянным, ведь поезд никуда не двигается.
Далее поезд продолжает движение с прежней скоростью. Без вычислений мы можем провести из точки, соответствующей концу остановки, прямую параллельную первой части графика.
Теперь построим тут же график движения для второго поезда (рисунок 4).
Он начинает свое движение не из начала координат, а из точки, соответствующей времени $t_{02} = 10 space мин$.
Он движется со скоростью $40 frac{км}{ч}$. Это означает, что за $1 space ч = 60 space мин$ он проходит путь, равный $40 space км$. Отметим эту точку на координатной плоскости и соединим с точкой начала движения.
Итак, графически мы получили, что
- Второй поезд догонит первый в момент времени $t = 40 space мин$
- Поезда встретятся на расстоянии $S = 20 space км$ от места отправления
Теперь подтвердим полученные данные вычислениями. Поезда встретятся друг с другом, пройдя определенный путь $S$. Это случится через определенное время $t$:
$S = S_1 = S_2$,
$S_1 = upsilon_1 t$,
$S_2 = upsilon_2 (t — t_{02})$.
Найдем это время:
$upsilon_1 t = upsilon_2 (t — t_{02})$,
$upsilon_2 t — upsilon_1 t = upsilon_2 t_{02}$,
$t (upsilon_2 — upsilon_1) = upsilon_2 t_{02}$,
$t = frac{upsilon_2 t_{02}}{upsilon_2 — upsilon_1}$.
Перед расчетом переведем $мин$ в $ч$: $t_{02} = 10 space мин = frac{10}{60} space ч = frac{1}{6} space ч$.
Теперь рассчитаем время встречи двух поездов:
$t = frac{40 frac{км}{ч} cdot frac{1}{6} space ч}{40 frac{км}{ч} — 30 frac{км}{ч}} = frac{4}{6} space ч = frac{2}{3} space ч = 40 space мин$.
Используя полученное значение времени и скорость движения первого поезда, рассчитаем расстояние, на котором встретятся поезда:
$S = upsilon_1 t$,
$S = 30 frac{км}{ч} cdot frac{2}{3} space ч = 20 space км$.
Ответ: $t = 40 space мин$, $S = 20 space км$.
Задача №11
Поезд прошел $25 space км$ за $35 space мин$, причем первые $10 space км$ он прошел в течение $18 space мин$, вторые $10 space км$ в течение $12 space мин$, а последние $5 space км$ за $5 space мин$. Определите среднюю скорость поезда на каждом участке и на всем пути.
Дано:
$S = 25 space км$
$t = 35 space мин$
$S_1 = 10 space км$
$t_1 = 18 space мин$
$S_2 = 10 space км$
$t_2 = 12 space мин$
$S_3 = 5 space км$
$t_3 = 5 space мин$
$upsilon_{1ср} — ?$, $upsilon_{2ср} — ?$, $upsilon_{3ср} — ?$
$upsilon_{ср} — ?$
Показать решение и ответ
Скрыть
Решение:
Переведем время из $мин$ в $ч$:
- $t = 35 space мин = frac{35}{60} space ч = frac{7}{12} space ч$
- $t_1 = 18 space мин = frac{18}{60} space ч = frac{3}{10} space ч = 0.3 space ч$
- $t_2 = 12 space мин = frac{12}{60} space ч = frac{1}{5} space ч = 0.2 space ч$
- $t_3 = 5 space мин = frac{5}{60} space ч = frac{1}{12} space ч$
Теперь рассчитаем среднюю скорость на каждом участке пути:
- $upsilon_{1ср} = frac{S_1}{t_1}$,
$upsilon_{1ср} = frac{10 space км}{0.3 space ч} approx 33.3 frac{км}{ч}$ - $upsilon_{2ср} = frac{S_2}{t_2}$,
$upsilon_{2ср} = frac{10 space км}{0.2 space ч} = 50 frac{км}{ч}$ - $upsilon_{3ср} = frac{S_3}{t_3}$,
$upsilon_{3ср} = frac{5 space км}{frac{1}{12} space ч} = 60 frac{км}{ч}$
Рассчитаем среднюю скорость на на всем пути:
$upsilon_{ср} = frac{S}{t}$,
$upsilon_{ср} = frac{25 space км}{frac{7}{12} space ч} approx 42.9 frac{км}{ч}$
Ответ: $upsilon_{1ср} approx 33.3 frac{км}{ч}$, $upsilon_{2ср} = 50 frac{км}{ч}$, $upsilon_{3ср} = 60 frac{км}{ч}$, $upsilon_{ср} approx 42.9 frac{км}{ч}$.
Памятка «Учимся решать задач на движение»
В задачах на движение рассматриваются три взаимосвязанные величины:
S – расстояние (пройденный путь),
t – время движения и
V – скорость – расстояние, пройденное за единицу времени.
Расстояние – это произведение скорости на время движения
S = V ● t
Скорость – это частное от деления расстояния на время движения
V = S : t
Время – это частное от деления расстояния на скорость движения
t = S : V
Задачи на встречное движение
Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V
Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?
Схема к задаче:
Решение:
S = V ● t
V сближ. = 1V + 2V
1 способ:
1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи
2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи
3) 36 + 42 = 78 (км)
2 способ:
1) 12 + 14 = 26 (км/ч) – скорость сближения
2) 26 • 3 = 78 (км)
Ответ: расстояние между посёлками 78 км.
Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?
Схема к задаче:

Решение:
V сближ. = 1V + 2V
t = S : V
1) 80 + 60 = 140 (км/ч) – скорость сближения
2) 280 : 140 = 2 (ч)
Ответ: машины встретятся через 2 часа.
Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?
Схема к задаче:
Решение:
V = S : t
2V = V сближ. – 1V
1) 340 : 2 = 170 (км/ч) – скорость сближения
2) 170 – 80 = 90 (км/ч)
Ответ: 90 км/ч. скорость второй машины
Задачи на движение в противоположных направлениях
Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях.
V удал. = 1V + 2V
Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?
Схема к задаче:
Решение:
S = V ● t
1 способ
1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч
2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч
3)36 + 42 = 78 (км)
2 способ
V удал. = 1V + 2V
S = V ● t
1)12 + 14 = 26 (км/ч) – скорость удаления
2)26 • 3 = 78 (км)
Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.
Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?
Схема к задаче:
Решение:
V удал. = 1V + 2V
t = S : V
1) 80 + 60 = 140 (км/ч) – скорость удаления
2) 280 : 140 = 2 (ч)
Ответ: через 2 часа расстояние между машинами будет 280 км
Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?
Схема к задаче:
Решение:
V = S : t
2V = V удал. – 1V
1) 340 : 2 = 170 (км/ч) – скорость удаления машин
2) 170 – 80 = 90 (км/ч)
Ответ: скорость второй машины 90 км/ч.