Как найти путь заряда

Как найти расстояние между зарядами

Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами .

О существовании электромагнитных сил знали еще древние греки. Но систематическое, количественное изучение физических явлений, в которых проявляется электромагнитное взаимодействие тел, началось только в конце XVIII века. Трудами многих ученых в XIX веке завершилось создание стройной науки, изучающей электрические и магнитные явления. Эта наука, которая является одним из важнейших разделов физики, получила название электродинамики .

Основными объектами изучения в электродинамике являются электрические и магнитные поля, создаваемые электрическими зарядами и токами.

Электрическое поле

1.1. Электрический заряд. Закон Кулона

Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Электрический заряд обычно обозначается буквами или .

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

Существует два рода электрических зарядов, условно названных положительными и отрицательными.

Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда .

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.

С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду .

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером . Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.

Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:

Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными . Элементарный заряд является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом и Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.

В обычных лабораторных опытах для обнаружения и измерения электрических зарядов используется электрометр – прибор, состоящий из металлического стержня и стрелки, которая может вращаться вокруг горизонтальной оси (рис. 1.1.1). Стержень со стрелкой изолирован от металлического корпуса. При соприкосновении заряженного тела со стержнем электрометра, электрические заряды одного знака распределяются по стержню и стрелке. Силы электрического отталкивания вызывают поворот стрелки на некоторый угол, по которому можно судить о заряде, переданном стержню электрометра.

Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов (рис. 1.1.2), отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка .

Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами .

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.

На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой .

Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.

Коэффициент пропорциональности в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).

Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения .

Коэффициент в системе СИ обычно записывают в виде:
где – электрическая постоянная .

В системе СИ элементарный заряд равен:

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.

Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Рис. 1.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.

Принцип суперпозиции является фундаментальным законом природы. Однако, его применение требует определенной осторожности, в том случае, когда речь идет о взаимодействии заряженных тел конечных размеров (например, двух проводящих заряженных шаров 1 и 2). Если к системе из двух заряженных шаров поднсти третий заряженный шар, то взаимодействие между 1 и 2 изменится из-за перераспределения зарядов .

Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.

Закон Кулона

Закон Кулона количественно описывает взаимодействие заряженных тел. Он является фундаментальным законом, то есть установлен при помощи эксперимента и не следует ни из какого другого закона природы. Он сформулирован для неподвижных точечных зарядов в вакууме. В реальности точечных зарядов не существует, но такими можно считать заряды, размеры которых значительно меньше расстояния между ними. Сила взаимодействия в воздухе почти не отличается от силы взаимодействия в вакууме (она слабее менее чем на одну тысячную).

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.

Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.

На основании многочисленных опытов Кулон установил следующий закон:

Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними. Она направлена вдоль прямой, соединяющей заряды, и является силой притяжения, если заряды разноименные, и силой отталкивания, если заряды одноименные.

Если обозначить модули зарядов через |q₁| и |q₂|, то закон Кулона можно записать в следующей форме:

Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц.

Полная формула закона Кулона:

( F ) — Сила Кулона

( q_1 q_2 ) — Электрический заряд тела

( r ) — Расстояние между зарядами

( varepsilon_0 = 8,85*10^ ) — Электрическая постоянная

( varepsilon ) — Диэлектрическая проницаемость среды

( k = 9*10^9 ) — Коэффициент пропорциональности в законе Кулона

Силы взаимодействия подчиняются третьему закону Ньютона: ( vec_=vec_ ) . Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках.

Электрический заряд обычно обозначается буквами q или Q .

Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:

Существует два рода электрических зарядов, условно названных положительными и отрицательными.

Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.

Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.

Отметим, чтоб выполнялся закон Кулона необходимо 3 условия:

• Точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.
• Неподвижность зарядов. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд .
• Взаимодействие зарядов в вакууме.

В Международной системе СИ за единицу заряда принят кулон (Кл) .

Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А . Единица силы тока (Ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.

Закон Кулона простым языком

Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.

Рисунок 1. Закон Кулона

История открытия

Эксперименты с заряженными частицами проводили много физиков:

• Г. В. Рихман;
• профессор физики Ф. Эпинус;
• Д. Бернулли;
• Пристли;
• Джон Робисон и многие другие.

Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.

Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).

Рис. 2. Крутильные весы

У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10 -9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1 º . Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.

Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.

Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.

Формулировка

Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.

Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F₁|=|F₂|=(k_e*q₁*q₂) / r 2

Рис. 3. Взаимодействие точечных зарядов

Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.

Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.

Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:

• соблюдение точечности зарядов;
• неподвижность заряженных тел;
• закон выражает зависимости между зарядами в вакууме.

Границы применения

Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.

Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 – 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.

Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 10 18 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.

Кулоновские силы подпадают под действие третьего закона Ньютона: F₁ = – F₂. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m₁* m₂ ) / r 2 , где m₁ и m₂ – массы взаимодействующих тел, а r – расстояние между ними.

Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.

Коэффициент k

Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.

Коэффициент k в СИ выражается следующим образом: k = 1/4πε₀, где ε₀ – электрическая постоянная: ε₀ = 8,85 ∙10 -12 Кл 2 /Н∙м 2 . Выполнив несложные вычисления, мы находим: k = 9×10 9 H*м 2 / Кл 2 . В метрической системе СГС k =1.

На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.

Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.

Закон Кулона в диэлектриках

Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε₀.

Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.

Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.

Применение на практике

Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.

Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.

На базе электростатики появилось много изобретений:

• конденсатор;
• различные диэлектрики;
• антистатические материалы для защиты чувствительных электронных деталей;
• защитная одежда для работников электронной промышленности и многое другое.

На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).

Рис. 4. Большой адронный коллайдер

Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.

1. Движение вдоль линий напряженности

Рассмотрим сначала случай, когда действующей на тело силой тяжести можно пренебречь по сравнению с силой, которая действует на тело со стороны электрического поля. Это всегда имеет место, когда речь идет о движении заряженных микрочастиц, например электронов. Напомним, кстати, что электрон имеет отрицательный заряд, а протон – положительный.

? 1. Объясните, почему при рассмотрении движения частицы в электрическом поле нельзя пренебрегать массой частицы даже в том случае, когда сила тяжести пренебрежимо мала по сравнению с силой, действующей на частицу со стороны электрического поля.

? 2. Заряженная частица движется в однородном электрическом поле. Что можно сказать о начальной скорости этой частицы, если траектория ее движения – прямолинейная?

Рассмотрим, как при таком движении изменяется кинетическая и потенциальная энергия частицы.

? 3. Электрон движется прямолинейно в однородном электрическом поле из точки с потенциалом 700 В в точку с потенциалом 200 В.
а) Совпадает ли направление начальной скорости электрона с направлением линий напряженности поля или эти направления противоположны?
б) Как изменилась полная энергия электрона?
в) Чему равно изменение потенциальной энергии электрона?
г) Чему равно изменение кинетической энергии электрона?
д) Какова минимальная начальная скорость электрона?

При движении в электрическом поле заряженная частица может изменить направление движения на противоположное.

? 4. Электрон влетает в однородное электрическое поле с начальной скоростью 8 * 10⁶ м/с. Потенциал поля в точке, в которую влетает электрон, равен 500 В. Направление начальной скорости электрона совпадает с направлением линий напряженности поля.
а) До точки с каким минимальным значением потенциала поля долетит электрон?
б) С какой по модулю скоростью электрон вернется в начальную точку?
в) Чему равна напряженность поля, если электрон вернулся в начальную точку через 9,1 * 10^-9 с?
г) Чему равен путь, пройденный электроном до его возвращения в начальную точку?

Сравним движение в одном и том же поле двух частиц с одинаковыми по модулю зарядами, но с различными массами.

? 5. Электрон и протон находятся на одной линии напряженности однородного электрического поля на расстоянии 1 см друг от друга. Они начинают двигаться из состояния покоя в противоположные стороны.
а) Чему равна напряженность поля, если через 10^-8 с расстояние между частицами стало равным 9,8 см?
б) На какое расстояние от своей начальной точки удалился к этому моменту протон?
в) Чему равны в этот момент скорости электрона и протона?

2. Движение заряженной частицы в конденсаторе

Если силой тяжести можно пренебречь по сравнению с силой, действующей на заряженную частицу со стороны электрического поля, то ее движение в поле конденсатора будет аналогично движению тела, брошенного горизонтально или под углом к горизонту, только роль силы тяжести будет играть сила, действующая на заряженную частицу со стороны электрического поля.

? 6. По какой траектории будет двигаться заряженная частица в однородном электрическом поле, если ее начальная скорость направлена под углом к линиям напряженности поля?

При рассмотрении тела, брошенного горизонтально или под углом к горизонту, мы использовали горизонтально направленную ось координат x и вертикально направленную ось y. В данном случае также удобно ввести оси координат x и y, как показано на рисунке 56.1.

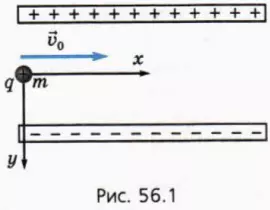
Если начальная скорость частицы направлена горизонтально, направление оси y удобно выбрать так, чтобы проекция силы, действующей на эту частицу со стороны электрического поля конденсатора, была положительной. Начало координат совместим с начальным положением частицы.

? 7. Частица с зарядом q и массой m влетает в электрическое поле плоского конденсатора в точке, находящейся посередине между пластинами (рис. 56.1). Пластины конденсатора расположены горизонтально. Расстояние между пластинами равно d, длина пластин l, напряжение между пластинами U. Начальная скорость частицы равна по модулю v0 и направлена горизонтально.
а) Чему равны проекции ускорения частицы на оси координат при ее движении внутри конденсатора?
б) Как зависят от времени проекции скорости частицы?
в) Как зависят от времени координаты частицы?
г) Сколько времени частица будет лететь сквозь весь конденсатор, если не столкнется с его пластиной?
д) При каком соотношении между указанными выше параметрами частица пролетит сквозь весь конденсатор и вылетит из него?
е) Чему равен тангенс угла между скоростью частицы и горизонталью в тот момент, когда частица вылетает из конденсатора?
ж) Чему равен модуль скорости частицы, когда она вылетает из конденсатора?

? 8. Электрон влетает в конденсатор посередине между его пластинами со скоростью, направленной параллельно пластинам. Расстояние между пластинами равно 1 см, длина пластин 10 см. Начальная скорость электрона 5 * 10⁷ м/с.
а) Какова должна быть разность потенциалов между пластинами конденсатора, чтобы электрон не пролетел сквозь весь конденсатор?
б) На какую пластину в таком случае попадет электрон?
в) На каком расстоянии от положительной пластины будет находиться электрон в момент вылета из конденсатора, если напряжение между его пластинами равно 100 В?
г) Чему в этом случае будет равен тангенс угла между скоростью электрона и горизонталью в момент его вылета из конденсатора?
д) Как в этом случае изменится потенциальная энергия электрона за время его движения в конденсаторе?
е) На сколько процентов увеличится кинетическая энергия электрона за время движения в конденсаторе?

Рассмотрим случай, когда начальная скорость частицы направлена под углом к пластинам конденсатора.

Возможные типы траектории движения частицы схематически изображены на рисунке 56.2. Для определенности мы выбрали положительно заряженную частицу.

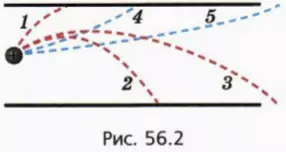
? 9. Каков знак заряда верхней пластины конденсатора, если положительно заряженная частица движется по одной из траекторий, изображенных красным пунктиром? синим пунктиром?

3. Движение заряженного тела в электрическом поле с учетом силы тяжести

Рассмотрим теперь случай, когда надо учитывать не только силу, действующую на тело со стороны электрического поля, но и силу тяжести.

? 10. Две большие пластины заряженного плоского конденсатора расположены вертикально (рис. 56.3). Разность потенциалов между пластинами равна U, а расстояние между ними равно d. Посередине между пластинами находится шарик с зарядом q и массой m. В начальный момент шарик покоится. Через некоторое время после того, как шарик отпустили, он столкнулся с одной из пластин конденсатора. Направим оси координат, как показано на рисунке.
56.3
а) Чему равна по модулю сила, действующая на шарик со стороны электрического поля?
б) Чему равна проекция ускорения шарика на ось х?
в) Через какой промежуток времени шарик столкнется с пластиной? Каков знак заряда этой пластины?
г) Насколько уменьшится высота шарика над землей к моменту столкновения по сравнению с его начальной высотой?
д) Какова форма траектории шарика?
е) Чему равно ускорение шарика во время движения?
ж) Чему равна скорость шарика в момент столкновения с пластиной?

Дополнительно вопросы и задания

11. Крупинка массой 10^-5 г влетает в электрическое поле горизонтально расположенного плоского конденсатора в точке, находящейся посередине между пластинами. Верхняя пластина конденсатора заряжена положительно. Начальная скорость крупинки направлена горизонтально. Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение между пластинами 1 кВ. Начальная скорость пылинки 6 м/с. Заряд крупинки равен по модулю 3 * 10^-12 Кл.
а) Чему равно отношение модулей силы тяжести и силы, действующей на крупинку со стороны электрического поля? При каком знаке заряда крупинки эти силы направлены одинаково?
б) Чему равно и как направлено ускорение крупинки, если у нее избыток электронов? недостаток электронов?
в) При каком знаке заряда крупинки она пролетит конденсатор насквозь?

12. Заряженная частица влетает в однородное электрическое поле с начальной скоростью, перпендикулярной линиям напряженности поля. В момент вылета из поля направление ее скорости составляет угол 60º с направлением начальной скорости. Во сколько раз увеличилась кинетическая энергия частицы при движении в электрическом поле? Считайте, что силой тяжести можно пренебречь.

Содержание:

Работа по перемещению заряда в электростатическом поле:

В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.

Работа по перемещению заряда в однородном электростатическом поле

Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.

Пусть в однородном электростатическом поле напряженностью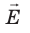

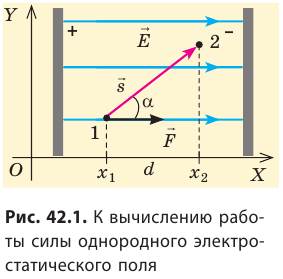
Вычислим работу А, которую совершает сила 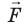, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.

Поле однородное, поэтому сила 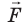постоянна, ее модуль равен: F=qE, а scosα=d=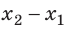является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( 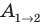) равна:

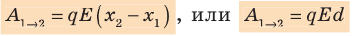
Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.

Обратите внимание! Формула 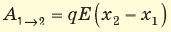будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.

Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:

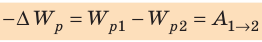
Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:

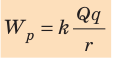
Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( < 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.

Что называют потенциалом электростатического поля

Потенциал 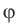электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к значению q этого заряда:

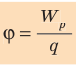
Единица потенциала в Си — вольт: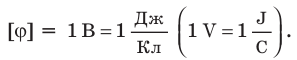

Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле: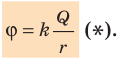

Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.

Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 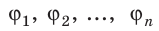полей, созданных каждым зарядом:

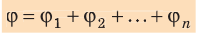
Как определяют разность потенциалов

Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: 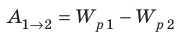. Поскольку 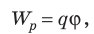то 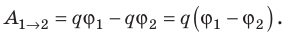Выражение 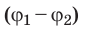называют разностью потенциалов, где 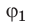— значение потенциала в начальной точке траектории движения заряда, 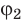— значение потенциала в ее конечной точке.

Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:

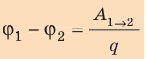
Единица разности потенциалов в Си — вольт: 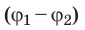= 1 В (V).

Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов 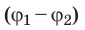− также называют напряжением (U). Важно не путать изменение потенциала 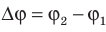и разность потенциалов (напряжение) .

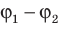Как связаны напряженность однородного электростатического поля и разность потенциалов

Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).

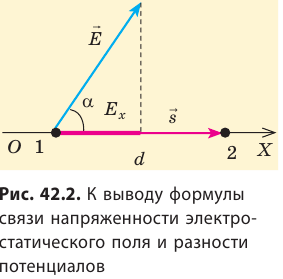
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: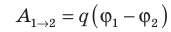; 2) через напряженность поля: 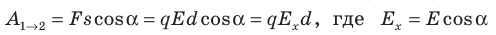— проекция вектора 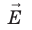на ось Ох, проведенную через точки 1 и 2.

Приравняв оба выражения для работы, получим: 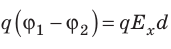, откуда: 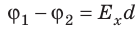, или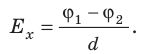

Если заряд перемещается в направлении напряженности электрического поля () , последняя формула примет вид:

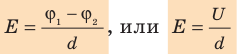
Из последней формулы следует единица напряженности в Си — вольт на метр:

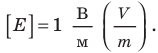
Какие поверхности называют эквипотенциальными

Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.

Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.

Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).

Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( 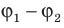), а на эквипотенциальной поверхности .

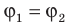Работу электростатического поля также можно представить через силу 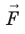, действующую на заряд со стороны поля: A F= scosα , где α — угол между векторам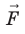и и 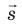. Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы 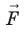, а следовательно, и вектор напряженности 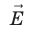поля в любой точке перпендикулярны вектору перемещения .

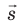Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).

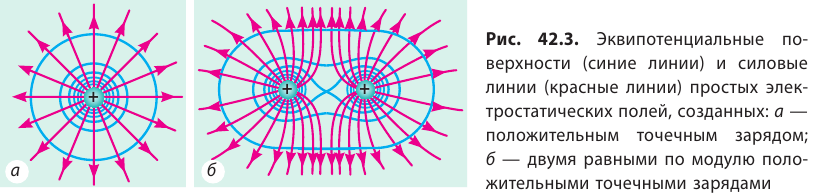
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.

• Заказать решение задач по физике

Пример решения задачи

Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона 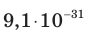кг, заряд 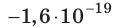Кл.

Заряд электрона — отрицательный, его начальная скорость 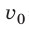= 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.

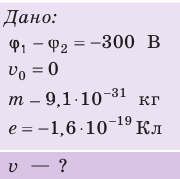
Решение:

Поиск математической модели, решение Согласно теореме о кинетической энергии:

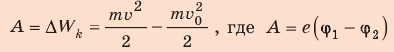— работа сил поля.

Таким образом, 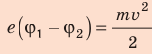, отсюда .

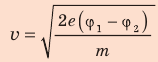Проверим единицу, найдем значение искомой величины:

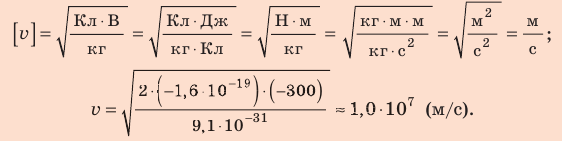
Ответ: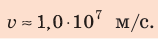

Выводы:

Если снять шерстяной свитер в сухую погоду, мы услышим треск. А если снимать свитер в темноте, иногда можно даже заметить искорки электрических разрядов.

Если расчесывать в сухую погоду сухие волосы пластмассовой расческой, то происходит ее электризация трением. Наэлектризованная расческа получит заряд и сможет притягивать небольшие кусочки бумаги.

Проделывая опыт с расческой и сухими волосами, можно убедиться, что наэлектризованные волосы и расческа буду притягиваться. Мы наблюдаем притяжение, значит, волосы и расческа обладают противоположными зарядами. Приближая расческу к волосам, обнаружим, что притяжение между ними возрастает.

Этот опыт позволил убедиться, что заряды действуют друг на друга на расстоянии. Чем ближе заряды находятся, тем сильнее их взаимное действие друг на друга.

Из механики известно, что существует ударное взаимодействие тел, когда, например, один бильярдный шар ударяется о другой такой же шар. В школьной физике рассматривают два вида ударного взаимодействия – абсолютно упругий и абсолютно неупругий удар.

Существует, так же, безударное взаимное действие тел – их притяжение, или отталкивание. К примеру, в механике, силу притяжения между телами, имеющими массу, вычисляют с помощью закона всемирного тяготения.

А силу взаимодействия электрических зарядов описывает закон Кулона.

Взаимодействие зарядов передается без участия вещества

Заряды будут притягиваться и отталкиваться не только в воздухе, но, даже в безвоздушном пространстве. В этом легко убедиться, если поместить заряженный электроскоп под колокол и откачать из-под колокола воздух. Полоски бумаги, имеющие одинаковые заряды, все так же, продолжат отталкиваться, независимо от того, в воздухе ли они находятся, либо в безвоздушном пространстве.

Это значит, что передача взаимодействия зарядов происходит не через вещество.

Ученые из Англии – Майкл Фарадей и Джеймс Максвелл, долгое время изучали электрические заряды. Они выяснили, что заряды окружены особым видом материи, которую они назвали электрическим полем.

Любой заряд окружен электрическим полем — особым видом материи.

Теории дальнодействия и близкодействия

Физики выдвигали различные теории, пытаясь объяснить взаимодействие зарядов. Наибольшее распространение получили две – их называют теориями близкодействия и дальнодействия.

Дальнодействие

Теория дальнодействия сообщает, что один заряд действует на другой заряд непосредственно. То есть, чтобы передать действие одного заряда на другой, посредники не нужны.

Кроме того, взаимодействие происходит мгновенно на любых расстояниях. Это значит, что если убрать один из взаимодействующих зарядов, то его действие на оставшийся заряд прекратится мгновенно.

Близкодействие

В противоположность этой теории Майкл Фарадей предложил свою теорию близкодействия.

Эта теория заявляет о том, что непосредственно действовать друг на друга заряды не могут. То есть, для передачи своего воздействия заряду нужна некоторый помощник. И каждый заряд создает в пространстве вокруг себя этого помощника. Фарадей назвал его электрическим полем.

На другие заряды будет действовать не сам заряд, а поле, созданное этим зарядом. Такое поле распространяется в пространстве не мгновенно, а с конечной скоростью.

Примечание: Как выяснилось позже, это очень большая скорость – триста тысяч километров в секунду. Ее называют скоростью света.

Поэтому, если один из взаимодействующих зарядов быстро убрать, то второй заряд узнает о его исчезновении не мгновенно, а через некоторое, пусть небольшое, время.

Получается, что взаимодействие зарядов протекает не непосредственно, а в виде цепочки. Каждый заряд создает вокруг себя поле, именно поле действует на другой заряд, помещенный в него.

А сила, действующая на заряд, расположенный в какой-либо точке пространства, зависит от характеристик поля в этой точке.

В настоящее время общепринятой теорией, объясняющей взаимодействие зарядов, является теория близкодействия Фарадея. Так как эта теория полностью подтвердилась экспериментально.

Примечание: Кроме электрических существуют, так же, магнитные поля. В отличие от электростатического, магнитное поле не имеет своих магнитных источников. Оно возникает в пространстве вокруг движущихся зарядов. То есть, магнитное поле – это поле электрических зарядов, находящихся в движении.

Джеймс Клерк Максвелл в середине 19-го века показал, что электрическое и магнитное поля связаны и это электромагнитное поле распространяется в пространстве с очень большой, но конечной скоростью.

Поле и вещество – это два вида материи

Мир, окружающий нас, материален. Значит, материя – это то, что существует реально, независимо от того, наблюдаем ли мы за ней, или нет.

Она может проявлять себя в виде двух частей — вещества и поля. Нас окружает вещество, а атомы и молекулы — это мельчайшие единицы вещества.

Поле – это еще один вид материи. Поле веществом не является, однако, оно существует реально.

Как обнаружить электрическое поле

Мы не чувствуем электрическое поле, так как у нас нет органов чувств, способных его обнаружить.

Но, используя нечто, что обладает чувствительностью к электрическому полю, можно убедиться, что поле, окружающее заряды, существует.

В качестве чувствительного элемента можно использовать любой электрический заряд. Потому, что любой заряд окружен своим собственным электрическим полем и, благодаря ему может чувствовать подобные поля, создаваемые другими зарядами. Такой заряд, используемый для обнаружения поля, физики называют пробным.

Примечания:

1. Некоторые живые существа могут чувствовать электрические поля, например, некоторые виды рыб.
2. Электрическое поле можно обнаружить по его действию на заряды, а, так же, с помощью различных приборов.
3. Поле заряда действует с некоторой силой на расположенный рядом другой заряд. То есть, заряды действуют друг на друга благодаря своим электрическим полям.

Мы можем обнаружить электрическое поле благодаря его действию на другие заряды. Электрическая сила — это сила, с которой поле действует на внесенный в него пробный заряд.

Примечание: Не следует путать пробный и элементарный заряд.

Две характеристики электростатического поля

Поле, окружающее неподвижные заряды, называют электростатическим полем.

Электрическое поле можно описать двумя величинами – векторной величиной — напряженностью (large vec{E}) и скалярной величиной – потенциалом (large varphi ).

Примечание: Применяют, так же, еще одну характеристику электрического поля — вектор электрической индукции (large vec{D}).

Описываем электрическое поле с помощью вектора

Рассмотрим два неподвижных точечных электрических заряда. Один заряд обозначим большой буквой Q:

(large Q left( text{Кл}right) ) – этот заряд создает вокруг себя электрическое поле.

Чтобы обнаружить это поле, на некотором расстоянии от заряда Q поместим еще один заряд.

(large r left( text{м}right) ) — расстояние между зарядами.

(large q left( text{Кл}right) ) — второй заряд, будем называть его пробным.

Примечания:

1. Заряд точечный, если его размерами можно пренебречь;
2. Обычно знак такого пробного заряда выбирают положительным. Пробный заряд имеет небольшую величину, такую, что поле, создаваемое им, на другие заряды почти не влияет.

Свойство 1: Поле, создаваемое зарядом, влияет только на другие заряды. Это поле не влияет на заряд, породивший его.

Благодаря своим электрическим полям заряды q и Q действуют друг на друга. Силу их взаимодействия можно рассчитать по закону Кулона:

[large |vec{F}| = k cdot frac {|q| cdot |Q|}{r^{2}} ]

(large F left( H right) ) – сила, с которой два точечных заряда притягиваются, или отталкиваются;

Для нас важным сейчас является само наличие взаимодействия. Чтобы не выяснять, будет ли сила воздействия силой притяжения, или отталкивания, каждый заряд поместим внутрь модуля.

Свойство 2: Электрическое поле, принадлежащее заряду Q в какой-либо точке пространства, не зависит от того, есть ли в этой точке какой-то другой заряд.

Что такое напряженность поля

Введем физическую величину, которая описывает поле заряда Q и не зависит от пробного q заряда. Для этого разделим обе части уравнения на пробный q заряд:

[large frac {|vec{F}|}{|q|} = k cdot frac {|Q|}{r^{2}} ]

Обратите внимание, что правая часть полученного уравнения не зависит от пробного заряда. Потому, что пробный заряд, обозначенный малой буквой q, не входит в правую часть. Правая часть зависит только от заряда, создавшего поле и обозначенного большой буквой Q.

Введем обозначение для дроби, расположенной в левой части полученного уравнения:

[large boxed { vec{E} = frac {vec{F}}{q} } ]

( large vec{E} left( frac {B}{text{м}} right) ) – напряженность электрического поля, измеряется в Вольтах, деленных на метр, или в Ньютонах, деленных на Кулон;

Напряженность электростатического поля в выбранной точке пространства – это векторная величина. Она равна отношению силы, действующей на пробный заряд, находящийся в выбранной точке поля к величине этого заряда. В различных точках поля силы могут быть разными, значит, будут различаться и напряженности в этих точках.

Чтобы найти (длину) модуль вектора E напряженности поля, создаваемого точечным зарядом, приравняем к величине E правую часть полученного выше выражения:

[large boxed {|vec{E}| = k cdot frac {|Q|}{r^{2}} } ]

(large k = 9cdot 10^{9}  left( H cdot frac{text{м}^{2}}{text{Кл}^{2}}right)) – постоянная величина;

(large |Q| left( text{Кл}right) ) — заряд, создающий в пространстве вокруг себя электрическое поле;

(large r left( text{м}right) ) – расстояние от заряда Q до точки, в которую мы поместили пробный заряд.

Примечание: Поле мы измеряем в той точке, в которую помещаем пробный заряд.

Напряженность – это вектор. Две главные характеристики вектора – его длина и направление.

Величина ( large vec{E} ) является силовой характеристикой электрического поля. Чем больше напряженность E, тем больше сила F, действующая на пробный заряд, помещенный в это поле.

[large boxed { frac {1 Н}{ 1 text{Кл}} = frac {1 B}{ 1 text{м}} } ]

Если на заряд 1 Кулон, помещенный в электростатическое поле, действует сила 1 Ньютон, то напряженность этого поля равна единице.

По третьему закону Ньютона, силы, с которыми взаимодействуют два заряда, будут равными.

Каждый неподвижный заряд создает свое собственное электростатическое поле. Если заряды имеют различные величины, то напряженности их полей различаются.

Куда направлен вектор Е

Обратим в очередной раз внимание на формулу:

[large vec{E} = frac {vec{F}}{q} ]

Заряд q – скалярная величина. А сила F – векторная.

Воспользуемся математическими свойствами векторов: разделив вектор F на скаляр q, мы получим новый вектор E:

1. его длина отличается от вектора F.
2. направления векторов F и E совпадают (либо векторы F и E направлены в противоположные стороны).

Вектор E сонаправлен с вектором силы, действующей на помещенный в поле пробный заряд. Для положительного заряда его вектор E направлен от этого заряда. А для отрицательного заряда его вектор E направлен к этому заряду.

Примечание: Однонаправленные или противоположно направленные, то есть, параллельные векторы, называют коллинеарными. У них может отличаться длина.

Как изменяется длина вектора Е с расстоянием

Длина вектора напряженности с расстоянием быстро убывает. Об этом можно судить с помощью формулы, описывающей модуль данного вектора:

[large E = k cdot frac {Q}{r^{2}} ]

Расстояние r возводится в квадрат и расположено в знаменателе. Это значит, что если расстояние увеличится в 2 раза, то напряженность уменьшится в 4 раза.

А если, например, расстояние увеличится в 3 раза, то напряженность уменьшится в 9 раз.

На рисунке 9 отражено изменение длины вектора напряженности. Обратите внимание на направление этого вектора и знак заряда:

Мы можем выразить зависимость напряженности от расстояния с помощью знака пропорции:

[large E sim frac {1}{r^{2}} ]

Подобную зависимость на графике можно отразить такой кривой:

Как видно из рисунка 10, увеличение расстояния до заряда в четыре раза вызывает ослабление напряженности его поля в шестнадцать раз.

Как по известной напряженности вычислить силу, с которой поле действует на заряд

Если известна напряженность поля, то силу, которая действует на заряд, помещенный в это поле, можно вычислить по формуле:

[large boxed{ vec{E} cdot q = vec{F} } ]

(large q left( text{Кл}right) ) – заряд, положительный, или отрицательный, помещенный в выбранную точку пространства, в которой существует электрическое поле;

Формула записана в векторном виде. Это значит, что она позволяет найти обе характеристики силы, действующей на заряд — направление вектора силы и его модуль.

Умножив заряд на напряженность в выбранной точке поля, можно вычислить силу, действующую на заряд со стороны поля.

Так как напряженность входит в формулу для вычисления силы, ее называют силовой характеристикой электрического поля.

Зная силу, мы можем по второму закону Ньютона вычислить ускорение заряда. А с помощью формул кинематики для равнопеременного движения, зная ускорение, можно определить перемещение заряда или траекторию его движения.

Как изобразить электрическое поле единичного заряда

Пусть неподвижный положительный точечный заряд создает в пространстве, окружающем его, электрическое поле. Нарисуем несколько векторов напряженности этого поля.

Красной точкой на рисунке обозначен заряд. А черным цветом обозначены точки, в которые помещали пробный заряд и измеряли поле.

По длине векторов можно сделать вывод, чем ближе к заряженному телу расположен пробный заряд, тем сильнее на него действует поле. Увеличив же расстояние между заряженным телом и пробным зарядом, заметим, что действие поля уменьшится.

Поля, действие которых будет различаться в разных точка пространства, называют неоднородными. Значит, электрическое поле вокруг точечных зарядов, неоднородное.

Изображаем неоднородное электрическое поле силовыми линиями

Как видно, мы можем изобразить поле с помощью нарисованных в различных точках векторов напряженности. Однако, есть более удобный способ.

Присмотревшись к рисунку, можно заметить, что векторы напряженности, окружающие заряд, располагаются на некоторых прямых. Эти прямые обозначены пунктирными линиями на рисунке. Из называют линиями электрического поля, или линиями напряженности.

Примечание: Изображать электростатическое поле удобнее не с помощью векторов, а с помощью линий напряженности.

Если заряд единственный, а поблизости от него других зарядов нет, то его поле изображают радиально расходящимися во все стороны линиями.

Линии положительных зарядов направлены от них, а линии отрицательных зарядов – к этим зарядам, так же, как векторы напряженности.

Мы помним, что вектор напряженности описывает силу, с которой поле, созданное зарядом может действовать на другие заряды. Поэтому, линии напряженности, так же, часто называют силовыми линиями поля.

Как выглядит поле двух взаимодействующих зарядов

Рассмотрим теперь поле взаимодействующих зарядов — положительного и отрицательного.

Как видно, линии взаимодействующих зарядов искривляются и, их конфигурация искажается.

Мы знаем, что поле одного точечного заряда неоднородное. Поле двух взаимодействующих зарядов, так же, неоднородное.

Теперь проведем обобщение, на рисунке неоднородное поле изображают:

• либо прямыми линиями, радиально расходящимися во все стороны от одиночного заряда, либо
• кривыми линиями, для взаимодействующих зарядов.

По мере удаления от зарядов расстояние между линиями будет увеличиваться. Чем дальше линии располагаются одна от другой в некоторой области пространства, тем слабее поле в этой области.

Будет ли поле действовать на заряд, расположенный между силовыми линиями

У начинающих изучать электростатику часто возникает вопрос, а будет ли на заряд, находящийся на рисунке между силовыми линиями, действовать сила с стороны электрического поля? Конечно, будет.

Не имеет значения, находится ли заряд на силовой линии на рисунке, или в пространстве между силовыми линиями. Поле существует во всех точках рассматриваемой области, поэтому на заряд будет действовать сила в любой точке поля, независимо, находится ли эта точка на силовой линии, или нет.

Примечание: Силовые линии – это всего лишь способ графического обозначения поля в некоторой области пространства. Поле существует во всех точках пространства, а не только на силовых линиях.

Свойства силовых линий электростатического поля

Можно выделить два свойства силовых линий поля, создаваемого неподвижными зарядами:

1. Силовые линии имеют начало и конец – они начинаются на положительных и заканчиваются на отрицательных зарядах.
2. Напряженность поля больше в той области, в которой линии располагаются гуще.

Примечание: Существует, так же, вихревое электрическое поле. Это поле не связано с неподвижными зарядами. Его линии замкнуты сами на себя. Картина такого поля представляет собой нечто похожее на вихрь, отсюда и появилось его название. Подробнее о вихревом электрическом поле написано в статье, посвященной электромагнитным волнам.

Поле сильней там, где его линии располагаются ближе одна к другой, а так же там, где длиннее вектор Е.

Где заканчиваются линии единственного заряда

Линии электростатического поля, начавшись на положительном заряде, должны закончиться на каком-либо отрицательном заряде.

Если поблизости от какого-либо заряда не располагается второй заряд, имеющий противоположный знак, то линии поля такого одинокого заряда уходят в бесконечность.

Там, далеко, на бесконечности, всегда найдется заряд, имеющий противоположный знак, на котором будут заканчиваться линии рассматриваемого одиночного заряда.

Почему заряды называют источниками электрического поля

Электростатическое поле имеет свои электрические источники.

Нам известно, что линии электростатического поля имеют начало и конец. Они начинаются на положительных зарядах, а на отрицательных зарядах заканчиваются.

Поэтому, положительные заряды называют источниками поля, а отрицательные – стоками.

Как изобразить однородное электрическое поле

Если равномерно распределить заряды по двум плоским поверхностям, расположив эти поверхности на некотором расстоянии параллельно, то в пространстве между этими поверхностями электрическое поле будет однородным.

Примечание: Система из двух параллельных проводящих поверхностей, расположенных на некотором расстоянии одна от другой, называют электрическим конденсатором.

Однородное поле на рисунке изображают параллельными прямыми линиями, расстояние между которыми не изменяется.

Такие поля можно создать только в некоторой ограниченной области пространства. Их удобно изучать, потому, что в любой точке такого поля вектор напряженности будет иметь одно и то же направление и длину.

Если во всех точках пространства, в которых существует электрическое поле, вектор напряженности имеет одинаковое направление и длину, то это поле называют однородным.

Примечание: Если говорить начистоту, то у концов плоских поверхностей линии поля будут искривляться. Это значит, что у краев поле не будет однородным.

Поэтому, для создания однородного электрического поля в учебной литературе рассматривают абстрактные бесконечно протяженные плоскости.

Читайте отдельную статью том, как обозначают распределенные заряды (откроется в новой вкладке).

Связь между векторами E неоднородного поля и линиями напряженности

Рассмотрим еще раз рисунок, на котором изображено поле двух взаимодействующих зарядов. Выберем на нем одну силовую линию. Вычислим длины нескольких векторов E и нарисуем их в выбранных точках, расположенных на этой линии.

Если через каждый вектор напряженности провести прямую линию, можно заметить, что эти линии образуют семейство касательных. Такие касательные прямые линии ограничивают собой кривую. Эта кривая и будет являться силовой линией.

Теперь можно дать определение силовых линий:

Силовая линия электростатического поля – это линия, касательная к которой в любой выбранной точке будет сонаправлена с вектором напряженности электрического поля в этой же точке.

В отдельной статье будет рассказано о работе электрического поля и еще одной его характеристике — потенциале.