Как найти пятого класса

5 класс – новый этап в школьном этапе обучения… Но все также большое количество домашней работы, теперь она только сложней и объемнее. Школьники начинают придумывать способы как поскорее избавиться от домашки и скорее пойти гулять с друзьями или просто отдохнуть. Бездумное списывание у одноклассников на переменках перед уроком обычно еще и с ошибками решенного задания, придумывание глупых отмазок “собака съела тетрадь с работой” и в том же духе обман. Все это обычно приводит к “двойкам” в дневнике и вызов родителей в школу…

Чтобы избежать этого, а выполнение уроков перестало быть нерешаемой проблемой, можно воспользоваться помощью ГДЗ для 5 класса. Ты найдешь решебник по любому предмету школьной программы 5 класса: Математика, Русский, Английский, Немецкий язык, География, История и другие дисциплины. Ответы на задания из учебников, рабочих тетрадей, книг для чтения, сборников задач, дидактических материалов дополнены краткими и доступными пояснениями или поэтапным решением. ГДЗ предназначено для того, чтобы помочь тебе с выполнением домашнего задания, ты можешь проверить правильность решенного упражнения и увидеть ошибки в решении. Мы надеемся, что решебник станет для тебя помощником.

Наименьшее общее кратное

Общее кратное

Число может быть кратно не одному, а сразу нескольким числам, такое число называется общим кратным данных чисел.

Числу 3 кратны числа: 6, 9, 12, 15 и т. д.

Числу 4 кратны числа: 8, 12, 16, 20 и т. д.

Можно заметить, что одно и тоже число (12) делится нацело сразу на оба числа 3 и 4. Следовательно, число 12 есть общее кратное чисел 3 и 4.

Общее кратное чисел — это любое число, которое делится без остатка на каждое из данных чисел.

Найти общее кратное нескольких натуральных чисел достаточно легко, можно просто перемножить данные числа, полученное произведение и будет их общим кратным.

Пример. Найти общее кратное для чисел 2, 3, 4, 6.

2 · 3 · 4 · 6 = 144.

Число 144 — общее кратное чисел 2, 3, 4 и 6.

Для любого количества натуральных чисел существует бесконечно много кратных.

Пример. Для чисел 12 и 20 кратными будут числа: 60, 120, 180, 240 и т. д. Все они являются общими кратными для чисел 12 и 20.

Наименьшее общее кратное

Наименьшее общее кратное (НОК) нескольких чисел — это самое маленькое натуральное число, которое делится без остатка на каждое из этих чисел.

Пример. Наименьшим общим кратным чисел 3, 4 и 9 является число 36, никакое другое число меньше 36 не делится одновременно на 3, 4 и 9 без остатка.

Наименьшее общее кратное записывается так:

Числа в круглых скобках могут быть указаны в любом порядке.

Пример. Запишем наименьшее общее кратное чисел 3, 4 и 9:

Как найти НОК

Рассмотрим два способа нахождения наименьшего общего кратного: с помощью разложения чисел на простые множители и нахождение НОК через НОД.

С помощью разложения на простые множители

Чтобы найти НОК нескольких натуральных чисел, надо разложить эти числа на простые множители, затем взять из этих разложений каждый простой множитель с наибольшим показателем степени и перемножить эти множители между собой.

Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.

Решение: разложим каждое из этих чисел на простые множители:

99 = 3 · 3 · 11 = 3 2 · 11 ,

54 = 2 · 3 · 3 · 3 = 2 · 3 3 .

Наименьшее общее кратное должно делиться на 99, значит, в его состав должны входить все множители числа 99. Далее НОК должно делиться и на 54, т. е. в его состав должны входить множители и этого числа.

Выпишем из этих разложений каждый простой множитель с наибольшим показателем степени и перемножим эти множители между собой. Получим следующее произведение:

2 · 3 3 · 11 = 594.

Это и есть наименьшее общее кратное данных чисел. Никакое другое число меньше 594 не делится нацело на 99 и 54.

Ответ: НОК (99, 54) = 594.

Так как взаимно простые числа не имеют одинаковых простых множителей, то их наименьшее общее кратное равно произведению этих чисел.

Пример. Найдите наименьшее общее кратное двух чисел 12 и 49.

Решение: разложим каждое из этих чисел на простые множители:

12 = 2 · 2 · 3 = 2 2 · 3,

Применяя к этому случаю правило, мы придём к заключению, что взаимно простые числа надо просто перемножить:

2 2 · 3 · 7 2 = 12 · 49 = 980.

Ответ: НОК (12, 49) = 980.

Таким же образом надо поступать, когда нужно найти наименьшее общее кратное простых чисел.

Пример. Найдите наименьшее общее кратное чисел 5, 7 и 13.

Решение: так как данные числа являются простыми, то просто перемножим их:

Ответ: НОК (5, 7, 13) = 455.

Если большее из данных чисел делится на все остальные числа, то это число и будет наименьшим общим кратным данных чисел.

Пример. Найдите наименьшее общее кратное чисел 24, 12 и 4.

Решение: разложим каждое из этих чисел на простые множители:

24 = 2 · 2 · 2 · 3 = 2 3 · 3,

12 = 2 · 2 · 3 = 2 2 · 3,

Можно заметить, что разложение большего числа содержит все множители остальных чисел, значит большее из этих чисел делится на все остальные числа (в том числе и само на себя) и является наименьшим общим кратным:

Ответ: НОК (24, 12, 4) = 24.

Нахождение НОК через НОД

НОК двух натуральных чисел равно произведению этих чисел, поделённого на их НОД.

Правило в общем виде:

Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.

Теперь мы можем вычислить НОК этих чисел по формуле:

НОК (99, 54) = 99 · 54 : НОД (99, 54) = 5346 : 9 = 594.

Ответ: НОК (99, 54) = 594.

Чтобы найти НОК трёх или более чисел используется следующий порядок действий:

1. Находят НОК любых двух из данных чисел.
2. Затем находят наименьшее общее кратное найденного НОК и третьего числа и т. д.
3. Таким образом поиск НОК продолжается до тех пор, пока есть числа.

Пример. Найдите наименьшее общее кратное чисел 8, 12 и 9.

Решение: сначала находим наибольший общий делитель любых двух из этих чисел, например, 12 и 8:

Вычисляем их НОК по формуле:

НОК (12, 8) = 12 · 8 : НОД (12, 8) = 96 : 4 = 24.

Теперь найдём НОК числа 24 и оставшегося числа 9. Их НОД:

Вычисляем НОК по формуле:

НОК (24, 9) = 24 · 9 : НОД (24, 9) = 216 : 3 = 72.

Ответ: НОК (8, 12, 9) = 72.

Калькулятор НОК

Данный калькулятор поможет вам найти наименьшее общее кратное чисел. Просто введите числа через пробел или запятую и нажмите кнопку Вычислить НОК .

Источник

Наименьшее общее кратное

Для того, чтобы находить общий знаменатель при сложении и вычитании дробей с разными знаменателями необходимо знать и уметь рассчитывать наименьшее общее кратное (НОК).

Кратное числу « a » — это число, которое само делится на число « a » без остатка.

Числа кратные 8 (то есть, эти числа разделятся на 8 без остатка): это числа 16, 24, 32 …

Кратные 9: 18, 27, 36, 45 …

Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество.

Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.

Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.

Как найти НОК

НОК можно найти и записать двумя способами.

Первый способ нахождения НОК

Данный способ обычно применяется для небольших чисел.

1. Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
2. Кратное числа « a » обозначаем большой буквой «К».

Пример. Найти НОК 6 и 8 .

Второй способ нахождения НОК

Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.

1. Разложить данные числа на простые множители. Подробнее правила разложения на простые множители вы можете прочитать в теме как найти наибольший общий делитель (НОД).
2. Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним — разложение остальных чисел.

Количество одинаковых множителей в разложениях чисел может быть разное.

Подчеркнуть в разложении меньшего числа (меньших чисел) множители, которые не вошли в разложение бóльшего числа (в нашем примере это 2 ) и добавить эти множители в разложение бóльшего числа.
НОК (24, 60) = 2 · 2 · 3 · 5 · 2

Полученное произведение записать в ответ.
Ответ: НОК (24, 60) = 120

Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК (12, 16, 24) .

24 = 2 · 2 · 2 · 3

Как видим из разложения чисел, все множители 12 вошли в разложение 24 (самого бóльшего из чисел), поэтому в НОК добавляем только одну 2 из разложения числа 16 .

НОК (12, 16, 24) = 2 · 2 · 2 · 3 · 2 = 48

Ответ: НОК (12, 16, 24) = 48

Особые случаи нахождения НОК

1. Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.

Например, НОК (60, 15) = 60
Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел.

На нашем сайте вы также можете с помощью специального калькулятора найти наименьшее общее кратное онлайн, чтобы проверить свои вычисления.

Источник

Математика. 5 класс

Конспект урока

Наименьшее общее кратное (НОК)

Перечень рассматриваемых вопросов:

– разложение на простые множители;

Кратное число – это число, делящееся на данное целое число без остатка.

Простое число – это такое натуральное число, которое больше 1 и делится только на 1 и само на себя.

Составные числа – это непростые натуральные числа, большие 1.

Взаимно простые числа – это числа, которые не имеют общих простых делителей

Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.

1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Ранее мы узнали, что такое кратное, ввели понятие делителя, научились находить наибольший общий делитель, а можно ли каким-либо способом найти общее кратное нескольких чисел? Оказывается, можно, этим сегодня мы и будем заниматься. Но находить не просто общее кратное нескольких чисел, а их наименьшее общее кратное – НОК.

Итак, для начала вспомним, что называется кратным. Это число, делящееся на данное натуральное число без остатка.

Теперь найдём, например, общие кратные чисел 12 и 15. Для этого выпишем все кратные чисел 12 и 15.

12 – его кратные 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …

15 – его кратные 15, 30, 45, 60, 75, 90, 105, 120, 135, …

Из представленных чисел общие кратные – это числа 60 и 120. Меньшее из них – 60. Это и есть наименьшее общее кратное чисел.

Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.

Для нахождения наименьшего общего кратного двух чисел можно использовать несколько способов. Один из них мы рассмотрели на примере нахождения НОК 12 и 15. Этот способ заключается в том, что выписываются все кратные двух чисел и затем находится наименьший общий из них.

Узнаем ещё одно правило нахождения НОК.

Во-первых, разложим числа на простые множители. Далее подчеркнём одинаковые множители этих чисел. Затем перемножим общие множители одного из чисел и добавим произведение всех остальных множителей от каждого числа. Это и будет НОК заданных чисел.

Найдём НОК (15; 16). Разложим числа на простые множители:

Видно, что из всех множителей общий лишь единица, значит, это взаимно простые числа.

НОК взаимно простых чисел – это произведение всех их множителей или произведение этих чисел.

В данном случае НОК равен 240.

Т. е. НОК любых двух простых чисел или двух соседних натуральных чисел будет равен произведению этих чисел.

Найдём НОК (10; 100). Разложим числа на простые множители:

Выделим общие делители у этих чисел, это 2 и 5.

Умножим их, а результат умножим ещё на оставшиеся простые множители от чисел 100 и 10.

НОК (10; 100) = 2 · 5 · 2 · 5 = 100

Обратите внимание на то, что 100 делится нацело на 10, и НОК тоже равен 100. Поэтому можно сделать вывод: если одно из двух чисел делится нацело на другое, то НОК этих чисел равен большему из них.

Некоторые задачи можно решить при помощи НОК проще, чем каким-либо другим способом. Например, рассмотрим такую задачу.

Девочка решила купить несколько плиток шоколада по 38 руб. , но у неё только 5-рублёвые монеты, а в магазине нет сдачи. Какое наименьшее количество плиток шоколада она сможет купить?

Решение: чтобы решить эту задачу, нужно найти НОК (5;38).

Разложим числа на множители:

Мы видим, что НОК (5; 38) = 5 · 38 = 190 – это будет сумма покупки за шоколад.

Теперь найдём, сколько девочка купит плиток.

Для этого сумму покупки разделим на стоимость одной плитки шоколада.

190 : 38 руб. = 5 – наименьшее количество плиток шоколада, которые сможет купить девочка.

№ 1. Какую цифру нужно подставить в число НОК (7; 2_) вместо пропуска, чтобы получить НОК = 21?

Варианты ответов: 1; 2; 3.

Решение: для решения этой задачи, надо разложить на множители оба числа, при этом вместо пропуска нужно подставить по порядку все цифры. А далее найти подходящий НОК этих чисел, равный 21.

Из всех разложений на множители под НОК (7; 2_) = 21 подходит только число 21.

Ответ: искомая цифра – 1.

№ 2. Какой наименьшей длины должен быть рулон ткани, чтобы от него без остатка можно было отрезать куски по 3 м и 7 м?

Решение: чтобы решить эту задачу, нужно найти НОК заданных чисел, он и будет являться искомым ответом, т. е. наименьшей длиной рулона ткани.

Источник

Нахождение наименьшего общего кратного: способы, примеры нахождения НОК

Продолжим разговор о наименьшем общем кратном, который мы начали в разделе « НОК – наименьшее общее кратное, определение, примеры». В этой теме мы рассмотрим способы нахождения НОК для трех чисел и более, разберем вопрос о том, как найти НОК отрицательного числа.

Вычисление наименьшего общего кратного (НОК) через НОД

Мы уже установили связь наименьшего общего кратного с наибольшим общим делителем. Теперь научимся определять НОК через НОД. Сначала разберемся, как делать это для положительных чисел.

Найти наименьшее общее кратное через наибольший общий делитель можно по формуле НОК ( a , b ) = a · b : НОД ( a , b ) .

Необходимо найти НОК чисел 126 и 70 .

Решение

Примем a = 126 , b = 70 . Подставим значения в формулу вычисления наименьшего общего кратного через наибольший общий делитель НОК ( a , b ) = a · b : НОД ( a , b ) .

Найдет НОД чисел 70 и 126 . Для этого нам понадобится алгоритм Евклида: 126 = 70 · 1 + 56 , 70 = 56 · 1 + 14 , 56 = 14 · 4 , следовательно, НОД ( 126 , 70 ) = 14 .

Вычислим НОК: НОК ( 126 , 70 ) = 126 · 70 : НОД ( 126 , 70 ) = 126 · 70 : 14 = 630 .

Ответ: НОК ( 126 , 70 ) = 630 .

Найдите нок чисел 68 и 34 .

Решение

НОД в данном случае нейти несложно, так как 68 делится на 34 . Вычислим наименьшее общее кратное по формуле: НОК ( 68 , 34 ) = 68 · 34 : НОД ( 68 , 34 ) = 68 · 34 : 34 = 68 .

Ответ: НОК ( 68 , 34 ) = 68 .

В этом примере мы использовали правило нахождения наименьшего общего кратного для целых положительных чисел a и b : если первое число делится на второе, что НОК этих чисел будет равно первому числу.

Нахождение НОК с помощью разложения чисел на простые множители

Теперь давайте рассмотрим способ нахождения НОК, который основан на разложении чисел на простые множители.

Для нахождения наименьшего общего кратного нам понадобится выполнить ряд несложных действий:

• составляем произведение всех простых множителей чисел, для которых нам нужно найти НОК;
• исключаем их полученных произведений все простые множители;
• полученное после исключения общих простых множителей произведение будет равно НОК данных чисел.

Этот способ нахождения наименьшего общего кратного основан на равенстве НОК ( a , b ) = a · b : НОД ( a , b ) . Если посмотреть на формулу, то станет понятно: произведение чисел a и b равно произведению всех множителей, которые участвуют в разложении этих двух чисел. При этом НОД двух чисел равен произведению всех простых множителей, которые одновременно присутствуют в разложениях на множители данных двух чисел.

У нас есть два числе 75 и 210 . Мы можем разложить их на множители следующим образом: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . Если составить произведение всех множителей двух исходных чисел, то получится: 2 · 3 · 3 · 5 · 5 · 5 · 7 .

Если исключить общие для обоих чисел множители 3 и 5 , мы получим произведение следующего вида: 2 · 3 · 5 · 5 · 7 = 1050 . Это произведение и будет нашим НОК для чисел 75 и 210 .

Найдите НОК чисел 441 и 700 , разложив оба числа на простые множители.

Решение

Найдем все простые множители чисел, данных в условии:

441 147 49 7 1 3 3 7 7

700 350 175 35 7 1 2 2 5 5 7

Получаем две цепочки чисел: 441 = 3 · 3 · 7 · 7 и 700 = 2 · 2 · 5 · 5 · 7 .

Произведение всех множителей, которые участвовали в разложении данных чисел, будет иметь вид: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 · 7 . Найдем общие множители. Это число 7 . Исключим его из общего произведения: 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 . Получается, что НОК ( 441 , 700 ) = 2 · 2 · 3 · 3 · 5 · 5 · 7 · 7 = 44 100 .

Ответ: НОК ( 441 , 700 ) = 44 100 .

Дадим еще одну формулировку метода нахождения НОК путем разложения чисел на простые множители.

Раньше мы исключали из всего количества множителей общие для обоих чисел. Теперь мы сделаем иначе:

• разложим оба числа на простые множители:
• добавим к произведению простых множителей первого числа недостающие множители второго числа;
• получим произведение, которое и будет искомым НОК двух чисел.

Вернемся к числам 75 и 210 , для которых мы уже искали НОК в одном из прошлых примеров. Разложим их на простые множители: 75 = 3 · 5 · 5 и 210 = 2 · 3 · 5 · 7 . К произведению множителей 3 , 5 и 5 числа 75 добавим недостающие множители 2 и 7 числа 210 . Получаем: 2 · 3 · 5 · 5 · 7 . Это и есть НОК чисел 75 и 210 .

Необходимо вычислить НОК чисел 84 и 648 .

Решение

Разложим числа из условия на простые множители: 84 = 2 · 2 · 3 · 7 и 648 = 2 · 2 · 2 · 3 · 3 · 3 · 3 . Добавим к произведению множителей 2 , 2 , 3 и 7 числа 84 недостающие множители 2 , 3 , 3 и
3 числа 648 . Получаем произведение 2 · 2 · 2 · 3 · 3 · 3 · 3 · 7 = 4536 . Это и есть наименьшее общее кратное чисел 84 и 648 ​​​​​​ ​.

Ответ: НОК ( 84 , 648 ) = 4 536 .

Нахождение НОК трех и большего количества чисел

Независимо от того, с каким количеством чисел мы имеем дело, алгоритм наших действий всегда будет одинаковым: мы будем последовательно находить НОК двух чисел. На этот случай есть теорема.

Предположим, что у нас есть целые числа a 1 , a 2 , … , a k . НОК m k этих чисел находится при последовательном вычислении m 2 = НОК ( a 1 , a 2 ) , m 3 = НОК ( m 2 , a 3 ) , … , m k = НОК ( m k − 1 , a k ) .

Теперь рассмотрим, как можно применять теорему для решения конкретных задач.

Необходимо вычислить наименьшее общее кратное четырех чисел 140 , 9 , 54 и 250 .

Решение

Введем обозначения: a 1 = 140 , a 2 = 9 , a 3 = 54 , a 4 = 250 .

Начнем с того, что вычислим m 2 = НОК ( a 1 , a 2 ) = НОК ( 140 , 9 ) . Применим алгоритм Евклида для вычисления НОД чисел 140 и 9 : 140 = 9 · 15 + 5 , 9 = 5 · 1 + 4 , 5 = 4 · 1 + 1 , 4 = 1 · 4 . Получаем: НОД ( 140 , 9 ) = 1 , НОК ( 140 , 9 ) = 140 · 9 : НОД ( 140 , 9 ) = 140 · 9 : 1 = 1 260 . Следовательно, m 2 = 1 260 .

Теперь вычислим по тому е алгоритму m 3 = НОК ( m 2 , a 3 ) = НОК ( 1 260 , 54 ) . В ходе вычислений получаем m 3 = 3 780 .

Нам осталось вычислить m 4 = НОК ( m 3 , a 4 ) = НОК ( 3 780 , 250 ) . Действуем по тому же алгоритму. Получаем m 4 = 94 500 .

НОК четырех чисел из условия примера равно 94500 .

Ответ: НОК ( 140 , 9 , 54 , 250 ) = 94 500 .

Как видите, вычисления получаются несложными, но достаточно трудоемкими. Чтобы сэкономить время, можно пойти другим путем.

Предлагаем вам следующий алгоритм действий:

• раскладываем все числа на простые множители;
• к произведению множителей первого числа добавляем недостающие множители из произведения второго числа;
• к полученному на предыдущем этапе произведению добавляем недостающие множители третьего числа и т.д.;
• полученное произведение будет наименьшим общим кратным всех чисел из условия.

Необходимо найти НОК пяти чисел 84 , 6 , 48 , 7 , 143 .

Решение

Разложим все пять чисел на простые множители: 84 = 2 · 2 · 3 · 7 , 6 = 2 · 3 , 48 = 2 · 2 · 2 · 2 · 3 , 7 , 143 = 11 · 13 . Простые числа, которым является число 7 , на простые множители не раскладываются. Такие числа совпадают со своим разложением на простые множители.

Теперь возьмем произведение простых множителей 2 , 2 , 3 и 7 числа 84 и добавим к ним недостающие множители второго числа. Мы разложили число 6 на 2 и 3 . Эти множители уже есть в произведении первого числа. Следовательно, их опускаем.

Продолжаем добавлять недостающие множители. Переходим к числу 48 , из произведения простых множителей которого берем 2 и 2 . Затем добавляем простой множитель 7 от четвертого числа и множители 11 и 13 пятого. Получаем: 2 · 2 · 2 · 2 · 3 · 7 · 11 · 13 = 48 048 . Это и есть наименьшее общее кратное пяти исходных чисел.

Ответ: НОК ( 84 , 6 , 48 , 7 , 143 ) = 48 048 .

Нахождение наименьшего общего кратного отрицательных чисел

Для того, чтобы найти наименьшее общее кратное отрицательных чисел, эти числа необходимо сначала заменить на числа с противоположным знаком, а затем провести вычисления по приведенным выше алгоритмам.

НОК ( 54 , − 34 ) = НОК ( 54 , 34 ) , а НОК ( − 622 , − 46 , − 54 , − 888 ) = НОК ( 622 , 46 , 54 , 888 ) .

Такие действия допустимы в связи с тем, что если принять, что a и − a – противоположные числа,
то множество кратных числа a совпадает со множеством кратных числа − a .

Необходимо вычислить НОК отрицательных чисел − 145 и − 45 .

Решение

Произведем замену чисел − 145 и − 45 на противоположные им числа 145 и 45 . Теперь по алгоритму вычислим НОК ( 145 , 45 ) = 145 · 45 : НОД ( 145 , 45 ) = 145 · 45 : 5 = 1 305 , предварительно определив НОД по алгоритму Евклида.

Получим, что НОК чисел − 145 и − 45 равно 1 305 .

Ответ: НОК ( − 145 , − 45 ) = 1 305 .

Источник

Основные правила математики с примерами. 5 класс

Содержание

Натуральные числа

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число 0 меньше любого натурального числа.

0<1, 0<100

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

4352⏟4>999⏟3

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

3561>3559

Свойства сложения

Переместительный закон: 

15+10=10+15

Сочетательный закон:

(23+15)+25=23+(15+25)

Формула пути

S=V·t
,где S — пройденный путь, V — скорость движения, t — время, за которое пройден путь S

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

2·x+10=16

x = 3 — корень, так как 
2·3+10=16

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

• Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

20слагаемое+xслагаемое=100суммаx = 100 — 20x = 80

• Чтобы найти неизвестное уменьшаемое, надо к разности при­бавить вычитаемое.

xуменьшаемое—10вычитаемое=40разностьx = 40 + 10x = 50

• Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

50уменьшаемое—xвычитаемое=40разностьx = 50 — 40x = 10

• Чтобы найти неизвестный множитель, надо произведение раз­делить на известный множитель.

xмножитель·7множитель=56произведениеx = 56 : 7x = 8

• Чтобы найти неизвестное делимое, надо делитель умножить на частное.

xделимое:8делитель=9частноеx = 9 · 8x = 72

• Чтобы найти неизвестный делитель, надо делимое разделить на частное.

42делимое:xделитель=7частноеx = 42 : 7x = 6

Отрезок, прямая, луч

Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

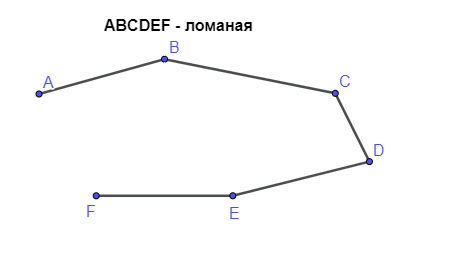
Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

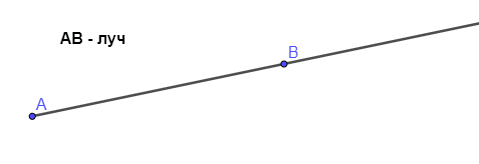
Луч

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Угол

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

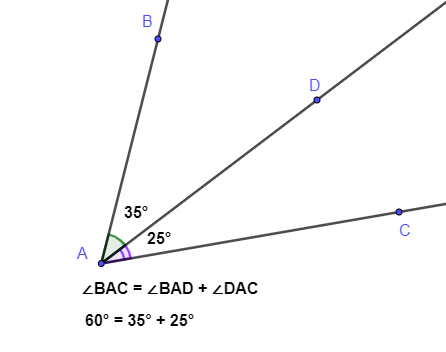
Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера  ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения

Умножение

• Если один из двух множителей равен 1, то произведение равно второму множителю.

• Если один из множителей равен нулю, то произведение равно нулю.

• Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

• Переместительный закон умножения:

• Сочетательный закон умножения: 

• Распределительное свойство умножения относительно сложения:  

2·(3+10) = 2·3 + 2·103·11 + 3·4 = 3·(11 + 4)

• Распределительное свойство умножения относительно вычитания:

2·(15—7) = 2·15 — 2·73·10 — 3·4 = 3·(10 — 4)

Деление. Деление с остатком

Деление

Для натуральных чисел равенство   является правильным, если является правильным равенство

15 : 5 = 3 -правильное равенство, так как  равенство 5 · 3 = 15 верное

В равенстве    число называют делимым, число — делителем, число и   запись  — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа  правильными являются равенства:

,

Деление с остатком

, где  — делимое, — делитель, — неполное частное, — остаток, .

154делимое=50делитель · 3неполное частное + 4остаток,    4<50

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

,

где  — площадь квадрата,  — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

• ,

где — объем параллелепипеда, , и  — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

• ,

где  — площадь основания параллелепипеда, — его высота.

Объем куба

,

где  — объем куба,  — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей

• Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

• Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

• Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

• Любая неправильная дробь больше любой правильной дроби.

Сложение и вычитание дробей с одинаковыми знаменателями

• Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

• Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

Сложение и вычитание смешанных чисел

• Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

• Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

• числитель разделить на знаменатель;
• полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

227= смешанное число? 7322—211  227=317      

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

• целую часть числа умножить на знаменатель дробной части;
• к полученному произведению прибавить числитель дробной части;
• эту сумму записать как числитель неправильной дроби;
• в его знаменателе записать знаменатель дробной части смешанного числа.

523= неправильная дробь?523=5*3+23=15+23=173

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

2,23  = 2,230 = 2,230000005,50000=5,50000=5,5

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

• с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
• после чего сравнить полученные дроби поразрядно.

Сравнить 5,03 и 5,0375.5,03⏟2=5,0300⏟4    и     5,0375⏟4  ; 5,0300 < 5,0375.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

• все следующие за этим разрядом цифры отбросить.
• если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4, то последнюю из цифр, которые оставляют, не меняют;
• если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

Округлить 5,248 и 3,952:а) до десятых:5,248≈5,2; 3,952≈4,0;б) до сотых:5,248≈5,25;3,952≈3,95.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

•  уравнять количество цифр после запятых;
•  записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
•  сложить полученные числа так, как складывают натуральные числа;
• поставить в полученной сумме запятую под запятыми.

Сложить 2,5 и 3,623.2,500⏟3 и 3,263⏟3;2,500+3,2635,763

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

•  уравнять количество цифр после запятых;
• записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
•  выполнить вычитание так, как вычитают натуральные числа;
• поставить в полученной разности запятую под запятыми.

Вычесть 3,27 и 3,009.3,270⏟3  и 3,009⏟3;3,270—3,0090,261

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

• перемножить их как натуральные числа, не обращая внимания на запятые;
• в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Умножить 1,5 и 2,25.2×2,2511,5+1125225·33,375 —количество цифр после запятой

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Умножить 1,235 на 10, 100, 1000.а) на 10:1,235 ×10⏟1=12,35б) на 100:1,235 ×100⏟2 = 123,5в) на 1000:1,235 ×1000⏟3=1235,0 = 1235

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Умножить 512,3 на 0,1,   0,01 и  0,001.а) на 0,1:512,3 ×0,1⏟1=51,23б) на 0,01:512,3 ×0,01⏟2=5,123в) на 0,001:512,3 ×0,001⏟3=0,5123

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

• перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
• выполнить деление на натуральное число.

Разделить 24,2 на 0,02.24,2 : 0,02⏟ 2= 2420,0 : 2 = 2420 : 2 = 1210.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

 Разделить 25,5 на 10, 100, 1000.а)  на 10:25,5 : 10⏟1=2,55;б) на 100:25,5 : 100⏟2=0,255;в)  на 1000:25,5 : 1000⏟3=0,0255;

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Примечание:

Процент

Процентом  называют сотую часть величины или числа 1%=

Найти 4% от числа 20.20 : 100 = 0,2  (0,2 —это 1% от числа 20);0,2 × 4 =0,8( 0,8—искомое число).Или   4% = 4100 = 0,04;0,04 ×20 = 0,8.