Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник». Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением Rэкв,
и вся схема представляется в виде схемы
на рис. 1.3, где R=Rэкв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.
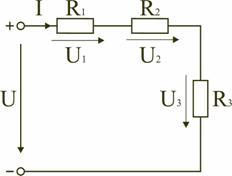
Электрическая
цепь с последовательным соединением
элементов
|
|
|
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U1
+ U2
+ U3 или
IRэкв
= IR1
+ IR2
+ IR3,
откуда
следует
(1.5)
Rэкв
= R1
+ R2
+ R3.
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
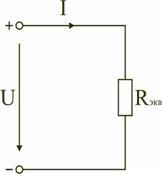
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением Rэкв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
,
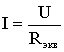и
по вышеприведенным формулам рассчитывают
падение напряжений U1,
U2,
U3
на соответствующих участках электрической
цепи (рис. 1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
Электрическая
цепь с параллельным соединением элементов
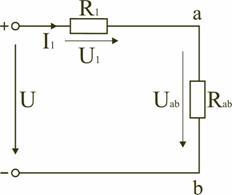
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
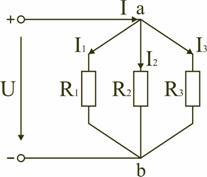
Рис.
1.6
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа (1.3) можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I1
+ I2
+ I3,
т.е.
,
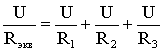откуда
следует, что
(1.6)
.
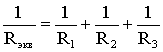В
том случае, когда параллельно включены
два сопротивления R1
и R2,
они заменяются одним эквивалентным
сопротивлением
(1.7)
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
gэкв
= g1
+ g2
+ g3.
По
мере роста числа параллельно включенных
потребителей проводимость цепи gэкв
возрастает, и наоборот, общее сопротивление
Rэкв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IRэкв
= I1R1
= I2R2 =
I3R3.
Отсюда
следует, что
,
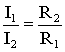т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
Электрическая
цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
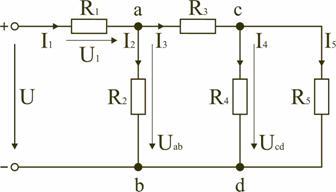
Рис.
1.7
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R1=R2=R3=R4=R5=R.
Сопротивления R4
и R5
включены параллельно, тогда сопротивление
участка цепи cd равно:
.
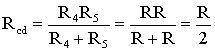В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
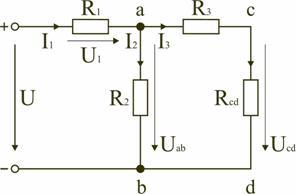
Рис.
1.8
На
схеме (рис. 1.8) сопротивление R3
и Rcd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
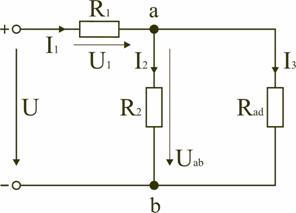
Рис.
1.9
На
схеме (рис. 1.9) сопротивление R2
и Rad
соединены параллельно, тогда сопротивление
участка цепи аb равно
.
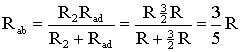Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R1
и Rab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
.
|
|
|
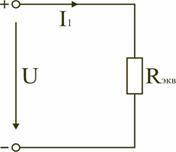
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
Rэкв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
Соединение
элементов электрической цепи по схемам
«звезда» и «треугольник»
В
электротехнических и электронных
устройствах элементы цепи соединяются
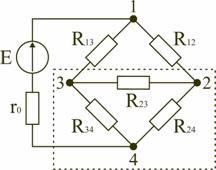
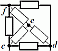
по мостовой схеме (рис. 1.12). Сопротивления
R12,
R13,
R24,
R34
включены в плечи моста, в диагональ 1–4
включен источник питания с ЭДС Е, другая
диагональ 3–4 называется измерительной
диагональю моста.
|
|
|
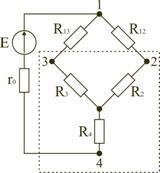
В
мостовой схеме сопротивления R13,
R12,
R23
и R24,
R34,
R23
соединены по схеме «треугольник».
Эквивалентное сопротивление этой схемы
можно определить только после замены
одного из треугольников, например
треугольника R24
R34
R23
звездой R2
R3
R4
(рис. 1.13). Такая замена будет
эквивалентной, если она не вызовет
изменения токов всех остальных элементов
цепи. Для этого величины сопротивлений
звезды должны рассчитываться по следующим
соотношениям:
(1.8)
;
;
.
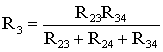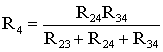Для
замены схемы «звезда» эквивалентным
треугольником необходимо рассчитать
сопротивления треугольника:
(1.9)
;
;
.
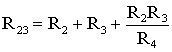После
проведенных преобразований (рис. 1.13)
можно определить величину эквивалентного
сопротивления мостовой схемы (рис. 1.12)
.
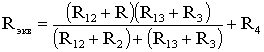Содержание
- 1 Как найти эквивалентное сопротивление в цепи?
- 2 Чему равно эквивалентное сопротивление?
- 3 Как найти R в параллельном соединении?
- 4 Как найти общее R?
- 5 Как найти эквивалентное сопротивление?
- 6 Как найти общий ток в цепи?
- 7 Как найти напряжение в электрической цепи?
- 8 Как складывается сопротивление?
- 9 Что называется эквивалентным сопротивлением?
- 10 Как найти ток в параллельной цепи?
- 11 Как складываются сопротивления при параллельном соединении?
- 12 Как найти емкость конденсатора при параллельном соединении?
- 13 Как найти сопротивление R?
- 14 Как найти коэффициент сопротивления воздуха?
Как найти эквивалентное сопротивление в цепи?
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
Чему равно эквивалентное сопротивление?
Резисторы соединены последовательно, если по ним течет один и тот же ток. Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме их сопротивлений: .
Общее сопротивление цепи при параллельном соединении проводников определяется по формуле: 1 R = 1 R 1 + 1 R 2 . Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников. Для проверки формулы можно использовать омметр.
Как найти общее R?
Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I. Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.
Как найти эквивалентное сопротивление?
3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R, где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Как найти общий ток в цепи?
Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений ; .
Как найти напряжение в электрической цепи?
Закон Ома для участка цепи:
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=frac.
- U — напряжение (в системе СИ измеряется — Вольт)
Как складывается сопротивление?
R = R1 + R2. При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников. Этот результат справедлив для любого числа последовательно соединенных проводников.
Что называется эквивалентным сопротивлением?
Если несколько сопротивлений соединенных последовательно, параллельно заменяется одним равным по значению, то такое сопротивление — эквивалентное.
Как найти ток в параллельной цепи?
Общая сила тока в параллельной цепи равна сумме силы тока на каждом элементе этой цепи. То есть, если известна сила тока на каждом резисторе, сложите эти силы тока, чтобы найти общую силу тока в параллельной цепи: IT = I1 + I2 + I3 + … Общее сопротивление в параллельной цепи.
Как складываются сопротивления при параллельном соединении?
Из закона Ома и первого и второго правил Кирхгофа следует: При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей. При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Как найти емкость конденсатора при параллельном соединении?
C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3, т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.
Как найти сопротивление R?
Сопротивление проводника прямо пропорционально напряжению на его концах и обратно пропорционально величине силы тока, протекающего через него. Формула для нахождения сопротивления по закону Ома, если известны сила тока и напряжение: R = U I {R= dfrac{U}{I}} R=IU, где R — сопротивление, U — напряжение, I — сила тока.
Как найти коэффициент сопротивления воздуха?
Pv = cx·S·v2·ρ/2, где S – площадь фронтальной проекции автомобиля, м2; v – скорость движения автомобиля относительно воздуха, м/с; ρ – плотность воздуха, кг/м3; cх – коэффициент аэродинамического сопротивления.
Главная
→
Примеры решения задач ТОЭ
→
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
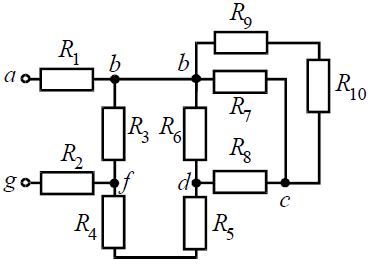
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
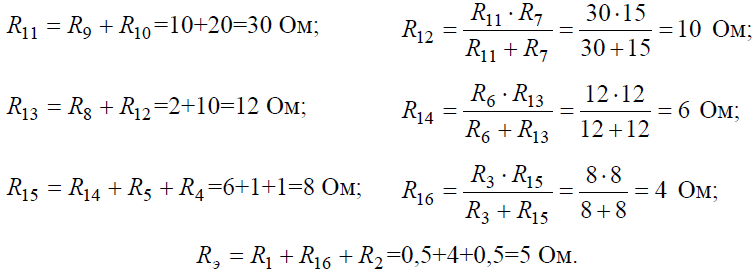
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
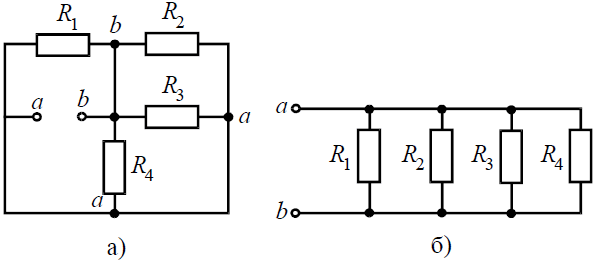Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
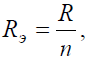где R — величина сопротивления, Ом;
n — количество параллельно соединенных сопротивлений.
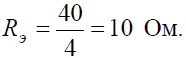
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
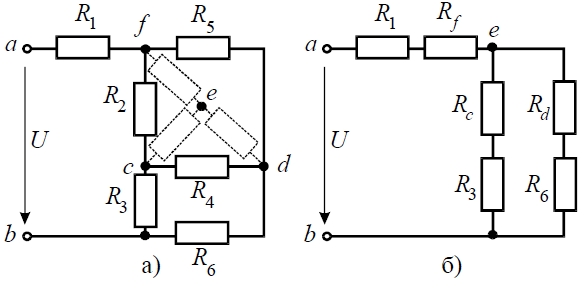
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
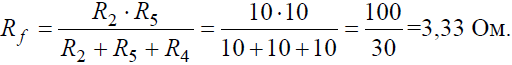По условию задачи величины всех сопротивлений равны, а значит:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
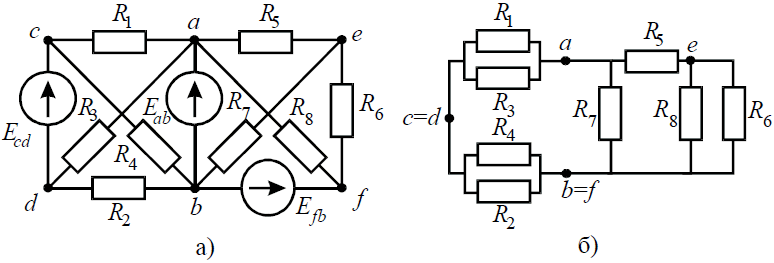
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
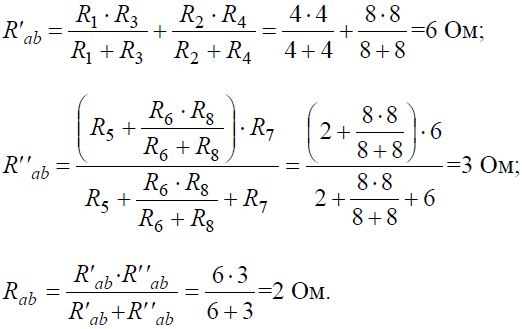
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
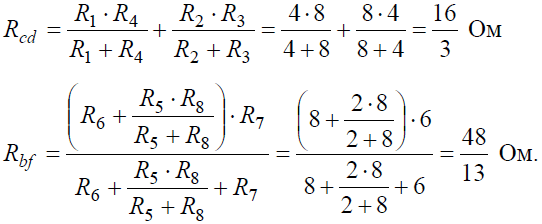
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
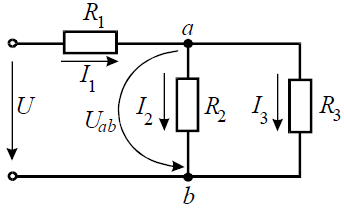
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
американские сигареты парламент.
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
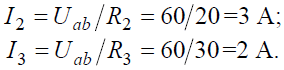
Баланс мощностей:
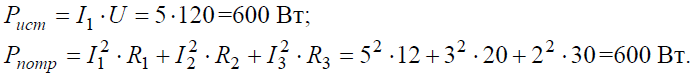
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
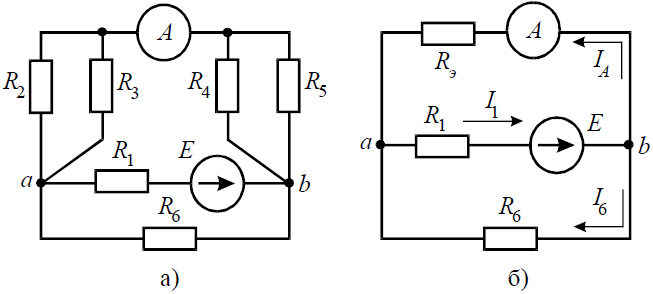
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
проститутки академическая. Смотри здесь строительство и ремонт деревянного дома.
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
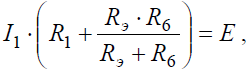
откуда ток I1:
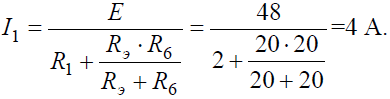
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
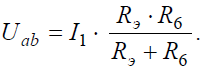
Тогда амперметр покажет ток:
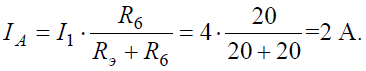
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
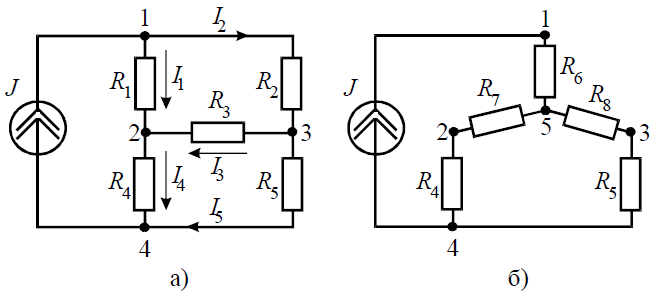
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
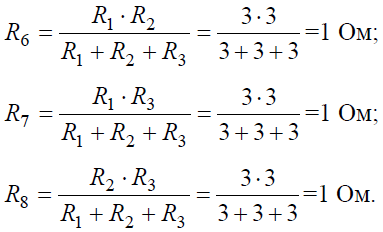
Преобразуем параллельное соединение ветвей между узлами 4 и 5
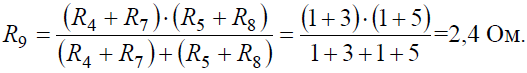
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
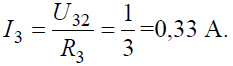
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
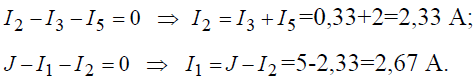
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Метод эквивалентных преобразований
Расчет эквивалентного сопротивления электрической цепи
Любое последовательное соединение можно преобразовать к последовательному соединению одного эквивалентного резистора и одного источника ЭДС. Причем, сопротивление эквивалентного резистора равно сумме всех сопротивлений входящих в соединение, а ЭДС эквивалентного источника равна алгебраической сумме ЭДС источников входящих в соединение.
R4=20 Ом, R5=40 Ом, R6=15 Ом (пример)
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.
9. СОЕДИНЕНИЕ ЗВЕЗДОЙ И ТРЕУГОЛЬНИКОМ
Схему еоедииения трех ветвей, образующих замкнутый контур с тремя узлами называют треугольником.
взаимные замены треугольника и звезды сопротивлений должны быть эквивалентными, т. е. при соответственно равных напряжениях между вершинами А, Б и В треугольника и звезды токи IA, IБ, 1В в подводящих проводах, соединяющих эти вершины с остальной частью цепи, должны остаться без изменений. Равенство токов должно выполняться при любых изменениях и переключениях в остальной части цепи и, в частности, при обрывах некоторых ее ветвей.
Рис 2.8 Соединение резисторов треугольником (а) и звездой (б)
Сопротивления эквивалентной звезды rа, rб, rв находятся в определенных соотношениях с сопротивлениями треугольника rаб, rбв, rва. Для выяснения этой зависимости допустим сначала, что в вершине А произошел обрыв подводящего провода и, следовательно, ток Iа=0. Сопротивления между двумя оставшимися присоединенными вершинами Б и В для обеих схем должны быть одинаковы, чтобы были соответственно равны токи IБ и Iв в обеих схемах.
Чтобы преобразовать треугольник в звезду при заданных сопротивлениях сторон треугольника rаб,rбв, rва, требуется определить сопротивления лучей эквивалентной звезды rа, rб, rв . Для этого составим полусумму левых и правых частей уравнений (2.15) и (2.16):
и вычтем из полученного выражения уменьшенные вдвое левую и правую части (2.14). В результате получим
(2.17)
Аналогично получим
(2.18)
(2.19)
сли сопротивления треугольника равны друг другу: rаб = rбв=rва=rΔ, то будут равны друг другу и сопротив
ления звезды, т. е. rа = rб=rв=r λ, причем из формул (2.17)—(2.19) получается простое соотношение
(2.20)
При обратном преобразовании звезды в эквивалентный треугольник, т. е. при заданных сопротивленияхrа, rб, rв, надо решить три уравнения (2.17)—(2 19) относительно сопротивлений rаб, rбв:
Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем же вершинам, что и сторона треугольника, и их произведения, деленного на сопротивление третьего луча звезды.
11. Режимы работы электрической цепи
· Режим короткого замыкания ( КЗ )
В режиме короткого замыкания источник питания замкнут накоротко. Режим является аварийным. Ток короткого замыкания КЗ во много раз превышает значение номинального тока.
Rн = 0 I = max
· Режим холостого хода ( ХХ )
В режиме холостого хода источник питания отсоединен от нагрузки и работает вхолостую. Сопротивление внешнего участка цепи и ток равен 0. Rн = ∞
· Режим согласованной нагрузки
Свойства электрической цепи – наибольшая мощность нагрузки развивается источником, когда сопротивление нагрузки ровно внутреннему сопротивлению источника.
Rн = I0
Из графика видно с ростом сопротивления нагрузки растёт мощность на нагрузке при Rн = I0 мощность нагрузки наибольшая при дальнейшем росте Rн – PRн уменьшается.
Мощность электрического тока
P = UI
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом. Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны. Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
Требуется рассчитать токи на всех резистивных элементах.
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте.
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Стоит заметить! Ток, протекающий через R4 и R5, по своему значению равен току на отрезке, не имеющем разветвления.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Equivalent resistance is defined as the total resistance of the circuit for the resistors connected in series or parallel combination. Resistors are electrical devices that limit the current flow in a circuit and obey Ohm’s law, V = IR. A circuit may have more than one resistor present due to which equivalent resistance is evaluated accordingly. The value of current and voltage depends on the orientation of resistors in the circuit.
In this article, we will learn about the Equivalent Resistance Formula in Series and Parallel combinations in detail.
What is the Equivalent Resistance?
Equivalent Resistance is the total resistance of the combination of all the resistances in the circuit. Suppose there are n resistance added in the circuit either in series or in parallel combination and if we replace all the resistance with a single resistance such that the current and the voltage difference in the circuit do not change it is called equivalent resistance.
Unit of Equivalent Resistance
Equivalent resistance is denoted by the symbol Req. SI unit of the measurement of Equivalent Resistance is Ohm (Ω) and the dimensional formula of the Equivalent Resistance [M1L2A−2T−3].
Formula for Equivalent Resistance
Equivalent Resistance is calculated using the Equivalent Resistance Formula, and the equivalent resistance formula is different in series and parallel combinations, i.e., we have two different equivalent resistance formulas they are,
- Equivalent Resistance Formula for Series Combination.
- Equivalent Resistance Formula for Parallel Combination.
Now, let’s learn about both formulas in detail in this article,
Equivalent Resistance Formula for Series Combination
In a series circuit of resistors, n resistors (n > 1) are connected adjacently one after the other, such that the collection of these resistors can be replaced by a single equivalent resistor to give the same resistance value. Here, the sum of the individual resistances will be the equivalent resistance of a series of resistors. The current through each resistor is the same but the voltage gets divided into n parts among the resistors.
.png)
Req = R1 + R2 + R3 + ….. + Rn
where,
Req is the equivalent resistance,
R1 is the resistance of the first resistor,
R2 is the resistance of the second resistor,
R3 is the resistance of the third resistor,
Rn is the resistance of the nth resistor,
Equivalent Resistance Formula for Parallel Combination
In a parallel circuit of resistors, n resistors (n > 1) are connected parallelly via wires that start from a common point. Here, the sum of the reciprocals of individual resistances equals the reciprocal of the equivalent resistance. The voltage through each resistor is the same but the current gets divided into n parts among the resistors.
.png)
1/Req = 1/R1 + 1/R2 + 1/R3 + ….. + 1/Rn
where,
Req is the equivalent resistance,
R1 is the resistance of the first resistor,
R2 is the resistance of the second resistor,
R3 is the resistance of the third resistor,
Rn is the resistance of the nth resistor,
How to find Equivalent Resistance?
The equivalent resistance of any circuit can easily be calculated using the steps given below,
Step 1: Study the electric circuit and mark all the resistance in the circuit along with the voltage of the battery.
Step 2: Check whether the resistance added is in series or parallel combination or both.
Step 3: Use the Equivalent Resistance Formula for Series Combination or Parallel combination accordingly.
Step 4: Simplify the formula in step 3 to get the Equivalent Resistance.
Read, More
- Electrical Resistance and Resistivity
- Temperature Dependence of Resistance
- Electrical Resistance Formula
Solved Examples on Equivalent Resistance Formula
Example 1: What is the equivalent resistance if three resistances of 4 Ω, 2 Ω, and 5 Ω are connected in series?
Solution:
We have,
R1 = 4 Ω
R2 = 2 Ω
R3 = 5 ΩUsing the formula we get,
Req = R1 + R2 + R3
= 4 + 2 + 5
= 11 Ω
Example 2: Find the unknown resistance if three resistances of 2 Ω, 5 Ω, and x Ω are connected in series to give an equivalent resistance of 10 Ω.
Solution:
We have,
R1 = 2 Ω
R2 = 5 ΩReq = 10 Ω
Using the formula we get,
Req = R1 + R2 + R3
10 = 2 + 5 + x
10 = 7 + x
x = 3 Ω
Example 3: Find the unknown resistance if three resistances of 7 Ω, 3 Ω, and X Ω are connected in series to give an equivalent resistance of 15 Ω.
Solution:
We have,
R1 = 7 Ω
R2 = 3 ΩReq = 15 Ω
Using the formula we get,
Req = R1 + R2 + R3
15 = 7 + 3 + X
15 = 10 +
x = 5 Ω
Example 4: What is the equivalent resistance if three resistances of 6 Ω, 3 Ω, and 8 Ω are connected in parallel?
Solution:
We have,
R1 = 6 Ω
R2 = 3 Ω
R3 = 8 ΩUsing the formula we get,
1/Req = 1/R1 + 1/R2 + 1/R3
1/Req = 1/6 + 1/3 + 1/8
1/Req = (4+8+3)/24
1/Req = 15/24
Req = 24/15 Ω = 1.6 Ω
Example 5: Find the unknown resistance if three known resistances of 4 Ω, 2 Ω, and 1 Ω connected in series with an unknown resistance of X Ω give an equivalent resistance of 0.5 Ω.
Solution:
We have,
R1 = 4 Ω
R2 = 2 Ω
R3 = 1 ΩReq = 0.5 Ω
Using the formula we get,
1/Req = 1/R1 + 1/R2 + 1/R3 + 1/R4
1/0.5 = 1/4 + 1/2 + 1/1 + 1/R4
1/R4 = 1/4 + 1/2 + 1/1 – 1/0.5
1/R4 = 1/4
R4 = 4 Ω
FAQs on Equivalent Resistance Formula
Question 1: What is the “equivalent resistance” formula in the Series combination?
Answer:
The “equivalent resistance” formula in the Series combination is given below,
Req = R1 + R2 + R3 + ….. + Rn
Question 2: What is the condition for the series combination of resistance?
Answer:
For the resistor to be connected in series combination the important conditions are,
- The current passing through each resistor is the must be same.
- The resistors are connected in a linear manner.
Question 3: What is the “equivalent resistance” formula in the Parallel combination?
Answer:
The “equivalent resistance” formula in the Parallel combination is given below,
1/Req = 1/R1 + 1/R2 + 1/R3 + ….. + 1/Rn
Question 4: What is the condition for the parallel combination of resistance?
Answer:
For the resistor to be connected in parallel combination the important conditions are,
- The voltage difference across each resistor is the same.
- The resistors are connected parallel to each other.
Last Updated :
21 Mar, 2023
Like Article
Save Article
