Модуль изменения импульса |Δp| камня, брошенного под углом к горизонту, за время полёта равен 2,4 кг • м/с. Дальность полета S = 5 м. Масса камня m = 0,2 кг. Найти работу, совершаемую при бросании камня.
Источник: “Методические указания и задания для индивидуальной работы со студентами по разделу МЕХАНИКА”, Московский технический университет связи и информатики.
Ответ: A = Δp2/(8m) + s2m3g2/(2Δp2). Но непонятно, как этот ответ должен быть получен.
Теги:
- криволинейное движение
- законы сохранения
- импульс
- задачи с подсказками
- версия для печати
Тема: Работа, совершенная при бросании тела (Прочитано 15080 раз)
0 Пользователей и 1 Гость просматривают эту тему.
inna213
Тело массой 1 кг, брошенное под углом 30°, достигло максимальной высоты 5 м. Работа, совершённая при бросании тела, равна…
Капельян, Малашонок, 2011 г, стр 64 №9
« Последнее редактирование: 15 Декабря 2012, 15:49 от alsak »

Записан
Работа, совершенная при бросании тела, равна изменению кинетической энергии тела. Но так как тело вначале не двигалось, то Wk0 = 0 и
A = ΔWk = Wk.
Найдем скорость тела сразу же после броска. Для этого воспользуемся следующими уравнениями (и учтем, что на максимальной высоте υy = 0) (рис. 1):
[begin{array}{c} {h_{max } =frac{upsilon _{y}^{2} -upsilon _{0y}^{2} }{2g_{y} } =frac{upsilon _{0y}^{2} }{2g} ,; ; ; upsilon _{0y}^{2} = 2gcdot h,} \ {upsilon _{0} =frac{upsilon _{0y} }{sin alpha },; ; ; A=W_{k} =frac{mcdot upsilon _{0}^{2} }{2} =frac{m}{2} cdot frac{upsilon _{0y}^{2} }{sin ^{2} alpha } =frac{m}{2} cdot frac{2gcdot h}{sin ^{2} alpha } = frac{mcdot gcdot h}{sin ^{2} alpha } ,} end{array}]
А = 200 Дж.
PS Тема «Движение под углом к горизонту» не входит в школьную программу по физики РБ, и ее нет в программе для подготовки к ЦТ.
« Последнее редактирование: 13 Января 2013, 13:02 от alsak »

Записан
inna213

Записан
Движение тела под углом к горизонту, теория и онлайн калькуляторы
Движение тела под углом к горизонту
Начальные условия
Рассмотрим движение тела (материальной точки) брошенного под углом к горизонту с некоторой высоты $h_0$. Начальная
скорость тела равна ${overline{v}}_0$, вектор ${overline{v}}_0$ составляет угол $alpha $ с горизонтом (рис.1). Систему отсчета, в которой движется тело, свяжем с Землей. Ось X направим параллельно земле, ось Y вертикально вверх.
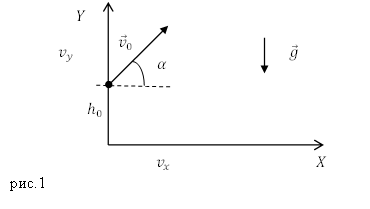
Движение тела под углом к горизонту происходит в поле тяжести Земли под воздействием силы тяжести. Силой сопротивления воздуха пренебрежём. В этом случае ускорение тела ($overline{a}$) совпадает с ускорением свободного падения ($overline{g}$):
[overline{a}=overline{g}left(1right),]
где $g=9,8 frac{м}{с^2}$.
Запишем начальные условия движения тела (рис.1):
[ left{ begin{array}{c}
xleft(t=0 right)=0, \
yleft(t=0 right)=h, \
v_xleft(t=0 right){=v}_{0x}=v_0{cos alpha , } \
v_yleft(t=0 right){=v}_{0y}=v_0{sin alpha . } end{array}
right.left(2right).]
Уравнение для перемещения тела, брошенного под углом к горизонту. Траектория его движения
Перемещение тела, которое бросили под углом к горизонту является равноускоренным, следовательно, для написания уравнения движения воспользуемся векторным уравнением для перемещения ($overline{s}$) при равнопеременном движении в виде, учтем равенство (1):
[overline{s}(t)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(3right).]
Векторное уравнение (3) в проекции на оси координат X и Y даст нам два скалярных уравнения:
[left{ begin{array}{c}
x(t)=v_0{cos alpha }t \
y(t)=h_0+v_0{sin alpha }t-frac{gt^2}{2} end{array}
right.left(4right).]
Из системы уравнений (4) мы видим, что при рассматриваемом нами движении происходит наложение двух прямолинейных движений.
Причем по оси X тело под углом к горизонту движется с постоянной скоростью ${ v}_{0x}=v_0{cos alpha , }$ а по оси Y материальная точка перемещается с постоянным ускорением $overline{g}$. Уравнение траектории движения тела можно получить, если из первого уравнения системы (4) выразить время ($t$) полученный результат подставить во вторую формулу системы:
[t=frac{x}{v_0{cos alpha }};; ]
[y(x)=h_0 tg alpha -frac{g}{2}{left(frac{x}{v_0{cos б }}right)}^2left(5right).]
Уравнение $y(x)$ (функция (5)) показывает, что тело движется по параболе в плоскости, в которой лежат векторы $overline{g}$ и ${overline{v}}_0.$
Уравнение скорости движения тела брошенного под углом к горизонту
В векторном виде уравнение для скорости движения рассматриваемого нами тела в произвольный момент времени запишем:
[overline{v}(t)={overline{v}}_0+overline{g}tleft(6right).]
В скалярном виде уравнение (6) представим в виде системы уравнений:
[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(7right).]
В системе уравнений (7) мы еще раз видим, что движение тела под углом к горизонту по оси X равномерное, по оси Y равнопеременное. Причем, двигаясь вверх, тело уменьшает свою скорость от $v_{0y}$ до нуля, затем падая вниз скорость тела увеличивается.
Модуль вектора скорости в производный момент времени для рассматриваемого нами движения найдем как:
[v=sqrt{v^2_x{+v}^2_y left(8right).}]
Время подъема и полета тела
Время, которое тело тратит на полет вверх в рассматриваемом движении можно найти из второго уравнения системы (7). В точке максимального подъема вектор скорости точки параллелен оси X, значит $v_y=0$, тогда время подъема ($t_p$):
[t_p=frac{v_0{sin alpha }}{g}left(9right).]
Время, которое тело находилось в воздухе (время полета($t_{pol}$)) получим из второго уравнения системы (4), приравняв ординату $y$ к нулю:
[t_{pol}=frac{v_0{sin alpha +sqrt{v^2_0{sin}^2alpha +2gh_0} }}{g}left(10right).]
При $h_0=0$ мы видим, что $t_{pol}=2t_p.$
Дальность полета и высота подъема
Для того чтобы найти горизонтальную дальность полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (4) подставим время полета ($t_{pol}$) (10). При $h_0=0,$ дальность полета равна:
[s=frac{v^2_0{sin left(2alpha right) }}{g}left(11right).]
Максимальную высоту подъема тела под углом к горизонту ($h_{max}$) находят из второго уравнения системы (4), подставляя в него время подъема ($t_p$) (9):
[h_{max}=h_0+frac{{v_0}^2{{sin}^2 б }}{2g}left(12right).]
Примеры задач с решением
Пример 1
Задание. Каким будет угол ($alpha $) под которым бросили тело к горизонту, если оказалось, что максимальная высота подъема ($h$) тела в четыре раза меньше, чем дальность его полета ($s$)? Сопротивление воздуха можно не учитывать.
Решение. Выберем систему отсчета связанную с Землей. Будем считать, что тело бросили из начала координат (рис.2).
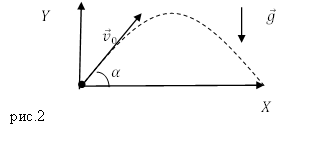
Запишем кинематические уравнения движения тела в поле тяжести земли:
[overline{s}(t)={overline{s}}_0+{overline{v}}_0t+frac{overline{g}t^2}{2}left(1.1right).]
[overline{v}(t)={overline{v}}_0+overline{g}tleft(1.2right)]
Исходя из начальных условий, нашей задачи:
[left{ begin{array}{c}
{overline{s}}_0=0 \
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha } end{array}
right. left(1.3right).]
В проекциях на оси уравнения (1.1) и (1.2)предстанут в виде:
[left{ begin{array}{c}
x(t)=v_0{cos alpha }t \
y(t)=v_0{sin alpha }t-frac{gt^2}{2} end{array}
right.left(1.4right).]
[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(1.5right).]
Время подъема из второго уравнения системы (1.5) равно:
[t_p=frac{v_0{sin alpha }}{g} left(1.6right).]
Тогда максимальная высота подъема равна:
[h=yleft(t_pright)=frac{v^2_0{sin}^2alpha }{2g}left(1.7right).]
Если тело бросили из начала координат, то $t_{pol}=2t_p,$ дальность полета найдем, подставив время полета в первое уравнение системы (1.4):
[s=xleft(t_{pol}right)=2v^2_0frac{{{cos alpha }sin alpha }}{g} left(1.8right).]
По условию задачи: $h=frac{s}{4}$, используем уравнения (1.7) и (1.8):
[frac{v^2_0{sin}^2alpha }{2g}=v^2_0frac{{{cos alpha }sin alpha }}{2g}to {sin alpha }={cos alpha }to alpha =frac{pi }{4}.]
Ответ. $alpha =frac{pi }{4}$
Пример 2
Задание. Какова скорость падения тела брошенного под углом горизонта $alpha $ со скоростью $v_0$? Если тело бросили с земли. Сопротивление воздуха можно не учитывать.
Решение. За основу решения задачи примем кинематическое уравнение для скорости движения тела в поле тяжести Земли:
[overline{v}left(tright)={overline{v}}_0+overline{g}tleft(2.1right).]
Начальные условия движения нашего тела:
[left{ begin{array}{c}
{overline{s}}_0=0 \
v_{0x}=v_0{cos alpha , } \
v_{0y}=v_0{sin alpha } end{array}
right. left(2.2right).]
В проекциях на оси X и Y уравнение (2.1):
[left{ begin{array}{c}
v_xleft(tright)=v_0{cos alpha , } \
v_yleft(tright)=v_0{sin alpha }-gt end{array}
right.left(2.3right).]
Время подъёма тела, принимая во внимание, что $v_yleft(t_pright)=0$ из второго уравнения (2.3) равно:
[t_p=frac{v_0{sin alpha }}{g} left(2.4right).]
Если тело бросили из начала координат, то $t_{pol}=2t_p:$
[t_{pol}=frac{2v_0{sin alpha }}{g}left(2.5right).]
Зная время полета, найдем $v_yleft(t_{pol}right)$, подставив его во второе уравнение (2.3):
[v_yleft(t_{pol}right)=-v_0{sin alpha left(2.6right). }]
Модуль вектора скорости в момент падения найдем как:
[v(t_{pol})=sqrt{v^2_x{+v}^2_y }=v_0.]
Ответ. При заданных условиях величина скорости падения равна модулю скорости бросания.
Читать дальше: динамика прямолинейного движения связанных тел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.
Кинематические характеристики движения
Важные факты!
Графически движение горизонтально брошенного тела описывается следующим образом:
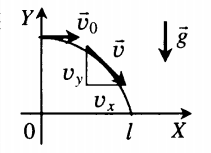
- Вектор скорости горизонтально брошенного тела направлен по касательной к траектории его движения.
- Проекция начальной скорости на ось ОХ равна v0: vox = v0. Ее проекция на ось ОУ равна нулю: voy = 0.
- Проекция мгновенной скорости на ось ОХ равна v0: vx = v0. Ее проекция на ось ОУ равна нулю: vy = –gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
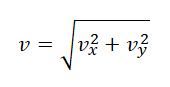
Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:
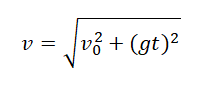
Минимальная скорость в течение всего времени движения равна начальной скорости: vmin = v0.
Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: vmax = v.
Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
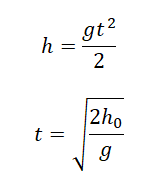
h0 — высота, с которой тело бросили в горизонтальном направлении.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0tпад
Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид:
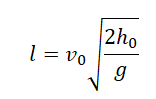
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
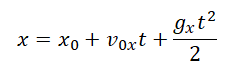
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:
x = v0t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
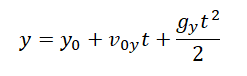
Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?
Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:
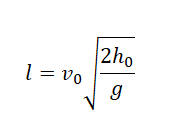
Выразим начальную скорость и вычислим ее:
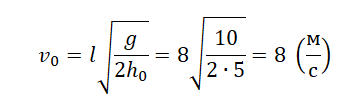
Горизонтальный бросок тела с горы
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.
График горизонтального броска тела с горы
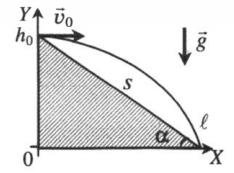
α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения
Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
l = s • cosα
Начальная высота — высота, с которой было брошено тело. Обозначается h0. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:
h0 = s sinα
Пример №2. На горе с углом наклона 30о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
Выразим это расстояние через дальность полета:
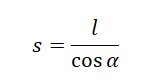
Дальность полета выражается по формуле:
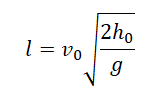
Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:
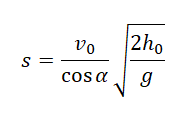
Выразим с учетом формулы начальной высоты:
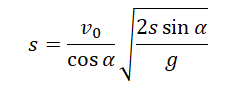
Преобразуем:
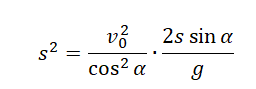
Поделим обе части выражения на общий множитель s:
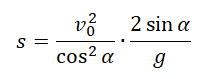
Подставим известные значения:
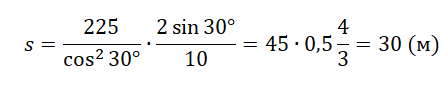
Задание EF18083
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
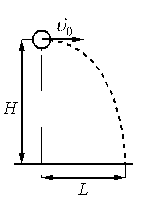
В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2υ0.
Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости и массы.
- Определить характер изменения физической величины при увеличении начальной скорости и массы шарика.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
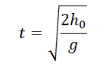
Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
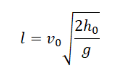
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 313.
Ответ: 313
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18048
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
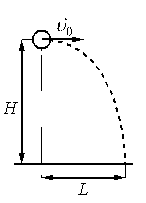
Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости.
- Определить характер изменения физической величины при уменьшении начальной скорости.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
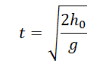
Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
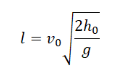
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 323.
Ответ: 323
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 18.1k
Что такое движение тела брошенного под углом к горизонту
Определение
Движением тела под углом к горизонту в физике называют сложное криволинейное перемещение, которое состоит из двух независимых движений, включая равномерное прямолинейное движение в горизонтальном направлении и свободное падение по вертикали.
В процессе подбрасывания объекта вверх под углом к горизонту вначале наблюдают его равнозамедленный подъем, а затем равноускоренное падение. Скорость перемещения тела, относительно поверхности земли, остается постоянной.
На графике изображено схематичное движение тела, которое подбросили под углом к горизонту. В этом случае α является углом, под которым объект начал свое перемещение. Характеристики такого процесса будут следующими:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Направление вектора скорости тела, которое подбросили под определенным углом к горизонту, будет совпадать с касательной к траектории его перемещения.
- Начальная скорость отличается от направления горизонтальной линии, а обе ее проекции не равны нулю.
- Проекция скорости в начале движения на ось ОХ составляет (V_{ox}=V_{0}cos alpha).
- Проекция начальной скорости на ось ОУ равна (V_{oy}=V_{0}sin alpha).
- Проекция мгновенной скорости на ось ОХ следующая: (V_{x}=V_{0}cos alpha).
- Проекция мгновенной скорости на ось ОУ обладает нулевым значением и рассчитывается следующим образом: (V_{x}=V_{0}sin alpha-gt).
- Ускорение свободного падения на ось ОХ обладает нулевой проекцией, или (g_{x}=0).
- Проекция ускорения свободного падения на ось ОУ равна (–g), или (g_{y}=-g).
К числу кинематических характеристик движения тела, которое подбросили под углом к горизонту, относят модуль мгновенной скорости в определенное время t. Данный показатель можно рассчитать с помощью теоремы Пифагора:
(V=sqrt{V^{2}_{x}+V^{2}_{y}})
Минимальная скорость тела будет замечена в самой верхней точке траектории, а максимальная величина данной характеристики будет достигнута, когда объект только начинает перемещаться, а также в точке падения на поверхность земли. Время подъема представляет собой время, необходимое для достижения телом верхней точки траектории. За полное время объект совершает полет, то есть перемещается от начальной точки к точке приземления.
Дальность полета является перемещением объекта по отношению к оси ОХ. Такую кинематическую характеристику обозначают буквой l. По отношению к оси ОХ тело перемещается, сохраняя постоянство скорости.
Определение
Горизонтальным смещением тела называют смещение данного объекта, относительно оси ОХ.
Расчет горизонтального смещения тела в какой-либо момент времени t выполняют с помощью уравнения координаты х:
(x=x_{0}+V_{0x}t+frac{gxt^{2}}{2})
Зная следующие условия:
- (x_{0}=0);
- проекция ускорения свободного падения, относительно оси ОХ, также имеет нулевое значение;
- проекция начальной скорости на ось ОХ составляет (V_{0}cos alpha).
Записанная формула приобретает следующий вид:
(x=V_{0}cos alpha t)
Мгновенной высотой принято считать высоту, на которой находится объект в определенный момент времени t. Наибольшей высотой подъема является расстояние от поверхности земли до верхней точки траектории движения тела под углом к горизонту.
Вывод формулы, как найти угол и дальность полета
Перемещение объекта, который был брошен под углом к горизонту, необходимо изобразить с помощью суперпозиций, характерных для двух типов движений:
- равномерное горизонтальное движение;
- равноускоренное перемещение в вертикальном направлении с ускорением свободного падения.
Скорость тела будет рассчитываться таким образом:
(v_{0x}=v_{x}=v_{0} cos alpha =const)
(v_{0y}=v_{0}sin alpha)
(v_{y}=v_{0}sin alpha-gt)
Уравнение координаты записывают в следующем виде:
(x=v_{0}cos alpha times t)
(y=v_{0}sin alpha times t-frac{gt^{2}}{2})
В любое время значения скорости тела будут равны:
(v=sqrt{v_{x}^{2}+v_{y}^{2}})
Определить угол между вектором скорости и осью ОХ можно таким образом:
(tan beta =frac{v_{y}}{v_{x}}=frac{v_{0}sin alpha -gt}{v_{0}cos alpha })
Время подъема на максимальную высоту составляет:
(t=frac{v_{0}sin alpha }{g})
Максимальная высота подъема будет рассчитана следующим образом:
(h_{max}=frac{v_{0}^{2}sin ^{2}alpha}{2g})
Полет тела будет длиться определенное время, которое можно рассчитать с помощью формулы:
(t=frac{2v_{0}sin alpha }{g})
Максимальная дальность полета составит:
(L_{max}=frac{v_{0}^{2}sin 2alpha }{g})
Примеры решения задач
В примерах, описывающих движение тела, на которое действует сила тяжести, следует учитывать, что а=g=9,8 м/с2.
Задача 1
Небольшой камень был брошен с ровной горизонтальной поверхности под углом к горизонту. Необходимо определить, какова максимальная высота подъема камня при условии, что, спустя 1 секунду после его начала движения, скорость тела обладала горизонтальным направлением.
Решение
Направление скорости будет горизонтальным в верхней точке перемещения камня. Таким образом, время, за которое он поднимется, составляет 1 секунду. С помощью уравнения времени подъема можно представить формулу произведения скорости в начале полета на синус угла, под которым бросили камень:
(V_{0}sin alpha =gt)
Данное равенство следует подставить в уравнение для расчета максимальной высоты, на которую поднимется камень, и выполнить вычисления:
(h=frac{V_{0}sin ^{2}alpha }{2g}=frac{(gt)^{2}}{2g}=frac{gt^{2}}{2}=frac{10times 1}{2}=5)
Ответ: максимальная высота подъема камня, который бросили под углом к горизонту, составляет 5 метров.
Задача 2
Из орудия выпустили снаряд, начальная скорость которого составляет 490 м/с, под углом 30 градусов к горизонту. Нужно рассчитать, какова высота, дальность и время полета снаряда без учета его вращения и сопротивления воздуха.
Решение
Систему координат и движение тела можно представить схематично:
Составляющие скорости, относительно осей ОХ и ОУ, будут совпадать во время начала движения снаряда:
(V_{0x}=V_{0} cos alpha) сохраняет стабильность значения в любой промежуток времени во время всего перемещения тела.
(V_{0y}=V_{0}sin alpha) будет меняться, согласно формуле равнопеременного движения (V_{y}=V_{0}sin alpha-gt).
В максимальной точке, на которую поднимется снаряд:
(V_{y}=V_{0}sin alpha-gt_{1}=0)
Из этого равенства следует:
(t=frac{V_{0sin alpha }}{g})
Полное время полета тела будет рассчитано по формуле:
(t=2t_{1}=frac{2V_{0}sin alpha }{g}=50)
Высота, на которую поднимется снаряд, определяется с помощью уравнения равнозамедленного перемещения тела:
(h=V_{0y}t_{1}-frac{gt_{1}^{2}}{2}=frac{V_{0}^{2}sin ^{2}alpha }{2g}=3060)
Дальность полета снаряда будет рассчитана таким образом:
(S=V_{0x}t=frac{V_{0}^{2}sin 2alpha }{g}=21000)
Ответ: высота составляет 3060 метров, дальность полета равна 21000 метров, время движения составит 50 секунд.

