Импульс тела
Импульсом тела называется величина, равная произведению массы тела на его скорость.
Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:
$p↖{→}=mυ↖{→}$
Направление вектора импульса всегда совпадает с направлением скорости.
За единицу импульса в СИ принимают импульс тела массой $1$ кг, движущегося со скоростью $1$ м/с, следовательно, единицей импульса является $1$ кг $·$ м/с.
Если на тело (материальную точку) действует постоянная сила в течение промежутка времени $∆t$, то постоянным будет и ускорение:
$a↖{→}={{υ_2}↖{→}-{υ_1}↖{→}}/{∆t}$
где, ${υ_1}↖{→}$ и ${υ_2}↖{→}$ — начальная и конечная скорости тела. Подставив это значение в выражение второго закона Ньютона, получим:
${m({υ_2}↖{→}-{υ_1}↖{→})}/{∆t}=F↖{→}$
Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:
${p_2}↖{→}-{p_1}↖{→}=F↖{→}∆t$
Здесь ${p_2}↖{→}-{p_1}↖{→}=∆p↖{→}$ — изменение импульса за время $∆t$. Тогда предыдущее уравнение примет вид:
$∆p↖{→}=F↖{→}∆t$
Выражение $∆p↖{→}=F↖{→}∆t$ представляет собой математическую запись второго закона Ньютона.
Произведение силы на время ее действия называют импульсом силы. Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.
Выражение $∆p↖{→}=F↖{→}∆t$ называется уравнением движения тела. Следует заметить, что одно и то же действие — изменение импульса точки — может быть получено малой силой за большой промежуток времени и большой силой за малый промежуток времени.
Импульс системы тел. Закон изменения импульса
Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:
${p_{сист}}↖{→}={p_1}↖{→}+{p_2}↖{→}+…$
Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.
Рассмотрим систему, состоящую из двух тел. Силы ($F_{12}$ и $F_{21}$ на рисунке, с которыми тела системы взаимодействуют между собой, называются внутренними.
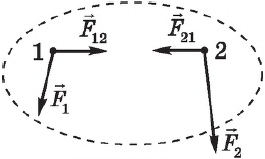
Пусть кроме внутренних сил на систему действуют внешние силы ${F_1}↖{→}$ и ${F_2}↖{→}$. Для каждого тела можно записать уравнение $∆p↖{→}=F↖{→}∆t$. Сложив левые и правые части этих уравнений, получим:
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_{12}}↖{→}+{F_{21}}↖{→}+{F_1}↖{→}+{F_2}↖{→})∆t$
Согласно третьему закону Ньютона ${F_{12}}↖{→}=-{F_{21}}↖{→}$.
Следовательно,
${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$
В левой части стоит геометрическая сумма изменений импульсов всех тел системы, равная изменению импульса самой системы — ${∆p_{сист}}↖{→}$.С учетом этого равенство ${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$ можно записать:
${∆p_{сист}}↖{→}=F↖{→}∆t$
где $F↖{→}$ — сумма всех внешних сил, действующих на тело. Полученный результат означает, что импульс системы могут изменить только внешние силы, причем изменение импульса системы направлено так же, как суммарная внешняя сила. В этом суть закона изменения импульса механической системы.
Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.
Закон сохранения импульса
Из уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ вытекает закон сохранения импульса. Если на систему не действуют никакие внешние силы, то правая часть уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ обращается в ноль, что означает неизменность суммарного импульса системы:
${∆p_{сист}}↖{→}=m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=const$
Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.
Закон сохранения импульса гласит:
Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.
Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.
Реактивное движение
Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.
Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.
Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.
На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.
Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Согласно закону сохранения импульса, импульс $m_{p}υ_p$, приобретаемый ракетой, должен быть равен импульсу $m_{газ}·υ_{газ}$ выброшенных газов:
$m_{p}υ_p=m_{газ}·υ_{газ}$
Отсюда следует, что скорость ракеты
$υ_p=({m_{газ}}/{m_p})·υ_{газ}$
Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.
Формула $υ_p=({m_{газ}}/{m_p})·υ_{газ}$ является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты была получена в 1897 г. К. Э. Циолковским и носит его имя.
Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости.
Работа силы
Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.
Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:
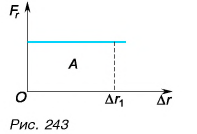
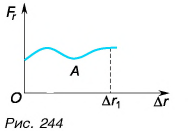
$A=F|∆r↖{→}|cosα$
где $F$ — сила, действующая на тело, $∆r↖{→}$ — перемещение, $α$ — угол между силой и перемещением.
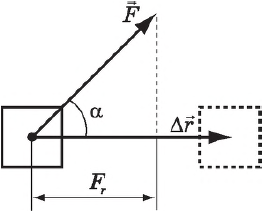
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖{→}$ и $∆r↖{→}$.
Работа — величина скалярная. Если $α < 90°$, то $А > 0$, а если $90° < α < 180°$, то $A < 0$; если же $α = 90°$, то $А = 0$. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. Также при движении спутника по круговой орбите сила тяготения не совершает работу.
При действии на тело нескольких сил полная работа (сумма работ всех сил) равна работе результирующей силы.
Единицей работы в СИ является джоуль ($1$ Дж). $1$ Дж — это работа, которую совершает сила в $1$ Н на пути в $1$ м в направлении действия этой силы. Эта единица названа в честь английского ученого Дж. Джоуля (1818-1889): $1$ Дж = $1$ Н $·$ м. Часто применяются также килоджоули и миллиджоули: $1$ кДж $= 1 000$ Дж, $1$ мДж $= 0.001$ Дж.
Работа силы тяжести
Рассмотрим тело, скользящее по наклонной плоскости с углом наклона $α$ и высотой $Н$.
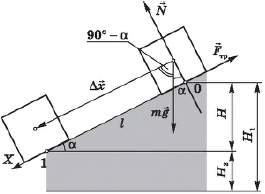
Выразим $∆x$ через $H$ и $α$:
$∆x={H}/{sinα}$
Учитывая, что сила тяжести $F_т=mg$ составляет угол ($90° – α$) с направлением перемещения, используя формулу $∆x={H}/{sin}α$, получим выражение для работы силы тяжести $A_g$:
$A_g=mg·cos(90°-α)·{H}/{sinα}=mgH$
Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.
Отсюда следует, что:
- работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
- при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).
Работа сил реакции, равна нулю, поскольку сила реакции ($N$) направлена перпендикулярно перемещению $∆x$.
Работа силы трения
Сила трения направлена противоположно перемещению $∆x$ и составляет с ним угол $180°$, поэтому работа силы трения отрицательна:
$A_{тр}=F_{тр}∆x·cos180°=-F_{тр}·∆x$
Так как $F_{тр}=μN, N=mg·cosα, ∆x=l={H}/{sinα},$ то
$A_{тр}=μmgHctgα$
Работа силы упругости
Пусть на нерастянутую пружину длиной $l_0$ действует внешняя сила $F↖{→}$, растягивая ее на $∆l_0=x_0$. В положении $x=x_0F_{упр}=kx_0$. После прекращения действия силы $F↖{→}$ в точке $х_0$ пружина под действием силы $F_{упр}$ сжимается.
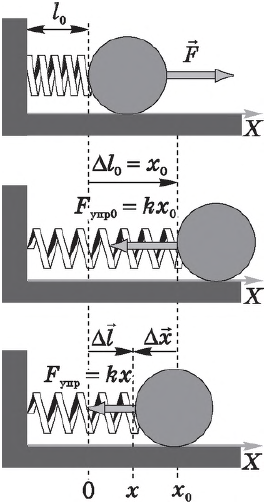
Определим работу силы упругости при изменении координаты правого конца пружины от $х_0$ до $х$. Поскольку сила упругости на этом участке изменяется линейно, в законе Гука можно использовать ее среднее значение на этом участке:
$F_{упр.ср.}={kx_0+kx}/{2}={k}/{2}(x_0+x)$
Тогда работа (с учетом того, что направления ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$ совпадают) равна:
$A_{упр}={k}/{2}(x_0+x)(x_0-x)={kx_0^2}/{2}-{kx^2}/{2}$
Можно показать, что вид последней формулы не зависит от угла между ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$. Работа сил упругости зависит лишь от деформаций пружины в начальном и конечном состояниях.
Таким образом, сила упругости, подобно силе тяжести, является консервативной силой.
Мощность силы
Мощность — физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.
Другими словами, мощность показывает, какая работа совершается за единицу времени (в СИ — за $1$ с).
Мощность определяется формулой:
$N={A}/{∆t}$
где $N$ — мощность, $А$ — работа, совершенная за время $∆t$.
Подставив в формулу $N={A}/{∆t}$ вместо работы $A$ ее выражение $A=F|{∆r}↖{→}|cosα$, получим:
$N={F|{∆r}↖{→}|cosα}/{∆t}=Fυcosα$
Мощность равна произведению модулей векторов силы и скорости на косинус угла между этими векторами.
Мощность в системе СИ измеряется в ваттах (Вт). Один ватт ($1$ Вт) — это такая мощность, при которой за $1$ с совершается работа $1$ Дж: $1$ Вт $= 1$ Дж/с.
Эта единица названа в часть английского изобретателя Дж. Ватта (Уатта), построившего первую паровую машину. Сам Дж. Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (л. с.), которую он ввел для того, чтобы можно было сравнивать работоспособности паровой машины и лошади: $1$ л.с. $= 735.5$ Вт.
В технике часто применяются более крупные единицы мощности — киловатт и мегаватт: $1$ кВт $= 1000$ Вт, $1$ МВт $= 1000000$ Вт.
Кинетическая энергия. Закон изменения кинетической энергии
Если тело или несколько взаимодействующих между собой тел (система тел) могут совершать работу, то говорят, что они обладают энергией.
Слово «энергия» (от греч. energia — действие, деятельность) нередко употребляется в быту. Так, например, людей, которые могут быстро выполнять работу, называют энергичными, обладающими большой энергией.
Энергия, которой обладает тело вследствие движения, называется кинетической энергией.
Как и в случае определения энергии вообще, о кинетической энергии можно сказать, что кинетическая энергия — это способность движущегося тела совершать работу.
Найдем кинетическую энергию тела массой $m$, движущегося со скоростью $υ$. Поскольку кинетическая энергия — это энергия, обусловленная движением, нулевым состоянием для нее является то состояние, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем его кинетическую энергию.
Для этого подсчитаем работу на участке перемещения $∆r↖{→}$ при совпадении направлений векторов силы $F↖{→}$ и перемещения $∆r↖{→}$. В этом случае работа равна
$A=F·∆x,$
где $∆x=∆r$
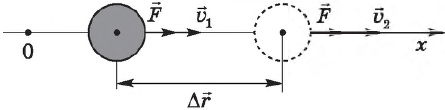
Для движения точки с ускорением $α=const$ выражение для перемещения имеет вид:
$∆x=υ_1t+{at^2}/{2},$
где $υ_1$ — начальная скорость.
Подставив в уравнение $A=F·∆x$ выражение для $∆x$ из $∆x=υ_1t+{at^2}/{2}$ и воспользовавшись вторым законом Ньютона $F=ma$, получим:
$A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$
Выразив ускорение через начальную $υ_1$ и конечную $υ_2$ скорости $a={υ_2-υ_1}/{t}$ и подставив в $A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$ имеем:
$A={m(υ_2-υ_1)}/{2}·(2υ_1+υ_2-υ_1)$
или
$A={mυ_2^2}/{2}-{mυ_1^2}/{2}$
Приравняв теперь начальную скорость к нулю: $υ_1=0$, получим выражение для кинетической энергии:
$E_K={mυ}/{2}={p^2}/{2m}$
Таким образом, движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую необходимо совершить, чтобы увеличить скорость тела от нуля до значения $υ$.
Из $E_K={mυ}/{2}={p^2}/{2m}$ следует, что работа силы по перемещению тела из одного положения в другое равна изменению кинетической энергии:
$A=E_{K_2}-E_{K_1}=∆E_K$
Равенство $A=E_{K_2}-E_{K_1}=∆E_K$ выражает теорему об изменении кинетической энергии.
Изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за это время силой, действующей на тело.
Потенциальная энергия
Потенциальной энергией называется энергия, определяемая взаимным расположением взаимодействующих тел или частей одного и того же тела.
Поскольку энергия определяется как способность тела совершать работу, то потенциальную энергию, естественно, определяют как работу силы, зависящую только от взаимного расположения тел. Таковой является работа силы тяжести $A=mgh_1-mgh_2=mgH$ и работа силы упругости:
$A={kx_0^2}/{2}-{kx^2}/{2}$
Потенциальной энергией тела, взаимодействующего с Землей, называют величину, равную произведению массы $m$ этого тела на ускорение свободного падения $g$ и на высоту $h$ тела над поверхностью Земли:
$E_p=mgh$
Потенциальной энергией упруго деформированного тела называют величину, равную половине произведения коэффициента упругости (жесткости) $k$ тела на квадрат деформации $∆l$:
$E_p={1}/{2}k∆l^2$
Работа консервативных сил (тяжести и упругости) с учетом $E_p=mgh$ и $E_p={1}/{2}k∆l^2$ выражается следующим образом:
$A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$
Эта формула позволяет дать общее определение потенциальной энергии.
Потенциальной энергией системы называется зависящая от положения тел величина, изменение которой при переходе системы из начального состояния в конечное равно работе внутренних консервативных сил системы, взятой с противоположным знаком.
Знак «минус» в правой части уравнения $A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$ означает, что при совершении работы внутренними силами (например, падение тела на землю под действием силы тяжести в системе «камень — Земля») энергия системы убывает. Работа и изменение потенциальной энергии в системе всегда имеют противоположные знаки.
Поскольку работа определяет лишь изменение потенциальной энергии, то физический смысл в механике имеет только изменение энергии. Поэтому выбор нулевого уровня энергии произволен и определяется исключительно соображениями удобства, например, простотой записи соответствующих уравнений.
Закон изменения и сохранения механической энергии
Полной механической энергией системы называется сумма ее кинетической и потенциальной энергий:
$E=E_k+E_p$
Она определяется положением тел (потенциальная энергия) и их скоростью (кинетическая энергия).
Согласно теореме о кинетической энергии,
$E_k-E_{k_1}=A_p+A_{пр},$
где $А_р$ — работа потенциальных сил, $А_{пр}$ — работа непотенциальных сил.
В свою очередь, работа потенциальных сил равна разности потенциальной энергии тела в начальном $Е_{р_1}$ и конечном $Е_р$ состояниях. Учитывая это, получим выражение для закона изменения механической энергии:
$(E_k+E_p)-(E_{k_1}+E_{p_1})=A_{пр}$
где левая часть равенства — изменение полной механической энергии, а правая — работа непотенциальных сил.
Итак, закон изменения механической энергии гласит:
Изменение механической энергии системы равно работе всех непотенциальных сил.
Механическая система, в которой действуют только потенциальные силы, называется консервативной.
В консервативной системе $А_{пр} = 0$. Отсюда следует закон сохранения механической энергии:
В замкнутой консервативной системе полная механическая энергия сохраняется (не изменяется со временем):
$E_k+E_p=E_{k_1}+E_{p_1}$
Закон сохранения механической энергии выводится из законов механики Ньютона, которые применимы для системы материальных точек (или макрочастиц).
Однако закон сохранения механической энергии справедлив и для системы микрочастиц, где сами законы Ньютона уже не действуют.
Закон сохранения механической энергии является следствием однородности времени.
Однородность времени состоит в том, что при одинаковых начальных условиях протекание физических процессов не зависит от того, в какой момент времени эти условия созданы.
Закон сохранения полной механической энергии означает, что при изменении кинетической энергии в консервативной системе должна меняться и ее потенциальная энергия, так что их сумма остается постоянной. Это означает возможность превращения одного вида энергии в другой.
В соответствии с различными формами движения материи рассматривают различные виды энергии: механическую, внутреннюю (равную сумме кинетической энергии хаотического движения молекул относительно центра масс тела и потенциальной энергии взаимодействия молекул друг с другом), электромагнитную, химическую (которая складывается из кинетической энергии движения электронов и электрической энергии их взаимодействия друг с другом и с атомными ядрами), ядерную и пр. Из сказанного видно, что деление энергии на разные виды достаточно условно.
Явления природы обычно сопровождаются превращением одного вида энергии в другой. Так, например, трение частей различных механизмов приводит к превращению механической энергии в тепло, т. е. во внутреннюю энергию. В тепловых двигателях, наоборот, происходит превращение внутренней энергии в механическую; в гальванических элементах химическая энергия превращается в электрическую и т. д.
В настоящее время понятие энергии является одним из основных понятий физики. Это понятие неразрывно связано с представлением о превращении одной формы движения в другую.
Вот как в современной физике формулируется понятие энергии:
Энергия — общая количественная мера движения и взаимодействия всех видов материи. Энергия не возникает из ничего и не исчезает, она может только переходить из одной формы в другую. Понятие энергии связывает воедино все явления природы.
Простые механизмы. КПД механизмов
Простыми механизмами называются приспособления, изменяющие величину или направление приложенных к телу сил.
Они применяются для перемещения или подъема больших грузов с помощью небольших усилий. К ним относятся рычаг и его разновидности — блоки (подвижный и неподвижный), ворот, наклонная плоскость и ее разновидности — клин, винт и др.
Рычаг. Правило рычага
Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.
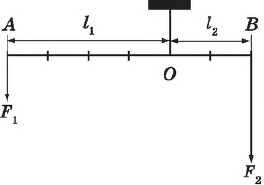
Правило рычага гласит:
Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:
${F_2}/{F_1}={l_1}/{l_2}$
Из формулы ${F_2}/{F_1}={l_1}/{l_2}$, применив к ней свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), можно получить такую формулу:
$F_1l_1=F_2l_2$
Но $F_1l_1=M_1$ — момент силы, стремящейся повернуть рычаг по часовой стрелке, а $F_2l_2=M_2$ — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, $M_1=M_2$, что и требовалось доказать.
Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту $147$ м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу $2.5$ тонн!
В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).
Неподвижный блок

Действие неподвижного блока аналогично действию рычага с равными плечами: $l_1=l_2=r$. Приложенная сила $F_1$ равна нагрузке $F_2$, и условие равновесия имеет вид:
$F_1=F_2$
Неподвижный блок применяют, когда нужно изменить направление силы, не меняя ее величину.
Подвижный блок

Подвижный блок действует аналогично рычагу, плечи которого составляют: $l_2={l_1}/{2}=r$. При этом условие равновесия имеет вид:
$F_1={F_2}/{2}$
где $F_1$ — приложенная сила, $F_2$ — нагрузка. Применение подвижного блока дает выигрыш в силе в два раза.
Полиспаст (система блоков)
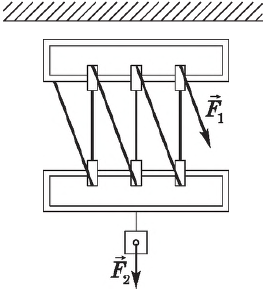
Обычный полиспаст состоит из $n$ подвижных и $n$ неподвижных блоков. Его применив дает выигрыш в силе в $2n$ раз:
$F_1={F_2}/{2n}$
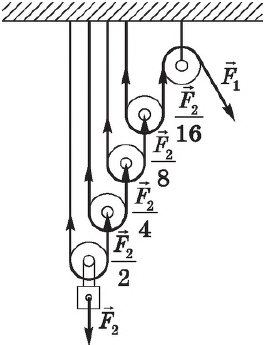
Степенной полиспаст состоит из п подвижных и одного неподвижного блока. Применение степенного полиспаста дает выигрыш в силе в $2^n$ раз:
$F_1={F_2}/{2^n}$
Винт
Винт представляет собой наклонную плоскость, навитую на ось.
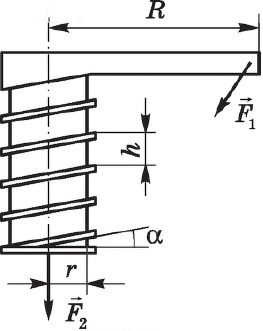
Условие равновесия сил, действующих на винт, имеет вид:
$F_1={F_2h}/{2πr}=F_2tgα, F_1={F_2h}/{2πR}$
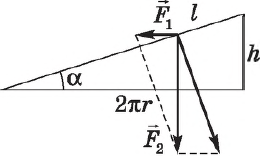
где $F_1$ — внешняя сила, приложенная к винту и действующая на расстоянии $R$ от его оси; $F_2$ — сила, действующая в направлении оси винта; $h$ — шаг винта; $r$ — средний радиус резьбы; $α$ — угол наклона резьбы. $R$ — длина рычага (гаечного ключа), вращающего винт с силой $F_1$.
Коэффициент полезного действия
Коэффициент полезного действия (КПД) — отношение полезной работы ко всей затраченной работе.
Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой $η$ («эта»):
$η={A_п}/{A_3}·100%$
где $А_п$ — полезная работа, $А_3$ — вся затраченная работа.
Полезная работа всегда составляет лишь часть полной работы, которую затрачивает человек, используя тот или иной механизм.
Часть совершенной работы тратится на преодоление сил трения. Поскольку $А_3 > А_п$, КПД всегда меньше $1$ (или $< 100%$).
Когда КПД немного меньше $1$, можно считать, что затраченная работа примерно равна полезной: $А_3 ≈ А_п$.
Поскольку каждую из работ в этом равенстве можно выразить в виде произведения соответствующей силы на пройденный путь, то его можно переписать так: $F_1s_1≈F_2s_2$.
Отсюда следует, что, выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот. Этот закон называют золотым правилом механики.
Золотое правило механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.
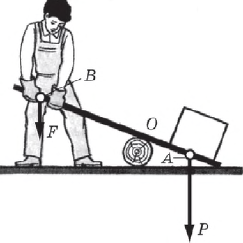
Так, например, благодаря этому правилу сразу можно сказать, что рабочему, изображенному на рисунке, при двукратном выигрыше в силе подъема груза на $10$ см придется опустить противоположный конец рычага на $20$ см.
Столкновение тел. Упругий и неупругий удары
Законы сохранения импульса и механической энергии применяются для решения задачи о движении тел после столкновения: по известным импульсам и энергиям до столкновения определяются значения этих величин после столкновения. Рассмотрим случаи упругого и неупругого ударов.
Абсолютно неупругим называется удар, после которого тела образуют единое тело, движущееся с определенной скоростью. Задача о скорости последнего решается с помощью закона сохранения импульса системы тел с массами $m_1$ и $m_2$ (если речь идет о двух телах) до и после удара:
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=(m_1+m_2)υ↖{→}$
Очевидно, что кинетическая энергия тел при неупругом ударе не сохраняется (например, при ${υ_1}↖{→}=-{υ_2}↖{→}$ и $m_1=m_2$ она становится равной нулю после удара).
Абсолютно упругим называется удар, при котором сохраняется не только сумма импульсов, но и сумма кинетических энергий ударяющихся тел.
Для абсолютно упругого удара справедливы уравнения
$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=m_1{υ’_1}↖{→}+m_2{υ’_2}↖{→};$
${m_{1}υ_1^2}/{2}+{m_{2}υ_2^2}/{2}={m_1(υ’_1)^2}/{2}+{m_2(υ’_2)^2}/{2}$
где $m_1, m_2$ — массы шаров, $υ_1, υ_2$ —скорости шаров до удара, $υ’_1, υ’_2$ —скорости шаров после удара.
Содержание:
Три закона Ньютона являются основой механики. Выдающийся американский физик XX ст. P Фейнман в своих знаменитых «Фейнмановских лекциях» отметил, что вся классическая механика содержится в этих законах. C их помощью в принципе можно решить любую задачу о движении тел с малыми скоростями.
Значение законов Ньютона заключается не только в этом. Они позволили создать стройную физическую теорию механического движения тел, ввести такие фундаментальные физические величины, как энергия и импульс, установить для них законы сохранения, являющиеся фундаментальными законами природы. C помощью этих законов в динамике решаются задачи, когда силы взаимодействия тел неизвестны. Например, при столкновении тел трудно определить значения сил взаимодействия между ними.
Законы сохранения в механике
Все изменения, наблюдаемые нами в природе, -результат взаимодействия между телами. Взаимодействия бывают электромагнитные, гравитационные и ядерные. Их интенсивность зависит не только от их природы, но и от расстояний между телами, их характеристик.
При определенных условиях один вид взаимодействия может быть интенсивнее другого. Так, на больших расстояниях существенным является гравитационное взаимодействие, в то время как ядерное будет существенным только на расстояниях, соизмеримых с размерами ядра атома.
Одновременно сделать расчеты всех взаимодействий тяжело, да и не всегда нужно. Поэтому ученые, как правило, рассматривают физические явления, пренебрегая некоторыми второстепенными взаимодействиями. Например, при расчетах силы трения, действующей на колеса автомобиля, существенной является сила притяжения Земли, а действием Луны можно пренебречь.
Ученые, рассматривая физические явления, как правило, пренебрегают второстепенными взаимодействиями.
При расчетах движения межпланетного корабля в пределах Солнечной системы нельзя пренебречь действием на корабль Солнца и планет, а вот действие далеких звезд можно не принимать во внимание.
Таким образом, в общей картине природы рассматривается лишь некоторая совокупность физических тел, условно изолированных от окружающей среды и объединенных общими признаками.
Группа объединенных по общим признакам тел, на которые не действуют другие тела или их действие несущественно в данных условиях, называется замкнутой (изолированной) системой.
Замкнутость системы – понятие относительное и определяется задачами, которые ставятся перед исследованиями, и уровнем развития их экспериментального или теоретического методов решения. Если система по определенным соображениям объявляется замкнутой, то она не становится абсолютно изолированной, «вне природы», в ней действуют те же физические законы. Это подтверждается многочисленными исследованиями, свидетельствующими об однородности пространства. Ни одной точке пространства нельзя дать преимущество по сравнению с другими точками, а протекание физических явлений не изменяется в случае перехода из одной точки пространства в другую. Поэтому не случайно закон гравитационного взаимодействия называется всемирным.
Наличие однородности в полной мере присуще и времени. Течение времени в разных точках пространства происходит одинаково. Поэтому некоторые физические величины в замкнутых системах остаются неизменными, например масса, энергия, импульс, т. е. подчиняются законам сохранения. В механике основными такими законами являются закон сохранения энергии и закон сохранения импульса.
Импульс тела и импульс системы тел
Еще в XVII в. в механике появилось понятие «количество движения». В настоящее время количество движения тела называют импульсом тела (от латинского impulses — толчок). Чему он равен? Как его можно изменить?
В механике Ньютона импульсом тела называется векторная величина, равная произведению массы тела на скорость его движения:

Импульс тела направлен так же, как скорость движения тела. Единица импульса в СИ — I килограмм-метр в секунду 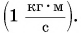
Из определения следует, что импульс зависит и от скорости, и от массы. Например, импульс груженого самосвала БЕЛАЗ гораздо больше импульса движущегося с такой же скоростью автомобиля (рис. 225).
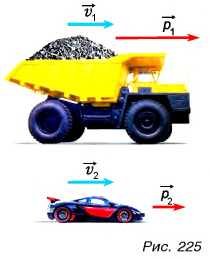
Согласно первому закону Ньютона скорость движения тела, на которое не действуют силы или действие сил скомпенсировано, постоянна. Значит, в этом случае постоянен и его импульс. Изменить импульс тела можно, только приложив к нему силу.
Рассмотрим пример. Тележку массой т, имеющую начальную скорость 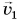 в течение промежутка времени
в течение промежутка времени 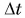 разгоняют, действуя постоянной силой F (рис. 226). Па сколько изменится импульс тележки?
разгоняют, действуя постоянной силой F (рис. 226). Па сколько изменится импульс тележки?
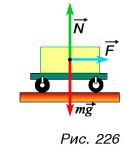
Найдем результирующую силу, действующую на тележку. Силами сопротивления можно пренебречь, сила реакции N и сила тяжести mg (рис. 226) компенсируют друг друга. Тогда по второму закону Ньютона
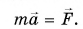
Подставляя в эту формулу ускорение 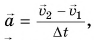 получим
получим 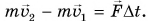 Действие силы F привело к изменению импульса тележки:
Действие силы F привело к изменению импульса тележки:

Величину 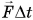 называют импульсом силы.
называют импульсом силы.
Импульс силы — это векторная величина, равная произведению силы на время ее действия.
Формула (2) выражает закон изменения импульса тела.
Изменение импульса тела равно импульсу результирующей всех сил, приложенных к нему.
Из данного закона следует:
- изменение импульса тела
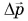 направлено так же, как результирующая сила F;
направлено так же, как результирующая сила F; - изменение импульса тела тем больше, чем больше приложенная к нему сила и чем продолжительнее время ее действия.
Формулу (2) можно записать в виде

Для любознательных:
Равенство 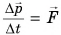 соответствует формулировке, которая была дана второму закону динамики самим Ньютоном: «Изменение количества движения пропорционально приложенной движущей силе и происходит по прямой, по которой эта сила действует».
соответствует формулировке, которая была дана второму закону динамики самим Ньютоном: «Изменение количества движения пропорционально приложенной движущей силе и происходит по прямой, по которой эта сила действует».
Закон изменения импульса объясняет целый ряд явлений повседневной жизни.
Проделаем простой опыт. Возьмем две нити: обычную 1 и резиновую 2 (рис. 227) одинаковой прочности и длины. Привяжем их к одинаковым грузам и дадим грузам возможность падать с одинаковой высоты. Нить 1 порвется, а нить 2 — нет (рис. 227). Почему это происходит?
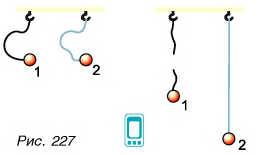
Дело в том, что промежуток времени торможения At для груза на обычной нити 1 был во много раз меньше, чем для груза на резиновой, легко деформируемой нити 2. Из формулы (3) следует, что сила F тем больше, чем меньше 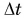 (при равных изменениях импульса). Значит, на обычную нить действовала большая сила.
(при равных изменениях импульса). Значит, на обычную нить действовала большая сила.
Это необходимо учитывать в технике. Нельзя делать резких рывков при подъеме грузов и при буксировке транспортных средств. Может произойти обрыв троса.
Чтобы избежать тяжелых последствий при столкновениях, следует уменьшить силу или увеличить время, за которое импульс уменьшится до нуля. Для этой цели вагоны снабжают буферными пружинными амортизаторами (рис. 228), автомобили — бамперами, ремнями безопасности, автоматически срабатывающими воздушными подушками (рис. 229).


И наоборот, для получения больших сил используют удар, при котором импульс изменяется за очень малый промежуток времени At (см. формулу (3)). Примерами служат забивание свай падающим молотом (рис. 230), разрушающее действие пуль, снарядов и т. д.
Мы рассмотрели изменение импульса одного тела. А как изменяется суммарный импульс нескольких тел?
В механике группу из нескольких тел называют механической системой. Тела, не входящие в систему, называются внешними телами.

Например, механической системой является пассажирский вагон (рис. 231). В механическую систему «вагон» входят: корпус вагона, люди, находящиеся в вагоне, багаж и т. д. Внешними телами будут: Земля, локомотив, рельсы, остальные вагоны поезда и т. д.
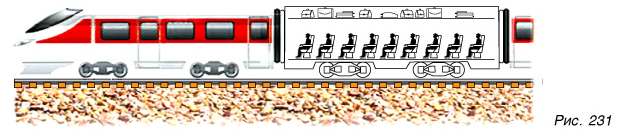
Силы взаимодействия тел системы друг с другом называют внутренними. Например, в системе «вагон» внутренней будет сила, с которой багаж давит на полку, и сила, с которой полка действует на багаж. Силы, действующие на тела системы со стороны внешних тел, называют внешними силами. Например, сила тяжести, с которой Земля действует на багаж, — это внешняя сила.
Каждое из тел механической системы имеет свой импульс. Векторная сумма импульсов всех тел, входящих в систему, называется импульсом механической системы:
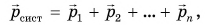
где п — количество тел системы.
Рассмотрим систему из двух тел (1 и 2) (рис. 232). Силы их взаимодействия 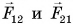 — это внутренние силы. Пусть на тела 1 и 2 действуют также и внешние силы. Обозначим их
— это внутренние силы. Пусть на тела 1 и 2 действуют также и внешние силы. Обозначим их 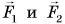 . За время
. За время 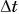 из-за действия сил произойдет изменение импульса:
из-за действия сил произойдет изменение импульса:
- •для тела 1:
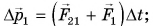
- •для тела 2:
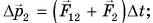
- •для всей системы:
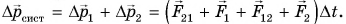
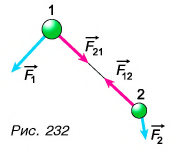
По третьему закону Ньютона силы взаимодействия тел 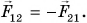
С учетом этого
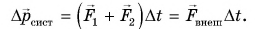
А если в механическую систему входит больше двух тел? Сумма всех внутренних сил будет по-прежнему равна нулю, а изменение импульса механической системы

где 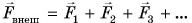 — результирующая всех внешних сил, действующих на тела системы.
— результирующая всех внешних сил, действующих на тела системы.
Формула (4) выражает закон изменения импульса механической системы.
Изменение импульса механической системы равно импульсу результирующей внешних сил.
Таким образом, только внешние силы могут вызвать изменение импульса механической системы. Внутренние силы не изменяют импульс механической системы в целом, но могут изменить импульс отдельных тел системы.
Ответьте самостоятельно: какая сила увеличивает импульс вагона на участке разгона? Какие силы уменьшают импульс вагона при его торможении? Могут ли пассажиры, находящиеся в вагоне, вызвать изменение импульса механической системы «вагон»?
Главные выводы:
- Импульс тела — это векторная величина, равная произведению массы тела на скорость его движения.
- Направление импульса тела совпадает с направлением его скорости.
- Изменение импульса тела равно импульсу результирующей всех сил, приложенных к нему.
- Изменить импульс механической системы могут только внешние силы. Это изменение равно импульсу результирующей внешних сил.
Пример №1
Шарик массой 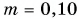 кг свободно надает без начальной скорости с высоты h = 0,20 м на горизонтальную плиту и отскакивает от нее. Считая, что модули скорости шарика перед ударом и сразу после удара равны (рис. 233), определите среднюю силу, с которой шарик во время удара действовал на плиту. Время соударения
кг свободно надает без начальной скорости с высоты h = 0,20 м на горизонтальную плиту и отскакивает от нее. Считая, что модули скорости шарика перед ударом и сразу после удара равны (рис. 233), определите среднюю силу, с которой шарик во время удара действовал на плиту. Время соударения 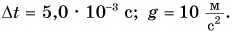
Решение

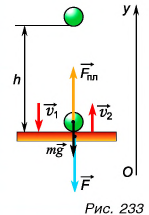
Так как на шарик во время удара действуют сила тяжести и сила, приложенная к нему со стороны плиты, то изменение импульса шарика за время удара 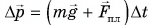 , где
, где 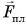 — средняя сила действия плиты на шарик. Отсюда
— средняя сила действия плиты на шарик. Отсюда
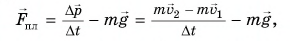
где 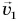 — скорость шарика перед ударом, a
— скорость шарика перед ударом, a 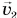 – сразу после удара.
– сразу после удара.
В проекции на ось Оу.
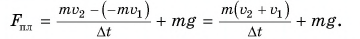
Так как шарик свободно падал без начальной скорости с высоты h, то 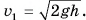 По условию задачи
По условию задачи 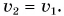 Значит,
Значит,
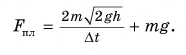
По третьему закону Ньютона средняя сила, с которой шарик во время удара действовал на плиту, 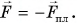 В результате для модуля F получим:
В результате для модуля F получим:
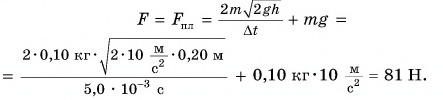
Сила, с которой шарик во время удара действовал на плиту, направлена по вертикали вниз. Модуль средней силы удара в 81 раз больше, чем вес покоящегося шарика.
Закон сохранения импульса и реактивное движение
Знаменитый французский философ и математик Рене Декарт (1596— 1650) утверждал: «Во Вселенной есть известное количество движения, которое никогда не изменяется. И если одно тело приводит в движение другое, то оно теряет столько своего движения, сколько его сообщает». Как вывести это утверждение из закона изменения импульса?
В предыдущем параграфе мы доказали, что импульс системы тел может измениться только под действием внешних сил:

А если результирующая внешних сил 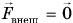 ? Тогда изменение импульса
? Тогда изменение импульса 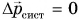 , и импульс системы остается постоянным:
, и импульс системы остается постоянным:

Векторное равенство (2) выражает закон сохранения импульса. Импульс механической системы сохраняется, если результирующая внешних сил, действующих на нее, равна нулю.
В каких случаях можно применять закон сохранения импульса? Прежде всего — когда на систему вообще не действуют внешние силы. Такие системы называют замкнутыми. Импульс замкнутой системы не изменяется (сохраняется), как и утверждал Декарт.
Реальные механические системы не бывают замкнутыми. На все окружающие нас тела действует Земля, на Землю действует Солнце и т. д. Однако закон сохранения импульса можно применять и для незамкнутых систем, если:
Например, закон сохранения импульса применяют при решении задач о столкновениях тел, выстрелах и т. д., когда в течение крайне малых промежутков времени внутри системы возникают огромные силы. Рассмотрим пример. Деревянный кубик массой М лежит на горизонтальном столе. В кубик попадает пуля массой 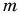 и застревает в нем (рис. 234). Скорость пули
и застревает в нем (рис. 234). Скорость пули 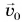 перед соударением горизонтальна. Требуется найти скорость
перед соударением горизонтальна. Требуется найти скорость 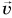 которую приобрел кубик.
которую приобрел кубик.
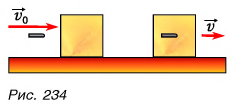
Замкнута ли система «кубик + пуля»? Нет. Но сила тяжести системы скомпенсирована силой реакции опоры, а сила трения кубика о стол мала. Значит, величиной 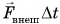 (где
(где 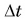 — время соударения) можно пренебречь и приравнять импульс системы «кубик + пуля» до соударения (равный
— время соударения) можно пренебречь и приравнять импульс системы «кубик + пуля» до соударения (равный 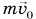 ) к импульсу этой системы после соударения
) к импульсу этой системы после соударения 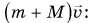
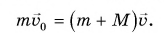
Значит, скорость кубика вместе с пулей после удара

Соударение, в результате которого тела объединяются и ведут себя как единое целое, называют абсолютно неупругим ударом.
Рассмотренный пример — частный случай такого удара. Другими примерами являются соединение вагонов при сценке, слипание пластилиновых шариков при соударении и т. д.
Рассмотрим теперь пример, в котором происходит не объединение, а разделение частей системы.
На горизонтальном рельсовом пути стоит платформа (рис. 235) с закрепленной на ней пушкой. Установка может свободно катиться по рельсам. Ствол орудия горизонтален. Пушка производит выстрел. Платформа приобретает скорость, направленную противоположно скорости снаряда.
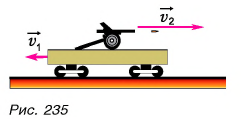
Как найти скорость 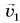 платформы? Сила тяжести, действующая па установку, компенсирована силой реакции рельсов. Трением качения можно пренебречь. Значит, как и в предыдущем примере, можно применить закон сохранения импульса.
платформы? Сила тяжести, действующая па установку, компенсирована силой реакции рельсов. Трением качения можно пренебречь. Значит, как и в предыдущем примере, можно применить закон сохранения импульса.
Так как импульс системы до выстрела был равен нулю, то после выстрела:

где 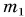 — масса установки,
— масса установки, 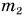 — масса снаряда,
— масса снаряда, 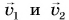 — их скорости после выстрела (рис. 235). Из равенства (4) находим скорость платформы:
— их скорости после выстрела (рис. 235). Из равенства (4) находим скорость платформы:

Почему платформа пришла в движение? Потому что пороховые газы, образовавшиеся в канале ствола при выстреле, действовали как на снаряд, так и на пушку. Сила, приложенная к пушке, вызвала движение платформы с пушкой в направлении, противоположном движению снаряда («отдачу»). Аналогичное явление можно наблюдать на простом опыте. Прикрепим к игрушечному автомобилю надутый воздушный шарик (рис. 236). Проколем его в точке А иглой. Образуется струя воздуха, вырывающегося из шарика, и автомобиль приходит в движение. Оно возникло при отделении от тела его части со скоростью, не равной нулю. Его называют реактивным движением, а силу, ускоряющую тело, — реактивной силой.
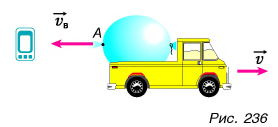
Реактивная сила возникает при отделении от тела какой-либо его части со скоростью, не равной нулю (относительно тела).
Устройство, создающее реактивную силу, называется реактивным двигателем.
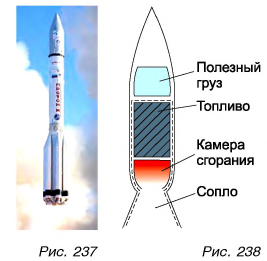
Реактивными двигателями оснащены скоростные самолеты, современные космические корабли (рис. 237). Упрощенная схема реактивного двигателя показана на рисунке 238.
Какую скорость 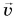 приобретет ракета массой
приобретет ракета массой 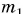 , если ее двигатель выбросит порцию газа массой
, если ее двигатель выбросит порцию газа массой 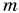 со скоростью
со скоростью 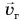 ?
?
По закону сохранения импульса из формулы (5) находим модуль скорости, приобретаемой ракетой:
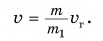
Значит, ракета набирает тем большую скорость, чем больше скорость истечения газов из ее сопла и чем меньше масса ракеты. Отсюда понятна выгода использования многоступенчатых ракет (рис. 238). После выгорания топлива в ступени ее отделяют. Масса ракеты уменьшается, что облегчает ее дальнейший разгон. С помощью многоступенчатых ракет выводят на орбиту искусственные спутники Земли, исследуют околоземное и межпланетное космическое пространство.
Первый в мире искусственный спутник Земли был запущен в 1957 г. в СССР. Первый орбитальный полет человека вокруг Земли совершил летчик-космонавт Ю. Гагарин в 1961 г. Американские астронавты Н. Армстронг и Э. Олдрин в 1969 г. первыми высадились на поверхность Луны.
Ракетно-космические исследования стали неотъемлемой частью современной цивилизации. Среди космонавтов есть уроженцы Беларуси: П. И. Климук, В. В. Коваленок, О. В. Новицкий. С космодрома «Байконур» 22 июля 2012 г. был запущен Белорусский космический аппарат (БКА) — спутник массой 400 кг. Он обеспечивает дистанционное зондирование территории Беларуси путем съемки из космоса.
Главные выводы:
- Если результирующая внешних сил равна нулю, то импульс системы сохраняется.
- Закон сохранения импульса можно применить к незамкнутым системам, если влиянием внешних сил можно пренебречь.
- Реактивная сила возникает при отделении от тела какой-либо его части с не равной нулю скоростью.
Пример №2
Два вагона массами 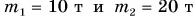 двигались по горизонтальному участку пути навстречу друг другу. Модули скорости движения вагонов
двигались по горизонтальному участку пути навстречу друг другу. Модули скорости движения вагонов 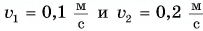 соответственно. Определите модуль и направление скорости движения вагонов после срабатывания автосцепки.
соответственно. Определите модуль и направление скорости движения вагонов после срабатывания автосцепки.
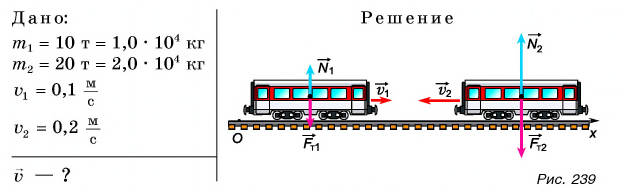
На систему из двух вагонов (рис. 239) действуют внешние силы: силы тяжести 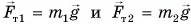 и компенсирующие их силы реакции рельсов
и компенсирующие их силы реакции рельсов 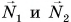 . Силы трения качения малы, ими можно пренебречь.
. Силы трения качения малы, ими можно пренебречь.
В итоге сумма внешних сил, действующих на вагоны, равна нулю. Значит, к системе из двух вагонов можно применить закон сохранения импульса: 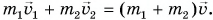 Здесь
Здесь 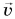 — скорость вагонов после сцепки. В проекции на ось Ох получим:
— скорость вагонов после сцепки. В проекции на ось Ох получим: 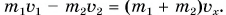
Отсюда 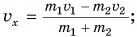

Знак «—» указывает на то, что после автосцепки вагоны будут двигаться противоположно направлению оси Ох.
Ответ: скорость v направлена противоположно оси Ох; 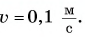
Механическая работа и мощность
В 7-м классе вы познакомились с физической величиной, называемой «механическая работа». Вы узнали, что; в случае когда направление силы F совпадает с направлением движения, работа, которую совершает эта сила, определяется по формуле:
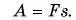
А если сила направлена под углом к перемещению? Как определить работу в этом случае?
Рассмотрим пример. Трактор передвигает бетонный блок, действуя на него силой 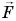 (рис. 242). Сила составляет угол а с перемещением блока
(рис. 242). Сила составляет угол а с перемещением блока 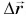 . Разложим силу
. Разложим силу 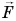 на две составляющие: перпендикулярную перемещению
на две составляющие: перпендикулярную перемещению 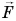 и параллельную ему
и параллельную ему 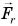 .
.
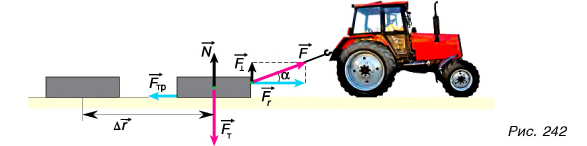
В направлении силы 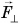 блок не перемещается. Эта сила работы не совершает. Значит, работа силы
блок не перемещается. Эта сила работы не совершает. Значит, работа силы 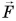 равна работе ее составляющей
равна работе ее составляющей 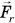 , которая направлена по движению блока:
, которая направлена по движению блока:
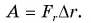
Так как 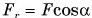 (рис. 242), то
(рис. 242), то

Механическая работа равна модулю силы, умноженному на модуль перемещения и на косинус угла между силой и перемещением.
Работа — скалярная величина.
Единицей работы в СИ является 1 джоуль (1 Дж). Он равен работе, совершаемой силой 1 ныотон при перемещении тела на 1 метр в направлении этой силы (1 Дж = 1 Н • м).
Работа силы может быть положительной, отрицательной или равной нулю. Это зависит от угла между силой и перемещением. Из формулы (1) следует:
- •если угол а острый, то cos а > 0 и работа положительна;
- •если прямой — равна нулю (cosа = 0);
- •если тупой — отрицательна (cos а < 0).
В нашем примере на бетонный блок, кроме силы натяжения троса 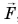 , действуют: сила тяжести
, действуют: сила тяжести 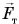 , сила реакции
, сила реакции 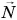 и сила трения
и сила трения 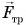 (рис. 242). Какой будет работа каждой из этих сил? Определите самостоятельно.
(рис. 242). Какой будет работа каждой из этих сил? Определите самостоятельно.
Построим график зависимости проекции силы Fr от модуля перемещения 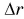 при Fr = const (рис. 243). Площадь закрашенного прямоугольника численно равна работе, совершенной этой силой при перемещении
при Fr = const (рис. 243). Площадь закрашенного прямоугольника численно равна работе, совершенной этой силой при перемещении 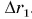 .
.
А если сила — переменная величина? В этом случае работа силы также определяется площадью фигуры под графиком зависимости силы Fr от модуля перемещения 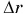 (рис. 244).
(рис. 244).
Подсчитаем работу для двух практически важных случаев.
Работа по подъему тела
Тело массой 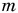 равномерно поднимают вверх. Для этого к нему прикладывают силу
равномерно поднимают вверх. Для этого к нему прикладывают силу 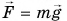 (рис. 245). Работа силы, необходимой для равномерного подъема груза по вертикали на высоту h, равна
(рис. 245). Работа силы, необходимой для равномерного подъема груза по вертикали на высоту h, равна

Работа но деформированию пружины
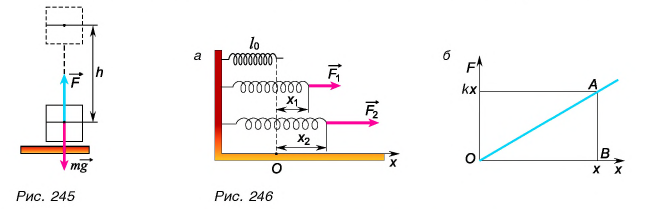
Растянем пружину жесткостью k внешней силой 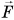 (рис. 246, а). При упругих деформациях модуль внешней силы прямо пропорционален растяжению пружины х т. е. F = kx. Работа силы F численно равна площади треугольника ОАВ на графике зависимости F от х (рис. 246, б):
(рис. 246, а). При упругих деформациях модуль внешней силы прямо пропорционален растяжению пружины х т. е. F = kx. Работа силы F численно равна площади треугольника ОАВ на графике зависимости F от х (рис. 246, б):

Равенство (3) выполняется и для работы по сжатию пружины.
Для любознательных:
Работа силы зависит от выбора системы отсчета. Рассмотрим пример. Вы находитесь в кабине движущегося лифта. Совершает ли работу действующая на вас сила тяжести? Да, если определять работу этой силы в системе отсчета, связанной с Землей. Нет, если системой отсчета является лифт. Докажите это самостоятельно.
Быстроту совершения работы характеризует мощность. Мощностью называют физическую величину, равную отношению работы к промежутку времени, за который работа совершена:

Мощность численно равна работе, совершаемой за единицу времени. Единицей мощности в СИ является 1 eamm( 1 Вт) — мощность, при которой работа 1 джоуль совершается за 1 секунду. Широко используются кратные единицы мощности: киловатт 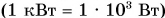 , мегаватт
, мегаватт 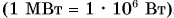 . Мощность автомобильных двигателей до сих пор указывают в лошадиных силах (л. е.). 1 л. с.
. Мощность автомобильных двигателей до сих пор указывают в лошадиных силах (л. е.). 1 л. с. 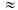 736 Вт.
736 Вт.
Согласно формуле (4) работа 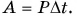 Поэтому в качестве единицы работы часто используют 1 киловатт час (1 кВт • ч), равный 3 600 ООО Дж.
Поэтому в качестве единицы работы часто используют 1 киловатт час (1 кВт • ч), равный 3 600 ООО Дж.
Именно за потребленное количество киловатт-часов (а не киловатт!) электроэнергии мы платим ежемесячно.
Установим связь мощности Р со скоростью движения тела и. Из формул 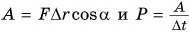 следует формула для определения мощности:
следует формула для определения мощности: 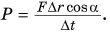 Учитывая, что
Учитывая, что 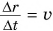 , получим:
, получим:
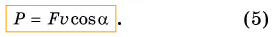
Равенство (5) показывает, что при одной и той же мощности двигателя молено:
- •либо двигаться с большой скоростью при сравнительно малой силе сопротивления движению (рис. 247, а);
- •либо преодолевать большую силу сопротивления, двигаясь с небольшой скоростью (рис. 247, б).

Это используют водители тяжелогруженых машин. При подъеме в гору они уменьшают скорость движения машины, чтобы увеличить силу тяги двигателя.
Главные выводы:
- Работа силы равна произведению модулей силы и перемещения на косинус угла между ними.
- Если угол между силой и перемещением острый, то работа силы положительна, если тупой — отрицательна.
- Силы, перпендикулярные перемещению тела, работу не совершают.
- Мощность численно равна работе, совершаемой за единицу времени.
- Мощность пропорциональна произведению действующей силы и скорости движения тела.
Пример №3
Из колодца глубиной l = 12 м равномерно поднимают ведро воды массой 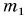 = 10 кг с помощью каната, каждый метр которого имеет массу
= 10 кг с помощью каната, каждый метр которого имеет массу 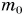 = 0,20 кг. Определите совершенную при этом работу. Принять
= 0,20 кг. Определите совершенную при этом работу. Принять 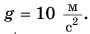

Решение
Учтем, что при подъеме ведра различные точки каната проходят разные пути (от s = 0 для верхней точки каната до s = l для его нижней точки). Тогда работа против сил тяжести, действующих на ведро
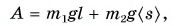
где 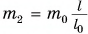 — масса каната,
— масса каната, 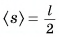 — среднее значение пути для точек каната.
— среднее значение пути для точек каната.
Отсюда 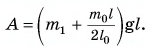
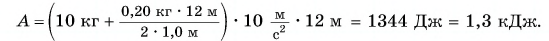
Ответ: 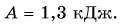
Пример №4
Автомобиль массой m = 2,0 т, развивающий мощность Р = 40 л. c., поднимается в гору с постоянной скоростью, модуль которой 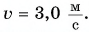 Определите угол наклона горы к горизонту. Силами сопротивления движению пренебречь. Принять g
Определите угол наклона горы к горизонту. Силами сопротивления движению пренебречь. Принять g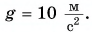
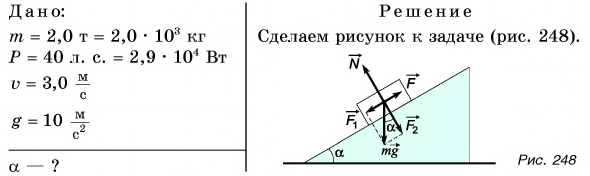
Мощность двигателя 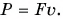 Модуль силы F (рис. 248), движущей автомобиль, равен модулю составляющей силы тяжести:
Модуль силы F (рис. 248), движущей автомобиль, равен модулю составляющей силы тяжести: 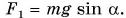 Тогда мощность
Тогда мощность 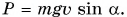
Отсюда 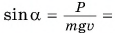

Ответ: 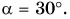
Потенциальная энергия
Вы уже знаете, что и для подъема тела на некоторую высоту, и для его деформации необходимо совершить работу. А какая физическая величина характеризует способность тел совершать работу?
Получим ответ, проведя опыт. О помощью нити и блока соединим гирю массой m с цилиндром немного меньшей массы 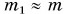 (рис. 249, а). Гиря опустится на уровень стола, а цилиндр поднимется на высоту h (рис. 249, б). За счет чего совершалась работа по подъему цилиндра? За счет работы силы тяжести
(рис. 249, а). Гиря опустится на уровень стола, а цилиндр поднимется на высоту h (рис. 249, б). За счет чего совершалась работа по подъему цилиндра? За счет работы силы тяжести 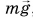 , с которой Земля притягивала гирю. Значит, способность совершать работу приобрела не гиря сама по себе, а система взаимодействующих тел «гиря + Земля». Мерой этой способности является физическая величина, называемая потенциальной энергией.
, с которой Земля притягивала гирю. Значит, способность совершать работу приобрела не гиря сама по себе, а система взаимодействующих тел «гиря + Земля». Мерой этой способности является физическая величина, называемая потенциальной энергией.
Потенциальная энергия — это мера способности сил взаимодействия механической системы совершать работу. Обозначим потенциальную энергию символом Еп. Она измеряется в тех же единицах, что и работа (в СИ — в джоулях). В дальнейшем мы будем говорить о потенциальной энергии тела, понимая, что речь идет о потенциальной энергии системы взаимодействующих тел.
Как определить потенциальную энергию тела
1. Нужно, прежде всего, определить нулевой уровень, т. е. состояние, в котором потенциальная энергия тела равна нулю. Например, можно принять, что потенциальная энергия гири равна пулю, когда гиря находится на поверхности стола, h = 0 (рис. 249).
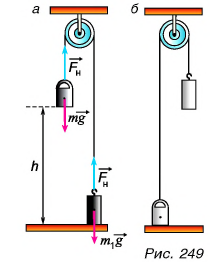
2. Затем следует найти работу А, которую совершают силы взаимодействия системы «гиря + Земля» при переходе тела из данного состояния в нулевое (в нашем опыте — при перемещении гири с высоты h на поверхность стола). Эта работа и определяет потенциальную энергию тела:

В нашем опыте работу Л совершала сила тяжести гири 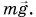 При перемещении гири с высоты h на нулевой уровень работа А = mgh. Значит, потенциальная энергия гири:
При перемещении гири с высоты h на нулевой уровень работа А = mgh. Значит, потенциальная энергия гири:

Совпадение выражения 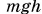 с работой по подъему тела (см. § 33) не случайно. Какая работа необходима для подъема тела (рис. 249, а), такую работу совершит сила тяжести при возвращении тела обратно (рис. 249, б). Определим теперь потенциальную энергию упруго деформированной пружины. Вам известно (§ 33), что работа, необходимая для деформации пружины,
с работой по подъему тела (см. § 33) не случайно. Какая работа необходима для подъема тела (рис. 249, а), такую работу совершит сила тяжести при возвращении тела обратно (рис. 249, б). Определим теперь потенциальную энергию упруго деформированной пружины. Вам известно (§ 33), что работа, необходимая для деформации пружины, 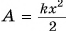 . Значит, потенциальная энергия упруго деформированной пружины:
. Значит, потенциальная энергия упруго деформированной пружины:

Формула (3) определяет потенциальную энергию любого упругого тела при деформациях сжатия или растяжения.
Для любознательных:
Формулы 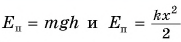 отличаются друг от друга, хотя обе описывают одну и ту же физическую величину — потенциальную энергию. Причина различия этих формул в том, что модуль силы тяжести
отличаются друг от друга, хотя обе описывают одну и ту же физическую величину — потенциальную энергию. Причина различия этих формул в том, что модуль силы тяжести 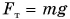 постоянен (график 1 на рис. 250), а модуль силы упругости
постоянен (график 1 на рис. 250), а модуль силы упругости 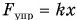 изменяется в процессе деформирования (график 3). Поэтому различаются и графики потенциальных энергий: наклонная прямая 2 и участок параболы 4 на рисунке 250.
изменяется в процессе деформирования (график 3). Поэтому различаются и графики потенциальных энергий: наклонная прямая 2 и участок параболы 4 на рисунке 250.
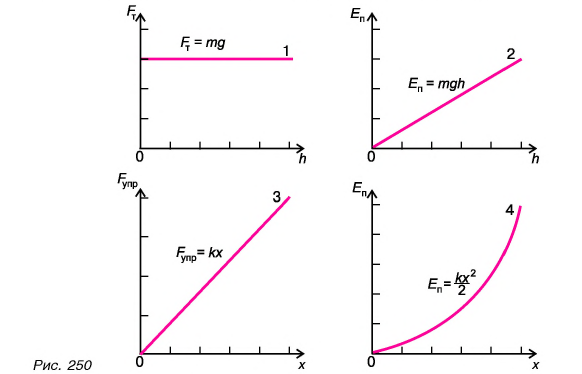
Рассмотрим еще два свойства потенциальной энергии.
1. Изменение потенциальной энергии и работа силы взаимодействия имеют противоположные знаки.
Например, при движении тела массой m вниз с высоты 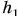 до высоты h2 (рис. 251) работа силы тяжести
до высоты h2 (рис. 251) работа силы тяжести 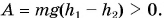 Изменение же потенциальной энергии
Изменение же потенциальной энергии 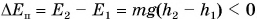 , т. е.
, т. е.

Равенство справедливо для всех видов потенциальной энергии.
2. Нулевой уровень потенциальной энергии можно выбрать произвольно. Значение потенциальной энергии зависит от выбора нулевого уровня. Например (см. рис. 249), если за нулевой уровень принять уровень поверхности пола, а не поверхности стола, то при высоте стола, равной Н, потенциальная энергия гири увеличится на 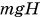 . Однако изменение потенциальной энергии
. Однако изменение потенциальной энергии 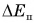 (формула (4)) от выбора нулевого уровня не зависит (докажите это самостоятельно). В каждом конкретном случае нулевой уровень выбирают так, чтобы решать задачу было проще.
(формула (4)) от выбора нулевого уровня не зависит (докажите это самостоятельно). В каждом конкретном случае нулевой уровень выбирают так, чтобы решать задачу было проще.
Главные выводы:
- Потенциальная энергия характеризует способность тела совершать работу.
- Потенциальная энергия равна работе силы взаимодействия, совершаемой при переходе тела из данного состояния на нулевой уровень.
- Изменение потенциальной энергии равно работе силы взаимодействия, взятой с противоположным знаком.
Пример №5
Недеформированную пружину жесткостью 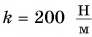 растянули от начальной длины
растянули от начальной длины 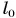 = 16 см до длины l = 20 см. Определите работу внешней силы по растяжению пружины, работу силы упругости и изменение потенциальной энергии пружины.
= 16 см до длины l = 20 см. Определите работу внешней силы по растяжению пружины, работу силы упругости и изменение потенциальной энергии пружины.
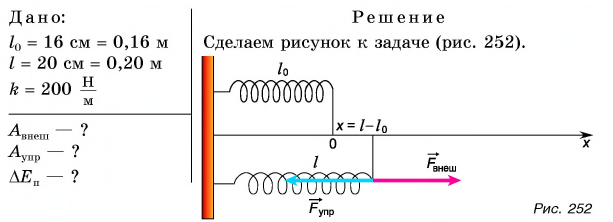
Работа внешней силы: 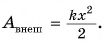 Из рисунка следует
Из рисунка следует 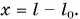
Тогда
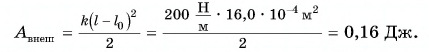
Работа силы упругости: 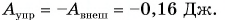 Изменение потенциальной энергии:
Изменение потенциальной энергии: 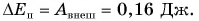 Работа внешней силы пошла на увеличение потенциальной энергии пружины.
Работа внешней силы пошла на увеличение потенциальной энергии пружины.
Ответ: 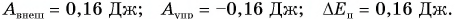
Кинетическая энергия и полная энергия системы тел
Из 7-го класса вы знаете, что, кроме потенциальной энергии, существует и кинетическая. Она зависит от массы и скорости движения тела. А как она связана с работой?
Обратимся к примерам. Молотком забивают в доску гвоздь (рис. 254, а). Движущийся вагон, сталкиваясь с покоящимся, сжимает буферные пружины. Силы, действующие со стороны движущихся молотка, вагона, совершали работу. Значит, движущиеся тела обладают способностью совершать работу. Количественной мерой этой способности является кинетическая энергия (обозначается Ек).
А как тело приобретает кинетическую энергию? В результате работы, произведенной над ним. Например, при метании молота или копья (рис. 254, б) работу совершает мускульная сила спортсмена. Чем больше эта работа, тем сильнее тело разгонится и тем большую кинетическую энергию приобретет.
Кинетическую энергию определяют как величину, равную работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости:

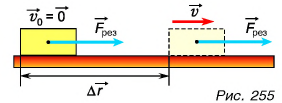
Найдем эту работу. Пусть тело массой т разгоняется из состояния покоя до скорости 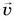 под действием сил, результирующая которых
под действием сил, результирующая которых 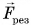 постоянна (рис. 255). Тело будет двигаться равноускоренно, а работа по разгону тела равна:
постоянна (рис. 255). Тело будет двигаться равноускоренно, а работа по разгону тела равна:

где 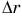 — модуль перемещения тела. При равноускоренном движении без начальной скорости (§ 12) квадрат скорости тела:
— модуль перемещения тела. При равноускоренном движении без начальной скорости (§ 12) квадрат скорости тела: 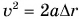 , по второму закону Ньютона
, по второму закону Ньютона 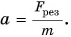 Тогда
Тогда 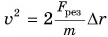 , откуда
, откуда 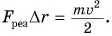
Так как 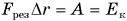 , то кинетическая энергия тела:
, то кинетическая энергия тела:

Кинетическая энергия — величина скалярная. Она зависит от модуля скорости, но не зависит от ее направления. Измеряется в тех же единицах, что и работа (в СИ — в джоулях).
А если начальная скорость движения тела 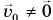 ? Тогда
? Тогда 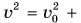
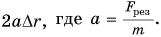 Несложно получить:
Несложно получить:

Работа пошла на изменение кинетической энергии тела.
Формула (4) выражает теорему об изменении кинетической энергии.
Изменение кинетической энергии тела равно работе результирующей всех сил, приложенных к нему.
Так как скорость движения относительна, то кинетическая энергия тоже относительна. Например, кинетическая энергия пассажира, сидящего в вагоне движущегося поезда, равна нулю относительно вагона и отлична от нуля относительно платформы. А что такое полная энергия? Чему она равна?
Рассмотрим пример. Пусть падающий мяч массой т в некоторый момент времени находится на высоте h и имеет скорость 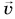 (рис. 256).
(рис. 256).
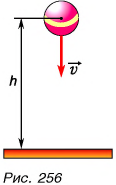
Найдем сумму кинетической и потенциальной энергии мяча. Эту сумму называют механической энергией тела:
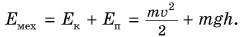
Найдена ли полная энергия? Нет.
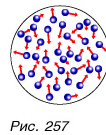
Как вы уже знаете, все тела состоят из микрочастиц — атомов, молекул и др. Эти частицы участвуют в хаотическом тепловом движении (рис. 257) и взаимодействуют (притягивают и отталкивают друг друга). Сумма кинетической энергии теплового движения микрочастиц и потенциальной энергии их взаимодействия друг с другом называется внутренней энергией тела  Значит, полная энергия Е тела равна:
Значит, полная энергия Е тела равна:

Главные выводы:
- Кинетическая энергия тела прямо пропорциональна его массе и квадрату скорости его движения.
- Значение кинетической энергии зависит от выбора системы отсчета.
- Изменение кинетической энергии равно работе результирующей всех сил, приложенных к телу.
- Механическая энергия тела есть сумма его кинетической и потенциальной энергии.
- Полная энергия тела складывается из его механической и внутренней энергии.
- Заказать решение задач по физике
Пример №6
Камень массой m = 0,50 кг брошен вертикально вверх со скоростью, модуль которой 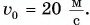 Какой кинетической энергией будет обладать камень через время
Какой кинетической энергией будет обладать камень через время 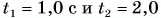 с от начала движения? Сопротивлением воздуха пренебречь. Принять
с от начала движения? Сопротивлением воздуха пренебречь. Принять 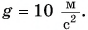

Решение
Найдем модули скорости движения камня 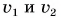 при
при 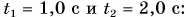
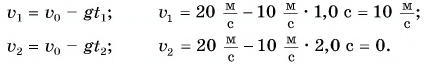
Кинетическая энергия камня через 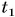 = 1,0 с:
= 1,0 с:

Через 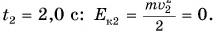
Ответ: 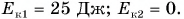
Закон сохранения энергии
Полная энергия системы складывается из ее механической энергии и внутренней энергии тел. входящих в систему. При каких условиях механическая и полная энергия системы изменяются? Остаются постоянными?
При подъеме тела возрастает его потенциальная энергия, а при увеличении скорости — кинетическая. А могут ли измениться и кинетическая, и потенциальная энергия одновременно? Рассмотрим пример. Будем поднимать со стола гирю массой m (рис. 258) с помощью прочной нити. Для механической системы «гиря + Земля» сила натяжения нити является внешней силой: 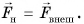 При
При 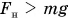 гиря не только поднимется на высоту hy но и увеличит свою скорость от
гиря не только поднимется на высоту hy но и увеличит свою скорость от 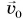 до
до 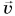 . Работа внешней силы вызовет изменение как кинетической, так и потенциальной энергии системы «гиря + Земля». Найдем связь между этими величинами. Примем за нулевой уровень поверхность стола. По теореме об изменении кинетической энергии
. Работа внешней силы вызовет изменение как кинетической, так и потенциальной энергии системы «гиря + Земля». Найдем связь между этими величинами. Примем за нулевой уровень поверхность стола. По теореме об изменении кинетической энергии

где А — работа результирующей силы 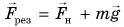 , равная:
, равная:

Из равенств (1) и (2) следует:
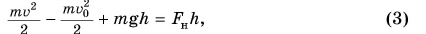
но 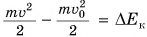 — изменение кинетической, mgh =
— изменение кинетической, mgh = 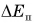 — изменение потенциальной энергии, a
— изменение потенциальной энергии, a 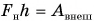 — работа внешней силы. Значит, в нашем примере
— работа внешней силы. Значит, в нашем примере

где 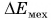 — изменение механической энергии системы. Это равенство применимо к любой механической системе, в которой действуют только силы тяжести или силы упругости. Внешними силами могут быть любые силы, например сила трения, сила сопротивления.
— изменение механической энергии системы. Это равенство применимо к любой механической системе, в которой действуют только силы тяжести или силы упругости. Внешними силами могут быть любые силы, например сила трения, сила сопротивления.
Изменение механической энергии системы, в которой действуют только силы тяжести или упругости, равно работе внешних сил.
Если система замкнута, т. е. на нее не действуют внешние силы, то из равенства (4) следует 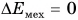 , а, значит,
, а, значит, 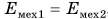 , или
, или

Механическая энергия замкнутой системы, в которой действуют только сила тяжести и силы упругости, остается постоянной (сохраняется). Это утверждение называют законом сохранения механической энергии.
Отметим, что сохраняются не кинетическая и потенциальная энергия по отдельности, а их сумма. В результате в замкнутой системе при уменьшении (увеличении) кинетической энергии настолько же возрастает (уменьшается) потенциальная: 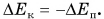
Обсудите, как кинетическая энергия переходит в потенциальную и обратно при движении тел, представленных на рисунке 259.
А что происходит, если система замкнута, но среди ее внутренних сил имеются силы трения и силы сопротивления? Проведем простой опыт. Придадим начальную скорость 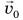 деревянному бруску массой m, находящемуся на поверхности стола. Пройдя некоторое расстояние, брусок остановится из-за действия силы трения — внутренней силы системы «брусок + стол» (рис. 260). Несмотря на то что внешняя сила (сила тяжести) работу не совершала, механическая энергия этой системы уменьшилась на величину
деревянному бруску массой m, находящемуся на поверхности стола. Пройдя некоторое расстояние, брусок остановится из-за действия силы трения — внутренней силы системы «брусок + стол» (рис. 260). Несмотря на то что внешняя сила (сила тяжести) работу не совершала, механическая энергия этой системы уменьшилась на величину 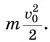
Из-за сил трения потери механической энергии происходят в любом реальном устройстве. Колебания тел, изображенных на рисунке 259, б, в, постепенно затухают, при выключенном двигателе теряет скорость автомобиль и т. д.
Исчезает ли при этом механическая энергия бесследно? При движении бруска по столу происходило нагревание бруска и стола. Только оно было мало, а потому незаметно. При торможении поезда, автомобиля нагреваются тормозные устройства. Под действием сил сопротивления воздуха раскаляются метеориты. При трении друг о друга нагреваются и далее могут плавиться куски льда.
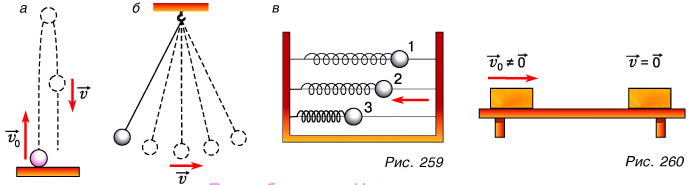
Нагревание происходит и при неупругих деформациях. Согните и разогните несколько раз подряд металлическую проволоку. Вы почувствуете, что в месте сгиба она нагрелась.
Что общего у всех этих явлений? То, что действие сил трения и со противления приводит к увеличению внутренней энергии тел. Хаотическое тепловое движение атомов и молекул становится более быстрым — растет внутренняя кинетическая энергия. Может увеличиться и внутренняя потенциальная энергия (например, при плавлении тел).
Весь накопленный опыт и специально проведенные эксперименты показывают, что в любой замкнутой системе уменьшение механической энергии в точности равно увеличению внутренней, а их сумма (т. е. полная энергия) остается постоянной:

Полная энергия замкнутой системы сохраняется.
Так формулируется один из важнейших законов природы — закон сохранения энергии.
Закон сохранения энергии не знает исключений. Он выполняется для всех физических, химических, биологических и других явлений. Этот закон используется в самых различных областях науки и техники, служит научной основой важнейшей области производства — энергетики.
Добыча энергоносителей (нефти, газа, угля), использование различных источников энергии (воды, ветра, солнечного излучения и т. д.), передача энергии на большие расстояния, борьба с потерями энергии (энергосбережение) являются важнейшими задачами всего мирового сообщества.
Главные выводы:
- Изменение механической энергии системы, в которой действуют силы тяжести и упругости, равно работе внешних сил.
- Полная энергия замкнутой системы сохраняется всегда, а ее механическая энергия сохраняется только при отсутствии сил трения и сопротивления.
- Закон сохранения энергии выполняется для всех явлений природы.
Пример №7
Пакет с цементом массой m = 20 кг поднимают вертикально вверх, прикладывая постоянную силу, модуль которой 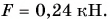 Определите кинетическую энергию пакета в момент, когда он окажется на высоте h = 2,0 м от начального положения. Начальная скорость пакета равна нулю. Сопротивлением воздуха пренебречь; модуль ускорения свободного падения принять
Определите кинетическую энергию пакета в момент, когда он окажется на высоте h = 2,0 м от начального положения. Начальная скорость пакета равна нулю. Сопротивлением воздуха пренебречь; модуль ускорения свободного падения принять 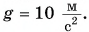

По условию задачи: 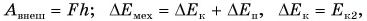
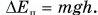 Тогда из равенства
Тогда из равенства 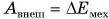 получим
получим 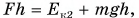 откуда
откуда 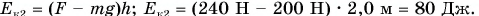
Ответ: 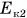 = 80 Дж.
= 80 Дж.
Законы сохранения
Механической системой (от греческого слова 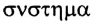 — составление; целое, состоящее из частей) называется группа взаимодействующих тел, рассматриваемых в данном случае.
— составление; целое, состоящее из частей) называется группа взаимодействующих тел, рассматриваемых в данном случае.
Силы взаимодействия тел рассматриваемой системы называются внутренними. Силы, действующие на тела рассматриваемой системы со стороны тел, не входящих в нее, называют внешними.
Система называется замкнутой, если тела, ее образующие, взаимодействуют только между собой. В замкнутой системе внешние силы отсутствуют. Систему можно считать замкнутой, если внешними силами можно пренебречь.
Важной динамической характеристикой тела или материальной точки, применяемой для характеристики механического движения, является импульс, или количество движения 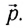
Импульс тела
Импульс тела 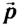 — векторная физическая величина, равная произведению массы тела т на его скорость
— векторная физическая величина, равная произведению массы тела т на его скорость 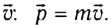
Как следует из определения, направление импульса совпадает с направлением скорости тела, а его единицей в СИ является килограмм на метр в секунду 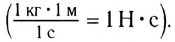
Запишем второй закон Ньютона в импульсной форме: 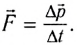
Напомним, что в полученном выражении 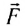 представляет собой равнодействующую всех сил, приложенных к телу (МТ). Из последнего равенства можно выразить изменение импульса
представляет собой равнодействующую всех сил, приложенных к телу (МТ). Из последнего равенства можно выразить изменение импульса 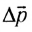 тела за время
тела за время 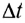 действия силы:
действия силы:

Векторная величина 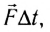 называемая импульсом силы, характеризует не только модуль и направление силы, но и время ее действия.
называемая импульсом силы, характеризует не только модуль и направление силы, но и время ее действия.
Изменение импульса тела (МТ) относительно инерциальной системы отсчета равно импульсу равнодействующей всех сил, действующих на него.
Таким образом, причиной изменения импульса тела является действие на него сил со стороны других тел. Соответственно, при отсутствии такого действия импульс тела измениться не может — он сохраняет свое значение сколь угодно долго. В этом случае
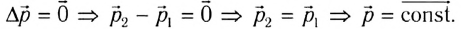
Подчеркнем, что основной закон динамики, записанный в импульсной форме, носит более общий характер, поскольку он справедлив и в том случае, когда масса тела при движении изменяется. Кроме того, в такой форме записи второй закон Ньютона справедлив и в релятивистской динамике, т. е. при движении со скоростями, сравнимыми со скоростью света в вакууме.
При рассмотрении незамкнутой механической системы тел необходимо учитывать, что каждое из тел системы может взаимодействовать как с телами этой системы, так и с телами, не входящими в нее.
Поскольку согласно третьему закону Ньютона внутренние силы в системе возникают парами и при суммировании компенсируют друг друга, то их вклад в равнодействующую равен нулю. Следовательно, изменение импульса механической системы в целом может происходить только под действием внешних сил, приложенных к ней.
При действии нескольких внешних сил 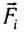 на данную механическую систему выполняется закон изменения импульса незамкнутой системы:
на данную механическую систему выполняется закон изменения импульса незамкнутой системы:
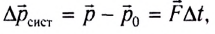
где 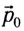 — начальный импульс системы,
— начальный импульс системы, 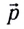 — конечный импульс системы,
— конечный импульс системы,
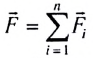 — результирующая сила,
— результирующая сила, 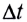 — время действия сил.
— время действия сил.
Изменение импульса незамкнутой механической системы относительно инерциальной системы отсчета равно импульсу равнодействующей всех внешних сил, действующих на нее.
Если результирующая внешняя сила, действующая на механическую систему, равна нулю 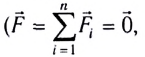 система замкнута), то изменение импульса системы также равно нулю:
система замкнута), то изменение импульса системы также равно нулю:
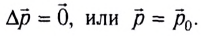
Таким образом, для замкнутых механических систем выполняется закон сохранения импульса:
- векторная сумма импульсов тел в замкнутой механической системе остается постоянной при любых взаимодействиях тел системы между собой.
Поскольку число взаимодействующих объектов во Вселенной велико, то, строго говоря, замкнутая система — это идеализация. Однако в случае кратковременного взаимодействия (столкновение, удар, взрыв), при котором  импульс силы будет мал, и им можно пренебречь. Для таких процессов
импульс силы будет мал, и им можно пренебречь. Для таких процессов 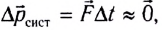 и закон сохранения импульса остается справедливым.
и закон сохранения импульса остается справедливым.
В случае, когда система незамкнута, но сумма проекций сил на какую-либо ось равна нулю, система называется частично замкнутой или замкнутой на данную ось. Например, если проекция равнодействующей на ось Оу равна нулю 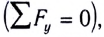 то изменение проекции импульса системы на эту ось также равно нулю
то изменение проекции импульса системы на эту ось также равно нулю 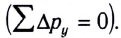 Следовательно, в этом случае сохраняется проекция импульса системы на заданную ось:
Следовательно, в этом случае сохраняется проекция импульса системы на заданную ось: 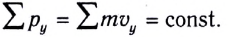
Реактивное движение
Закон сохранения импульса позволяет объяснить возникновение реактивного движения, широко используемого в науке и технике, например при космических полетах. Его также можно наблюдать в живой природе.
Рассмотрим простейшую ракету как систему двух взаимодействующих тел (рис. 51), одно из которых представляет собой замкнутую оболочку (трубку) с соплом, а второе — содержащуюся внутри ракеты горючую смесь (топливо).

При горении смеси раскаленные газы с большой скоростью выбрасываются из ракеты. Оболочка при этом разгоняется в противоположную сторону в соответствии с законом сохранения импульса. После выгорания топлива ракета, подобно брошенному камню, совершает свой дальнейший полет по баллистической траектории.
До начала работы двигателей сумма импульсов ракеты 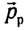 и горючей смеси
и горючей смеси 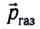 равна нулю
равна нулю 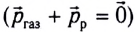 (см. рис. 51). Следовательно, согласно закону сохранения импульса и после включения двигателей сумма импульсов ракеты и газов также равна нулю:
(см. рис. 51). Следовательно, согласно закону сохранения импульса и после включения двигателей сумма импульсов ракеты и газов также равна нулю:

где М — масса ракеты, 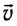 — скорость ракеты, m — масса одновременно выброшенных газов,
— скорость ракеты, m — масса одновременно выброшенных газов, 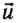 — скорость истечения газов относительно ракеты (рис. 52).
— скорость истечения газов относительно ракеты (рис. 52).
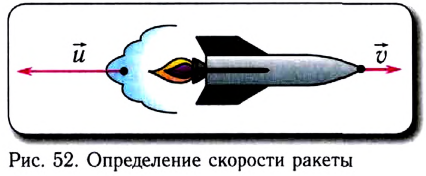
Отсюда получаем

Отметим, что эта формула справедлива при условии незначительного изменения массы М ракеты в результате работы ее двигателей.
Из второго закона Ньютона, записанного в импульсной форме

следует, что изменение импульса тела, связанное с действием силы, может возникать не только при изменении скорости тела, но и при изменении его массы.
Законы движения тел с переменной массой (ракет) были исследованы русскими учеными И. В. Мещерским и К. Э. Циолковским.
Циолковский одним из первых обосновал идею космических полетов с помощью ракет и выхода человека в космос, а также получил широко известную формулу, связывающую массу ракеты с ее скоростью.
Уравнение Мещерского позволяет определить реактивную силу, действующую на ракету со стороны реактивной струи газов.
Пусть в данной ИСО в некоторый момент времени t скорость ракеты равна 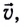 а ее масса — М. Через малый промежуток времени
а ее масса — М. Через малый промежуток времени 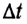 масса ракеты за счет сгорания топлива и истечения газов уменьшится до значения
масса ракеты за счет сгорания топлива и истечения газов уменьшится до значения 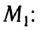
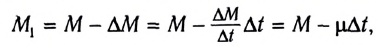
где 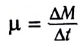 — масса, теряемая ракетой в единицу времени (расход топлива).
— масса, теряемая ракетой в единицу времени (расход топлива).
За это время скорость ракеты увеличится до значения 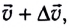 а масса истекших газов будет
а масса истекших газов будет 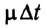 и их скорость в данной ИСО будет равна
и их скорость в данной ИСО будет равна 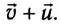
Из закона сохранения импульса
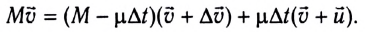
Раскрывая скобки и пренебрегая членом, содержащим произведение двух малых величин 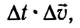 получаем
получаем
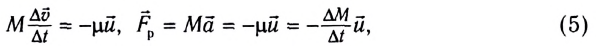
где 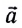 — ускорение ракеты,
— ускорение ракеты, 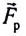 — реактивная сила тяги.
— реактивная сила тяги.
Таким образом, реактивная сила тяги, действующая на ракету, определяется скоростью истечения газов  относительно ракеты и расходом топлива
относительно ракеты и расходом топлива 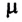 и направлена в сторону, противоположную направлению истечения газов. Движение тела, возникающее вследствие отделения от него части его массы с некоторой скоростью
и направлена в сторону, противоположную направлению истечения газов. Движение тела, возникающее вследствие отделения от него части его массы с некоторой скоростью 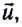 называют реактивным.
называют реактивным.
Особенностью реактивного движения является тот факт, что оно может быть реализовано как в земных, так и в космических условиях, поскольку реактивная сила тяги практически не зависит от свойств окружающей среды и от скорости движения объекта. Это обстоятельство обеспечило широкое распространение
реактивных двигателей при создании современных высокоскоростных судов, самолетов, космических ракет.
Работа и мощность в механике
Работа — скалярная физическая величина, прямо пропорциональная модулю силы F, совершающей работу, и пройденному пути s: A=Fs, если направление силы совпадает с направлением движения.
При динамическом подходе к описанию механического движения определяющим понятием является импульс силы, зависящий от времени ее воздействия.
Для описания действия силы при перемещении тела на определенное расстояние вводится скалярная физическая величина, называемая работой силы.
Если под действием силы 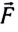 тело совершает перемещение
тело совершает перемещение 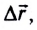 то говорят, что сила совершила над телом некоторую работу А.
то говорят, что сила совершила над телом некоторую работу А.
Работа — скалярная физическая величина, равная произведению модуля силы F, модуля перемещения 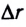 и косинуса угла а между
и косинуса угла а между 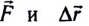 (рис. 53):
(рис. 53):

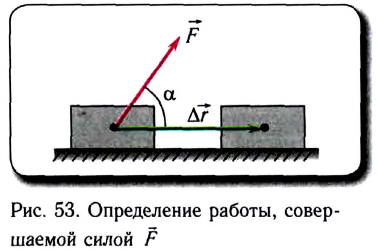
Данное определение справедливо для постоянной (как по модулю, так и по направлению) силы 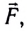 перемещающей тело по отрезку прямой линии.
перемещающей тело по отрезку прямой линии.
В СИ единицей работы является джоуль (1 Дж= 1 Н • 1 м).
Один джоуль — это работа, которую совершает сила в один ньютон, действующая на тело в направлении его перемещения, на пути в один метр.
Если графически изобразить зависимость проекции силы 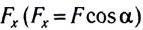 от модуля вектора перемещения
от модуля вектора перемещения 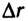 на направление перемещения (ось Ох), то работа А силы будет численно равна площади прямоугольника ОАВС (рис. 54).
на направление перемещения (ось Ох), то работа А силы будет численно равна площади прямоугольника ОАВС (рис. 54).

Рассмотрим некоторые наиболее распространенные случаи вычисления работы: 1.Если угол между направлением силы, совершающей работу, и перемещением равен нулю (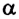 = 0), то работа вычисляется по формуле
= 0), то работа вычисляется по формуле

Так, сила тяги, создаваемая двигателем автомобиля, совершает положительную работу при его разгоне.
2. Если угол между направлением силы и перемещением 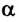 = 90°, то
= 90°, то
А = 0. (3)
Так, при вращении шарика на нити сила натяжения нити не совершает работу и модуль скорости шарика не меняется.
3. Если угол между направлением силы и перемещением 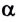 = 180°, то работа вычисляется по формуле:
= 180°, то работа вычисляется по формуле:

Так, сила сопротивления среды совершает отрицательную работу, что при выключенном двигателе автомобиля приводит к уменьшению его скорости до полной его остановки.
Во многих случаях в процессе движения сила меняется и по модулю, и по направлению, т. е. не выполняются условия, при которых справедлива формула для работы (1). Тогда для нахождения работы необходимо весь путь разделить на такие малые участки 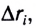 для которых эти условия соблюдаются, и подсчитать сумму работ на всех участках. При графическом вычислении работы она будет численно равна площади фигуры ОАВС, где АВ — график зависимости
для которых эти условия соблюдаются, и подсчитать сумму работ на всех участках. При графическом вычислении работы она будет численно равна площади фигуры ОАВС, где АВ — график зависимости 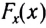 (рис. 55).
(рис. 55).
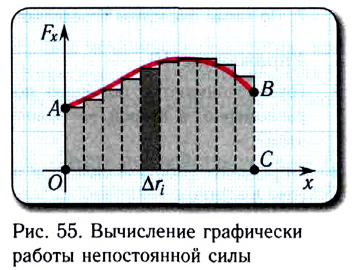
Существует два класса сил — потенциальные (консервативные) и непотенциальные (неконсервативные).
Если работа силы не зависит от траектории движения тела, а определяется только его начальным и конечным положениями в пространстве, то сила является потенциальной. Следует подчеркнуть, что модуль потенциальных сил определяется только расположением тел в пространстве, т. е. расстояниями между взаимодействующими телами.
Можно показать, что работа потенциальной силы при перемещении тела по любой замкнутой траектории всегда равна нулю.
Заметим, что если на каком-либо участке пути потенциальные силы совершают некоторую работу А над телом, то при движении по той же траектории в обратном направлении будет совершена работа — А.
Потенциальными являются силы упругости, силы гравитационного притяжения, сила тяжести.
Если работа силы зависит от траектории движения тела, то говорят о непотенциальной силе, примером которой является сила трения. Действительно, работа силы трения отрицательна при перемещении тела по участку траектории, как в прямом, так и в обратном направлении.
Величину работы, совершаемой постоянной силой 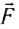 в единицу времени, характеризует мощность:
в единицу времени, характеризует мощность:

Мощность Р — скалярная физическая величина, определяющая быстроту совершения работы.
Единицей мощности в СИ является ватт 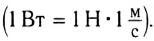
Средняя мощность равна отношению совершенной работы А к промежутку времени 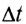 ее выполнения:
ее выполнения:
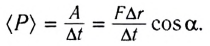
С учетом того, что 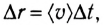 получаем
получаем
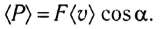
Следовательно, мгновенную мощность Р можно определить по формуле:

Таким образом, мгновенная мощность силы равна произведению модуля силы, модуля скорости тела и косинуса угла 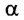 между
между 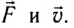
Подчеркнем, что полученная формула справедлива и в случае изменяющихся с течением времени значений силы и скорости.
Кинетическая и потенциальная энергии. Закон сохранения энергии в механике
Кинетическая энергия тела — скалярная физическая величина, равная работе, совершенной при разгоне данного тела из состояния покоя до данной скорости, или величина, равная работе силы, необходимой для остановки данного тела. Потенциальная энергия — это энергия, обусловленная расположением взаимодействующих тел или частей тела.
Работа силы связана с изменением механической энергии при переходе системы из одного состояния в другое. Энергия — это скалярная физическая величина, характеризующая способность тела или системы тел совершать работу. Изменение энергии системы определяется работой, совершенной внешними силами, приложенными к системе.
Термин «энергия» был введен В. Дж. Ренкиным в 1853 г. при рассмотрении закона сохранения энергии в немеханических системах. Он образован от греческого слова 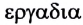 — работа и приставки
— работа и приставки 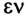 — в, внутри.
— в, внутри.
В механике состояние системы определено, если известно положение тел системы (их координаты) и импульсы всех тел системы. В соответствии с этим в механике существуют два вида энергии — потенциальная и кинетическая.
Кинетическая энергия (энергия движения) — вид механической энергии, которой обладают тела вследствие их движения. Кинетическая энергия движущегося тела в заданной ИСО равна работе, которую нужно совершить для полной остановки тела.
Рассмотрим тело, движущееся со скоростью 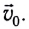 Пусть под действием силы
Пусть под действием силы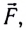 направленной противоположно
направленной противоположно 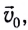 оно остановилось, совершив перемещение
оно остановилось, совершив перемещение 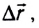 тогда
тогда
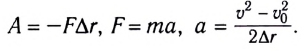
Вследствие того, что конечная скорость тела v = 0, получаем
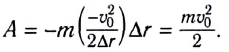
Таким образом, при поступательном движении твердого тела его кинетическая энергия определяется по формуле

где m — масса тела, v — скорость любой точки тела (например, центра тяжести).
Отметим, что эта формула верна лишь для скоростей движения V, намного меньших скорости света с, т. е. при 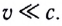
Теорема о кинетической энергии:
изменение кинетической энергии 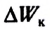 тела при его переходе из одного состояния в другое равно работе А всех сил, действующих на тело:
тела при его переходе из одного состояния в другое равно работе А всех сил, действующих на тело:

где 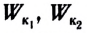 — кинетическая энергия тела в начальном и конечном состоянии соответственно.
— кинетическая энергия тела в начальном и конечном состоянии соответственно.
Потенциальная энергия
Потенциальная энергия (энергия положения) — вид механической энергии, обусловленной взаимодействием тел или частей одного и того же тела и зависящей только от координат тел.
Потенциальная энергия системы взаимодействующих тел — это физическая величина, численно равная работе, совершаемой силами взаимодействия при взаимном удалении всех тел системы из данного положения на бесконечное расстояние друг от друга. В этом положении потенциальная энергия считается равной нулю.
На тело, находящееся у поверхности Земли, действует сила тяжести. Для изменения положения тела над поверхностью Земли сила тяжести 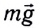 должна совершить работу, равную изменению потенциальной энергии
должна совершить работу, равную изменению потенциальной энергии 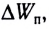 взятую с противоположным знаком
взятую с противоположным знаком
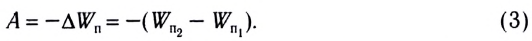
Такой выбор знака приводит к тому, что работа силы тяжести положительна при движении тела вниз, а значит, потенциальная энергия 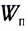 убывает. И, наоборот, при движении тела вверх энергия
убывает. И, наоборот, при движении тела вверх энергия 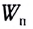 возрастает, а работа — отрицательна.
возрастает, а работа — отрицательна.
В однородном поле силы тяжести (вблизи поверхности Земли) потенциальной энергией 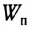 называют физическую величину
называют физическую величину 
где h — высота над уровнем, условно принятым за нулевой. Отметим, что эта высота должна быть намного меньше радиуса R планеты, т. е. 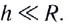
Выбор состояния, энергия которого принимается за нулевой уровень, совершенно произволен и определяется только соображениями удобства.
Потенциальная энергия упруго деформированного тела определяется работой, которую совершают силы упругости, возвращая тело в недеформированное состояние. Модуль силы упругости 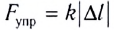 по мере возвращения тела в недеформированное состояние будет равномерно убывать до нуля. Следовательно, в данном случае необходимо рассчитать работу переменной силы. Вследствие того, что зависимость силы упругости от абсолютного удлинения (сжатия)
по мере возвращения тела в недеформированное состояние будет равномерно убывать до нуля. Следовательно, в данном случае необходимо рассчитать работу переменной силы. Вследствие того, что зависимость силы упругости от абсолютного удлинения (сжатия) 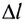 линейная, находим
линейная, находим
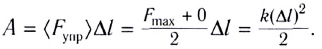
Потенциальной энергией упруго деформированного тела является величина
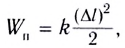
где k — жесткость образца, 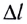 — абсолютное удлинение (сжатие).
— абсолютное удлинение (сжатие).
Единицей энергии, как и работы, в СИ является джоуль (1 Дж).
Сумма кинетической и потенциальной энергий называется полной механической энергией системы:
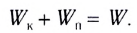
Таким образом, в общем случае работа А, совершенная над системой тел, равна приращению ее энергии 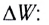
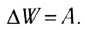
Если механическая система является консервативной, т. е. если внешние и внутренние силы, действующие на тела системы, являются потенциальными и работа внешних сил равна нулю, то
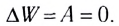
Следовательно,
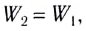
т. е. механическая энергия системы сохраняется.
Для таких систем выполняется закон сохранения механической энергии: полная механическая энергия консервативной физической системы является величиной постоянной:
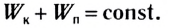
Закон сохранения механической энергии справедлив и для незамкнутых систем в том случае, если внешнее силовое ноле потенциально и стационарно.
Закон сохранения механической энергии является частным случаем закона сохранения и превращения энергии:
при любых процессах энергия не увеличивается и не уменьшается. Энергия может превращаться из одного вида в другой и передаваться от одного тела другому, но ее полная величина сохраняется постоянной.
Границы применения физических законов и теорий
Физики установили существование четырех видов взаимодействия между частицами: сильное, электромагнитное, слабое и гравитационное (отмечено в порядке уменьшения интенсивности). Современные теории всех взаимодействий являются квантовыми.
Интенсивность любого взаимодействия принято характеризовать с помощью так называемого постоянного взаимодействия, которое определяет вероятность процессов, обусловленных данным видом взаимодействия. Отношение значений констант показывает относительную интенсивность соответствующих взаимодействий, которая дает возможность сравнить их.
Самым универсальным среди взаимодействий является гравитационное -оно возникает между любыми телами, имеющими массу.
В физике частиц гравитационное взаимодействие не имеет никакого значения на расстояниях больше 10-35 м. При меньших расстояниях или очень больших энергиях это взаимодействие по значению сравнивается с другими взаимодействиями.
Электромагнитное взаимодействие возникает между телами, имеющими электрический заряд.
Слабое и сильное взаимодействия – ядерные. Слабое взаимодействие руководит распадом тяжелых частиц на более легкие и изменяет внутреннюю природу частиц. Сильное взаимодействие – это взаимодействие между кварками, которое и обусловливает ядерное взаимодействие, а также разные ядерные реакции. Это взаимодействие почти в 1037 раз сильнее гравитационного.
Каждому фундаментальному взаимодействию соответствует своя частица, переносящая это взаимодействие. Для гравитации – это гравитоны, для электромагнитного взаимодействия – фотоны, сильное взаимодействие обусловливается глюонами, слабое – векторными бозонами.
Как же осуществляются эти взаимодействия?
Электромагнитное взаимодействие: переносчик – фотон. Гравитационное взаимодействие: переносчики – кванты поля тяготения – гравитоны. И фотоны, и гравитоны не имеют массы (массы покоя) и всегда движутся со скоростью света. Слабые взаимодействия: переносчики – векторные бозоны. Существенным отличием переносчиков слабого взаимодействия от фотона и гравитона является их массивность. Переносчики сильных взаимодействий – глюоны (англ, glue – «клей») с массой покоя, равной нулю.
Ряд существенных открытий, сделанных в фундаментальной физике, особенно в физике высоких энергий, важные экспериментальные результаты открывают глубокую взаимосвязь частиц и скрытых сил, действующих внутри вещества. Ученые выдвинули гипотезу, согласно которой вся природа подчинена действию некоей суперсилы, являющейся достаточно мощной, чтобы создать нашу Вселенную и наделить ее светом, энергией, материей и предоставить ей структуру. В суперсиле материя, пространство-время и взаимодействие слиты в неразделимое гармоничное целое, порождающее такое единство Вселенной, которого раньше никто и не предполагал.
Фундаментальные законы достаточно абстрактно сформулированы, и не являются следствием экспериментов. Обычно фундаментальные законы «угадываются», а не выводятся из эмпирических. Количество таких законов очень ограничено (например, классическая механика имеет лишь четыре фундаментальных закона: три закона Ньютона и закон всемирного тяготения). Многочисленные эмпирические законы являются последствиями (иногда вовсе не очевидными) фундаментальных. Критерием истинности последних является соответствие конкретных последствий экспериментальным наблюдениям. Все известные сегодня фундаментальные законы описываются достаточно простыми математическими выражениями. Границы применения фундаментальных законов ограничены. Эта ограниченность не связана с математическими неточностями, а имеет более фундаментальный характер: при выходе за границы
применения фундаментального закона начинают терять смысл сами понятия, используемые в формулировках. Так, для микрообъектов оказывается невозможным строгое определение понятий ускорения и силы, которая ограничивает применение законов Ньютона.
Ограниченность применения фундаментальных законов естественно приводит к вопросу о существовании еще более общих законов. Такими являются законы сохранения. Существующий опыт развития естествознания показывает, что законы сохранения не теряют своего смысла при замене одной системы фундаментальных законов другой. В большинстве случаев законы сохранения не способны дать такого полного описания явлений, которое дают фундаментальные законы, а лишь накладывают определенные запреты на реализацию тех или иных состояний при эволюции системы.
Мы уже говорили, что первый закон Ньютона выполняется только в инерциальных системах отсчета. Второй закон также выполняется лишь в инерциальных системах. Третий закон выполняется и в неинерциальных системах, но не всегда. Он не выполняется для так называемых сил инерции. Следовательно, первым ограничением законов Ньютона является то, что они выполняются только в инерциальных системах отсчета.
Механика Ньютона является механикой малых скоростей (сравнительно со скоростью распространения света). Движение в микромире (мире молекул, атомов и элементарных частиц) подчиняется другим законам. Поэтому механика Ньютона неприменима к микромиру, она является механикой больших тел (конечно, сравнимых с размерами молекул).
Следовательно, классическая механика Галилея-Ньютона выполняется лишь в инерциальных системах для больших тел, движущихся с малыми скоростями, а потому считать ее универсальной нельзя.
Каждый физический закон имеет свои границы применения. Это, в первую очередь, касается закона сохранения механической энергии. Первое важное ограничение данного закона – система рассматриваемых тел должна быть изолирована от внешних влияний. Такую систему называют замкнутой. Второе ограничение связано с тем, что не всегда работа однозначно определяется изменением потенциальной энергии тела при перемещении его с одной точки поля в другую. Однозначное определение работы как меры изменения потенциальной энергии имеет место лишь для определенных типов полей, которые называют потенциальными. Примерами таких полей является гравитационное или электростатическое поле. Потенциальными считаются поля, работа сил которых не зависит от траектории движения тела в поле. Соответственно, силы этих полей называют консервативными. Если работа сил зависит от формы пути или силы зависят от скорости движения, то механическая энергия системы не сохраняется. Например, силы трения, не являющиеся консервативными, присутствуют во всех случаях. Следовательно, закон сохранения механической энергии выполняется лишь для идеализированных ситуаций.
Изучая закон Гука, следует помнить, что он имеет определенные границы применения или границы, в которых он выполняется, а именно «предел упругости».
Закон Ома также имеет границы применения, хотя и достаточно широкие – вплоть до чрезвычайно малых токов. Закон Ома не выполняется в тех случаях, когда ток очень слабый (или очень большой), и начинают проявляться флуктуации числа носителей тока – электронов в металле. Тогда закон, имеющий принципиально статистический характер, не выполняется.
Законы прямолинейного распространения света, отражения и преломления выполняются лишь при определенных условиях, когда длина световых волн намного меньше размеров отверстий и экранов, с которыми взаимодействует свет при распространении.
Фундаментальный характер законов сохранения в природе
Фундаментальные физические законы – самое полное, но приближенное отражение объективных процессов в природе. Разные формы движения материи описываются разными фундаментальными теориями. Каждая из этих теорий описывает полностью определенные явления: механическое или тепловое движение, электромагнитные явления.
Законы сохранения – утверждения, согласно которым числовые значения этих величин не меняются со временем в любых процессах.
Идея сохранения появилась сначала как сугубо философская точка зрения о наличии неизменного, стабильного в вечно переменчивом мире. Еще античные философы-материалисты пришли к понятию материи как неуничтожимой и несоздаваемой. С другой стороны, наблюдение постоянных изменений в природе приводило к представлению о вечном движении материи как важном ее свойстве. С появлением материалистической формулировки механики на этой основе появились законы сохранения.
Самыми важными законами сохранения, которые выполняются для любых изолированных систем, являются закон сохранения энергии и закон сохранения импульса.
Закон сохранения энергии в механических процессах. Механическая энергия разделяется на два вида: потенциальную (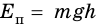 – если тело
– если тело
поднято на определенную высоту над Землей, 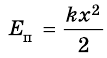 если тело упруго деформировано) и кинетическую
если тело упруго деформировано) и кинетическую 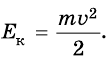 И потенциальная, и кинетическая энергии изменяются только в результате такого взаимодействия тел, при котором силы, действующие на тела, выполняют работу, отличающуюся от нуля.
И потенциальная, и кинетическая энергии изменяются только в результате такого взаимодействия тел, при котором силы, действующие на тела, выполняют работу, отличающуюся от нуля.
Рассмотрим теперь вопрос об изменении энергии при взаимодействии тел, образующих замкнутую систему. Если несколько тел взаимодействуют между собой лишь силами тяготения и силами упругости и никакие внешние силы не действуют, то при любых взаимодействиях сумма кинетической и потенциальной энергий тел остается постоянной. Это утверждение называют законом сохранения энергии в механических процессах.
Сумму кинетической и потенциальной энергий тел называют полной механической энергией 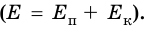 Поэтому закон сохранения энергии можно сформулировать следующим образом: полная механическая энергия замкнутой системы тел, взаимодействующих силами притяжения и упругости, остается постоянной: Е = const. Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергий.
Поэтому закон сохранения энергии можно сформулировать следующим образом: полная механическая энергия замкнутой системы тел, взаимодействующих силами притяжения и упругости, остается постоянной: Е = const. Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергий.
Закон сохранения полной механической энергии в процессах при участии сил упругости и гравитационных сил является одним из основных законов механики. Знание данного закона упрощает решение многих задач, имеющих практическое значение. Например, для получения электроэнергии широко используют энергию рек. С этой целью строят плотины, перегораживают реки. Под действием сил притяжения вода из водохранилища по плотине движется вниз ускоренно и приобретает определенную кинетическую энергию. При столкновении потока воды с лопатками гидравлической турбины происходит превращение кинетической энергии поступательного движения воды в кинетическую энергию вращательного движения роторов турбины, а потом с помощью электрического генератора – в электрическую энергию.
Механическая энергия не сохраняется, если между телами действует сила трения. Автомобиль, движущийся по горизонтальному участку дороги, после выключения двигателя проходит определенный путь и под действием сил трения останавливается. При торможении автомобиля происходит нагревание тормозных колодок, шин автомобиля, асфальта. В результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул. Следовательно, при любых физических взаимодействиях энергия не возникает, а только превращается из одного вида в другой. Этот экспериментально установленный факт называют законом сохранения и превращения энергии. Источники энергии на Земле большие и разнообразные. В давние времена люди знали только один источник энергии – силу мышц и силу домашних животных. Энергия возобновлялась за счет потребления еды.
Энергия окружающего космического пространства аккумулируется Солнцем в виде энергии атомных ядер, химических элементов, электромагнитных и гравитационных полей. Солнце, в свою очередь, обеспечивает Землю энергией в виде энергии ветра и волн, приливов и отливов, в форме геомагнетизма, разного вида излучений, энергии мышц животного мира.
Геофизическая энергия высвобождается в виде природных стихийных явлений, обмена веществ в живых организмах, полезной работы по перемещению тел, изменения их структуры, качества, передачи информации, запаса энергии в разного рода аккумуляторах, в упругой деформации пружин, мембран.
Любые виды энергии, превращаясь друг в друга с помощью механического движения, химических реакций и электромагнитных излучений, в конце концов, переходят в тепло и рассеиваются в окружающем пространстве. Это явление проявляется в виде взрывных процессов, горения, гниения, плавления, испарения, деформации, радиоактивного распада.
Происходит кругооборот энергии в природе, который характеризуется не только хаотичностью, но и обратным ей процессом – упорядочиванием структуры, которые наглядно прослеживаются, в первую очередь, в звездообразовании, трансформации и возникновении новых электромагнитных и гравитационных полей, и они опять несут свою энергию новым «солнечным системам».
Закон сохранения механической энергии сформулировал немецкий ученый Готфрид Лейбниц. Потом немецкий ученый Юлиус Майер, английский физик Джеймс Джоуль и немецкий ученый Генрих Гельмгольц экспериментально открыли законы сохранения энергии в немеханических явлениях.
Закон сохранения импульса
Покой и движение тела относительны, скорость движения зависит от выбора системы отсчета. Согласно второму закону Ньютона, независимо от того, находится ли тело в покое или движется равномерно и прямолинейно, изменение его скорости движения может происходить только под действием силы, то есть в результате взаимодействия с другими телами.
Есть физическая величина, которая одинаково изменяется у всех тел под действием одинаковых сил. Она определяется произведением массы тела и его скорости и называется импульсом тела. Импульс тела – величина векторная, сонаправленная со скоростью движения тела. Импульс тела является количественной характеристикой поступательного движения тел. Экспериментальные исследования взаимодействия разных тел – от планет и звезд до атомов и электронов, элементарных частиц – показали, что в любой системе взаимодействующих между собой тел геометрическая сумма импульсов этих тел остается постоянной: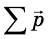 = const.
= const.
Систему тел, невзаимодействующих с другими телами, невходящими в эту систему, называют замкнутой. Таким образом, в замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называют законом сохранения импульса.
Необходимым условием применения закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета. На законе сохранение импульса основывается реактивное движение, его используют при расчете направленных взрывов, например при прокладке тоннелей в горах. Полеты в космос стали возможными благодаря использованию многоступенчатых ракет.
- Международная система единиц СИ
- Математика – язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
- Ядерная энергетика в физике
- Динамика в физике
- Статика в физике
- Кинематика в физике
Законы сохранения в механике

Содержание
- Импульс тела
- Импульс системы тел
- Закон сохранения импульса
- Работа силы
- Мощность
- Работа как мера изменения энергии
- Кинетическая энергия
- Потенциальная энергия
- Закон сохранения механической энергии
- Основные формулы по теме «Законы сохранения в механике»
Импульс тела
Импульс тела – это векторная физическая величина, равная произведению массы тела на его скорость:
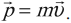
Обозначение – ( p ), единицы измерения – (кг·м)/с.
Импульс тела – это количественная мера движения тела.
Направление импульса тела всегда совпадает с направлением скорости его движения.
Изменение импульса тела равно разности конечного и начального значений импульса тела:
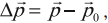
где ( p_0 ) – начальный импульс тела,
( p ) – конечный импульс тела.
Если на тело действует нескомпенсированная сила, то его импульс изменяется. При этом изменение импульса тела равно импульсу подействовавшей на него силы.
Импульс силы – это количественная мера изменения импульса тела, на которое подействовала эта сила.
Обозначение – ( F!Delta t ), единицы измерения — Н·с.
Импульс силы равен изменению импульса тела:
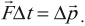
Направление импульса силы совпадает по направлению с изменением импульса тела.
Второй закон Ньютона (силовая форма):
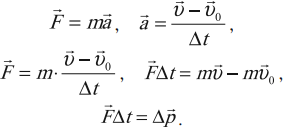
Важно!
Следует всегда помнить, что совпадают направления векторов:
• силы и ускорения: ( vec{F}uparrowuparrowvec{a} );
• импульса тела и скорости: ( vec{p}uparrowuparrowvec{v} );
• изменения импульса тела и силы: ( Deltavec{p}uparrowuparrowvec{F} );
• изменения импульса тела и ускорения: ( Deltavec{p}uparrowuparrowvec{a} ).
Импульс системы тел
Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:
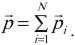
При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которых мы изучаем, называется механической системой или просто системой.
Рассмотрим систему, состоящую из трех тел. На тела системы действуют внешние силы, а между телами действуют внутренние силы.
( F_1,F_2,F_3 ) – внешние силы, действующие на тела;
( F_{12}, F_{23}, F_{31}, F_{13}, F_{21}, F_{32} ) – внутренние силы, действующие между телами.
Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в виде уравнения:
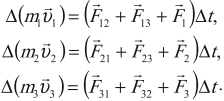
В левой части каждого уравнения стоит изменение импульса тела за малое время ( Delta t ).
Обозначим: ( v_0 ) – начальные скорости тел, а ( v^{prime} ) – конечные скорости тел.
Сложим левые и правые части уравнений.
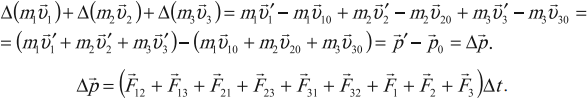
Но силы взаимодействия любой пары тел в сумме дают нуль.
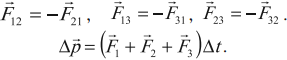
Важно!
Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.
Закон сохранения импульса
Закон сохранения импульса
Векторная сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой:
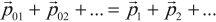
Замкнутая система – это система, на которую не действуют внешние силы.
Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций.
При абсолютно упругом ударе взаимодействующие тела до и после взаимодействия движутся отдельно.
Закон сохранения импульса для абсолютно упругого удара:
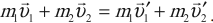
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
Закон сохранения импульса для абсолютно неупругого удара:
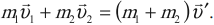
Реактивное движение – это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-то его части.
Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.
Для осуществления реактивного движения не требуется взаимодействия тела с окружающей средой, поэтому реактивное движение позволяет телу двигаться в безвоздушном пространстве.
Реактивные двигатели
Широкое применение реактивные двигатели в настоящее время получили в связи с освоением космического пространства. Используются они также для метеорологических и военных ракет различного радиуса действия. Кроме того, все современные скоростные самолеты оснащены воздушно-ракетными двигателями.
Реактивные двигатели делятся на два класса:
- ракетные;
- воздушно-реактивные.
В ракетных двигателях топливо и необходимый для его горения окислитель находятся непосредственно внутри двигателя или в его топливных баках.
Ракетный двигатель на твердом топливе
При горении топлива образуются газы, имеющие очень высокую температуру и оказывающие давление на стенки камеры. Сила давления на переднюю стенку камеры больше, чем на заднюю, где находится сопло. Выходящие через сопло газы не встречают на своем пути стенку, на которую могли бы оказать давление. В результате появляется сила, толкающая ракету вперед.
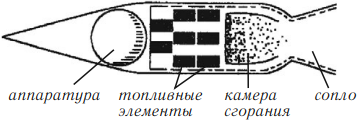
Сопло – суженная часть камеры, служит для увеличения скорости истечения продуктов сгорания, что, в свою очередь, повышает реактивную силу. Сужение струи газа вызывает увеличение его скорости, так как при этом через меньшее поперечное сечение в единицу времени должна пройти такая же масса газа, что и при большем поперечном сечении.
Ракетный двигатель на жидком топливе
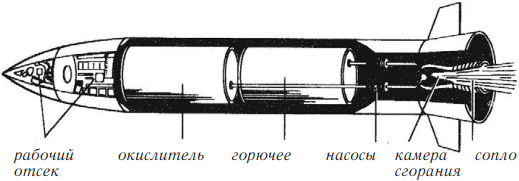
В ракетных двигателях на жидком топливе в качестве горючего используют керосин, бензин, спирт, жидкий водород и др., а в качестве окислителя – азотную кислоту, жидкий кислород, перекись водорода и пр.
Горючее и окислитель хранятся отдельно в специальных баках и с помощью насосов подаются в камеру сгорания, где температура достигает 3000 0С и давление до 50 атм. В остальном работает так же, как и двигатель на твердом топливе.
Воздушно-реактивный двигатель
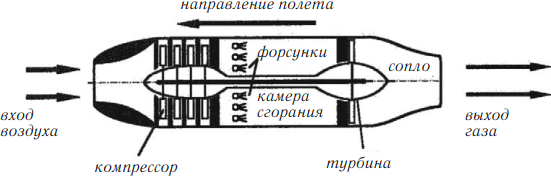
В носовой части находится компрессор, засасывающий и сжижающий воздух, который затем поступает в камеру сгорания. Жидкое горючее (керосин) попадает в камеру сгорания с помощью специальных форсунок. Раскаленные газы выходят через сопло, вращают газовую турбину, приводящую в движение компрессор.
Основное отличие воздушно-реактивных двигателей от ракетных двигателей состоит в том, что окислителем для горения топлива служит кислород воздуха, поступающего внутрь двигателя из атмосферы.
Алгоритм применения закона сохранения импульса к решению задач:
- Запишите краткое условие задачи.
- Определите характер движения и взаимодействия тел.
- Сделайте рисунок, на котором укажите направление векторов скоростей тел до и после взаимодействия.
- Выберите инерциальную систему отсчета с удобным для нахождения проекций векторов направлением координатных осей.
- Запишите закон сохранения импульса в векторной форме.
- Спроецируйте его на выбранные координатные оси (сколько осей, столько и уравнений в системе).
- Решите полученную систему уравнений относительно неизвестных величин.
- Выполните действия единицами измерения величин.
- Запишите ответ.
Работа силы
Механическая работа – это скалярная векторная величина, равная произведению модулей вектора силы, действующей на тело, вектора перемещения и косинуса угла между этими векторами.
Обозначение – ( A ), единицы измерения – Дж (Джоуль).
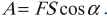
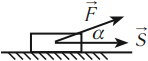
1 Дж – это работа, которую совершает сила в 1 Н на пути в 1 м:
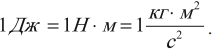
Механическая работа совершается, если под действием некоторой силы, направленной не перпендикулярно, тело перемещается на некоторое расстояние.
Зависимость механической работы от угла ( alpha )
- ( alpha=0^{circ},, cosalpha=1,, A=FS,,A>0; )
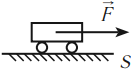
- ( 0^{circ}<alpha<90^{circ},, A=FScosalpha,,A>0; )
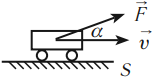
- ( alpha=90^{circ},, cosalpha=0,, A=0; )
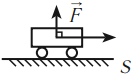
- ( 90^{circ}<alpha<180^{circ},, A=FScosalpha,,A<0; )
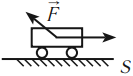
( alpha=180^{circ},, cosalpha=-1,, A=-FS,,A<0; )
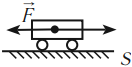
Геометрический смысл механической работы
На графике зависимости ( F=F(S) ) работа силы численно равна площади фигуры, ограниченной графиком, осью перемещения и прямыми, параллельными оси силы.
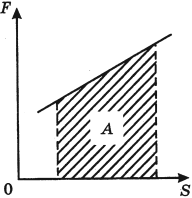
Формулы для вычисления работы различных сил
Работа силы тяжести:
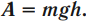
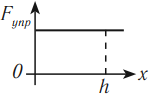
Работа силы упругости:
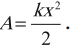
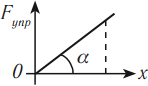
Коэффициент полезного действия механизма (КПД) — это физическая величина, равная отношению полезной работы, совершенной механизмом, ко всей затраченной при этом работе.
Обозначение – ( eta ), единицы измерения – %.
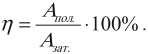
( A_{mathit{пол.}} ) – полезная работа – это та работа, которую нужно сделать;
( A_{mathit{зат.}} ) – затраченная работа – это та работа, что приходится делать на самом деле.
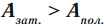
Важно!
КПД любого механизма не может быть больше 100%.
Мощность
Мощность – это количественная мера быстроты совершения работы.
Обозначение – ( N ), единицы измерения – Вт (Ватт).
Мощность равна отношению работы к времени, за которое она была совершена: .
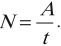
1 Вт – это мощность, при которой за 1 с совершается работа в 1 Дж:
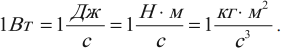
1 л. с. (лошадиная сила) = 735 Вт.
Связь между мощностью и скоростью равномерного движения:
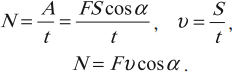
Таким образом, мощность равна произведению модуля вектора силы на модуль вектора скорости и на косинус угла между направлениями этих векторов.
Важно!
Если интервал времени стремится к нулю, то выражение представляет собой мгновенную мощность, определяемую через мгновенную скорость.
Работа как мера изменения энергии
Если система тел может совершать работу, то она обладает энергией.
Работа и изменение кинетической энергии (теорема о кинетической энергии)
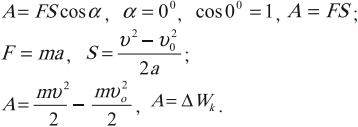
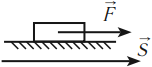
Если под действием силы тело совершило перемещение и вследствие этого его скорость изменилась, то работа силы равна изменению кинетической энергии.
Силы, работа которых не зависит от формы траектории, называются консервативными.
Работа и изменение потенциальной энергии тела, поднятого над землей
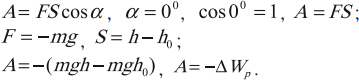
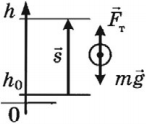
Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.
Работа и изменение потенциальной энергии упруго деформированного тела
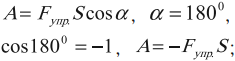
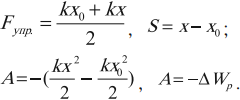
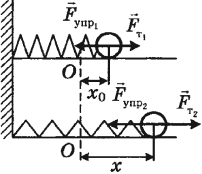
Работа силы упругости равна изменению потенциальной энергии, взятому с противоположным знаком.
Кинетическая энергия
Кинетическая энергия – это энергия, которой обладает тело вследствие своего движения.
Обозначение – ( W_k (E_k) ), единицы измерения – Дж.
Кинетическая энергия равна половине произведения массы тела на квадрат его скорости:
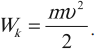
Важно!
Так как кинетическая энергия отдельного тела определяется его массой и скоростью, то она не зависит от того, взаимодействует ли это тело с другими телами или нет. Значение кинетической энергии зависит от выбора системы отсчета, как и значение скорости. Кинетическая энергия системы тел равна сумме кинетических энергий отдельных тел, входящих в эту систему.
Потенциальная энергия
Потенциальная энергия – это энергия взаимодействия тел или частей одного и того же тела.
Обозначение – ( W_p (E_p) ), единицы измерения – Дж.
Потенциальная энергия тела, поднятого на некоторую высоту над землей, равна произведению массы тела, ускорения свободного падения и высоты, на которой он находится:
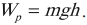
Потенциальная энергия упруго деформированного тела равна половине произведения жесткости на квадрат удлинения:
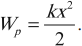
Важно!
Величина потенциальной энергии зависит от выбора нулевого уровня. Нулевым называется уровень, на котором потенциальная энергия равна нулю. Нулевой уровень выбирается произвольно, исходя из удобства решения задачи.
Закон сохранения механической энергии
Полная механическая энергия – это энергия, равная сумме кинетической и потенциальной энергий.
Обозначение – ( W (E) ), единицы измерения – Дж.
Закон сохранения механической энергии
В замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т. е. не изменяется с течением времени:
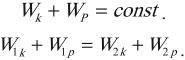
Если между телами системы действуют кроме сил тяготения и упругости другие силы, например сила трения или сопротивления, действие которых приводит к превращению механической энергии в тепловую, то в такой системе тел закон сохранения механической энергии не выполняется.
Важно!
В случае, если кроме консервативных сил (тяжести, упругости, тяготения) существуют еще и неконсервативные силы, например сила трения, а также внешние силы, то

Теорема о кинетической энергии справедлива для сил любой природы:
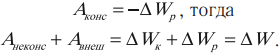
Если на систему тел действуют неконсервативные и внешние силы, то изменение полной энергии равно сумме работ неконсервативных и внешних сил.
Закон сохранения и превращения энергии
Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой или передается от одного тела к другому.
Основные формулы по теме «Законы сохранения в механике»


Законы сохранения в механике
3.1 (62.98%) 47 votes
Движение в природе не возникает из ничего и не исчезает – оно передаётся от одного объекта к другому. При определённых условиях, движение в состоянии накапливаться, но, высвобождаясь, обнаруживает своё свойство к сохранению.
Задумывались ли вы когда-нибудь почему:
- Мяч, летящий с большой скоростью, футболист может остановить ногой или головой, а вагон, движущийся по рельсам даже очень медленно, человек не остановит (масса вагона намного больше массы мяча).
- Стакан с водой находится на длинной полоске прочной бумаги. Если тянуть полоску медленно, то стакан движется вместе с бумагой. а если резко дернуть полоску бумаги – стакан остается неподвижный. (стакан останется неподвижным из-за инерции – явления сохранения скорости тела постоянной при отсутствии действия на него других тел)
- Теннисный мяч, попадая в человека, вреда не причиняет, однако пуля, которая меньше по массе, о движется с большой скоростью (600—800 м/с), оказывается смертельно опасной (скорость пули намного болше, чем мяча).
Значит, результат взаимодействия тел зависит и от массы тел и от их скорости одновременно.
Еще великий французский философ, математик, физик и физиолог, основатель новоевропейского рационализма и один из влиятельнейших метафизиков Нового времени Рене Декарт ввел такое понятие как “количество движения”. Он же высказал закон сохранения количества движения, дал понятие импульса силы.

“Я принимаю, что во Вселенной… есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает.” Р. Декарт
Декарт, судя по его высказываниям, понимал фундаментальное значение введенного им в XVII веке понятия количества движения — или импульса тела — как произведения массы тела на величину его скорости. И хотя он совершил ошибку, не рассматривая количество движения как векторную величину, сформулированный им закон сохранения количества движения выдержал с честью проверку временем. В начале XVIII века ошибка была исправлена, и триумфальное шествие этого закона в науке и технике продолжается по сию пору.
Как один из основополагающих законов физики, он дал неоценимое орудие исследования ученым, ставя запрет одним процессам и открывая дорогу другим. Взрыв, реактивное движение, атомные и ядерные превращения — везде превосходно работает этот закон. А в скольких самых обиходных ситуациях помогает разобраться понятие импульса, сегодня, мы надеемся, вы убедитесь сами.
Количество движения – мера механического движения, равная для материальной точки произведению её массыm на скорость v.Количество движения mv — величина векторная, направленная так же, как скорость точки. Иногда Количество движения называют ещёимпульсом. Количество движения, в любой момент времени, характеризуется скоростью объекта определённой массы при перемещении его из одной точки пространства в другую.
Импульсом тела (или количеством движения) называют векторную величину, равную произведению массы тела на его скорость:

Импульс тела направлен в ту же сторону, что и скорость тела.
Единицей измерения импульса в СИ является 1 кг·м/с.
Изменение импульса тела происходит при взаимодействии тел, например, при ударах. (Видео “Бильярдные шары). При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу.
Виды соударений:
Абсолютно неупругий удар – это такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
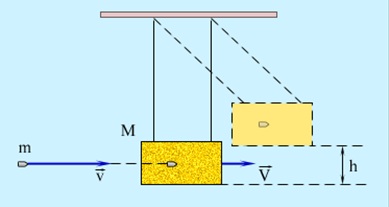
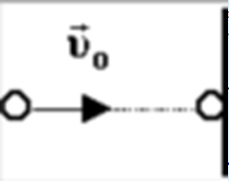
Пуля застревает в бруске и далее они движутся как одно целое Кусок пластелина прилипает к стене
Абсолютно упругий удар – это столкновение, при котором сохраняется механическая энергия системы тел.
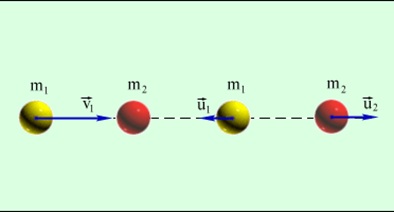
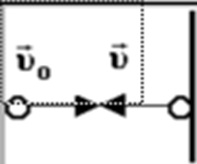
Шарики после столкновения отскакивают друг от друга в разные стороны Мяч отскакивает от стены
Пусть на тело массой m в течение некоторого малого промежутка времени Δt действовала сила F.
Под действием этой силы скорость тела изменилась на ![]()
Следовательно, в течение времени Δt тело двигалось с ускорением 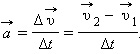
Из основного закона динамики (второго закона Ньютона) следует:
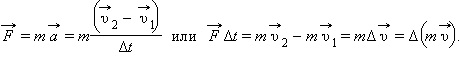
Физическая величина, равная произведению силы на время ее действия, называется импульсом силы: ![]()
Импульс силы также является векторной величиной.
Импульс силы равен изменению импульса тела (II закон Ньютона в импульсной форме):
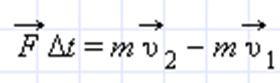
Обозначив импульс тела буквой p второй закон Ньютона можно записать в виде: 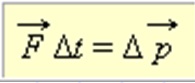
Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу.
Для определения изменения импульса удобно использовать диаграмму импульсов, на которой изображаются вектора импульсов, а также вектор суммы импульсов, построенный по правилу параллелограмма.
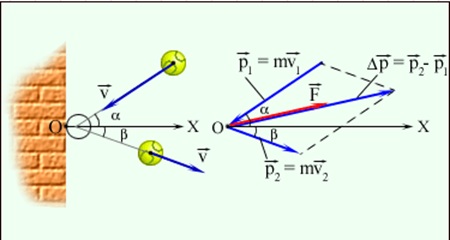
При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которой мы изучаем, называется механической системой или просто системой.
В механике часто встречаются задачи, когда необходимо одновременно рассматривать несколько тел, движущихся по-разному. Таковы, например, задачи о движении небесных тел, о соударении тел, об отдаче огнестрельного оружия, где и снаряд и пушка начинают двигаться после выстрела, и т. д. В этих случаях говорят о движении системы тел: солнечной системы, системы двух соударяющихся тел, системы «пушка — снаряд» и т. п. Между телами системы действуют некоторые силы. В солнечной системе это силы всемирного тяготения, в системе соударяющихся тел — силы упругости, в системе «пушка — снаряд» — силы, создаваемые пороховыми газами.
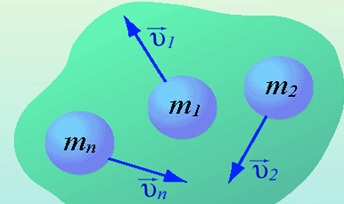
Импульс системы тел будет равен сумме импульсов каждого из тел. входящих в систему.
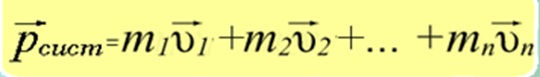
Кроме сил, действующих со стороны одних тел системы на другие («внутренние силы»), на тела могут действовать еще силы со стороны тел, не принадлежащих системе («внешние» силы); например, на соударяющиеся бильярдные шары действует еще сила тяжести и упругость стола, на пушку и снаряд также действует сила тяжести и т. п. Однако в ряде случаев всеми внешними силами можно пренебрегать. Так, при изучении соударения катящихся шаров силы тяжести уравновешены для каждого шара в отдельности и потому не влияют на их движение; при выстреле из пушки сила тяжести окажет свое действие на полет снаряда только после вылета его из ствола, что не скажется на величине отдачи. Поэтому часто можно рассматривать движения системы тел, полагая, что внешние силы отсутствуют.
Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
ЗАМКНУТАЯ СИСТЕМА – ЭТО СИСТЕМА ТЕЛ, КОТОРЫЕ ВЗАИМОДЕЙСТВУЮТ ТОЛЬКО ДРУГ С ДРУГОМ.
Закон сохранения импульса.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
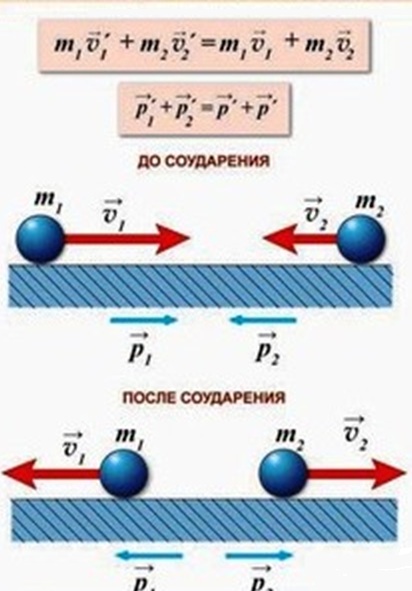

Закон сохранения импульса служит основой для объяснения обширного круга явлений природы, применяется в различных науках:
- Закон строго выполняется в явлениях отдачи при выстреле, явлении реактивного движения, взрывных явлениях и явлениях столкновения тел.
- Закон сохранения импульса применяют: при расчетах скоростей тел при взрывах и соударениях; при расчетах реактивных аппаратов; в военной промышленности при проектировании оружия; в технике – при забивании свай, ковке металлов и т.д
Энергетические характеристики движения вводятся на основе понятия механической работы или работы силы.
Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.
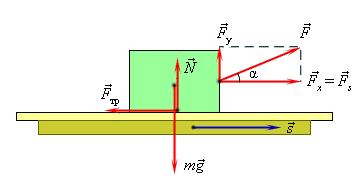
Механическая работа – это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы и вектором перемещения (или скорости).
A = Fs cos α
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.
В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
[1 Дж=1 Н·м]
Работа силы, совершаемая в единицу времени, называется мощностью.
Мощность N – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:
N=A/t
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
Внесистемная единица мощности 1 л.с.=735 Вт
Связь между мощностью и скоростью при равномерном движении:
N=A/t так как A=FScosα тогда N=(FScosα)/t, но S/t = v следовательно
N=Fvcos α
В технике используются единицы работы и мощности:
1 Вт·с = 1 Дж; 1Вт·ч = 3,6·103 Дж; 1кВт·ч = 3,6·106 Дж
Если тело способно совершить работу, то говорят, что оно обладает энергией.
Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.
Обозначается Е Единица энергии в СИ [1Дж = 1Н*м]
Механическая работа есть мера изменения энергии в различных процессах А = ΔЕ.
Различают два вида механической энергии – кинетическая Ек и потенциальная Еp энергия.
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергий
Е = Ек + Еp
Кинетическая энергия – это энергия тела, обусловленная его движением.
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергиейтела:
![]()
Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью ![]() равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
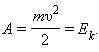
Если тело движется со скоростью ![]() , то для его полной остановки необходимо совершить работу
, то для его полной остановки необходимо совершить работу
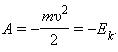
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятиепотенциальной энергии или энергии взаимодействия тел.
Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела.
Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения тела и определяется только начальным и конечным положениями. Такие силы называются консервативными. Работа консервативных сил на замкнутой траектории равна нулю.
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Потенциальная энергия тела в поле силы тяжести (потенциальная энергия тела, поднятого над землёй):
Ep = mgh
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Понятие потенциальной энергии можно ввести и для упругой силы. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Можно просто удлинить пружину на величину x, или сначала удлинить ее на 2x, а затем уменьшить удлинение до значения x и т. д. Во всех этих случаях упругая сила совершает одну и ту же работу, которая зависит только от удлинения пружины x в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A, взятой с противоположным знаком :
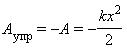
где k – жесткость пружины.
Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
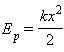
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x1, тогда при переходе в новое состояние с удлинением x2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:
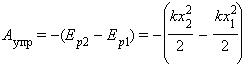
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
A = –(Ep2 – Ep1).
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
A = Ek2 – Ek1
Следовательно Ek2 – Ek1 = –(Ep2 – Ep1) или Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.
Сумму E = Ek + Ep называют полной механической энергией.
Полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход энергии от одного тела к другому.
Е = Ек + Еp = const
Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
P1_11_2012.pdf
Скачиваний:
91
Добавлен:
03.06.2015
Размер:
772.96 Кб
Скачать
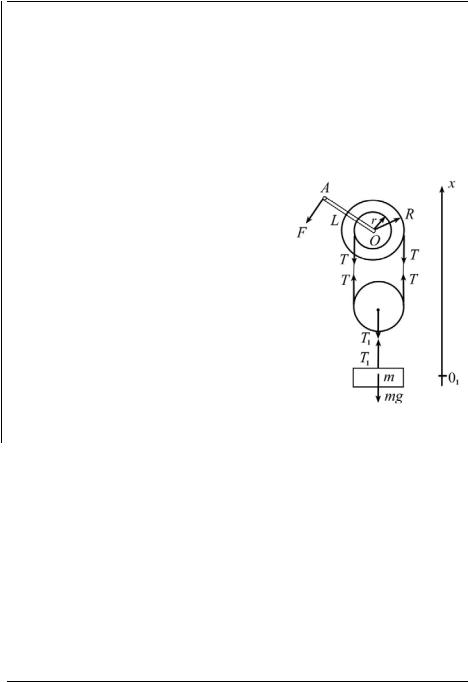
2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
Массами цилиндров, рукоятки, троса, подвижного блока и трением в
|
осях пренебречь. |
Ускорение |
свободного падения принять |
равным |
|
g =10 м/с2 . |
F, которую необходимо приложить к |
||
|
Найдите минимальную силу |
|||
|
рукоятке ворота, |
чтобы поднимать груз массой m =140 кг. |
(МФТИ, |
|
|
2008г.) |
Решение. Изобразим на рис. 17 силы, действующие на цилиндры и груз, где через T обозначена сила натяжения троса, связывающего под-
вижный блок с дифференциальным воротом, через T1 − сила натяжения троса, на котором к подвижному блоку подвешен груз, а через mg −
сила тяжести груза.
Поскольку массой подвижного блока можно пренебречь, то в проекциях на ось
O1 x можно записать
2T −T1 = 0.
Для груза, находящегося в равновесии, в проекциях на ту же ось имеем:
T1 −mg = 0.
Для моментов сил, действующих на дифференциальный ворот, относительно оси ворота, проходящей через точку O, спра-
ведливо уравнение:
TR −Tr − FL = 0.
Решая совместно три написанных уравнения, найдём
|
F = |
R −r |
mg = 70 H. |
Рис. 17 |
|
2L |
|||
Решение механических задач часто облегчается применением законов изменения и сохранения импульса и энергии тела. Особенно эффективным является использование этих законов в тех случаях, когда действующие силы переменны во времени и непосредственное решение уравнений динамики с помощью методов элементарной математики затруднительно. r
Напомним, что импульсом тела называется векторная величина p, равная произведению массы m тела на его скорость v : p = mvr.
Импульсом системы тел P называют векторную сумму импульсов всех тел, составляющих этуrсистему. Например, если система состоит из
трёх тел с импульсами pr1 , p2 и pr3 , то импульс такой системы тел равен
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
18

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
Pr = pr1 + pr2 + pr3.
В общем случае импульс тела в процессе движения может изменяться как по величине, так и по направлению. При этом справедлив закон изменения импульса тела: приращение импульса тела равно произве-
дению равнодействующей силы F на промежуток времени t, в тече-
|
ние |
которого она действует на |
тело: pr = F t. |
Произведение |
|
Fr |
t называют импульсом силы. |
Аналогичное соотношение спра- |
|
|
ведливо и для системы тел, только в этом случае под F надо понимать |
|||
|
равнодействующую только внешних сил: приращение |
P импульса си- |
||
|
стемы тел равно импульсу равнодействующей F внешних сил, дей- |
|||
|
ствующих на систему: P = Fr t. |
Внутренние силы взаимодействия |
между телами, входящими в систему, не могут изменить импульс системы.
Из сказанного следует закон сохранения импульса системы тел (или отдельноr взятого тела). Импульс системы тел (тела) сохраняется (т.
е. P =0 ) при любых взаимодействиях тел системы, если импульс рав-
нодействующей F внешних сил F t равен нулю. Это возможно в ка-
ком-либо из трёх случаев:
1) если внешние силы на систему (тело) не действуют вообще (система изолированная);
2) если равнодействующая F внешних сил, действующих на систему (тело), равна нулю;
3) если промежуток времени t, в течение которого на систему (теr– ло) действуют внешние силы, мал ( t →0), а равнодействующая F ограничена по модулю (не бесконечно большая).
Встречаются ситуации, когда импульс системы тел (тела) в целом не сохраняется, но сохраняется проекция Px импульса на некоторое на-
правление Ox ( Px =0). Это возможно в трёх случаях:
1) если внешние силы, действующие на систему (тело), направлены перпендикулярно оси Ox;
2) если проекция Fx на ось Ox равнодействующей F внешних сил равна нулю;
3) если промежуток времени t мал, а проекция Fx ограничена по
модулю (Fx ≠ ∞).
Часто при решении задач для определения импульса системы тел бывает удобно воспользоваться понятием центраr масс рассматрива-емой
системы. Можно показать, что импульс P системы тел равен
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
19

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
|
произведению массы M |
системы (т. |
е. суммы масс тел, входящих в |
|
|
систему) |
и скорости |
vrc движения |
её центра масс (точки C ): |
|
Pr = M vrc . |
В связи с этим справедлива теорема о движении центра |
масс: центр масс системы тел движется так, как двигалась бы материальная точка, масса которой равна массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на систему. Использование сформулированной теоремы позволяет порой существенно упростить процесс решения задачи.
Изменение импульса тела (системы) характеризует действие силы в течение конкретного промежутка времени. Для характеристики действия силы на определённом перемещении служит физическая величина,
называемая механической работой.
|
Пусть материальная точка движется по некоторой |
не обязательно |
||||||||||
|
прямолинейной траектории (рис. 18). Пусть также на |
материальную |
||||||||||
|
точку действует сила F, которая в общем случае в процессе движения |
|||||||||||
|
FS |
может меняться как по модулю, так и по на- |
||||||||||
|
правлению. Разобьём траекторию на множество |
|||||||||||
|
сколь угодно малых участков, каждый из котоr– |
|||||||||||
|
Si |
|||||||||||
|
рых можно считать прямолинейным, а силу |
F |
||||||||||
|
F |
|||||||||||
|
на каждом таком участке можно считать посто- |
|||||||||||
|
i =1,2,… |
янной. Рассмотрим малое перемещение |
Sri , |
|||||||||
|
Sr |
Рис. 18 |
Работой |
Ai силы F на малом перемещении |
||||||||
|
называют величину, равную скалярному произведению векторов Fr |
|||||||||||
|
i |
r |
r |
r |
||||||||
|
и Si : |
Ai = F |
Si . |
|||||||||
|
По определению скалярного произведения можно записать: |
|||||||||||
|
Ai = F Si cosαi = FS ,i Si = F Si,F , |
|||||||||||
|
где αi – rугол между векторами F и |
Si , FS ,i − проекция F на направ- |
||||||||||
|
ление |
Si , |
Si,F − проекция Si на направление F. |
|||||||||
|
Работа |
A силы F на всём участке траектории равна алгебраической |
||||||||||
|
сумме работ |
Ai , совершаемых силой Fr на каждом из малых участ- |
||||||||||
|
ков, на которые разбита траектория: |
A = ∑ Ai . Когда на материальную |
точку действуют n сил, их общая работа i A равна алгебраической сум-
ме работ каждой из сил в отдельности: A = ∑n Ai , j =1,2,…, n.
j=1
Если мы имеем дело не с материальной точкой, а с твёрдым телом или системой тел, то данное выше определение работы остаётся спра-
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
20

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
ведливым, но в этом случае надо только иметь в виду, что под S сле-
дует понимать перемещение точки приложения силы F. Игнорирова-
ние этого обстоятельства зачастую приводит к ошибочным результатам. Часто говорят о работе, которую совершает или может совершить над телом какое-либо другое тело. Здесь, во избежание недоразумений, надо чётко понимать, что по определению работу над телом совершает
сила, действующая на него со стороны рассматриваемого другого тела.
Способность конкретного тела совершать работу характеризуют с помощью энергии. Кинетической энергией K движущейся материальной точки называют половину произведения массы m точки на квадрат
её скорости v, т. е. K = mv2 / 2.
Для определения кинетической энергии конкретного твёрдого тела его следует мысленно разбить на множество материальных точек. Ки-
нетическая энергия K тела будет равна алгебраической сумме кине-
|
тических энергий Ki этих материальных точек: K = ∑Ki = ∑ |
m v2 |
|
|
i i |
. |
|
|
2 |
||
|
i |
В случае, когда тело массой m движется поступательно (не вращаясь), скорости vi составляющих его материальных точек в каждый кон-
кретный момент времени одинаковы и равны скорости v поступательного движения тела. Тогда кинетическая энергия K такого тела в соответствии со сказанным выше в каждый момент времени равна
|
K = ∑Ki = ∑ |
m v2 |
= |
v2 |
∑mi . |
||
|
i |
||||||
|
2 |
2 |
|||||
|
i |
i |
i |
||||
|
Очевидно, что ∑mi = m, |
где m − масса тела. Следовательно, кине- |
|||||
|
i |
тическая энергия K тела массой m, движущегося поступательно со скоростью v, равна K = m2v2 . Если движение тела не поступательное
(присутствует вращение), то для нахождения его кинетической энергии эта формула непосредственно не применима!
Так, например, в случае, когда однородный обруч массой m катится без проскальзывания со скоростью v по горизонтальной поверхности,
его кинетическая энергия равна K = mv2 .
Кинетическая энергия тела есть мера его движения. Приращение ки-
нетической энергии K рассматриваемого тела равно суммарной работе A всех сил, действующих на тело:
|
K = A. |
(13) |
|
Здесь K − разность между конечным K2 и начальным K1 значения- |
|
|
ми кинетической энергии K = K2 − K1. Утверждение (13) |
называется |
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
21

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
теоремой об изменении кинетической энергии.
Силы, действующие на тело, могут различаться по своей природе и свойствам. В механике сложилось, в частности, разделение сил на консервативные и неконсервативные. Консервативными (или потенциальными) называются силы, работа которых не зависит от траектории движения тела, а определяется только начальным и конечным его положением. Такими силами являются, например, сила тяжести и сила упругости. В общем случае работа любых консервативных сил может быть представлена как убыль некоторой величины П, которую называют по-
тенциальной энергией тела:
|
А= П1 − П2 . |
(14) |
|
|
(Убыль величины отличается от приращения знаком: |
П1 − П2 = − П. ) |
|
|
Например, потенциальная энергия тела массы m, |
находящегося на |
|
|
высоте h |
над поверхностью земли, равна П = mgh, |
если за «нулевой |
|
уровень» |
условно принята поверхность земли. Потенциальная энергия |
тела, находящегося под действием упругой силы деформированной пружины равна П = kx2 / 2, где x − величина деформации (сжатия или растяжения) пружины, k − коэффициент жёсткости пружины.
Неконсервативными называются силы, работа которых зависит от формы траектории и пройденного пути. Для таких сил равенство (14) несправедливо (понятие потенциальной энергии не применяется). Неконсервативными являются, например, сила трения скольжения, силы сопротивления воздуха или жидкости (зависящие от скорости).
Физическую величину, равную сумме кинетической и потенциальной энергий тела, называют его механической энергией E = K + П. Можно показать, что приращение механической энергии равно суммарной работе А неконсервативных сил, действующих на тело в процессе движе-
ния. Следовательно, если неконсервативные силы отсутствуют или таковы, что не совершают работы над телом в течение интересующего нас времени, то механическая энергия тела остаётся постоянной за это время: E =const. Это утверждение известно как закон сохране-
ния механической энергии.
Взаимодействия тел, изучаемые в механике, отличаются большим разнообразием. Частным случаем таких взаимодействий являются столкновения тел. Среди них выделяют так называемые упругие и неупругие столкновения. Следует отметить, что в учебной литературе наблюдается некоторая неопределённость терминологии на этот счёт. Здесь мы будем называть столкновения, при которых сохраняется суммарная механическая энергия тел, абсолютно упругими (или просто
упругими). Так, например, в большинстве случаев можно считать абсо-
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
22

2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
лютно упругим центральное столкновение двух стальных шаров. Столкновения, при которых изменяется суммарная механическая
энергия взаимодействующих тел, будем называть неупругими. Изменение суммарной механической энергии при таких столкновениях характеризуется её убылью и сопровождается, например, выделением тепла. Причём количество выделившейся теплоты в точности равно убыли механической энергии системы. Если тела после столкновения движутся как единое целое (с одинаковыми по величине и направлению скоростями), то такое столкновение будем называть абсолютно неупругим.
Задача 10. С наклонной плоскости одновременно без начальных скоростей начинают соскальзывать брусок и скатываться без проскальзывания обруч. При каком коэффициенте трения скольжения между бруском и наклонной плоскостью оба тела будут двигаться, не обгоняя друг друга? Угол наклона плоскости к горизонту равен α.
Решение. Из динамики известно, что ускорение a1 бруска, скользя-
щего по наклонной плоскости вниз, равно a1 = g (sinα −μcosα).
Пусть обруч скатывается с наклонной плоскости в течение времени t. За это время его центр масс пройдёт путь l, равный длине наклонной плоскости. Пусть скорость центра масс обруча в конце этого пути равна
|
v. Из кинематики известно, |
что |
l = |
a t |
2 |
, v = a t |
(где |
a − |
ускорение |
|||||
|
2 |
|||||||||||||
|
2 |
2 |
2 |
|||||||||||
|
центра масс обруча). |
|||||||||||||
|
обруча |
за |
время |
t |
равно |
|||||||||
|
Приращение |
кинетической энергии |
||||||||||||
|
K = K |
2 |
− K . Поскольку K = 0 |
(по условию), |
а |
K |
2 |
= M v2 , |
где |
M − |
||||
|
1 |
1 |
С другой стороны, |
|||||||||||
|
масса обруча, то |
K = M v2 . |
по теореме об измене- |
нии кинетической энергии эта величина равна работе всех сил, действующих на обруч в течение времени t. С учётом этого имеем:
M v2 = Mgl sinα,
где Mgl sinα − работа силы тяжести (покажите это самостоятельно).
Сила нормальной реакции опоры работы не совершает, так как направлена перпендикулярно перемещению центра масс обруча. Работа силы трения также равна нулю, так как обруч катится без проскальзывания и, следовательно, в каждый момент времени скорость точки касания обруча с наклонной плоскостью (точки приложения силы трения) равна ну-
лю. Учитывая кинематические уравнения, найдём a2 = g2 sinα. Тела не будут обгонять друг друга, если a1 = a2 . Отсюда μ = 12 tgα.
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
23
2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
Задача 11. На подвижной тележке массой
|
M , находящейся на горизонтальной плоско- |
|
|
сти, с помощью лёгкого стержня, который |
|
|
может свободно вращаться вокруг точки O |
|
|
(рис. 19), подвешен маленький шарик массой |
|
|
m. Вначале система покоилась. Шарику крат- |
|
|
ковременным ударом сообщают горизонталь- |
|
|
ную скорость v. На какую наибольшую вы- |
|
|
соту H по сравнению с первоначальным уро- |
Рис. 19 |
|
внем поднимется шарик? Считать, что угол |
отклонения стержня от вертикали не превышает 90o. Трением и массой колёс тележки пренебречь. (Институт криптографии, связи и информатики Академии ФСБ РФ, 2005 г.)
Решение. В горизонтальном направлении на систему «шарик– тележка» никакие силы не действуют (трения нет). Сила упругости стержня, на котором подвешен шарик, является внутренней силой и импульса системы изменить не может. Таким образом, проекция импульса системы «шарик – тележка» на горизонтальное направление сохраняется. В начальный момент она была равна mv, а в момент
достижения шариком максимальной высоты H шарик и тележка движутся с одинаковой скоростью v1 в горизонтальном направлении (на
рис. 19 – вправо). С учётом сохранения проекции импульса на направление движения тележки имеем:
mv =(m + M )v1.
Считая потенциальную энергию шарика в поле силы тяжести в начальный момент равной нулю, можно записать по закону сохранения
|
механической энергии: |
mv2 |
= mgH + |
(m + M )v12 |
. |
|||
|
2 |
2 |
||||||
|
M v2 |
|||||||
|
Из двух написанных уравнений получаем ответ: |
H = |
||||||
|
. |
|||||||
|
2(M + m)g |
Задача 12. Тело движется со скоростью v1 = 6м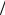 с и догоняет такое же тело, движущееся со скоростью v2 =3м
с и догоняет такое же тело, движущееся со скоростью v2 =3м с (вдоль той же прямой).
с (вдоль той же прямой).
Определите скорости тел после центрального абсолютно упругого уда-
ра. (МИЭМ, 2006 г.)
Решение. Удар называется центральным, если скорости тел до удара направлены вдоль линии, соединяющей центры масс тел (рис. 20 а). За-
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
24
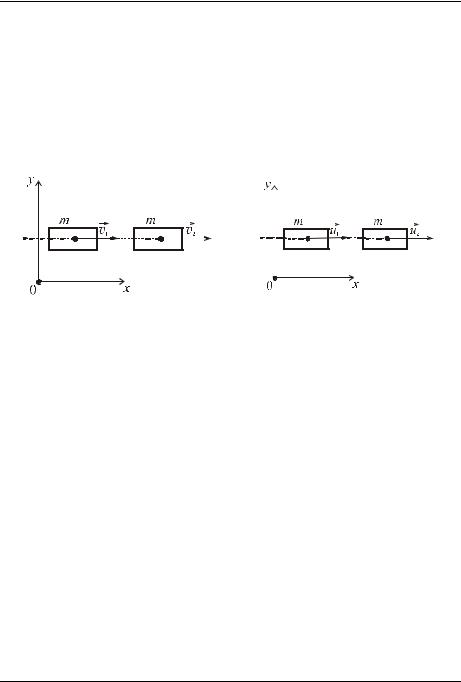
2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
данные скорости v1 и v2 направлены вдоль одной прямой. Направим ось Ox параллельно этой прямой в сторону движения тел. Пусть скоро-
сти тел после удара равны u1 и u2 . Эти скорости в данном случае могут
быть только параллельными оси Ox. Предположительно направим их так, как показано на рис. 20 б.
Систему тел будем считать замкнутой (в условии иного не оговорено). По закону сохранения импульса суммарный импульс тел до удара равен суммарному импульсу тел после удара. В проекциях на ось Ox можно, следовательно, записать:
|
mv1 + mv2 = mu1x + mu2x , |
(15) |
||||||||
Рис. 20 а Рис. 20 б
где u1x и u2x − проекции на ось Ox векторов u1 и u2 соответственно. (Если направления векторов u1 и u2 выбраны правильно, то u1x =u1, а u2 x =u2 . ) По условию удар абсолютно упругий, следовательно суммарная механическая энергия тел сохраняется. Тогда
|
mv |
2 |
+ |
mv |
2 |
2 |
= |
mu |
2 |
+ |
mu |
2 |
. |
(16) |
|
1 |
1 |
2 |
|||||||||||
|
2 |
2 |
2 |
2 |
||||||||||
При этом, в связи с выше сказанным, независимо от знака проекций
|
u1x и u2 x |
|||||
|
u 2 |
= u |
2 и |
u 2 |
= u 2 . |
(17) |
|
1 |
1x |
2 |
2x |
||
|
Перегруппируем слагаемые в (15) и сократим на m. Тогда получим: |
|||||
|
v1 −u1x |
=u2x |
−v2 . |
(18) |
||
|
Аналогично уравнение (16) преобразуем к виду: |
|||||
|
v 2 |
−u 2 |
=u 2 −v 2 . |
|||
|
Или с учётом (17) |
1 |
1 |
2 |
2 |
|
|
v 2 |
−u 2 |
= u 2 |
−v 2 . |
||
|
1 |
1x |
2x |
2 |
Воспользовавшись алгебраической формулой для разности квадратов, можно записать: (v1 −u1x )(v1 +u1x )=(u2x −v2 )(u2x + v2 ).
Поскольку v1 −u1x =u2x −v2 (см. выше) и, очевидно, v1 −u1x ≠ 0 и
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
25
Рис. 21
2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
u2x − v2 ≠ 0, то, сократив на эти выражения, получим:
|
v1 +u1x |
= u2x |
+ v2 . |
(19) |
|
|
Вычитая (18) из (19), найдём u1x |
= v2 . |
Складывая (18) и (19), получим |
||
|
u2x = v1. Видим, что u1x |
и u2x |
получились положительными. |
Значит |
|
|
направления скоростей u1 |
и u2 указаны на рис. 20 б верно. В рассмат- |
риваемом случае тела в результате удара «обмениваются» скоростями: u1 = v2 =3м с, u2 = v1 = 6м
с, u2 = v1 = 6м с.
с.
|
Задача 13. Лёгкий пластилиновый шарик массы m летит со скоро- |
|||||
|
стью vr и сталкивается с массивной плитой, дви- |
u |
||||
|
жущейся навстречу шарику со скоростью u |
|||||
|
(рис. 21). Какое количество теплоты выделится |
v |
m |
|||
|
при абсолютно неупругом столкновении шарика с |
|||||
|
плитой? Массу M плиты считать много большей |
M |
||||
|
массы шарика (M >> m). |
. |
x |
|||
|
Решение. Направим ось Ox в сторону движния |
0 |
плиты, как показано на рис. 21. Пусть u1−совмест-
ная скорость плиты с шариком после столкновения (на рис. 21 не показана). Считая, что после столкновения плита с шариком движутся в том же направлении, что и плита до столкновения, по закону сохранения импульса (система тел замкнута) можно записать в проекциях на ось Ox уравнение:
|
Mu −mv =(M +m)u1. |
||||||||||||||||||||||||||||
|
Отсюда скорость |
u равна: u |
= |
Mu −mv |
= |
M |
u − |
m |
v. |
||||||||||||||||||||
|
1 |
1 |
M |
+ m |
M + m |
M + m |
|||||||||||||||||||||||
|
Преобразуем это выражение следующим образом: |
m |
|||||||||||||||||||||||||||
|
M |
m |
1 |
||||||||||||||||||||||||||
|
u = |
u − |
v = |
u − |
M |
v. |
|||||||||||||||||||||||
|
m |
||||||||||||||||||||||||||||
|
1 |
M |
1+ |
m |
M |
1+ |
m |
1+ |
1+ |
m |
|||||||||||||||||||
|
M |
M |
|||||||||||||||||||||||||||
|
M |
M |
|||||||||||||||||||||||||||
|
Считая отношение |
m |
близким к нулю (по условию M >> m ) и пре- |
||||||||||||||||||||||||||
|
M |
||||||||||||||||||||||||||||
|
m |
||||||||||||||||||||||||||||
|
небрегая им по сравнению с единицей |
<<1 |
в знаменателе умень- |
||||||||||||||||||||||||||
|
M |
шаемого, а вычитаемое по той же причине отбрасывая вовсе, получим u1 =u, то есть после столкновения шарик с плитой движутся с той же
скоростью, что и плита до столкновения. Иными словами, скорость плиты не изменилась. Перейдём в систему отсчёта, связанную с пли-
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
26
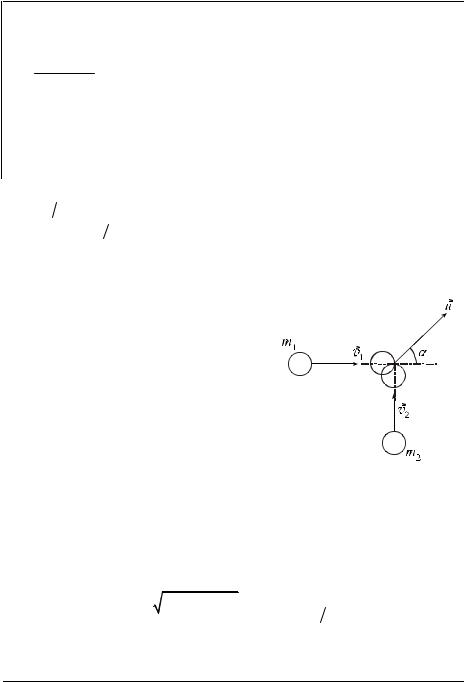
. После столкновения в выбранной системе отсчёта плита
2012-2013 уч. год, № 1, 11 кл. Физика. Основные законы механики
той. В свете сказанного эту систему отсчёта можно считать инерциальной. В ней плита покоится, а шарик до удара движется навстречу плите со скоростью v +u. Следовательно, перед столкновением
K = m(u + v)2
2
и шарик покоятся, их суммарная механическая энергия равна нулю. Убыль суммарной механической энергии тел равна искомому количеству теплоты
|
Q = |
m(v +u)2 |
. |
|
|
2 |
|||
|
Задача |
14. Шар массой m1 = 2 кг, |
движущийся со скоростью |
|
|
v1 = 2м с, |
сталкивается с шаром массой m2 =1 кг, движущимся со ско- |
||
|
ростью v2 |
=3м с. В результате столкновения шары слипаются. Опре- |
делите количество выделившейся при столкновении теплоты и совместную скорость шаров после столкновения. В момент столкновения скорости шаров взаимно перпендикулярны.
|
Решение. Из условия задачи следует, |
|||||||||||||||
|
что столкновение абсолютно неупругое, |
|||||||||||||||
|
и после него шары будут двигаться как |
|||||||||||||||
|
одно целое (рис. 22). Считая систему тел |
|||||||||||||||
|
замкнутой, по закону сохранения им- |
|||||||||||||||
|
пульса имеем: |
|||||||||||||||
|
m1vr1 +m2 vr2 =(m1 + m2 )ur, |
|||||||||||||||
|
где |
ur − совместная скорость слипшихся |
||||||||||||||
|
шаров после столкновения. |
Написан- |
||||||||||||||
|
ное |
уравнение |
проиллюстрировано на |
|||||||||||||
|
рис. 22. Возведём обе части этого урав- |
|||||||||||||||
|
нения в квадрат: |
|||||||||||||||
|
m12 vr12 + 2m1m2 vr1 vr2 +m22 vr2 |
2=(m1 + m2 )2 ur2. |
Рис. 22 |
|||||||||||||
|
Поскольку по условию скорости v |
и v |
взаимно перпендикулярны, то |
|||||||||||||
|
1 |
2 |
r |
r |
||||||||||||
|
их скалярное произведение равно нулю: v1 |
v2 =0. Учитывая также, что |
||||||||||||||
|
vr12 |
= v12 , vr2 |
2 = v22 , |
ur2 =u2 , |
получим |
m12 v12 + m22 v22 =(m1 + m2 )2 u2 . |
||||||||||
|
Откуда модуль искомой скорости u равен |
|||||||||||||||
|
u = |
m12 v12 + m22 v22 |
= |
5 м |
≈1,7 м с. |
|||||||||||
|
m + m |
3 с |
||||||||||||||
|
Направление скорости u |
1 |
2 |
|||||||||||||
|
составляет угол α с направлением скорости |
© 2012, ЗФТШ МФТИ. Чугунов Алексей Юрьевич
27
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
