Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
Понятие механической работы
В статье мы расскажем о главных энергетических характеристиках движения: работе и мощности. Дадим этим физическим величинам определение и рассмотрим их основные свойства.
В общем случае под работой в физике понимают меру воздействия силы. Затронем самые простые её разновидности, те, что объясняются законами классической механики.
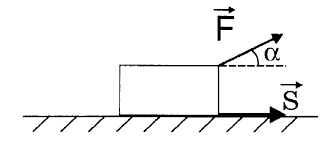
Определение
Механическая работа – это скалярная величина, равная произведению модуля силы и модуля перемещения на косинус угла между ними.
Формула работы в механике следующая:
[A=|F|*|s|* cos alpha]
[boldsymbol{F}]– сила, действующая на тело, [boldsymbol{S}] – перемещение тела, [boldsymbol{a}] – угол между ними.
Механическая работа: основные формулы
Работа, совершаемая внешней силой против деформации тела, может быть записана в виде формулы:
A = k*(x2 – x1)2/2, где k – коэффициент упругости тела. x1 и x2 – начальное и конечное удлинение тела. Получается, что работа в этом случае зависит лишь от координат.
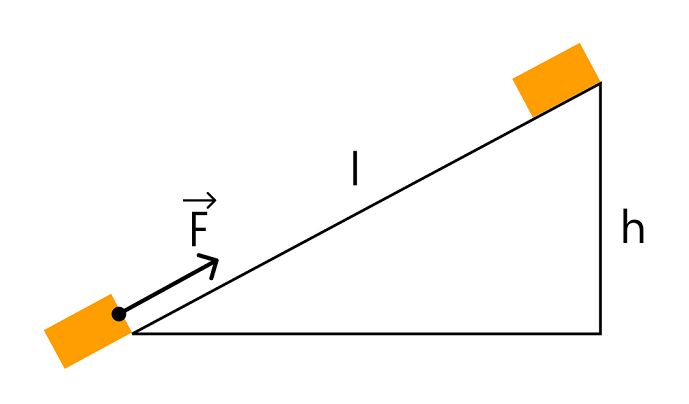
Работа силы тяжести записывается по формуле:
A = m*g*(h2 – h1), где m – масса тела. g – ускорение свободного падения. h1 и h2 – начальная и конечная высота тела. От траектории тела работа сил тяжести (если считать поле тяготения постоянным и однородным) не зависит.
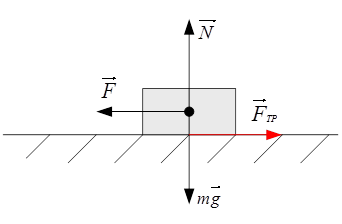
Работа сил трения записывается по формуле:
A = -Fтр* S, где Fтр – сила трения. S – путь пройденный телом. Обратите внимание, сила взята со знаком минус. Силы трения всегда противоположны перемещению, куда бы тело не двигалось.
В международной системе СИ единицей измерения механической работы считается Джоуль. Он равен работе совершённой силой в 1 Н при перемещении тела в направлении её действия на 1 м.
Результирующая работа сил
Результирующая механическая работа нескольких сил равна сумме работ каждой из них.
[mathrm{A}=sum Delta A i=sum F Delta S i]
Если считать перемещения предельно малыми (ΔSi→0), то можно перейти к интегралу [mathrm{A}=int_{b}^{a} F(x) d x].
Графически работа изображается как площадь фигуры на графике показывающем зависимость силы от координаты.
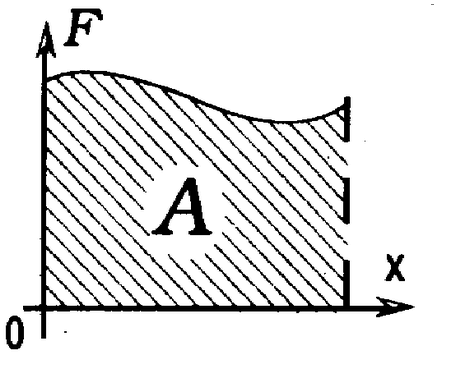
Случаи, когда механическая работа не совершается
Рассмотрим их:
- Сила действует, но тело своего местоположения не меняет и не деформируется. Например, когда мы пытаемся сдвинуть с места большой, тяжёлый шкаф;
- Тело движется, но на него не действуют никакие силы либо их действие скомпенсировано. Например, когда тело движется в безвоздушном пространстве только по инерции;
- Сила и перемещение перпендикулярны друг другу. Например, когда на тело действует центростремительная сила.
Из выше сказанного следует, что для совершения работы обязательно наличие действующей на тело силы и перемещение его под действием этой силы.
Нет времени решать самому?
Наши эксперты помогут!
Мощность: определение, формулы
Определение
Мощностью в физике называют количество работы, которое было совершено за единицу времени.
Формула выражения работы через мощность выглядит следующим образом: [boldsymbol{N=(A / Delta t)}].
По виду это выражение очень сильно напоминает формулу выражения скорости, только там вместо работы стоит перемещение. Это не просто совпадение. Мощность действительно можно охарактеризовать, как скорость совершения работы.
Вот ещё несколько формул для выражения мощности:
N = F*S/ Δt = F* v = F* v cos α
v – вектор скорости, v – абсолютная величина скорости, α – угол между скоростью тела и линией действия на него силы.
Из приведённой выше первой формулы для мощности вытекает единица её измерения. Если работа измеряется в джоулях, а время в секундах, то логично предположить, что в системе СИ мощность будет мериться в Джоулях на секунду Дж/с. Так и есть. Единица измерения мощности называется Ватт. 1 Ватт равен работе в 1 Джоуль, которая совершается за 1 секунду. Однако подобная мощность столь мала, что на практике чаще всего используют единицу измерения в тысячу Ватт. Называют её Киловатт (кВт).
На практике мощность нередко указывают в лошадиных силах. Это внесистемная един6ица измерения мощности. 1 лошадиная сила равна 0,735 киловатт или 745.7 Вт. Это так называемая электрическая лошадиная сила, традиционно используется именно в России. Есть ещё механическая лошадиная сила, метрическая лошадиная сила, гидравлическая лошадиная сила и т. д. Все они несколько отличаются от заявленной выше величины.
Как найти работу силы тяжести
Под воздействием силы тяжести тело может совершать работу. Простейший пример — свободное падение тела. Понятие работы отражает перемещение тела. Если тело остается на месте, работы оно не совершает.

Инструкция
Сила тяжести тела — приблизительно постоянная величина, равная произведению массы тела на ускорение свободного падения g. Ускорение свободного падения g ≈ 9,8 ньютон на килограмм, или метр на секунду в квадрате. g является константой, величина которой незначительно колеблется лишь для разных точек земного шара.
По определению, элементарная работа силы тяжести — произведение силы тяжести на бесконечно малое передвижение тела: dA = mg · dS. Перемещение S является функцией от времени: S = S(t).
Чтобы найти работу силы тяжести на всем пути L, надо взять интеграл от функции элементарной работы по L: A = ∫dA = ∫(mg · dS) = mg · ∫dS.
Если в задаче задана функция скорости от времени, то зависимость перемещения от времени можно найти путем интегрирования. Для этого понадобится знать начальные условия: начальную скорость, координату и т.д.
Если известна зависимость ускорения от времени t, придется интегрировать два раза, ведь ускорение — вторая производная от перемещения.
Если в задаче дано координатное уравнение, то нужно понять, что перемещение отражает разность начальной и конечной координаты.
Помимо силы тяжести, на физическое тело могут действовать и другие силы, так или иначе влияющие на его положение в пространстве. Важно помнить, что работа — аддитивная величина: работа результирующей силы равна сумме работ слагаемых сил.
Согласно теореме Кёнига, работа силы по перемещению материальной точки равняется приращению кинетической энергии этой точки: A(1-2) = K2 – K1. Зная это, можно попробовать найти работу силы тяжести через кинетическую энергию.
Полезный совет
Для интегрирования применяйте табличные интегралы простейших функций и правила интегрирования. Помните, что интегрирование – обратная процедура дифференцированию (нахождению производной).
Источники:
- «Механика», Д.В. Сивухин, 2006.
- Найдите работу силы тяжести
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
- Подробности
- Обновлено 30.05.2018 20:11
- Просмотров: 706

Задачи по физике – это просто!
Вспомним
Формулы, по которым можно вычислить работу силы:



Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Типовые задачи из курса школьной физики по динамике на расчет работы, совершаемой силой тяжести.
Задача 1
Автомобиль массой 500 кг движется вверх по наклонной плоскости, расположенной под угломм 30o к горизонту. Найти работу силы тяжести на пути в 200 метров.

Задача 2
Какую работу совершит сила тяжести при падении мяча массой 0,5 кг на землю из состояния покоя с высоты 5 метров?

Задача 3
Какую работу совершает сила тяжести при отскоке мяча от земли, если он поднимается на высоту 2-х метров? Масса мяча составляет 0,4 кг.

Задача 4
Скорость падающего кирпича массой 2 кг на некотором отрезке пути изменилась от 3 м/с до 6 м/с. Определить работу, совершенную силой тяжести.


у
Найдем работу, которую совершает сила
тяжести
![]() ,
,
действующая на падающее тело массойm,
при его перемещении из точки 1 в точку
2 по произвольному пути (рис.4.6).
Полная работа:
![]() .
.
Силу тяжести при
![]() можно считать постоянной, тогда
можно считать постоянной, тогда
![]() .
.
Так как
направление вектора
![]() противоположно возрастанию высотыh(α = 180), то
противоположно возрастанию высотыh(α = 180), то
![]()
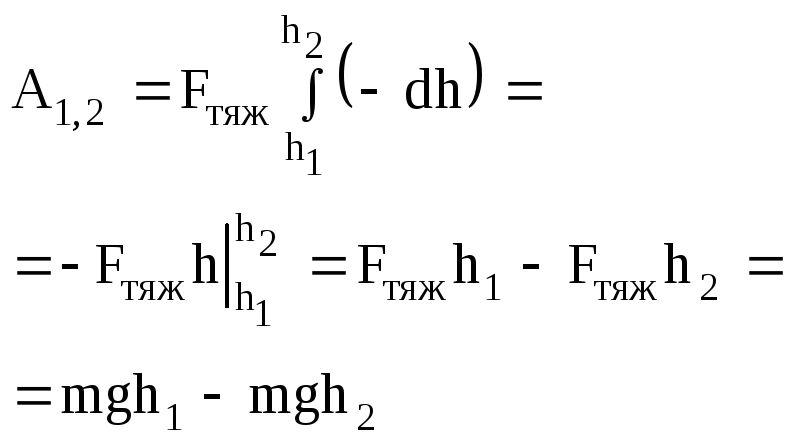
![]() .
.
Работа силы тяжести равна убыли
потенциальной энергии, зависит от
начального и конечного положений тела
над Землей и не зависит от формы траектории
его движения. Следовательно, сила тяжести
есть консервативная сила.
3.6.3. Потенциальная энергия пружины
Внешняя сила, сжимая или растягивая
пружину, совершает работу. Освобожденная
от внешнего воздействия, пружина
восстанавливает свою форму, а потенциальная
энергия, запасенная пружиной в процессе
деформации, превращается в другие виды
энергии. Мерой энергии превратившейся
в другие виды, является величина работы,
совершенная упругой силой.
Работа упругой силы
![]() на участкеdx
на участкеdx
dA = Fхdx = – kxdx,
Полная
работа при изменении длины пружины на
Δх = х2 – х1
 (3.25)
(3.25)
Потенциальная энергия деформированной
пружины
![]() (3.26)
(3.26)
где
С = 0, так как потенциальная энергия
недеформированной пружины равна нулю.
Р абота
абота
упругой силы не зависит от того, как
произошло изменение длины пружины.
Поэтому упругая сила так же как и сила
гравитационного притяжения консервативна.
3.6.4. Потенциальный барьер и яма
Потенциальная энергия может быть
представлена графически. График,
выражающий зависимость потенциальной
энергии от соответствующей координаты,
называется потенциальной кривой. По
характеру потенциальной кривой
определяется величина и направление
силы, действующей на тело вдоль
соответствующего направления.
Проанализируем одну из возможных
потенциальных кривых. Возьмем кривую
изменения потенциальной энергии Епсистемы тел, когда в системе одно тело
перемещается вдоль оси х (рис. 3.12). Сила
действующая на тело
![]()
![]() .
.
где
![]() – угол наклона к оси касательной
– угол наклона к оси касательной
проведенной в соответствующей точке
кривой Еп=f(x)
.
B точке х1(![]() ,
,
поэтому![]() )cила противоположна
)cила противоположна
направлению х и препятствует удалению
тела из системы. В точке х2(tgα < 0,
силаFх > 0)
силаFхсовпадает
с направлением оси х, и способствует
движению тела в данном направлении. В
точке х0(tgα = 0) сила на
тело не действует. Величину силы можно
определить по крутизне потенциальной
кривой: чем круче кривая, тем больше
численное значениеtgα,
например, величина силы в точке 2 больше,
чем в точке 1.
Резкое возрастание потенциальной кривой
вдоль направления движения тела
определяет потенциальный барьер, который
характеризуется высотой и шириной. Так,
для тела, находящейся в точке с координатой
х1, высота потенциального барьера
ΔЕп, ширина Δх = (х2– x1).
Если потенциальный барьер встречается
на пути движения тела, как в положительном,
так и в отрицательном направлении оси,
то, оно находится в потенциальной яме.
Форма и глубина потенциальной ямы
зависят от природы сил взаимодействия
и конфигурации системы тел.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
17.05.20158.11 Mб14курс лекций новый.doc
- #
- #
- #
- #

