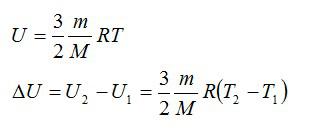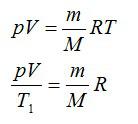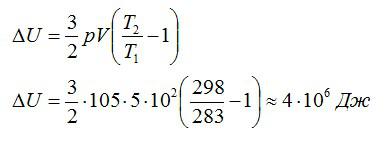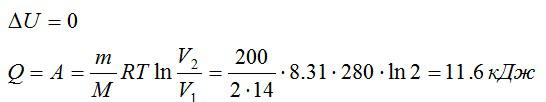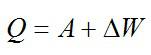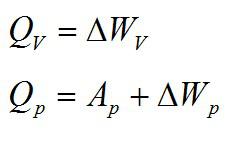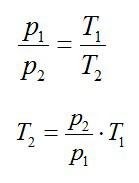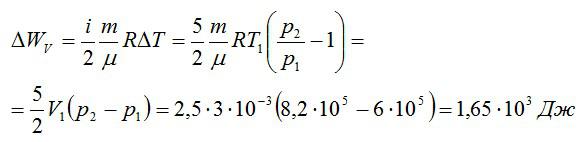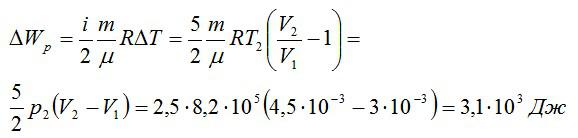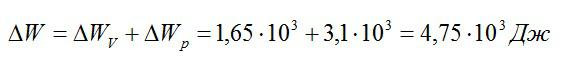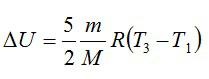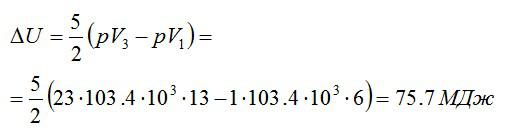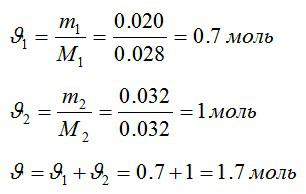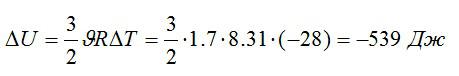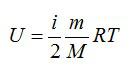Физика, 10 класс
Урок 23. Внутренняя энергия. Работа. Количество теплоты
Список вопросов, рассмотренных в уроке: внутренняя энергия; способы изменения внутренней энергии; различные виды теплообмена; уравнение теплового баланса; работа в термодинамике; нахождение численного значения работы в различных тепловых процессах.
Глоссарий по теме
Термодинамическая система представляет собой систему тел, которые взаимодействуют и обмениваются энергией и веществом.
Состояние равновесия – это состояние системы, в которой нет теплообмена между телами, составляющими систему.
Термодинамический процесс – процесс изменения состояния системы, который изменяет параметры системы.
Внутренняя энергия представляет собой сумму кинетической энергии хаотичного теплового движения и потенциальной энергии взаимодействия всех молекул, составляющих тело.
Теплоемкость представляет собой энергию, которая численно равна количеству тепла, которое выделяется или поглощается, когда температура тела изменяется на 1 К.
Теплопередача- это передача энергии от одного тела другому без выполнения работы.
Количество тепла является количественной мерой изменения внутренней энергии во время теплообмена.
Работа в термодинамике – это взаимодействие системы с внешними объектами, в результате чего изменяются параметры системы.
Список литературы
Г.Я. Мякишев., Б. Буховцев., Н. Н. Соцкий. Физика.10. Учебник для образовательных организаций М .: Просвещение, 2017. – С. 243-254.
Рымкевич А.П. Сборник задач по физике. 10-11 класс М.: Дрофа, 2009.- с.75-84
Основное содержание урока
Внутренняя энергия тела – это полная энергия всех молекул, которые его составляют. Внутренняя энергия идеального газа пропорциональна его температуре.
U = 3/2 · ν · R · T
Чтобы изменить внутреннюю энергию вещества, надо сообщить ему некоторое количество тепла или совершить работу.
Работа в термодинамике равна изменению внутренней энергии системы: A = ΔU.
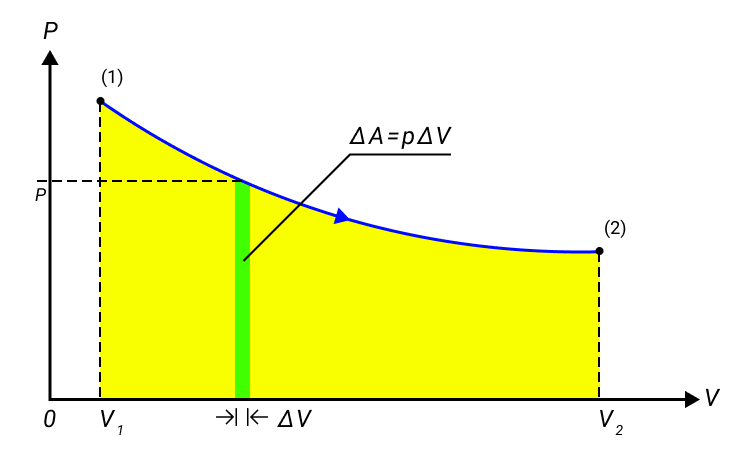
Работа газа в изобарном процессе равна A = P · ΔV. Если газ расширяется, то А > 0, если газ сжимается, то А < 0.
Кроме того, работа газа может быть определена с использованием графика давления в зависимости от объема.
Работа газа численно равна площади под графиком давления.
Количество теплоты – это энергия, которую система получает или теряет во время теплообмена.
Количество тепла для различных термических процессов определяется по-разному.
При нагревании и охлаждении: Q = c_ ∙ m ∙ ΔT;
Во время плавления и кристаллизации: Q = ℷ ∙ m;
Во время испарения и конденсации; Q = r ∙ m;
При сжигании: Q = q ∙ m.
Для замкнутой и адиабатически изолированной системы тел выполняется уравнение теплового баланса: Q1 + Q2 + … + Qn = 0
Выражение для внутренней энергии одноатомного идеального или разреженного реального газа имеет следующий вид:
U = 3/2 ν ∙ R ∙ T
Для идеального газа из молекул с двумя, тремя или более атомами необходимо учитывать кинетическую энергию вращения молекул (они больше не могут считаться материальными точками), поэтому выражение для их внутренней энергии отличается от U = 3/2 ν ∙ R ∙ T числовым коэффициентом.
Для двухатомного газа (например, O2, CO и т. д.):
U = 5/2 ν ∙ R ∙ T
Для газа с тремя атомами или более (например, O3, CH4):
U = 3ν · R · T
Изменить внутреннюю энергию вещества можно, передав ему некоторое количество тепла или выполнить над ним работу.
Существует три типа теплопередачи:
1) Теплопроводность представляет собой процесс переноса энергии от более теплого тела к менее нагретому телу с прямым контактом или от более нагретых частей тела к менее нагретым, осуществляемый хаотично движущимися частицами тела (атомы, молекулы, электроны , и т.д.). Простым примером является нагревание чашки, в которую выливают горячий чай.
2) Конвекция – это своего рода передача тепла, в которой внутренняя энергия передается снизу вверх струями или потоками жидкости или газа. Пример: нагревание воды в чайнике, который стоит на горячей плите.
3) Лучистый обмен или излучение – это процесс передачи энергии через электромагнитное излучение. Простой пример: солнечный свет.
Механическая работа изменяет механическую энергию тела. Термодинамическая работа изменяет внутреннюю энергию газа.
Если газ расширяется, то работа газа считается положительной. Если он сжат, то отрицательной.
Формула для нахождения работы газа в изобарном процессе имеет следующий вид:
A = p · ΔV
Для изотермического процесса формула принимает следующий вид: A = ν ∙ R ∙ T ∙ ln (V_2 / V_1)
Разбор тренировочных заданий
1. Объём газа, расширяющегося при постоянном давлении 100 кПа, увеличился на 20 литров. Работа, выполняемая газом в этом процессе, – _____.
Варианты ответов:
2000 Дж;
20 000 Дж;
200 Дж;
50 МДж.
Правильный вариант / варианты (или правильные комбинации вариантов): 3) 2000 Дж.
Совет: используйте формулу работы.
2. Чтобы из 5 кг снега, при температуре 0ºС, получить воду при 20ºС, необходимо сжигать в печке с КПД 40% __ кг дров.
Решение: при сгорании дров выделится количество теплоты:

из этого количества на полезную работу пойдёт только:
Для плавления снега необходимо количество теплоты:

для нагревания воды понадобится:
Согласно уравнению теплового баланса:

Отсюда следует:
Подставим числовые значения в формулу:
Ответ: 0,5175 кг.
Термодинамика – раздел физики, изучающий превращения энергии в макроскопических системах и основные свойства этих систем.
Термодинамика опирается на общие закономерности тепловых процессов и свойств макроскопических систем. Выводы термодинамики эмпирические, то есть опираются на факты, проверенные опытным путем с использованием молекулярно-кинетической модели.
Для описания термодинамических процессов в системах, состоящих из большого числа частиц, используются величины, не применимые к отдельным молекулам и атомам: температура, давление, концентрация, объем, энтропия)
Термодинамическое равновесие – состояние макросопической системы, когда описывающие ее макроскопические величины остаются неизменными.
В термодинамике рассматриваются изолированные системы тел, находящиеся в термодинамическом равновесии. То есть в системах с прекращением всех наблюдаемых макроскопических процессов. Особую важность представляет свойство, которое получило название выравнивания температуры всех ее частей.
При внешнем воздействии на термодинамическую систему наблюдается переход в другое равновесное состояние. Он получил название термодинамического процесса. Когда время его протекания достаточно медленное, система приближена к состоянию равновесия. Процессы, состоящие из последовательности равновесных состояний, называют квазистатическими.
Внутренняя энергия. Формулы
Внутренняя энергия считается важнейшим понятием термодинамики. Макроскопические тела (системы) имеют внутреннюю энергию, состящую из энергии каждой молекулы. Исходя из молекулярно-кинетической теории, внутренняя энергия состоит из кинетической энергии атомов и молекул, а также потенциальной энергии их взаимодействия.
Например, внутренняя энергия идеального газа равняется сумме кинетических энергий частиц газа, которые находятся в непрерывном беспорядочном тепловом движении. После подтверждений большим количеством экспериментов, был получен закон Джоуля:
Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема.
Применение молекулярно-кинетической теории говорит о том, что выражение для определения внутренней энергии 1 моля одноатомного газа, с поступательными движениями молекул записывается как:
U=32NАkT=32RT.
Зависимость от расстояния между молекулами у потенциальной энергии очевидна, поэтому внутренняя U и температура Т обусловлены изменениями V:
U=U(T, V).
Определение внутренней энергии U производится с помощью наличия макроскопических параметров, характеризующих состояние тела. Изменение внутренней энергии происходит по причине действия на тело внешних сил, совершающих работу. Внутренняя энергия является функцией состояния системы.
Когда газ в цилиндре сжимается под поршнем, то внешние силы совершают положительную работу A’. Силы давления газа на поршень также совершают работу, но равную A=-A’. При изменении объема газа на величину ∆V, говорят, что он совершает работу pS∆x=p∆V, где p – давление газа, S – площадь поршня, ∆x – его перемещение. Подробно показано в примере на рисунке 1.
Наличие знака перед работой говорит о работе газа в разных состояниях: положительная при расширении и отрицательная при сжатии. Переход из начального в конечное состояние работы газа может быть описан с помощью формулы:
A=∑pidVi или в пределе при ∆Vi→0:
A=∫V1V2pdV.
Рисунок 1. Работа газа при расширении.
Обратимые и необратимые процессы
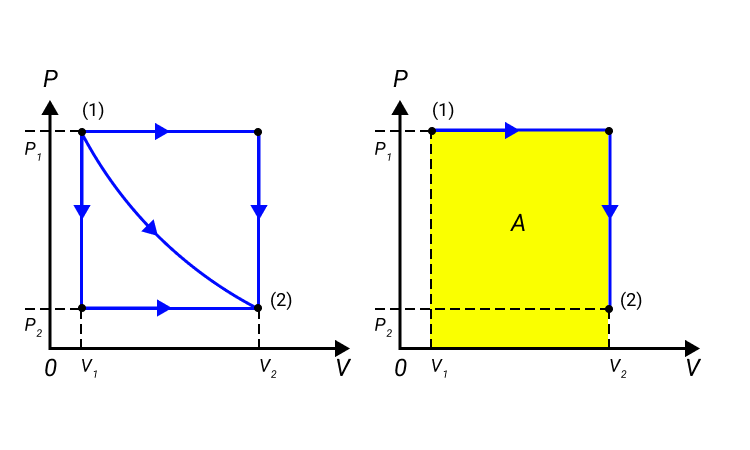
Работа численно равняется площади процесса, изображенного на диаграмме p, V. Величина А зависит от метода перехода от начального состояния в конечное. Рисунок 2 показывает 3 процесса, которые переводят газ из состояние (1) в состояние (2). Во всех случаях газ совершает работу.
Рисунок 2. Три различных пути перехода из состояния (1) в состояние (2). Во всех трех случаях газ совершает разную работу, равную площади под графиком процесса.
Процессы из рисунка 2 возможно провести в обратном направлении. Тогда произойдет изменение знака А на противоположный.
Процессы, которые возможно проводить в обоих направлениях, получили название обратимых.
Жидкости и твердые тела могут незначительно изменять свой объем, поэтому при совершении работы разрешено им пренебречь. Но их внутренняя энергия подвергается изменениям посредствам совершения работы.
Механическая обработка деталей нагревает их. Это способствует изменению внутренней энергии. Имеется еще один пример опыта Джоуля 1843 года, служащий для определения механического эквивалента теплоты, изображенного на рисунке 3. Во время вращения катушки, находящейся в воде, внешние силы совершают положительную работу A’>0, тогда жидкость повышает температуру из-за наличия силы трения, то есть происходит увеличение внутренней энергии.
Процессы примеров не могут проводиться в противоположных направлениях, поэтому они получили название необратимых.
Рисунок 3. Упрощенная схема опыта Джоуля по определению механического эквивалента теплоты.
Изменение внутренней энергии возможно при наличии совершаемой работы и при теплообмене. Тепловой контакт тел позволяет увеличиваться энергии одного тела с уменьшением энергии другого. Иначе это называется тепловым потоком.
Количество теплоты
Количество теплоты Q, полученное телом, называется его внутренней энергией, получаемой в результате теплообмена.
Рисунок 4. Модель работы газа.
Процесс передачи тепла тел возможен только при разности их температур.
Направление теплового потока всегда идет к холодному телу.
Количество теплоты Q считается энергетической величиной и измеряется в джоулях (Дж).
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
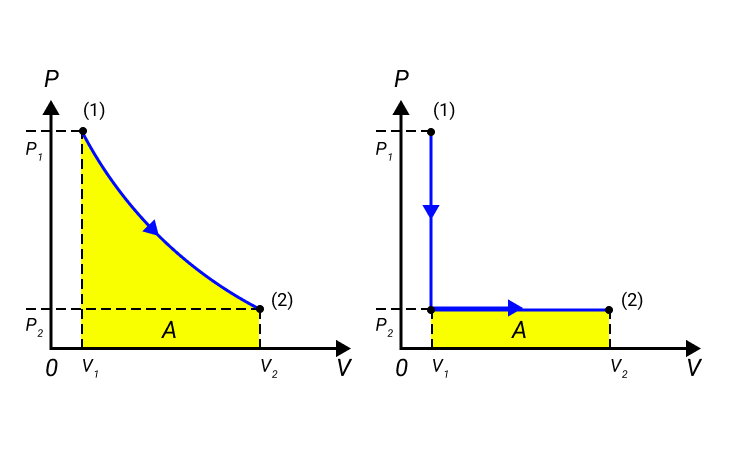
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
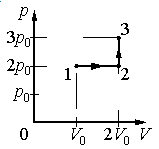
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15k
Внутренняя энергия, теплота, работа
Понятие
энергии в механике связывают либо с
движением тел, либо с положением этих
тел в силовом поле. Сохранение энергии
рассматривается как постоянство
суммы кинетической и потенциальной
энергии, при этом не принимается во
внимание внутреннее состояние этих
тел. Однако движущееся тело имеет не
только кинетическую и потенциальную
энергии, но и определенную тепловую
энергию (температуру). При контакте
этого тела с другим телом, температура
которого ниже первого, начнется переход
тепловой энергии от первого тела ко
второму, при этом внутреннее состояние
обоих тел изменится, так как меняется
запас энергии. С другой стороны, увеличение
«запаса теплоты» может быть достигнуто
за счет уменьшения кинетической энергии
(например, удар пули о твердую поверхность
приводит к повышению температуры и
поверхности, и пули). Нагретое тело при
охлаждении может стать источником
механической энергии, что реализуется
в тепловых машинах.
Внутренняя
энергия
системы
(U)
включает в себя все виды энергии системы
(кинетическую энергию поступательного,
вращательного, колебательного движения
молекул и все формы движения атомов,
электронов, ядер и т.д.) за исключением
кинетической и потенциальной энергии
всего тела (системы). Изучение двух
последних видов энергии не входит в
задачи термодинамики.
Как
и любую энергию, внутреннюю энергию
нельзя измерить. Однако, можно определить
ее изменение при переходе из одного
состояния в другое.
В
термодинамике обычно исследуют две
формы передачи энергии от одной системы
к другой – теплоту Q и работу А.
Теплота
– неупорядоченная форма передачи
энергии, которая переходит путем
хаотического столкновения молекул
соприкасающихся тел, т.е. путем
теплопроводности или теплоизлучения.
В термодинамике положительной (Q > 0)
считается теплота, подведенная к системе.
В термохимии подводимая к системе
теплота имеет противоположный знак (Q
< 0).
Работа
– упорядоченная форма передачи энергии,
общей чертой которой является перемещение
масс, состоящих из очень большого числа
молекул, под действием каких-либо сил.
Положительной (А > 0) считается работа,
совершаемая системой против действия
внешних сил.
Теплота
и работа характеризуют качественно и
количественно две различные формы
передачи энергии от одной части
материального мира к другой.
В
отличие от внутренней энергии, теплота
и работа зависят от способа проведения
процесса, т.е. являются функциями пути.
Первый закон термодинамики. Понятие об энтальпии
Первый
закон термодинамики является частным
случаем закона сохранения энергии
применительно к процессам, в которых
выделяется, поглощается или преобразуется
тепловая энергия.
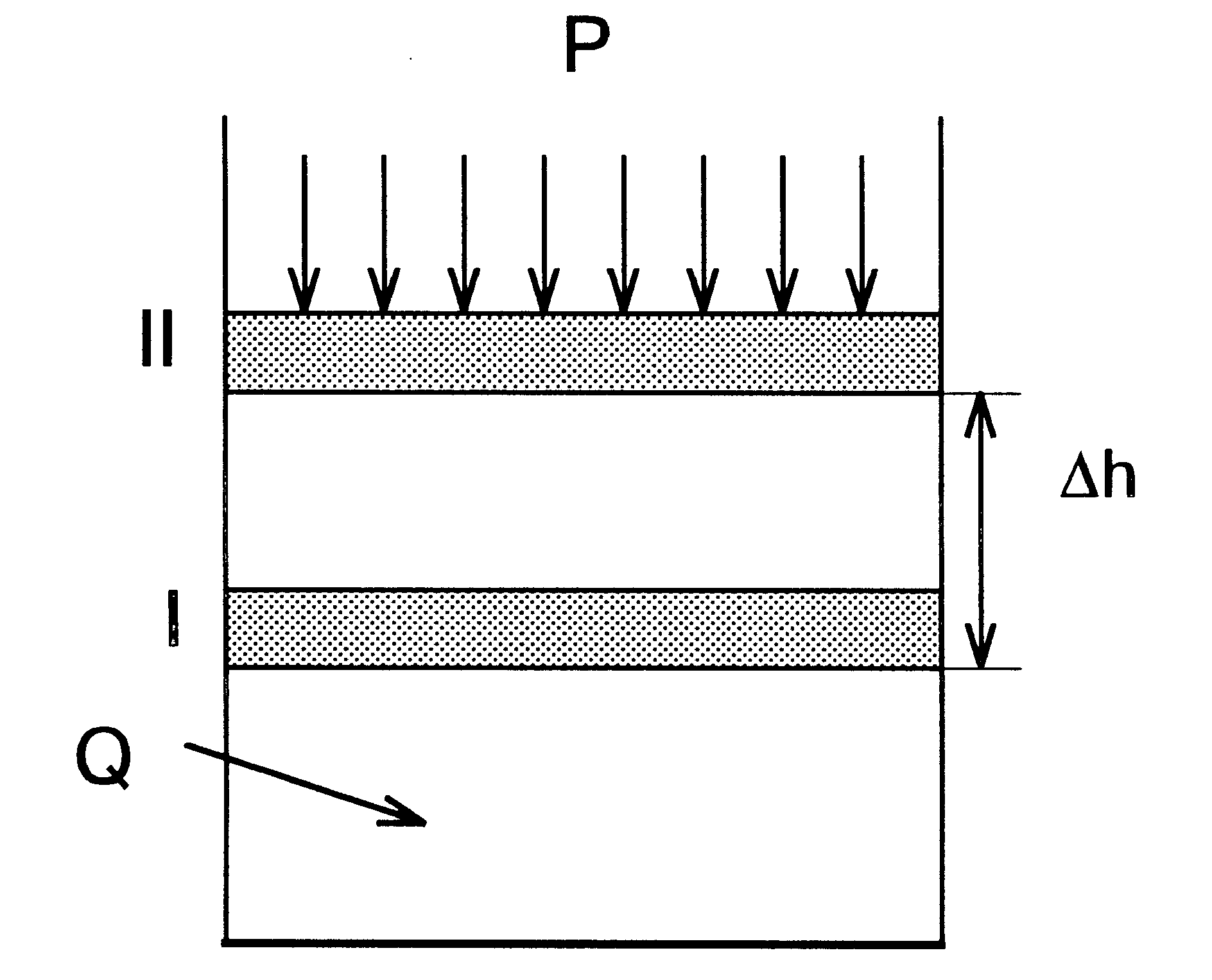
Рассмотрим,
как изменяется внутренняя энергия DU
при проведении процесса, в котором
система (газ, находящийся при постоянном
давлении р = const в цилиндре под поршнем)
получает некоторое количество тепловой
энергии Qр,
в результате чего газ нагревается (Т2
> T1,
U2
> U1)
и расширяется (V2
> V1)
(рис. 1).
Рис.
1. К выводу первого закона термодинамики
Если
положение поршня не зафиксировано, то
поршень будет перемещаться до тех пор,
пока внешняя сила F, приложенная к поршню,
не уравновесит силу, действующую на
поршень со стороны системы.
Тогда
имеем
F
= p.s,
где
p – внешнее давление,
s
– площадь поперечного сечения цилиндра.
При
этом движении совершается работа против
сил внешнего давления, равная
A
= F .Dh,
где
Dh
– величина перемещения поршня.
Поскольку
произведение площади поперечного
сечения цилиндра на величину перемещения
поршня есть приращение объема системы
DV,
то можно записать
A
= F .Dh
= р.
s.
Dh
= p .
DV.
Таким
образом, тепловая энергия (-QР),
сообщенная газу, при постоянном давлении
(p=const) идет частично на увеличение
внутренней энергии DU,
а частично на работу расширения A
|
–
Данное Уравнение |
|
|
Учитывая, -QP |
|
Сумма
внутренней энергии и произведения
давления на объем (H = U + pV) получила
название энтальпии
или энергосодержания.
Энтальпия
и внутренняя энергия являются функциями
состояния данной системы.
Если
подвод тепла к цилиндру с поршнем
осуществлен в изобарных условиях, т.е.
при постоянном давлении (p=const) , как это
предполагалось при выводе уравнения
(2), то
-QP
=
DН.
Если
закрепить поршень и подвести теплоту
при постоянном объеме (V
= const),
то
V=0,
и вся теплота пойдет на увеличение
внутренней энергии:
-QV
=
DU.
Так
как чаще всего реакции проводят при
постоянном объеме (например, атмосферном)
давлении, далее в расчетах мы будем
использовать величину DН.
Так
как энтальпия является функцией
состояния, то все общие свойства функции
состояния распространяются и на неё.
Свойства
энтальпии:
1.
Разность энтальпий системы в конечном
и начальном состояниях не зависит от
пути перехода системы из одного состояния
в другое.
2.Энтальпия
системы равна сумме энтальпий частей,
составляющих систему, т.е. энтальпия –
величина аддитивная.
3.Абсолютное
значение энтальпии системы (как и
абсолютное значение потенциальной
энергии тела) является принципиально
неопределяемым.
Однако,
как и в случае с потенциальной энергией,
при термодинамических расчетах нас
интересует не абсолютные величины
энтальпии, а их изменение при переходе
системы из одного состояния в другое.
Вспомним, что при расчете изменения
потенциальной энергии при переходе с
одного уровня на другой произвольно
выбирают уровень, на котором потенциальную
энергию тела полагают равной нулю (не
важно, что ниже этого уровня потенциальная
энергия тела оказывается отрицательной,
так как это не скажется на результате
расчета величины изменения потенциальной
энергии). Точно также может быть
произвольно выбрано единое начало
отсчета энтальпии для всех химических
систем.
Энтальпия
любой системы равна сумме энтальпий
веществ, входящих в её состав. В свою
очередь, энтальпия вещества зависит от
его строения, количества, температуры
и давления. Следовательно, за начало
отсчета для веществ любого строения
следует выбрать (произвольно) одни и
те же условия (стандартные условия).
За
точку
отсчета
принимают значение энтальпии образования
простых веществ при 298К (25оС),
давлении 101,3 кПа (1атм.), если они при
этих условиях, называемых стандартными,
находятся в устойчивом состоянии.
Стандартные
термодинамические величины обозначают
определенным образом (например
– стандартная энтальпия вещества А).
Невозможность определения абсолютной
энтальпии распространяется и на
абсолютные величины стандартных
энтальпий веществ, поэтому они не могут
быть использованы для расчета теплот
реакций. Однако для этих целей можно
пользоваться относительными величинами,
например, величинамиэнтальпий
образования веществ.
При
этом полагают (это также является
произвольно выбранным условием), что
любое вещество образуется из простых
веществ, каждое из которых находится в
стандартных условиях, причем в модификации,
устойчивой при этих условиях. В
соответствии с этим положением,
стандартные энтальпии образования всех
простых веществ, устойчивых в стандартном
состоянии, равны нулю
(например,
).
В скобках указывается агрегатное
состояние вещества: тв – твердое, ж –
жидкое, г – газообразное. Например,,
а,
что не характерно для натрия в газообразном
состоянии при стандартных условиях.
Для
характеристики энтальпии сложного
вещества вводят понятие стандартная
энтальпия образования,
которая
равна количеству теплоты с обратным
знаком, выделяющейся или поглощающейся
при образовании одного моля вещества
из простых веществ, находящихся в
устойчивых агрегатных состояниях в
стандартных условиях.
Размерность
энтальпии образования
вещества
– кДж/моль. Стандартные энтальпии
образования большинства сложных веществ
имеют отрицательные значения, так как
образуются из простых веществ с выделением
теплоты.
Стандартные
энтальпии образования определены для
большого количества веществ и сведены
в таблицы термодинамических величин
(см. Приложение, табл .2).
На
примере реакции горения метана покажем,
почему и как тепловой эффект реакции
может быть рассчитан с использованием
величин стандартных энтальпий образования
веществ
CH4(г)
+
2О2(г)
CО2(г)
+ 2Н2О(г)
, DНор
исходные
вещества продукты реакции,
где
DНр
– изменение энтальпии для данной
реакции, кДж (при расчете
стандартная энтальпия образования
каждого вещества (кДж/моль) умножается
на число его молей в соответствии с
уравнением реакции).
Исходные
и конечные вещества могут быть получены
из одних и тех же простых веществ С(ТВ)
+ 2Н2(Г)
+ 2О2(Г),
взятых
в одних и тех же количествах
С(ТВ)
+ 2Н2(Г)
+ 2О2(Г)
CH4(г)+
2О2(г),
DН1
простые
вещества исходные вещества
С(ТВ)
+ 2Н2(Г)
+ 2О2(Г)
CО2(Г)
+
2Н2О(Г),
DН2.
простые
вещества продукты реакции
Энтальпия
– функция состояния, поэтому её изменение
в процессах
простые
вещества
продукты реакции,
простые
вещества
исходные вещества
продукты реакции
одинаковы
(одно из свойств функций состояния):
DН2
=
DН1
+ DНр,
где
и
В
стандартных условиях:
Разница
суммы энтальпий образования продуктов
реакции и исходных веществ определяет
тепловой эффект (QP)
реакции, взятый с обратным знаком (так
как DНор
=
– QР).
Рассчитать
DНо298,р.
для данной реакции можно, пользуясь
табличными данными (см. Приложение,
табл.2):
DНо
298,
р
=
(DНоСО2+
2 DНоН2О
)
– (DНоСН4+
2 DНоО2)
, кДж.
DНо
298,р
=
(DНоСО2+
2 DНоН2О
)
– (DНоСН4+
2 DНоО2)
=
=
[(-393,5) + 2(-241,8) – (DНоСН4)
– 2(0)] кДж = – 802,2 кДж.
Для
точного расчета теплового эффекта
реакции, протекающей в нестандартных
условиях
(например
р = 101,3 кПа, Т298
К), следует рассчитать энтальпии
образования всех участвующих веществ
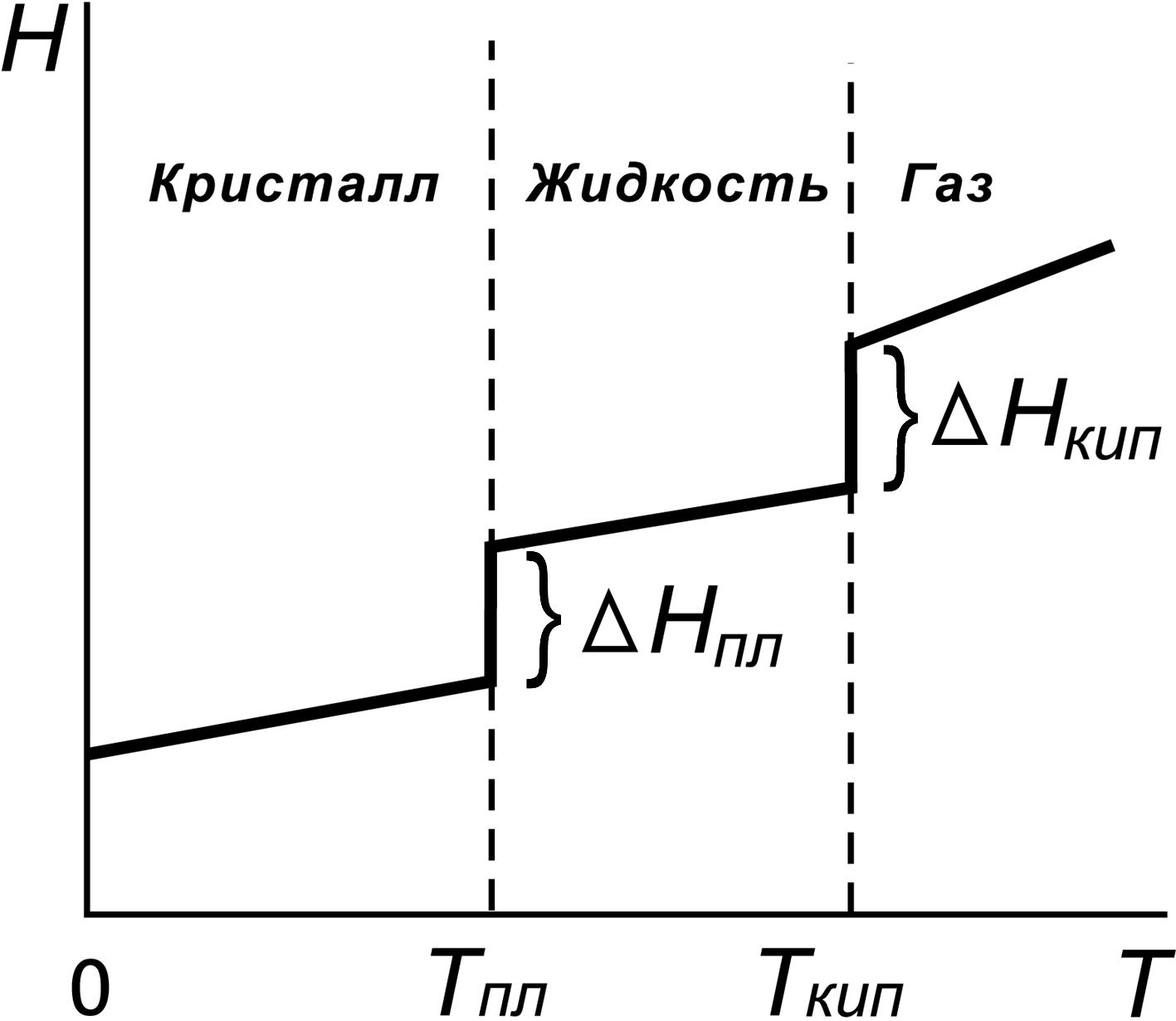
при этих условиях. В общем виде зависимость
энтальпии образования от температуры
показана на рис.2, из которого видно, что
при фазовых переходах изменение энтальпии
происходит скачкообразно на величину,
соответственно, теплоты плавления
∆Нпл.
или парообразования (кипения) ∆Нкип.,
взятых с обратным знаком.
Рис.
2. Зависимость энтальпии образования
вещества от температуры
В
пределах одного фазового состояния
(газового, жидкого и т.д.) изменение
энтальпии при изменении температуры
невелико, поэтому при приближенных
расчетах этим изменением пренебрегают.
Уравнение
температурной зависимости энтальпии
моля вещества в пределах одного фазового
состояния:
,
где
СР
– мольная
теплоемкость
при
постоянном давлении,
которая равна количеству теплоты,
необходимому для нагревания 1 моля
вещества на один градус.
СР
зависит от природы и агрегатного
состояния вещества, а также от температуры.
Однако в небольшом температурном
интервале зависимостью СР
от Т можно пренебречь и считать, что
DН
= СРDТ.
С помощью этого соотношения можно
рассчитать энтальпии веществ для
различных температур (в пределах одного
агрегатного состояния).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение задач – занятие, которое любит далеко не каждый. Здесь мы стараемся сделать так, чтобы оно занимало у вас поменьше времени без ущерба для качества самого решения. Тема этой статьи — задачи на внутреннюю энергию.
Подписывайтесь на наш телеграм и читайте полезные материалы для студентов каждый день!
Решение задач: внутренняя энергия
Прежде чем приступать к задачам на внутреннюю энергию тела, посмотрите общую памятку по решению физических задач. И пусть под рукой на всякий случай всегда будут основные физические формулы.
Задача №1. Изменение внутренней энергии
Условие
Воздушный шар объёмом 500 м3 наполнен гелием под давлением 105 Па. В результате нагрева температура газа в аэростате поднялась от 10 °С до 25 °С. Как увеличилась внутренняя энергия газа?
Решение
Для решения будем использовать формулу внутренней энергии идеального газа:
Массу гелия выразим из уравнения Клапейрона-Менделеева:
Тогда можно записать:
Ответ: 4 МДж.
Задача №2. Внутренняя энергия и работа
Условие
Азот массой 200 г расширяется изотермически при температуре 280 К, причем объём газа увеличивается в 2 раза. Найти:
- Изменение ∆U внутренней энергии газа.
- Совершенную при расширении газа работу А.
- Количество теплоты Q, полученное газом.
Решение
Так как процесс изотермический, то изменение внутренней энергии равно нулю, а работа равна количеству теплоты, полученному газом:
Ответ: 0; 11,6 кДж; 11,6 кДж.
Задача №3. Изменение внутренней энергии при изобарном и изохорном процессе
Условие
Кислород занимает объём V1= 3 л при давлении p1= 820 кПа. В результате изохорного нагревания и изобарного расширения газ переведён в состояние с объёмом V2= 4,5 л и давлением p2= 600 кПа. Найти количество теплоты, полученное газом; изменение внутренней энергии газа.
Решение
Теплота, подведенная к газу, идет на совершение работы и изменение внутренней энергии:
В изохорном и изобарном процессе соответственно:
Изохорное нагревание:
Изменение внутренней энергии при изохорном процессе:
Изменение внутренней энергии при изобарном процессе:
Общее изменение внутренней энергии:
Ответ: 4,75 кДж.
Задача №4. Изменение внутренней энергии двухатомного газа
Условие
Кислород массой 2 кг занимает объём 6 м3 и находится под давлением 1 атм. Газ был нагрет сначала при постоянном давлении до объёма 13 м3, а затем при постоянном объёме – до давления 23 атм. Найти изменение внутренней энергии газа.
Решение
Изменение внутренней энергии находим по формуле:
Эту форму можно преобразовать, используя уравнение Клапейрона-Менделеева:
Ответ: 75,7 МДж.
Задача №5. Внутренняя энергия смеси газов
Условие
В закрытом сосуде находится масса m1 = 20 г азота и масса m2 = 32 г кислорода. Определить изменение ΔU внутренней энергии смеси газов при охлаждении ее на ΔТ = 28 К.
Решение
Определим количество молей азота и кислорода, а затем общее количество вещества в смеси соответственно:
Изменение внутренней энергии:
Знак «минус» означает, что внутренняя энергия уменьшается.
Ответ: -539 Дж.
Вопросы на тему «Внутренняя энергия тела»
Вопрос 1. Что такое внутренняя энергия?
Ответ. Для начала, внутренняя энергия чего? Бутылки с пивом, воздуха в шарике, тазика с водой? Все макроскопические тела обладают энергией, заключенной внутри них: атомы твердого тела колеблются в кристаллической решетке около положений равновесия, молекулы газа находятся в постоянном хаотическом движении и т.д.
По определению:
Внутренняя энергия вещества – это энергия, которая складывается из кинетической энергии всех атомов и молекул, и потенциальной энергии их взаимодействия друг с другом.
Для идеального газа с числом степеней свободы i внутренняя энергия вычисляется по формуле:
Вопрос 2. От чего зависит внутренняя энергия идеального газа?
Ответ. Эта величина не зависит от объёма и определяется только температурой.
Вопрос 3. Как изменяется внутренняя энергия тела?
Ответ. Если тело совершает работу, его внутренняя энергия уменьшается. Например, газ передвигает поршень. Если же работа совершается над телом, то внутренняя энергия увеличивается.
Вопрос 4. Что такое функция состояния?
Ответ. Функция состояния – это один из параметров, которым можно описать термодинамическую систему. Функция состояния не зависит от того, как система пришла в то или иное состояние, а определяется несколькими переменными состояния.
Внутренняя энергия – это функция состояния термодинамической системы. В общем случае она зависит от температуры и объёма.
Вопрос 5. Можно ли изменить внутреннюю энергию тела, не совершая над ним работы?
Ответ. Да, еще один способ изменения внутренней энергии – теплопередача. В процессе теплопередачи внутренняя энергия тел изменяется.
Нужна помощь в решении задач по любой теме и других студенческих заданий? Профессиональный студенческий сервис поспособствует в выполнении работы вне зависимости от ее сложности.