Просмотров 1.2к. Опубликовано 30.12.2022
Большинство современных двигателей преобразуют внутреннюю энергию углеводородного топлива в механическую энергию. То есть являются тепловыми машинами. Первым ученым, который задался вопросом о создании самой эффективной тепловой машины стал французский физик Сади Карно. В 1824 в его работе – «Размышления о движущей силе огня и о машинах, способных развивать эту силу», предложен идеальный термодинамический цикл тепловой машины. Цикл, позволяющий получить максимальный теоретический КПД, затем назвали именем Карно.

Главной характеристикой, на которую обращают внимание при проектировании любого двигателя является коэффициент полезного действия или КПД. Коэффициент КПД показывает, насколько эффективно протекает трансформация тепловой энергии в системе в полезную механическую работу. КПД любого цикла вычисляется путем отношения полезной работы к затраченной энергии (которую передают системе).
- Полезная работа – та, которую получаем на выходе системы в результате выполнения цикла.
- Затраченная энергия – та, что была подведена к системе за цикл.
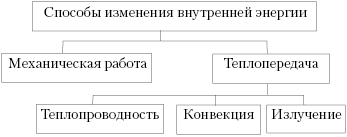
Термодинамические процессы и циклы.
Цикл Карно состоит из двух изотермических и двух адиабатных процессов. Чтобы понять, что из себя представляют эти процессы, обратимся к первому закону термодинамики:
∆U = A + Q,
где ∆U – внутренняя энергия рабочего тела или системы,
A – совершаемая в цикле работа,
Q – количество теплоты, переданное за цикл, системе.
Формулировка первого закона термодинамики: при переходе системы из одного состояния в другое, изменение внутренней энергии системы равно сумме количества теплоты, переданного системе, и работы внешних сил.
Что такое изотермический и адиабатный процессы?
Изотермический процесс
Изотермический процесс – процесс, перехода рабочего тела из одного состояния в другое без изменения температуры ∆T=0.

Например, изменение объёма и давления газа при неизменной температуре.
При постоянной температуре изменение внутренней энергии газа ∆U будет равно нулю, так как ∆T = 0.
Тогда, согласно первому закону термодинамики: Q = A. Это значит:
- получая теплоту, газ будет расширяться, совершая положительную работу. При этом всё количество тепла будет потрачено на совершение работы.
- и наоборот, при отдаче теплоты объем газа будет уменьшаться.
Адиабатный процесс
Адиабатный процесс – такой процесс, который протекает без передачи или получения тепла Q от окружающей среды. То есть, процесс протекает в теплоизолированной системе или с бесконечно большой скоростью, при которой теплообменом можно пренебречь Q = 0.
Согласно первому закону термодинамики: A = -∆U.
Это значит:
- работу газ совершает за счет уменьшения внутренней энергии;
- и наоборот, приложенная к системе работа, затрачивается только на повышение внутренней энергии.

Из каких процессов состоит цикл Карно
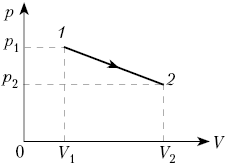
Главная особенность всех круговых процессов или циклов состоит в том, что их работа невозможна, если приводить рабочее тело в контакт только с одним источником теплоты. Любой тепловой двигатель устроен таким образом, что за счет теплообмена между двумя источниками теплоты он способен преобразовать тепло в механическую работу. Температуры этих источников должны отличаться, но, при этом, быть постоянными.
Чтобы понять, как работает цикл Карно, нужно представить простой тепловой двигатель, например цилиндр с поршнем, внутри которого находится газ. К газу может подводиться и отводится тепло. Источники тепла, при этом, называются:
- нагреватель – источник, имеющий высокую постоянную температуру TН
- холодильник – с постоянной низкой температурой TХ.
Цикл Карно имеет четыре обратимых процесса – два изотермических, и два – адиабатных.

Изотермические процессы протекают при постоянной температуре T. Адиабатные процессы – при постоянной энтропии S, без теплообмена с окружающей средой.
Для удобства, цикл Карно представляют в:
- T-S координатах – зависимость энтропии S от температуры T.
- p-V координатах – зависимость давления p от удельного объёма V.

Изотермическое расширение
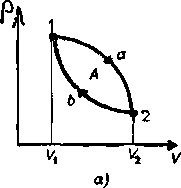
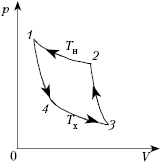
Изотермическое расширение или изотермический подвод тепла – показано процессом AB. В начале рабочее тело находится в точке A. На данном этапе рабочее тело или газ имеет начальную температуру TН. Затем, к телу подводится энергия в виде теплоты Q1. Снижение температуры при расширении отсутствует, так как подводится теплота Q1, от нагревателя. Увеличения температуры тоже не будет, так как совершается работа A1=Q1. Поэтому, при расширении рабочего тела его температура остается постоянной – изотермическое расширение TН=const. При этом, энтропия рабочего тела увеличивается, из-за увеличения его объема. Происходит это за счет совершения механической работы.

Адиабатическое расширение
Адиабатическое расширение – показано процессом BC. После окончания изотермического подвода тепла газ находится в состоянии, характеризуемом точкой B. Далее следует адиабатическое расширение рабочего тела. На этом этапе газ в двигателе изолирован от обоих тепловых источником – как от горячего, так и от холодного. Поэтому ни источники, ни рабочее тело получают и не теряют тепло. Такой процесс называется адиабатическим. Из-за отсутствия теплообмена с окружающей средой Q=0 энтропия рабочего тела остается постоянной S=const. Работа осуществляется только за счет внутренней энергии A = -∆U. Поэтому происходит снижение температуры газа.

Рабочее тело, расширяясь, заставляет поршень двигаться вверх. Давление газа под поршнем постепенно снижается. Выталкивая подвижный поршень вверх, рабочее тело совершает механическую работу, в результате чего теряет определенное количество внутренней энергии. Количество этой энергии равно проделанной работе A = -∆U. В процессе расширения рабочего тела его температура уменьшается и становится равной TХ.
Изотермическое сжатие
Изотермическое сжатие – процесс CD. На данном этапе рабочее передаёт тепло холодному источнику при температуре TХ. К газу подводится работа сжатия путем перемещения поршня вниз. В результате этого процесса, рабочее тело передает холодильнику количество теплоты равное подводимой работе Q2=А2. Изменения внутренней энергии не будет ∆U=0. Поэтому, этот процесс считается изотермическим сжатием TХ=const. Энтропия газа уменьшается.

Адиабатическое сжатие
Адиабатическое сжатие – процесс DA. После завершения отвода тепла, газ находится в состоянии, характеризуемом точкой D. На последней стадии цикла рабочее тело снова остается изолированным обоих источников Q=0. Предполагается, что поршень движется без трения, а процесс является обратимым. Работа продолжает подводиться и поршень движется вниз, сжимая газ. В результате этого внутренняя энергия газа возрастает A = +∆U. Под давлением поршня температура рабочего тела поднимается до температуры нагревателя TН, но энтропия остается неизменной. Итогом этого этапа является то, что рабочее тело возвращается к своему изначальному состоянию в точку А.

Поскольку цикл Карно идеальный, то принято допущение, что температуры рабочего тела в процессах AB и CD равна температуре горячего и холодного источника или отличаются на бесконечно малую величину.
Формула расчета цикла Карно
Коэффициент КПД показывает, насколько совершенен цикл и входящие в него термодинамические процессы. Термический КПД любого термодинамического цикла рассчитывается по формуле:

Где Q1 – тепло, подведенное к рабочему телу от нагревателя;
Q2 – тепло, отведенное от рабочего тела к холодильнику.
Применительно для расчета КПД цикла Карно используется формула:

Где TН -температура горячего источника;
TХ -температура холодно источника.
Температура формуле вычисления КПД цикла Карно в кельвинах [К].
Обратный цикл Карно
Описанный выше цикл теплового двигателя Карно полностью обратим. Это значит, что можно пройти все процессы в обратном направлении:
- процесс отвода тепла станет процессом подвода тепла
- процесс сжатия – расширением.
При проходе процессов в обратном направлении получим циклом холодильной машины Карно или теплового насоса. Диаграммы остаются абсолютно такими же, измениться лишь направление процессов.
Единственное отличие обратного цикла Карно — это противоположные направления всех четырёх термодинамических процессов.

Тепло в обратном цикле Карно будет поглощаться из холодильника, и далее отводиться к нагревателю. Чтобы это осуществить, в соответствии со вторым законом термодинамики, необходимо затратить работу. Работа затрачивается на сжатие газа.
В результате того, что к данной системе прикладывается работа, тепло перемещается от холодного источника к горячему.
Подробнее про обратный цикл Карно и холодильные машины рекомендуем прочитать в статье.
Теорема Карно
Теорема Карно – это теорема, выявляющая некоторые ограничения для предела КПД реальных тепловых машин. Описал ее Сади Карно в своем труде о движущей силе огня. Но некоторые из современных авторов считают, что рассуждения Карно позволяют сформулировать сразу две теоремы. Звучат они так:
- КПД любого обратимого теплового двигателя, работающего по циклу Карно, не зависит от природы рабочего тела и конструкции самой машины, а является лишь функцией температур нагревателя и холодильника:
Из этой теоремы можно сделать вывод, что самую большую роль, определяющую КПД тепловой машины, играет разница температур горячего и холодного источников.
- КПД любого теплового двигателя, работающего по необратимому циклу, должен быть меньше КПД двигателя с обратимым циклом Карно, при условии равных температур нагревателей и холодильников.
Эта трактовка теоремы дает понять, что реальные двигатели неидеальны, в отличии от теоретической модели Карно. Поэтому, из-за наличия неизбежных потерь энергии, КПД реального двигателя будет снижаться в зависимости от объема этих потерь.
Исходя из этого, уравнение расчета КПД цикла Карно показывает максимальную эффективность работы для любого двигателя, в котором задействованы соответствующие температурные параметры.
Следствие теоремы Карно – все обратимые двигатели, которые работают между идентичными источниками тепла, имеют одинаковую эффективность.

Отсюда можно сделать вывод: понижение температуры холодного резервуара сильнее влияет на максимальный КПД тепловой машины, чем увеличение температуры горячего резервуара на такую же величину. На практике добиться этого довольно сложно, так как чаще всего источником для охлаждения является окружающая среда со своей температурой.
Максимальный КПД достигается только в том случае, когда значение энтропии не изменяется в течение цикла. Например, в течение цикла энтропия может изменяться при наличии трения, в результате которого при механической работе выделяется тепло. В данной ситуации цикл нельзя назвать обратимым.
Обобщенный цикл Карно
Согласно описанной ранее теореме Карно, КПД абсолютно любого реального цикла не может быть выше КПД в цикле Карно при идентичных температурных параметрах. Несмотря на это существуют примеры, термический КПД которых, при определенных условиях, равен циклу Карно. Такие циклы имеют отличия в изображении на T-S диаграмме. В данных циклах используется регенерация теплоты, поэтому они называются регенеративными.
Термодинамический цикл с регенерацией теплоты
Происходит процесс регенерации следующим образом. Доля тепла, отдаваемая рабочим телом холодильнику, переходит обратно к рабочему телу для его нагревания. Такой метод повышает термический КПД рабочего цикла, позволяя сделать расход теплоты более выгодным, и используется в теплосиловых устройствах. Например, в современных тепловых электрических станциях.
Рассмотрим T-S диаграмму регенеративного цикла.

Данный цикл состоит из двух изотермических (1-2) и (3-4) и двух политропных (произвольных) (2-3) и (4-1) обратимых и эквидистантных процессов.
- Горячий источник (нагреватель), имея начальную температуру T1, по изотерме (1-2) передает теплоту рабочему телу.
- В точке 2 начинается расширение рабочего тела в направлении (2-3) – политропный процесс. На данной кривой происходит отвод теплоты регенерации qрег.
- Точка 3 на диаграмме находится левее, чем в диаграмме для идеального цикла Карно, поскольку вследствие отвода теплоты регенерации уменьшается энтропия рабочего тела.
- Далее, на изотермической прямой (3-4) происходит сжатие рабочего тела и отведение теплоты к холодному источнику с температурой T2 (холодильник).
- В точке 4 начинается политропный процесс сжатия по кривой (4-1). Одновременно с этим к рабочему телу подводится теплота qрег.
Рабочее тело принимает и отдает равное количество теплоты qрег, значит в данном процессе происходит перенос теплоты из одной части цикла в другую, это и называется процессом регенерации.
Термический КПД регенеративного цикла
Термический КПД регенеративного цикла будет равен термическому КПД Карно при идентичных параметрах температуры. Поэтому такой регенеративный цикл так же называют обобщенным циклом Карно (только если он обратим). Подобные явления находят массовое практическое применение на различных промышленных объектах и предприятиях.
К примеру, по принципу регенерации происходит подогрев воды в паровых турбинах и подогрев воздуха в газовых турбинах.
Говоря об обобщенном цикле Карно, стоит отметить, что его реализация в идеальном виде невозможна. Обусловлено это тем, что в идеале такая система должна содержать бесконечно большое количество промежуточных регенераторов. При этом, для каждого из них температура отводимой и подводимой теплоты должна быть определенной. Любые методы регенерации, которые используются на практике, являются в определенной мере приближенными к идеальному циклу.
Эффективность реальных тепловых двигателей.
Обратимые двигатели в реальности невозможны. Реальные машины имеют еще меньший КПД, чем КПД машины Карно. Помимо этого, реальные двигатели, работающие по принципу Карно, можно встретить крайне редко. Несмотря на это, данное уравнение не теряет своей актуальности для определения максимального КПД, который можно спрогнозировать для определенной пары источников теплоты. Двигатель, работающий по принципу Карно должен рассматриваться как теоретическая модель тепловых двигателей.

Важнейшей технической задачей является повышение КПД тепловых двигателей и приближение этого значение к максимально возможному. Сравним значения термических КПД некоторых тепловых двигателей:
- Паровой двигатель – 8%
- Газотурбинная установка – 25-38%
- Паротурбинная установка – 40-50%
Начальные и конечные температуры пара для паровой турбины имеют такие приблизительные значения: Tн = 800 К, Tх = 300 К. Максимальное теоретическое значение КПД при данных температурах – 62%. Но, вследствие различных потерь энергии, в реальности экономичность достигает 45%.
На сегодня, КПД самых экономичных паротурбинных блоков на сверхперегретом паре с развитой системой регенерации и промежуточным перегревом пара достигает 52%.

Заключение
Модель работы идеального теплового двигателя, предложенная Сади Карно почти 200 лет назад, хоть и нереализуема на практике, но определенно остается актуальной и в нынешнее время.
Цикл Карно – теоретический инструмент, позволяющий рассчитать максимальную эффективность для любого теплового двигателя, что является немаловажной задачей для каждого инженера, занимающегося разработкой и моделированием термодинамических систем.
В этой статье рубрики «физика для чайников» рассмотрим подробное решение нескольких задач на работу в термодинамике. Тем, кто хочет научиться решать задачи, рекомендуем систематически тренироваться, предварительно ознакомившись с теорией. А еще, полезно почитать памятку по решению физических задач и держать под рукой основные физические формулы.
Чтобы не заскучать, подписывайтесь на наш телеграм-канал. Там вас ждет ежедневная рассылка, которая будет полезна всем учащимся.
Примеры решения задач на работу в термодинамике
Задача №1. Работа расширения
Условие
При адиабатическом расширении 1 кг воздуха его объем увеличился в 10 раз. Найти работу расширения, если начальное давление 1 атм, а начальная температура 15 °С.
Решение

Зная молярную массу воздуха (29 г/моль), начальный объем можно найти из уравнения Клапейрона-Менделеева:

Не забываем переводить все физические величины из условия в систему СИ.
Из условия находим конечный объем:

Работа равна:

Ответ: 751 кДж.
Задача №2. Работа в цикле Карно
Условие
Температура нагревателя идеальной тепловой машины составляет 227 °С, а охладителя — 27 °С. За один рабочий цикл тепловая машина получает количество теплоты, равное 100Дж. Какую работу совершает рабочее тело идеальной тепловой машины за один цикл?
Решение
Из формулы для КПД можно выразить искомую работу:
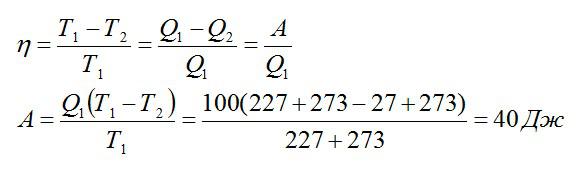
Ответ: 40 Дж.
Задача №3. Работа при выдувании мыльного пузыря
Условие
Определить работу, которую необходимо совершить, чтобы выдуть мыльный пузырь диаметром 10 см.
Решение
Работа, которую нужно совершить, чтобы, выдувая мыльный пузырь, увеличить площадь поверхности мыльной пленки на дельта S, равна:

Здесь сигма – коэффициент поверхностного натяжения для мыльного раствора (берется из таблицы). S – общая площадь двух сферических поверхностей пленки мыльного пузыря (внешней и внутренней). S нулевое – площадь этих поверхностей до выдувания пузыря (этой величиной можно пренебречь).

Ответ: 2,5 мДж.
Задача №4. Графическое представление работы
Условие
Газ расширяется от объёма V1 до объёма V2 один раз изотермически, другой изобарно и третий адиабатно. При каком процессе газ совершает большую работу и при каком газу передаётся большее количество теплоты?

Решение
Работа численно равна площади криволинейной трапеции. Из рисунка очевидно, что работа при изобарном процессе будет максимальной, при адиабатном минимальной, т. е.

Ответ: см. выше.
Задача №5. Работа газа
Условие
Газ совершает круговой процесс, состоящий из нескольких этапов. Сначала газ изохорно охлаждается до температуры, при которой его давление равно P2 = 105 Па. Затем он изобарно охлаждается до состояния, из которого возвращается в начальное состояние таким образом, что его давление изменяется с изменением объема по закону Р = αV (α – постоянная величина). Начальные объем и давление газа известны: V1 = 2 м3, Р1 = 4·105 Па. Нарисовать график данного кругового процесса на РV-диаграмме и найти работу, совершенную газом.
Решение
Сначала выполним рисунок:

Точки состояния газа 1 и 3 лежат на прямой, проходящей через центр координат:

C учетом этого, получаем:

Работа газа в данном случае равна площади треугольника 123:

Подставим найденное ранее значение для V3, преобразуем и подставим значения из условия:

Ответ: 2,25*10^5 Дж.
Вопросы на тему «Работа в термодинамике»
Вопрос 1. Что такое работа в термодинамике?
Ответ. Работа – одна из форм обмена энергией термодинамической системы с окружающими телами. Работа, как и энергия, измеряется в Джоулях.
Вопрос 2. Сформулируйте первое начало термодинамики.
Ответ. Первое начало термодинамики гласит:
Изменение внутренней энергии системы равно сумме совершаемой над системой работы внешних сил и количества теплоты, переданной системе.
У первого начала термодинамики исторически есть несколько формулировок. Одна из них: невозможно построить вечный двигатель первого рода.
Вопрос 3. При каком из изопроцессов работа газа равна нулю?
Ответ. При изохорном процессе объем системы остается неизменным. Следовательно, газ в данном процессе не совершает работу.
Вопрос 4. Как, совершая работу, можно изменить внутреннюю энергию?
Ответ. Если работа совершается над телом (системой), то его внутренняя энергия увеличивается, если же тело само совершает работу, это ведет к уменьшению его внутренней энергии.
Вопрос 5. Как определить работу газа геометрически?
Ответ. Величина работы газа равна площади фигуры под графиком на диаграмме pV
Нужна помощь в решении задач или в выполнении других студенческих заданий? Обращайтесь в профессиональный студенческий сервис.
Спецвыпуск
Г. А.
Белуха
Работа газа в термодинамике
··· Орловский выпуск ···
Г.А.БЕЛУХА,
школа № 4, г. Ливны, Орловская обл.
Работа газа в термодинамике
Методические рекомендации по
изучению темы, 10-й класс
При изучении работы газа в
термодинамике учащиеся неизбежно сталкиваются с
трудностями, обусловленными слабыми навыками
вычисления работы переменной силы. Поэтому к
восприятию этой темы необходимо готовиться,
начиная уже с изучения работы в механике и решая
с этой целью задачи на работу переменной силы
путём суммирования элементарных работ на всём
пути с помощью интегрирования.
Например, при вычислениях работы силы
Архимеда, силы упругости, силы всемирного
тяготения и т.п. надо учиться суммировать
элементарные величины с помощью простейших
дифференциальных соотношений типа dA = Fds.
Опыт показывает, что старшеклассники легко
справляются с этой задачей, – дугу траектории, на
которой сила увеличивается или уменьшается,
нужно разбить на такие промежутки ds, на
которых силу F можно считать постоянной
величиной, а затем, зная зависимость F = F(s),
подставить её под знак интеграла. Например, 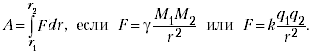
Работа этих сил вычисляется с помощью
простейшего табличного интеграла 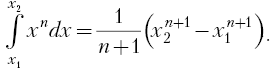
Такая методика облегчает адаптацию
будущих студентов к восприятию курса физики в
вузе и устраняет методические сложности,
связанные с умением находить работу переменной
силы в термодинамике и др.
После того как учащиеся усвоили, что
такое внутренняя энергия и как найти её
изменение, целесообразно дать обобщающую схему:
Усвоив, что работа – это один из
способов изменения внутренней энергии,
десятиклассники легко рассчитывают работу газа
в изобарном процессе. На данном этапе необходимо
подчеркнуть, что сила давления газа на всём пути
не меняется, и по третьему закону Ньютона |F2| = |F1|,
знак работы находим из формулы A = Fs cos![]() . Если
. Если ![]() = 0°, то A > 0,
= 0°, то A > 0,
если ![]() = 180°,
= 180°,
то A < 0. На графике зависимости р(V)
работа численно равна площади под графиком.
Пусть газ расширяется или сжимается
изотермически. Например, газ сжимается под
поршнем, давление изменяется, и в любой момент
времени 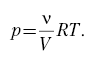
При бесконечно малом перемещении
поршня на dl мы получим бесконечно малое
изменение объёма dV, а давление р можно
считать постоянным. По аналогии с нахождением
механической работы переменной силы, составим
простейшее дифференциальное соотношение dA = pdV,
тогда 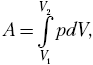 и, зная
и, зная
зависимость р (V), запишем  Это табличный интеграл
Это табличный интеграл
типа  Работа
Работа
газа в этом случае отрицательна, т.к. ![]() = 180°:
= 180°:
![]()
т.к. V2 < V1.
Полученную формулу можно переписать,
используя соотношение 
Для закрепления решим задачи.
1. Газ переходит из состояния 1
(объём V1, давление р1) в
состояние 2 (объём V2, давление р2)
в процессе, при котором его давление зависит от
объёма линейно. Найдите работу газа.
Решение. Построим примерный
график зависимости p от V. Работа равна
площади под графиком, т.е. площади трапеции:
![]()
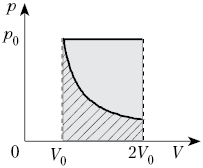
2. Один моль воздуха, находящийся при
нормальных условиях, расширяется от объёма V0
до 2V0 двумя способами – изотермически
и изобарно. Сравните работу, совершённую
воздухом в этих процессах.
Решение
При изобарном процессе Ap = р0![]() V, но р0 =
V, но р0 = ![]() RT0/V0,
RT0/V0,
![]() V = V0,
V = V0,
следовательно, Ap = ![]() RT0.
RT0.
При изотермическом процессе:
![]()
Сравним: ![]()
Изучив первый закон термодинамики и
его применение к изопроцессам и закрепив
решением задач тему о работе в термодинамике,
учащиеся подготовились к восприятию наиболее
сложной части термодинамики «Работа циклов и КПД
тепловых машин». Этот материал я излагаю в
следующей последовательности: работа циклов –
цикл Карно – КПД тепловых машин – круговые
процессы.
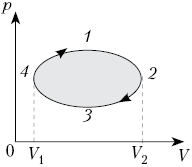 Круговым
Круговым
процессом (или циклом) называется
термодинамический процесс, в результате
которого тело, пройдя ряд состояний,
возвращается в исходное состояние. Если все
процессы в цикле равновесные, то цикл считается
равновесным. Его можно изобразить графически в
виде замкнутой кривой.
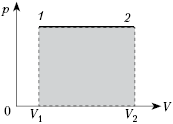
На рисунке показан график зависимости
давления p от объёма V (диаграмма p, V)
для некоторого цикла 1–2–3–4–1. На участках 1–2
и 4–1 газ расширяется и совершает
положительную работу А1, численно
равную площади фигуры V1412V2.
На участке 2–3–4 газ сжимается и совершает
работу А2, модуль которой равен
площади фигуры V2234V1. Полная
работа газ за цикл А = А1 + А2,
т.е. положительна и равна площади фигуры 12341.
Если равновесный цикл изображается
замкнутой кривой на р, V-диаграмме,
которая обходится по часовой стрелке, то работа
тела положительна, а цикл накзывается прямым.
Если замкнутая кривая на р, V-диаграмме
обходится против часовой стрелки, то газ
совершает отрицательную работу за цикл, а цикл
называется обратным. В любом случае модуль
работы газа за цикл равен площади фигуры,
ограниченной графиком цикла на р, V-диаграмме.
В круговом процессе рабочее тело
возвращается в исходное состояние, т.е. в
состояние с первоначальной внутренней энергией.
Это значит, что изменение внутренней энергии за
цикл равно нулю: ![]() U = 0.
U = 0.
Так как, по первому закону термодинамики, для
всего цикла Q = ![]() U + A, то Q = A.
U + A, то Q = A.
Итак, алгебраическая сумма всех количеств
теплоты, полученных за цикл, равна работе тела за
цикл: Aц = Qн + Qх = Qн
– |Qх|. 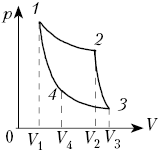
Рассмотрим один из круговых процессов
– цикл Карно. Он состоит из двух изотермических и
двух адиабатических процессов. Пусть рабочим
телом является идеальный газ. Тогда на участке 1–2
изотермического расширения, согласно первому
закону термодинамики, всё получаемое газом тепло
идёт на совершение положительной работы: Q12 = A12.
То есть нет никаких потерь тепла в окружающее
пространство и никакого изменения внутренней
энергии: ![]() U = 0,
U = 0,
т.к. T12 = const (потому что газ –
идеальный).
На участке 2–3 адиабатного
расширения газ совершает положительную работу
за счёт изменения внутренней энергии, т.к. Qад = 0
= ![]() U23 + Aг23
U23 + Aг23 ![]() Aг23 = –
Aг23 = –![]() U23.
U23.
Здесь также нет потерь тепла, по определению
адиабатного процесса.
На участке 3–4 над газом
совершается положительная работа внешней силой,
но он не нагревается (изотермический процесс).
Благодаря достаточно медленно протекающему
процессу и хорошему контакту с холодильником газ
успевает отдавать получаемую за счёт работы
энергию в виде тепла холодильнику. Сам же газ
совершает при этом отрицательную работу: Q34 = Aг34
< 0.
На участке 4–1 газ адиабатно (без
теплообмена) сжимается до исходного состояния.
При этом он совершает отрицательную работу, а
внешние силы – положительную: 0 = ![]() U41 + Aг41
U41 + Aг41
![]() Aг41 = –
Aг41 = –![]() U41.
U41.
Таким образом, за цикл газ получает
тепло только на участке 1–2, изотермически
расширяясь:
![]()
Холодильнику тепло отдаётся только
при изотермическом сжатии газа на участке 3–4:
![]()
Согласно первому закону термодинамики
Aц = Qн – |Qx|;
поэтому
![]()
КПД машины, работающей по циклу Карно,
найдём по формуле 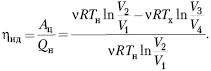
Согласно закону Бойля–Мариотта для
процессов 1–2 и 3–4, а также уравнению
Пуассона для процессов 2–3 и 4–1, легко
доказать, что ![]()
(Хорошо бы увидеть, как автор это
делает: ведь уравнение Пуассона для диабаты
идеального газа надо ещё получить. – Ред.)
После сокращений получим формулу КПД
тепловой машины, работающей по циклу Карно: ![]()
 Работу тепловых машин, работающих по
Работу тепловых машин, работающих по
обратному циклу, методически правильно, как
показывает опыт, изучать на примере работы
обратного цикла Карно, т.к. он обратим и его можно
провести в обратном направлении: расширять газ
при понижении температуры от Tн до Tx
(процесс 1–4) и при низкой температуре Tx
(процесс 4–3), а затем сжимать (процессы 3–2
и 2–1). Теперь двигатель совершает работу,
чтобы привести в действие холодильную машину.
Рабочее тело отнимает количество теплоты Qx
у продуктов внутри при низкой температуре Tх,
а отдаёт количество теплоты Qн
окружающим телам, за пределами холодильника, при
более высокой температуре Tн. Таким
образом, машина, работающая по обратному циклу
Карно, уже не тепловая, а идеальная холодильная.
Роль нагревателя (отдающего тепло) выполняет
тело с более низкой температурой. Но, сохранив
названия элементов, как в тепловой машине,
работающей по прямому циклу, мы можем
представить блок-схему холодильника в следующем
виде:
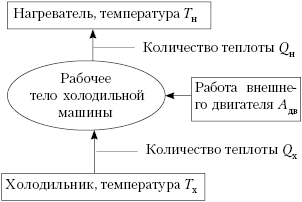
Обратим внимание, что тепло от
холодного тела переходит в холодильной машине к
телу с более высокой температурой не
самопроизвольно, а за счёт работы внешней силы.
Важнейшей характеристикой
холодильника является холодильный коэффициент ![]() , определяющий
, определяющий
эффективность работы холодильника и равный
отношению количества теплоты, отнятого от
холодильной камеры Qх к затраченной
энергии внешнего источника ![]()
За один обратный цикл рабочее тело
получает от холодильника количество теплоты Qх
и отдаёт в окружающее пространство количество
теплоты Qн, что больше Qх на
работу Aдв, совершаемую
электродвигателем над газом за цикл: |Qн| = |Qх| + Адв.
Энергия, затраченная двигателем
(электроэнергия в случае компрессорных
электрических холодильников), идёт на полезную
работу над газом, а также на потери при
нагревании обмоток двигателя электрическим
током QR и на трение в схеме Атр.
Если пренебречь потерями на трение и
джоулево тепло в обмотках двигателя, то
холодильный коэффициент
![]()
Учитывая, что в прямом цикле
![]()
после несложных преобразований
получим:
![]()
Последнее соотношение между
холодильным коэффициентом и КПД тепловой машины,
которая может работать и по обратному циклу,
показывает, что холодильный коэффициент может
быть больше единицы. В этом случае тепла
отнимается от холодильной камеры и возвращается
в комнату больше, чем для этого используется
энергии двигателем.
В случае идеальной тепловой машины,
работающей по обратному циклу Карно (идеального
холодильника), холодильный коэффициент имеет
максимальное значение:
![]()
В реальных холодильниках ![]() т.к. не вся получаемая
т.к. не вся получаемая
двигателем энергия идёт на работу над рабочим
телом, о чём написано выше.
Решим задачу:
• Оцените стоимость изготовления 1 кг
льда в домашнем холодильнике, если температура
испарения фреона –tх °С,
температура радиатора tн °С.
Стоимость одного киловатт-часа электроэнергии
равна Ц. Температура в комнате t.
Дано:
m, c, t, tн, tх,
![]() , Ц.
, Ц.
____________
Д – ?
Решение
Стоимость Д изготовления льда равна
произведению работы электродвигателя на тариф Ц:
Д = ЦА.
Для превращения воды в лёд с
температурой 0 °С необходимо отвести от неё
количество теплоты Q = m(ct + ![]() ). Считаем
). Считаем
приближённо, что над фреоном совершается
обратный цикл Карно с изотермами при
температурах Tн и Tх.
Используем формулы для холодильного
коэффициента: по определению, ![]() = Q/A и для
= Q/A и для
идеального холодильника ![]() ид = Tх/(Tн – Tх).
ид = Tх/(Tн – Tх).
Из условия следует, что ![]()
![]()
![]() ид.
ид.
Решаем совместно три последних
уравнения:
![]()
Разбирая с учащимися эту задачу,
необходимо обратить внимание на то, что основная
работа холодильного устройства идёт не на
охлаждение продуктов, а на поддержание
температуры внутри холодильного шкафа путём
периодической откачки тепла, проникающего
сквозь стенки холодильника.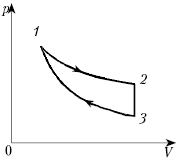
Для закрепления темы можно решить
задачу:
• КПД тепловой машины, работающей по
циклу, состоящему из изотермического процесса 1–2,
изохорического 2–3 и адиабатического 3–1,
равен ![]() , а
, а
разность максимальной и минимальной температур
газа в цикле равна ![]() T. Найдите работу, совершённую
T. Найдите работу, совершённую ![]() моль одноатомного
моль одноатомного
идеального газа в изотермическом процессе.
Решение
При решении задач, в которых
фигурирует КПД цикла, полезно предварительно
проанализировать все участки цикла, используя
первый закон термодинамики, и выявить участки,
где тело получает и отдаёт тепло. Проведём
мысленно ряд изотерм на р, V-диаграмме.
Тогда станет ясно, что максимальная температура
в цикле на изотерме, а минимальная – в т. 3.
Обозначим их через T1 и T3
соответственно.
На участке 1–2 изменение
внутренней энергии идеального газа U2 – U1 = 0.
По первому закону термодинамики, Q12 = (U2 – U1) + А12.
Так как на участке 1–2 газ расширялся, то
работа газа А12 > 0. Значит, и
подведённое к газу количество теплоты на этом
участке Q12 > 0, причём Q12 = А12.
На участке 2–3 работа газа равна
нулю. Поэтому Q23 = U3 – U2.
Воспользовавшись выражениями U2=
![]() cVT1
cVT1
и тем, что T1 – T3 = ![]() T, получим Q23 = –
T, получим Q23 = –![]() cV
cV ![]() T < 0.
T < 0.
Это означает, что на участке 2–3 газ получает
отрицательное количество теплоты, т.е. отдаёт
тепло.
На участке 3–1 теплообмена нет,
т.е. Q31 = 0 и, по первому закону
термодинамики, 0 = (U1 – U3) + A31.
Тогда работа газа
A31 = U3 – U1 = ![]() cV(T3 –T1) = –
cV(T3 –T1) = –![]() cV
cV ![]() T.
T.
Итак, за цикл газ совершил работу A12 + А31 = А12 – ![]() cV
cV ![]() T и получил
T и получил
тепло только на участке 1–2. КПД цикла
![]()
Так как ![]() то работа газа на изотерме равна
то работа газа на изотерме равна
![]()
Геннадий Антонович Белуха –
заслуженный учитель РФ, педагогический стаж 20
лет, ежегодно его ученики занимают призовые
места на различных этапах всероссийской
олимпиады по физике. Хобби – компьютерная
техника.

Осевое сечение тепловой машины Карно. На этой диаграмме abcd — цилиндрический сосуд, cd — подвижный поршень, а A и B — тела с постоянной температурой. Сосуд может контактировать с любым телом или отодвигаться от обоих (как здесь)[1].
Тепловая машина Карно или тепловой двигатель Карно[2] — это теоретический двигатель, работающий по циклу Карно. Базовая модель этого двигателя была разработана Сади Карно в 1824 году. Модель теплового двигателя Карно была графически расширена Бенуа Полем Эмилем Клапейроном в 1834 году и математически исследована Рудольфом Клаузиусом в 1857 году, работа, которая привела к фундаментальной термодинамической концепции энтропии.
Каждая термодинамическая система существует в определённом состоянии. Термодинамический цикл происходит, когда система проходит через серию различных состояний и, наконец, возвращается в исходное состояние. В процессе прохождения этого цикла система может выполнять работу над своим окружением, тем самым действуя как тепловой двигатель.
Тепловой двигатель действует, передавая энергию из более тёплой области в более холодную область пространства и, при этом, преобразуя часть этой энергии в механическую работу. Цикл также может быть обратным. На систему можно воздействовать внешней силой, и в процессе она может передавать тепловую энергию от более холодной системы к более тёплой, тем самым действуя как холодильник или как тепловой насос, а не как тепловая машина.
Диаграмма Карно[править | править код]
На соседней диаграмме из работы Карно 1824 года «Размышления о движущей силе огня»[3] изображены «два тела A и B, каждое из которых поддерживается при постоянной температуре, причем температура A выше, чем у B. Мы можем отдавать тепло этим телам или забирать тепло без изменения их температуры. Эти тела выполняют функции двух неограниченных резервуаров теплорода. Первое мы назовем печью, а второе — холодильником»[4]. Затем Карно объясняет, как мы можем получить движущую силу, то есть «работу», перенося определённое количество тепла от тела A к телу B. Подобная машина, приводимая в движение внешней силой, также может действовать как холодильник, совершая цикл в обратном направлении.
Современная диаграмма[править | править код]

Схема тепловой машины Карно (современная) — где количество тепла QH течёт из высокотемпературного нагревателя TH через вещество «рабочего тела», а оставшееся тепло QC течёт в охладитель TC, таким образом заставляя рабочее вещество совершать механическую работу W над окружающей средой посредством циклов сжатия и расширения.
На предыдущем изображении показана оригинальная диаграмма в виде поршня и цилиндра, которую Карно использовал при обсуждении своих идеальных двигателей. На рисунке справа показана блок-схема типового теплового двигателя, такого как двигатель Карно. На схеме «рабочее тело» (система), термин, введенный Клаузиусом в 1850 году, может быть любым твердым, жидким или газообразным веществом, через которое тепло Q может вводиться или передаваться для производства работы. Карно постулировал, что рабочим телом может быть любое вещество, способное к расширению, например пары воды, пары спирта, пары ртути, постоянный газ или воздух и так далее. Хотя в те ранние годы двигатели выпускались в различных конфигурациях, обычно теплотаQH подводилась с помощью котла, в котором вода кипятилась над топкой; теплотаQC отнималась потоком холодной проточной воды в виде конденсатора, который являлся отдельной частью двигателя. Выходная работа W представляет движение поршня, когда он используется для поворота кривошипа, который, в свою очередь, обычно использовался для приведения в действие насоса, использовавшегося для откачки воды из затопленных соляных шахт. Карно определял работу как «поднятие тяжестей на высоту».
Цикл Карно[править | править код]
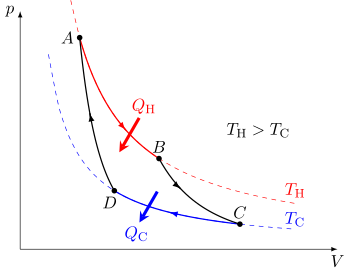
Рисунок 1: Цикл Карно, изображенный на PV-диаграмме, чтобы проиллюстрировать проделанную работу.
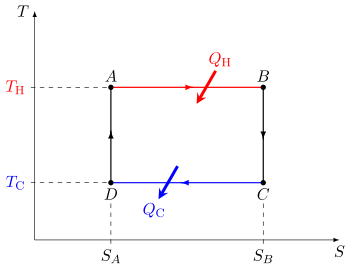
Рисунок 2: Цикл Карно, действующий как тепловая машина, проиллюстрированный на диаграмме температура-энтропия. Цикл происходит между горячим резервуаром при температуре T H и холодным резервуаром при температуре T C. Вертикальная ось — температура, горизонтальная ось — энтропия.
Цикл Карно при работе в качестве теплового двигателя состоит из следующих этапов:
- Обратимое изотермическое расширение газа при «горячей» температуре TH (изотермическое добавление или поглощение тепла). На этом этапе (от A до B) газ расширяется, и он воздействует на окружающую среду. Температура газа не изменяется во время процесса, и поэтому расширение является изотермическим. Расширение газа происходит за счёт поглощения тепловой энергии QH и энтропии.
из высокотемпературного резервуара.
- Изоэнтропическое (обратимое адиабатическое) расширение газа (изоэнтропическая работа на выходе). Для этого этапа (от B до C) предполагается, что поршень и цилиндр имеют теплоизоляцию, поэтому они не получают и не теряют тепло. Газ продолжает расширяться, воздействуя на окружающую среду и теряя эквивалентное количество внутренней энергии. Расширение газа вызывает его охлаждение до «холодной» температуры TC. Энтропия остается неизменной.
- Обратимое изотермическое сжатие газа при «холодной» температуре, ТС. (отвод изотермического тепла) (от C до D) Теперь газ подвергается воздействию холодного температурного резервуара, в то время как окружающая среда воздействует на газ, сжимая его (например, посредством обратного сжатия поршня), вызывая при этом некоторое количество тепловой энергии QC и энтропии
перетечь из газа в низкотемпературный резервуар. (Это то же количество энтропии, которое было поглощено на шаге 1.) Эта работа меньше, чем работа, выполняемая с окружающей средой на этапе 1, потому что она происходит при более низком давлении, учитывая отвод тепла в холодный резервуар, когда происходит сжатие (то есть сопротивление сжатию ниже на этапе 3, чем сила расширения на шаге 1).
- Изоэнтропическое сжатие газа. (D — A) И снова предполагается, что поршень и цилиндр теплоизолированы, а резервуар для холодной температуры удален. Во время этого шага окружающая среда продолжает работу по дальнейшему сжатию газа, при этом температура и давление повышаются теперь, когда радиатор был удален. Эта дополнительная работа увеличивает внутреннюю энергию газа, сжимая его и вызывая повышение температуры до TH. Энтропия остается неизменной. В этот момент газ находится в том же состоянии, что и в начале шага 1.
Теорема Карно[править | править код]
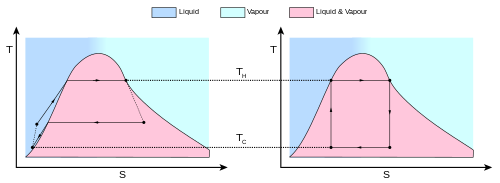
Реальные идеальные двигатели (слева) по сравнению с циклом Карно (справа). Энтропия реального материала изменяется с температурой. Это изменение показано кривой на диаграмме TS . На этом рисунке кривая указывает на парожидкостное равновесие (см. Цикл Ренкина). Необратимые системы и потери тепла (например, из-за трения) препятствуют достижению идеала на каждом этапе.
Теорема Карно является формальным утверждением этого факта: КПД любого теплового двигателя работающего по циклу Карно между двумя тепловыми резервуарами, независимо от устройства двигателя, является функцией только температур холодного и горячего резервуаров и всегда больше КПД любого другого теплового двигателя работающего по иному циклу между теми же резервуарами.

Объяснение Эта максимальная эффективность 
- W — работа, совершаемая системой,
тепло, поступающее в систему,
— абсолютная температура холодного резервуара, а
— абсолютная температура горячего резервуара.
Следствие теоремы Карно гласит, что: все реверсивные двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны.
Эффективность η максимальна, когда весь циклический процесс является обратимым. Это означает, что полная энтропия полной системы (энтропии горячей печи, «рабочего тела» теплового двигателя и холодного стока) остается постоянной, когда «рабочее тело» завершает один цикл и возвращается в исходное состояние. (В общем случае полная энтропия этой комбинированной системы увеличилась бы в общем необратимом процессе).
Поскольку «рабочая жидкость» возвращается в то же состояние после одного цикла, а энтропия системы является функцией состояния; изменение энтропии системы «рабочей жидкости» равно 0. Таким образом, это означает, что полное изменение энтропии печи и стока равно нулю, чтобы процесс был обратимым, а КПД двигателя был максимальным. Этот вывод проводится в следующем разделе.
Коэффициент полезного действия (COP) теплового двигателя обратно пропорционален его КПД.
КПД реальных тепловых машин[править | править код]
Для настоящего теплового двигателя полный термодинамический процесс обычно необратим. Рабочая жидкость возвращается в исходное состояние после каждого цикла, и, таким образом, изменение энтропии жидкостной системы равно 0, но сумма изменений энтропии в горячем и холодном резервуаре в этом циклическом процессе больше 0.
Внутренняя энергия жидкости — это функция состояния, поэтому её полное изменение за один цикл равно 0. Таким образом, общая работа, выполняемая системой W, равна теплу, подводимому к системе. 


|
Для реальных двигателей — пути 1 и 3 цикла Карно; в котором тепло поглощается «рабочей жидкостью» из горячего резервуара и передаётся ей соответственно в холодный резервуар; больше не остаются идеально обратимыми, и существует разница температур между температурой резервуара и температурой жидкости во время теплообмена.
При передаче тепла от горячего резервуара при 



|
где температура жидкости T всегда немного меньше, чем 
Итак, получилось бы:

|
Точно так же во время передачи тепла из жидкости в холодный резервуар для величины изменения общей энтропии 
 , ,
|
где во время этого процесса передачи тепла в холодный резервуар температура жидкости T всегда немного больше, чем 
Мы рассмотрели здесь только величину изменения энтропии. Поскольку полное изменение энтропии жидкой системы для циклического процесса равно 0, то

|
Предыдущие три уравнения в совокупности дают:

|
Уравнения (2) и (7) вместе дают

|
Следовательно,

|
где 



Следовательно, эффективность реального двигателя всегда ниже, чем у идеального двигателя Карно.
Уравнение (7) означает, что полная энтропия всей системы (два резервуара + жидкость) увеличивается для реального двигателя, потому что прирост энтропии холодного резервуара как 



Согласно второй теореме «КПД двигателя Карно не зависит от природы рабочего тела».
Примечания[править | править код]
- ↑ Figure 1 in Carnot (1824, p. 17) and Carnot (1890, p. 63). In the diagram, the diameter of the vessel is large enough to bridge the space between the two bodies, but in the model, the vessel is never in contact with both bodies simultaneously. Also, the diagram shows an unlabeled axial rod attached to the outside of the piston.
- ↑ In French, Carnot uses machine à feu, which Thurston translates as heat-engine or steam-engine. In a footnote, Carnot distinguishes the steam-engine (machine à vapeur) from the heat-engine in general. (Carnot, 1824, p. 5 and Carnot, 1890, p. 43)
- ↑ Sometimes translated as Reflections on the Motive Power of Heat. Дата обращения: 26 апреля 2021. Архивировано 23 января 2020 года.
- ↑ English translation by Thurston (Carnot, 1890, p. 51-52).
2.4.1. Работа тепловых машин. Цикл Карно
Процессы в системе
бывают обратимые и необратимые.
Термодинамический процесс называется
обратимым,
если он может происходить как в прямом,
так и в обратном направлении. Если такой
процесс происходит сначала в прямом, а
затем в обратном направлении и система
возвращается в исходное состояние, то
в окружающей среде и в этой системе не
происходит никаких изменений. Всякий
процесс, не удовлетворяющий этим
условиям, является необратимым.
Круговым
процессом (или циклом)
называется процесс, при котором система,
пройдя через ряд состояний, возвращается
в исходное. На диаграмме процессов цикл
изображается замкнутой кривой (рис 84.)
Цикл, совершаемый идеальным газом, можно
разбить на процессы расширения (1—2)
и сжатия
(2—1) газа.
Работа расширения (определяется площадью
фигуры la2V2V1l)
положительна
(dV>0),
работа сжатия (определяется площадью
фигуры 2blV1V22)
отрицательна
(dV<0).
Следовательно, работа, совершаемая
газом за цикл, определяется площадью,
охватываемой замкнутой кривой. Если за
цикл
совершается
положительная работа (цикл протекает
по часовой стрелке), то он называется
прямым
(рисунок –
2.26,а), если
за цикл совершается отрицательная
работа (цикл протекает против часовой
стрелки), то он называется обратным
(рисунок –
2.26,6).
Прямой цикл
используется в тепловых
машинах, совершающих механическую
работу за счет полученной извне теплоты.
Обратный цикл используется в холодильных
машинах, где за счет работы внешних сил
теплота переносится к телу с более
высокой температурой. В результате
кругового процесса система возвращается
в исходное состояние и, следовательно,
полное изменение внутренней энергии
газа равно нулю. Поэтому первое начало
термодинамики для кругового процесса
|
Q=∆U+A=A, |
(2.60), |
т.е. работа,
совершаемая за цикл, равна количеству
полученной извне теплоты. Однако в
результате кругового процесса где Q1–
количество теплоты, полученное системой,
Q2
– количество
теплоты, отданное системой. Поэтому
термический
коэффициент полезного действия
для кругового процесса
|
η |
(2.61). |
Тепловая машина,
кроме тела с высокой температурой Ti
(нагреватель),
за счет внутренней энергии которого
будет совершаться работа, и холодильника
с температурой Т2,
служащего
для отвода части теплоты, должна иметь
еще «рабочее тело». Действие тепловой
машины происходит по следующей схеме.
От теплового резервуара (нагревателя
с температурой T1)
теплота
передается рабочему телу и частично
преобразуется последним в работу;
частично же теплота от рабочего тела
передается холодильнику (с температурой
Т2),
а рабочее
тело возвращается в исходное состояние.
В соответствии с первым началом
термодинамики необходимо, чтобы
выполнялось равенство dQ1=dA+dQ2
. Работа за
один цикл зависит от его формы и измеряется
площадью, охваченной кривой, описывающей
процесс.
Если ввести
коэффициент
полезного действия
такой машины
как отношение η
= dA/dQ1
, то
нетрудно получить следующее выражение
для КПД
идеальной машины:
|
η |
или
|
η |
(2.62). |
Итак, КПД идеальной
машины определяется только температурами
нагревателя и холодильника. Мощность
тепловой машины определяется произведением
работы, совершаемой за один цикл, на
число циклов, происходящих за 1 с. Одной
из возможных схем действия такой машины
является работа по так называемому
циклу Карно, впервые рассмотренному
Сади Карно (1796—1832). На рисунке – 2.27
представлен цикл тепловой машины,
работающей по циклу Карно. Он состоит
из двух адиабат и двух изотерм. Работа,
совершаемая рабочим телом за цикл,
положительна. При переводе системы из
состояния 1
в состояние 2
нагреватель отдает рабочему телу
количество теплоты Q1
при температуре Т1,
а при переводе системы из состояния 3
в состояние
4
рабочее тело передает холодильнику
количество теплоты Q2
при температуре
Т2.
Рассмотрим более
подробно работу идеальной машины Карно,
в которой рабочим телом служит идеальный
газ, взятый в количестве 1 моль. На участке
1, 2 рабочее
тело находится в контакте с
|
|
|
|
|
Рисунок |
Рисунок |
нагревателем.
Происходит изотермическое расширение
газа от объема V1
до объема
V2.
Количество
теплоты, переданное газу на этом участке,
равно:
|
Q1 |
(2.63). |
Эта теплота
полностью переходит в работу расширения.
На участке 3,
4 газ
изотермически сжимают при температуре
Т2.
При этом
сжатии холодильнику отдается количество
теплоты, равное:
|
Q2 |
(2.64). |
Адиабатическим
сжатием на участке 4,
1 рабочее
тело приводят в исходное состояние. Так
как внутренняя энергия рабочего тела
за цикл не меняется, то алгебраическая
сумма количеств теплоты, переданных
газу, и работы, совершенной при его
расширении и сжатии, должна быть равна
нулю. На адиабатных участках работы
расширения и сжатия газа взаимно
компенсирую друг друга, так как процесс
идет между двумя изотермами с температурами
T1
и T2.
Поэтому работа, совершаемая газом при
изотермических процессах, является
полезной работой; она равна:
|
A |
(2.65) |
или с учетом
выражений для Q1
и Q2:
|
A= |
(2.66). |
Зная выражение
для полезной работы, нетрудно найти КПД
машины, работающей по циклу Карно:
|
η |
(2.67). |
Из уравнений
Пуассона, описывающих процессы 1,
4 и 2, 3, нетрудно
найти связь между объемами:
|
|
(2.68). |
Поэтому для КПД
машины получаем:
|
η |
(2.69), |
т. е. КПД обратимого
цикла Карно равен КПД идеальной тепловой
машины и является наибольшим возможным
в заданном интервале температур (Т1,Т2).
Кроме тепловых
машин, в технике и быту широкое
распространение получили холодильные,
машины — устройства, в которых за счет
внешней механической работы теплота
передается от тела с меньшей температурой
телу с более высокой температурой.
Идеальной холодильной машиной может
служить машина Карно, работающая по
обращенному циклу. В обращенном цикле
Карно рабочее тело проходит те же
промежуточные состояния, что и в прямом
цикле, только в обратном направлении.
Результатом обращенного цикла Карно
будет перенос теплоты от холодного тела
к более нагретому за счет совершения
работы внешними телами.
КПД идеального
цикла Карно не зависит от рода рабочего
тела (теорем
Карно). Это
можно доказать с помощью следующего
мысленного эксперимента. Представим
себе, что одна из машин Карно (с идеальным
газом) работает по прямому циклу Карно
и приводит в действие вторую машину,
где рабочим телом служит какое-либо
вещество, не являющееся идеальным газом.
При этом обе машины работают с одними
и теми же резервуарами теплоты (с
температурами Т1
и Т2).
Пусть КПД
первой машины есть η1,
а второй (при прямом цикле) — η2.
Совершая прямой
цикл, первая машина получает из резервуара
1
количество теплоты Q1
и отдает
резервуару 2
количество
теплоты Q2.
Работа машины
A=Q1—Q2
затрачивается
на приведение в действие второй машины.
Вторая машина, совершая обратный цикл,
отдаст резервуару 1
количество
теплоты Q1,
а у резервуара
2 отнимет
количество теплоты Q2.
Если КПД машин неодинаков (например,
η1<η2),
то Q11≠Q1.
Сделав
частоты циклов n1
и п1‘
различными
{всегда между машинами можно поставить
редуктор, меняющий число их оборотов в
единицу времени), можно добиться,
например, равенства: п1‘
Q11
= n1
Q1.
При этом
резервуар 1
не претерпит
никаких изменений. Но в резервуаре 2
произойдут
изменения: первая машина отдаст ему
количество теплоты n1Q2,.
а вторая заберет количество теплоты
п1‘Q21
которое
отлично от n1Q2,
так как не равны КПД машин. Следовательно,
наша система, не получая теплоты извне,
совершит работу за счет отнятия теплоты
от резервуара 2,
что противоречит законам термодинамики.
Предположив, что
η1<η2.
мы поменяем
роли машин и придем к такому же невозможному
результату. Следовательно, остается
допустить, что оба КПД одинаковы и КПД
идеального цикла Карно не зависит от
рода рабочего тела.