Как найти работу физика количество теплоты

Физика, 10 класс

Урок 23. Внутренняя энергия. Работа. Количество теплоты

Список вопросов, рассмотренных в уроке: внутренняя энергия; способы изменения внутренней энергии; различные виды теплообмена; уравнение теплового баланса; работа в термодинамике; нахождение численного значения работы в различных тепловых процессах.

Глоссарий по теме

Термодинамическая система представляет собой систему тел, которые взаимодействуют и обмениваются энергией и веществом.

Состояние равновесия – это состояние системы, в которой нет теплообмена между телами, составляющими систему.

Термодинамический процесс – процесс изменения состояния системы, который изменяет параметры системы.

Внутренняя энергия представляет собой сумму кинетической энергии хаотичного теплового движения и потенциальной энергии взаимодействия всех молекул, составляющих тело.

Теплоемкость представляет собой энергию, которая численно равна количеству тепла, которое выделяется или поглощается, когда температура тела изменяется на 1 К.

Теплопередача- это передача энергии от одного тела другому без выполнения работы.

Количество тепла является количественной мерой изменения внутренней энергии во время теплообмена.

Работа в термодинамике – это взаимодействие системы с внешними объектами, в результате чего изменяются параметры системы.

Список литературы

Г.Я. Мякишев., Б. Буховцев., Н. Н. Соцкий. Физика.10. Учебник для образовательных организаций М .: Просвещение, 2017. – С. 243-254.

Рымкевич А.П. Сборник задач по физике. 10-11 класс М.: Дрофа, 2009.- с.75-84

Основное содержание урока

Внутренняя энергия тела – это полная энергия всех молекул, которые его составляют. Внутренняя энергия идеального газа пропорциональна его температуре.

U = 3/2 · ν · R · T

Чтобы изменить внутреннюю энергию вещества, надо сообщить ему некоторое количество тепла или совершить работу.

Работа в термодинамике равна изменению внутренней энергии системы: A = ΔU.

Работа газа в изобарном процессе равна A = P · ΔV. Если газ расширяется, то А > 0, если газ сжимается, то А < 0.

Кроме того, работа газа может быть определена с использованием графика давления в зависимости от объема.

Работа газа численно равна площади под графиком давления.

Количество теплоты – это энергия, которую система получает или теряет во время теплообмена.

Количество тепла для различных термических процессов определяется по-разному.

При нагревании и охлаждении: Q = c_ ∙ m ∙ ΔT;

Во время плавления и кристаллизации: Q = ℷ ∙ m;

Во время испарения и конденсации; Q = r ∙ m;

При сжигании: Q = q ∙ m.

Для замкнутой и адиабатически изолированной системы тел выполняется уравнение теплового баланса: Q1 + Q2 + … + Qn = 0

Выражение для внутренней энергии одноатомного идеального или разреженного реального газа имеет следующий вид:

U = 3/2 ν ∙ R ∙ T

Для идеального газа из молекул с двумя, тремя или более атомами необходимо учитывать кинетическую энергию вращения молекул (они больше не могут считаться материальными точками), поэтому выражение для их внутренней энергии отличается от U = 3/2 ν ∙ R ∙ T числовым коэффициентом.

Для двухатомного газа (например, O2, CO и т. д.):

U = 5/2 ν ∙ R ∙ T

Для газа с тремя атомами или более (например, O3, CH4):

U = 3ν · R · T

Изменить внутреннюю энергию вещества можно, передав ему некоторое количество тепла или выполнить над ним работу.

Существует три типа теплопередачи:

1) Теплопроводность представляет собой процесс переноса энергии от более теплого тела к менее нагретому телу с прямым контактом или от более нагретых частей тела к менее нагретым, осуществляемый хаотично движущимися частицами тела (атомы, молекулы, электроны , и т.д.). Простым примером является нагревание чашки, в которую выливают горячий чай.

2) Конвекция – это своего рода передача тепла, в которой внутренняя энергия передается снизу вверх струями или потоками жидкости или газа. Пример: нагревание воды в чайнике, который стоит на горячей плите.

3) Лучистый обмен или излучение – это процесс передачи энергии через электромагнитное излучение. Простой пример: солнечный свет.

Механическая работа изменяет механическую энергию тела. Термодинамическая работа изменяет внутреннюю энергию газа.

Если газ расширяется, то работа газа считается положительной. Если он сжат, то отрицательной.

Формула для нахождения работы газа в изобарном процессе имеет следующий вид:

A = p · ΔV

Для изотермического процесса формула принимает следующий вид: A = ν ∙ R ∙ T ∙ ln⁡ (V_2 / V_1)

Разбор тренировочных заданий

1. Объём газа, расширяющегося при постоянном давлении 100 кПа, увеличился на 20 литров. Работа, выполняемая газом в этом процессе, – _____.

Варианты ответов:

2000 Дж;

20 000 Дж;

200 Дж;

50 МДж.

Правильный вариант / варианты (или правильные комбинации вариантов): 3) 2000 Дж.

Совет: используйте формулу работы.

2. Чтобы из 5 кг снега, при температуре 0ºС, получить воду при 20ºС, необходимо сжигать в печке с КПД 40% __ кг дров.

Решение: при сгорании дров выделится количество теплоты:

из этого количества на полезную работу пойдёт только:

Для плавления снега необходимо количество теплоты:

для нагревания воды понадобится:

Согласно уравнению теплового баланса:

Отсюда следует:

Подставим числовые значения в формулу:

Ответ: 0,5175 кг.

Содержание:

Работа в термодинамике:

В 9 классе вы узнали, что работа силы (механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. Работу силы рассматривают как меру изменения энергии физической системы. А как определить работу в термодинамике? Как может быть выражена эта работа через макроскопические параметры — давление и об1

Рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, закрытом подвижным поршнем (рис. 52).

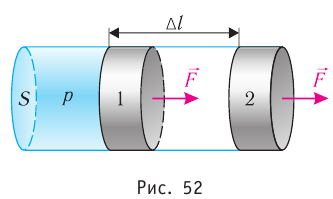
Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением р, которое газ оказывает на них. Допустим, что в результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние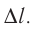

Модуль силы давления газа, действующей на поршень, F = pS. Эта сила совершает работу по перемещению поршня

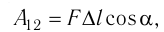 (10.1)

где а — угол между направлениями силы и перемещения. В рассматриваемом примере а = 0, тогда

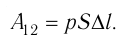
Произведение 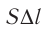определяет приращение объёма 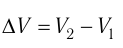(см. рис. 52), поэтому работа газа при его изобарном расширении

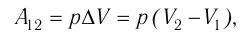 (10.2)

где 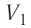— начальный объём газа, 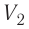— объём газа в конечном состоянии.

Так как давление р газа всегда величина положительная, из формулы (10.2) следует, что, если газ расширяется 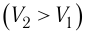, работа, совершённая силой давления газа, положительная (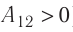), а в случае сжатия (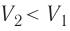) работа отрицательная ().

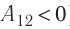Процесс медленного изобарного сжатия газа из состояния 2 с начальным объёмом 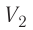в состояние 1 с конечным объёмом 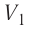можно характеризовать работой 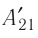внешних сил над газом:
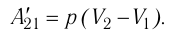 (10.З)

Из сравнения равенств (10.2) и (10.3) вытекает соотношение между работой 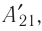у совершённой внешними силами, и работой 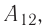совершённой силой давления газа: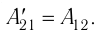Это соотношение согласуется с третьим законом Ньютона (внешняя сила 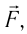действующая на газ со стороны поршня, имеет
направление, противоположное силе давления 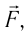действующей на поршень со стороны газа). Из формулы (10.3) видно, что работа, совершённая внешними силами, положительная 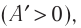если происходит сжатие газа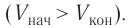
Если газ расширяется 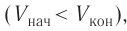), то работа, совершённая внешними силами отрицательная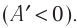

Геометрическое толкование работы

Построим график зависимости давления газа от его объёма при р = const. Как видно из рисунка 53, при изобарном расширении газа работа, совершённая силой давления газа, численно равна площади прямоугольника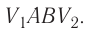

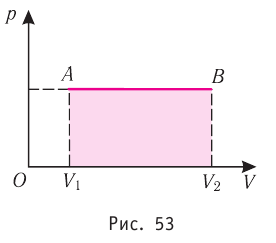
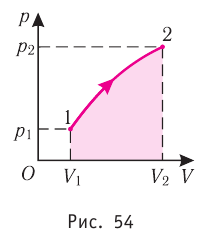
Если процесс перехода газа из начального состояния в конечное не является изобарным, то работа, совершённая силой давления газа при изменении его объёма от 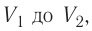численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов 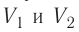(рис. 54).

Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, снова возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 55). Работа, совершаемая системой при циклическом процессе, или работа цикла, равна площади фигуры, ограниченной линиями, которые изображают цикл: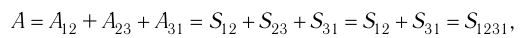

где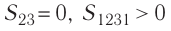 на рисунке 55, а и 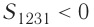на рисунке 55, б.

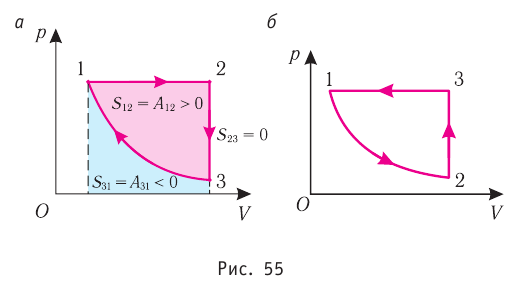
Если «кривая расширения» (изобара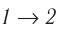) (см. рис. 55, а) расположена выше «кривой сжатия» (изотерма 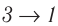), то полная работа, совершённая системой за цикл (работа цикла), положительная. Если же, как изображено на рисунке 55, б, «кривая сжатия» (изобара 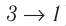) расположена выше «кривой расширения» (изотерма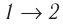), то работа цикла отрицательная.

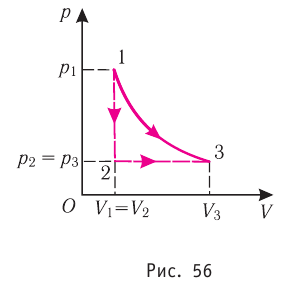
Из рисунка 56 видно, что численное значение работы цикла определяется не только начальным и конечным состояниями системы, но и видом процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения, либо сначала изохорно понизив его давление до значения 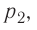а затем изобарно увеличив его объём от значения 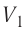до значения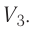

Как видно из рисунка 56, в первом случае работа, совершённая силами давления газа, больше, чем во втором. Следовательно, работа, совершаемая при переходе термодинамической системы из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.

Количество теплоты и удельная теплоёмкость

Итак, существуют два способа передачи энергии от одного тела к другому. Первый характеризуется передачей энергии в процессе механического взаимодействия тел — механическая энергия одного тела переходит в энергию хаотического движения частиц вещества другого тела или, наоборот, убыль энергии хаотического движения частиц вещества одного тела сказывается на увеличении механической энергии другого тела. Такую форму передачи энергии в термодинамике (как и в механике) называют работой. Так, например, в рассмотренной нами ранее термодинамической системе (газ в цилиндрическом сосуде под поршнем) расширение газа приводит к перемещению поршня. При этом убыль внутренней энергии газа равна работе, совершённой силой давления газа, под действием которой поршень переместился.

Второй способ передачи энергии осуществляется при непосредственном обмене энергией между хаотически движущимися частицами взаимодействующих тел. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей энергии частицам более холодного тела. В результате внутренняя энергия первого тела уменьшается, а второго тела увеличивается. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей. Как вы уже знаете, существуют три вида теплопередачи: теплопроводность, конвекция и излучение.

Количественной мерой энергии, переданной телу в процессе теплопередачи, является количество теплоты Q. В СИ единицей количества теплоты является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию (1 кал = 4,19Дж).

Если процесс теплопередачи не сопровождается изменением агрегатного состояния вещества, то
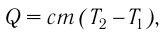 (10,4)
где m — масса тела, 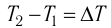— разность температур в конце и в начале процесса теплопередачи, с — удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое получает или отдаёт вещество массой 1 кг при изменении его температуры на 1 К. Удельную
теплоемкость измеряют в джоулях, деленных на килограмм, кельвин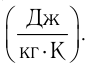
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкости тела. Обозначают теплоёмкость тела С и измеряют в джоулях на кельвин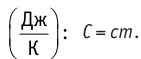Теплоёмкость, в отличие от удельной теплоёмкости, является тепловой характеристикой тела, а не вещества.
 

Удельная теплота плавления

Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления 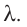Для плавления тела массой m, предварительно нагретого до температуры плавления, ему необходимо сообщить количество теплоты 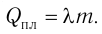При кристаллизации тела выделяется количество теплоты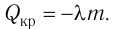

Удельная теплота парообразования

Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Количество теплоты, необходимое для превращения жидкости массой m, предварительно нагретой до температуры кипения, в пар, определяют по формуле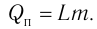Конденсация пара сопровождается выделением количества теплоты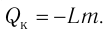

Удельная теплота сгорания топлива

Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания топлива q. Количество теплоты, выделившееся при полном сгорании некоторой массы m топлива, определяют по формуле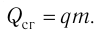Оно передаётся телам, образующим термодинамическую систему, и по отношению к ним является положительной величиной.

Отметим, что в результате теплопередачи могут изменяться как обе составляющие внутренней энергии тела, так и одна из них. При нагревании (охлаждении) изменяются кинетическая энергия хаотического движения частиц, которые составляют тело, и потенциальная энергия их взаимодействия. При плавлении (кристаллизации), кипении (конденсации) изменяется только потенциальная энергия взаимодействия частиц вещества.

При совершении работы также может изменяться как кинетическая, так и потенциальная энергия частиц вещества. Следовательно, как при теплопередаче, так и при совершении работы происходит изменение кинетической и потенциальной энергий частиц вещества, что приводит к изменению внутренней энергии тела.

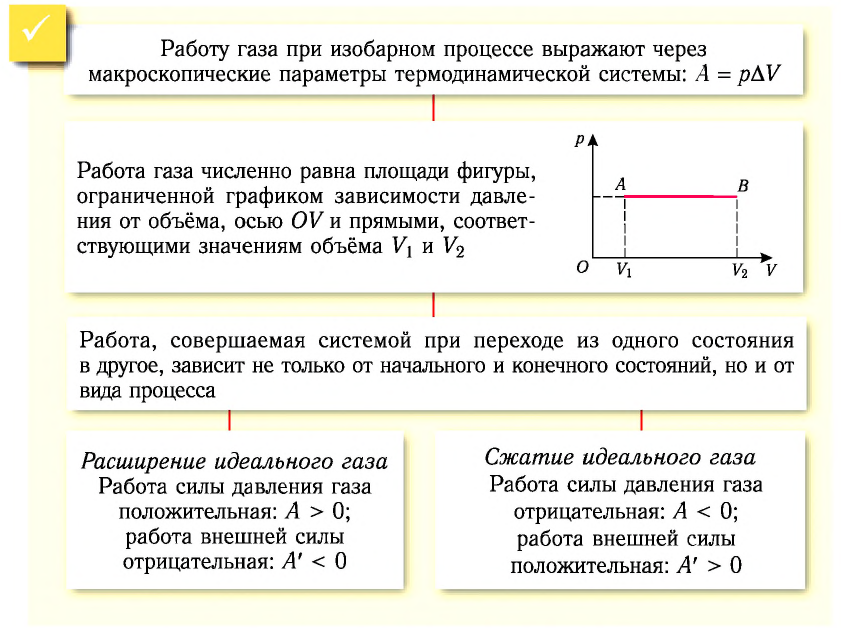
1. Работу газа при изобарном процессе выражают через макроскопические параметры термодинамической системы:

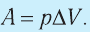
2.    Работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёмов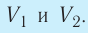

3.    Работа, совершаемая при переходе системы из одного состояния в другое, зависит не только от начального и конечного состояний, но и от вида процесса.

4.    Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей.

Пример №1

Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 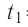= 12 °С до 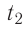= 87 °С, если давление газа и его начальный объём соответственно p=190кПа и 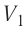= 6,Одм’5.

Дано:

Пример №2

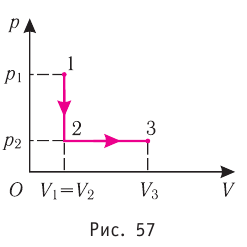
Состояние идеального газа, взятого в количестве v=l,0 моль при температуре 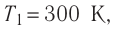изменяется так, как показано на рисунке 57. Определите работу газа в ходе всего процесса, если на изохоре 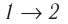его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.

Дано:

v = 1,0 моль

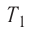= 300 к

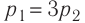
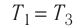
А — ?

Решение. Работа Л газа в ходе всего процесса равна сумме работ на участках 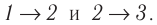Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный 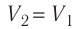), то работа газа 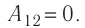. Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (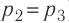)следовательно, работа газ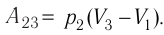а Тогда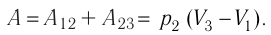
Так как по условию 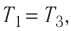то воспользуемся уравнением Клапейрона (5.2):

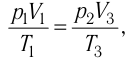откуда  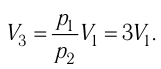Следовательно,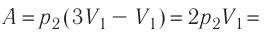
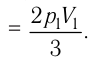Согласно уравнению Клапейрона—Менделеева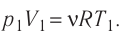

Тогда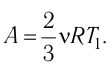

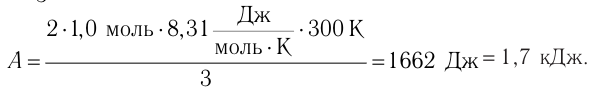
Ответ: А = 1,7 кДж.

Работа в термодинамике

В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.

Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.

Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.

Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.

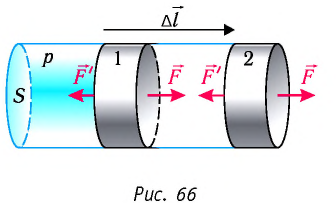
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре 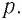В результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние 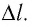Модуль силы давления газа  на поршень 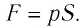Эта сила совершила работу по перемещению поршня, равную    

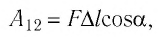
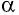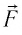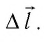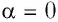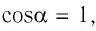где — угол между направлениями силы  и перемещения поршня Поскольку в рассматриваемом примере и то

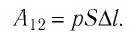
Произведение 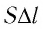 определяет изменение объёма  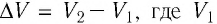— начальный объём газа; 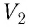— объём газа в конечном состоянии (см. рис. 66).

Таким образом, работа силы давления газа при его изобарном расширении:

Так как давление р газа — величина положительная, то из формулы (12.1) следует, что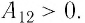

При изобарном расширении газа из состояния 1 в состояние 2 работа силы 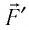(см. рис. 66):

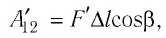
где 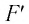— модуль силы, действующей на газ со стороны поршня (внешняя сила); 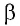— угол между направлениями силы 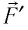и перемещения 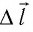поршня.

Перемещение 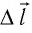поршня одно и то же, а сила давления 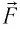газа на поршень и сила давления 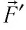поршня на газ — силы, подчиняющиеся третьему закону Ньютона:

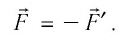
Следовательно, работы 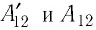отличаются только знаком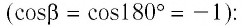

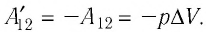
Таким образом, можно сделать следующие выводы.

 

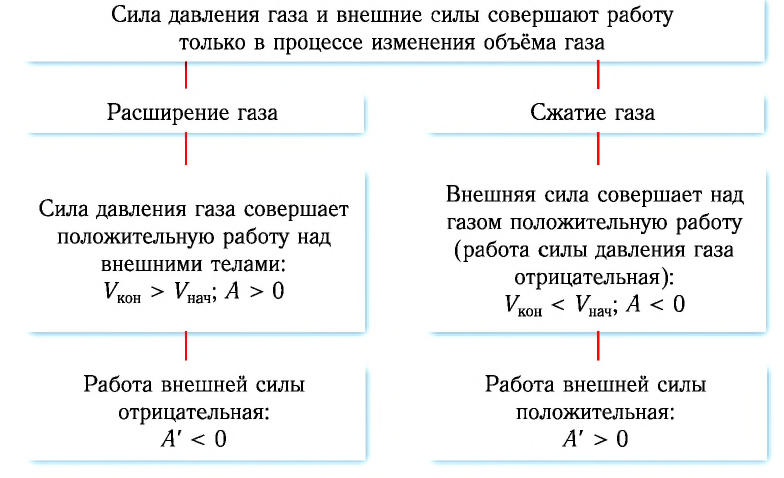
Геометрическое толкование работы:

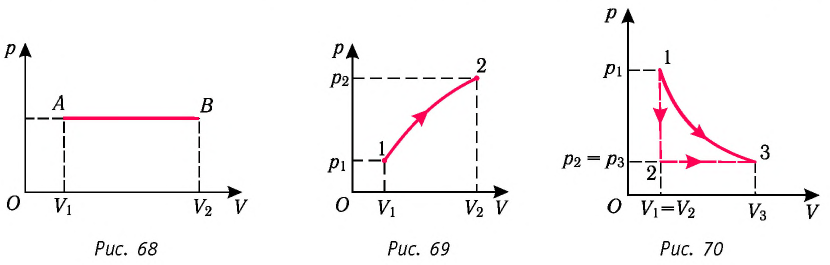
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при 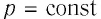(рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника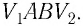 

Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от 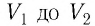численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов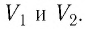 

Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения 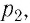а затем изобарно увеличив его объём до значения В первом случае работа газа больше, чем во втором.

Следовательно, работа, совершаемая термодинамическом системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.

Пример №3

Определите работу, совершаемую силой давления идеального газа определённой 200 массы при переходе из состояния 1 в состояние 3 (рис. 73).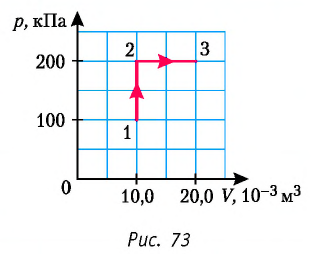   

Решение. 1 способ. Работа А газа в ходе всего процесса равна сумме работ на участках 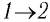и 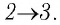Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс 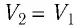), то работа, совершаемая силой давления газа, 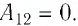В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу

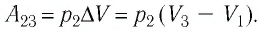
Тогда при переходе из состояния 1 в состояние 3 работа

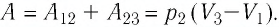
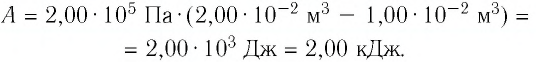
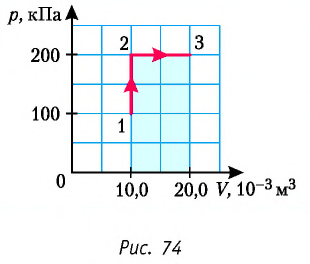
2 способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёма 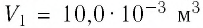и 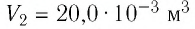(закрашенная область на рисунке 74).

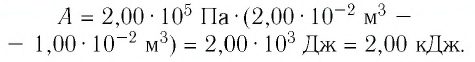
Ответ: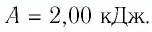

Пример №4

Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 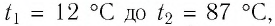если давление газа 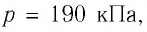а его начальный объём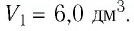

Решение. Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому

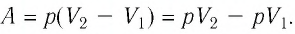
Согласно уравнению Клапейрона—Менделеева,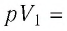
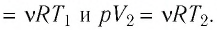Следовательно,

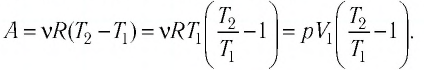
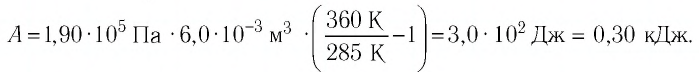
Ответ: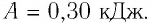

Как определить работу в термодинамике

В конце XVIII в. английский физик Бенджамин Томпсон (граф Румфорд) исследовал тепло, выделяющееся при сверлении бронзовых пушек. Румфорд успевал вскипятить поставленные на пушки котлы с водой за счет тепла, которое выделялось, пока лошади приводили в движение очень тупое сверло. В данном случае энергия механического движения сверла превращалась в энергию хаотического движения молекул бронзы и воды. А можно ли сделать наоборот?

Почему при изменении объема газа изменяется его внутренняя энергия

Внутренняя энергия газа может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ сжимают (газ совершает отрицательную работу) (рис. 37.1) и он при этом не отдает энергию окружающей среде, то скорость движения молекул газа, а соответственно, и внутренняя энергия, и температура газа увеличиваются. И наоборот: если газ расширяется (то есть совершает положительную работу), то скорость движения молекул, температура и внутренняя энергия газа уменьшаются.

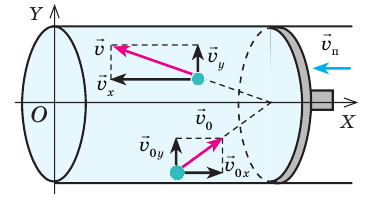
Рис. 37.1. При сжатии газа скорость его молекул после столкновения с поршнем увеличивается (v > 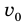) — газ нагревается. (Аналогично увеличивается скорость мяча после удара волейболиста, когда его рука движется навстречу мячу.)

Как вычислить работу газа

Вычислим работу, которую совершает сила давления газа при изменении его объема от 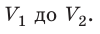По определению работы: A=Fscosα. Если газ расширяется изобарно, то сила, действующая со стороны газа на поршень, постоянна: F=pS (p — давление газа; S — площадь поршня); модуль перемещения поршня 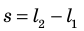(рис. 37.2, а); α = 0.

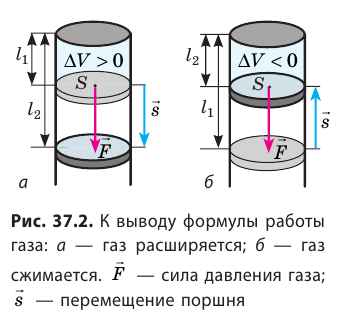
Таким образом, работа газа при его изобарном расширении равна:

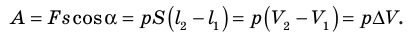
Работе газа при изобарном расширении (или сжатии) можно дать простое геометрическое толкование: работа газа численно равна площади прямоугольника под графиком зависимости p(V) (рис. 37.3).

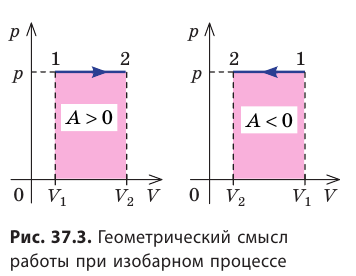
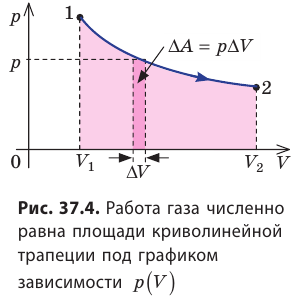
Пусть некоторый газ переходит из состояния 1 в состояние 2 (рис. 37.4). Если изменение объема газа (∆V) достаточно мало, то давление газа можно считать неизменным. Тогда работа газа численно равна площади выделенной на рисунке полосы. Полная работа при изменении объема от 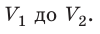будет равна сумме площадей всех полос, то есть площади криволинейной трапеции под графиком зависимости p (V).

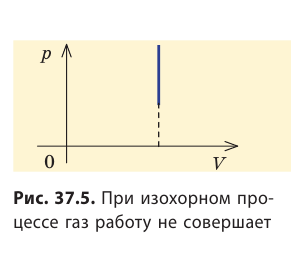
Очевидно, что при изохорном процессе (V = const) площадь фигуры под графиком зависимости p (V) равна нулю (рис. 37.5), — газ работу не совершает (A = 0) . Работа газа зависит от того, каким образом происходил переход газа из начального состояния в конечное (рис. 37.6).

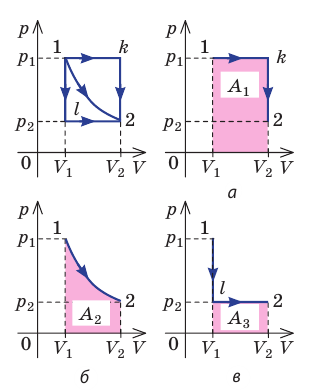
Рис. 37.6. три пути перехода газа из состояния 1 в состояние 2: а — газ изобарно расширяется (участок 1k), затем изохорно охла ждается (участок k2); б — газ изотермически расширяется; в — газ изохорно охлаждается (участок 1l), затем изобарно расширяется (участок l2). сравнив площади фигур под графиками, видим, что:

Пример №5

На рисунке графически изображен циклический процесс, совершаемый идеальным газом. Определите работу газа за цикл.

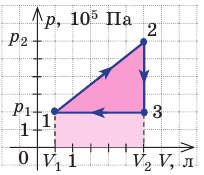
Решение:

Полная работа за цикл равна сумме работ, совершенных газом в ходе каждого процесса цикла. Работа газа в ходе процесса 1–2 численно равна площади трапеции, основания которой равны 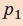и 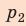, а высота — 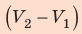; объем газа увеличивается, поэтому работа газа положительна. Работа газа в ходе процесса 2–3 равна нулю, поскольку этот процесс изохорный. Работа газа в ходе процесса 3–1 численно равна площади прямоугольника со сторонам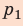и и 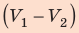; объем газа уменьшается, поэтому работа отрицательна. Следовательно, для определения работы за весь цикл нужно из площади трапеции вычесть площадь прямоугольника. То есть, как видно из рисунка, работа газа за цикл численно равна площади прямоугольного треугольника 1–2–3:

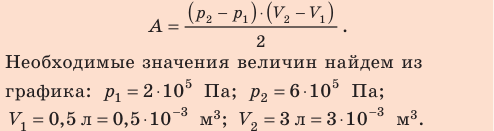
Выводы:

• При отсутствии теплообмена с окружающей средой, если над газом совершают работу, внутренняя энергия газа увеличивается; если газ сам совершает работу, его внутренняя энергия уменьшается.
• Если объем газа увеличивается, то газ совершает положительную работу. Если объем газа уменьшается, то работа газа отрицательна.
• Работа газа численно равна площади фигуры под графиком зависимости p (V). При изобарном процессе работу газа можно определить по формуле A=p∆V, при изохорном процессе работа газа равна нулю: A = 0.

Вычисление полезной работы через КПД

Измерять КПД принято в процентах. Например, КПД 35%, означает, что почти две трети энергии пошли на ненужные траты, стали рассеянным в пустую теплом, были потрачены на истирание деталей машины, образование искр и т. п.

Важно. 35% совсем не плохой КПД. У паровозов первой половины 20 века он составлял всего 10%. Лишь одна десятая образующегося при сгорании топлива тепла шла на перемещение состава, остальное рассеивалось в атмосфере. Среднеэксплуатационный КПД у современных тепловозов 20-22%. КПД машин на бензиновом ДВС равен 25%. КПД дизеля – 33%. Хорошо на этом фоне выглядит КПД электромобилей. Он у них около 90%.

В формуле нахождения полезной работы да в физике в основном КПД обозначают буквой из греческого алфавита η (эта).

Полезная работа в физике и ненужные траты энергии

Прежде чем говорить о том, как найти полезную работу в физике, следует сказать о ней самой. Дело в том что полезная работа в физике – величина очень даже субъективная. Она напрямую связана с человеческим восприятием, с тем, чего нам нужно получить от системы. Поэтому часто, когда говорят о КПД, имеют в виду различные технические устройства, а не природные объекты.

Хотя технологии постоянно развиваются избежать значительных потерь энергии всё же не удаётся. Получается, что:

Aзатр > Aполез

Aзатр – затраченная работа, Aполез – полезная работа, та что идёт на осуществление нужного нам процесса.

Как бы мы ни пытались уменьшить ненужные потери энергии, полностью от них избавиться не получиться. Непреодолимой преградой для этого является первый закон термодинамики. Из него явственно следует, что КПД любого устройства и механизма ни при каких обстоятельствах не может быть больше единицы и даже стать равным ей.

Мощность представляет собой работу, совершённую за единицу времени. В связи с этим КПД можно посчитать как отношение входной мощности системы к выходной. Т. е.

η = Pвх/Pвых.

Как найти полезную работу в физике используя формулы для разных физических процессов

Вид формул, как найти полезную работу в физике, зависит от природы физических явлений, использующихся для преобразования затраченной энергии в нужную.

Как найти полезную работу в физике механической системы

Лучше всего это показать на конкретном примере. Допустим, нам требуется найти КПД процесса, при котором мальчик вкатывает санки весом 4 кг на горку длиной 12, высотой 2 м. Он прикладывает для этого силу, равную 15 Н.

Решение:

Напомним, что общая формула для КПД

η = (Aполез/Aзатр) * 100%

Aполез в нашем случае равна потенциальной энергии (Eп), которую нужно потратить на то, чтобы поднять санки на высоту, т. е.  Aполез = m*g*h.

Затраченная мальчиком работа равна произведению силы на перемещение, т. е. Aзатр = F*S.

Подставляем в общую формулу для КПД

η = (m*g*h*100)/(F*S)

При подстановке численных значений получаем

η = 4*9,8*2/15*12 * 100% = 78,4/180 * 100% ≃ 43,6 %

Из этого примера ясно, чему равна полезная работа в физике механической системы, выраженная через КПД.

Формула полезной работы в физике термодинамической системы

Именно по ней судят об эффективности тепловых машин. Допустим, нам нужно отыскать КПД тепловой машины, рабочее тело которой берёт от нагревателя 20кДж, а холодильнику отдаёт 10кДж.

Решение:

Тепловая машина работает следующим образом: нагреватель передаёт определённое количество теплоты рабочему телу, оно из-за этого расширяется, совершая тем самым механическую работу. Однако в последнюю переходит далеко не вся часть переданной тепловой энергии. Чтобы вернуть систему в исходное состояние и начать новый цикл приходится использовать холодильник.

Из выше сказанного можно сделать вывод, что Aполез равна разности энергии взятой от нагревателя и энергии, забранной холодильником, т. е.

Aполез = Qнагревателя – Qхолодильника

Затраченная работа равняется количеству той теплоты, которая была сообщена нагревателю.

Если всё это подставим в формулу для КПД, то получим

[eta=(text { Qнагревателя }-text { Qхолодильника })^{*} 100 / text { Qнагревателя }]

После подстановки численных значений будем иметь

η = (20 – 10)/20*100% = 50%

Теперь ясно, как определить полезную работу в физике термодинамической системы.

Формула полезной работы в физике электродинамической системы

Очень важный класс явлений. Каждый день все пользуются самыми разными электрическими устройствами: телевизором, компьютером, телефоном и т. д. Но мы рассмотрим случай попроще. Вычислим КПД электрического чайника. Допустим воде было передано 22176 Дж тепла за 2 мин. Напряжение в электросети стандартное 220 В. Сила тока равняется 1,4 А.

Решение:

Aполез будем считать работу, которая пошла на нагрев воды. Хотя она нам и дана из условия, формулу вспомнить всё равно не будет лишним.

• Q = cm(tконечная-tначальная)
• Q — количество теплоты [Дж]
• c — удельная теплоёмкость вещества [Дж/кг*˚C]
• m — масса [кг]
• tконечная — конечная температура [˚C]
• tначальная — начальная температура [˚C]
• Работа тока вычисляется по формуле
• A = (I^2)*Rt = (U^2)/R *t = UIt
• A — работа электрического тока [Дж]
• I — сила тока [А]
• U — напряжение [В]
• R — сопротивление [Ом]
• t — время [c]

В нашем примере она примет вид

η = Q/A *100% = Q/UIt *100%

Переводим минуты в секунды и, подставляя численные значения, получаем

η = 22176/220*1,4*120 *100% = 60%

Формула полезной работы электродинамической системы будет:

Содержание:

1. Теплота и работа
2. Энергия движения и взаимодействия молекул. Внутренняя энергия тел
3. Изменение внутренней энергии тела
4. Единица количества теплоты
5. Понятие о теплоёмкости тела. Удельная теплоёмкость вещества
6. Измерение удельной теплоёмкости
7. Развитие взглядов на природу теплоты
8. Механический эквивалент теплоты
9. Закон сохранения и превращения энергии

Теплота представляет собой такую форму передачи энергии, которая определяется либо непосредственным контактом между телами (см. теплопроводность, конвекция), либо лучистым переносом энергии. Работа представляет собой иной механизм передачи энергии, при котором обязательно имеет место изменение объёма тела.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Теплота и работа

Работа – путем упорядоченного движения молекул. Внутренняя энергия – энергия взаимодействия всех частиц. Все величины являются энергией и измеряются в джоулях. Первый закон термодинамики. Теплота, подведенная к системе, расходуется на изменение внутренней энергии и совершение работы.

Энергия движения и взаимодействия молекул. Внутренняя энергия тел

Мы теперь знаем, что молекулы, из которых состоят тела, находятся в движении. Молекулы газа движутся поступательно с разными скоростями и в разных направлениях. Для газа характерна хаотичность движения молекул. В жидкостях молекулы могут колебаться, вращаться и поступательно перемещаться относительно друг друга. В твёрдых телах молекулы и атомы колеблются около некоторых средних положений.

Как и всякие движущиеся тела, молекулы обладают кинетической энергией.

Мы знаем также, что молекулы в теле связаны между собой силами сцепления, в газах слабо, в жидкостях и твёрдых телах очень сильно. Поэтому молекулы обладают также потенциальной энергией, зависящей от их взаимного расположения.

Кинетическая энергия движения частиц, из которых состоит тело, вместе с потенциальной энергией взаимодействия этих частиц составляют внутреннюю энергию тела.

Имея всегда какой-то запас внутренней энергии, тело одновременно может обладать механической энергией. Например, снаряд движущийся на некоторой высоте, кроме внутренней энергии, обладает ещё механической энергией — потенциальной и кинетической.

Изменение внутренней энергии тела

Внутренняя энергия тела не является какой-то постоянной величиной: у одного и того же тела она может изменяться. При повышении температуры, например, внутренняя энергия тела увеличивается, так как увеличивается средняя кинетическая энергия движения молекул этого тела. С понижением же температуры, наоборот, внутренняя энергия тела уменьшается.

Внутренняя энергия меняется также при переходе тела из одного агрегатного состояния в другое, при деформации тела, при раздроблении тела на более мелкие части, так как во всех этих случаях меняется взаимное расположение частиц, а значит, и их потенциальная энергия.

Из всего сказанного следует, что внутренняя энергия тела зависит от состояния этого тела. С изменением состояния тела меняется и его внутренняя энергия.

Рассмотрим теперь, в результате каких процессов происходит изменение внутренней энергии тела.

Если движущееся тело производит работу против сил трения, то его механическая энергия уменьшается; одновременно меняется и состояние тела. При трении тела нагреваются, дробятся на части и даже могут переходить из одного агрегатного состояния в другое (например, при трении плавятся кусочки льда). Следовательно, в процессе совершения работы внутренняя энергия тела изменяется.

Внутреннюю энергию тела можно изменять и иным путём. Вода в чайнике, поставленном на плиту, закипает, её внутренняя энергия изменяется. Воздух и различные предметы в комнате нагреваются от печки; следовательно, их внутренняя энергия увеличивается, так как увеличивается кинетическая энергия молекул.

Но при этом работа не совершается. Значит, изменение внутренней энергии может происходить не только в результате совершения работы, но и при различных тепловых процессах.

Процесс изменения внутренней энергии тела без совершения работы называется теплопередачей. Теплопередача осуществляется и при непосредственном контакте тел (чайник на плите) и если тела разделены расстоянием (нагревание предметов от печки или от солнца).

Итак, внутреннюю энергию тела можно изменять двумя путями: путём совершения работы и путём теплопередачи.

Когда тело увеличивает запас своей внутренней энергии, то это значит, что оно получает какое-то количество энергии извне; наоборот, уменьшение запаса внутренней энергии означает, что тело отдаёт часть своей энергии.

Мерой энергии, получаемой или отдаваемой телом в процессе теплопередачи, служит особая величина, называемая количеством теплоты.

Единица количества теплоты

В те времена, когда впервые стали производить измерения количества теплоты (вторая половина XVIII в.), понятиями работы и энергии в науке ещё не пользовались (они были введены в XIX в.).

Для измерения количества теплоты была введена особая единица. За единицу количества теплоты принято то количество теплоты, которое необходимо для нагревания 1 г воды на 1°С. Эта единица называется калорией ¹ (сокращённое обозначение: кал). Употребляют также и единицу, в 1000 раз большую — килокалорию ккал).

¹ Калория — от латинского слова калор — жар.

Рихман Георг (1711—1753) — замечательный русский учёный. Родился в 1711 г., в один год с  Ломоносовым. Учился в Петербургской Академии наук. В 1741 г. был назначен профессором академии. Его работы касались главным образом исследования теплоты и электричества. В области теплоты он заложил основы калориметрии. Совместно с  Ломоносовым впервые в России начал изучение электрических явлений. Рихман впервые применил электроскоп для исследования электрических зарядов на телах.

Тщательные измерения показывают, что для нагревания 1 г воды на 1°С требуется несколько большее или меньшее количество теплоты, в зависимости от исходной температуры.

Так, для нагревания 1 г воды от 1 до 2° требуется приблизительно на 1% больше количества теплоты, чем для нагревания от 31 до 32°. При точных измерениях принято считать за 1 калорию количество теплоты, необходимое для нагревания 1 г чистой воды от 19,5 до 20,5°С.

Понятие о теплоёмкости тела. Удельная теплоёмкость вещества

Нагревая тела с одинаковой массой, но состоящие из различных веществ (железа, дерева, кирпича и т. д.), можно обнаружить, что для повышения их температуры на данное число градусов требуются различные количества теплоты.

Количество теплоты, необходимое для нагревания тела на 1°, называется теплоёмкостью этого тела.

Опыт показывает, что для нагревания тела не на 1° С, а на t° требуется в t раз большее количество теплоты. При остывании на t° тело отдаёт такое же количество теплоты, которое поглощает при нагревании на t°.

Чем больше масса тела, тем больше его теплоёмкость, т. е. тем большее количество теплоты требуется для нагревания его на 1° С.

Теплоёмкость однородного тела пропорциональна его массе и зависит от вещества, из которого оно состоит.

Сравнивать между собой можно теплоёмкости различных веществ, имеющих одинаковую массу, равную, например, единице массы.

Количество теплоты, необходимое для нагревания 1 г вещества на 1° С, называется удельной теплоёмкостью вещества.

Пусть Q — количество теплоты, которое надо передать телу, масса которого m, чтобы повысить температуру его от до  Чтобы определить удельную теплоёмкость вещества с, надо количество теплоты Q разделить на массу тела m и на разность температур Таким образом,

Удельные теплоёмкости обычно выражают в  или в 

Удельная теплоёмкость воды при нагревании от 19,5°С до 20,5°С равна 1  При других температурах она отличается от 1 но это отличие очень незначительно, и мы его в дальнейшем учитывать не будем. Вообще удельная теплоёмкость любого вещества с изменением температуры хотя и незначительно, но меняется.

Во многих случаях при расчётах пользуются средним значением удельной теплоёмкости. Для некоторых веществ такие значения удельной теплоемкости приведены в следующей таблице:

• Водород……..3,41
• Гелий……..1,26
• Спирт……..0,58
• Эфир……..0,56
• Керосин……..0,51
• Лёд……..0,48
• Воздух……..0,24
• Алюминий……..0,22
• Стекло……..0,19
• Алмаз……..0,12
• Железо……..0,11
• Медь……..0,09
• Серебро……..0,05
• Ртуть……..0,03
• Олово……..0,05
• Свинец……..0,03

Зная удельную теплоёмкость вещества, по формуле 

можно рассчитать количество теплоты, идущее на нагревание тела.

Измерение удельной теплоёмкости

Для измерения удельной теплоёмкости твёрдых, жидких и газообразных веществ существуют различные способы. Мы рассмотрим наиболее простой способ измерения теплоёмкости твёрдых веществ.

Испытуемое тело нагревают до определенной температуры и затем погружают его в особый прибор — калориметр, в который налито определённое количество воды (рис. 129).

Рис. 129. Схема установки по определению удельной теплоёмкости вещества с помощью калориметра.

Если вода в калориметре имеет температуру ниже, чем температура опущенного в неё тела, то она нагревается, а тело охлаждается до тех пор, пока их температуры не сравняются. Количество теплоты, отданное телом, равно количеству теплоты, полученному калориметром и водой. Этот опытный факт и даёт возможность определить удельную теплоёмкость тела.

Пусть масса калориметра равна m₁ его удельная теплоёмкость c₁ , масса воды в калориметре m₂, удельная теплоёмкость воды с, начальная температура воды и калориметра t⁰₁ , масса испытуемого тела m, его удельная теплоёмкость с_х и начальная температура общая температура калориметра и тела (греч. «тэта»). Тогда результат указанного опыта можно выразить уравнением:

    (1)

Это уравнение  теплового баланса. Оно показывает, что при теплообмене между испытуемым телом и калориметром количество теплоты, отданное телом, равно количеству теплоты, полученному калориметром.

Из уравнения (1) определяется искомая удельная теплоёмкость:

Надо иметь в виду, что, кроме обмена энергией между внесённым телом и калориметром, такой обмен возможен между телом и окружающими калориметр предметами. При точных измерениях необходимо по возможности уменьшать потери энергии и_вводить в вычисления поправки, учитывающие ту часть энергии, которая передаётся в процессе опыта окружающей среде.

Развитие взглядов на природу теплоты

В XVIII в. господствовало мнение, что теплота есть особая невидимая и невесомая жидкость, способная переходить из одного тела в другое. Такая жидкость, называвшаяся  теплородом, находилась, по мнению сторонников этой гипотезы, во всех телах.

Гипотезы теплорода в своё время придерживались знаменитые учёные — Ньютон, Лавуазе Лаплас, Гей-Люссак  и др. Само название «теплоёмкость» введено было потому, что оно указывало на содержание теплорода.

В то время как большинство учёных XVIII в. принимали гипотезу теплорода, против неё выступил М. В. Ломоносов.

В 1745 г. М. В. Ломоносов опубликовал работу «Размышления о причине теплоты и холода», начинавшуюся так: «Весьма известно, что тепло возбуждается движением: руки от взаимного трения согреваются, дерево загорается, искры вылетают при ударе кремнём о сталь, железо накаливается при ковании его частыми, сильными ударами; по прекращению их тепло уменьшается, и полученный огонь потухает… Из всего этого совершенно очевидно, что имеется достаточное основание теплоты в движении. А так как никакое движение без материи происходить не может, то необходимо,чтобы достаточное основание теплоты состояло в движении какой-либо материи».

По Ломоносову, теплота возникает в телах в результате сообщения им движения; следовательно, сущность теплоты — в движении частиц, образующих тело.

Учение Ломоносова о природе теплоты нашло признание среди ряда крупнейших учёных его времени. Так, например, знаменитый математик и физик Эйлер в письме, адресованном Ломоносову, писал: «Всякий знает, что появившиеся до сих пор трактаты о причинах теплоты ещё не разъяснили вполне этого предмета, и занимающиеся его исследованием заслуживают величайшей похвалы. Вас нельзя не поблагодарить за то, что вы рассеяли мрак, покрывавший доселе этот вопрос».

Знал о работах Ломоносова и известный итальянский физик Вольта. В 1786 г. он отметил «то чрезвычайное остроумие, с которым господин Ломоносов в своё время опроверг теплород».

Дальнейшее развитие и опытное обоснование учение о природе теплоты нашло в работах английских учёных  Румфорда и Дэви.

В 1798 г. Румфорд писал: «Когда я присутствовал в мюнхенском арсенале при сверлении пушек, меня поразила высокая температура, которую металл быстро принимал при сверлении, и ещё более высокая температура металлических стружек, которая превышала температуру кипения воды».

Желая убедиться, существует ли теплород, Румфорд произвёл ряд опытов, при которых тщательно изолировал испытуемый предмет от нагревания какими-либо другими предметами. Он сверлил металлический цилиндр, поместив его в ящик, наполненный холодной водой, и убедился, что через короткое время вода начинает кипеть. «Трудно описать недоумение и удивление, отразившееся на лицах присутствующих, когда они увидели, что столь большое количество воды было доведено до кипения без помощи огня».

Румфорд заметил, что чем дольше работает лошадь, приводящая в движение сверло, тем больше выделяется теплоты. На основании этого наблюдения он сделал вывод, что «нельзя считать веществом то, что можно получить в неограниченном количестве из изолированного тела, и нельзя представить себе теплоту иначе, чем некоторым движением».

В 1802 г. Дэви показал на опыте, что при трении двух кусков льда образуется вода, теплоёмкость которой в два раза больше, чем теплоёмкость льда. Этот опыт Дэви повторяет, помещая кусок льда под колокол воздушного насоса. И в этом случае, хотя лёд не мог ниоткуда получить «теплорода», он обращается в воду, на что затрачивается теплота.

Несмотря на убедительность доводов Ломоносова, Румфорда, Дэви, опровергавших существование теплорода, гипотеза теплорода ещё довольно долго существовала в науке. Для доказательства её несостоятельности потребовались новые опыты, новые научные исследования.

Механический эквивалент теплоты

В начале XIX в. в промышленность и транспорт широко внедряются паровые двигатели. Одновременно изыскиваются возможности повышения их экономичности. В связи с этим перед физикой и техникой ставится вопрос большой практической важности: как при наименьшей затрате топлива в машине совершить возможно больше работы.

Первый шаг в решении этой задачи сделал французский инженер Сади Карпов  1824 г., изучая вопрос о коэффициенте полезного действия паровых машин.

В 1842 г. немецкий учёный Роберт Майер теоретически определил, какое количество механической работы можно получить при затрате одной килокалории теплоты.

В основу своих расчётов Майер положил различие в теплоёмкостях газа.

У газов различают две теплоёмкости: теплоёмкость при постоянном давлении (с_р) и теплоёмкость при постоянном объёме (c_v).

Теплоёмкость газа при постоянном давлении измеряется количеством теплоты, которое идёт на нагревание данной массы газа на 1°С без изменения его давления.

Теплоёмкость же при постоянном объёме численно равна количеству теплоты, идущей на нагревание данной массы газа на 1°С без изменения объёма, занимаемого газом.

У всякого газа теплоёмкость при постоянном давлении больше теплоёмкости при постоянном объёме. Так, например, для воздуха удельные теплоёмкости с_р и c_v имеют следующие значения:

Объясняется это различие в теплоёмкостях газа следующим образом. При нагревании газа при постоянном объёме увеличивается только внутренняя энергия газа.

При нагревании же газа при постоянном давлении увеличивается, как и в первом случае, внутренняя энергия газа, но, кроме того, газ при расширении совершает работу. Проследим ход рассуждений Майера.

Рис. 130. Рисунок, поясняющий теоретический расчёт Майера механического эквивалента теплоты.

Допустим, что в сосуде (рис. 130), площадь основания которого 1 м², заключён при температуре 0° и давлении 760 мм рт. ст. 1 м³ воздуха. Воздух, заключённый в сосуде, закрыт поршнем АВ, который Майер в своих рассуждениях считал невесомым.

Масса 1 м³ воздуха равна 1,293 кг. Если нагреть этот воздух на 1°С, то он расширится и

поднимет поршень на (в положение А₁В₁).

Перемещая поршень, воздух в сосуде производит работу по преодолению силы атмосферного давления Гак как атмосферное давление равно 1,0332 то сила, действующая на поршень сверху, равна:

Работа, совершаемая расширяющимся воздухом по преодолению этой силы, равна:

Количество теплоты, идущей на нагревание воздуха в сосуде при постоянном давлении, равно:

Для нагревания же этого количества воздуха при постоянном объёме требуется:

За счёт количества теплоты  газ совершил работу, равную 37,82 кГм.

Из этих расчётов вытекает, что 0,0886 ккал эквивалентны 37,82 кГм. Отсюда количество механической работы, эквивалентное 1 ккал теплоты, равно:

Внутреннюю энергию тела, как было установлено в § 71, можно изменять двумя путями: путём совершения работы и путём теплопередачи.

Количество механической работы, которое вызывает такое же изменение внутренней энергии тела, как и сообщение ему единицы количества теплоты, называется механическим эквивалентом теплоты.

Рис. 131. Схема опыта Джоуля по определению механического эквивалента теплоты. Чтобы вода не увлекалась движением лопаточек, калориметр был разделён перегородками с вырезами в них для прохождения лопаточек.

Опытные определения механического эквивалента теплоты впервые были произведены Джоулем в период с 1840 по 1849 г. Один из наиболее известных его способов определения механического эквивалента теплоты состоял в следующем.

В калориметр А (разрез его показан на рис. 131) наливалась вода. Падающие грузы W и W’  приводили во вращение ось К с лопаточками L. Калориметр имел перегородки N; он был устроен так для того, чтобы увеличить трение подвижной части прибора о воду. Вследствие трения лопаточек о воду последняя нагревалась (температура внутри калориметра измерялась термометром).

Джемс Прескотт Джоуль (1818— 1889) — выдающийся английский физик, сыграл большую роль в опытном обосновании закона сохранения и превращения энергии.

Он впервые точно определил на опыте механический эквивалент теплоты. Одновременно с русским физиком Э. X. Ленцем открыл закон, который определяет количество теплоты, выделяемое электрическим током при прохождении по проводнику. Совместно с В. Томсоном открыл явление понижения температуры газа при его расширении.

Именем Джоуля названа единица работы джоуль.

По высоте падения h и массе грузов m подсчитывалась произведённая работа А = mgh. По повышению температуры в калориметре подсчитывалось количество теплоты Q, выделенное при трении подвижной части калориметра о воду. На эту величину увеличивалась внутренняя энергия воды.

Многочисленные измерения показали, что отношение работы А к количеству теплоты Q, на которое увеличивалась внутренняя энергия воды, в результате совершения этой работы, представляет постоянную величину. Эта величина и является механическим эквивалентом теплоты. Механический эквивалент обозначается буквой J:

Джоуль заменял воду ртутью и получал тот же результат. Наконец, вместо работы трения лопаточек о воду Джоуль измерял в калориметре работу трения двух кусков металла. Измерения дали ту же величину механического эквивалента теплоты.

Зная механический эквивалент теплоты, легко выразить единицу измерения количества теплоты через единицы работы:

Закон сохранения и превращения энергии

Рассмотрим более подробно описанный выше опыт Джоуля. В этом опыте потенциальная энергия падающих грузов превращалась в кинетическую энергию вращающихся лопаток; благодаря работе против сил трения кинетическая энергия лопаток превращалась во внутреннюю энергию воды. Мы сталкиваемся здесь со случаем превращения одного вида энергии в другой. Потенциальная энергия падающих грузов превращается во внутреннюю энергию воды, количество теплоты Q является мерой превращенной энергии. Таким образом, количество энергии сохраняется при её превращениях в другие виды энергии.

Естественно поставить вопрос: сохраняются ли при превращениях количества других видов энергии, например кинетической, электрической и т. д.? Допустим, что летит пуля массой  со скоростью Ее кинетическая энергия равна  Пуля попала в какой-либо предмет и застряла в нём. Кинетическая энергия пули превращается при этом во внутреннюю энергию пули и предмета, измеряемую количеством теплоты Q, которая вычисляется по известной формуле (§ 73). Если кинетическая энергия при превращении во внутреннюю энергию не теряется, то должно иметь место равенство:

Опыт подтверждает это заключение. Количество энергии сохраняется.

При прохождении электрического тока проводник нагревается: электрическая энергия превращается во внутреннюю энергию проводника. Опыт показывает, что при работе электрического тока в 1 получается всегда количество теплоты, равное 860 ккал. Таким образом, сохраняется общее количество энергии. Этот вывод относится ко всем видам энергии.

Тысячелетняя практика показала, что ни один из видов энергии никогда не возникает из ничего. Это положение подтверждается фактом невозможности осуществления вечного двигателя (см. ч. 1, § 78). Большой опытный материал показал также, что энергия и не исчезает при всех своих превращениях. Все явления природы происходят в соответствии с законом сохранения и превращения энергии, который формулируется так:

Во всех процессах, происходящих в природе, энергия не возникает и не исчезает, она только превращается из одного вида в другой в эквивалентных количествах.

Все формы энергии: кинетическая, потенциальная, электромагнитная, химическая, внутриатомная и др. — способны превращаться друг в друга.

Именно возможность взаимного превращения всех форм энергии обусловливает богатство и разнообразие явлений природы.

Для иллюстрации этого великого закона природы рассмотрим несколько примеров.

Солнечные лучи несут определённый запас энергии. Падая на поверхность Земли, лучи нагревают её. Энергия солнечных лучей при этом превращается во внутреннюю энергию почвы и тел, находящихся на поверхности Земли. Последняя передаётся окружающему Землю воздуху; воздушные массы приходят в движение, появляется ветер — происходит превращение в механическую (кинетическую) энергию. Часть энергии солнечных лучей поглощается на поверхности Земли листьями растений; при этом в растениях происходят сложные химические реакции, в результате которых образуются органические соединения — происходит превращение в химическую энергию.

В § 57 и 58 говорилось об использовании энергии движущейся воды; последняя возникает также в результате превращения энергии солнечного излучения.

Наконец, в настоящее время наука овладевает возможностями превращения внутриатомной энергии в другие, нужные для практики виды энергии.

Закон сохранения и превращения энергии широко используется при исследовании явлений природы. Этот закон представляет научную основу для разнообразных расчётов во всех областях техники.

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Масса
7. Взаимодействия тел
8. Механическая энергия
9. Импульс
10. Вращение твердого тела
11. Криволинейное движение тел
12. Колебания
13. Колебания и волны
14. Механические колебания и волны
15. Бегущая волна
16. Стоячие волны
17. Акустика
18. Звук
19. Звук и ультразвук
20. Движение жидкости и газа
21. Молекулярно-кинетическая теория
22. Молекулярно-кинетическая теория строения вещества
23. Молекулярно – кинетическая теория газообразного состояния вещества
24. Температура и теплота
25. Термодинамические процессы
26. Идеальный газ
27. Уравнение состояния идеального газа
28. Изменение внутренней энергии
29. Переход вещества из жидкого состояния в газообразное и обратно
30. Кипение, свойства паров, критическое состояние вещества
31. Водяной пар в атмосфере
32. Плавление и кристаллизация
33. Тепловое расширение тел
34. Энтропия
35. Процессы перехода из одного агрегатного состояния в другое
36. Тепловое расширение твердых и жидких тел
37. Свойства газов
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома