Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
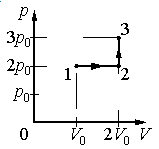
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 14.9k
В этой заметке рассмотрим как можно вычислить работу идеального газа при различных изо-процессах. Это будет полезно тем, кто только начинает изучать термодинамику и МКТ. Для простоты изображения всех процессов возьмем самые популярные P-V диаграммы.
Есть такое понятие как термодинамический процесс. Изменение любого параметра термодинамической системы (к параметрам можно отнести температуру T, давление p, объем V, энтропию S). Но так как все параметры термодинамической системы взаимосвязаны, то частенько, когда изменяется один параметр, то и изменяются другие параметры.
Если термодинамические процессы не протекают, то система находится в равновесном состоянии. То есть равновесное состояние — такое абстрактное состояние системы, при котором все термодинамические параметры системы остаются сколь угодно долго неизменными, если над системой не совершают никаких внешних воздействий. То есть система предоставлена сама себе. Почему же это состояние абстрактно? Потому что в реальной жизни очень тяжело изолировать систему от внешнего влияния окружающего мира. Таким образом, в каждый момент времени протекают какие-то термодинамические процессы.
Однако, процессы могут протекать настолько медленно, что система изменяется почти незаметно. Иногда это дает возможность рассматривать состояние системы из последовательных равновесных состояний. Такие процессы еще называются квазистатическими. Под квазистатичностью можно понимать что-то ооочень медленное, настолько медленной, что оно длится намного дольше, чем время релаксации (время, за которое амплитудное значение внешнего возмущения, которое начало менять систему, уменьшилось в e раз).
Еще система может постоянно возвращаться к исходному состоянию. Такой круговой процесс называется циклом (примерно по таким процессам работают тепловые машины и ДВС).
Что нужно чтобы изучить какую-либо термодинамическую систему?
1. Определить работу, совершаемую в данном процессе
2. Определить изменение внутренней энергии системы
3. Определить количество теплоты, которое вошло в систему или которое отдала система.
4. Установить связи между отдельными величинами, которые характеризуют состояние рабочего тела (газа)
Основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.
И далее мы с вами выведем работы в этих основных процессах.
1. Изохорный процесс
Изохорным процесс — термодинамический процесс, который протекает при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.
2. Изотермический процесс
Изотермический процесс — термодинамический процесс, который протекает при постоянной температуре. На практике очень сложно осуществить этот процесс. Потому что при сжатии или расширении газа, нужны условия, при которых газ будет успевать обмениваться температурой с внешней средой, чтобы поддерживать свою температуру неизменной.
3. Изобарный процесс
Изобарный процесс — термодинамический процесс, который протекает при постоянном давлении. Помещение газа в плотный цилиндр с подвижным поршнем, на который действует постоянная сила ( например сила тяжести со стороны груза ) при отводе и подводе теплоты, может смоделировать такой процесс.
4. Адиабатный процесс
Адиабатный процесс — термодинамический процесс, который протекает без теплообмена (Q = 0) рабочего тела (газа) с окружающей средой. Также сложно осуществимый процесс. Примерная модель: газ помещают в цилиндр с подвижным поршнем. При этом цилиндр и поршень выполнены из высококачественного теплоизолирующего материала.
5. Политропный процесс (p∙Vⁿ = const )
Этот процесс является обобщением всех предыдущих. Все параметры в этом процессе могут меняться. А процессы выше являются его частными случаями. n – показатель политропы, некоторая постоянная, которая может принимать любые значения от -∞ до +∞.
n = 0 – изобарный процесс p = const
n = 0 – изотермический процесс T = const
n = γ – адиабатный процесс p∙Vⁿ = const
n = +∞ или n = -∞ – изохорный процесс V = const
Любые формулы для этого процесса аналогичны адиабатному процессу. При этом работа выводится точно также. Только коэффициент адиабаты (γ) в общем случае заменяется на коэффициент политропы (n).
Понравился разбор задачи ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Как найти работу газа
Работа газа осуществляется при изменении его объема. Именно при изменении объема газа приходят в движение узлы тепловых двигателей, будь то двигатель внутреннего сгорания или пуля в стволе ружья. При различных процессах работа газа вычисляется по-разному.

Вам понадобится
- – манометр;
- – термометр.
Инструкция
Если работа газа осуществляется при изобарном процессе (при постоянном давлении), то для того чтобы найти работу газа с помощью манометра, измерьте давление газа. После этого замерьте его объем перед выполнением работы и после. Найдите изменение объема газа, отняв от конечного значения начальное. После этого найдите произведение давления газа на изменение его объема. Это и будет работа газа при постоянном давлении A=p•ΔV.
Для идеального газа вычислить работу при постоянном давлении можно, применив уравнение Клапейрона-Менделеева. Найдите работу газа, умножив его массу на число 8,31 (универсальную газовую постоянную) и изменение температуры при выполнении работы. Результат поделите на молярную массу газа A=m•R•ΔT/M. При расчетах учитывайте то, что если работа выполняется газом (он расширяется), то она положительна. Если же работа выполняется над газом (его сжимают сторонние силы), то работа отрицательна.
Если работа выполняет при изотермическом расширении (когда температура постоянна), узнайте изменение объема газа и значение его температуры. Для того чтобы найти работу газа, умножьте его массу на число 8,31 (универсальную газовую постоянную) и температуру при выполнении работы. Результат поделите на молярную массу газа. Получившееся число умножьте на логарифм натуральный из отношения конечного и начального объемов газа A=m•R•T•ln(V2/V1)/M.
В общем случае, чтобы найти работу газа возьмите интеграл из функции давления по объему. Границы интеграла – от начального до конечного объема ∫pdV. Если есть график газового процесса в координатах (V,p), как правило, он представляет собой прямую линию, найдите площадь трапеции ограниченной по бокам линиями перпендикулярными оси Vв точках V1 и V2, снизу осью V, а сверху графиком функции. В более сложных случаях ищется площадь криволинейной трапеции.
Полезный совет
Если объем газа не изменяется, работа им не выполняется.
Источники:
- как изменяется объем газа
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
|
|
Макеты страниц

Рис. 4.3. Работа, произведенная газом, расширяющимся при постоянном давлении. На p—V – диаграмме работа изображается площадью (в данном случае заштрихованной) под горизонтальной линией, представляющей процесс (расширение при постоянном давлении). Работа определяется следующим выражением:

Теперь разобьем эту площадь на полоски, как показано на нижнем рисунке. Площадь первой полоски равна 





Здесь использовано стандартное математическое обозначение: 


Теперь вернемся к случаю изменяющегося давления. На рис. 4.4 изображена изотерма — кривая, которая представляет связь между p и V в процессе их изменения при постоянной температуре. Для изотермического расширения, т. е. процесса, происходящего при постоянной температуре вдоль изображенной кривой, совершенная газом работа равна заштрихованной площади под кривой между начальным и конечным значениями объема. Задача заключается в ее вычислении. Начнем с того, что разобьем полное изменение объема на ряд малых изменений, точно так же, как мы сделали в случае постоянного давления. Далее предположим, что в течение каждого такого малого изменения объема давление остается постоянным. Результирующий график напоминает полку с книгами, высота которых постепенно уменьшается. Если сложить все площади 




Рис. 4.4. Работа газа, расширяющегося при постоянной температуре. Величина работы по-прежнему определяется заштрихованной площадью под кривой (изотермой), изображающей ход процесса, но теперь она не равна произведению давления на изменение объема, поскольку давление также изменяется. Для вычисления работы необходимо прибегнуть к интегрированию, т. е. разбить площадь на большое число очень тонких полос. Работа определяется выражением

В пределе, когда величина 



Но чтобы выполнить суммирование величины pdV, как показано на рис. 4.4, нужно знать величину p для каждого dV. Для этого обратимся к уравнению состояния. Для простоты расчета возьмем уравнение идеального газа. Согласно данному уравнению, в каждый момент времени pV — nRT; разрешая последнее уравнение относительно p, найдем, что p = nRT/V. Тогда получаем

Такое выражение справедливо для любого процесса расширения. В изотермическом случае, который мы рассматриваем, его можно упростить, заметив, что все 

где мы снова использовали некоторые математические обозначения.
Символ 



Они просто означают,что процесс суммирования(интегрирования) проводится по интервалу от начального объема 








Суммы или интегралы, подобные фигурирующим в выражении (7), так важны и так часто встречаются, что мы сделаем теперь небольшое отступление и покажем, как они вычисляются. Чтобы этот экскурс оказался действительно полезным, следует знать кое-что о логарифмах. Читателям, уже знакомым с логарифмами, полезно познакомиться с приведенным ниже обзором, заключенным в рамку. Тот, кто не сталкивался с таким представлением чисел, должен потратить некоторое время и ознакомиться с приложением II.
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ПРЕДИСЛОВИЕ АВТОРА
- БЛАГОДАРНОСТИ
- 1. ПЕРВЫЕ ШАГИ
- ГОРЯЧЕЕ И ХОЛОДНОЕ
- ПРЕОБРАЗОВАНИЕ РАБОТЫ В ТЕПЛОТУ
- ТЕПЛОТА И РАБОТА — НЕ ОДНО И ТО ЖЕ
- В ДЕЙСТВИЕ ВСТУПАЕТ ГРЕК ГЕРОН
- СНАЧАЛА ВОЗНИКЛО ОГНЕСТРЕЛЬНОЕ ОРУЖИЕ
- ВНОВЬ О ПАРЕ
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- 2. НАСКОЛЬКО ГОРЯЧО ГОРЯЧЕЕ?
- СТЕПЕНЬ НАГРЕТОСТИ, ОПРЕДЕЛЯЕМАЯ НА ОЩУПЬ
- ПЕРВЫЕ ТЕРМОМЕТРЫ
- ЧТО ЖЕ ТАКОЕ ТЕМПЕРАТУРА!
- ГАЗОВЫЕ ТЕРМОМЕТРЫ
- МЕЖДУНАРОДНАЯ ШКАЛА ТЕМПЕРАТУР
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- 3. СИСТЕМЫ, ПАРАМЕТРЫ СОСТОЯНИЯ И СОСТОЯНИЯ
- СПЕЦИАЛЬНЫЕ ЗНАЧЕНИЯ НЕКОТОРЫХ ОБЩИХ ТЕРМИНОВ
- ПОЧЕМУ ТЕМПЕРАТУРА ВХОДИТ В РАССМОТРЕНИЕ!
- СООТНОШЕНИЯ, В КОТОРЫЕ ВХОДИТ ТЕМПЕРАТУРА
- МОЛИ И МОЛЕКУЛЫ
- АТОМНАЯ ТЕОРИЯ: КРАТКИИ ОБЗОР
- ЗАКОН ИДЕАЛЬНОГО ГАЗА
- ДРУГИЕ УРАВНЕНИЯ СОСТОЯНИЯ
- УРАВНЕНИЯ СОСТОЯНИЯ В ВИРИАЛЬНОЙ ФОРМЕ
- НЕКОТОРЫЕ ТИПИЧНЫЕ ЗАДАЧИ
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- 4. ВНОВЬ О РАБОТЕ
- ОБЩЕЕ ОПРЕДЕЛЕНИЕ МЕХАНИЧЕСКОЙ РАБОТЫ
- РАБОТА ПРИ РАСШИРЕНИИ ГАЗА
- РАБОТА ПРИ ИЗМЕНЕНИИ ДАВЛЕНИЯ
- КРАТКО О ЛОГАРИФМАХ
- ВНОВЬ ОБ ИЗОТЕРМИЧЕСКОМ РАСШИРЕНИИ
- ПРИМЕР
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- 5. БОЛЕЕ ПОДРОБНО О ТЕПЛОТЕ
- ТЕПЛООБМЕН — ЭТО ПРОЦЕСС
- СКОЛЬКО ТЕПЛОТЫ ПЕРЕДАЕТСЯ?
- ЧТО ВЫЗЫВАЕТ ТЕПЛООБМЕН?
- КОНЦЕПЦИЯ ТЕПЛОРОДА И СВЕРЛИЛЬНЫЙ СТАНОК РУМФОРДА
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- 6 У ИСТОКОВ АНАЛИЗА ЦИКЛИЧЕСКИХ ПРОЦЕССОВ
- ЭТО НЕ ИГРУШКА, ЭТО МАШИНА
- ПОНЯТИЕ ЦИКЛА
- ЗНАМЕНИТЫЙ ЦИКЛ КАРНО
- СЛЕДСТВИЯ ВЗАИМОСВЯЗИ ПРОЦЕССОВ В ЦИКЛЕ КАРНО
- ТЕПЛОВЫЕ МАШИНЫ И ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- ПРИМЕР
- КРАТКИЕ ВЫВОДЫ
- 7. ЭКВИВАЛЕНТНОСТЬ ТЕПЛОТЫ И РАБОТЫ И ИХ СВЯЗЬ С ЭНЕРГИЕЙ
- СМЕНА ДЕКОРАЦИИ: ОБОРУДОВАНИЕ ДЛЯ ПИВОВАРЕНИЯ
- МЕХАНИКА И ПРОИСХОЖДЕНИЕ ПОНЯТИЯ ЭНЕРГИИ
- РАБОТА И КОНСЕРВАТИВНЫЕ СИСТЕМЫ
- ВЫХОД ЗА РАМКИ МЕХАНИКИ
- ТЕПЕРЬ ДОБАВИМ ТЕПЛОТУ
- ДРУГИЕ ВИДЫ ЭНЕРГИИ
- ПРИМЕРЫ
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- 8. РАЗРЕШЕНИЕ ОДНОЙ «ДИЛЕММЫ»
- ОДНОВРЕМЕННО В РАЗНЫХ СТРАНАХ
- НА НЕКОТОРЫЕ ДАВНО ИЗВЕСТНЫЕ ФАКТЫ
- НАГРЕВАНИЕ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
- РАБОТА БЕЗ ТЕПЛООБМЕНА — АДИАБАТИЧЕСКОЕ РАСШИРЕНИЕ И СЖАТИЕ
- ЦИКЛ КАРНО С НОВОЙ ТОЧКИ ЗРЕНИЯ
- ПРИМЕР
- УПРАЖНЕНИЯ
- 9. ИТАК. ЧТО НАМ ИЗВЕСТНО?
- 10. ПТМ МОЖЕТ МНОГОЕ РАССКАЗАТЬ
- ПТМ НА ЭЛЕКТРОСТАНЦИИ
- ПТМ И НАУКА
- ПРИМЕРЫ
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- II. ПТМ И АВТОМОБИЛЬНЫЙ ДВИГАТЕЛЬ
- ЦИКЛ ОТТО, ИЛИ ДВИГАТЕЛЬ С ИСКРОВЫМ ВОСПЛАМЕНЕНИЕМ
- ИГРА С ОКТАНОВЫМ ЧИСЛОМ
- ПОСЛУШНЫЙ ДВИГАТЕЛЬ ДИЗЕЛЯ
- КПД И ОКРУЖАЮЩАЯ СРЕДА
- ПРИМЕР
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- 12. ПОЗНАКОМИМСЯ С ЭНТРОПИЕЙ
- ЕЩЕ О СВЯЗИ ПАРАМЕТРОВ И ВЗАИМОДЕЙСТВИЙ
- ВЫЧИСЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ В НЕКОТОРЫХ СЛУЧАЯХ
- К ВОПРОСУ О НЕЗАВИСИМОСТИ ОТ ПУТИ
- ДОПОЛНИТЕЛЬНОЕ УПРАЖНЕНИЕ
- КРАТКИЕ ВЫВОДЫ
- УПРАЖНЕНИЯ
- 13. ВСЕ КОНЧАЕТСЯ ЭНТРОПИЕЙ
- ИЗМЕНЕНИЯ ЭНТРОПИИ В ИЗОЛИРОВАННЫХ СИСТЕМАХ
- ЭНТРОПИЯ И ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
- СВЯЗЬ МЕЖДУ РАЗЛИЧНЫМИ ФОРМУЛИРОВКАМИ ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
- СУЩНОСТЬ ЭНТРОПИИ
- ПОРЯДОК И ХАОС
- ПРИЛОЖЕНИЯ I. МЕХАНИЧЕСКИЕ ВЕЛИЧИНЫ-ЕДИНИЦЫ И ИЗМЕРЕНИЕ
- ВРЕМЯ
- ДЛИНА
- МАССА
- СИЛА
- ПРОИЗВОДНЫЕ ЕДИНИЦЫ
- II. ПУТЕВОДИТЕЛЬ ПО СТРАНЕ ЛОГАРИФМОВ
- III. ВСЕ ИМЕЕТ ЭНТРОПИЮ











