Как найти работу газа графически

В этой заметке рассмотрим как можно вычислить работу идеального газа при различных изо-процессах. Это будет полезно тем, кто только начинает изучать термодинамику и МКТ. Для простоты изображения всех процессов возьмем самые популярные P-V диаграммы.

Есть такое понятие как термодинамический процесс. Изменение любого параметра термодинамической системы (к параметрам можно отнести температуру T, давление p, объем V, энтропию S). Но так как все параметры термодинамической системы взаимосвязаны, то частенько, когда изменяется один параметр, то и изменяются другие параметры.

Если термодинамические процессы не протекают, то система находится в равновесном состоянии. То есть равновесное состояние — такое абстрактное состояние системы, при котором все термодинамические параметры системы остаются сколь угодно долго неизменными, если над системой не совершают никаких внешних воздействий. То есть система предоставлена сама себе. Почему же это состояние абстрактно? Потому что в реальной жизни очень тяжело изолировать систему от внешнего влияния окружающего мира. Таким образом, в каждый момент времени протекают какие-то термодинамические процессы.

Однако, процессы могут протекать настолько медленно, что система изменяется почти незаметно. Иногда это дает возможность рассматривать состояние системы из последовательных равновесных состояний. Такие процессы еще называются квазистатическими. Под квазистатичностью можно понимать что-то ооочень медленное, настолько медленной, что оно длится намного дольше, чем время релаксации (время, за которое амплитудное значение внешнего возмущения, которое начало менять систему, уменьшилось в e раз).

Еще система может постоянно возвращаться к исходному состоянию. Такой круговой процесс называется циклом (примерно по таким процессам работают тепловые машины и ДВС).

Что нужно чтобы изучить какую-либо термодинамическую систему?
1. Определить работу, совершаемую в данном процессе
2. Определить изменение внутренней энергии системы
3. Определить количество теплоты, которое вошло в систему или которое отдала система.
4. Установить связи между отдельными величинами, которые характеризуют состояние рабочего тела (газа)

Основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.

И далее мы с вами выведем работы в этих основных процессах.

1. Изохорный процесс

Изохорным процесс — термодинамический процесс, который протекает при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.

2. Изотермический процесс

Изотермический процесс — термодинамический процесс, который протекает при постоянной температуре. На практике очень сложно осуществить этот процесс. Потому что при сжатии или расширении газа, нужны условия, при которых газ будет успевать обмениваться температурой с внешней средой, чтобы поддерживать свою температуру неизменной.

3. Изобарный процесс

Изобарный процесс — термодинамический процесс, который протекает при постоянном давлении. Помещение газа в плотный цилиндр с подвижным поршнем, на который действует постоянная сила ( например сила тяжести со стороны груза ) при отводе и подводе теплоты, может смоделировать такой процесс.

4. Адиабатный процесс

Адиабатный процесс — термодинамический процесс, который протекает без теплообмена (Q = 0) рабочего тела (газа) с окружающей средой. Также сложно осуществимый процесс. Примерная модель: газ помещают в цилиндр с подвижным поршнем. При этом цилиндр и поршень выполнены из высококачественного теплоизолирующего материала.

5. Политропный процесс (p∙Vⁿ = const )

Этот процесс является обобщением всех предыдущих. Все параметры в этом процессе могут меняться. А процессы выше являются его частными случаями. n – показатель политропы, некоторая постоянная, которая может принимать любые значения от -∞ до +∞.

n = 0 – изобарный процесс p = const
n = 0 – изотермический процесс T = const
n = γ – адиабатный процесс p∙Vⁿ = const
n = +∞ или n = -∞ – изохорный процесс V = const

Любые формулы для этого процесса аналогичны адиабатному процессу. При этом работа выводится точно также. Только коэффициент адиабаты (γ) в общем случае заменяется на коэффициент политропы (n).

Понравился разбор задачи ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Работа расширения или сжатия газа

Одним
из основных термодинамических процессов,
совершающихся в большинстве тепловых
машин, является процесс расширения газа
с совершением работы. Легко определить
работу, совершаемую при изобарном
расширении газа.

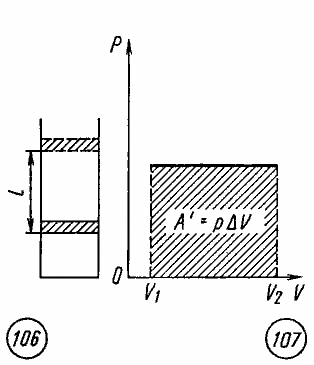
   Если
при изобарном расширении газа от объема
V₁
до объема V₂
происходит перемещение поршня в цилиндре
на расстояние l
(рис. 7.3), то работа A’,
совершенная газом, равна

,
(7.27)

где
p
— давление газа,
—
изменение его объема.

3

Рис
7.3 Рис 7.4

Как
видно из рисунка 7.4, при изображении
изобарного процесса расширения газа в
координатных осях p
, V
площадь фигуры, ограниченной графиком
процесса, координатами V₁
и V₂,
осью абсцисс, пропорциональна работе
газа A’.

Работа
при произвольном процессе расширения
газа.
Произвольный процесс расширения газа
от объема V₁
до объема V₂
можно представить как совокупность
чередующихся изобарных и изохорных
процессов.

   При
изохорных процессах работа равна нулю,
так как поршень в цилиндре не перемещается.
Работа при изобарных процессах
пропорциональна площади фигуры на
диаграмме p,
V
под соответствующим участком изобары
(рис. 7.5).

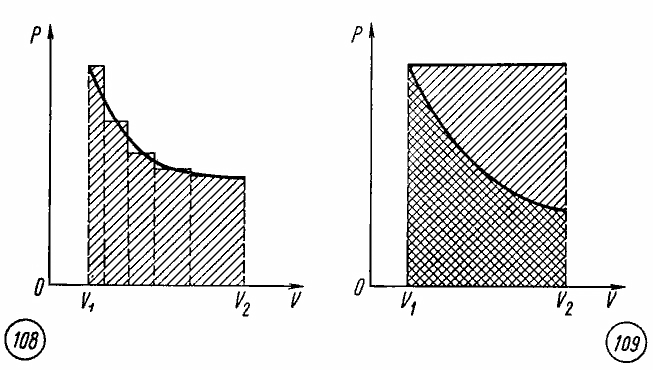
Рис.
7.5
Рис. 7.6

Следовательно,
работа при произвольном процессе
расширения газа прямо пропорциональна
площади фигуры под соответствующим
участком графика процесса на диаграмме
p,
V.

Работа
при изотермическом расширении газа.
Сравнивая площади фигур под участками
изотермы и изобары (рис. 7.6), можно сделать
вывод, что расширение газа от объема V₁
до объема V₂
при одинаковом начальном значении
давления газа сопровождается в случае
изобарного расширения совершением
большей работы.

Работа
при сжатии газа.
При расширении газа направление вектора
силы давления газа совпадает с направлением
вектора перемещения, поэтому работа
A’,
совершенная газом, положительна (A’
> 0), а работа А
внешних сил отрицательна: A
= –A’
< 0.

   При
сжатии газа направление вектора внешней
силы совпадает с направлением перемещения,
поэтому работа А
внешних сил положительна (A
> 0), а работа A’,
совершенная газом, отрицательна (A’
< 0).

Адиабатный
процесс.
Кроме изобарного, изохорного и
изотермического процессов, в термодинамике
часто рассматриваются адиабатные
процессы.

   Адиабатным
процессом
называется процесс, происходящий в
термодинамической системе при отсутствии
теплообмена с окружающими телами, т. е.
при условии Q
= 0.

   Отсутствие
теплообмена с окружающей средой может
быть обеспечено хорошей теплоизоляцией
газа. Быстрые процессы расширения или
сжатия газа могут быть близкими к
адиабатному и при отсутствии теплоизоляции,
если время, за которое происходит
изменение объема газа, значительно
меньше времени, необходимого для
установления теплового равновесия газа
с окружающими телами.

 Примерами
адиабатных процессов могут служить
процессы сжатия воздуха в цилиндре
воздушного огнива, в цилиндре двигателя
внутреннего сгорания. В соответствии
с первым законом термодинамики, при
адиабатном сжатии изменение внутренней
энергии газа
равно
работе внешних сил А:

(7.28)

Так
как работа внешних сил при сжатии
положительна, внутренняя энергия газа
при адиабатном сжатии увеличивается,
его температура повышается.

   При
адиабатном расширении газ совершает
работу A’
за счет уменьшения своей внутренней
энергии:

,
(7.29)

поэтому
температура газа при адиабатном
расширении понижается. Это можно
обнаружить в следующем опыте. Если в
бутылку, содержащую насыщенный водяной
пар, накачивать с помощью насоса воздух,
то пробка вылетает (рис. 7.7).

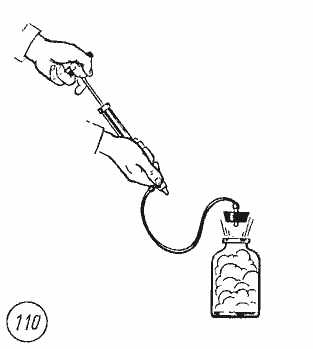
Рис.
7.7

Работа
A’
по выталкиванию пробки совершается
воздухом за счет уменьшения его внутренней
энергии, так как расширение воздуха
происходит за очень короткое время и
теплообмен с окружающей средой не
успевает произойти. Образование капель
тумана доказывает, что при адиабатном
расширении воздуха его температура
понизилась и опустилась ниже точки
росы.

График
адиабатного процесса.
Поскольку при адиабатном сжатии
температура газа повышается, то давление
газа с уменьшением объема растет быстрее,
чем при изотермическом процессе.
Понижение температуры газа при адиабатном
расширении приводит к тому, что давление
газа убывает быстрее, чем при изотермическом
расширении.

   График
адиабатного процесса в координатных
осях p,
V
представлен на рисунке 1.8. На том же
рисунке для сравнения приведен график
изотермического процесса.

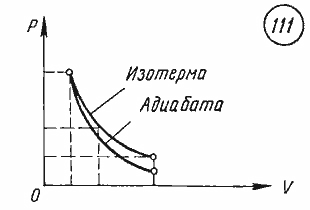
Рис.
7.8

Вну́тренняя
эне́ргия
тела (обозначается как E
или U) —
полная энергия этого тела за вычетом
кинетической
энергии
тела как целого и потенциальной
энергии
тела во внешнем поле сил. Следовательно,
внутренняя энергия складывается из
кинетической энергии хаотического
движения молекул,
потенциальной энергии взаимодействия
между ними и внутримолекулярной энергии.

Внутренняя
энергия является однозначной функцией
состояния системы. Это означает, что
всякий раз, когда система оказывается
в данном состоянии, её внутренняя энергия
принимает присущее этому состоянию
значение, независимо от предыстории
системы. Следовательно, изменение
внутренней энергии при переходе из
одного состояния в другое будет всегда
равно разности между ее значениями в
конечном и начальном состояниях,
независимо от пути, по которому совершался
переход.

Внутреннюю
энергию тела нельзя измерить напрямую.
Можно определить только изменение
внутренней энергии:

где

—подведённая
к телу теплота,
измеренная в джоулях

—работа,
совершаемая телом против внешних сил,
измеренная в джоулях

Эта
формула является математическим
выражением первого
начала термодинамики

Для
квазистатических
процессов
выполняется следующее соотношение:

где

—температура,
измеренная в кельвинах

—энтропия,
измеренная в джоулях/кельвин

—давление,
измеренное в паскалях

—химический
потенциал

—количество
частиц в системе

Идеальные
газы

Согласно
закону Джоуля, выведенному эмпирически,
внутренняя энергия идеального
газа
не зависит от давления или объёма. Исходя
из этого факта, можно получить выражение
для изменения внутренней энергии
идеального газа. По определению молярной
теплоёмкости
при постоянном объёме,
.
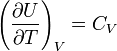Так как внутренняя энергия идеального
газа является функцией только от
температуры, то

.
(7.30)

Эта
же формула верна и для вычисления
изменения внутренней энергии любого
тела, но только в процессах при постоянном
объёме (изохорных
процессах);
в общем случае C_V
(T,V)
является функцией и температуры, и
объёма.

Если
пренебречь изменением молярной
теплоёмкости при изменении температуры,
получим:

ΔU
= νC_VΔT,
(7.31)

где
ν — количеств о вещества, ΔT —
изменение температуры.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ранее мы достаточно плотно познакомились с процессами и методами работы с ними. Среди часто используемых способов работы с процессами выделяются два: уравнение Менделеева-Клапейрона (для описания состояния идеального газа) и первое начало термодинамики. Из нескольких друг за другом идущих разных процессов можно составить общий циклический процесс.

Круговой процесс (цикл) – составной термодинамический процесс, в результате совершения которого рабочее тело (газ) возвращается в исходное состояние. Таким образом, начальное и конечное состояние газа (давление газа , объём газа  и температура газа ) одинаковы. Попробуем изобразить такой процесс в координатах  (рис. 1).

Например, наш циклический процесс 1.1 состоит из двух изохор, двух изотерм, а процесс 1.2 — из двух изобар и двух изохор. Таким образом, исходя из текстовых условий любой задачи и знания общего вида изопроцессов (именно из них чаще всего составляется цикл), можно нарисовать рисунок.

Для энергетического описания процесса (или цикла) через первое начало термодинамики необходимо обдумать два вопроса:

1. как изменяется внутренняя энергия газа ()
2. чему равна работа газа ()

• где

Для циклов есть небольшие фишки, которые удобно использовать для убыстрения задачи.

Так, изменение внутренней энергии газа зависит только от изменения температуры, а т.к. в цикле начальное и конечное состояние газа одинаково, то изменение внутренней энергии идеального газа за цикл равно 0 ().

Поиск работы для газа также можно несколько упростить. Попробуем в координатах  нарисовать график изобарического процесса и найти работу газа (рис. 2). Пусть газ находится в состоянии (давление  и объём ), далее газ изобарически перевели в состояние 2 (давление  и объём ). Тогда по определению работы газа:

(1)

Геометрически (рис. 2), произведение давления на разность объёмов численно равна площади прямоугольника, ограниченного сверху прямой (процессом), а снизу осью. В целом, эту логику можно расширить на любые процессы, тогда работа газа численно равна площади под кривой в координатах .

Также в рамках школьной физики присутствует условное деление циклов на прямые и обратные:

Прямой цикл – круговой, в котором рабочее тело совершает положительную работу за счёт сообщённой ему теплоты.

Обратный цикл — круговой, в котором рабочее тело совершает отрицательную работу.

Анализируя (1) вопрос о положительной и отрицательной работе, сводится к вопросу о соотношении между начальным и конечным объёмами, если:

• — газ расширяется, работа положительна,
• — газ сжимается, работа отрицательна.

Для графиков можно использовать следующую логику: в случае, если площадь под графиком расширения газа больше соответствующей площади для сжатия, значит цикл — прямой (рис. 3), если наоборот — обратный (рис. 4).

Таким образом, разница в прямом и обратном цикле может быть в очерёдности процессов. Так, прямой процесс, в нашем примере, — это 1-2-3-4-1, а обратный — 1-4-3-2-1.

Вывод: в задачах на циклические процессы нужно быть очень внимательным при прочтении, т.к. часть слов будет иметь глубокий физический смысл. Лучше всего процессы в таких задачах прорисовывать на графиках в координатах . Если график уже есть, то это к лучшему. Определяемся с конкретными изопроцессами, заданными в задаче, и используем это знание или через уравнение Менделеева-Клапейрона, или через первое начало термодинамики.

Данная работа представляет собой
пример проведения урока по решению графических
задач по теме “Работа в термодинамике”. Данный
метод позволяет во-первых, предоставить учащимся
возможность решить задачу у доски, не рискуя
получить неудовлетворительную отметку при
совершении ошибки, т.е. обеспечивается
психологический комфорт на уроке; во-вторых,
учащиеся, решающие задачу на своём рабочем месте,
могут сравнить своё решение с решением на доске и
участвовать в его обсуждении; в-третьих, учащиеся
могут решать задачи опережающими темпами (выбор
индивидуального образовательного маршрута);
в-четвёртых, учащиеся могут самостоятельно
выбрать себе домашнее задание, варьируя как
количество задач так и их сложность. В качестве
дидактического материала должен использоваться
раздаточный материал, содержащий как сами
задачи, так и алгоритм решения задач каждого
типа. При наличии проектирующих устройств на
экран проецируется алгоритм и задачи данного
типа. Важным фактом является то, что задачи
подобного типа являются не только
самостоятельными в данной теме, но и элементом,
лежащим в основе решения комбинированных задач
по теме “Газовые законы. Термодинамика”, т.е.
задач части “С” ЕГЭ.

Исходными данными для решения задач
являются графики pV -, pT – и VT – зависимостей. В
качестве подготовки к данному уроку учащиеся
должны повторить способы определения изменения
параметров газа по графикам происходящих с ними
процессов. Урок строится по следующему
алгоритму: учитель объясняет принцип решения
задачи данного типа, затем учащиеся
самостоятельно решают предложенные задачи
данного типа. При этом должны соблюдаться
следующие принципы:

– каждая последующая задача решается у
доски другим учащимся;

– перед учащимися, решающими задачи на
рабочем месте, ставиться цель по возможности
решить задачу быстрее, чем решение появится на
доске, и сравнить решения;

– количество предлагаемых к решению
задач должно быть избыточным, чтобы каждый
учащийся мог в соответствии со своим темпом
решить максимально возможное количество задач;

– за одну – две минуты до окончания
решения задач данного типа учащимся может быть
предложено перерисовать себе графики нерешённых
задач в качестве домашнего задания.

Определение знака работы газа
(положительная, отрицательная).

Объяснение учителя.

Работа газа прямо пропорциональна
изменению его объёма, из чего следует, что знак
работы газа определяется знаком изменения его
объёма.

Учитель показывает решение на примере
изображённого на рис.1 графика. Из графика
очевидно вытекает, что объём газа увеличивается,
т.е. его изменение – положительная величина, из
чего следует, что работа газа положительна и газ
совершает работу над внешними силами. Это можно
записать символьным способом:

А_г~V

V^=> V>0=> А_г>0,
т.е. газ совершает работу над внешними силами.

Составить задачи для решения на уроке
не представляет трудности: среди них должны быть
графики как изо-, так и не изопроцессов; объём
газа должен быть задан в них как в явном так и в
неявном виде, объём газа должен как
увеличиваться, так и уменьшаться и оставаться
неизменным (работа газа равна 0, т.е. газ не
совершает работу). Количество решаемых на уроке
задач определяется степенью подготовленности
класса, т.е. скоростью их решения , и количеством
времени, отводимом учителем на решение задач
данного типа; количество предлагаемых для
решения задач должно быть избыточным. Подборка
возможных задач дана ниже.

Сравнение работы газа в различных
процессах.

Объяснение учителя.

Модуль работы газа численно равен
площади под графиком зависимости p(V). Поэтому
сравнение работ газа в различных процессах
сводится к сравнению площадей под графиком
процесса в осях pV.

Учитель показывает решение на примере
изображённого на рисунке графика. Из графика
очевидно следует, что площадь под графиком
процесса 2-3 больше площади под графиком процесса
1-3 (заштрихованные площади). Из этого делается
вывод о том, что работа в процессе 2-3 больше
работы газа в процессе 1-2.

При решении задач учащимися они должны
обозначать и заштриховывать площади
соответствующих фигур под графиками.

При подборке задач необходимо
предусмотреть такие, в которых

– графики процессов представлены в
осях pV.

– работы газа в обоих процессах
положительны; отрицательны; работа газа в одном
из процессов положительна, в другом –
отрицательна; работа газа в одном из процессов
отрицательна, в другом – равна 0; работа газа в
одном из процессов положительна, в другом –
отрицательна, но они равны по модулю.

– при возможности полезно представить
графики процессов в осях VT или pT, провоцируя их на
ошибку делать вывод, сравнивая площади фигур под
графиками не тех зависимостей. При этом возможно
сравнить работы газа в процессах, если в одном из
них работа не совершается (изохорный процесс). В
противном случае необходимо перерисовать
графики процессов в осях pV (задача повышенного
уровня сложности).

В процессе решения задач учащимися
необходимо обратить внимание на то, что
сравниваются модули работы газа.

Количество предлагаемых учащимся для
решения задач как и в предыдущем случае
определяется учителем исходя из отводимого для
этого времени и степени подготовленности класса.
Подборка возможных задач дана ниже.

Определение работы газа в процессе,
изображённом на графике.

Объяснение учителя.

Модуль работы газа численно равен
площади под графиком зависимости p(V). Поэтому
решение задачи сводится к решению
геометрической задачи по определению площади
под графиком зависимости p(V). Рассмотрим пример
на рисунке 3.

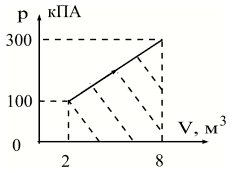
рис. 3

Модуль работы газа численно равен
площади заштрихованной фигуры, т.е. трапеции. Из
геометрии известно, что площадь трапеции равна
произведению полусуммы её оснований на высоту.

Введём обозначения: p₁ = 100 кПа; p₂
= 300 кПа; V₁ = 2 м³; V₂ = 8 м³.
Введённые обозначения полезно нанести на график
для лучшего понимания учащимися вывода формулы
для решения задачи.

| А_г| = S (численно) => | А_г| =
0,5·( p₁+ p₂)·( V₂ – V₁) = 0,5·(100·10³
+300·10³)Па·( 8 – 2) м³ = 1,2·10⁶ Дж.

Последующие задачи учащиеся решают
самостоятельно, в т.ч. и у доски.

При подборе задач необходимо
предусмотреть такие, чтобы в них присутствовали
графики:

– процессов с отрицательной работой
газа;

– нескольких последовательных
процессов, в которых в отдельных процессах
работа газа была как положительной, так и
отрицательной (и равной 0 – изохорные процессы);

– циклических процессов как с
положительной так и отрицательной работой газа
за цикл.

Полезно так же варьировать единицы
измерения давления и объёма газа. При наличии
учебного времени можно предложить графики
процессов, представленных в осях VT и pT, в этом
случае учащимся придётся сначала изобразить
процесс в осях pV с соответствующим расчётом
параметров состояний газа, а затем уже
определять работу газа.

В качестве домашнего задания учащимся
предлагается как минимум решить дома ещё раз
задачи, решённые в классе. В этом случае у них
появляется возможность самопроверки
правильности решения. Домашнее задание в большем
объёме регулируется учителем исходя из
поставленных учебных задач. При этом каждый
учащийся может выбрать для себя домашнее задание
требуемого объёма и уровня сложности.

Таким образом, реализация этого метода
позволяет

– создать комфортный психологический
климат на уроке;

– предоставить возможность большему,
чем при традиционных методах, количеству
учащихся решить задачу у доски под контролем
учителя;

– получить опыт проверки чужих решений,
сравнения со своим решением и при необходимости
его корректировке;

– каждому учащемуся выбрать свой
образовательный маршрут, регулируя как
количество решаемых на уроке задач, так и объём
домашнего задания по количеству и уровню
сложности выбираемых задач.

Ниже предложены возможные задачи для
использования на уроке. Очевидно, что учитель
может сделать свою подборку в соответствии с
уровнем подготовленности класса.

Задачи на определение знака работы.

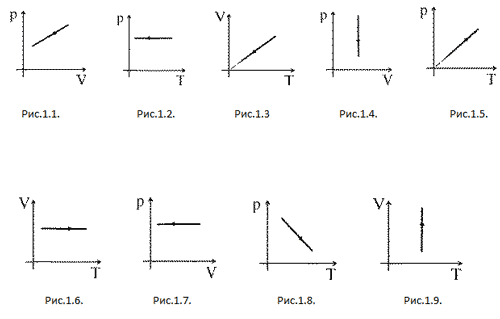
Задачи на сравнение газа в различных
процессах.

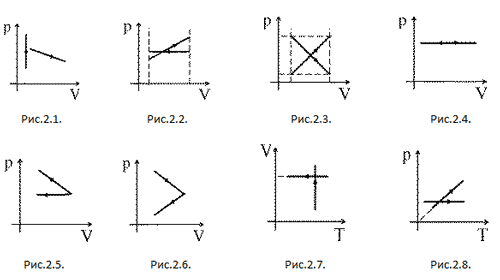
Задачи на определение работы газа.

Термодинамика

Термодинамика – это раздел физики, изучающий тепловые свойства макроскопических тел и систем тел, находящихся в состоянии теплового равновесия, на основе закона сохранения энергии, без учета внутреннего строения тел, составляющих систему.

Термодинамика не рассматривает микроскопические величины – размеры атомов и молекул, их массы и количество.

Законы термодинамики устанавливают связи между непосредственно наблюдаемыми физическими величинами, характеризующими состояние системы, такими как давление ​( p )​, объем ​( V )​, температура ​( T )​.

Внутренняя энергия

Внутренняя энергия – это физическая величина, равная сумме кинетической энергии теплового движения частиц тела и потенциальной энергии их взаимодействия друг с другом.

Обозначение – ​( U )​, в СИ единица измерения – Джоуль (Дж).

В термодинамике внутренняя энергия зависит от температуры и объема тела.

Внутренняя энергия тел зависит от их температуры, массы и агрегатного состояния. С ростом температуры внутренняя энергия увеличивается. Наибольшая внутренняя энергия у вещества в газообразном состоянии, наименьшая – в твердом.

Внутренняя энергия идеального газа представляет собой только кинетическую энергию теплового движения его частиц; потенциальная энергия взаимодействия частиц равна нулю.

Внутренняя энергия идеального газа прямо пропорциональна его температуре, а от объема не зависит (молекулы идеального газа не взаимодействуют друг с другом):

где ​( i )​ – коэффициент, равный числу степеней свободы молекулы, ​( nu )​ – количество вещества, ​( R )​ – универсальная газовая постоянная, ​( T )​ – абсолютная температура.

Число степеней свободы равно числу возможных движений частицы.

Важно!
Для одноатомных газов коэффициент ​( i )​ = 3, для двухатомных газов ​( i )​ = 5.

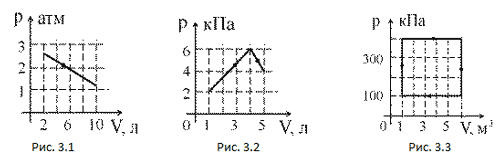
На практике часто важно уметь находить изменение внутренней энергии:

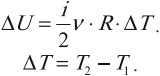
При решении задач можно записать формулу для вычисления внутренней энергии, используя уравнение Менделеева–Клапейрона:

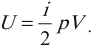
где ​( p )​ – давление, ​( V )​ – объем газа.

Внутренняя энергия реальных газов зависит как от температуры, так и от объема.

Изменить внутреннюю энергию можно за счет изменения температуры (при теплопередаче) и за счет изменения давления и объема (при совершении работы).

Тепловое равновесие

Тепловое равновесие – это состояние системы, при котором все ее макроскопические параметры остаются неизменными сколь угодно долго.

Величины, характеризующие состояние макроскопических тел без учета их молекулярного строения, называются макроскопическими параметрами. К ним относятся давление и температура, объем, масса, концентрация отдельных компонентов смеси газа и др. В состоянии теплового равновесия отсутствует теплообмен с окружающими телами, отсутствуют переходы вещества из одного агрегатного состояния в другое, не меняются температура, давление, объем.

Любая термодинамическая система переходит самопроизвольно в состояние теплового равновесия. Каждому состоянию теплового равновесия, в которых может находиться термодинамическая система, соответствует определенная температура.

Важно!
В состоянии теплового равновесия объем, давление могут быть различными в разных частях термодинамической системы, и только температура во всех частях термодинамической системы, находящейся в состоянии теплового равновесия, является одинаковой. Микроскопические процессы внутри тела не прекращаются и при тепловом равновесии: меняются положения молекул, их скорости при столкновениях.

Теплопередача

Теплопередача – процесс изменения внутренней энергии тела без совершения работы.

Существуют три вида теплопередачи: теплопроводность, конвекция и излучение (лучистый теплообмен). Теплопередача происходит между телами, имеющими разную температуру. Тепло передается от тела с более высокой температурой к телу с более низкой температурой.

Теплопроводность – это процесс переноса энергии от более нагретых тел (частей тела) к менее нагретым в результате движения и взаимодействия частиц тела. Высокую теплопроводность имеют металлы – так, лучшие проводники тепла – медь, золото, серебро. Теплопроводность жидкостей меньше, а газы являются плохими проводниками тепла. Пористые тела плохо проводят тепло, так как в порах содержится воздух. Вещества с низкой теплопроводностью используют в качестве теплоизоляторов. Теплопроводность невозможна в вакууме. При теплопроводности не происходит переноса вещества.

Явление теплопроводности газов аналогично явлению диффузии. Быстрые молекулы из слоя с более высокой температурой перемещаются в более холодный слой, а молекулы из холодного слоя перемещаются в более нагретый. За счет этого средняя кинетическая энергия молекул более теплого слоя уменьшается, и его температура становится ниже.

В жидкостях и твердых телах при повышении температуры какого-либо участка твердого тела или жидкости его частицы начинают колебаться сильнее. Соударяясь с соседними частицами, где температура ниже, эти частицы передают им часть своей энергии, и температура этого участка возрастает.

Конвекция – перенос энергии потоками жидкости или газа.

Объяснить механизм конвекции можно на основе теплового расширения тел и закона Архимеда. При нагревании объем жидкости увеличивается, а плотность уменьшается. Нагретый слой под действием силы Архимеда поднимается вверх, а холодный опускается вниз. Это естественная конвекция. Она возникает при неравномерном нагревании жидкости или газа снизу в поле тяготения.

При вынужденной конвекции перемещение вещества происходит под действием насосов, лопастей вентилятора. Такая конвекция применяется в состоянии невесомости. Интенсивность конвекции зависит от разности температур слоев среды и агрегатного состояния вещества. Конвекционные потоки поднимаются вверх. При конвекции происходит перенос вещества.

В твердых телах конвекция невозможна, так как частицы не могут из-за сильного взаимодействия покидать свои места. В вакууме конвекция также невозможна.

Примером конвективных потоков в природе являются ветры (бризы дневной и ночной, муссоны).

Излучение (лучистый теплообмен) – перенос энергии электромагнитными волнами. Перенос тепла излучением возможен в вакууме. Источником излучения является любое тело, температура которого отлична от нуля К. При поглощении энергия теплового излучения переходит во внутреннюю энергию. Темные тела быстрее нагреваются излучением, чем тела с блестящей поверхностью, но и остывают быстрее. Мощность излучения зависит от температуры тела. С увеличением температуры тела энергия излучения увеличивается. Чем больше площадь поверхности тела, тем интенсивнее излучение.

Количество теплоты. Удельная теплоемкость вещества

Количество теплоты – это скалярная физическая величина, равная энергии, которую тело получило или отдало при теплопередаче.

Обозначение – ​( Q )​, в СИ единица измерения – Дж.

Удельная теплоемкость – это скалярная физическая величина, численно равная количеству теплоты, которое тело массой 1 кг получает или отдает при изменении его температуры на 1 К.

Обозначение – ​( c )​, в СИ единица измерения – Дж/(кг·К).

Удельная теплоемкость определяется не только свойствами вещества, но и тем, в каком процессе осуществляется теплопередача. Поэтому выделяют удельную теплоемкость газа при постоянном давлении – ​( c_P )​ и удельную теплоемкость газа при постоянном объеме – ​( c_V )​. Для нагревания газа на 1 К при постоянном давлении требуется большее количество теплоты, чем при постоянном объеме – ​( c_P > c_V )​.

Формула для вычисления количества теплоты, которое получает тело при нагревании или отдает при охлаждении:

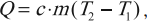
где ​( m )​ – масса тела, ​( c )​ – удельная теплоемкость, ​( T_2 )​ – конечная температура тела, ​( T_1 )​ – начальная температура тела.

Важно!
При решении задач на расчет количества теплоты при нагревании или охлаждении можно не переводить температуру в кельвины. Так как 1К=1°С, то​( Delta T=Delta t )​.

Работа в термодинамике

Работа в термодинамике равна изменению внутренней энергии тела.

Обозначение работы газа – ​( A’ )​, единица измерения в СИ – джоуль (Дж). Обозначение работы внешних сил над газом – ​( A )​.

Работа газа ​( A’ =-A )​.

Работой расширения идеального газа называют работу, которую газ совершает против внешнего давления.

Работа газа положительна при расширении и отрицательна при его сжатии. Если объем газа не изменяется (изохорный процесс), то работы газ не совершает.

Графически работа газа может быть вычислена как площадь фигуры под графиком зависимости давления от объема в координатных осях ​( (p,V) )​, ограниченная графиком, осью ​( V )​ и перпендикулярами, проведенными из точек начального и конечного значений объема.

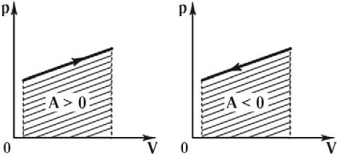
Формула для вычисления работы газа:

в изобарном процессе ​( A’=pcdotDelta V. )​

в изотермическом процессе ( A’=frac{m}{M}RTlnfrac{V_2}{V_1}. )​

Уравнение теплового баланса

Если система тел является теплоизолированной, то ее внутренняя энергия не будет изменяться несмотря на изменения, происходящие внутри системы. Если ​( A )​ = 0, ​( Q )​ = 0, то и ​( Delta U )​ = 0 .

При любых процессах, происходящих в теплоизолированной системе, ее внутренняя энергия не изменяется (закон сохранения внутренней энергии).

Рассмотрим теплоизолированную систему из двух тел с разными температурами. При контакте между ними будет проходить теплообмен. Тело с большей температурой будет отдавать некоторое количество теплоты, а тело с меньшей температурой – получать, пока температуры тел не станут равными. Так как суммарная внутренняя энергия не должна изменяться, то, на сколько уменьшится внутренняя энергия более нагретого тела, на столько должна увеличиться внутренняя энергия второго тела. Так как работа не совершается, то изменение внутренней энергии равно количеству теплоты.

Количество теплоты, отданное при теплообмене телом с большей температурой, равно по модулю количеству теплоты, полученному телом с меньшей температурой:

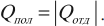
Другая формулировка: если тела образуют замкнутую систему и между ними происходит только теплообмен, то алгебраическая сумма отданных ​( Q_{отд} )​ и полученных ( Q_{пол} ) количеств теплоты равна нулю:

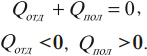
Первый закон термодинамики

Закон сохранения и превращения энергии, распространенный на тепловые явления, называется первым законом (началом) термодинамики.

Можно дать формулировку этого закона исходя из способов изменения внутренней энергии.

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

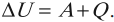
Если рассматривать работу самой системы над внешними телами, то закон может быть сформулирован так:

количество теплоты, переданное системе, идет на изменение ее внутренней энергии и совершение системой работы над внешними телами:

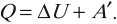
Если система изолирована и над ней не совершается работа и нет теплообмена с внешними телами, то в этом случае внутренняя энергия не изменяется. Если к системе не поступает теплота, то работа системой может совершаться только за счет уменьшения внутренней энергии. Это значит, что невозможно создать вечный двигатель – устройство, способное совершать работу без каких-либо затрат топлива.

Первый закон термодинамики для изопроцессов

Изотермический процесс: ​( Q=A’,(T=const, Delta U=0) )​
Физический смысл: все переданное газу тепло идет на совершение работы.

Изобарный процесс: ( Q=Delta U+A’ )​
Физический смысл: подводимое к газу тепло идет на увеличение его внутренней энергии и на совершение газом работы.

Изохорный процесс: ( Q=Delta U,(V=const, A’=0) )​
Физический смысл: внутренняя энергия газа увеличивается за счет подводимого тепла.

Адиабатный процесс: ​( Delta U=-A’ )​ или ​( A=Delta U,mathbf{(Q=0)} )​
Физический смысл: внутренняя энергия газа уменьшается за счет совершения газом работы. Температура газа при этом понижается.

Задачи об изменении внутренней энергии тел

Такие задачи можно разделить на группы:

• При взаимодействии тел изменяется их внутренняя энергия без совершения работы над внешней средой.
• Рассматриваются явления, связанные с превращением одного вида энергии в другой при взаимодействии двух тел. В результате происходит изменение внутренней энергии одного тела вследствие совершенной им или над ним работы.

При решении задач первой группы:

• установить, у каких тел внутренняя энергия уменьшается, а у каких – возрастает;
• составить уравнение теплового баланса ​( (Delta U=0) ), при записи которого в выражении ​( Q =cm(t_2 – t_1) )​ для изменения внутренней энергии нужно вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака;
• решить полученное уравнение относительно искомой величины;
• проверить решение.

При решении задач второй группы:

• убедиться, что в процессе взаимодействия тел теплота извне к ним не подводится, т.е. действительно ли ​( Q = 0 )​;
• установить, у какого из двух взаимодействующих тел изменяется внутренняя энергия и что является причиной этого изменения – работа, совершенная самим телом, или работа, совершенная над телом;
• записать уравнение ​( Q = Delta U + A )​ для тела, у которого изменяется внутренняя энергия, учитывая знак перед работой и КПД рассматриваемого процесса;
• если работа совершается за счет уменьшения внутренней энергии одного из тел, то ​( А= -Delta U )​, а если внутренняя энергия тела увеличивается за счет работы, совершенной над телом, то ​( A=Delta U )​;
• найти выражения для ​( Delta U )​ и ​( A )​;
• подставить в исходное уравнение вместо ( Delta U ) и ( A ) выражения для них, получить окончательное соотношение для определения искомой величины;
• решить полученное уравнение относительно искомой величины;
• проверить решение.

Второй закон термодинамики

Все процессы в природе протекают только в одном направлении. В обратном направлении самопроизвольно они протекать не могут. Необратимым называется процесс, обратный которому может протекать только как составляющая более сложного процесса.

Примеры необратимых процессов:

• переход тепла от более нагретого тела к менее нагретому телу;
• переход механической энергии во внутреннюю энергию.

Первый закон термодинамики ничего не говорит о направлении процессов в природе.

Второй закон термодинамики выражает необратимость процессов, происходящих в природе. Существует несколько его формулировок.

Второй закон термодинамики (формулировка Клаузиуса):
невозможно перевести тепло от более холодной системы к более горячей при отсутствии одновременных изменений в обеих системах или окружающих телах.

Второй закон термодинамики (формулировка Кельвина):
невозможно осуществить такой периодический процесс, единственным результатом которого было бы получение работы за счет теплоты, взятой от одного источника.

Эта формулировка говорит также и о том, что невозможно построить вечный двигатель второго рода, то есть двигатель, совершающий работу за счет охлаждения какого-либо одного тела.

Важно!
В формулировке второго закона термодинамики большое значение имеют слова «единственным результатом». Если процессы, о которых идет речь, не являются единственными, то запреты снимаются. Например, в холодильнике происходит передача тепла от более холодного тела к нагретому и при этом осуществляется компенсирующий процесс превращения механической энергии окружающих тел во внутреннюю энергию.

Второй закон термодинамики выполняется для систем с огромным числом частиц. В системах с малым количеством частиц возможны флуктуации – отклонения от равновесия.

КПД тепловой машины

Коэффициентом полезного действия (КПД) тепловой машины (двигателя) называется отношение работы ​( A )​, совершаемой двигателем за цикл, к количеству теплоты ​( Q_1 )​, полученному за цикл от нагревателя:

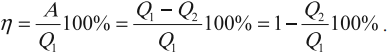
Тепловая машина с максимальным КПД была создана Карно. В машине осуществляется круговой процесс (цикл Карно), при котором после ряда преобразований система возвращается в начальное состояние.

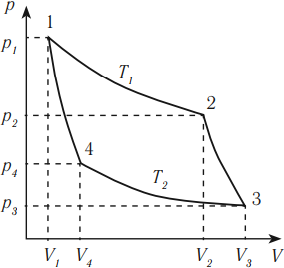
Цикл Карно состоит из четырех стадий:

1. Изотермическое расширение (на рисунке — процесс 1–2). В начале процесса рабочее тело имеет температуру ​( T_1 )​, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передает ему количество теплоты ​( Q_1 )​. При этом объем рабочего тела увеличивается.
2. Адиабатное расширение (на рисунке — процесс 2–3). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника ​( T_2 )​.
3. Изотермическое сжатие (на рисунке — процесс 3–4). Рабочее тело, имеющее к тому времени температуру ​( T_2 )​, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты ​( Q_2 )​.
4. Адиабатное сжатие (на рисунке — процесс 4–1). Рабочее тело отсоединяется от холодильника. При этом его температура увеличивается до температуры нагревателя ​( T_1 )​.

КПД цикла Карно:

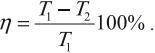
Отсюда видно, что КПД цикла Карно с идеальным газом зависит только от температуры нагревателя ​( (T_1) )​ и холодильника ( (T_2) ).

Из уравнения следуют выводы:

• для повышения КПД тепловой машины нужно увеличить температуру нагревателя и уменьшить температуру холодильника;
• КПД тепловой машины всегда меньше 1.

Цикл Карно обратим, так как все его составные части являются равновесными процессами.

КПД тепловых двигателей: двигатель внутреннего сгорания — 30%, дизельный двигатель — 40%, паровая турбина — 40%, газовая турбина — 25–30%.

Принципы действия тепловых машин

Тепловым двигателем называют устройство, преобразующее внутреннюю энергию топлива в механическую энергию.

Основные части теплового двигателя:

• Нагреватель – тело с постоянной температурой, преобразующее внутреннюю энергию топлива в энергию газа. В каждом цикле работы двигателя нагреватель передает рабочему телу некоторое количество теплоты.
• Рабочее тело – это газ, совершающий работу при расширении.
• Холодильник – тело с постоянной температурой, которому рабочее тело передает часть тепла.

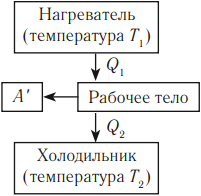
Любая тепловая машина получает от нагревателя некоторое количество теплоты ​( Q_1 )​ и передает холодильнику количество теплоты ​( Q_2 )​. Так как ​( Q_1 > Q_2 )​, то совершается работа ​( A’ = Q_1 – Q_2 )​.

Тепловой двигатель должен работать циклически, поэтому расширение рабочего тела должно сменяться его сжатием. Работа расширения газа должна быть больше работы сжатия, совершаемой внешними силами (условие совершения полезной работы). Температура газа при расширении должна быть выше, чем температура при сжатии. Тогда давление газа во всех промежуточных состояниях при сжатии будет меньше, чем при расширении.

В реальных тепловых машинах нагревателем является камера сгорания. В них рабочее тело нагревается за счет тепла, выделяющегося при сгорании топлива. Количество теплоты, выделяющееся при сгорании топлива, вычисляется по формуле:

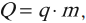
где ​( q )​ – удельная теплота сгорания топлива, ​( m )​ – масса топлива.

Холодильником чаще всего у реальных двигателей служит атмосфера.

Виды тепловых двигателей:

• паровой двигатель;
• турбина (паровая, газовая);
• двигатель внутреннего сгорания (карбюраторный, дизельный);
• реактивный двигатель.

Тепловые двигатели широко используются на всех видах транспорта: на автомобилях – двигатели внутреннего сгорания; на железнодорожном транспорте – дизельные двигатели (на тепловозах); на водном транспорте – турбины; в авиации – турбореактивные и реактивные двигатели. На тепловых и атомных электростанциях тепловые двигатели приводят в движение роторы генераторов переменного тока.

Проблемы энергетики и охрана окружающей среды

Тепловые двигатели широко применяются на транспорте и в энергетике (тепловые и атомные электростанции). Использование тепловых двигателей сильно влияет на состояние биосферы Земли. Можно выделить следующие вредные факторы:

• при сжигании топлива используется кислород из атмосферы, что приводит к снижению содержания кислорода в воздухе;
• при сгорании топлива в атмосферу выделяется углекислый газ. Концентрация углекислого газа в атмосфере повышается. Это изменяет прозрачность атмосферы, так как молекулы углекислого газа поглощают инфракрасное излучение, что ведет к повышению температуры (парниковый эффект);
• при сжигании угля в атмосферу поступают азотные, серные соединения и соединения свинца, вредные для здоровья человека.

Решение проблемы охраны окружающей среды от вредного воздействия предприятий тепловой энергетики требует комплексного подхода. Массовыми загрязнителями при работе тепловых электростанций являются летучая зола, диоксид серы и оксиды азота. Методы сокращения выбросов зависят от свойств топлива и условия его сжижения. Предотвращение загрязнения летучей золой достигается очисткой всего объема продуктов сгорания твердого топлива в высокоэффективных золоуловителях. Сокращение выбросов оксидов азота с продуктами сгорания топлива на тепловых электростанциях, а также в парогазовых и газотурбинных установках обеспечивается, главным образом, технологией сжигания топлива. Уменьшение выброса диоксида серы может быть достигнуто различными методами облагораживания и переработки топлива вне тепловых электростанций либо непосредственно на тепловых электростанциях, а также очисткой дымовых газов.

Контроль за выбросом вредных веществ электростанций осуществляется специальными приборами.

В ряде случаев достаточно эффективным решением вопросов очистки выбросов в атмосферу остается сооружение фильтров-уловителей и дымовых труб. У дымовой трубы два назначения: первое — создавать тягу и тем самым заставлять воздух — обязательный участник процесса горения — в нужном количестве и с должной скоростью входить в топку; второе — отводить продукты горения (вредные газы и имеющиеся в дыме твердые частицы) в верхние слои атмосферы. Благодаря непрерывному турбулентному движению вредные газы и твердые частицы уносятся далеко от источника их возникновения и рассеиваются.

Для рассеивания сернистого ангидрида, содержащегося в дымовых трубах тепловых электростанций, сооружаются дымовые трубы высотой 180, 250 и 320 м. Тепловые электростанции России, работающие на твердом топливе, за год выбрасывают в отвалы около 100 млн т золы и шлаков. Зола и шлаки занимают большие площади земель, неблагоприятно влияют на окружающую среду.

Более половины всех загрязнений создает транспорт. Один из путей решения проблемы защиты окружающей среды заключается в переходе на дизельные двигатели, электродвигатели, повышение КПД.

Алгоритм решения задач раздела «Термодинамика»:

• выделить систему тел и определить ее тип (замкнутая, адиабатически замкнутая, замкнутая в механическом смысле, незамкнутая);
• выяснить, как изменяются параметры состояния ​( (p,V,T) )​ и внутренняя энергия каждого тела системы при переходе из одного состояния в другое;
• записать уравнения, связывающие параметры двух состояний системы, формулы для расчета изменения внутренней энергии каждого тела системы при переходе из одного состояния в другое;
• определить изменение механической энергии системы и работу внешних сил по изменению ее объема;
• записать формулу первого закона термодинамики или закона сохранения и превращения энергии;
• решить систему уравнений относительно искомой величины;
• проверить решение.

Основные формулы раздела «Термодинамика»