Как найти работу газа при изобарном процессе

В этой заметке рассмотрим как можно вычислить работу идеального газа при различных изо-процессах. Это будет полезно тем, кто только начинает изучать термодинамику и МКТ. Для простоты изображения всех процессов возьмем самые популярные P-V диаграммы.

Есть такое понятие как термодинамический процесс. Изменение любого параметра термодинамической системы (к параметрам можно отнести температуру T, давление p, объем V, энтропию S). Но так как все параметры термодинамической системы взаимосвязаны, то частенько, когда изменяется один параметр, то и изменяются другие параметры.

Если термодинамические процессы не протекают, то система находится в равновесном состоянии. То есть равновесное состояние — такое абстрактное состояние системы, при котором все термодинамические параметры системы остаются сколь угодно долго неизменными, если над системой не совершают никаких внешних воздействий. То есть система предоставлена сама себе. Почему же это состояние абстрактно? Потому что в реальной жизни очень тяжело изолировать систему от внешнего влияния окружающего мира. Таким образом, в каждый момент времени протекают какие-то термодинамические процессы.

Однако, процессы могут протекать настолько медленно, что система изменяется почти незаметно. Иногда это дает возможность рассматривать состояние системы из последовательных равновесных состояний. Такие процессы еще называются квазистатическими. Под квазистатичностью можно понимать что-то ооочень медленное, настолько медленной, что оно длится намного дольше, чем время релаксации (время, за которое амплитудное значение внешнего возмущения, которое начало менять систему, уменьшилось в e раз).

Еще система может постоянно возвращаться к исходному состоянию. Такой круговой процесс называется циклом (примерно по таким процессам работают тепловые машины и ДВС).

Что нужно чтобы изучить какую-либо термодинамическую систему?
1. Определить работу, совершаемую в данном процессе
2. Определить изменение внутренней энергии системы
3. Определить количество теплоты, которое вошло в систему или которое отдала система.
4. Установить связи между отдельными величинами, которые характеризуют состояние рабочего тела (газа)

Основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.

И далее мы с вами выведем работы в этих основных процессах.

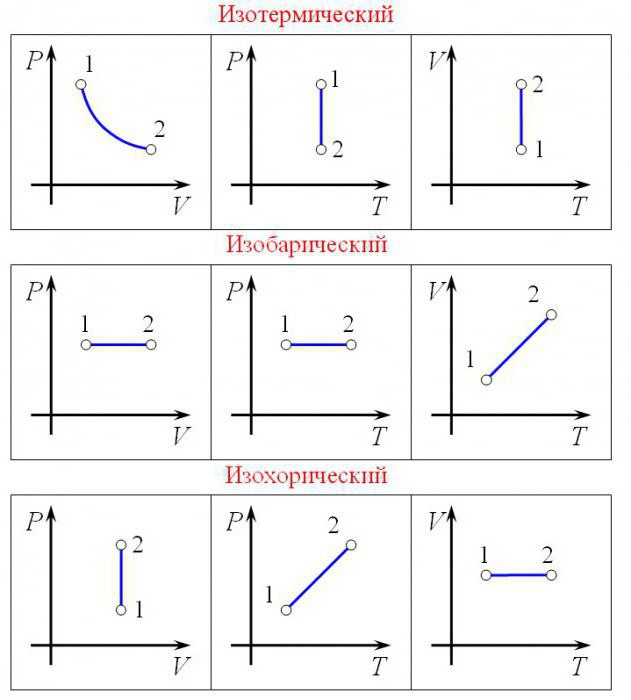
1. Изохорный процесс

Изохорным процесс — термодинамический процесс, который протекает при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.

2. Изотермический процесс

Изотермический процесс — термодинамический процесс, который протекает при постоянной температуре. На практике очень сложно осуществить этот процесс. Потому что при сжатии или расширении газа, нужны условия, при которых газ будет успевать обмениваться температурой с внешней средой, чтобы поддерживать свою температуру неизменной.

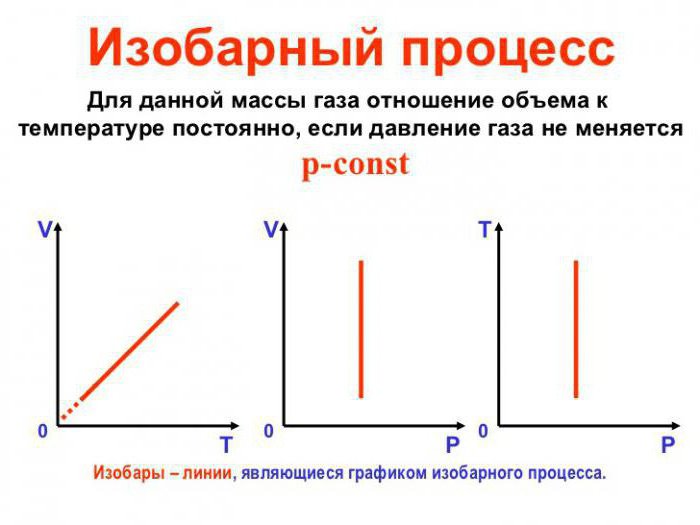
3. Изобарный процесс

Изобарный процесс — термодинамический процесс, который протекает при постоянном давлении. Помещение газа в плотный цилиндр с подвижным поршнем, на который действует постоянная сила ( например сила тяжести со стороны груза ) при отводе и подводе теплоты, может смоделировать такой процесс.

4. Адиабатный процесс

Адиабатный процесс — термодинамический процесс, который протекает без теплообмена (Q = 0) рабочего тела (газа) с окружающей средой. Также сложно осуществимый процесс. Примерная модель: газ помещают в цилиндр с подвижным поршнем. При этом цилиндр и поршень выполнены из высококачественного теплоизолирующего материала.

5. Политропный процесс (p∙Vⁿ = const )

Этот процесс является обобщением всех предыдущих. Все параметры в этом процессе могут меняться. А процессы выше являются его частными случаями. n – показатель политропы, некоторая постоянная, которая может принимать любые значения от -∞ до +∞.

n = 0 – изобарный процесс p = const
n = 0 – изотермический процесс T = const
n = γ – адиабатный процесс p∙Vⁿ = const
n = +∞ или n = -∞ – изохорный процесс V = const

Любые формулы для этого процесса аналогичны адиабатному процессу. При этом работа выводится точно также. Только коэффициент адиабаты (γ) в общем случае заменяется на коэффициент политропы (n).

Понравился разбор задачи ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Изобарный процесс, связанные с ним уравнения и вывод формулы работы

Изобарный процесс (также называемый изобарическим процессом) является одним из термодинамических процессов, которые происходят при постоянном показателе давления. Масса газа системы при этом также остается постоянной. Наглядное представление о графике, демонстрирующем изобарный процесс, дает термодинамическая диаграмма в соответствующей системе координат.

Примеры

Наиболее простым примером изобарического процесса можно назвать нагревание некоторого объема воды в открытом сосуде. В качестве еще одного примера можно привести расширение идеального газа в цилиндрическом объеме, где поршень имеет свободный ход. В каждом из этих случаев давление будет постоянным. Оно равно обыкновенному атмосферному давлению, что вполне очевидно.

Обратимость

Изобарный процесс можно считать обратимым в том случае, если давление в системе совпадает с внешним давлением и равно во все моменты времени процесса (то есть оно постоянно по своему значению), а температура изменяется очень медленно. Таким образом, термодинамическое равновесие в системе сохраняется в каждый момент времени. Именно совокупность вышеперечисленных факторов дает нам возможность считать изобарный процесс обратимым.

Чтобы осуществить в системе изобарический процесс, теплоту к ней нужно или подводить, или отводить. При этом теплота должна расходоваться на работу расширения идеального газа и на изменение его внутренней энергии. Формулу, демонстрирующую зависимость величин друг от друга при изобарном процессе, называют законом Гей-Люссака. Она показывает, что объем пропорционален температуре. Давайте выведем эту формулу на основании поверхностных знаний.

Вывод закона Гей-Люссака (первичное понимание)

Человек, хотя бы немного разбирающийся в молекулярной физике, знает, что многие задачи связаны с определенными параметрами. Имя им – давление газа, объем газа и температура газа. В тех или иных случаях в ход идут молекулярная и молярная масса, количество вещества, универсальная газовая постоянная и другие показатели. И здесь есть определенная связь. Давайте поговорим об универсальной газовой постоянной подробнее. На тот случай, если кто-то не знает, каким образом ее получили.

Получение универсальной газовой постоянной

Эту константу (постоянное число с определенной размерностью) принято также называть постоянной Менделеева. Она присутствует также в уравнении Менделеева-Клапейрона для идеального газа. Как же получил наш знаменитый физик эту константу?

Как мы знаем, уравнение идеального газа имеет следующую форму: PV/T (что озвучивается так: “произведение давления на объем, деленное на температуру”). По отношению к универсальной газовой постоянной применим так называемый закон Авогадро. Он гласит о том, что если мы возьмем любой газ, то одинаковое его количество молей при одинаковой температуре и одинаковом давлении займет одинаковый объем.

По сути дела, это есть словесная формулировка уравнения состояния идеального газа, которое было записано в виде формулы немного ранее. Если мы возьмем нормальные условия (а это когда температура газа равна 273,15 Кельвинов, давление равно 1 атмосфере, соответственно, 101325 Паскалей, а объем моля газа равен 22,4 литра) и подставим их в уравнение, все перемножим и разделим, то получим, что совокупность подобных действий дает нам численный показатель, равный 8,31. Размерность дается в Джоулях, деленных на произведение моля на Кельвин (Дж/моль*К).

Уравнение Менделеева-Клапейрона

Давайте возьмем уравнение состояния идеального газа и перепишем его в новом виде. Изначальное уравнение, напомним, имеет вид PV/T=R. А теперь умножим обе части на температурный показатель. Получим формулу PV(м)=RT. То есть произведение давления на объем равно произведению универсальной газовой постоянной на температуру.

Теперь умножим обе части уравнения на то или иное количество молей. Обозначим их количество буквой, скажем, X. Таким образом, получим следующую формулу: PV(м)X=XRT. Но ведь мы знаем, что произведение V с индексом “м” дает нам в результате просто объем V, а число молей X раскрывается в виде деления частной массы на молярную массу, то есть имеет вид m/M.

Таким образом, конечная формула будет выглядеть следующим образом: PV=MRT/m. Это и есть то самое уравнение Менделеева-Клапейрона, к которому пришли оба физика практически одновременно. Мы можем умножить правую часть уравнения (и в то же время разделить) на число Авогадро. Тогда получим: PV = XN(a)RT/N(a). Но ведь произведение количества молей на число Авогадро, то есть XN(a), дает нам не что иное, как общее число молекул газа, обозначаемое буквой N.

В то же время частное от универсальной газовой постоянной и числа Авогадро – R/N(a) даст постоянную Больцмана (обозначается k). В итоге мы получим еще одну формулу, но уже в несколько другом виде. Вот она: PV=NkT. Можно раскрыть эту формулу и получить следующий результат: NkT/V=P.

Работа газа при изобарном процессе

Как мы выяснили ранее, изобарным процессом называется термодинамический процесс, при котором давление остается величиной постоянной. А чтобы выяснить, как будет определяться работа при изобарном процессе, нам придется обратиться к первому началу термодинамики. Общая формула выглядит следующим образом: dQ = dU + dA, где dQ – это количество теплоты, dU – изменение внутренней энергии, а dA – работа, совершаемая в ходе выполнения термодинамического процесса.

Теперь рассмотрим конкретно изобарный процесс. Примем во внимание тот фактор, что давление остается постоянным. Теперь попытаемся переписать первое начало термодинамики для изобарного процесса: dQ = dU + pdV. Чтобы получить наглядное представление о процессе и работе, нужно изобразить его в системе координат. Ось абсцисс обозначим p, ось ординат V. Пускай объем будет увеличиваться. В двух отличных друг от друга точках с соответствующим значением p (конечно же, фиксированным) отметим состояния, представляющие собой V1 (первоначальный объем) и V2 (конечный объем). В этом случае график будет представлять собой прямую линию, параллельную оси абсцисс.

Найти работы в таком случае проще простого. Это будет просто площадь фигуры, ограниченная с двух сторон проекциями на ось абсцисс, а с третьей стороны – прямой линией, соединяющей точки, лежащие, соответственно, в начале и конце изобарной прямой. Попробуем вычислить значение работы при помощи интеграла.

Он будет вычисляться следующим образом: A = p (интеграл в пределах от V1 до V2) dV. Раскроем интеграл. Получим, что работа будет равна произведению давления на разность объемов. То есть выглядеть формула будет следующим образом: A = p (V2 – V1). Если мы раскроем некоторые величины, то получим еще одну формулу. Она выглядит так: A = xR (T2 – T2), где x – количество вещества.

Универсальная газовая постоянная и ее смысл

Можно сказать, что последнее выражение будет определять физический смысл R – универсальной газовой постоянной. Чтобы было понятнее, давайте обратимся к конкретным числам. Возьмем для проверки один моль какого-либо вещества. В то же время пускай температурная разница будет составлять 1 Кельвин. В этом случае легко заметить, что работа газа будет равна универсальной газовой постоянной (или же наоборот).

Заключение

Этот факт можно подать немного в другом свете, перефразировав формулировку. Например, универсальная газовая постоянная будет численно равна работе, совершаемой при изобарном расширении одним молем идеального газа, если он нагревается на один Кельвин. Вычислить работу при других изопроцессах будет несколько сложнее, но главное – при этом применять логику. Тогда все быстро встанет на свои места, и вывод формулы окажется проще, чем вы думаете.

Изобарический процесс

Вы будете перенаправлены на Автор24

Что такое изобарический процесс

Изобарическим (или изобарным) процессом называется процесс, происходящий в неизменной массе газа при постоянном давлении.

Запишем уравнение для двух состояний идеального газа:

[pV_1=nu RT_1left(1right),] [pV_2=nu RT_2 left(2right).]

Разделим уравнение (2) на уравнение (1), получим уравнение изобарного процесса:

Уравнение (4) называют законом Гей-Люссака.

Внутренняя энергия и количество теплоты изобарического процесса

Этот процесс происходит с подводом тепла, если объем увеличивается, или его отводом, чтобы уменьшать объем. Запишем первое начало термодинамики, последовательно получим выражения для работы, внутренней энергии и количества теплоты изобарного процесса:

где $delta Q $- элементарное тепло, подводимое к системе, $dU$- изменение внутренней энергии газа в проводимом процессе, $dA$- элементарная работа, которую совершает газ в процессе, i-число степеней свободы молекулы газа, R — универсальная газовая постоянная, d – количество молей газа.

Изменение внутренней энергии газа:

Уравнение (8) определяет работу для изобарного процесса. Вычтем из (2) уравнение (1), получим еще одно уравнение для работы газа в изобарном процессе:

[p<(V>_2-V_1)=nu R<(T>_2-T_1)to A=nu R<(T>_2-T_1) (9)] [triangle Q=frac<2>нR<(T>_2-T_1)+nu R<(T>_2-T_1)=c_<mu p>nu triangle T (10),]

где $c_<mu p>$ — молярная теплоёмкость газа при изобарном процессе. Уравнение (10) определяет количество теплоты, сообщаемое газу массы m в изобарном процессе при увеличении температуры на $triangle T.$

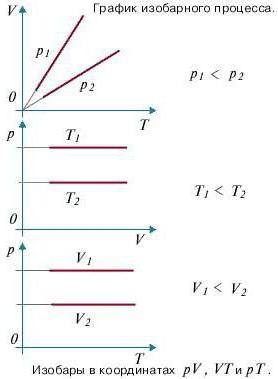
Изопроцессы очень часто изображают на термодинамических диаграммах. Так, линия, изображающая на такой диаграмме изобарический процесс, называется изобарой (рис.1).

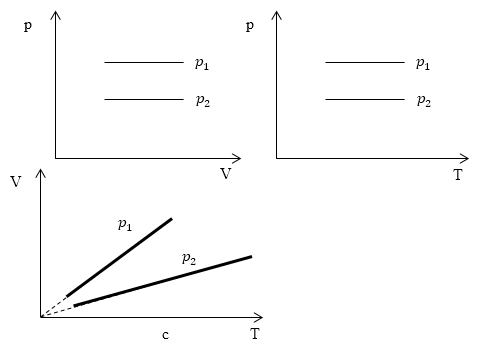
Задание: Определите, как соотносятся давления $p_1$ и $p_2$ на диаграмме V(T) рис 1с.

Проведем изотерму $T_1$

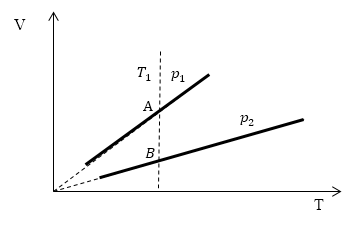
В точках А и В температуры одинаковы, следовательно, газ подчиняется закону Бойля — Мариотта:

[p_AV_A=p_BV_B (1.2)] [V_A > V_Bto p_A Ответ: Давления $p_1 > p_2$.

Готовые работы на аналогичную тему

Задание: При неизменном давлении p=3$cdot <10>^5$Па газ расширился от объема $V_1=2л$ до $V_2=4л.$ Найти работу, совершаемую газом.

За основу решения задачи примем формулу работы при расширении газа в изобарном процессе:

Переведем данные объемы в СИ: $V_1=2л=2<cdot 10>^<-3>м^3$, $V_2=4л=4<•10>^<-3>м^3$

Ответ: Работа газа в изобарном процессе 600 Дж.

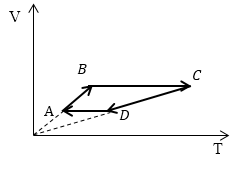
Задание: Сравните работу газа в процессе ABC и работу над газом в процессе CDA рис 3.

За основу решения примем формулу, определяющую работу газа:

Из геометрического смысла определенного интеграла известно, что работа — есть площадь фигуры, которая ограничена функцией подынтегрального выражения, осью абсцисс, и изохорами в точках $V_1 и V_2$ (оси p(V)). Переведем графики процессов в оси p(V).

Рассмотрим каждый отрезок графиков процессов изображенных на рисунке (3).

АВ: Изохорный процесс (p=const), $Vuparrow left( Объем растетright), Tuparrow $;

ВС: Изохорный процесс (V =const), $Tuparrow $ (из графика), p$uparrow $, из закона для изохорного процесса ($frac

=const$);

CD: (p=const), $Vdownarrow , Tdownarrow ;$

DA: (V =const), $Tdownarrow , pdownarrow .$

Изобразим графики процессов в осях p(V) (рис.4):

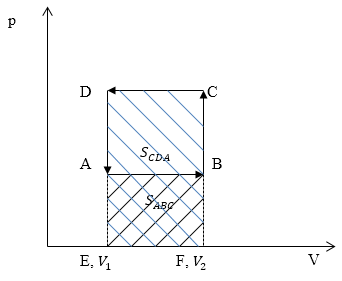
Работа газа $A_=S_$ ($S_$ — площадь прямоугольника ABFE) (рис. 3). Работа над газом $A_=S_$ ($S_$)$ -площадь прямоугольника $EFCD.Очевидно, что $A_>A_.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 18 12 2021

Первый закон термодинамики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1 ).

Работа газа равна:

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2 ).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1) .

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3 ):

Рис. 3. Работа газа как площадь

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.

Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4 ).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Так, в процессе расширения газ совершает положительную работу 0 right )’ alt=’left ( A> 0 right )’ /> ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 right )’ alt=’left ( ‘ > 0 right )’ /> .

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:

Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Всё подведённое к газу тепло идёт на совершение газом работы.

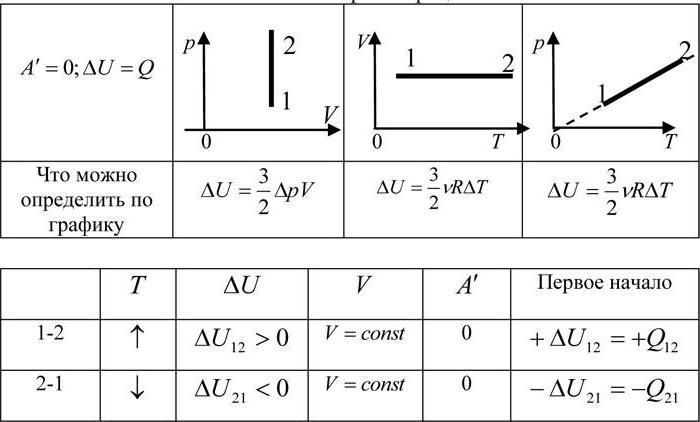
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1) ). Имеем:

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет , поэтому 0′ alt=’Delta U > 0′ /> : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5 ).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

[spoiler title=”источники:”]

http://spravochnick.ru/fizika/molekulyarnaya_fizika/izobaricheskiy_process/

http://ege-study.ru/ru/ege/materialy/fizika/pervyj-zakon-termodinamiki/

[/spoiler]

Что такое изобарический процесс

«Изобарический процесс» 👇

Работа в термодинамике

В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.

Рассмотрим работу газа при изобарическом расширении.

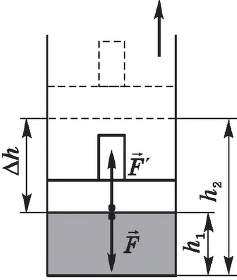
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:

$A’=F’∆h=pS∆h=p∆V$

Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V < 0$, поскольку $∆h < 0$.

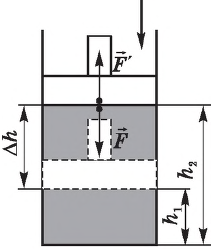
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:

$A=-A’=-p∆V$

Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.

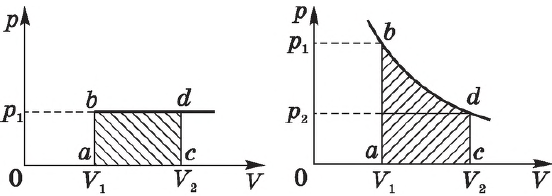
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.

Первый закон термодинамики

Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.

Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).

Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.

Первый закон термодинамики формулируется так:

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

$∆U=A+Q$

где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.

Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.

При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.

Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:

$Q=∆U+A’$

где $А’$ — работа, совершаемая системой ($А’=-А$).

Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.

Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.

Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.

Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.

Применение первого закона термодинамики к различным процессам

Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.

Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.

Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.

Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.

При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,

$∆U=Q$

т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.

Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q < 0$ и $∆U < 0$, внутренняя энергия уменьшается.

Изотермический процесс графически изображается изотермой.

Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.

Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:

$Q=A’$

При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q < 0$ и $А’ < 0$. В этом случае над газом совершается работа внешними силами. Для внешних сил работа положительна. Геометрически работа при изотермическом процессе определяется площадью под кривой $р(V)$.

Изобарный процесс на термодинамической диаграмме изображается изобарой.

Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.

Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.

При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:

$Q=∆U+A’$

Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).

Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.

Адиабатический процесс

Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).

Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.

Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе

$∆U=A$

где $А$ — работа внешних сил.

При адиабатном расширении газа $А < 0$.

Следовательно,

$∆U={i}/{2}·{m}/{M}R∆T < 0,$

что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.

На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.

Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).

Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.

Принцип действия тепловых двигателей

Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.

Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.

Таким образом, основными элементами любого теплового двигателя являются:

1. рабочее тело (газ или пар), совершающее работу;
2. нагреватель, сообщающий энергию рабочему телу;
3. холодильник, поглощающий часть энергии от рабочего тела.

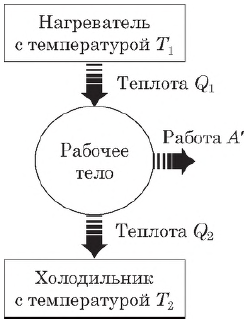
Коэффициент полезного действия теплового двигателя

Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:

$A’=|Q_1|-|Q_2|$

где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.

Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:

$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$

Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η < 1$.

КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 – T_2=0$ двигатель не может работать.

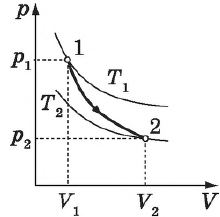
Цикл Карно

Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.

Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».

Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.

Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.

Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.

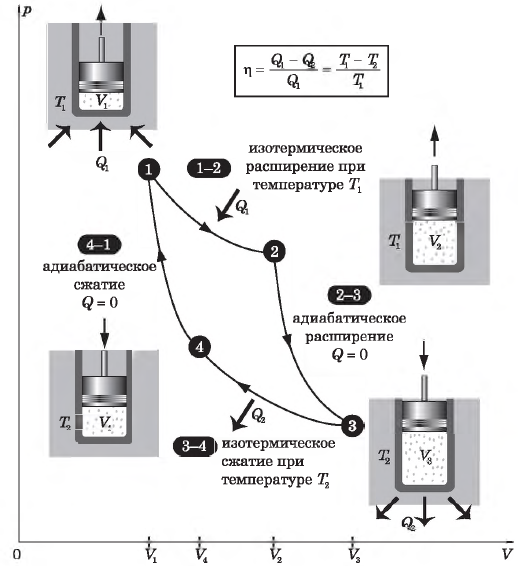
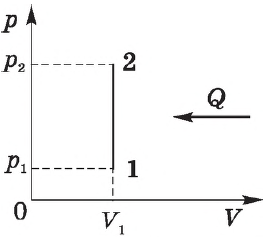
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:

$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:

$A_{23}=-∆U_{23}$

Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2 < Т_1$. В процессе ($3-4$) газ изотермически сжимается, передавая холодильнику количество теплоты $Q_2$:

$A_{34}=Q_2,$

Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.

Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:

$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$

Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.

Работу
газа, совершаемую при изопроцессах,
можно найти следующим образом: При
изобарном процессе (
):

;

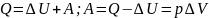
При
изохорном процессе (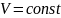
):

;

При
изотермическом процессе (

):

;

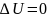
При
адиабатном процессе (
):

,
где

– теплоёмкость газа при постоянном
объёме.

Теплоемкость
газа — это отношение тепла, сообщенного
газу, к изменению температуры

,
которое при этом произошло.

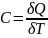
Молярная
теплоемкость — теплоемкость 1 моля
газа.

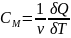
Теплоемкость
идеального газа в изопроцессах:

Адиабатический.В
адиабатическом процессе теплообмена
с окружающей средой не происходит, то
есть

.
При изменении объема температура и
давление меняются, то есть . Следовательно,
теплоемкость идеального газа в
адиабатическом процессе также равна
нулю:

.

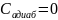
Изотермический
В
изотермическом процессе постоянна
температура, то есть

.
При изменении объема газу передается
(или отбирается) некоторое количество
тепла. Следовательно, теплоемкость
идеального газа стремится к бесконечности:

.

Изохорный
В
изохорическом процессе постоянен объем,
то есть

.
Таким образом,


где

число степеней свободы частиц газа.

Изобарный
В изобарном
процессе

:

Полезные
формулы:

Изменение
внутренней энергии 

идеального
одноатомного газа.

К
оличество
теплоты, переданное телу, 

идет
на изменение его внутренней энергии 

и
на совершение им работы (Первый
закон термодинамики). 

 Количество
теплоты при
нагревании и охлаждении газа.

Работа
газа при
изобарном процессе (p = const)

22,Закон сохранения энергии в изо- и адиабатном процессах.

Закон
сохр-я энергии в изо- и адиабатном
процессах и есть первое начало
термодинамики. Оно гласит о том, что
кол-во теплоты газа равна сумме работы,
которую совершил газ и изменению
внутренней энергии газа.

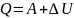
Или
для бесконечно малых величин:

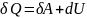
Этот
закон применим для каждого изопроцесса:

1. Изотермический
   процесс
   (T=const)

dU=0

отсюда:

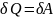
– вся теплота расходуется на совершение
работы.

;

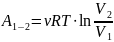
1. Изохорный
   процесс
   (V=const)

dV=0
; dA=0

– вся подводимая
теплота идёт во внутреннюю энергию.

– молярная
теплоёмкость;

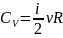
– удельная теплоёмкость

1. Изобарный
   процесс
   (P=const)

– здесь полностью
выполняется 1ое начало ТД.

1. Адиабатный
   процесс
   (Q=0)
   

– газ совершает
работу

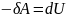
– над газом
совершают работу

23.Термодинамический цикл. Цикл Карно.

Замкнутый
процесс – это любой процесс, в результате
которого газ выходит из одного состояния,
проходит стадию и возвращается в
начальное состояние.

Цикл
Карно.

Состоит
из 4ёх стадий. При переводе газа из
состояния 1 в состояние 2 протекает
изотермический процесс. При переводе
газа из 2 в 3 протекает адиабатный процесс,
из состояния 3 в 4 протекает изотермический,
и при переводе из 4 в 1 протекает адиабатный
процесс. Рассмотрим эти стадии.

1-2

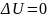
2-3

;

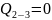
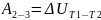
3-4

4-1

;

КПД
(коэфф. полезного действия) вычисляется
по ф-ле:

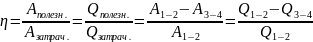
Также
работу, совершаемую газом, можно найти
путём вычисления площади подкривой
процесса.

Зная
теплоёмкость газа, которая вычисляется
по ф-ле

можно найти КПД замкнутого цикла:

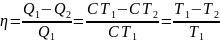
Где

– сообщённая теплота

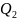
– теплота, которую
забрали у газа

– температура той
системы, от которой газ поглотил тепло

– температура
холодильника, при которой отводилась
теплота

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #