В этой заметке рассмотрим как можно вычислить работу идеального газа при различных изо-процессах. Это будет полезно тем, кто только начинает изучать термодинамику и МКТ. Для простоты изображения всех процессов возьмем самые популярные P-V диаграммы.
Есть такое понятие как термодинамический процесс. Изменение любого параметра термодинамической системы (к параметрам можно отнести температуру T, давление p, объем V, энтропию S). Но так как все параметры термодинамической системы взаимосвязаны, то частенько, когда изменяется один параметр, то и изменяются другие параметры.
Если термодинамические процессы не протекают, то система находится в равновесном состоянии. То есть равновесное состояние — такое абстрактное состояние системы, при котором все термодинамические параметры системы остаются сколь угодно долго неизменными, если над системой не совершают никаких внешних воздействий. То есть система предоставлена сама себе. Почему же это состояние абстрактно? Потому что в реальной жизни очень тяжело изолировать систему от внешнего влияния окружающего мира. Таким образом, в каждый момент времени протекают какие-то термодинамические процессы.
Однако, процессы могут протекать настолько медленно, что система изменяется почти незаметно. Иногда это дает возможность рассматривать состояние системы из последовательных равновесных состояний. Такие процессы еще называются квазистатическими. Под квазистатичностью можно понимать что-то ооочень медленное, настолько медленной, что оно длится намного дольше, чем время релаксации (время, за которое амплитудное значение внешнего возмущения, которое начало менять систему, уменьшилось в e раз).
Еще система может постоянно возвращаться к исходному состоянию. Такой круговой процесс называется циклом (примерно по таким процессам работают тепловые машины и ДВС).
Что нужно чтобы изучить какую-либо термодинамическую систему?
1. Определить работу, совершаемую в данном процессе
2. Определить изменение внутренней энергии системы
3. Определить количество теплоты, которое вошло в систему или которое отдала система.
4. Установить связи между отдельными величинами, которые характеризуют состояние рабочего тела (газа)
Основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.
И далее мы с вами выведем работы в этих основных процессах.
1. Изохорный процесс
Изохорным процесс — термодинамический процесс, который протекает при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.
2. Изотермический процесс
Изотермический процесс — термодинамический процесс, который протекает при постоянной температуре. На практике очень сложно осуществить этот процесс. Потому что при сжатии или расширении газа, нужны условия, при которых газ будет успевать обмениваться температурой с внешней средой, чтобы поддерживать свою температуру неизменной.
3. Изобарный процесс
Изобарный процесс — термодинамический процесс, который протекает при постоянном давлении. Помещение газа в плотный цилиндр с подвижным поршнем, на который действует постоянная сила ( например сила тяжести со стороны груза ) при отводе и подводе теплоты, может смоделировать такой процесс.
4. Адиабатный процесс
Адиабатный процесс — термодинамический процесс, который протекает без теплообмена (Q = 0) рабочего тела (газа) с окружающей средой. Также сложно осуществимый процесс. Примерная модель: газ помещают в цилиндр с подвижным поршнем. При этом цилиндр и поршень выполнены из высококачественного теплоизолирующего материала.
5. Политропный процесс (p∙Vⁿ = const )
Этот процесс является обобщением всех предыдущих. Все параметры в этом процессе могут меняться. А процессы выше являются его частными случаями. n – показатель политропы, некоторая постоянная, которая может принимать любые значения от -∞ до +∞.
n = 0 – изобарный процесс p = const
n = 0 – изотермический процесс T = const
n = γ – адиабатный процесс p∙Vⁿ = const
n = +∞ или n = -∞ – изохорный процесс V = const
Любые формулы для этого процесса аналогичны адиабатному процессу. При этом работа выводится точно также. Только коэффициент адиабаты (γ) в общем случае заменяется на коэффициент политропы (n).
Понравился разбор задачи ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Ранее мы достаточно плотно познакомились с процессами и методами работы с ними. Среди часто используемых способов работы с процессами выделяются два: уравнение Менделеева-Клапейрона (для описания состояния идеального газа) и первое начало термодинамики. Из нескольких друг за другом идущих разных процессов можно составить общий циклический процесс.
Круговой процесс (цикл) – составной термодинамический процесс, в результате совершения которого рабочее тело (газ) возвращается в исходное состояние. Таким образом, начальное и конечное состояние газа (давление газа 
, объём газа 
и температура газа 
) одинаковы. Попробуем изобразить такой процесс в координатах (рис. 1).
Рис. 1. Примеры циклических процессов
Например, наш циклический процесс 1.1 состоит из двух изохор, двух изотерм, а процесс 1.2 — из двух изобар и двух изохор. Таким образом, исходя из текстовых условий любой задачи и знания общего вида изопроцессов (именно из них чаще всего составляется цикл), можно нарисовать рисунок.
Для энергетического описания процесса (или цикла) через первое начало термодинамики необходимо обдумать два вопроса:
- как изменяется внутренняя энергия газа (
)
- чему равна работа газа (
)
- где
Для циклов есть небольшие фишки, которые удобно использовать для убыстрения задачи.
Так, изменение внутренней энергии газа зависит только от изменения температуры, а т.к. в цикле начальное и конечное состояние газа одинаково, то изменение внутренней энергии идеального газа за цикл равно 0 ().
Рис. 2. Графическая интерпретация работы газа
Поиск работы для газа также можно несколько упростить. Попробуем в координатах нарисовать график изобарического процесса и найти работу газа (рис. 2). Пусть газ находится в состоянии (давление
и объём 
), далее газ изобарически перевели в состояние 2 (давление 
и объём ). Тогда по определению работы газа:
(1)
Геометрически (рис. 2), произведение давления на разность объёмов численно равна площади прямоугольника, ограниченного сверху прямой (процессом), а снизу осью. В целом, эту логику можно расширить на любые процессы, тогда работа газа численно равна площади под кривой в координатах .
Также в рамках школьной физики присутствует условное деление циклов на прямые и обратные:
Прямой цикл – круговой, в котором рабочее тело совершает положительную работу за счёт сообщённой ему теплоты.
Обратный цикл — круговой, в котором рабочее тело совершает отрицательную работу.
Анализируя (1) вопрос о положительной и отрицательной работе, сводится к вопросу о соотношении между начальным и конечным объёмами, если:
— газ расширяется, работа положительна,
— газ сжимается, работа отрицательна.
Для графиков можно использовать следующую логику: в случае, если площадь под графиком расширения газа больше соответствующей площади для сжатия, значит цикл — прямой (рис. 3), если наоборот — обратный (рис. 4).
Рис. 3. Прямой циклический процесс
Рис. 4. Обратный циклический процесс
Таким образом, разница в прямом и обратном цикле может быть в очерёдности процессов. Так, прямой процесс, в нашем примере, — это 1-2-3-4-1, а обратный — 1-4-3-2-1.
Вывод: в задачах на циклические процессы нужно быть очень внимательным при прочтении, т.к. часть слов будет иметь глубокий физический смысл. Лучше всего процессы в таких задачах прорисовывать на графиках в координатах . Если график уже есть, то это к лучшему. Определяемся с конкретными изопроцессами, заданными в задаче, и используем это знание или через уравнение Менделеева-Клапейрона, или через первое начало термодинамики.
Содержание:
Работа в термодинамике:
В 9 классе вы узнали, что работа силы (механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. Работу силы рассматривают как меру изменения энергии физической системы. А как определить работу в термодинамике? Как может быть выражена эта работа через макроскопические параметры — давление и об1
Рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, закрытом подвижным поршнем (рис. 52).
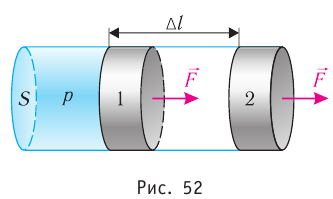
Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением р, которое газ оказывает на них. Допустим, что в результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние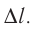 
Модуль силы давления газа, действующей на поршень, F = pS. Эта сила совершает работу по перемещению поршня
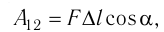(10.1)
где а — угол между направлениями силы и перемещения. В рассматриваемом примере а = 0, тогда
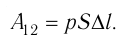
Произведение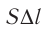 
определяет приращение объёма 
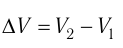(см. рис. 52), поэтому работа газа при его изобарном расширении
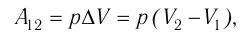(10.2)
где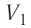 
— начальный объём газа, 
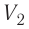— объём газа в конечном состоянии.
Так как давление р газа всегда величина положительная, из формулы (10.2) следует, что, если газ расширяется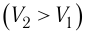 
, работа, совершённая силой давления газа, положительная (
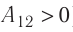), а в случае сжатия (
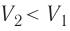) работа отрицательная (
).
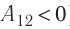Процесс медленного изобарного сжатия газа из состояния 2 с начальным объёмом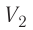 
в состояние 1 с конечным объёмом 
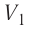можно характеризовать работой 
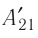внешних сил над газом:
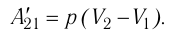(10.З)
Из сравнения равенств (10.2) и (10.3) вытекает соотношение между работой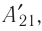 
у совершённой внешними силами, и работой 
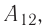совершённой силой давления газа:
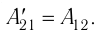Это соотношение согласуется с третьим законом Ньютона (внешняя сила 
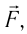действующая на газ со стороны поршня, имеет
направление, противоположное силе давления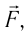 
действующей на поршень со стороны газа). Из формулы (10.3) видно, что работа, совершённая внешними силами, положительная 
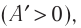если происходит сжатие газа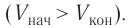 
Если газ расширяется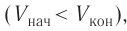 
), то работа, совершённая внешними силами отрицательная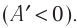 
Геометрическое толкование работы
Построим график зависимости давления газа от его объёма при р = const. Как видно из рисунка 53, при изобарном расширении газа работа, совершённая силой давления газа, численно равна площади прямоугольника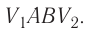 
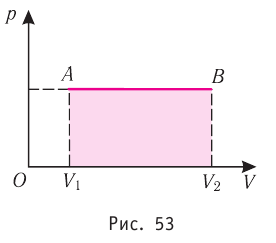
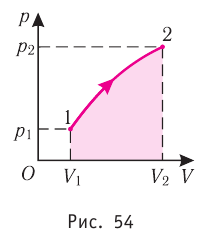
Если процесс перехода газа из начального состояния в конечное не является изобарным, то работа, совершённая силой давления газа при изменении его объёма от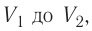 
численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов 
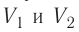(рис. 54).
Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, снова возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 55). Работа, совершаемая системой при циклическом процессе, или работа цикла, равна площади фигуры, ограниченной линиями, которые изображают цикл: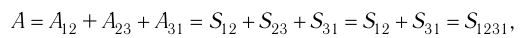
где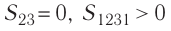
на рисунке 55, а и 
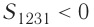на рисунке 55, б.
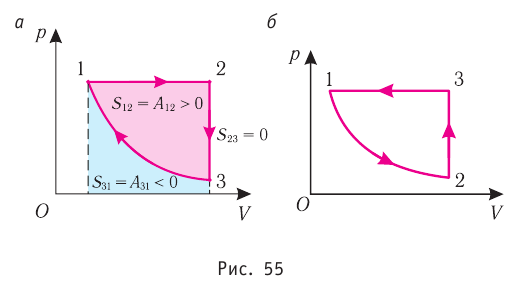
Если «кривая расширения» (изобара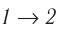
) (см. рис. 55, а) расположена выше «кривой сжатия» (изотерма 
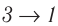), то полная работа, совершённая системой за цикл (работа цикла), положительная. Если же, как изображено на рисунке 55, б, «кривая сжатия» (изобара 
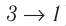) расположена выше «кривой расширения» (изотерма
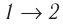), то работа цикла отрицательная.
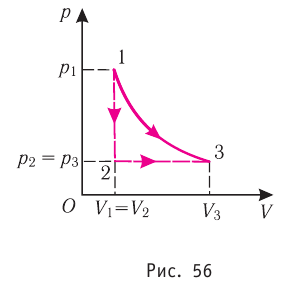
Из рисунка 56 видно, что численное значение работы цикла определяется не только начальным и конечным состояниями системы, но и видом процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения, либо сначала изохорно понизив его давление до значения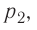 
а затем изобарно увеличив его объём от значения 
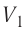до значения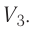 
Как видно из рисунка 56, в первом случае работа, совершённая силами давления газа, больше, чем во втором. Следовательно, работа, совершаемая при переходе термодинамической системы из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Количество теплоты и удельная теплоёмкость
Итак, существуют два способа передачи энергии от одного тела к другому. Первый характеризуется передачей энергии в процессе механического взаимодействия тел — механическая энергия одного тела переходит в энергию хаотического движения частиц вещества другого тела или, наоборот, убыль энергии хаотического движения частиц вещества одного тела сказывается на увеличении механической энергии другого тела. Такую форму передачи энергии в термодинамике (как и в механике) называют работой. Так, например, в рассмотренной нами ранее термодинамической системе (газ в цилиндрическом сосуде под поршнем) расширение газа приводит к перемещению поршня. При этом убыль внутренней энергии газа равна работе, совершённой силой давления газа, под действием которой поршень переместился.
Второй способ передачи энергии осуществляется при непосредственном обмене энергией между хаотически движущимися частицами взаимодействующих тел. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей энергии частицам более холодного тела. В результате внутренняя энергия первого тела уменьшается, а второго тела увеличивается. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей. Как вы уже знаете, существуют три вида теплопередачи: теплопроводность, конвекция и излучение.
Количественной мерой энергии, переданной телу в процессе теплопередачи, является количество теплоты Q. В СИ единицей количества теплоты является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию (1 кал = 4,19Дж).
Если процесс теплопередачи не сопровождается изменением агрегатного состояния вещества, то
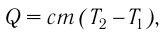(10,4)
где m — масса тела,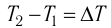 
— разность температур в конце и в начале процесса теплопередачи, с — удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое получает или отдаёт вещество массой 1 кг при изменении его температуры на 1 К. Удельную
теплоемкость измеряют в джоулях, деленных на килограмм, кельвин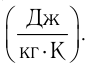
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкости тела. Обозначают теплоёмкость тела С и измеряют в джоулях на кельвин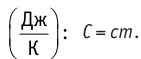
Теплоёмкость, в отличие от удельной теплоёмкости, является тепловой характеристикой тела, а не вещества.
Удельная теплота плавления
Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления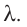 
Для плавления тела массой m, предварительно нагретого до температуры плавления, ему необходимо сообщить количество теплоты 
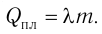При кристаллизации тела выделяется количество теплоты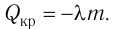 
Удельная теплота парообразования
Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Количество теплоты, необходимое для превращения жидкости массой m, предварительно нагретой до температуры кипения, в пар, определяют по формуле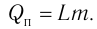
Конденсация пара сопровождается выделением количества теплоты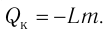 
Удельная теплота сгорания топлива
Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания топлива q. Количество теплоты, выделившееся при полном сгорании некоторой массы m топлива, определяют по формуле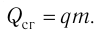
Оно передаётся телам, образующим термодинамическую систему, и по отношению к ним является положительной величиной.
Отметим, что в результате теплопередачи могут изменяться как обе составляющие внутренней энергии тела, так и одна из них. При нагревании (охлаждении) изменяются кинетическая энергия хаотического движения частиц, которые составляют тело, и потенциальная энергия их взаимодействия. При плавлении (кристаллизации), кипении (конденсации) изменяется только потенциальная энергия взаимодействия частиц вещества.
При совершении работы также может изменяться как кинетическая, так и потенциальная энергия частиц вещества. Следовательно, как при теплопередаче, так и при совершении работы происходит изменение кинетической и потенциальной энергий частиц вещества, что приводит к изменению внутренней энергии тела.
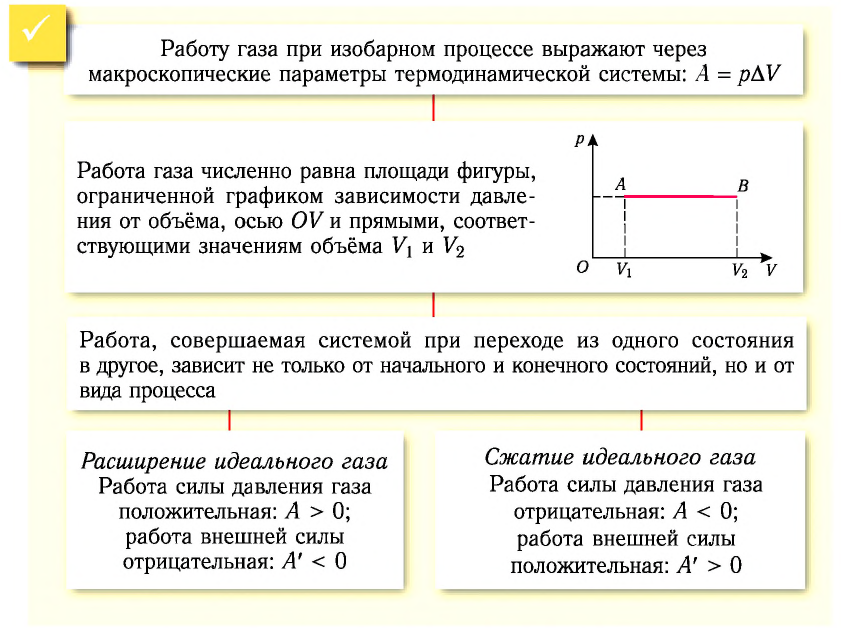
1. Работу газа при изобарном процессе выражают через макроскопические параметры термодинамической системы:
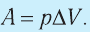
2. Работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёмов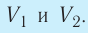 
3. Работа, совершаемая при переходе системы из одного состояния в другое, зависит не только от начального и конечного состояний, но и от вида процесса.
4. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей.
Пример №1
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от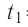 
= 12 °С до 
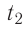= 87 °С, если давление газа и его начальный объём соответственно p=190кПа и 
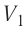= 6,Одм’5.
Дано:
Пример №2
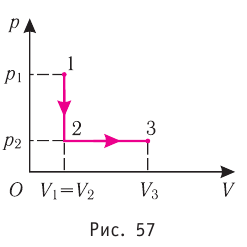
Состояние идеального газа, взятого в количестве v=l,0 моль при температуре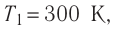 
изменяется так, как показано на рисунке 57. Определите работу газа в ходе всего процесса, если на изохоре 
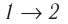его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.
Дано:
v = 1,0 моль
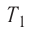= 300 к
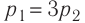
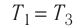
А — ?
Решение. Работа Л газа в ходе всего процесса равна сумме работ на участках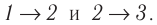 
Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный 
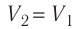), то работа газа 
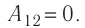. Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (
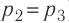)следовательно, работа газа 
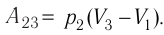Тогда 
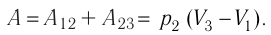
Так как по условию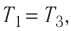 
то воспользуемся уравнением Клапейрона (5.2):
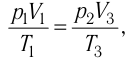откуда 
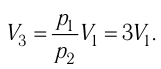Следовательно,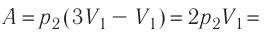 
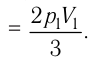Согласно уравнению Клапейрона—Менделеева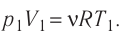 
Тогда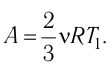 
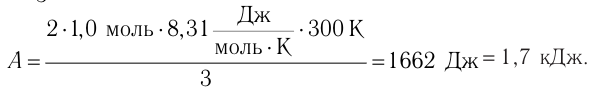
Ответ: А = 1,7 кДж.
Работа в термодинамике
В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.
Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.
Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.
Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.
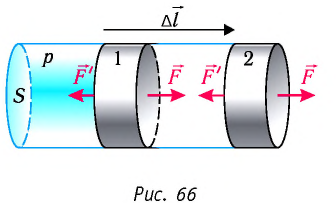
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре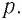 
В результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние 
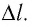Модуль силы давления газа на поршень 
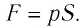Эта сила совершила работу по перемещению поршня, равную
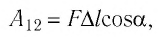
где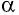 
— угол между направлениями силы 
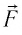и перемещения поршня 
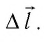Поскольку в рассматриваемом примере 
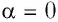и 
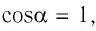то
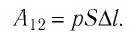
Произведение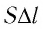 
определяет изменение объёма 
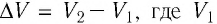— начальный объём газа; 
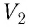— объём газа в конечном состоянии (см. рис. 66).
Таким образом, работа силы давления газа при его изобарном расширении:
Так как давление р газа — величина положительная, то из формулы (12.1) следует, что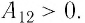 
При изобарном расширении газа из состояния 1 в состояние 2 работа силы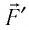 
(см. рис. 66):
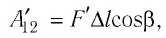
где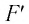 
— модуль силы, действующей на газ со стороны поршня (внешняя сила); 
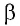— угол между направлениями силы 
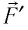и перемещения 
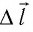поршня.
Перемещение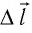 
поршня одно и то же, а сила давления 
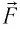газа на поршень и сила давления 
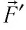поршня на газ — силы, подчиняющиеся третьему закону Ньютона:
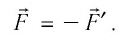
Следовательно, работы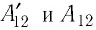 
отличаются только знаком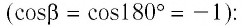 
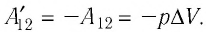
Таким образом, можно сделать следующие выводы.
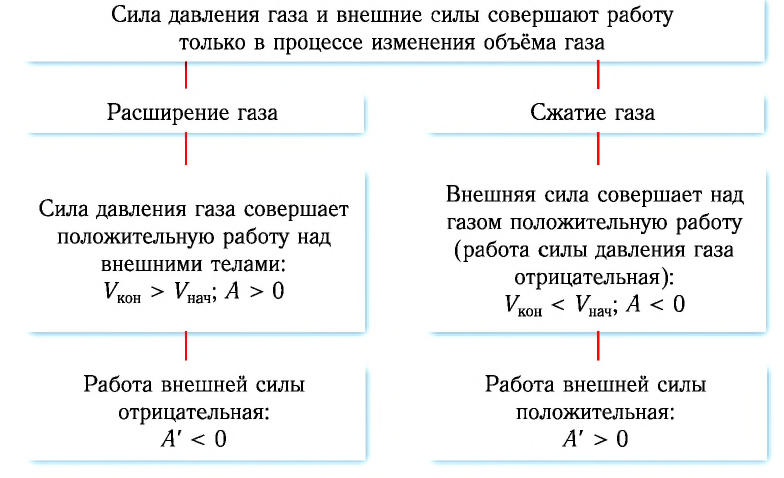
Геометрическое толкование работы:
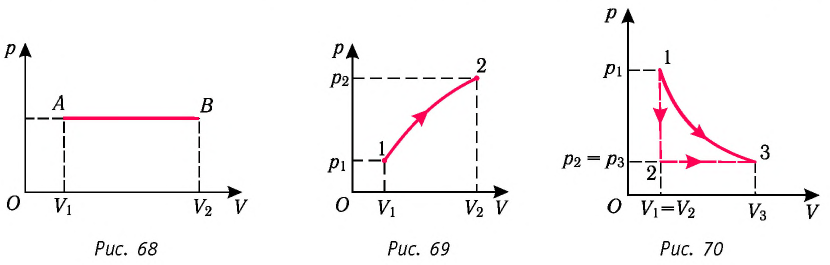
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при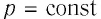 
(рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника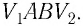 
Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от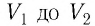 
численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов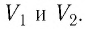 
Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения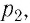 
а затем изобарно увеличив его объём до значения 
В первом случае работа газа больше, чем во втором.
Следовательно, работа, совершаемая термодинамическом системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Пример №3
Определите работу, совершаемую силой давления идеального газа определённой 200 массы при переходе из состояния 1 в состояние 3 (рис. 73).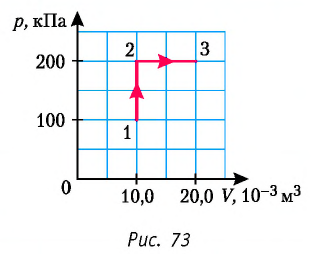 
Решение. 1 способ. Работа А газа в ходе всего процесса равна сумме работ на участках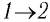 
и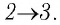 
Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс 
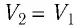), то работа, совершаемая силой давления газа, 
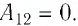В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу
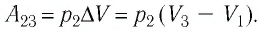
Тогда при переходе из состояния 1 в состояние 3 работа
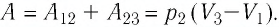
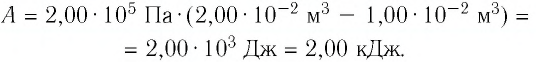
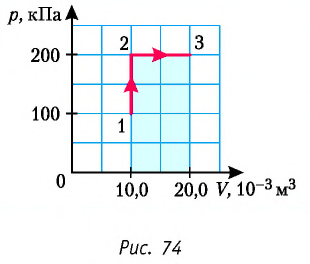
2 способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёма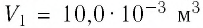 
и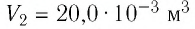 
(закрашенная область на рисунке 74).
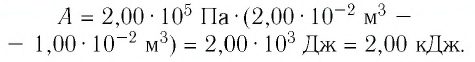
Ответ: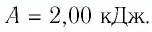 
Пример №4
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от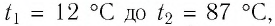 
если давление газа 
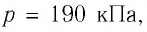а его начальный объём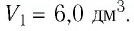 
Решение. Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
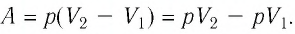
Согласно уравнению Клапейрона—Менделеева,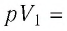 
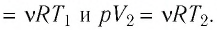Следовательно,
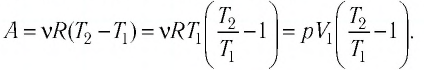
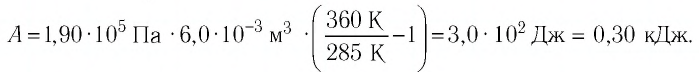
Ответ: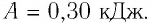 
Как определить работу в термодинамике
В конце XVIII в. английский физик Бенджамин Томпсон (граф Румфорд) исследовал тепло, выделяющееся при сверлении бронзовых пушек. Румфорд успевал вскипятить поставленные на пушки котлы с водой за счет тепла, которое выделялось, пока лошади приводили в движение очень тупое сверло. В данном случае энергия механического движения сверла превращалась в энергию хаотического движения молекул бронзы и воды. А можно ли сделать наоборот?
Почему при изменении объема газа изменяется его внутренняя энергия
Внутренняя энергия газа может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ сжимают (газ совершает отрицательную работу) (рис. 37.1) и он при этом не отдает энергию окружающей среде, то скорость движения молекул газа, а соответственно, и внутренняя энергия, и температура газа увеличиваются. И наоборот: если газ расширяется (то есть совершает положительную работу), то скорость движения молекул, температура и внутренняя энергия газа уменьшаются.
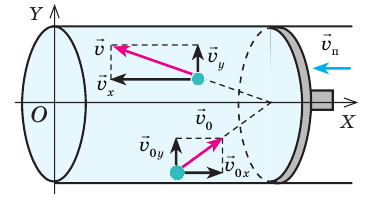
Рис. 37.1. При сжатии газа скорость его молекул после столкновения с поршнем увеличивается (v >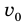 
) — газ нагревается. (Аналогично увеличивается скорость мяча после удара волейболиста, когда его рука движется навстречу мячу.)
Как вычислить работу газа
Вычислим работу, которую совершает сила давления газа при изменении его объема от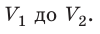 
По определению работы: A=Fscosα. Если газ расширяется изобарно, то сила, действующая со стороны газа на поршень, постоянна: F=pS (p — давление газа; S — площадь поршня); модуль перемещения поршня 
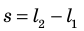(рис. 37.2, а); α = 0.
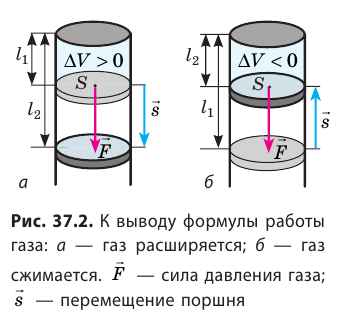
Таким образом, работа газа при его изобарном расширении равна:
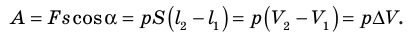
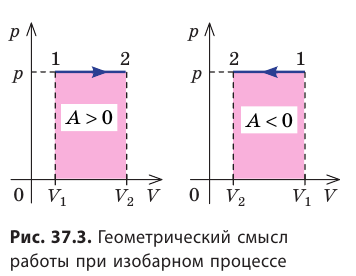
Работе газа при изобарном расширении (или сжатии) можно дать простое геометрическое толкование: работа газа численно равна площади прямоугольника под графиком зависимости p(V) (рис. 37.3).
Пусть некоторый газ переходит из состояния 1 в состояние 2 (рис. 37.4). Если изменение объема газа (∆V) достаточно мало, то давление газа можно считать неизменным. Тогда работа газа численно равна площади выделенной на рисунке полосы. Полная работа при изменении объема от 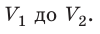будет равна сумме площадей всех полос, то есть площади криволинейной трапеции под графиком зависимости p (V).
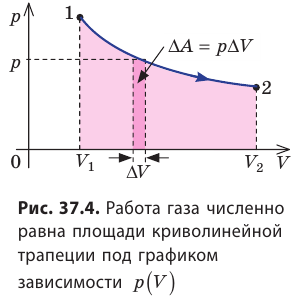
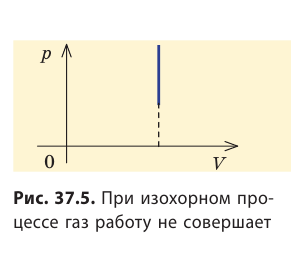
Очевидно, что при изохорном процессе (V = const) площадь фигуры под графиком зависимости p (V) равна нулю (рис. 37.5), — газ работу не совершает (A = 0) . Работа газа зависит от того, каким образом происходил переход газа из начального состояния в конечное (рис. 37.6).
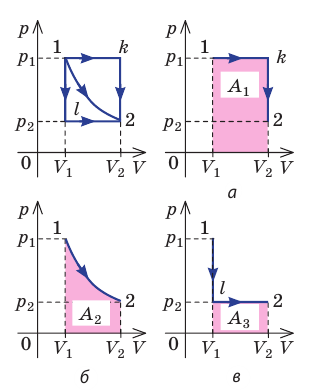
Рис. 37.6. три пути перехода газа из состояния 1 в состояние 2: а — газ изобарно расширяется (участок 1k), затем изохорно охла ждается (участок k2); б — газ изотермически расширяется; в — газ изохорно охлаждается (участок 1l), затем изобарно расширяется (участок l2). сравнив площади фигур под графиками, видим, что: 
Пример №5
На рисунке графически изображен циклический процесс, совершаемый идеальным газом. Определите работу газа за цикл.
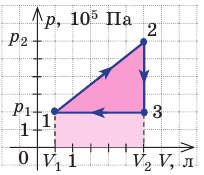
Решение:
Полная работа за цикл равна сумме работ, совершенных газом в ходе каждого процесса цикла. Работа газа в ходе процесса 1–2 численно равна площади трапеции, основания которой равны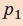 
и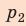 
, а высота — 
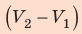; объем газа увеличивается, поэтому работа газа положительна. Работа газа в ходе процесса 2–3 равна нулю, поскольку этот процесс изохорный. Работа газа в ходе процесса 3–1 численно равна площади прямоугольника со сторонам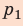и 
и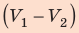 
; объем газа уменьшается, поэтому работа отрицательна. Следовательно, для определения работы за весь цикл нужно из площади трапеции вычесть площадь прямоугольника. То есть, как видно из рисунка, работа газа за цикл численно равна площади прямоугольного треугольника 1–2–3:
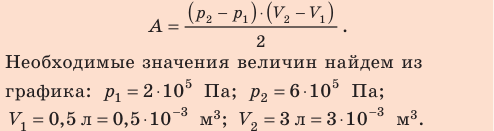
Выводы:
- При отсутствии теплообмена с окружающей средой, если над газом совершают работу, внутренняя энергия газа увеличивается; если газ сам совершает работу, его внутренняя энергия уменьшается.
- Если объем газа увеличивается, то газ совершает положительную работу. Если объем газа уменьшается, то работа газа отрицательна.
- Работа газа численно равна площади фигуры под графиком зависимости p (V). При изобарном процессе работу газа можно определить по формуле A=p∆V, при изохорном процессе работа газа равна нулю: A = 0.
- Первый закон термодинамики
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Термодинамика – основные понятия, формулы и определения
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория
Речь в статье пойдет о КПД различных циклов, проводимых с газом. При этом давайте помнить, что внутренняя энергия изменяется тогда, когда изменяется температура, а в адиабатном процессе передачи тепла не происходит, то есть для совершения работы в таком процессе газ “изыскивает внутренние резервы”. Кроме того, работа численно равна площади под кривой процесса, а работа за цикл – площади внутри цикла.
Задача 1.
На рисунке представлена диаграмма цикла с одноатомным идеальным газом. Участки 
и – адиабаты. Вычислите КПД данной тепловой машины и максимально возможный КПД .
К задаче 1
КПД тепловой машины можно вычислить как
Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:
Работа численно равна площади, ограниченной циклом. Поэтому
Участк и по условию – адиабаты, то есть передачи тепла газу на этих участках не происходит, следовательно, работа будет совершена за счет «внутренних резервов» – то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.
Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и , и , это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать . Но, так как , а ,то изменение внутренней энергии будет равно
Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке :
Ответ: , .
Задача 2.
Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж. В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу кДж. Найдите КПД данной тепловой машины.
К задаче 2
Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.
Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД
Ответ: .
Задача 3.
КПД тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе кДж. Найдите разность максимальной и минимальной температур газа в цикле.
К задаче 3
Полная площадь под кривой процесса 1-2 равна кДж. При этом, так как КПД машины 25%, то площадь внутри цикла равна , а под кривой 3-1 – . В процессе 1-2 изменения внутренней энергии не было, так как температура не менялась, а в процессе 3-1 газу не передавали тепло, следовательно, работа совершена за счет внутренней энергии. Т.е.
Ответ: 500 K.
Условие задачи:
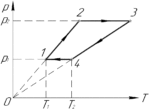Определите работу, совершаемую одним молем газа за цикл, если (frac{p_2}{p_1}=2), (T_1=280) К, (T_2=360) К (схема к условию приведена справа).
Задача №5.4.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(nu=1) моль, (frac{p_2}{p_1}=2), (T_1=280) К, (T_2=360) К, (A-?)
Решение задачи:
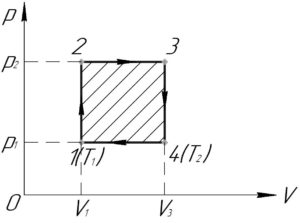Приведённый в условии график для нахождения работы газа в цикле (A) перестроим в координатах p-V. Для этого нужно произвести анализ каждого из процессов.
Итак, начнём. Процесс 1-2 – изохорный ((V=const)), поскольку график этого процесса в координатах p-T лежит на прямой, проходящей через начало координат. Так как температура газа в процессе увеличивается, то по закону Шарля давление растёт (хотя это итак понятно из исходного графика). Аналогично, изохорным является процесс 3-4, но так как температура газа в этом процессе уменьшается, то будет уменьшаться и давление.
Процесс 2-3 – изобарный ((p=const)). Температура газа в процессе растёт, поэтому по закону Гей-Люссака будет увеличиваться и объем. Также изобарным является процесс 4-1. Объем газа в этом процессе уменьшается, так как уменьшается температура.
С учётом всего вышесказанного получим следующий график (смотрите схему к решению).
Работа газа в цикле (A) равна площади этого цикла в координатах p-V. Если цикл обходится по часовой стрелке, то работа положительна (что имеет место в нашем случае), иначе – отрицательна. Тогда:
[A = left( {{p_2} – {p_1}} right)left( {{V_3} – {V_1}} right);;;;(1)]
Запишем закон Гей-Люссака для изобарного процесса 4-1:
[frac{{{V_3}}}{{{T_2}}} = frac{{{V_1}}}{{{T_1}}}]
[{V_3} = {V_1}frac{{{T_2}}}{{{T_1}}};;;;(2)]
Учитывая выражение (2) и то, что по условию (frac{p_2}{p_1}=2), формула (1) примет вид:
[A = left( {2{p_1} – {p_1}} right)left( {{V_1}frac{{{T_2}}}{{{T_1}}} – {V_1}} right) = {p_1}{V_1}left( {frac{{{T_2}}}{{{T_1}}} – 1} right)]
Теперь запишем уравнение Клапейрона-Менделеева для состояния газа в точке 1:
[{p_1}{V_1} = nu R{T_1}]
Тогда:
[A = nu R{T_1}left( {frac{{{T_2}}}{{{T_1}}} – 1} right)]
[A = nu Rleft( {{T_2} – {T_1}} right)]
Посчитаем ответ:
[A = 1 cdot 8,31 cdot left( {360 – 280} right) = 664,8;Дж]
Ответ: 664,8 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.4.33 Газообразный водород массой 1 кг при начальной температуре 300 К охлаждают
5.4.35 В сосуде объемом 2 л находится гелий при давлении 100 кПа и температуре 200 К
5.4.36 Два одинаковых сосуда, содержащих одинаковое число молекул азота, соединены
