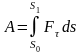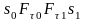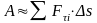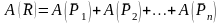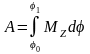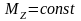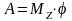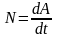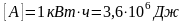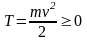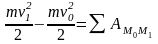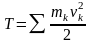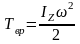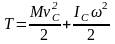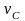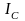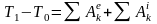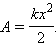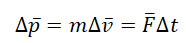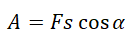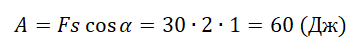Е
сли
изменение
задано
в виде графика
,
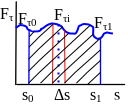
то работа выражается криволинейным
интегралом
.
Графически этот интеграл равен площади
криволинейной трапеции
,
которую можно заменить суммой площадей
трапеций равных
,
то есть
.
1 3.1.7 Теоремы о работе силы:
Теорема
1:
Работа
равнодействующей силы
на
некотором перемещении равна алгебраической
сумме работ составляющих сил на этом
же перемещении
.
Теорема
2:
Работа
постоянной
по модулю и направлению силы
на результирующем перемещении равна
алгебраической сумме работ этой силы
на соответствующих перемещениях
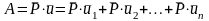
Следствие
1:Работу
постоянной силы на криволинейном
перемещении можно заменить работой на
прямолинейном перемещении.
Следствие
2:
В случае замкнутого контура перемещения
и работа постоянной силы равна нулю.
13.1.8 Работа сил приложенных к вращающемуся телу
.
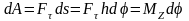
Элементарная
работа силы приложенной к вращающемуся
телу равно произведению момента
относительно оси вращения на элементарный
угол
.
Работа
момента относительно оси вращения при
повороте на угол φ
равна
.
Если
,
то
.
Если
значение
задано в виде графика, то работа может
быть определена графически аналогично
работе силы.
13.2 Мощность. Коэффициент полезного действия
13.2.1
Мощностью
называют скалярную величину равную
работе совершаемую силой в единицу
времени.
.
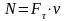
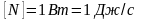
736
Вт=75кГм/с.
Работу,
произведенную машиной, измеряют
произведением мощности на время
.
.
Мощность,
развиваемая моментом силы (пары сил)
равна
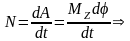
13.2.2
Коэффициентом полезного действия
(КПД) системы (механизма, машины, агрегата
и т.д.) за некоторый промежуток времени
называют отношение совершенной полезной
работы к затраченной работе сил,
действующих на систему. Это средний
КПД
за этот промежуток времени.
.
Мгновенный
КПД равен:
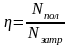
13.3 Кинетическая энергия
13.3.1
Кинетической энергией материальной
точки
называется скалярная величина равная
половине произведения массы точки на
квадрат ее скорости
,
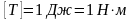
Теорема
об изменении кинетической энергии
материальной точки:
Изменение кинетической энергии
материальной точки при некотором ее
перемещении равно алгебраической сумме
работ всех действующих на точку сил на
этом же перемещении.
.
Следствие
1:
При несвободном движении точки с любыми
связями N:
.
Следствие
2:
В случае идеально гладкой поверхности
реакции связей N
перпендикулярны к траектории движения
точки и
.
Следствие
3:
Этим выражением можно пользоваться и
в случае шероховатых связей. Для этого
в число активных сил включают силы
трения.
13.3.2
Кинетической энергией материальной
системы
называют скалярную величину равную
сумме кинетических энергий всех точек
системы
.
Если
система состоит из нескольких тел, то
ее кинетическая энергия равна сумме
кинетических энергий этих тел.
13.3.3
Формулы для определения кинетической
энергии твердых тел
определяются видом их движения.
Поступательное
движение:
,
где
М – масса тела;
–
скорость любой
точки тела.
Вращение
вокруг неподвижной оси Z:
,
где
– момент инерции тела относительно оси
вращения Z;
–
угловая скорость тела.
Плоское
движение:
,
где
– скорость центра масс тела;
–
момент инерции тела относительно оси
проходящей через центр масс перпендикулярно
плоскости движения.
При
плоском движении тела его кинетическая
энергия равна сумме поступательного
движения всех его точек со скоростью
центра масс и вращения вокруг центра
масс.
13.3.4
Теорема об изменении кинетической
энергии системы:
Изменение кинетической энергии системы
при некотором ее перемещении равно
сумме работ всех внешних и внутренних
сил действующих на систему при этом
перемещении.
.
Частные
случаи:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Графический способ вычисления работы
Вычисление работы си ты на конечном пути по установленным формулам, без знания закона движения точки приложения силы, возможно лишь в частных случаях (например, при постоянной силе).
Для вычисления же работы силы в общем случае, когда сила может зависеть от времени, координат и скорости, нужно знать закон движения точки приложения силы. Только в этом случае можно выразить, как мы видели при решении задачи 86, все переменные в функции времени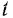 
и вычислить соответствующий интеграл.
Если же закон движения точки приложения силы неизвестен, то для вычисления работы силы нужно сначала найти этот закон, т. е. решить вторую основную задачу динамики.
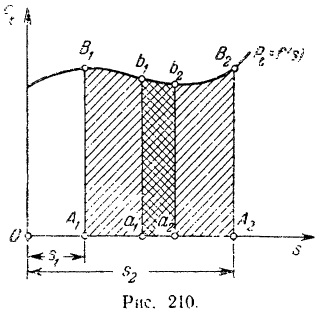
На практике для определения работы часто пользуются графическим способом, используя для этой цели график зависимости
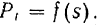
По оси абсцисс этого графика (рис. 210) отложены, в некотором масштабе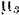 
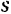
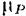
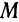
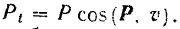
значения дуговой координаты 
точки приложения силы, а по оси ординат, также в каком-то масштабе 
, соответствующие им значения проекции этой силы на направление скорости точки 
, т.е.
Элементарная работа силы будет равна
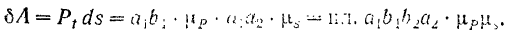
Работа силы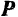 
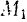
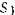
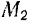
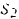
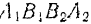
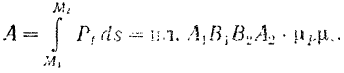
на конечном перемещении ее точки приложения из положения 
с дуговой координатой 
в положение 
с координатой 
будет выражаться в некотором масштабе площадью фигуры 
(рис. 210):
Работа силы на некотором перемещении ее точки приложения выражается в определенном масштабе площадью фигуры, ограниченной осою абсцисс, кривой
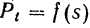
и двумя ординатами, соответствующими начальному и конечному положениям точки приложение силы.
На рис. 210 алгебраические значения касательной составляющей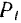 
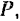
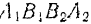
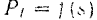
силы отложены и положительную сторону соответствующей оси и потому работа силы 
изображаемая площадью фигуры , будет положительной. Если же построенная кривая
будет расположена от оси абсцисс в сторону отрицательных значений 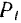, то соответствующая площадь будет изображать отрицательную работу.
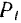
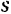
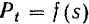
К графическому способу определения работы силы приходится прибегать в тех случаях, когда нам известны значения силы только для отдельных значении , установление же аналитической зависимости
затруднительно или даже невозможно. В ряде случаев (например, при определении работы пара или газа в цилиндрах паровой машины или двигателя) график зависимости
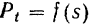
получается автоматически, при помощи самопишущих приборов, называемых индикаторами.
В заключение отметим следующее обстоятельство.
Хотя установленное в механике понятие работы (называемой иногда механической работой) и возникло из повседневного опыта, но оно не всегда совпадает с тем, что понимают под работой с физиологический точки зрения. Так, человек, неподвижно держащий па вытянутых руках тяжелый груз, не совершает, очевидно, с точки зрения механики, никакой работы (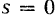
). С физиологической же точки зрения он совершает, конечно, определенную работу.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Механическая работа, или работа постоянной силы (скалярная величина) |
(A = vec{F} · Deltavec{r}), ((1)) где произведение векторов силы (vec{F}) и перемещения (Deltavec{r}) является скалярным. (A = FDelta rcosalpha), ((2)) где (alpha) — угол между направлениями (vec{F}) и (Deltavec{r}) |
| Единицы работы | [(A)] (= 1 Н · 1 м =1 Дж) |
|
Работа силы — аддитивная физическая величина (получаемая суммированием) |
Если на физический объект действует (N) сил (vec{F}_1, vec{F}_2)… (vec{F}_N), то (A = sumlimits_{i = 1}^{N}vec{F}_i · Deltavec{r}). ((3)) Например, на тело действуют силы тяжести (vec{F}_т), реакции опоры (vec{N}) и трения скольжения (vec{F}_{тр}), тогда работа результирующей всех сил при перемещении тела равна (A = (vec{F}_т + vec{F}_{тр} + vec{N}) · Deltavec{r}) ((4)) |
| Работа переменной силы |
Если сила, совершающая работу по перемещению тела, изменяется, то траектория движения объекта разбивается на такие участки, где значение силы постоянно и работа силы на данном участке вычисляется по формуле: (A_k = F_kDelta r_kcosalpha_k). ((5)) Работа силы на всей траектории вычисляется через суммирование по (k)-м участкам: (A = sumlimits_kA = sumlimits_kvec{F}_k · Deltavec{r}_k = sumlimits_kF_kDelta r_kcosalpha_k) ((6)) |
| Геометрическая интерпретация механической работы |
Работа постоянной силы вычисляется как площадь (S) фигуры (рис. (1)) в координатах ((F_x), (Delta r)), где (F_x = Fcosalpha).
Рис. (1). Графическое представление работы силы |
| Мощность |
Средняя мощность: (P_{ср} = frac{A}{Delta t}), ((7)) где (Delta t) — конечный временной интервал совершения работы. Мгновенная мощность (мощность): (P = limlimits_{Delta tto 0}frac{A}{Delta t} = limlimits_{Delta tto 0}frac{vec{F} · Deltavec{r}}{Delta t} = limlimits_{Delta tto 0}vec{F} · frac{Deltavec{r}}{Delta t} = vec{F} · vec{v},) ((8)) где (vec{v}) — вектор мгновенной скорости, символ (limlimits_{Delta tto 0}) — обозначение математического предела |
| Единицы мощности | [(P)] (= frac{1 Дж}{1 с} = 1 Вт) |
Нам удалось достаточно просто рассчитать работу постоянной силы — силы тяжести. Когда же сила меняется по модулю и направлению (§ 90), расчет работы значительно усложняется. В этих случаях удобен графический способ расчета.
Еще раз вернемся к задаче о работе силы тяжести. Допустим, что тело массы 
(рис. 5.15) падает вертикально под действием силы тяжести (направление вниз будем считать положительным). Будем отсчитывать длину пути 
от точки начала падения. Построим график зависимости силы тяжести 
от длины пути 
График будет иметь вид прямой, параллельной оси абсцисс, так как сила тяжести 
постоянна (рис. 5.16).
Рис. 5.15.
Рис. 5.16.
Рис. 5.17.
Рис. 5.18.
По определению работа, которую совершит сила тяжести на расстоянии 
равна
Произведение численно равно площади фигуры, показанной на графике. Это позволяет рассчитывать работу по таким графикам и в случае переменных сил.
Для примера проведем графический расчет работы силы упругости.
Пусть на пружине жесткостью 
подвешен груз массы 
под действием которого пружина растянута на величину 
(рис. 5.17). Как было показано в § 63, пружина при этом будет действовать на груз с силой упругости 
направленной к положению равновесия. Если груз не удерживать, то он начнет двигаться в направлении действия этой силы. Сила упругости при этом будет совершать положительную работу. Во время движения сила упругости постепенно уменьшается, поэтому формулу 
нельзя применить для расчета работы сразу для всего движения тела.
Построим график зависимости силы упругости 
от длины пути 
(рис. 5.18). Допустим, что тело проходит точку, длина пути до которой 
Выделим около этой точки такое малое расстояние 
чтобы можно было работу силы упругости на этом расстоянии подсчитать по формуле 
Произведение 
численно равно площади прямоугольника, заштрихованного на рисунке. Расположим 
так, чтобы ордината, соответствующая точке 
была средней линией этого прямоугольника. Тогда 
будет средней линией трапеции, ограниченной отрезком 
линии графика силы, ординатами точек 
и отрезком оси 
Произведение 
численно равно площади этой трапеции, т. е. и в этом случае работа силы упругости оказалась равной
площади фигуры, ограниченной линией графика силы, ординатами начальной и конечной точек движения и отрезком оси 
Используя этот результат, можно рассчитать работу сил упругости для любого конечного движения тела. Пусть тело, отклоненное на расстояние 
под действием силы упругости возвратилось в положение равновесия. Работа силы упругости в этом случае будет равна площади треугольника, показанного на рис. 5.19, т. е.
Если под действием силы упругости тело перешло из положения 
в положение 
(рис. 5.20), то, как видно из рис. 5.21, работа этой силы равна
Наш расчет обнаружил, что работа силы упругости полностью определяется начальным и конечным положениями тела. Можно показать, что эта работа не зависит от формы траектории, по которой двигалось тело под действием пружины. Поэтому сила упругости тоже является консервативной силой. Растягивая пружину, мы совершаем какую-то работу против силы упругости пружины. Если эту пружину затем освободить, то сила упругости вернет ее в нерастянутое состояние. При этом она полностью возвратит всю ту работу, которая была совершена при ее растяжении.
Рис. 5.19.
Рис. 5.20.
Рис. 5.21.
По площади треугольника на рис. 1.18.4 можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы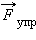 
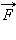
равна по модулю работе внешней силы 
и противоположна ей по знаку.
Если к телу приложено несколько сил, то общая работа всех сил равна алгебраической сумме работ, совершаемых отдельными силами. При поступательном движении тела, когда точки приложения всех сил совершают одинаковое перемещение, общая работа всех сил равна работе равнодействующей приложенных сил .
Источник
Графический способ вычисления работы
Графический способ вычисления работы
Вычисление работы си ты на конечном пути по установленным формулам, без знания закона движения точки приложения силы, возможно лишь в частных случаях (например, при постоянной силе).
Для вычисления же работы силы в общем случае, когда сила может зависеть от времени, координат и скорости, нужно знать закон движения точки приложения силы. Только в этом случае можно выразить, как мы видели при решении задачи 86, все переменные в функции времени 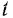и вычислить соответствующий интеграл.
Если же закон движения точки приложения силы неизвестен, то для вычисления работы силы нужно сначала найти этот закон, т. е. решить вторую основную задачу динамики.
На практике для определения работы часто пользуются графическим способом, используя для этой цели график зависимости
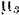
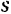
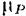
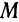
По оси абсцисс этого графика (рис. 210) отложены, в некотором масштабе значения дуговой координаты точки приложения силы, а по оси ординат, также в каком-то масштабе , соответствующие им значения проекции этой силы на направление скорости точки , т.е.
Элементарная работа силы будет равна
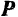
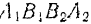
Работа силы на конечном перемещении ее точки приложения из положения с дуговой координатой в положение с координатой будет выражаться в некотором масштабе площадью фигуры (рис. 210):
Работа силы на некотором перемещении ее точки приложения выражается в определенном масштабе площадью фигуры, ограниченной осою абсцисс, кривой
и двумя ординатами, соответствующими начальному и конечному положениям точки приложение силы.
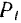
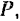
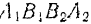
На рис. 210 алгебраические значения касательной составляющей силы отложены и положительную сторону соответствующей оси и потому работа силы изображаемая площадью фигуры , будет положительной. Если же построенная кривая
будет расположена от оси абсцисс в сторону отрицательных значений 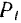, то соответствующая площадь будет изображать отрицательную работу.
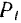
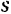
К графическому способу определения работы силы приходится прибегать в тех случаях, когда нам известны значения силы только для отдельных значении , установление же аналитической зависимости
затруднительно или даже невозможно. В ряде случаев (например, при определении работы пара или газа в цилиндрах паровой машины или двигателя) график зависимости
получается автоматически, при помощи самопишущих приборов, называемых индикаторами.
В заключение отметим следующее обстоятельство.
Хотя установленное в механике понятие работы (называемой иногда механической работой) и возникло из повседневного опыта, но оно не всегда совпадает с тем, что понимают под работой с физиологический точки зрения. Так, человек, неподвижно держащий па вытянутых руках тяжелый груз, не совершает, очевидно, с точки зрения механики, никакой работы (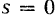). С физиологической же точки зрения он совершает, конечно, определенную работу.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
Механическая работа и мощность
теория по физике 🧲 законы сохранения
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
Модуль силы тяжести: Fтяж = mg
Работа силы тяжести: A = mgs cosα
Модуль силы трения скольжения: Fтр = μN = μmg
Работа силы трения скольжения: A = μmgs cosα
Модуль силы упругости: Fупр = kx
Работа силы упругости:
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0 о , то cosα = 1.
- Если 0 о o , то cosα > 0.
- Если α = 90 о , то cosα = 0.
- Если 90 о o , то cosα о , то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180 о ). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0 о ). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
Мощность
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела
Работа при равномерном прямолинейном движении определяется формулой:
Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна:
Мощность при равномерном подъеме груза
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому:
