В этой заметке рассмотрим как можно вычислить работу идеального газа при различных изо-процессах. Это будет полезно тем, кто только начинает изучать термодинамику и МКТ. Для простоты изображения всех процессов возьмем самые популярные P-V диаграммы.
Есть такое понятие как термодинамический процесс. Изменение любого параметра термодинамической системы (к параметрам можно отнести температуру T, давление p, объем V, энтропию S). Но так как все параметры термодинамической системы взаимосвязаны, то частенько, когда изменяется один параметр, то и изменяются другие параметры.
Если термодинамические процессы не протекают, то система находится в равновесном состоянии. То есть равновесное состояние — такое абстрактное состояние системы, при котором все термодинамические параметры системы остаются сколь угодно долго неизменными, если над системой не совершают никаких внешних воздействий. То есть система предоставлена сама себе. Почему же это состояние абстрактно? Потому что в реальной жизни очень тяжело изолировать систему от внешнего влияния окружающего мира. Таким образом, в каждый момент времени протекают какие-то термодинамические процессы.
Однако, процессы могут протекать настолько медленно, что система изменяется почти незаметно. Иногда это дает возможность рассматривать состояние системы из последовательных равновесных состояний. Такие процессы еще называются квазистатическими. Под квазистатичностью можно понимать что-то ооочень медленное, настолько медленной, что оно длится намного дольше, чем время релаксации (время, за которое амплитудное значение внешнего возмущения, которое начало менять систему, уменьшилось в e раз).
Еще система может постоянно возвращаться к исходному состоянию. Такой круговой процесс называется циклом (примерно по таким процессам работают тепловые машины и ДВС).
Что нужно чтобы изучить какую-либо термодинамическую систему?
1. Определить работу, совершаемую в данном процессе
2. Определить изменение внутренней энергии системы
3. Определить количество теплоты, которое вошло в систему или которое отдала система.
4. Установить связи между отдельными величинами, которые характеризуют состояние рабочего тела (газа)
Основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.
И далее мы с вами выведем работы в этих основных процессах.
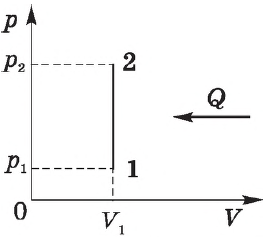
1. Изохорный процесс
Изохорным процесс — термодинамический процесс, который протекает при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.
2. Изотермический процесс
Изотермический процесс — термодинамический процесс, который протекает при постоянной температуре. На практике очень сложно осуществить этот процесс. Потому что при сжатии или расширении газа, нужны условия, при которых газ будет успевать обмениваться температурой с внешней средой, чтобы поддерживать свою температуру неизменной.
3. Изобарный процесс
Изобарный процесс — термодинамический процесс, который протекает при постоянном давлении. Помещение газа в плотный цилиндр с подвижным поршнем, на который действует постоянная сила ( например сила тяжести со стороны груза ) при отводе и подводе теплоты, может смоделировать такой процесс.
4. Адиабатный процесс
Адиабатный процесс — термодинамический процесс, который протекает без теплообмена (Q = 0) рабочего тела (газа) с окружающей средой. Также сложно осуществимый процесс. Примерная модель: газ помещают в цилиндр с подвижным поршнем. При этом цилиндр и поршень выполнены из высококачественного теплоизолирующего материала.
5. Политропный процесс (p∙Vⁿ = const )
Этот процесс является обобщением всех предыдущих. Все параметры в этом процессе могут меняться. А процессы выше являются его частными случаями. n – показатель политропы, некоторая постоянная, которая может принимать любые значения от -∞ до +∞.
n = 0 – изобарный процесс p = const
n = 0 – изотермический процесс T = const
n = γ – адиабатный процесс p∙Vⁿ = const
n = +∞ или n = -∞ – изохорный процесс V = const
Любые формулы для этого процесса аналогичны адиабатному процессу. При этом работа выводится точно также. Только коэффициент адиабаты (γ) в общем случае заменяется на коэффициент политропы (n).
Понравился разбор задачи ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
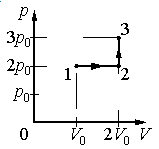
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k
Работа
идеального газа в изопроцессах.
Первый закон
термодинамики (закон сохранения энергии
для тепловых процессов) определяет
количественное соотношение между
изменением внутренней энергии системы
дельта U, количеством теплоты Q, подведенным
к ней, и суммарной работой внешних сил
A, действующих на систему.
Первый закон
термодинамики – Изменение внутренней
энергии системы при ее переходе из
одного состояния в другое равно сумме
количества теплоты, подведенного к
системе извне, и работы внешних сил,
действующих на нее:
Первый закон
термодинамики – количество теплоты,
подведенное к системе, идет на изменение
ее внутренней энергии и на совершение
системой работы над внешними телами:
Частные случаи
первого закона термодинамики для
изопроцессов
При изохорном
процессе объем газа остается постоянным,
поэтому газ не совершает работу. Изменение
внутренней энергии газа происходит
благодаря теплообмену с окружающими
телами:
При изотермическом
процессе количество теплоты, переданное
газу от нагревателя, полностью расходуется
на совершение работы:
Q=A’
При изобарном
расширении газа подведенное к нему
количество теплоты расходуется как на
увеличение его внутренней энергии и на
совершение работы газом:
Адиабатный процесс
– термодинамический процесс в
теплоизолированной системе.
Теплоёмкость идеального
газа —
отношение количества
теплоты,
сообщённого газу, к изменению температуры δТ,
которое при этом произошло.
Молярная
теплоёмкость — теплоёмкость
1 моля идеального
газа.
Адиабатический[править | править исходный текст]
В адиабатическом
процессе теплообмена
с окружающей средой не происходит, то
есть .
Однако, объём, давление и
температура меняются, то есть .
Следовательно,
теплоёмкость идеального газа в
адиабатическом процессе равна нулю: .
Изотермический[править | править исходный текст]
В изотермическом
процессе постоянна
температура, то есть .
При изменении объёма газу передаётся
(или отбирается) некоторое количество
тепла. Следовательно, теплоёмкость
идеального газа равна бесконечности:
Изохорный[править | править исходный текст]
В изохорном
процессе постоянен
объём, то есть .
Элементарная работа газа равна
произведению изменения объёма на
давление, при котором происходит
изменение ().
Первое Начало Термодинамики для
изохорного процесса имеет вид:
А для идеального газа
Таким образом,
где —
число степеней
свободы частиц
газа.
Другая
формула: ,
где γ — показатель
адиабаты,
R — универсальная
газовая постоянная.
Согласно Первому началу
термодинамики существует два способа
изменения внутренней энергии тела (в
нашем случае идеального газа): передать
ему некоторое количество теплоты или
совершить над ним работу.
dU=δQ+δA, где δA — работа
внешних сил над газом.
δAвнеш.сил=-δAгаза
δQ=dU+δAгаза
В расчете на 1 моль:
С=δQ/ΔT=(ΔU+pΔV)/ΔT
ΔU=CV*ΔT
C=CV+(pΔV/ΔT)в
данном процессе
Внутренняя энергия идеального газа
Исходя
из определения идеального газа, в нем
отсутствует потенциальная составляющая
внутренней энергии (отсутствуют силы
взаимодействия молекул, кроме ударного).
Таким образом, внутренняя
энергия идеального газа представляет
собой только кинетическую энергию
движения его молекул. Ранее
(уравнение 2.10) было показано, что
кинетическая энергия поступательного
движения молекул газа прямо пропорциональна
его абсолютной температуре
|
|
Используя
выражение универсальной газовой
постоянной (4.6), можно определить величину
константы α
|
|
Таким
образом, кинетическая энергия
поступательного движения одной молекулы
идеального газа будет определяться
выражением
|
|
(4.10) |
В
соответствии с кинетической теорией,
распределение энергии по степеням
свободы равномерное. У поступательного
движения 3 степени свободы. Следовательно,
на одну степень свободы движения молекулы
газа будет приходиться 1/3 ее кинетической
энергии
|
|
(4.11) |
Для
двух, трех и многоатомных молекул газа
кроме степеней свободы поступательного
движения есть степени свободы вращательного
движения молекулы. Для двухатомных
молекул газа число степеней свободы
вращательного движения равно 2, для трех
и многоатомных молекул – 3.
Поскольку
распределение энергии движения молекулы
по всем степеням свободы равномерное,
а число молекул в одном киломоле газа
равняется Nμ,
внутреннюю энергию одного киломоля
идеального газа можно получить, умножив
выражение (4.11) на число молекул в одном
киломоле и на число степеней свободы
движения молекулы данного газа
|
|
(4.12) |
где
Uμ –
внутренняя энергия киломоля газа в
Дж/кмоль,
i
– число степеней свободы движения
молекулы газа.
Для
1-атомного газа i = 3, для 2-атомного газа
i = 5, для 3-атомного и многоатомного газов
i = 6 (рис. 4.1).
Для
многоатомного газа i=6, так как существуют
3 степени свободы поступательного
движения и 3 степени свободы вращательного
движения молекул. Может быть еще
колебательное движение атомов в молекуле,
но его обычно учитывают для реальных
газов, используя экспериментальные
данные. Для идеальных газов колебательное
движение атомов в молекулах тоже может
быть учтено при расчете внутренней
энергии, об этом будет сказано в разделе
“Зависимость теплоемкостей идеальных
газов от температуры”. На данном этапе
изложения материала будем руководствоваться
молекулярно-кинетической теорией
идеального газа. В соответствии с
ней атомы
в молекулах идеального газа имеют
жесткие связи, т.е. колебательного
движения атомов в молекулах нет.
Для
одного килограмма идеального газа
удельная внутренняя энергия в Дж/кг
определяется делением выражения (4.12)
на молярную массу газа
|
|
(4.13) |
Для
произвольного количества газа внутренняя
энергия определяется как произведение
его массы на удельную внутреннюю энергию
этого газа
|
|
(4.14) |
где
m
– масса газа в кг,
U
– полная внутренняя энергия идеального
газа.
Если
система состоит из нескольких различных
по физическим свойствам газов, то,
подчиняясь закону сложения (аддитивности),
его полная внутренняя энергия будет
определяться суммой внутренних энергий
компонентов газовой смеси
|
|
(4.15) |
где
n
– число компонентов газа в системе.
Полученные
уравнения внутренней энергии идеального
газа (4.12) – (4.15) указывают на то, что
внутренняя энергия идеального газа
зависит только от абсолютной температуры
газа и числа степеней свободы движения
его молекул
|
|
или
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Работа в термодинамике
В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.
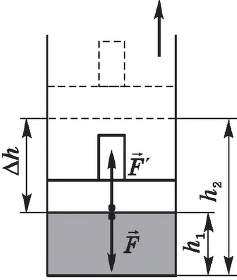
Рассмотрим работу газа при изобарическом расширении.
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:
$A’=F’∆h=pS∆h=p∆V$
Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V < 0$, поскольку $∆h < 0$.
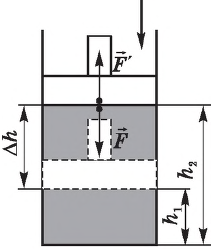
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:
$A=-A’=-p∆V$
Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.
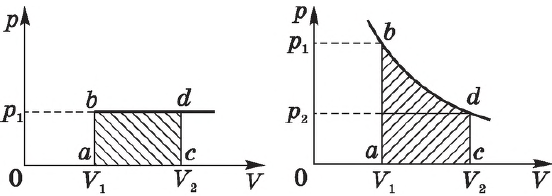
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.
Первый закон термодинамики
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
$∆U=A+Q$
где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.
Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:
$Q=∆U+A’$
где $А’$ — работа, совершаемая системой ($А’=-А$).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.
Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.
Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,
$∆U=Q$
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q < 0$ и $∆U < 0$, внутренняя энергия уменьшается.
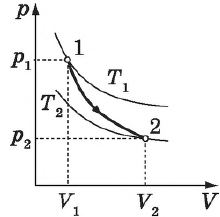
Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.
Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:
$Q=A’$
При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q < 0$ и $А’ < 0$. В этом случае над газом совершается работа внешними силами. Для внешних сил работа положительна. Геометрически работа при изотермическом процессе определяется площадью под кривой $р(V)$.
Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.
Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.
При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:
$Q=∆U+A’$
Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс
Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).
Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.
Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе
$∆U=A$
где $А$ — работа внешних сил.
При адиабатном расширении газа $А < 0$.
Следовательно,
$∆U={i}/{2}·{m}/{M}R∆T < 0,$
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.
Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
Принцип действия тепловых двигателей
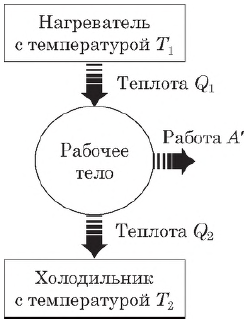
Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.
Таким образом, основными элементами любого теплового двигателя являются:
- рабочее тело (газ или пар), совершающее работу;
- нагреватель, сообщающий энергию рабочему телу;
- холодильник, поглощающий часть энергии от рабочего тела.
Коэффициент полезного действия теплового двигателя
Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:
$A’=|Q_1|-|Q_2|$
где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.
Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:
$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$
Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η < 1$.
КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 – T_2=0$ двигатель не может работать.
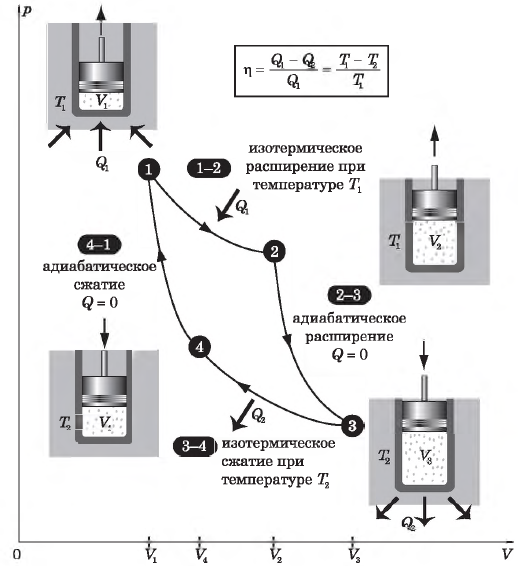
Цикл Карно
Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.
Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.
Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.
Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:
$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
$A_{23}=-∆U_{23}$
Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2 < Т_1$. В процессе ($3-4$) газ изотермически сжимается, передавая холодильнику количество теплоты $Q_2$:
$A_{34}=Q_2,$
Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.
Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:
$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$
Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.
Работа идеального газа
Рассмотрим газ, который находится в цилиндре, закрытом поршнем (рис.1).
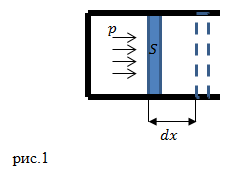
Пусть газ при расширении передвинет поршень на малое расстояние . Таким образом, газ выполнит работу над поршнем (
):
где F – сила, с которой газ действует на поршень, S – площадь поршня; p – давление газа на поршень; – изменение объёма газа под поршнем. Результирующая работа газа, если его объем изменяется от
до
находится как:
Более конкретный результат интегрирования определяет зависимость . Формула (2) для вычисления работы справедлива для изменения объема всех видов тел (газа, жидкости и твердого тела).
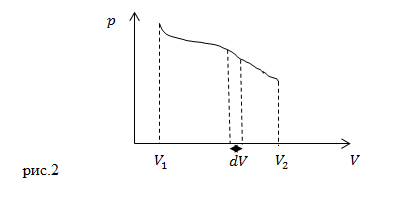
Часто работу газа изображают при помощи графиков в осях (рис.2). Если объем газа увеличивается на
, то работа газа (
) – это площадь криволинейной трапеции с основанием
на рис. 2. Суммарная работа, которую совершил газ, изменяя объем от
до
, определена площадью, которая ограничивается осью абсцисс, кривой
и прямыми
и
.
Работа идеального газа для отдельных процессов
В изобарном процессе () работа вычисляется при помощи формулы:
В изохорном процессе работа газа равна нулю, так как изменения объема не происходит:
Найдем работу для изотермического процесса ():
где из уравнения Менделеева – Клапейрона: – молярная масса газа; m – масса газа). Получили, что для изотермического процесса работа равна:
Для адиабатного процесса, который проходит без обмена теплом окружающей среды и газа работу проще найти из первого начала термодинамики:
Так как то получаем, что в адиабатном процессе газ выполняется работу за счет уменьшения внутренней энергии:
где i – число степеней свободы молекулы газа.





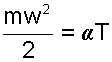

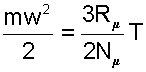





![Rendered by QuickLaTeX.com [A=int^{V_2}_{V_1}{pdV} qquad (2)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-307146ee2b5ca3587ed0509196a22027_l3.png)
![Rendered by QuickLaTeX.com [A_{p=const}=pint^{V_2}_{V_1}{dV=pleft(V_2-V_1right)} qquad (3)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fe5676918253ce4d339056f88171b922_l3.png)
