Как найти работу идеального одноатомного газа - Сайт, где вы сможете решить свои вопросы

Определение

Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.

Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:

U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV

i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.

Изменение внутренней энергии идеального газа в изопроцессах

Основная формула	ΔU=32·mMRT=32νRT=32νR(T2−T1)
Изотермический процесс	ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной.
Изобарное расширение	ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV
Изохорное увеличение давления	ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp
Произвольный процесс	ΔU=32νR(T2−T1)=32(p2V2−p1V1)

Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.

Работа идеального газа

Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:

A=Fscosα

Перемещение равно разности высот поршня в конечном и начальном положении:

s=h2−h1

Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:

Работа идеального газа

F=pS

p — давление газа, S — площадь поршня

Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:

A‘=p(V2−V1)=pΔV>0

Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.

Работа идеального газа при изобарном сжатии:

A‘=p(V2−V1)=pΔV<0

Работа идеального газа при нагревании газа:

A‘=νRΔT=νR(T2−T1)=mMνRΔT

Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.

Геометрический смысл работы в термодинамике

В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).

Примеры графических задач

Изобарное расширение: A‘=p(V2−V1) A‘>0
Изобарное сжатие: A‘=p(V2−V1) A‘<0
Изохорное охлаждение: V=const A‘=0
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0
Замкнутый цикл: 1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1)
Произвольный процесс: A‘=p1+p22(V2−V1)

Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A₂ к A₁ в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:

A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV

A1=p(V2−V1)=p(5V−V)=4pV

Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.

Задание EF17505

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?

Для каждой величины подберите соответствующий характер изменения:

1) увеличивается

2) уменьшается

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Определить по графику, как меняется давление.
Определить, как меняется объем.
Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.

Решение

На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.

Ответ: 123

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17758

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10⁵ Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10⁵ Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Алгоритм решения

1.Записать исходные данные.

2.Записать уравнение состояния идеального газа.

3.Записать формулу для расчета внутренней энергии газа.

4.Используя первое начало термодинамики, выполнить общее решение задачи.

5.Подставив известные данные, вычислить неизвестную величину.

Решение

Запишем исходные данные:

• Начальная температура газа: T₁ = 600 К.

• Начальное давление: p₁ = 4∙10⁵ Па.

• Конечное давление: p₂ = 10⁵ Па.

• Работа, совершенная газом: A = 2493 Дж.

Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:

pV=νRT

Внутренняя энергия одноатомного идеального газа пропорциональна температуре:

U=32νRT

Внутренняя энергия аргона до расширения и после него:

U1=32νRT1

U2=32νRT2

Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:

T=constV

T1V1=T2V2

Выразим конечную температуру:

T2=T1V1V2

Составим уравнение состояния газа для состояний аргона 1 и 2:

p1V1=νRT1

p2V2=νRT2

Отсюда:

νR=p1V1T1=p2V2T2

Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:

V1V2=p2T1p1T2

Подставим это отношение в формулу для конечной температуры:

T2=T1V1V2=p2T12p1T2

Отсюда:

T2=T1√p2p1

Отсюда внутренняя энергия газа в состоянии 2 равна:

U2=32νRT1√p2p1

Уменьшение внутренней энергии аргона составило (изначально она была выше):

ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)

В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:

ΔU=Q+A

Следовательно, газ отдал следующее количество теплоты:

Q=ΔU−A=32νRT1(1−√p2p1)−A

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17966

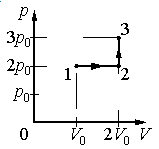
Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна

Ответ:

а) р₀V₀

б) 2р₀V₀

в) 4р₀V₀

г) 6р₀V₀

Алгоритм решения

1.Определить, на каком участке графика совершается работа.

2.Записать геометрический смысл работы.

3.Извлекая данные из графика, вычислить работу, совершенную газом.

Решение

Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.

Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).

Давление газа при этом равно 2p₀, а объем равен разности 2V₀ и V₀. Следовательно, работа, совершенная газом, будет равна произведению:

A=2p0(2V0−V0)=2p0V0

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 14.9k

Источник

Вывод формул работы идеального газа во всех изо-процессах

В этой заметке рассмотрим как можно вычислить работу идеального газа при различных изо-процессах. Это будет полезно тем, кто только начинает изучать термодинамику и МКТ. Для простоты изображения всех процессов возьмем самые популярные P-V диаграммы.

Есть такое понятие как термодинамический процесс. Изменение любого параметра термодинамической системы (к параметрам можно отнести температуру T, давление p, объем V, энтропию S). Но так как все параметры термодинамической системы взаимосвязаны, то частенько, когда изменяется один параметр, то и изменяются другие параметры.

Если термодинамические процессы не протекают, то система находится в равновесном состоянии. То есть равновесное состояние — такое абстрактное состояние системы, при котором все термодинамические параметры системы остаются сколь угодно долго неизменными, если над системой не совершают никаких внешних воздействий. То есть система предоставлена сама себе. Почему же это состояние абстрактно? Потому что в реальной жизни очень тяжело изолировать систему от внешнего влияния окружающего мира. Таким образом, в каждый момент времени протекают какие-то термодинамические процессы.

Однако, процессы могут протекать настолько медленно, что система изменяется почти незаметно. Иногда это дает возможность рассматривать состояние системы из последовательных равновесных состояний. Такие процессы еще называются квазистатическими. Под квазистатичностью можно понимать что-то ооочень медленное, настолько медленной, что оно длится намного дольше, чем время релаксации (время, за которое амплитудное значение внешнего возмущения, которое начало менять систему, уменьшилось в e раз).

Еще система может постоянно возвращаться к исходному состоянию. Такой круговой процесс называется циклом (примерно по таким процессам работают тепловые машины и ДВС).

Что нужно чтобы изучить какую-либо термодинамическую систему?
1. Определить работу, совершаемую в данном процессе
2. Определить изменение внутренней энергии системы
3. Определить количество теплоты, которое вошло в систему или которое отдала система.
4. Установить связи между отдельными величинами, которые характеризуют состояние рабочего тела (газа)

Основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.

И далее мы с вами выведем работы в этих основных процессах.

1. Изохорный процесс

Изохорным процесс — термодинамический процесс, который протекает при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.

2. Изотермический процесс

Изотермический процесс — термодинамический процесс, который протекает при постоянной температуре. На практике очень сложно осуществить этот процесс. Потому что при сжатии или расширении газа, нужны условия, при которых газ будет успевать обмениваться температурой с внешней средой, чтобы поддерживать свою температуру неизменной.

3. Изобарный процесс

Изобарный процесс — термодинамический процесс, который протекает при постоянном давлении. Помещение газа в плотный цилиндр с подвижным поршнем, на который действует постоянная сила ( например сила тяжести со стороны груза ) при отводе и подводе теплоты, может смоделировать такой процесс.

4. Адиабатный процесс

Адиабатный процесс — термодинамический процесс, который протекает без теплообмена (Q = 0) рабочего тела (газа) с окружающей средой. Также сложно осуществимый процесс. Примерная модель: газ помещают в цилиндр с подвижным поршнем. При этом цилиндр и поршень выполнены из высококачественного теплоизолирующего материала.

5. Политропный процесс (p∙Vⁿ = const )

Этот процесс является обобщением всех предыдущих. Все параметры в этом процессе могут меняться. А процессы выше являются его частными случаями. n – показатель политропы, некоторая постоянная, которая может принимать любые значения от -∞ до +∞.

n = 0 – изобарный процесс p = const
n = 0 – изотермический процесс T = const
n = γ – адиабатный процесс p∙Vⁿ = const
n = +∞ или n = -∞ – изохорный процесс V = const

Любые формулы для этого процесса аналогичны адиабатному процессу. При этом работа выводится точно также. Только коэффициент адиабаты (γ) в общем случае заменяется на коэффициент политропы (n).

Понравился разбор задачи ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Работа идеального газа

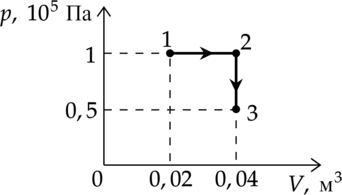
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)

Работа газа – площадь под графиком: [A=p_1cdot(V_2-V_1)=10^5text{ Па}cdot(0,04text{ м$^3$}-0,02text{ м$^3$})=2000text{ Дж}=2text{ кДж}]

Ответ: 2

Идеальный газ получил количество теплоты 300 Дж и при этом внутренняя энергия газа увеличилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)

Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=300text{ Дж}-100text{ Дж}=200 text{ Дж}]

Ответ: 200

Идеальный газ получил количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)

Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=100text{ Дж}-(-100text{ Дж})=200 text{ Дж}]

Ответ: 200

На pV-диаграмме изображены циклические процессы, совершаемые идеальным газом в количестве 1 моль. Определите отношение работы газа в циклическом процессе ВСDВ к работе газа в циклическом процессе АВDFА.

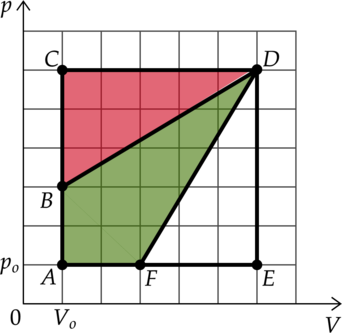
[frac{A_{BCDB}}{A_{ABDFA}}=frac{0,5cdot3cdot5}{5cdot5-2cdot0,5cdot3cdot5}=0,75]

Ответ: 0,75

В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы, сжав газ. Ответ выразите в кДж.

Первое начало термодинамики: [Q=Delta U+A_{text{г}}] [A_{text{г}}=Q-Delta U]
Подставим исходные значения: [A_{text{г}}=Q-Delta U=-10text{ кДж}-30text{ кДж}=-40 text{ кДж}] [A_{text{вн.с.}}=-A_{text{г}}=40 text{ кДж}]

Ответ: 40

В цилиндр с подвижным поршнем накачали (nu = 2) моля идеального одноатомного газа при температуре (t_1 = 50) (^{circ}C). Накачивание вели так, что давление газа было постоянным. Затем накачку прекратили и дали газу в цилиндре расшириться без теплообмена с окружающей средой до давления p = 1 атм. При этом газ остыл до температуры (t_2 = 20) (^{circ}C). Какую суммарную работу совершил газ в этих двух процессах? В исходном состоянии цилиндр был пуст и поршень касался дна. Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ дайте в кДж округлите до целых.

В первом процессе газ расширяется при постоянном давлении. От объема 0 до (V_1) [A_{1-2}=p(V_1-0)=pV_1=nu RT_1]
Без теплообмена с окружающей средой означает, что процесс – адиабатический [Q=Delta U+A_{2-3}=0] [A_{2-3}=-Delta U_{2-3}]
Подставим исходные значения: [A=A_{1-2}+A_{2-3}=nu RT_1+frac{3}{2}nu R(T_1-T_2)=] [=2text{ моль}cdot8,3text{ Дж/моль·К}cdot323text{ K}+frac{3}{2}cdot2text{ моль}cdot8,3text{ Дж/моль·К}cdot30{ K}approx 6000text{ Дж}approx 6 text{ кДж}]

Ответ: 6

С массой (m = 80) г идеального газа, молярная масса которого (M = 28) г/моль, совершается циклический процесс, изображенный на рисунке. Какую работу (A) совершает такой двигатель за один цикл, если (T_1 = 300) К, (T_2 = 1000) К, а при нагревании на участке 4 – 1 давление газа увеличивается в 2 раза? Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ округлите до целых.

1-2 и 3-4 – изобарные процессы
2-3 и 4-1 – изохорные процессы
Перерисуем график в координатах (pV)
Так как 2-3 и 4-1 – изохорные процессы, то (Tsim p). Давление увеличивается в 2 раза, то температура увеличивается в 2 раза. Следовательно: [T_4=frac{T_1}{2}=150 text{ К}] [T_3=frac{T_2}{2}=500 text{ К}]
Работа газа цикл – площадь внутри графика в координатах (pV) [A=(p_1-p_4)cdot(V_2-V_1)=(2p_4-p_4)cdot(V_2-V_1)=p_4cdot(V_2-V_1)=p_4V_2-p_4V_1]
Подставим исходные значения,переведя все единицы в систему СИ: [A=p_4V_2-p_4V_1=nu RT_3-nu RT_4=nu R(T_3-T_4)=frac{m}{M}R(T_3-T_4)=] [=frac{0,08text{ кг}}{0,028text{ кг/моль}}cdot8,31text{ Дж/(моль$cdot$ К)}cdot(500 text{ К} – 150 text{ К})= 8310 text{ Дж}]

Ответ: 8310

УСТАЛ? Просто отдохни

Источник

Работа идеального газа
равна

При расширении работа газа
положительна, при сжатии – отрицательна.

Чтобы получить функцию
давления в зависимости от объема, надо
использовать совместно с уравнением
процесса уравнение Менделеева-Клапейрона

4-1. В воздушном шарике
находится одноатомный идеальный газ.
Газ расширяется от объема

до объема

,
при этом его давление меняется по закону

а)

;
б)

;
в)

;
г)

.

Найти работу (в МДж),
совершенную газом в этом процессе.

p₀
= 10⁵
Па;

=
1 м³;

=2
м³.

Ответы: а) 0,15 МДж; б) 0,233 МДж;
в) 0,375 МДж; г) 0,62 МДж

4-2. В воздушном шарике
находится один моль одноатомного
идеального газа. Газ расширяется от
объема

до объема

,
при этом его температура меняется по
закону

а)

;
б)

;
в)

;
г)

Найти работу (в кДж),
совершенную газом в этом процессе.
Универсальная газовая постоянная

.
T₀
= 300 K;

=
1 м³;

=2
м³.

Ответы: а) 26,1 кДж; б) 45,2 кДж;
в) 79,4 кДж; г) 141 кДж

4-3. В воздушном шарике
находится один моль одноатомного
идеального газа. Газ расширяется от
объема

до объема

,
при этом его объем меняется по закону

а)

;
б)

;
в)

;
г)

Найти работу (в кДж),
совершенную газом в этом процессе.
Универсальная газовая постоянная

.

= 300 K;

=
1 м³;

=2
м³.

Ответы: а) 3,74 кДж; б) 5,82 кДж;
в) 9,35 кДж; г) 15,5 кДж

4-4. В воздушном шарике
находится один моль одноатомного
идеального газа. Газ расширяется от
объема

до объема

,
при этом его давление меняется по закону

.
Найти работу (в МДж), совершенную газом
в этом процессе. Универсальная газовая
постоянная

= 300 K;

= 10⁵
Па;

=
1 м³;

=2
м³.

Ответ: 6,02 МДж

4-5. В воздушном шарике
находится один моль одноатомного
идеального газа. Газ расширяется от
объема

до объема

,
при этом его температура меняется по
закону

.
Найти работу (в МДж), совершенную газом
в этом процессе. Универсальная газовая
постоянная

= 300 K;

= 10⁵
Па;

=
1 м³;

=2
м³.

Ответ: 6,02 МДж

4
-6э.
Идеальный газ совершает циклический
процесс 1-2-3-1, как показано на рисунке,
где процессы 2-3 – изохорический, а 3-1 –
изотермический. Площадь

фигуры 1-2-3 равна 10 Дж, а площадь

фигуры 1-3-В-А равна 15 Дж.

В процессе 3-1 газ отдал
окружающей среде тепло…

Ответ: 15 Дж

5. Теплоемкость.

Теплоемкость
газа равна

– теплота, необходимая для нагревания
тела (газа) на один Кельвин.

Зная теплоемкость, можно
определить теплоту, переданную газу
при нагревании:

Если задана зависимость
теплоемкости от температуры в виде
графика, то теплота есть площадь
под кривой

.

Изменение
внутренней энергии
идеального газа равна

где

– число степеней свободы молекулы. При
не очень высокой и не очень низкой
температуре (когда возбуждены вращательные
степени свободы, но не возбуждены
колебательные степени свободы) i
= 3 для одноатомного
газа, i
=5 для двухатомного
газа, i
= 6 для трех- и
(более)-атомного газа.

Первое начало термодинамики:

теплота, переданная газу
от нагревателя, идет на увеличение
внутренней энергии газа и на совершение
эти газом работы. Если внутренняя энергия
газа при этом уменьшается, то

.

Политропический процесс
– процесс с постоянной теплоемкостью.

5-1. Теплоемкость газа зависит
от температуры по закону

а)

;
б)

;
в)

;
г)

.

Найти тепло, полученное
газом, если его температура увеличилась
с

до

.

=1
Дж/К;

=300
К;

.

Ответы: а) 450 Дж; б) 1125 Дж; в)
3150 Дж; г) 9,56 кДж

5-2. Теплоемкость газа зависит
от температуры по закону

а)

;
б)

;
в)

;
г)

При изменении температуры
газа от

до

им была совершена работа А.
Найти изменение внутренней энергии
газа.

=1
Дж/К;

=300
К;

;
А =
100 Дж.

Ответы: а) 600 Дж; б) 1760 Дж; в)
5,39 кДж; г) 16,9 кДж

5-3. Теплоемкость одного моля
идеального одноатомного
газа зависит от температуры по закону
а)

;
б)

.

Найти работу, совершенную
газом, при изменении температуры газа
от

до

.
Универсальная газовая постоянная R
= 8,3 Дж/мольК;

=1
Дж/К;

=300
К;

Ответы: а) –3285 Дж; б) –2334 Дж

5-4. Теплоемкость одного моля
идеального двухатомного
газа зависит от температуры по закону
а)

;
б) .

Найти работу, совершенную
газом, при изменении температуры газа
от

до

.
Универсальная газовая постоянная R
= 8,3 Дж/моль×К;

=1
Дж/К;

=300
К;

Ответы: а) – 5775 Дж; б) – 4824
Дж

5-5. Теплоемкость одного моля
идеального трехатомного
газа зависит от температуры по закону
а)

;
б)

Найти работу, совершенную
газом, при изменении температуры газа
от

до

.
Универсальная газовая постоянная R
= 8,3 Дж/моль×К;

=1
Дж/К;

=300
К;

Ответы: а) – 7020 Дж; б) – 6069
Дж

5-6. Один моль идеального а)
одноатомного; б) двухатомного; в)
трехатомного газа совершает политропический
процесс. При этом его температура
увеличивается от

до

,
и газ совершает работу А.
Найти теплоемкость газа. Универсальная
газовая постоянная

=300
К;

;
А =
100 Дж.

Ответы: а) 12,8 Дж/К; б) 21,1 Дж/К;
в) 25,3 Дж/К

5-7. Один моль идеального а)
одноатомного; б) двухатомного ; в)
трехатомного газа совершает политропический
процесс с теплоемкостью С.
При этом его температура увеличивается
на

,
и газ совершает работу А.
Найти

.
Универсальная газовая постоянная

С = 30
Дж/К; А
= 100 Дж.

Ответы: а) 5,7 К; б) 10,8 К; в) 19,7
К

5-8. Один моль идеального а)
одноатомного; б) двухатомного; в)
трехатомного газа совершает политропический
процесс с теплоемкостью С.
При этом его температура увеличивается
на

,
и газ совершает работу А.
Найти А.
Универсальная газовая постоянная

С = 30
Дж/К;

= 10 К.

Ответы: а) 175 Дж; б) 92,3 Дж; в)
50,7 Дж

5
-9.
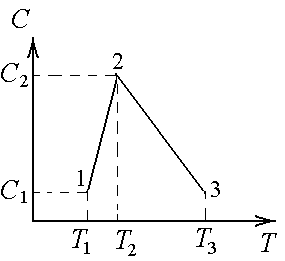
Идеальный газ совершает процесс 1–2–3.
Его теплоемкость зависит от температуры,
как показано на графике.

T₁
= 600 К; T₂
= 900 К; Т₃
= 1800 К.

С₁
= 1 Дж/К; С₂
= 5 Дж/К.

Найти

а) тепло, полученное газом
в этом процессе.

б) Во сколько раз тепло,
полученное на участке 2–3 больше тепла,
полученного на участке 1–2.

в) На сколько джоулей тепло,
полученное на участке 2–3 больше тепла,
полученного на участке 1–2.
Ответы: а) 3600 Дж; б) в 3 раза; в) 1800 Дж

5-10э.
Молярные теплоемкости азота в процессах

равны

соответственно. Их отношение

равно: а)

б)

в)

г)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

ТЕРМОДИНАМИКА

Внутренней энергией тела в молекулярно-кинетической теории называется суммарная кинетическая энергия хаотического движения всех молекул тела плюс суммарная потенциальная энергия взаимодействия этих молекул друг с другом (но не с другими телами).

Внутренняя энергия одноатомного идеального газа

В одноатомном идеальном газе молекулы не взаимодействуют друг с другом, по этому его внутренняя энергия такого газа будет определяться как кинетическая энергия беспорядочного движения молекул.

Тогда внутренняя энергия будет определяться как произведение средней кинетической энергии и количества молекул из которых состоит наш газ:

Вспоминаем что средняя кинетическая энергия поступательного движения молекул определяется как:

$[overline {E}=frac{3}{2}k T]$

А количество молекул в газе можно найти следующим образом:

Делаем небольшие алгебраические преобразования.

$[U= NE=frac{3}{2}nu N_A k T]$

Так как произведение числа Авогадро и постоянную Больцмана называют универсальной газовой постоянной , получаем:

$[U=frac{3}{2}nu RT]$

Из полученного уравнения видно что внутренняя энергия одноатомного идеального газа напрямую зависит от его температуры. В таком случае изменение внутренней энергии можно определить как:

$[Delta U=frac{3}{2}nu RDelta T]$

Работа газа при изобарном процессе

Работа газа при произвольном процессе равна площади под гафиком процесса в координатах (P,V). При линейной зависимости давления от объема равна:

$[A=p_{cp}Delta V = frac{p_1+p_2}{2}(V_2-V_1)]$

Первый закон термодинамики количество теплоты сообщаемое газу идет на изменение внутренней энергии этого газа (), а так же на совершение работы этим газом ().

Применение первого закона термодинамики к изопроцессам.

Изобарный

Изохорный

Изотермический

Адиабатный

Адиабатный процесс — процесс протекающий без внешнего теплообмена с окружающей средой.

Еще одна интерпретация первого закона термодинамики звучит следующим образом: «Изменение внутренней энергии () тела происходит в результате теплообмена (теплопередачи) либо совершения работы () над этим телом».

Количество теплоты () — энергия которую приобретает или теряет тело в результате теплообмена.
Теплопередача — это процесс передачи тепла от более нагретого тела жидкости или газа к менее нагретому. Можно выделить три вида теплопередачи: 1. Теплопроводность — передача тепла между различными частями одного тела, либо между телами при их непосредственном контакте; 2. Конвекция — вид теплообмена, при котором тепло передается струями и потоками жидкости или газа; 3. Излучение — передача тепла с помощью инфракрасного спектра электромагнитных волн.
Количество теплоты при нагревании или охлаждении

Удельная теплоемкость () — количество теплоты необходимое чтоб нагреть 1 килограмм данного вещества на 1 градус.
Количество теплоты при плавлении (кристаллизации) При плавлении тело получает тепло, по этому количество теплоты берется со знаком плюс, а при кристаллизации, жидкость напротив отдает свою энергию, по этому количество теплоты имеет отрицательное значение.

Удельная теплота плавления и кристаллизации () — количество теплоты необходимое для того, чтоб расславить 1 килограмм данного вещества.
Количество теплоты при парообразовании (конденсации) При кипении жидкость получает тепло, по этому количество теплоты берется со знаком плюс, а при конденсации, пар напротив теряет энергию, по этому количество теплоты имеет отрицательное значение.

Удельная теплота парообразования и конденсации () — количество теплоты необходимое для того, чтоб превратить в пар 1 килограмм жидкости.
Количество теплоты выделяемое при сгорании топлива

Удельная теплота сгорания () — количество теплоты выделяемое при сгорании одного килограмма топлива.

Уравнение теплового баланса В изолированной системе в результате теплообмена устанавливается тепловое равновесие, а католичества теплоты получаемые или отдаваемые телами этой системы в сумме будут равны нулю.

Тепловая машина

Тепловая машина — устройство, преобразующее тепловую энергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник).
В циклическом процессе изменение внутренней энергии за цикл равно нулю, а работа выполняемая машиной за цикл будет равна разности теплоты полученной от нагревателя и теплоты отданной холодильнику .