Во время протекания тока по однородному участку цепи электрическое поле совершает работу. За пройденное время Δt по цепи имеется заряд Δq=IΔt.
Электрическое поле выделенного участка выполняет работу, формулу которой мы запишем так: ΔA=(φ1–φ2) Δq=Δφ12IΔt=UIΔt, где U=Δφ12 – напряжение. Такая величина называется работой электрического тока.
Обе части формулы RI=U выражают закон Ома для однородного участка цепи с сопротивлением R, умноженным на IΔt. В итоге получим соотношение RI2Δt=UIΔt=ΔA, выражающее закон сохранения энергии для однородного участка цепи. Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике. ΔQ=ΔA=RI2Δt.
Закон Джоуля-Ленца
Дж. Джоуль и Э. Ленц установили закон преобразования работы тока в тепло.
Формула мощности электрического тока (измеряется в амперах) записывается в виде отношения изменения работы тока ΔA за определенный промежуток времени Δt:
P=∆A∆t=UI=I2R=U2R.
Работа и мощность электрического тока обратно пропорциональны.
По таблице СИ понятно, в чем измеряется мощность: в ваттах (ВТ), а работа в Джоулях (Дж).
Перейдем к рассмотрению полной цепи постоянного тока, которая состоит из источника с электродвижущей силой ε и внутренним сопротивлением r на участке R. Запись основного закона Ома для полной цепи имеет вид (R + r)I=ε. При умножении обеих частей на Δq=IΔt получаем, что соотношение для выражения сохранения энергии полной цепи постоянного тока запишется: R I2Δt+r I2Δt=ε IΔt=ΔAст. Из левой части видно, что ΔQ=R I2Δt обозначает выделяющееся тепло на внешнем участке за промежуток времени Δt, а ΔQист=rI2Δt – внутри источника за тот же время.
εIΔt – это обозначение работы сторонних сил ΔAст, действующих внутри. Если имеется замкнутая цепь, тогда ΔAст переходит в тепло, которое выделяется во внешней цепи (ΔQ) и внутри источника (ΔQист).
ΔQ+ΔQист=ΔAст=εIΔt.
Работа сторонних сил
Работа электрического поля не входит в данное соотношение, так как в замкнутой цепи работа не совершается, следовательно, тепло идет только от внутренних сторонних сил. В данном случае электрическое поле перераспределяет тепло по всем участкам цепи.
Внешняя цепь может иметь не только проводник с R сопротивлением, но и механизм, потребляющий мощность. Такой случай говорит о том, что R эквивалентно сопротивлению нагрузки. Энергия, которая выделяется по внешней цепи, преобразуется в тепло и другие виды энергии.
Работа, совершаемая сторонними силами за единицу времени, равняется Pист=εI=ε2R+r. Внешняя цепь характеризуется мощностью P=RI2=εI-rI2=ε2R(R+r)2.
Коэффициентом полезного источника называют отношение η=PPист, записываемое как η=PPист=1-rεI=RR+r.
Рисунок 1.11.1 показывает зависимость Pист, полезной Р, выделяемой во внешней цепи, кпд η от тока I для источника с ЭДС, равной ε, и внутренним сопротивлением r. Изменение тока в цепи происходит в пределах от I=0( при R=∞) до I=Iкз=εr( при R=0).
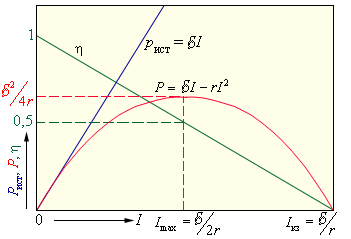
Рисунок 1.11.1. Зависимость мощности источника Pист, мощности во внешней цепи Р и КПД источника η от силы тока.
Приведенные графики показывают, что максимальная мощность во внешней цепи может быть достигнута при R=r и запишется Pmax=ε24r. Формула тока в цепи будет иметь вид Imax=12Iкз=ε2r, где КПД источника не превышает 50%. При I→0 может достигаться максимальное значение КПД, тогда сопротивление R→∞. При коротком замыкании значение мощности Р=0. Тогда она только выделяется внутри источника, что грозит перегревом, причем КПД обращается в ноль.
В этой статье я объясню, что такое работа электрического тока, какие единицы измерения для нее используются и какие важные формулы необходимо знать.
Что такое работа электрического тока?
Давайте рассмотрим обычную батарейку. По сути, батарейка преобразует химическую энергию в электрическую энергию электронов. Если теперь подключить её в электрическую цепь, то электроны могут совершать работу, используя свою электрическую энергию, например, зажигать лампочку.
Если вы хотите узнать, сколько электрической энергии было преобразовано в другой вид энергии, то вам нужно рассчитать работу электрического тока.
Определение понятия «электрическая работа» и её единицы измерения.
Работа электрического тока [A] позволяет определить, сколько электрической энергии было или может быть преобразовано в другие виды энергии.
Когда вы рассчитываете работу электрического тока, вы знаете, сколько электрической энергии было преобразовано в другие формы энергии. А уже какие другие формы энергии могут быть — это зависит от ситуации (несколько примеров в списке ниже):
- Ваш тостер преобразует электрическую энергию в тепловую;
- Когда вы включаете лампочку, электрическая энергия преобразуется в световую;
- Электродвигатель преобразует электрическую энергию в механическую.
Единицей измерения работы электрического тока в СИ является Джоуль [Дж], также часто используется в качестве единицы измерения Ватт-секунда [Вт·с]. Один джоуль всегда соответствует одной ватт-секунде. То есть 1 Дж = 1 Вт·с .
Другой важной единицей измерения является киловатт-час [кВт·ч]. Один киловатт-час равен 3 600 000 ватт-секунд или джоулей.
1 кВт·ч = 1 * 103 Вт·ч = 1 * 103 * 3600 Вт·с = 3,6 * 106 Вт·с = 3,6 * 106 Дж.
Полезный факт: а вы знали, что именно электрическую работу измеряют электросчётчики установленные в наших домах и квартирах! Электросчётчики измеряют работу электрического тока в кВт·ч.
По какой формуле вычисляется работа электрического тока?
Если вы на каком-либо участке электрической цепи под действием электрического напряжения U привели в движение заряд q, то вы можете рассчитать электрическую работу A как напряжение U, приложенное на концах этого участка цепи, умноженное на электрический заряд q, который прошёл по нему, то есть: A = U * q .
Зная, что электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения: q = I * t. Тогда электрическую работу A [Дж] можно определить как напряжение U [В], умноженное на силу тока I [А] и умноженное на время t [с], то есть: A = U * I * q .
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Чуть ниже в статье мы разберем два практических примера, которые покажут применение данных формул. Однако перед этим мы кратко рассмотрим еще несколько важных формул.
Примечание: Вы обязательно должны запомнить первые две формулы. Следующие ниже формулы менее важны, но могут быть полезны для вас при решении тех или иных задач.
Другие формулы для определения работы электрического тока.
Закон Ома для участка цепи связывает напряжение U и ток I. Это позволяет нам рассчитать электрическую работу A другим способом.
Итак, согласно закона Ома, U = I * R или I = U / R , где R — это электрическое сопротивление.
Тогда вы можете подставить эти формулы в A = U * I * t. В итоге получатся другие формулы для нахождения работы электрического тока:
- A = I2 * R * t ;
- A = (U2 * t ) / R .
Примеры задач
Пример 1.
У вас есть батарея, подающая постоянное напряжение 12 В и ток 2,3 А. Вы используете эту батарею для освещения лампочки в течение 1 часа. Теперь вы хотите знать, какая работа электрического тока была произведена.
Мы знаем формулу для определения работы электрического тока: A = U * I * q, тогда получаем:
A = 12 В * 2,3 А * 1 ч = 27,6 Вт·ч .
Чтобы дать вам представление о единицах измерения, давайте переведем результат в ватт-секунды и джоули
27,6 Вт·ч = 27,6 * 3600 Вт·с = 99360 Вт·с = 99360 Дж.
Пример 2.
У вас есть батарейка с напряжением 5 В. Эта батарейка совершает электрическую работу в 10*10-2 Вт·с. Нам нужно рассчитать рассчитать количество электрического заряда q, перемещенного между полюсами батареи.
Мы знаем формулу для определения работы электрического тока: A = U * q, тогда q = A / U. Подставляя значения в формулу получаем:
q = 10*10-2 Вт·с / 5 В = 0,02 Кл.
При прохождении тока в цепи электрическое поле совершает работу по перемещению заряда. В этом случае работу электрического поля называют работой электрического тока.
При прохождении заряда (q) по участку цепи электрическое поле будет совершать работу: (A=qcdot U), где (U) — напряжение электрического поля, (A) — работа, совершаемая силами электрического поля по перемещению заряда (q) из одной точки в другую.
Для выражения любой из этих величин можно использовать приведённый ниже рисунок.
Рис. (1). Зависимость между работой, напряжением и зарядом
Количество заряда, прошедшее по участку цепи, пропорционально силе тока и времени прохождения заряда:
q=I⋅t
.
Работа электрического тока на участке цепи пропорциональна напряжению на её концах и количеству заряда, проходящего по этому участку:
A=U⋅q
.
Работа электрического тока на участке цепи пропорциональна силе тока, времени прохождения заряда и напряжению на концах участка цепи:
A=U⋅I⋅t
.
Чтобы выразить любую из величин из данной формулы, можно воспользоваться рисунком.

Рис. (2). Зависимость между работой, силой тока и временем прохождения заряда
Единицы измерения величин:
работа электрического тока ([A]=1) Дж;
напряжение на участке цепи ([U]=1) В;
сила тока, проходящего по участку ([I]=1) А;
время прохождения заряда (тока) ([t]=1) с.
Для измерения работы электрического тока нужны вольтметр, амперметр и часы. Например, для определения работы, которую совершает электрический ток, проходя по спирали лампы накаливания, необходимо собрать цепь, изображённую на рисунке. Вольтметром измеряется напряжение на лампе, амперметром — сила тока в ней. А при помощи часов (секундомера) засекается время горения лампы.

Рис. (3). Схема и часы для измерения
Например:
I = 1,2 АU = 5 Вt = 1,5 мин = 90 сА = U⋅I⋅t = 5⋅1,2⋅90 = 540 Дж
Обрати внимание!
Работа чаще всего выражается в килоджоулях или мегаджоулях.
(1) кДж = 1000 Дж или (1) Дж = (0,001) кДж;
(1) МДж = 1000000 Дж или (1) Дж = (0,000001) МДж.
Для потребителей электрической энергии существуют приборы, позволяющие в пределах ошибки измерения получать числовые данные о ее расходе в единицу времени.

Рис. (4). Электросчетчик
Механическая мощность численно равна работе, совершённой телом в единицу времени:
N = Аt
. Чтобы найти мощность электрического тока, надо поступить точно также, т.е. работу тока,
A=U⋅I⋅t
, разделить на время.
Мощность электрического тока обозначают буквой (Р):
. Таким образом:
Мощность электрического тока равна произведению напряжения на силу тока:
P=U⋅I
.
Из этой формулы можно определить и другие физические величины.
Для удобства можно использовать приведённый ниже рисунок.
Рис. (5). Зависимость между мощностью, напряжением и силой тока
За единицу мощности принят ватт: (1) Вт = (1) Дж/с.
Из формулы
P=U⋅I
следует, что
(1) ватт = (1) вольт ∙ (1) ампер, или (1) Вт = (1) В ∙ А.
Обрати внимание!
Используют также единицы мощности, кратные ватту: гектоватт (гВт), киловатт (кВт), мегаватт (МВт).
(1) гВт = (100) Вт или (1) Вт = (0,01) гВт;
(1) кВт = (1000) Вт или (1) Вт = (0,001) кВт;
(1) МВт = (1 000 000) Вт или (1) Вт = (0,000001) МВт.
Пример:
Измерим силу тока в цепи с помощью амперметра, а напряжение на участке — с помощью вольтметра.
Рис. (6). Схема
Так как мощность тока прямо пропорциональна напряжению и силе тока, протекающего через лампочку, то перемножим их значения:
.
Ваттметры измеряют мощность электрического тока, протекающего через прибор. По своему назначению и техническим характеристикам ваттметры разнообразны.
В зависимости от сферы применения у них различаются пределы измерения.
|
Аналоговый ваттметр |
Аналоговый ваттметр |
Аналоговый ваттметр |
Цифровой ваттметр |
|
|
|
|
|
Рис. (7). Приборы для измерения
Подключим к цепи по очереди две лампочки накаливания, сначала одну, затем другую и измерим силу тока в каждой из них. Она будет разной.


Рис. (8). Лампы различной мощности в цепи
Сила тока в лампочке мощностью (25) ватт будет составлять (0,1) А. Лампочка мощностью (100) ватт потребляет ток в четыре раза больше — (0,4) А. Напряжение в этом эксперименте неизменно и равно (220) В. Легко можно заметить, что лампочка в (100) ватт светится гораздо ярче, чем (25)-ваттовая лампочка. Это происходит оттого, что её мощность больше. Лампочка, мощность которой в (4) раза больше, потребляет в (4) раза больше тока. Значит:
Обрати внимание!
Мощность прямо пропорциональна силе тока.
Что произойдёт, если одну и ту же лампочку подсоединить к источникам различного напряжения? В данном случае используется напряжение (110) В и (220) В.


Рис. (8). Лампа, подключенная к источнику тока с различным напряжением
Можно заметить, что при большем напряжении лампочка светится ярче, значит, в этом случае её мощность будет больше. Следовательно:
Обрати внимание!
Мощность зависит от напряжения.
Рассчитаем мощность лампочки в каждом случае:
| I=0,2АU=110ВP=U⋅I=110⋅0,2=22Вт | I=0,4АU=220ВP=U⋅I=220⋅0,4=88Вт. |
Можно сделать вывод о том, что при увеличении напряжения в (2) раза мощность увеличивается в (4) раза.
Не следует путать эту мощность с номинальной мощностью лампы (мощность, на которую рассчитана лампа). Номинальная мощность лампы (а соответственно, ток через нить накала и её расчётное сопротивление) указывается только для номинального напряжения лампы (указано на баллоне, цоколе или упаковке).
Рис. (9). Маркировка
В таблице дана мощность, потребляемая различными приборами и устройствами:
Таблица (1). Мощность различных приборов
|
Название |
Рисунок |
Мощность |
| Калькулятор |
|
(0,001) Вт |
| Лампы дневного света |
|
(15 — 80) Вт |
| Лампы накаливания |
|
(25 — 5000) Вт |
| Компьютер |
|
(200 — 450) Вт |
| Электрический чайник |
|
(650 — 3100) Вт |
| Пылесос |
|
(1500 — 3000) Вт |
| Стиральная машина |
|
(2000 — 4000) Вт |
| Трамвай |
|
(150 000 — 240000) Вт |
Источники:
Рис. 1. Зависимость между работой, напряжением и зарядом. © ЯКласс.
Рис. 3. Схема и часы для измерения. © ЯКласс.
Рис. 5. Зависимость между мощностью, напряжением и силой тока. © ЯКласс.
Рис. 6. Схема. © ЯКласс.
Таблица 1. Мощность различных приборов. Компьютер. Указание авторства не требуется, 2021-08-14, Pixabay License, https://pixabay.com/ru/photos/яблоко-стул-компьютер-1834328/.
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Ее принято называть работой тока.
Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:
A=ΔqU
Но сила тока равна:
I=ΔqΔt
Выразим заряд:
Δq=IΔt
Тогда работа тока равна:
A=IUΔt
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.
Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:
A=I2RΔt=U2RΔt
Работа тока измеряется в Джоулях (Дж).
Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.
A=IUΔt=16·220·10=35200 (Дж)=35,2 (кДж)
Закон Джоуля-Ленца
В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.
Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:
Закон Джоуля—Ленца
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
Q=I2RΔt
Количество теплоты измеряется в Джоулях (Дж).
Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.
Используем закон Ома и закон Джоуля—Ленца:
Q=I2RΔt=(UR)2Δt=U2RΔt=1222=72 (Дж)
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Определение
Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).
Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:
P=AΔt
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P=IU=I2R=U2R
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P=I2R=0,32·10=0,9 (Вт)
Выразив силу тока через заряд, прошедший за единицу времени, получим:
P=qUt
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P=(εR+r)2R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
Pmax=(εr+r)2r=ε24r
Мощность тока внутренней цепи:
Pвнутр=I2r=(εR+r)2r
Полная мощность:
Pполн=I2(R+r)=ε2R+r
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P=(εR+r)2R
Применим закон Ома для полной цепи:
I=εR+r
Выразим сопротивление внешней цепи:
R=εI−r
Отсюда:
P=(εεI−r+r)2(εI−r)=I2(εI−r)=Iε−rI2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
rI2−Iε+P=0
I2−1I+0,75=0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
| Объем проводника цилиндрической формы |
V=Sl |
| Масса проводника цилиндрической формы |
m=ρV=ρSl |
| Количество теплоты и изменение температуры |
Q=cmΔT |
Конденсатор в цепи постоянного тока
Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.
Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.
Подсказки к задачам
| Электроемкость, заряд и напряжение |
C=qU |
| Напряженность и напряжение |
E=Ud |
| Энергия конденсатора |
W=q22C=CU22 |
| Количество теплоты |
Q=ΔW |
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?
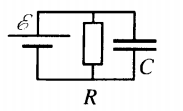
Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:
I=εR+r
Применим закон Ома:
I=UR
Приравняем правые части выражений и получим:
εR+r=UR
Отсюда напряжение на конденсаторе равно:
U=εRR+r
Напряженность электрического поля равна:
E=Ud=εRd(R+r)=9·80,002(8+1)=720,018=4000 (Вм)
Задание EF17564
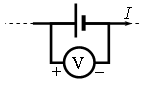 Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?
Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?
Ответ:
а) 5 Дж
б) 4 Дж
в) 3 Дж
г) 1 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу для нахождения количества теплоты, выделенной внутри источника тока.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 3 В.
• Внутреннее сопротивление источника тока: r = 1 Ом.
• Сила тока в цепи: I = 2 А.
• Напряжение на внешней цепи: U = 5 В.
Количество теплоты, выделенной внутри источника тока, равно:
Q=I2rt=22·1·1=4 (Дж)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17573
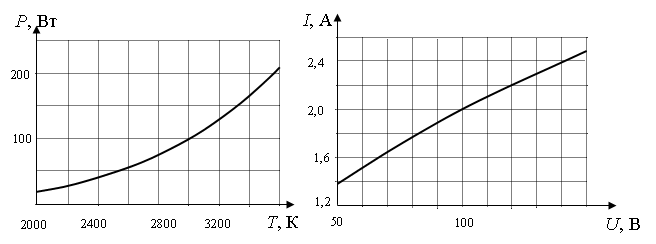
При нагревании спирали лампы накаливания протекающим по ней электрическим током основная часть подводимой энергии теряется в виде теплового излучения. На рисунке изображены графики зависимости мощности тепловых потерь лампы от температуры спирали P=P(T) и силы тока от приложенного напряжения I=I(U). При помощи этих графиков определите примерную температуру спирали лампы при силе тока I=2 A.
Ответ:
Алгоритм решения
1.Записать исходные данные.
2.С помощью графика зависимости силы тока от напряжения вычислить мощность.
3.С помощью графика зависимости мощности от температуры спирали определить ее температуру.
Решение
Нас интересует сила тока, равная 2 А. По графику зависимости силы тока от напряжения этому значение соответствует U = 100 В. Мощность определяется формулой:
P=IU=2·100=200 (Вт)
Этой мощности соответствует температура, равная около 3600 К.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17608
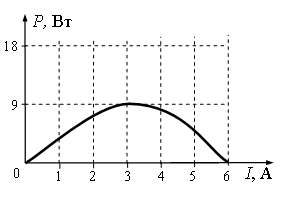 Ученик исследовал зависимость тепловой мощности Р, выделяющейся на реостате R, от силы тока в цепи. При проведении опыта реостат был подключён к источнику постоянного тока. График полученной зависимости приведён на рисунке.
Ученик исследовал зависимость тепловой мощности Р, выделяющейся на реостате R, от силы тока в цепи. При проведении опыта реостат был подключён к источнику постоянного тока. График полученной зависимости приведён на рисунке.
Какое из утверждений соответствует результатам опыта?
А. При коротком замыкании в цепи сила тока будет равна 6 А.
Б. При силе тока в цепи 3 А на реостате выделяется минимальная мощность.
Ответ:
а) только А
б) только Б
в) и А, и Б
г) ни А, ни Б
Алгоритм решения
- Проверить истинность каждого из утверждений.
- Выбрать верный ответ.
Решение
Согласно первому утверждению, при коротком замыкании в цепи сила тока будет равна 6 А. Это действительно так, потому что при этом значении силы тока мощность равна нулю. А это значит, что сопротивление на внешней цепи было нулевым.
Согласно второму утверждению, при силе тока в цепи 3 А на реостате выделяется минимальная мощность. Это не так. На графике этой силе тока соответствует максимальная мощность.
Верно только первое утверждение «А».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.3k
Содержание
- Как найти работу которую совершил источник тока
- Как найти работу которую совершил источник тока
- Работа электрического тока. Закон Джоуля-Ленца.
- Закон Джоуля-Ленца .
- Задачи на работу и мощность электрического тока с решением
- Работа и мощность тока: задачи с решением
- Задача №1. Мощность электрического тока
- Задача №2. Расчет мощности электрического тока
- Задача №3. Работа электрического тока
- Задача №4. Расчет работы электрического тока
- Задача №5 на закон Джоуля-Ленца
- Вопросы на работу и мощность электрического тока
Как найти работу которую совершил источник тока
Это соотношение выражает закон сохранения энергии для однородного участка цепи.
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца .
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением и внешнего однородного участка с сопротивлением . Закон Ома для полной цепи записывается в виде
Умножив обе части этой формулы на Δ = Δ, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
Первый член в левой части Δ = 2 Δ – тепло, выделяющееся на внешнем участке цепи за время Δ, второй член Δист = 2 Δ – тепло, выделяющееся внутри источника за то же время.
Выражение Δ равно работе сторонних сил Δст, действующих внутри источника.
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами , действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.
Внешняя цепь может представлять собой не только проводник с сопротивлением , но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под нужно понимать эквивалентное сопротивление нагрузки . Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.
На рис. 1.11.1 графически представлены зависимости мощности источника ист, полезной мощности , выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи для источника с ЭДС, равной , и внутренним сопротивлением . Ток в цепи может изменяться в пределах от = 0 (при ) до (при = 0).
Источник
Как найти работу которую совершил источник тока
При прохождении тока, т. е. при упорядоченном движении носителей заряда в проводнике, действующее на них электрическое поле, определяемое приложенным к концам проводника напряжением, совершает работу. Эту работу обычно называют работой электрического тока.
Работа сил электрического поля при перемещении носителей заряда равна произведению переносимого заряда на разность потенциалов между теми точками, где перемещается заряд:
При постоянном токе — время, в течение которого переносится заряд Поэтому работа постоянного тока за время на участке цепи, на концах которого поддерживается напряжение определяется соотношением
Мощность Р электрического тока, определяемая работой, совершаемой за единицу времени, равна
Электрический ток, совершая работу, может раскалять нить электролампы, вращать якорь электродвигателя, плавить металлы, вызывать химические превращения, заряжать аккумулятор и т. д. Во всех этих случаях работа тока определяет меру превращения электрической энергии в другие формы — внутреннюю энергию теплового движения, механическую энергию и т. д.
Работа электрического тока измеряется в тех же единицах, что и механическая работа. Это в системе СГСЭ и 1 Дж в
Мощность измеряется в ваттах: . Часто используются кратные единицы (киловатт) (мегаватт) Вт. Для работы тока часто используется внесистемная единица (киловатт-час) — работа, совершаемая за 1 час при развиваемой мощности
Закон Джоуля-Ленца. Прохождение электрического тока через проводник, обладающий сопротивлением, всеща сопровождается выделением теплоты. Количество выделившейся за время теплоты определяется законом Джоуля—Ленца:
В случае однородного участка, коща формулы (2) и (4) совпадают, т. е. количество выделяющейся теплоты равно работе тока, и работу тока можно выразить любым из эквивалентных способов:
В однородном участке цепи, например в резисторе, работа тока сводится только к выделению теплоты.
В качестве примера рассмотрим какой-нибудь электронагревательный прибор, отдающий выделяющуюся теплоту в окружающую среду. Скорость теплопередачи, т. е. количества теплоты, отдаваемой нагретым элементом в единицу времени, пропорциональна разности температур между нацзетым телом и окружающей средой:
Коэффициент к зависит от свойств тела (площади поверхности, размеров и формы). Будем считать его значение известным. Выделяющуюся джоулеву теплоту можно подсчитать по любой из формул (5). Поскольку обычно нагревательный прибор включается в сеть с заданным напряжением, то удобно воспользоваться выражением
Сразу после включения выделяющаяся джоулева теплота превосходит отдаваемую окружающей среде, так как происходит нагревание самого прибора. В конце концов устанавливается такая его температура Т, при которой Р и сравниваются наступает стационарное состояние, в котором разность температур прибора и окружающей среды уже не меняется.
Если сопротивление нагреваемого током элемента не зависит от температуры, то, приравнивая значения Р и немедленно получаем выражение для установившейся разности температур:
Однако в действительности, как правило, сопротивление зависит от температуры. Для металлической проволоки эту зависимость можно считать линейной (см. § 10):
где с хорошей точностью под можно понимать сопротивление при температуре окружающей среды. Если учитывать эту зависимость сопротивления от температуры, то, приравнивая Р и приходим уже к квадратному уравнению для
Имеющий физический смысл корень этого уравнения можно представить в следующем виде:
В условиях, когда мало, т. е. превышение температуры нагревательного элемента прибора над окружающей средой невелико, второй
член в подкоренном выражении мал по сравнению с единицей и можно воспользоваться приближенной формулой При этом получаем прежний результат
В другом предельном случае больших (как, например, у лампочки накаливания, температура нити которой составляет несколько тысяч градусов), можно, наоборот, в подкоренном выражении пренебречь единицей по сравнению со вторым членом. При этом для приближенно получаем
— разность температур теперь пропорциональна не квадрату, а первой степени приложенного напряжения.
В неоднородных участках цепи, где ток определяется формулой выделяющаяся теплота не равна работе тока. Это означает, что протекание тока в таком участке сопровождается не только выделением теплоты, но и другими процессами, связанными с превращением энергии.
Зарядка аккумулятора. В качестве примера энергетических превращений в неоднородной цепи рассмотрим зарядку аккумулятора. Не вдаваясь в детали происходящих в аккумуляторе процессов, а только учитывая, что при зарядке все химические процессы внутри него идут «вспять», легко сообразить, что ток идет в направлении, противоположном току при разрядке, когда аккумулятор является источником питания для внешней цепи. Поэтому аккумулятор включается в цепь так, как показано на рис. 86, а ток в цепи идет в направлении, указанном стрелкой. Так как ЭДС аккумулятора (сумма скачков потенциала внутри него) понижает потенциал в цепи в направлении протекания тока, то, в соответствии с законом Ома для неоднородного участка, ток в цепи равен
Рис. 86. Схема включения аккумулятора на зарядку
В этой формуле — внутреннее сопротивление аккумулятора, а сопротивление включено в цепь для регулировки зарядного тока. Легко видеть, что ток будет положительным и, следовательно, пойдет в указанном направлении только при условии, что подаваемое напряжение больше электродвижущей силы аккумулятора . Только при выполнении этого условия и можно зарядить аккумулятор.
Работа, совершаемая зарядной станцией (т. е. внешним источником напряжения в единицу времени, т. е. работа тока на всем рассматриваемом участке, равна На всех сопротивлениях,
включая внутреннее сопротивление аккумулятора, в единицу времени выделяется джоулева теплота, равная . Кроме зарядки аккумулятора и выделения теплоты других энергетических превращений в рассматриваемой цепи не происходит. Поэтому на основании закона сохранения энергии можно утверждать, что
где Рзар — мощность, идущая непосредственно на зарядку аккумулятора. Подставляя в (7) выражение для силы тока (6), получаем
Таким образом, при зарядке аккумулятор в единицу времени запасает энергию, равную 14. Разумеется, этого результата можно было ожидать из элементарных соображений: ведь процессы в аккумуляторе считаются обратимыми, а при разрядке аккумулятор развивает мощность
Обратим внимание, что, считая известными выражения для полной работы тока, для джоулевой теплоты и для работы зарядки аккумулятора, можно с помощью закона сохранения энергии получить выражение (6) для тока в цепи. Для этого нужно просто подставить в Это значит, что закон Ома для неоднородного участка можно получить как следствие закона сохранения энергии.
Работа источника тока. Источник тока — это устройство, поддерживающее разность потенциалов на концах подключенной к нему электрической цепи. Это происходит благодаря действию сторонних сил — сил неэлектростатической природы. Какие энергетические превращения при этом происходят?
Как мы видели, ЭДС источника равна сумме напряжений во внешнем и внутреннем участках цепи:
Домножим обе части этого равенства на заряд проходящий по цепи за время В левой части получившегося равенства будет стоять сумма работ электрического тока во внешнем и во внутреннем участках цепи. Справа будет стоять произведение
Электрический ток совершает работу за счет действия источника, т. е. сторонних сил. По закону сохранения энергии работа тока в цепи равна работе, совершаемой за это же время источником тока, т. е. работе действующих в нем сторонних сил.
Определение ЭДС. Итак, работа источника тока при перемещении по цепи заряда равна Поэтому электродвижущей силе источника можно дать и такое определение: электродвижущей силой называется величина, равная отношению работы Лстор сторонних сил
при перемещении по цепи заряда к этому заряду:
Поскольку работа источника тока равна то развиваемая им мощность
Мощность и КПД источника тока. Выясним, каким должно быть сопротивление нагрузки для того, чтобы получить максимальную силу тока в цепи, максимальную полезную мощность, максимальный коэффициент полезного действия.
Ток в цепи (рис. 87) определяется законом Ома: Поэтому полная мощность Р, развиваемая источником тока, равна . Полезная мощность т. е. мощность, выделяющаяся на нагрузке дается соотношением
Коэффициент полезного действия источника в этой цепи, определяемый как отношение полезной мощности к полной, зависит от сопротивления нагрузки:
Исследуем полученные выражения. Полная мощность Р и ток в цепи I различаются постоянным множителем поэтому их зависимость от сопротивления нагрузки одинакова (кривая 1 на рис. 88).
Рис. 87. К исследованию условий работы источника тока
Рис. 88. Зависимость мощности и КПД источника тока от сопротивления нагрузки
Максимальным значение этих величин будет при т. е. при коротком замыкании источника. Как видно из формул (12) и (13), при этом равны нулю полезная мощность и коэффициент полезного действия При полная мощность и ток равны половине своего максимального значения, коэффициент полезного действия равен 0,5, а полезная мощность достигает своего максимального значения,
равного половине мощности Р при этой нагрузке. Для того чтобы убедиться, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока полезная мощность максимальна, преобразуем правую часть выражения (12) следующим образом:
Полезная мощность будет максимальной, когда знаменатель правой части выражения (14) минимален. Преобразуем знаменатель:
Функция (15) достигает минимума тогда, когда выражение в скобках равно нулю, т. е. при Этот результат можно, разумеется, получить, приравнивая нулю производную по знаменателя правой части выражения (14).
При неограниченном увеличении сопротивления нагрузки как полная, так и полезная мощность стремится к нулю (кривая 2), а коэффициент полезного действия — к единице (кривая 3).
Из рис. 87 видно, что требования получения максимального тока в цепи, максимальной полезной мощности и максимального КПД противоречивы. Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника, но при этом близки к нулю полезная мощность и КПД: почти вся совершаемая источником тока работа идет на выделение теплоты на внутреннем сопротивлении Чтобы получить от данного источника тока максимальную полезную мощность, следует взять нагрузку с сопротивлением равным внутреннему сопротивлению источника. Значение максимальной полезной мощности но коэффициент полезного действия при этом равен всего лишь 0,5.
Любую полезную мощность меньшую максимальной, можно получить, как свидетельствует ход кривой 2 на рис. 88, при двух значениях сопротивления нагрузки. Практически для получения заданной полезной мощности следует выбирать нагрузку с большим сопротивлением так как КПД при этом выше. Для получения КПД, близкого к единице, следует брать нагрузку с сопротивлением, много большим внутреннего сопротивления источника тока, но при этом выделяющаяся мощность .
• Работа каких сил имеется в виду, когда говорят о работе, совершаемой электрическим током?
• В каких случаях работа электрического тока не равна выделяющейся в цепи джоулевой теплоте
• Для зарядки аккумулятора с ЭДС его включили в сеть с постоянным напряжением Какая доля потребляемой от сети энергии запасается в аккумуляторе?
• Каким образом работа сторонних сил связана с ЭДС источника тока? Аргументируйте свой ответ.
• Какой должна быть нагрузка, чтобы источник тока развивал максимальную полезную мощность? Каким при этом будет его КПД?
• Почему условия получения максимальной полезной мощности и максимального КПД от данного источника тока противоречат друг другу?
• Покажите, что два значения сопротивления нагрузки и при которых в нагрузке выделяется одинаковая джоулева теплота, связаны соотношением где — внутреннее сопротивление источника тока.
• Постройте графики зависимости мощности источника тока, полезной мощности и КПД от силы тока I в цепи.
Поле сторонних сил. Работа, совершаемая электрическим током при прохождении заряда по всей цепи, равна работе действующих в источнике сторонних сил. Поэтому ЭДС можно выразить через эти силы.
Введем новую величину Естор, которую назовем напряженностью поля сторонних сил. Это сила, действующая на единичный положительный заряд, обусловлена любыми причинами, кроме электростатического поля. Тогда полная сила, действующая на заряд, будет складываться из электростатической силы и сторонней силы:
Рассмотрим замкнутую цепь и рассчитаем полную работу, совершаемую всеми действующими на заряд силами при его перемещении по всей цепи. Работа электростатических сил на замкнутом контуре равна нулю, так как эти силы — потенциальные. Поэтому полная работа на замкнутом контуре равна работе только сторонних сил. Именно эта работа и определяет ЭДС источника тока.
Обратим внимание на кажущееся противоречие. Работа тока — это по определению работа сил электрического поля. В то же время, как мы видели, работа тока во всей цепи равна работе источника, т. е. работе сторонних сил. Но как мы только что выяснили, работа электростатического поля равна нулю. Как все это согласовать?
Дело в том, что, говоря о работе электрического тока, мы имели в виду работу электрических сил не на всем замкнутом пути, а только на тех участках цепи, где заряды движутся под действием электрических сил. Мы не включали работу электрических сил в местах скачков потенциала (где и действуют
сторонние силы), т. е. в местах, где электрическое поле направлено противоположно движению положительных зарядов. Именно в этих местах внутри источника тока движение зарядов против сил электрического поля обусловлено действием сторонних сил. Если учесть работу электрических сил и в этих местах, то полная их работа действительно будет равна нулю.
Здесь можно привести следующую механическую аналогию. Лыжник спускается с горы и, сделав круг, возвращается к ее подножию, а затем с помощью подъемника снова поднимается на вершину. Аналогом потенциального электростатического поля здесь является поле силы тяжести. Роль сторонних сил играют силы, поднимающие его наверх в подъемнике. Очевидно, что полная работа силы тяжести на всем замкнутом пути равна нулю. Однако в данном случае она не представляет интереса. Важна лишь та работа сил тяжести, что совершается при движении лыжника от вершины горы до ее основания. Эта работа как раз и равна работе «сторонних» сил, действующих на лыжника в подъемнике.
Работа и теплота в произвольной цепи. В неоднородном участке цепи, содержащем источник с ЭДС и внутренним сопротивлением когда , для работы тока А, работы источника и выделяющейся теплоты имеем
Выделяющаяся теплота равна сумме работы тока и работы источника:
Подчеркнем, что эти формулы справедливы во всех случаях, независимо от того, идет ли ток через источник в «естественном» направлении, когда он отдает энергию во внешнюю цепь, или в противоположном, как это бывает при зарядке аккумулятора, когда он потребляет энергию (в этом случае I и Ч имеют противоположные знаки и Лист При этом теплота окажется во всех случаях положительной.
Как связаны между собой работа сторонних сил и работа сил электрического поля при переносе заряда вдоль всей замкнутой цепи?
Поясните аналогию между работой электрических и сторонних сил и работой силы тяжести и «подъемной» силы при катании лыжника на горе с подъемником.
Источник
Работа электрического тока. Закон Джоуля-Ленца.

Для определения работы, которая совершается током, проходящим по некоторому участку цепи, нужно воспользоваться определением напряжения: . Значит,
где А — работа тока; q — электрический заряд, который прошел за определенное время через исследуемый участок цепи. Подставив в последнее равенство формулу q = It, имеем:
Работа электрического тока на участке цепи является произведением напряжения на концах этого участка на силу тока и на время, на протяжении которого совершалась работа.
Закон Джоуля-Ленца .
Закон Джоуля — Ленца гласит: количество теплоты, которое выделяется в проводнике на участке электрической цепи с сопротивлением R при протекании по нему постоянного тока I в течение времени t равно произведению квадрата тока на сопротивление и время:
Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которому удалось раскалить железную спираль, пропустив через нее электрический ток.
Из закона Джоуля — Ленца видно, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на проводнике с наибольшим сопротивлением. Это применяется в технике, например, для распыления металлов.

При параллельном соединении каждый проводник находятся под одинаковым напряжением, но токи в них разные. Из формулы (Q = I 2 Rt) видно, что, так как, согласно закону Ома , то

Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.
Если в формуле (А = IUt) выразить U через IR, воспользовавшись законом Ома, получим Закон Джоуля — Ленца. Это лишний раз подтверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.
Источник
Задачи на работу и мощность электрического тока с решением

В сегодняшней статье мы займемся решением задач на тему «Работа и мощность постоянного тока». Вдруг кому-нибудь пригодится.
Кстати, много полезной информации для студентов, а также приятные скидки, вы найдете на нашем телеграм-канале. Подписывайтесь!
Работа и мощность тока: задачи с решением
Перед непосредственным решением задач на работу и мощность электрического тока повторите теорию, ознакомьтесь с общей памяткой по решению задач. Также мы собрали для вас вместе более 40 формул по физике, держите их под рукой.
Задача №1. Мощность электрического тока
Условие
Сопротивление нити накала электрической лампы составляет 400 Ом, а напряжение на нити равно 100 В. Какова мощность тока в лампе?
Решение
По определению, мощность тока на участке цепи равна работе, деленной на время, за которое она была совершена:
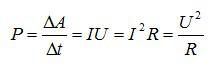
Подставим значения, и найдем мощность:
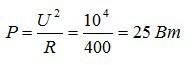
Ответ: 25 Вт.
Задача №2. Расчет мощности электрического тока
Условие
Два резистора соединены параллельно и последовательно. В каком из двух резисторов мощность тока больше (и во сколько раз) соответственно при параллельном и последовательном соединении?
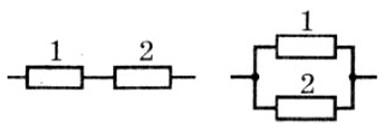
Решение
1) При последовательном соединении сила тока в каждом резисторе одинакова, а мощность тока напрямую зависит от сопротивления резисторов:
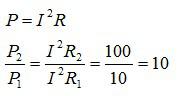
Мощность тока во втором резисторе больше в 10 раз.
2) При параллельном соединении на резисторах будет разная сила тока, но одинаковое напряжение. Для мощности тока целесообразно использовать формулу:
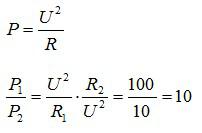
Мощность тока в первом резисторе больше в 10 раз.
Ответ: В 10 раз больше во втором резисторе; в 10 раз больше в первом резисторе.
Задача №3. Работа электрического тока
Условие
Какова работа электрического тока в паяльнике, если сила тока в цепи равна 3 А, а сопротивление паяльника – 40 Ом? Время работы паяльника – 30 минут. Какое количество теплоты выделится в паяльнике за это время?
Решение
По закону Джоуля-Ленца, работа тока на наподвижном проводнике с сопротивлением R, преобразуется в тепло.
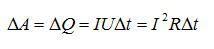

При вычислениях не забывайте переводит все величины в систему СИ.
Работа тока равна выделившемуся количеству теплоты.
Ответ: 648 кДж.
Задача №4. Расчет работы электрического тока
Условие
Какую работу ток совершает в электродвигателе за 20 минут, если сила тока в цепи равна 0,2 А, а напряжение составляет 12 В.
Решение
Применим формулу для работы тока:
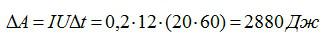
Ответ: 2880 Дж.
Напоследок мы приберегли для вас задачу посложнее.
Задача №5 на закон Джоуля-Ленца
Условие
Сила тока в проводнике сопротивлением R=20 Ом нарастает в течение времени Δt=2 с по линейному закону от I0=0 до Imax=6 А. Определить количество теплоты Q1, выделившееся в этом проводнике за первую секунду, и Q2 — за вторую, а также найти отношение этих количеств теплоты Q2/Q1.
Решение
Закон Джоуля – Ленца применим в случае постоянного тока (I =const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде:
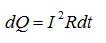
Здесь сила тока I является некоторой функцией времени. В нашем случае I=kt, где k — коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:
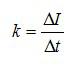
С учетом этого, формула для количества теплоты примет вид:
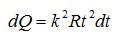
Для определения количества теплоты, выделившегося за конечный промежуток времени, выражение для бесконечно малого количества теплоты следует проинтегрировать в пределах от t1 до t2:
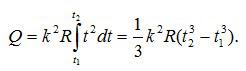
При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t1 =О, t2= 1 с и, следовательно, Q1=60 Дж, а за вторую секунду — пределы интегрирования t1= 1 с, t2=2 с и тогда Q2=420 Дж.
Кстати, читайте в нашем блоге о том, как считать интегралы.
За вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду.
Ответ: 60 Дж; 420 Дж; в 7 раз больше.
Вопросы на работу и мощность электрического тока
Вопрос 1. Что такое работа электрического тока?
Ответ. Работа электрического тока – это физическая величина, которая показывает, какая работа была совершена электрическим полем при перемещении зарядов по проводнику. Она равна произведению силы тока на участке цепи, напряжению на концах этого участка и времени, в течение которого протекает ток по проводнику.
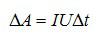
Единица измерения работы – 1 Джоуль.
Вопрос 2. Сформулируйте закон Джоуля-Ленца.
Ответ. Это эмпирический закон преобразования работы тока в тепло. Он был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем.
Работа электрического тока, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло, выделяющееся на проводнике.
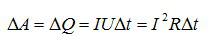
При прохождении тока по проводнику положительные ионы в узлах кристаллических решеток проводника за счет энергии тока начинают сильнее колебаться, что сопровождается увеличением внутренней энергии проводника, т.е. его нагреванием.
Вопрос 3. Что такое мощность электрического тока?
Ответ. Мощность тока – физическая величина, характеризующая скорость совершения током работы. Мощность равна отношению работы к интервалу времени, за которые она была совершена:
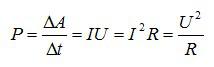
Единицей измерения мощности является Ватт. 1 Ватт – это мощность, при которой за одну секунду совершается работа в 1 Джоуль.
Вопрос 4. Приведите пример внесистемной единицы измерения работы.
Ответ. На практике часто пользуются единицей, называемой ватт-час (втч). Так как в часе 3 600 секунд, 1 ватт-час равен 3 600 Дж.
Вопрос 5. Как измерить работу тока?
Ответ. В простейшем случае для измерения работы тока нужны амперметр, вольтметр и часы. На практике работу электрического тока измеряют с помощью счетчиков.
Нужна помощь в решении задач и выполнении других заданий? Профессиональный сервис для учащихся всегда к вашим услугам.
- Контрольная работа от 1 дня / от 100 р. Узнать стоимость
- Дипломная работа от 7 дней / от 7950 р. Узнать стоимость
- Курсовая работа 5 дней / от 1800 р. Узнать стоимость
- Реферат от 1 дня / от 700 р. Узнать стоимость
![]()
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник












