- Авторы
- Резюме
- Файлы
Иванов Е.М.
Показано, что общепринятая формула для определения работы справедлива только для частных случаев. Правильное определение работы. Общепринятая формула работы тоже применима только к одному частному случаю.
Вот как определяет сущность работы О.Д. Хвольсон [1, Стр.91-92] «Сила совершает работу, когда её точка приложения перемещается… …следует отличать два случая производства работы: в первом сущность работы заключается в преодолевании внешнего сопротивления движению, которое совершается без увеличения скорости движения тела; во втором – работа обнаруживается увеличением скорости движения, к которому внешний мир относится индифферентно. На деле мы обыкновенно имеем соединение обоих случаев: сила преодолевает какие-либо сопротивления и в то же время меняет скорость движения тела».
Для вычисления работы постоянной силы предлагается формула:
(1)
где S – перемещение тела под действием силы F, a – угол между направлениями силы и перемещения. При этом говорят [2], что «если сила перпендикулярна перемещению, то работа силы равна нулю. Если же, несмотря на действие силы, перемещение точки приложения силы не происходит, то сила никакой работы не совершает. Например, если какой-либо груз неподвижно висит на подвесе, то действующая на него сила тяжести не совершает работы».
В [2] также говорится: «Понятие работы как физической величины, введенное в механике, только до известной степени согласуется с представлением о работе в житейском смысле. Действительно, например, работа грузчика по подъёму тяжести расценивается тем больше, чем больше поднимаемый груз и чем на большую высоту он должен быть поднят. Однако с той же житейской точки зрения мы склонны называть «физической работой» всякую деятельность человека, при которой он совершает известные физические усилия. Но, согласно даваемому в механике определению, эта деятельность может и не сопровождаться работой. В известном мифе об Атланте, поддерживающем на своих плечах небесный свод, люди имели в виду усилия, необходимые для поддержания огромной тяжести, и расценивали эти усилия как колоссальную работу. Для механики же здесь нет работы, и мышцы Атланта могли бы быть попросту заменены прочной колонной».
Эти рассуждения напоминают известное высказывание И.В. Сталина: «Есть человек – есть проблема, нет человека – нет проблемы».
В учебнике физики для 10 класса [3, Стр.138] предлагается следующий выход из данной ситуации: «При неподвижном удержании человеком груза в поле тяжести Земли совершается работа и рука испытывает усталость, хотя видимое перемещение груза равно нулю. Причиной этого является то, что мышцы человека испытывают постоянные сокращения и растяжения, приводящие к микроскопическим перемещениям груза». Всё хорошо, вот только как рассчитать эти сокращения-растяжения?
Получается такая ситуация: человек пытается переместить шкаф на расстояние S, для чего он действует силой F в течение времени t, т.е. сообщает импульс силы . Если шкаф имеет небольшую массу и нет сил трения, то шкаф перемещается и значит, работа совершается. Но если шкаф большой массы и большие силы трения, то человек, действуя тем же импульсом силы, шкаф не перемещает, т.е. работа не совершается. Что-то тут не вяжется с так называемыми законами сохранения. Или взять пример, показанный на рис. 1. Если сила F направлена горизонтально (
), то работа
, а если под углом a, то
. Так как
, то, естественно, возникает вопрос, куда же исчезла энергия, равная разности работ (
)?
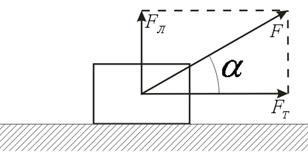
Рисунок 1. Сила F направлена горизонтально ( ), то работа
, а если под углом a, то
Приведем пример, показывающий, что работа совершается, если тело остаётся неподвижным. Возьмем электрическую цепь состоящую из источника тока, реостата и амперметра магнитоэлектрической системы. При полностью введенном реостате сила тока бесконечно мала и стрелка амперметра стоит на нуле. Начинаем постепенно двигать реохорд реостата. Стрелка амперметра начинает отклоняться, закручивая спиральные пружины прибора. Это совершает работу сила Ампера: сила взаимодействия рамки с током с магнитным полем. Если остановить реохорд, то установится постоянная сила тока и стрелка перестает двигаться. Говорят, что если тело неподвижно, то сила работы не совершает. Но амперметр, удерживая стрелку в том же положении, по прежнему потребляет энергию , где U – напряжение, подведенное к рамке амперметра,
– сила тока в рамке. Т.е. сила Ампера, удерживая стрелку, по прежнему совершает работу по удержанию пружин в закрученном состоянии.
Покажем, почему возникают подобные парадоксы. Вначале получим общепринятое выражение для работы. Рассмотрим работу разгона по горизонтальной гладкой поверхности первоначально покоящегося тела массы m за счет воздействия на него горизонтальной силой F в течение времени t. Этому случаю соответствует угол на рис.1. Запишем II закон Ньютона в виде
. Умножим обе части равенства на пройденный путь S:
. Поскольку
, то получим
или
. Отметим, что умножая обе части уравнения на S, мы тем самым отказываем в работе тем силам, которые не производят перемещение тела (
). Кроме того, если сила F действует под углом a к горизонту, мы тем самым отказываем в работе всей силе F, «разрешая» работу только её горизонтальной составляющей:
.
Проведем другой вывод формулы для работы. Запишем II закон Ньютона в дифференциальной форме
(2)
Левая часть уравнения – элементарный импульс силы, а правая
– элементарный импульс тела (количество движения). Отметим, что правая часть уравнения может быть равна нулю, если тело остается неподвижным (
) или движется равномерно (
), в то время как левая часть не равна нулю. Последний случай соответствует случаю равномерного движения, когда сила
уравновешивает силу трения
.
Однако вернемся к нашей задаче о разгоне неподвижного тела. После интегрирования уравнения (2), получим , т.е. импульс силы равен импульсу (количеству движения), полученному телом. Возведем в квадрат и разделив на
обе части равенства, получим
или
(3)
Таким образом мы получим другое выражение для вычисления работы
(4)
где – это импульс силы. Это выражение не связано с путем S, пройденным телом за время t, поэтому оно может быть использовано для вычисления работы, совершаемой импульсом силы и в том случае, если тело остается неподвижным.
В случае, если сила F действует под углом a (рис.1), то её раскладываем на две составляющие: силу тяги и силу
, которую назовем силой левитации, она стремится уменьшить силу тяжести. Если
будет равна
, то тело будет находиться в квазиневесомом состоянии (состояние левитации). Используя теорему Пифагора:
, найдем работу силы F
или
(5)
Поскольку , а
, то работу силы тяги можно представить в общепринятом виде:
.
Если сила левитации , то работа левитации будет равна
(6)
Это как раз та работа, которую выполнял Атлант, удерживая на своих плечах небесный свод.
А теперь рассмотрим работу сил трения. Если сила трения является единственной силой, действующей по линии движения (например, автомобиль, двигавшийся по горизонтальной дороге со скоростью , выключил двигатель и стал тормозить), то работа силы трения будет равна разности кинетических энергий и может быть рассчитана по общепринятой формуле:
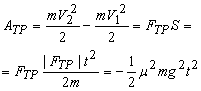
Однако, если тело движется по шероховатой горизонтальной поверхности с некоторой постоянной скоростью , то работу силы трения нельзя вычислять по общепринятой формуле
, поскольку в данном случае движения надо рассматривать как движение свободного тела (
), т.е. как движение по инерции, и скорость V создает не сила
, она была приобретена ранее. Например, тело двигалось по идеально гладкой поверхности с постоянной скоростью, и в тот момент, когда оно въезжает на шероховатую поверхность, включается сила тяги
. В данном случае путь S не связан с действием силы
. Если взять путь
м, то при скорости
м/с время действия силы будет составлять
с, при
м/с время
с, при
м/с время
с. Поскольку сила трения считают не зависящей от скорости, то, очевидно, на одном и том же отрезке пути
м сила
совершит гораздо большую работу за 200 с, чем за 10 с, т.к. в первом случае импульс силы
, а в последнем –
. Т.е. в данном случае работу силы трения надо рассчитывать по формуле:
(8)
Обозначая «обычную» работу трения через и учитывая, что
, формулу (8), опуская знак «минус», можно представить в виде
(9)
Зависимость от
, выраженных в долях
, показана на рис.2.
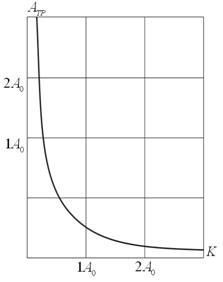
Рисунок 2. Зависимость от
, выраженных в долях
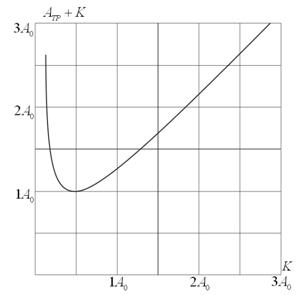
Рисунок 3. Зависимость суммы ( ) от величины
, выраженных так же в долях
На рис.3. показана зависимость суммы ( ) от величины
, выраженных так же в долях
. Эта сумма имеет минимум, равный
при
. То же самое относится и к случаю равномерного скольжения вниз по шероховатой наклонной плоскости (угол наклона
), когда сила трения равна скатывающей силе
или
, т.е.
. В этом случае, чтобы тело равномерно скользило вниз, оно должно получить начальный импульс
. Тогда работа силы трения будет определяться не длиной наклонной плоскости S, а временем скольжения
:
(10)
Учитывая, что ,
, а
, опуская знак «минус», получим
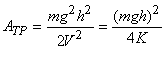
Зависимость от K совпадает с графиком (рис.2), только вместо
следует подставить (
), то же самое относится и к графику на рис. 3.
СПИСОК ЛИТЕРАТУРЫ
- Хвольсон О.Д. Курс физики. Т. I. Р.С.Ф.С.Р. Госуд.Изд-во, Берлин, 1923.
- Элементарный учебник физики. Т. I. – М.: Наука, 1972.
- Касьянов В.А. Физика. 10 класс. Учебн.-М.: Дрофа, 2003.
Библиографическая ссылка
Иванов Е.М. ОПРЕДЕЛЕНИЕ РАБОТЫ И РАБОТА СИЛЫ ТРЕНИЯ // Успехи современного естествознания. – 2005. – № 8.
– С. 10-13;
URL: https://natural-sciences.ru/ru/article/view?id=8991 (дата обращения: 19.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Как найти работу силы трения
Движение в реальных условиях не может продолжаться до бесконечности. Причина этому – сила трения. Она возникает при контакте тела с другими телами и всегда направлена противоположно направлению движения. Это означает, что сила трения всегда выполняет отрицательную работу, что нужно учитывать при расчетах.

Вам понадобится
- – рулетка или дальномер;
- – таблица ля определения коэффициента трения;
- – понятие о кинетической энергии;
- – весы;
- – калькулятор.
Инструкция
Если тело движется равномерно и прямолинейно, найдите силу, которая приводит его в движение. Она компенсирует силу трения, поэтому численно равна ей, но направлена в сторону движения. Измерьте рулеткой или дальномером расстояние S, на которое сила F передвинула тело. Тогда работа силы трения будет равна произведению силы на расстояние со знаком «минус» A=-F∙S.
Пример. Автомобиль движется по дороге равномерно и прямолинейно. Какую работу выполняет сила трения на дистанции 200 м, если сила тяги двигателя равна 800 Н? При равномерном прямолинейном движении сила тяги двигателя равна по модулю силе трения. Тогда ее работа будет равна A=-F∙S =-800∙200=-160000 Дж или -160 кДж.
Свойство поверхностей удерживаться друг за друга показывает коэффициент трения μ. Для каждой пары контактирующих поверхностей он разный. Его можно рассчитать или узнать в специальной таблице. Существует коэффициент трения покоя и коэффициент трения скольжения. При расчете работы силы трения берите коэффициент для скольжения, поскольку без перемещения работа не выполняется. Например, коэффициент трения скольжения дерева по металлу равен 0,4.
Определите работу силы трения, действующей на тело, расположенное на горизонтальной поверхности. Для этого определите его массу m в килограммах при помощи весов. Умножьте массу на коэффициент трения скольжения для данных поверхностей μ, ускорение свободного падения (g≈10 м/с²) и расстояние, на которое передвинулось тело, S. Перед формулой поставьте знак «минус», поскольку тело движется в сторону, противоположную направлению силы трения (A=-μ∙m∙g∙S).
Работа силы трения, когда действует только она, равна изменению кинетической энергии тела. Для ее определения найдите начальную v0 и конечную v скорости тела на исследуемом участке пути. Умножьте массу тела m на разность квадратов начальной и конечной скорости тела, а результат поделите на число 2 (А=m∙(v²-v0²)/2). Например, если автомобиль массой 900 кг, двигавшийся со скоростью 20 м/с, останавливается, то работа силы трения будет равна А=900∙(0²-20²)/2=-180000 Дж или -180 кДж.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
В специальном разделе физики – динамике, когда изучают движение тел, то рассматривают действующие на движущуюся систему силы. Последние могут выполнять как положительную, так и отрицательную работу. Рассмотрим в данной статье, что такое работа силы трения и как она рассчитывается.
Понятие работы в физике
В физике понятие “работа” отличается от обыденного представления об этом слове. Под работой понимают физическую величину, которая равна скалярному произведению вектора силы на вектор перемещения тела. Предположим, что имеется некоторый объект, на который действует сила F¯. Поскольку другие силы не действуют на него, то вектор его перемещения l¯ будет по направлению совпадать с вектором F¯. Скалярное произведение этих векторов в данном случае будет соответствовать произведению их модулей, то есть:
A = (F¯*l¯) = F*l.
Величина A – это работа силы F¯ по перемещению объекта на расстояние l. Учитывая размерности величин F и l, получаем, что работа измеряется в ньютонах на метр (Н*м) в системе СИ. Однако, единица Н*м имеет собственное название – это джоуль. Это означает, что концепция работы совпадает с концепцией энергии. Иными словами, если сила в 1 ньютон перемещает тело на 1 метр, то соответствующие энергетические затраты равны 1 джоулю.
Что такое сила трения?
Изучение вопроса работы силы трения возможно, если знать, о какой силе идет речь. Трением в физике называется процесс, который препятствует любому движению одного тела по поверхности другого, когда эти поверхности приведены в контакт.
Если рассматривать исключительно твердые тела, то для них существует три вида трения:
- покоя;
- скольжения;
- качения.
Эти силы действуют между соприкасающимися поверхностями и всегда направлены против движения тел.
Трение покоя препятствует возникновению самого движения, трение скольжения проявляет себя в процессе движения, когда поверхности тел скользят друг по другу, а трение качения существует между телом, которое катится по поверхности, и самой поверхностью.
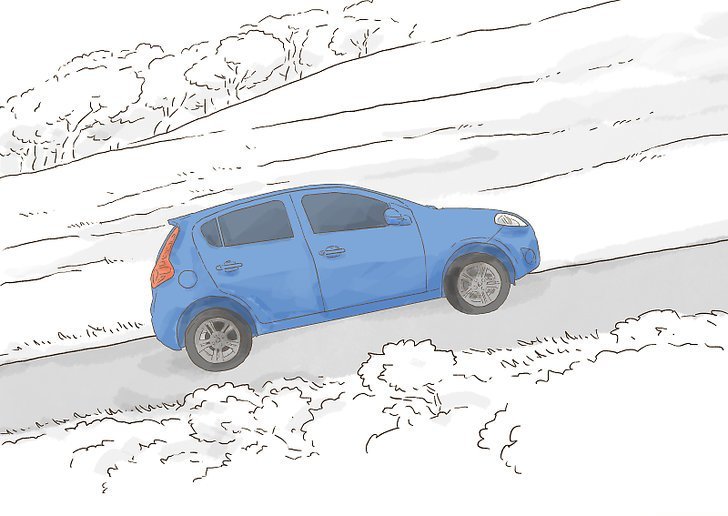
Примером действия трения покоя является автомобиль, который стоит на ручном тормозе на склоне холма. Трение скольжения проявляет себя при движении лыжника по снегу или конькобежца по льду. Наконец, трения качения действует во время движения колеса автомобиля по дороге.
Силы для всех трех видов трения вычисляются по следующей формуле:
Ft = µt*N.
Здесь N – реакции опоры сила, µt – коэфициент трения. Сила N показывает величину воздействия опоры на тело перпендикулярно плоскости поверхности. Что касается параметра µt, то он измеряется экспериментальным путем для каждой пары трущихся материалов, например, дерево-дерево, сталь-снег и так далее. Измеренные результаты собраны в специальные таблицы.
Для каждой силы трения коэффициент µt имеет собственное значения для выбранной пары материалов. Так, коэффициент трения покоя больше такового для трения скольжения на несколько десятков процентов. В свою очередь, коэффициент качения на 1-2 порядка меньше такового для скольжения.
Работа сил трения
Теперь, познакомившись с понятиями работы и с видами трения, можно переходить непосредственно к теме статьи. Рассмотрим по порядку все виды сил трения и разберемся, какую работу они выполняют.
Начнем с трения покоя. Этот вид проявляет себя тогда, когда тело не движется. Поскольку нет движения, значит, вектор его перемещения l¯ равен нулю. Последнее означает, что работа силы трения покоя также равна нулю.
Трение скольжения по своему определению действует только тогда, когда тело перемещается в пространстве. Поскольку сила этого вида трения направлена всегда против перемещения тела, значит, она совершает отрицательную работу. Величину A можно рассчитать по формуле:
A = -Ft*l = -µt*N*l.
Работа силы трения скольжения направлена на замедление движения тела. В результате совершения этой работы механическая энергия тела переходит в тепло.
Трение качение, как и скольжение, также предполагает движение тела. Сила трения качения совершает отрицательную работу, замедляя исходное вращение тела. Поскольку речь идет о вращении тела, то значение работы этой силы удобно вычислять через работу ее момента. Соответствующая формула записывается в виде:
A = -M*θ, где M = Ft*R.
Здесь θ – угол поворота тела в результате вращения, R – расстояние от поверхности до оси вращения (радиус колеса).
Задача с силой трения скольжения
Известно, что деревянный брусок находится на краю наклонной деревянной плоскости. Плоскость к горизонту наклонена под углом 40o. Зная, что коэффициент трения скольжения равен 0,4, длина плоскости равна 1 метр, и масса бруска соответствует 0,5 кг, необходимо найти работу трения скольжения.
Рассчитаем силу трения скольжения. Она равна:
Ft = m*g*cos(α)*µt = 0,5*9,81*cos(40o)*0,4 = 1,5 Н.
Тогда соответствующая работа A будет равна:
A = -Ft*l = -1,5*1 = -1,5 Дж.
Задача с силой трения качения
Известно, что колесо прокатилось по дороге некоторое расстояние и остановилось. Диаметр колеса равен 45 см. Количество оборотов колеса до остановки равно 100. Принимая во внимание коэффициент качения равный 0,03, необходимо найти, чему равна работа силы трения качения. Масса колеса равна 5 кг.
Сначала вычислим момент силы трения качения:
M = Ft*R = µt*m*g*D/2 = 0,03*5*9,81*0,45/2 = 0,331 Н*м.
Если количество оборотов, сделанных колесом, умножить на 2*pi радиан, то мы получим угол поворота колеса θ. Тогда формула для работы имеет вид:
A = -M*θ = -M*2*pi*n.
Где n – число оборотов. Подставляя момент M и число n из условия, получаем искомую работу: A = – 207,87 Дж.
Здесь нужно понимать физические процессы, которые происходят с телами во время трения и условия, при которых происходит трение.
если тело покоится, работа сил трения равно нулю. При перемещении тела под действием силы на расстояние s, тело совершает работу по перемещению тела А=F*s, s – перемещение, F – прилагаемая к телу сила. При движении возникает сила трения (тела с опорой) , которая также совершает работу, одновременно, в результате трения происходит нагрев тела и поверхности, с которой взаимодействует тело при движении (далее просто поверхности) , т. е. часть работы по перемещению тела расходуется на нагрев тел, что влечет за собой изменение тепловой энергии тела и поверхности.
На тело при движении действуют и другие силы сопротивления движению, которыми иногда можно пренебречь, а иногда нет.
Например при свободном падении тела на тело действует сила тяжести, которая совершает работу по перемещению тела. Воздух оказывает сопротивление движению, возникает сила сопротивления воздуха, часть этого сопротивления идет на нагрев тела, иногда и на деформацию тела. Падение спутника сопровождается сильным его нагревом, деформацией (вплоть до разделения на части) , т. е. работа по совершению деформации тела, и работа силы трения о воздух.
В простом случае
А_силы_трения = А_при_перемещении_тела – Q_энергия_затраченная_на_нагрев
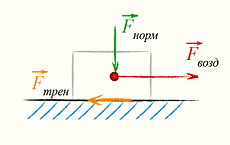
Работа против сил трения, формула
Если тело движется с постоянной скоростью (равномерно) против сил трения, то над ним совершается работа
W = Fs. При этом сила F совпадает по направлению с перемещением s и равна по величине силе трения Fтр.
Работа против сил трения превращается в тепловую энергию.
[
W = F_{тр} s = μ F_{норм} s
]
Здесь:
W — работа против сил трения (Джоуль),
Fтр — сила трения (Ньютон),
μ — коэффициент трения,
Fнорм — сила нормального давления (Ньютон),
s — перемещение (метр),
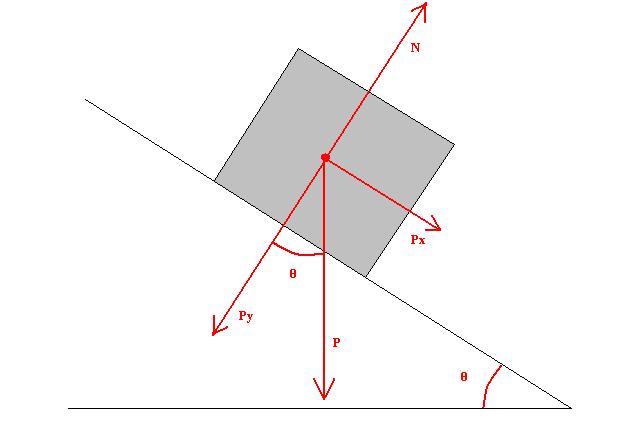
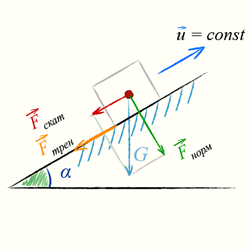
Работа силы трения на наклонной плоскости, формула
При движении тела вверх по наклонной плоскости совершается работа против силы тяжести и силы трения. В этом случае сила, действующая в направлении перемещения, складывается из скатывающей силы Fск и силы трения Fтр. В соответствии с формулой (1)
[
W = (F_{ск} + F_{тр})s = (F_{ск} + μ F_{норм})s
]
[
F_{ск} = G sin(α)
]
[
F_{норм} = G cos(α)
]
[
G = mg
]
[
W = mg (sin(α) + μ cos(α)) s
]
Вычислить, найти работу силы трения на наклонной плоскости по формуле (2)
Работа против сил трения |
стр. 463 |
|---|