Как найти работу момента силы

Работа,
совершаемая внешней силой при вращении
твердого тела, вокруг зак-

репленной
оси

φ

А = ∫ Мz
dφ,

o

где Мz
− проекция момента сил на неподвижную
ось вращения; dφ
− элементар-

ный угол
поворота.

Работа
постоянного момента силы М, вращающего
тело вокруг неподвижной

оси

А = Мφ,

где φ −
полный угол поворота.

Мощность
момента силы М, развиваемая при вращении

N
= Mω,

где ω −
угловая скорость.

7. Кинетическая энергия вращательного движения

Ек = I
ω²/2.

Кинетическая
энергия тела, катящегося по плоскости
без проскальзывания:

Eк
= mv²/2
+ Iω²/2,

где mv²/2
− кинетическая энергия его поступательного
движения, а Iω²/2
−

кинетическая
энергия вращательного движения.

1. Связь работы с изменением кинетической энергии при вращени

Работа
момента сил, действующего на тело, идет
на приращение вращатель-

ной кинетической
энергии тела

7

А
= Δ Ек = Iω²2/2
− Iω²1/2.

1. Гироскоп. Частота прецессии гироскопа

Гироскоп
− всякое массивное твердое тело,
вращающееся вокруг некоторой

оси с болшой
угловой скоростью. Если гироскоп
вращается вокруг некоторой

оси и на
негодействуют силой, закручивающей
его вокруг второй оси, перпен-

дикулярной
первой, то он начинает вращаться
(прецессировать) вокруг третьей

оси,
парнедикулярной первым двум. Частота
прецессии волчка под действием

силы тяжести
при отклонении его от вертикали

ωп
= mgh
/ Io
ω,

где m
− масса волчка, h
− расстояние от точки опоры до центра
масс, Io
и ω −

момент
инерции и угловая скорость относительно
первой оси.

ВОПРОСЫ
И УПРАЖНЕНИЯ

1. Дайте
определение твердого тела в механике.

2. Как
определяется момент силы M
относительно: а) точки;б) оси вращения?

Каковы
свойства этой величины? Какова размерность?

3. Исходя из
основного закона динамики в форме d
p
/ dt
= F,
получите урав-

нение динамики
вращательного движения для материальной
точки d
L/dt
= M.

4. Дайте
определение момента импульса L
относительно:
а) точки; б)оси вра-

щения. Каковы
свойства этой величины? Какова размерность?

5. Получите
уравнение моментов для материальной
точки, движущейся по ок-

ружности,
относительно неподвижной оси вращения
I
β = M
.

6.Чему равен
момент инерции I
материальной точки относительно оси
враще-

ния?

7. Запишите
выражение для кинетической энергии
твердого тела, вращающего-

ся вокруг
закрепленной оси. Чему равна кинетическая
энергия твердого тела

при плоском
движении?

8. Запишите
и сформулируйте теорему Штейнера.

9. Приведите
примеры вычисления для моментов инерции
однородных тел пра-

вильной
формы.

10. Сформулируйте
понятие об эллипсоиде инерции.

n

11. Покажите,
что для системы материальных точек d
L/dt
= M,
где L=
∑[ri
m
vi]

n

i=1

− момент
импульса системы, M
=∑Mi
− результирующий
момент внешних сил.

i=1

12. Дайте
определения собственного, орбитального
и полного момента импульса

твердого
тела.

13. Сформулируйте
закон сохранения момента импульса для
системы материаль-

ных точек.

14. Запишите
уравнение вращательного движения
твердого тела вокруг неподви-

жной оси.Чему
равен момент инерции твердого тела
относительно оси вращения?

Является ли
эта величина аддитивной?

15. Как
определить работу внешних сил при
вращении твердого тела вокруг непо-

движной оси?
Чему равна мощность при вращательном
движении?

ПРИМЕРЫ
РЕШЕНИЯ ЗАДАЧ

Пример 1.
Через неподвижный блок в виде однородного
сплошного цилиндра

массой m
= 160 г перекинута невесомая нить, к концам
которой подвешены грузы

массами m1
= 200 г и m2
= 300 г. Пренебрегая трением в оси блока
и сопротивле- 8

нием воздуха,
определить: 1) ускорение а грузов; 2)
силы натяжения нитей Т1

Т2
соответственно.

Рис.
14

Дано:
m
= 160 г = 0,16 кг, m1
= 200 г = 0,2 кг, m2
= 300 г = 0,3 кг.

О п р е
д е л и т ь: 1) a;
2) T1,
T2.

Р е ш е
н и е. Направив ось х вертикально
вниз (рис. 14), запишем для

каждого
груза уравнение движения (второй закон
Ньютона) в проекциях на эту

ось:

m1a
= T1 – m1g, (1)

m2a
= m2g − T2, (2)

где Т1 и Т2
− силы натяжения нитей; они неодинаковые;
так как Т2 > T1,
то

за счет этого
обеспечивается вращающий ммент,
действующий на блок.

Согласно
основному закону динамики вращательного
движения вращающий

момент,
приложенный к цилиндру

Мо
= Ioβ,
(3)

где Io
− момент инерции цилиндра относительно
оси вращения, перпендикуляр-

ной плоскости
чертежа; β
− угловое ускорение. С другой стороны

Мо
= ( Т2′ − Т1′) R,
(4)

где Т1′ и
Т2′ − силы, приложенные к ободу цилиндра;
R
− плечо этих сил, равное

радиусу
цилиндра. По третьему закону Ньютона,
с учетом невесомости нити Т1′=

= Т1 и Т2′ =
Т2. Воспользовавшись этим, получим,
приравняв (3) и (4),

Ioβ
= (Т2
– Т1)
R, (5)

где
− Io = mR²/2; β = a/R.

Решение
уравнений (1), (2), (5) после подстановки
значений Io
и β приводит

к искомому
выражению для ускорения:

a
= ( m2
– m1)g/(
m1
+ m2
+ m/2).

Из уравнений
(1) и (2) находим силы натяжения Т1 и
Т2:

T1
= m1(g + a); T2 = m2(g − a).

Вычисляя,
получим:
1) a = 1.69 м/c²;
2) T1 = 2.3 H; T2 = 2.44 H.

Пример
2. Человек сидит в центре скамьи
Жуковского, вращающейся с час-

тотой n1
= 30 минˉ¹. В вытянутых руках он держит
по гире массой m
= 5 кг каж-

дая. Расстояние
от каждой гири до оси вращения l1
= 60 см. Суммарный момент 9

инерции
человека и скамьи относительно оси
вращения Io
= 2 кг·м². Определить:

1) частоту
n2
вращения скамьи с человеком; 2) какую
работу А совершит чело-

век, если он
прижмет гантели к себе так, что рассояние
от каждой гири до оси

станет равным
l2
= 20 см.

Д а н о:
n1
= 30 минˉ¹, m
= 5 кг, l1=
60 cм
= 0.6 м, Io
= 2 кг·м², l2
= 20см = 0.2 м.

О п р е
д е л и т ь: 1) n2
; 2) A.

Р е ш
е н и е. По условию задачи момент внешних
сил относительно верти-

кальной оси
вращения равен нулю, поэтому момент
импульса этой системы сох-

раняется,
т.е.

J1ω1
= J2ω2,
(1)

где J1
= So
+ 2ml1²
и J2
= So
+ 2ml2²
− соответственно момент инерции всей
сис-

темы до
сближения и после сближения; m−
масса каждой гири.Угловая скорость

ω = 2πn.
Подставляя это выражение в уравнение
(1), получим искомую частоту

вращения:

n2
= ( So + 2ml1²)·n1/(
So + 2ml2²).

Работа,
совершаемая человеком, равна изменению
кинетической энергии сис-

темы:

A
= Eк2
− Ек1 = J2ω2²/2
− J1ω1²/2.

Выразив из
уравнения (1) ω2 = J1ω1²/J2,
получим:

A
= J1ω1²[(J1/J2
− 1)]/2 = J1ω1²(J1
− J2)/2J
= 2J1π²n1²(J1
− J2)/J2.

Вычисляя,
находим: 1) n2
= 70 минˉ¹; 2) A=
36.8 Дж.

Пример
3. Вычислить момент инерции Iz
молекулы NO2
относительно оси z,

проходящей
черз центр масс молекулы перпендикулярно
плоскости, содержащей

ядра атомов.
Межъядерное расстояние d
этой молекулы равно 0.118 нм, валент-

ный угол α
= 140°.

Р е ш е н
и е. Молекулу NO2
можно рассматривать как систему,
состоящую

из трёх
материальных точек общей массой

m
= 2m1
+ m2,
(1)

где m1
− масса атома кислорода; m2
− масса атома азота. Расположим молекулу

Рис. 15

относительно
координатных осей так, как это указано
на рис. 15 (начало коорди-

нат совместим
с центром масс С молекулы, ось z
направим перпендикулярно

плоскости
чертежа «к нам»).

Для
определения Iz
воспользуемся теоремой Штейнера:

I
= I
c
+ ma².

Для данного
случая эта теорема запишется в виде
Iz′
= Iz
+ ma²,
где Iz′
− момент

инерции
относительно оси z′,
параллельной оси z
и проходящей через атом азо-

та (точка О
на рис. 15). Отсюда искомый момент инерции
10

Iz
= Iz′
− ma².
(2)

Момент
инерции Iz′
находим как сумму моментов двух
материальных точек (ато-

мов кислорода):

Iz′
= 2m1d².
(3)

Расстояние
а между осями z
и z′
равно координате хс центра масс
системы

И поэтому
может быть выражено по формуле хс
=Σmixi/Σmi.
В данном случае

a
= xc
= (2m1x1
+ m2x2)/(2m1
+ m2),

или, учитывая,
что х1 = d
cos(α/2)
и х2 = 0,

а
= хс = 2m1d
cos(α/2)/
(2m1
+ m2).
(4)

Подставив
в вформулу (2) значения Iz′
, m,
а соответственно из выражений (3),

(1), (4), получим

Iz
= 2m1d²
− (2m1
+ m2)[
2m1/(2m1
+ m2)]²d²
cos²(α/2),

или после
преобразований

Iz
= 2m1d²[
1 − 2m1
cos²(α/2)/(2m1
+ m2)].
(5)

Зная
относительные атомные массы кислорода
( Ао =16) и азота (АN
= 14), запи-

шем массы
атомов этих элементов в атомных единицах
массы (а.е.м), а затем вы-

− 27
−27
− 27

разим в
килограммах ( 1 а.е.м. = 1.66 ·10 кг): m1
= 16·1.66·10 кг = 2.66·10 кг;

− 27
−27

m2
= 14·1.66 ·10 кг = 2.32·10 кг.

Значения
m1,
m2,
d
и α подставим* в формулу (5) и произведем
вычисления:

−46

Iz
= 6,80 ·10 кг·м².

(*Для вычисления
выражения, стоящего в скобках, вместо
масс атомов можно под-

ставить их
относительные массы, так как здесь массы
входят в виде отношения).

Пример
4. Маховик в виде диска массой m
= 50 кг и радиусом R
= 20 см

был раскручен
до частоты вращения n1
= 480 минˉ¹ и затем представлен самому

себе.
Вследствие трения маховик остановился.
Найти момент М сил трения, счи-

тая его
постоянным для двух случаев: 1) маховик
остановился через t
= 50 c;

2) маховик
до полной остановки сделал 200 оборотов.

Р е ш е н
и е. 1. По второму закону динамики
вращательного движения изме-

нение момента
импульса вращающегося тела равно
произведению момента силы,

действующего
на тело, на время действия этого момента:

MΔt
= Iω2
− Iω1,

где I
− момент инерции маховика; ω1 и ω2 −
начальная и конечная угловые ско-

рости. Так
как ω2 = 0 и Δt
= t,
то Мt
= − Iω1,
откуда

М
= − Iω1/t.
(1)

Момент
инерции диска относительно его
геометрической оси равен I
= mR²/2.

Подставив
это выражение в формулу (1), найдем
11

М = − mR²ω1/(2t).
(2)

Выразив
угловую скорость ω1 через частоту
вращения n1
и произведя вычи-

сления по
формуле (2), найдем

М = − 1Н·м.

1. В условии задачи
   дано число поворотов, сделанных маховиком
   до останов-

ки, т.е. его
угловое перемещение. Поэтому применим
формулу, выражающую связь

работы с
изменением кинетической энергии:

A
= Iω2²/2
− Iω1²/2,

или, учтя,
что ω2 = 0,

А = − Iω1²/2.
(3)

Работа
при вращательном движении определяется
по формуле А = Мφ. Под-

ставив
выражения работы и момента инерции
диска в формулу (3), получим

Мφ = − mR²ω1²/4.

Отсюда
момент сил трения

М = − mR²ω1²/(4φ).
(4)

Угол
поворота φ = 2πN
= 2·3.14·200 рад = 1256 рад. Произведя вычисления

по формуле
(4), получим

М = − 1Н·м.

Знак
минус показывает, что момент сил трения
оказывает тормозящее дейст-

вие.

Пример
5. Стержень длиной l
= 1.5 м и массой М = 10 кг может вращаться

вокруг
неподвижной оси, проходящей через
верхний конец стержня (рис. 16). В

середину
стержня ударяет пуля массой m
= 10 г, летящая в горизонтальном на-

правлении
со скоростью vo
= 500 м/c,
и застревает в стержне. На какой угол
φ

отклонится
стержень после удара?

Рис.16

Р е ш е н
и е. Удар пули следует рассматривать
как неупругий: после удара

и пуля, и
соответствующая точка стержня будут
двигаться с одинаковыми ско-

ростями.

12

Рассмотрим
подробнее явления, происходящие при
ударе. Сначала пуля, уда-

рившись о
стержень, за ничтожно малый промежуток
времени приводит его в

движение с
угловой скоростью ω и сообщает ему
кинетичекскую энергию

Ек
= Iω²/2,
(1)

где I
− момент инерции стержня относительно
оси вращения.

Затем
стержень поворачивается на искомый
угол φ, причём центр масс его

поднимается
на высоту h
= (l/2)(1
− cos
φ). В отклоненном положении стер-

жень будет
обладать потенциальной энергией

Еп
= Мg(l/2)(1
− cos
φ).
(2)

Потенциальная
энергия получена за счет кинетической
энергии и равна ей

по закону
сохранения энергии. Приравняв правые
части равенств (1) и (2), по-

лучим

Mg(l/2)(1−
cosφ)
= Iω²/2.

Отсюда

cosφ
= 1 − Iω²/(Mgl).

Подставив
в эту формулу выражение для момента
инерции стержня I
= Ml²/3,

получим

cosφ
=1 − lω²/(3g).
(3)

Чтобы из
выражения (3) найти φ, необходимо
предварительно определить

значение
ω. В момент удара на пулю и стержень
действуют силы тяжести, ли-

нии действия
которых проходят через ось вращения и
направлены вертикально

вниз. Моменты
этих сил относительно оси вращения
равны нулю. Поэтому при

ударе пули
о стержень будет справедлив закон
сохранения момента импульса.

В начальный
момент удара угловая скорость стержня
ωо = 0, поэтому его

собстенный
момент ипульса So1
= Iωo
= 0. Пуля коснулась стержня и начала уг-

лубляться
в стержень, сообщая ему угловое ускорение
и участвуя во вращении

около оси.
Начальный орбитальный момент импульса
пули Lo1
= mvor,
где r
−

расстояние
точки попадания от оси вращения. В
конечный момент удара стер-

жень имел
угловую скорость ω, а пуля − линейную
скорость v,
равную линей-

ной скорости
точек стержня, находящихся на расстоянии
r
от оси вращения.

так как v
= ωr,
то конечный момент импульса пули L2
= mvr
= mr²ω.

Применив
закон сохранения момента импульса,
можем написать

Lo1
+ Lo2 = L1 + L2, или
mvor = Iω + mr²ω,

откуда

ω
= mvor/(I + mr²), (4)

где I
= Ml²/3
− момент инерции системы стержень −
пуля.

Если
учесть, что в (4) mr²«
I
= Ml²/3,
а также, что r
= l/2,
то после неслож-

ных
преобразований получим

ω
= 3mvo/(2Ml).
(5)

Подставив
числовые значения величин в (5), найдем
13

ω
= 3·10ˉ²·500 /(2·10·1.5) рад = 0.5 рад.

По (3)
получим

cosφ
= 1 − 1.5(0.5)²/(3·9.8) = 0.987.

Следовательно,
φ = 9°20′.

ЗАДАЧИ
ГРУППЫ А

1.(В.3.3)
К ободу однородного диска радиусом R
= 0.2 м приложена ка-

сательная
сила F
= 98.1 Н. При вращении на диск действует
момент сил трения

Мтр = 4.9 Н·м.
Найти массу m
диска, если известно, что диск вращается
с уг-

ловым
ускорением β = 100 рад/c².

Ответ:
m
= 2( FR
– Mтр
)/βR²
= 7.36 кг.

2.(В.3.5)
Однородный
диск радиусом R
= 0.2 м и массой m
=5 кг вра-

щается вокруг
оси, проходящей через его центр
перпендикулярно к его плоско-

сти.
Зависимость угловой скорости ω
вращения диска от времени t
дается

уравнением
ω = А + Вt,
где В = 8 рад/c².
Найти касательную силу F,
прило-

женную к
ободу диска. Трением пренебречь.

Ответ:
F
= 4.0 H.

3.(В.3.9)
Маховое
колесо, момент инерции которого I
= 245 кг м², враща-

ется с
частотой n
= 20 об/c.
Через время t
= 1 мин после того, как на колесо

перестал
действовать момент сил М, оно остановилось.
Найти момент сил тре-

ния Мтр и
число оборотов N,
которое сделало колесо до полной
остановки пос-

ле прекращения
действия сил. Колесо считать однородным
диском.

Ответ:
Мтр = 513 Н·м;
N
= 600 об.

4.(В.3.12)
На барабан
радиусом R
= 0.5 м намотан шнур, к концу кото-

рого привязан
груз массой m
= 10 кг. Найти момент инерции I
барабана, если

известно,
что груз опускается с ускорением а =
2.04 м/c².

Ответ:
I
= 9.5 кг·м².

5.(В.3.14)
Две гири
с разными массами соединены нитью,
перекинутой че-

рез блок,
момент инерции которого I
= 50 кг·м² и радиус R
= 20 см. Момент сил

трения
вращающегося блока Мтр = 98.1 Н·м. Найти
разность сил натяжения нити

Т1 – Т2 по
обе стороны блока, если известно, что
блок вращается с угловым уско-

рением β =
2.36 рад/c².
Блок считать однородным диском.

Ответ:
Т1 – Т2 = (
Iβ
+ Mтр)
/R
= 1.08 кН.

6.(В.3.26)
Медный шар радиусом R
= 10 см вращается с частотой n
= 2 об/c

вокруг оси,
проходящей ерез его центр. Какую работу
надо совершить, чтобы уве-

личить
угловую скорость ω вращения шара вдвое?

Ответ:
A
= 3.2π³
R²*³ρn²
= 34.1 Дж, где ρ −плотность меди.

7.(В.3.27)
Найти
линейные ускорения а центров: 1)
шара, 2) диска и

3) обруча,
скатывающихся без скольжения с наклонной
плоскости. Угол наклона

плоскости
φ = 30°, начальная скорость всех тел vo
= 0. Сравнить найденные уско-

рения с
ускорением тела, соскальзывающего с
наклонной плоскости при отсутст-

вии
трения.

14

Ответ:

a
= mg sinφ/( m + I/R²); 1)a1 = 3.50 м/c²,
2) a2 = 3.27 м/c²,
3)a3 =2.44м/c²;

при
свободном скольжении а = g
sinφ
= 4.9 м/c².

8.(В.3.31)
Вентилятор
вращается с частотой n
= 900 об/мин. После выклю-

чения
вентилятор, вращаясь равнозамедленно,
сделал до остановки N
= 75 об. Ра-

бота сил
торможения А = 44.4 Дж. Найти момент
инерции I
вентилятора и мо-

мент сил
торможения М.

Ответ:
I
= 0.01 кг·м²; M
= 94·10ˉ³ H·м.

9.(В.3.32)
Маховое
колесо, момент инерции которого I
= 245 кг·м², враща-

ется с
частотой n
= 20 об/c.
После того как на колесо перестал
действовать вра-

щающий
момент, оно остановилось, сделав N
= 1000 об. Найти момент сил тре-

ния Мтр и
время t,
прошедшее от момента прекращения
действия вращающего

момента до
остановки колеса.

10.(В.3.34)
Маховое колесо начинает вращаться с
угловым ускорением β =

= 0.5 рад/c²
и через t1
= 15 c
после начала движения приобретает
момент импуль-

са L
= 73.5 кг·м²/c.
Найти кинетическую энергию Ек колеса
через время t2
= 20 c

после начала
движения.

Ответ:
Eк
= βLt2²/2t1
= 490 Дж.

11.(В.3.38)
Однородный стержень длиной l
= 85 см подвешен на горизон-

тальной оси,
проходящей через верхний конец стержня.
Какую минимальную ско-

рость vмин
надо сообщить нижнему концу стержня,
чтобы он сделал полный обо-

рот вокруг
оси?

Ответ:
vмин
= 7.1 м/с.

12.(В.3.40)
Горизонтальная
платформа массой m
=100 кг вращается вокруг

вертикальной
оси, проходящей через центр платформы,
с частотой n1
= 10 об/мин.

Человек
массой mo
= 60 кг стоит при этом на краю платформы.
С какой частотой

n2
начнет вращаться платформа, если
человек перейдёт от края платформы к
её

центру?Считатать
платформу однородным диском, а человека
− точечной массой.

Ответ:
n2
= n1(
m
+ 2mo)/m
= 22 об/мин.

13.(В.3.41)
Какую
работу А совершает человек при переходе
от края плат-

формы мы к
её центру в условиях предыдущей задачи?
Радиус платформы R
=

= 1.5 м.

Ответ:
А = 162 Дж.

ЗАДАЧИ
ГРУППЫ Б

1.(Ч.3.21)
Тонкий
однородный стержень длиной l
=50 см и массой
m=400
г

вращается
с угловым ускорением β = 3 рад /c²
около оси, проходящей перпенди-

кулярно
стержню через его середину. Определить
вращающий момент.

Ответ:
M
= ml²β/12
= 0.025 Н·м.

2.(Ч.3.25)
Через
блок, имеющий форму диска, перекинут
шнур. К концам

шнура
привязаны грузики массой m1
= 100 г и m2
= 110 г. С каким ускорением

а будут
двигаться грузики, если масса m
блока равна 400 г? Трение при враще-

нии блока
ничтожно мало.

Ответ:
a
= 2(m2
– m1)g/(m
+ 2m1
+ 2m2)
= 0.24 м/c².

15

3.(Ч.3.27)
Через
неподвижный блок массой m
= 0.2 кг перекинут шнур,

к концам
которого подвесили грузы массами m1
= 0.3 кг и m2
= 0.5 кг. Опреде-

лить силы
натяжения Т1 и Т2 шнура по обе стороны
бдлка во время движения

грузов, если
масса блока равномерно распределена
по ободу.

Ответ:
T1
= m1(m
+ 2m2)g/(m1
+ m2
+ m)
= 3.53 H,

T2
= m2(m
+ 2m1)g/(m1
+ m2
+ m)
= 3.92 H.

4.(Ч.3.28
Шар массой
m
= 10 кг и радиусом R
= 20 см вращается вокруг

оси, проходящей
через его центр. Уравнение вращения
шара имеет вид φ = А +

+ Вt²
+ Ct³,
где В = 4 рад/c²,
С = − 1 рад/c³.
Найти закон изменения момента сил,

действующих
на шар. Определить момент сил М в
момент времени t
= 2 c.

Ответ:
M
= 4/5 mR² ·(B + 3Ct) = − 0.64 H·м.

5.(Т.1.137)
Полная
кинетическая энергия Е диска, катящегося
по горизон-

тальной
поверхности, равна 24 Дж. Определить
кинетическую энергию Ек пост и

Ек вр
вращательного движения дска.

Ответ:
Ек пост
= 16 Дж, Ек вр = 8 Дж.

6.(Т.1.146)
Маховик
в виде сплошного диска, момент инерции
которого I=

= 1.5 кг·м²,
вращаясь при торможении равнозамедленно,
за время t
=1 мин умень-

шил частоту
своего вращенич с no
=240 об/мин до n1
= 120 об/мин. Определить:

1) угловое
ускорение маховика; 2) момент М силы
торможения; 3) работу тормо-

жения А.

Ответ:
1) 0.21
рад/c²
; 2) 0.047 Н·м ; 3) 355 Дж.

7.(Ч.3.36)
В центре
скамьи Жуковского стоит стоит человек
и держит в ру-

ках стержень
длиной l
= 2.4 м и
массой m
= 8 кг, расположенный вертикально

по оси
вращения скамьи. Скамья с человеком
вращается с частотой n1
= 1 cˉ¹.
С

какой частотой
n2
будет вращаться скамья с человеком,
если он повернёт стер-

жень в
горизонтальное положение? Суммарный
момент инерции I
человека и

скамьи равен
6 кг·м².

Ответ:
n2
= 12 I
n1/(12
I
+ ml²)
= 0.61 cˉ¹.

8.(Ч.3.39)
Маховик
вращается по закону, выражаемому
уравнением φ =

= А + Вt
+ Сt², где А = 2 рад, В = 32 рад/c,
C
= − 4 рад/c².
Найти среднюю мощ-

ность < N
>, развиваемую силами, действующими
на маховик при его вращении

до остановки,
если его момент инерции I
= 100 кг·м².

Ответ:
12.8 кВт.

9.(Ч.3.46)
Маховик,
момент инерции I
которого равен 40 кг·м², начал

вращаться
равноускоренно из состояния покоя под
действием момента силы М =

= 20 Н·м.
Вращение продолжалось в течение t
= 10 с. Опрделить кинетическую

энергию Ек,
приобретённую маховиком.

Ответ:
Ек =
М²(Δt)²/(2I)
= 500Дж.

10.(Ч.3.52)
Сколько
времени t
будет скатываться без скольжения обруч

c
наклонной плоскости длиной l
= 2 м и высотой
h
= 10 см?

Ответ:
t
= 2l√
gh
= 4.04 c.

11.(Т.1.152)
На
однородный сплошной цилиндрический
вал радиусом R=

= 20 см, момент
инерции которого I
= 0.15кг·м², намотана легкая нить, к концу
16

которой
прикреплен груз массой m
= 0.5кг. До начала вращения барабана высо-

та h
груза над полом составляла 2.3 м.
Определить: 1) время опускания груза

до пола ; 2)
силу натяжениянити; 3) инетическую
энергию груза в момент удара

о пол.

Ответ:
1) 2 с; 2) 4.31 H;
3) 1.32 Дж.

12.
Однородный сплошной цилиндр массой
m
и радиусом R
катится по

горизонтальной
поверхности со скоростью центра масс
Vo.
Определить момент

импульса
цилиндра Jo
относительно оси, параллельной оси
вращения и лежащей

на этой
повехности.

Ответ:
Jo
= (3/2) [ RomVo]

ЗАДАЧИ
ГРУППЫ С

1.(И.1.195)
К точке,
радиус- вектор которой относительно
оси координат

О равен r
= ai
+ bj,
приложена сила F
= Ai
+ Bj,
где а,b,A,B
− постоянные, i,j–

орты осей
х и у. Найти момент Мо
и плечо l
силы F
относительно
оси О.

Ответ:
Mo
= ( aB
– bA
) k,
где k
− орт оси
z;
l
= ‌‌‌‌‌|aB
– bA
|/√ A²
+ B².

2.(И.1.196)
Момент
импульса частицы относительно некоторой
точки О ме-

няется по
закону Jo
= a
+ bt²,
где a
и
b
− постоянные
векторы, причем a
пер-

пендикулярен
b.
Найти относительно точки О момент Мо
силы, действующей на

частицу,
когда угол между векторами Мо
и Jo
окажется равным 45°.

Ответ:
Мо
= 2b
√ a/b
.

3.(С.1.120)
Тело
массой m
брошено с начальной скоростью vo,
образующей

угол α с
горизонтом. Приняв плоскость, в которой
движется тело, за плоскость

х, у
и направив ось у
вверх, а
ось х −
по направлению движения, найти вектор

момента
импульса тела J
относительно точки бросания в момент,
когда тело на-

ходится в
верхней точке траектории. Сопротивлением
воздуха пренебречь.

Ответ:
J
= − (m
vo³
sin²α
cosα/2g)
k.

4.(С.1.125)
В условиях предыдущей задачи найти
зависимость от времени:

а)
момент M
силы, действующей на частицу;

б)
момент импульса частицы J.

Ответ:
а) М
= − mgvocosα
t
k
; б) J
= − (1/2) mgvocosα
t²k.

5.(И.1.198)
Небольшая
шайба массы m
= 50 г начинает скользить с верши-

ны гладкой
наклонной плоскости, высота которой
h
= 100 см и угол наклона к

горизонту
α = 15°(Рис 17). Найти модуль момента
импульса шайбы относитель-

но оси О,
перпендикулярной к плоскости рисунка,
через t
= 1.3 c
после начала

движения.

Рис.17

Ответ:
Jo
= (1/2)mght
sin
2α
= 0.16 кг·м²/c.

17

6.(И.1.204)
Частица
движется по замкнутой траектории в
центральном си-

ловом поле,
где её потенциальная энергия U
= kr²,
k
− положительная постоян-

ная, r
− расстояние частицы до центра поля О.
Найти массу частицы, если наи-

меньшее
расстояние её до точки О равно r1,
а скорость на наибольшем рассто-

янии от этой
точки − v2.

Ответ:
m
=2kr1²/v2².

7.(И.1.210)
Однородный
шар массы m
и радиуса R
начинает скатывать-

ся без
скольжения по наклонной плоскости,
составляющей угол α с горизон-

том. Найти
зависимость от времени момента импульса
шара относительно точ-

ки касания
в начальный момент. Как изменится
результат в случае абсолютно

гладкой
наклонной плоскости?

Ответ:
J
= Rmgt
sinα.

8.(И.1.226)
Космическое
тело А движется к Солнцу С, имея
вдали от

него скорость
vo
и прицельный параметр l
− плечо
вектора vo
относительно

Рис.
18

центра Солнца
(рис.18). Найти наименьшее расстояние, на
которое это тело при-

близится к
Солнцу.

Ответ:
rмин
= [√ 1 + (lvo²/γmc)²
− 1] γmc/vo²,
где mc
− масса Солнца.

9.(И.1.250)
Какую наименьшую работу надо совершить,
чтобы доставить

космический
корабль массы m
= 2.0 ·10³ кг с повехности Земли на Луну?
Cопро-

тивление
воздуха не учитывать.

Ответ:
A
≈ γm
( M1/R1
+ M2/R2
) = 1.3 ·10² ГДж, где М и R
− масса и

радиус
Земли и Луны.

10.(И.1.253)
Однородный шар массы m
= 4.0 кг движется поступательно по

поверхностистола
под действием постоянной силы F,
приложенной, как показано

Рис.19

на рис.19, где
угол α = 30°. Коэффициент трения между
шаром и столом μ= 0.20.

найти F
и ускорение шара.

Ответ:
F
= kmg/
[(1 + μ)
sinα]
= 13 H;
a
= μg
(ctgα
− 1)/(1+μ) = 1.2 м/c².

11.(И.1.255)
Найти
момент инерции:

а) тонкого
однородного стержня относительно оси,
перпендикулярной к стер-

жню и
проходящей через его конец, если масса
стержня m
и его длина l;

18

б) тонкой
однородной прямоугольной пластинки
относительно оси,проходящей

через одну
из вершин пластинки перпендикулярно к
еёё плоскости, если стороны

пластинки
равны a
и b,
а её масса −
m.

Ответ:
a)
I = ml²/3;
б)
I = m(
a²
+ b²)/3.

12.(И.1.257)
Вычислить момент инерции:

а) медного
однородного диска относительно оси
симметрии, перпендикуляр-

ной к плоскости
диска, если его толщина b
= 2.0 мм и радиус R
= 100 мм;

б)
однородного сплошного конуса
относительно его оси симметрии, если

масса конуса
m
и радиус его основания R.

Ответ:
a)
I = πρbR²*²/2 = 2.8 г·м²;
б)
I = (3/10) mR².

13.(И.1.268)
Однородный цилиндр радиуса R
раскрутили вокруг его оси

до угловой
скорости ωо и поместили затем в угол
(рис.20). Коэффициент тре-

Рис.20

ния между
стенками угла и цилиндром равен μ.
Сколько оборотов сделает ци-

линдр до
остановки?

Ответ:
n
= (1 + μ²)
ωo²R/8πμ
(μ
+ 1)g.

14.(И.1.270)
Однородный диск радиуса R
раскрутили до угловой скорос-

ти ω
и осторожно положили плашмя на
гаризонтальную поверхность. Сколь-

ко времени
диск будет вращаться на поверхности,
если коэффициент трения ра-

вен μ?

Ответ:
t
= 3ωR/4μg.

15.(И.1.294)
В системе,
показанной на рис.21 известны масса m
груза A,

масса М
ступенчатого блока В, момент инерции
I
последнего относительно

Рис.21

его оси и
радиусы ступеней блока R
и 2R.
Масса нитей пребрежимо мала. Най-

ти ускорение
груза А.

Ответ:
a
= g
( m
– M)/(
M
+ m
+ I/R²).

19

Занятие
5. Механика жидкостей и газов

СОДЕРЖАНИЕ
ТЕОРИИ

1. Законы гидростатики.

2. Стационарное
   течение идеальной жидкости или газа.

3. Течение вязкой
   жидкости. Формула Пуазейля.

4. Турбулентное
   течение вязкой жидкости. Число Рейнольдса.

ОСНОВНЫЕ
ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ

В общем курсе физики изучают два наиболее простых типа перемещения объектов в пространстве – это поступательное движение и вращение. Если динамика поступательного движения основана на использовании таких величин, как силы и массы, то для количественного описания вращения тел используют понятия моментов. В данной статье рассмотрим, по какой формуле момент силы вычисляют, и для решения каких задач пользуются этой величиной.

Момент силы

Вам будет интересно:Герой Российской Федерации Петров Дмитрий Владимирович, гвардии старший лейтенант: биография, подвиг

Представим себе простую систему, которая состоит из материальной точки, вращающейся вокруг оси на расстоянии r от нее. Если к этой точке приложить касательную силу F, которая будет перпендикулярна оси вращения, то она приведет к появлению углового ускорения точки. Способность силы приводить к вращательному движению систему называется крутящим моментом или моментом силы. Вычисляют по формуле следующей его:

M¯ = [r¯*F¯]

В квадратных скобках стоит векторное произведение радиус-вектора на силу. Радиус-вектор r¯ является направленным отрезком от оси вращения к точке приложения вектора F¯. Учитывая свойство векторного произведения, для значения модуля момента формула в физике запишется в таком виде:

M = r*F*sin(φ) = F*d, где d = r*sin(φ).

Здесь угол между векторами r¯ и F¯ обозначен греческой буквой φ. Величина d называется плечом силы. Чем оно больше, тем больший крутящий момент может создать сила. Например, если открывать дверь, надавливая на нее вблизи петель, то плечо d будет маленьким, поэтому необходимо приложить большую силу, чтобы повернуть дверь на петлях.

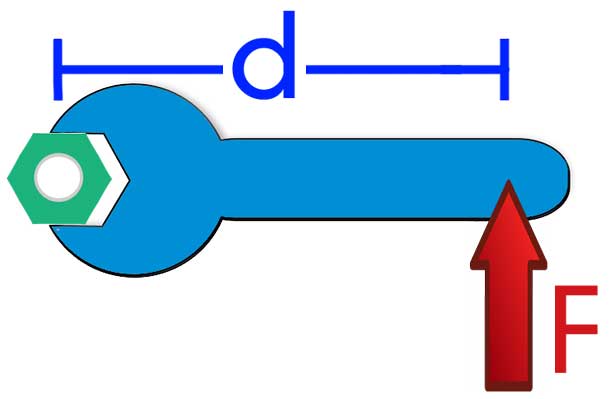
Как видно из формулы момента, величина M¯ – это вектор. Направлен он перпендикулярно плоскости, в которой лежат вектора r¯ и F¯. Направление M¯ определить легко с использованием правила руки правой. Чтобы им воспользоваться, необходимо четыре пальца руки правой направить вдоль вектора r¯ по направлению действия силы F¯. Тогда отогнутый большой палец покажет направление момента силы.

Момент силы в статике

Рассмотренная величина является очень важной при вычислении условий равновесия системы тел, имеющих ось вращения. Таких условий в статике всего два:

• равенство нулю всех внешних сил, которые оказывают на систему то или иное воздействие;
• равенство нулю моментов сил, связанных с внешними силами.

Оба условия равновесия математически можно записать так:

∑i(Fi¯) = 0;

∑i(Mi¯) = 0.

Как видно, вычислять необходимо именно векторную сумму величин. Что касается момента силы, то принято считать за его положительное направление, если сила совершает поворот против хода стрелки часов. В противном случае перед формулой определения момента следует использовать знак минус.

Отметим, если в системе ось вращения расположена на некоторой опоре, то соответствующая сила реакции момента не создает, поскольку ее плечо равно нулю.

Момент силы в динамике

Динамика движения вращения вокруг оси имеет так же, как и динамика поступательного перемещения, основное уравнение, на основе которого решаются многие практические задачи. Оно называется уравнением моментов. Формула соответствующая записывается в виде:

M = I*α.

По сути, это выражение является вторым законом Ньютона, если момент силы заменить на силу, момент инерции I – на массу, а угловое ускорение α – на аналогичную линейную характеристику. Чтобы лучше понимать это уравнение, отметим, что момент инерции выполняет ту же самую роль, что обычная масса при поступательном движении. Момент инерции зависит от распределения массы в системе относительно оси вращения. Чем больше расстояние тела до оси, тем больше величина I.

Угловое ускорение α вычисляется в радианах в секунду в квадрате. Оно характеризует быстроту изменения вращения.

Если момент силы равен нулю, тогда система не получает никакого ускорения, что свидетельствует о сохранении ее момента импульса.

Работа момента силы

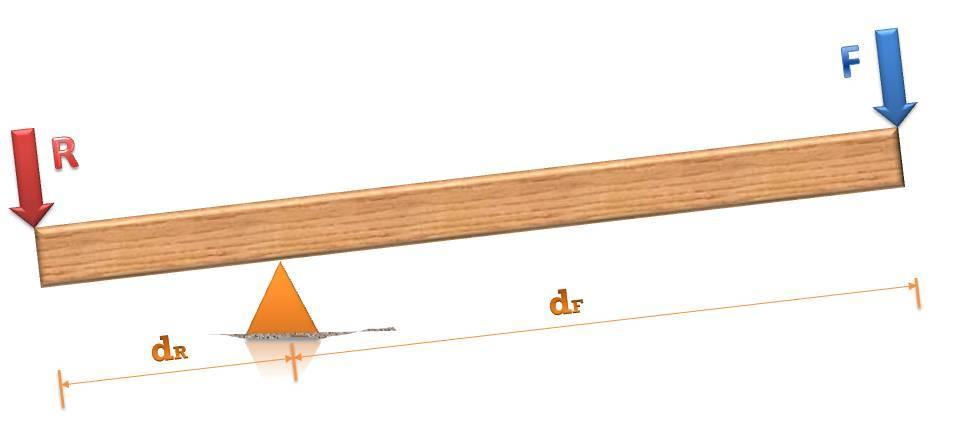
Поскольку изучаемая величина измеряется в ньютонах на метр (Н*м), то многие могут подумать, что ее можно заменить джоулем (Дж). Однако этого не делают потому, что в джоулях измеряется некоторая энергетическая величина, момент силы же – это силовая характеристика.

Так же как сила, момент M тоже может совершать работу. Вычисляется она по такой формуле:

A = M*θ.

Где греческой буквой θ обозначен угол поворота в радианах, на который повернулась система в результате действия момента M. Заметим, что в результате умножения момента силы на угол θ, единицы измерения сохраняются, однако, уже используют именно единицы работы, то есть, Джоули.

Жду ваши вопросы и мнения в комментариях

Вращение вокруг оси или точки различных объектов является одним из важных видов движения в технике и в природе, который изучают в курсе физики. Динамика вращения, в отличие от динамики линейного движения, оперирует понятием момента той или иной физической величины. Данная статья посвящена вопросу, что такое момент сил.

Понятие о моменте силы

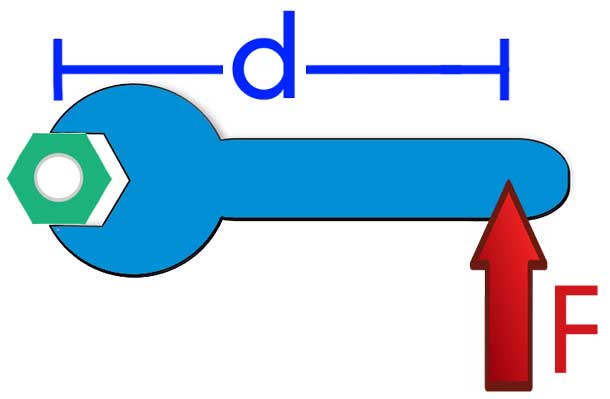
Каждый любитель велосипеда хотя бы один раз в своей жизни раскручивал рукой колесо своего “железного коня”. Если описанное действие выполнять, взявшись рукой за покрышку, то раскрутить колесо гораздо легче, чем взявшись за спицы ближе к оси вращения. Это простое действие описывается в физике с помощью момента силы или вращающего момента.

Что такое момент силы? Ответить на этот вопрос можно, если представить себе систему, которая может вращаться вокруг оси O. Если в некоторой точке P к системе приложить вектор силы F¯, тогда момент действующей силы F¯ будет равен:

M¯ = [OP¯*F¯].

То есть момент M¯ представляет собой векторную величину, равную произведению векторной силы F¯ на радиус-вектор OP¯.

Записанная формула позволяет отметить важный факт: если внешняя сила F¯ приложена под любым углом к любой точке оси вращения, то момента она не создает.

Абсолютная величина момента силы

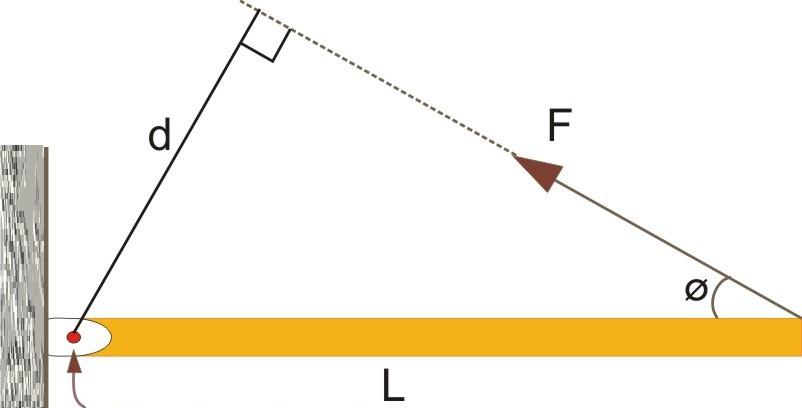
В предыдущем пункте мы рассмотрели определение, что такое момент силы относительно оси. Теперь обратимся к рисунку ниже.

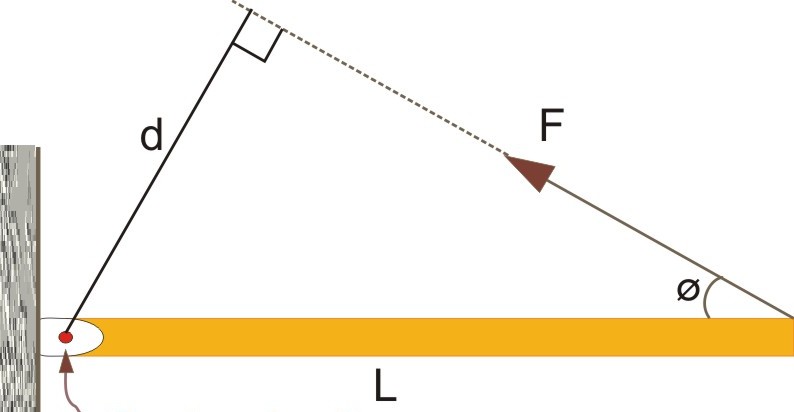
Здесь изображен некоторый стержень, имеющий длину L. С одной стороны он закреплен через шарнирное соединение на вертикальной стене. Другой конец стержня является свободным. На этот конец оказывает действие сила F¯. Также известен угол между стержнем и вектором силы. Он равен φ.

Вращающий момент определяется через векторное произведение. Модуль такого произведения равен произведению абсолютных значений векторов на синус угла между ними. Применяя тригонометрические формулы, приходим к следующему равенству:

M = L*F*sin(φ).

Обращаясь снова к рисунку выше, можно это равенство переписать в следующей форме:

M = d*F, где d = L*sin(φ).

Величина d, которая равна расстоянию от вектора силы до оси вращения, получила название рычага силы. Чем больше значение d, тем больший момент создаст сила F.

Направление момента силы и его знак

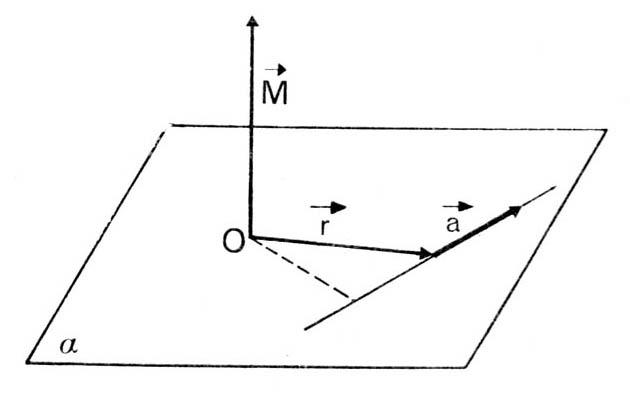
Изучение вопроса, что такое момент силы, не может быть полным, если не рассмотреть его векторную природу. Вспоминая свойства векторного произведения, можно с уверенностью сказать, что момент силы будет перпендикулярен плоскости, построенной на векторах-множителях.

Конкретное направление M¯ определяется однозначно, если применить так называемое правило буравчика. Звучит оно просто: вращая буравчик по направлению кругового движения системы, поступательным движением буравчика определяется направление момента силы.

Если смотреть на вращающуюся систему вдоль ее оси, то вектор момента силы, приложенный к точке, может быть направлен как на читателя, так и от него. В связи с этим при количественных расчетах используют понятие о положительном или об отрицательном моменте. В физике принято положительным считать тот момент силы, который приводит к вращению системы против хода часовой стрелки.

В чем смысл величины M¯?

Имеется в виду физический смысл. Действительно, в механике линейного движения известно, что сила – это мера возможности придать линейное ускорение телу. По аналогии, момент силы точки – это мера возможности сообщения углового ускорения системы. Момент силы является причиной появления углового ускорения и ему прямо пропорционален.

Разную возможность совершения вращения или поворота легко понять, если вспомнить, что дверь открывается легче, если ее толкнуть подальше от дверных петель, то есть в области ручки. Еще один пример: любой более-менее тяжелый предмет легче удержать, если прижать руку к телу, чем держать его на вытянутой руке. Наконец, открутить гайку проще, если воспользоваться длинным ключом. В названных примерах момент силы изменяется за счет уменьшения или увеличения рычага силы.

Здесь уместно привести аналогию философского характера, взяв за пример книгу Экхарта Толле “Сила момента Сейчас”. Книга относится к психологическому жанру и учит жить без стресса в данный момент своей жизни. Только текущее мгновение имеет смысл, только во время него совершаются все действия. Учитывая названную идею книги “Сила момента Сейчас” можно сказать, что вращающий момент в физике осуществляет ускорение или замедление вращения в текущий момент времени. Поэтому главное уравнение моментов имеет следующий вид:

dL = M*dt.

Где dL – изменение момента импульса за бесконечно малый промежуток времени dt.

Важность понятия о моменте силы для статики

Многие знакомы с задачами на рычаги разного рода. Практически во всех этих задачах статики требуется найти условия равновесия системы. Для нахождения этих условий проще всего воспользоваться концепцией момента силы.

Если система не движется и находится в состоянии равновесия, то сумма всех моментов сил относительно оси, точки или выбранной опоры должна быть равна нулю, то есть:

∑_i=1ⁿM_i¯ = 0.

Где n – число действующих сил.

Напомним, что абсолютные значения моментов M_i в равенство выше нужно подставлять с учетом их знака. Сила реакции опоры, которая рассматривается в качестве оси вращения, вращающего момента не создает. Ниже приводится видео, которое поясняет тему этого пункта статьи.

Момент силы и его работа

Многие читатели обратили внимание, что момент силы рассчитывается в ньютонах на метр. Это означает, что он имеет такую же размерность, что работа или энергия в физике. Тем не менее концепция момента силы – это величина векторная, а не скалярная, поэтому работой момент M¯ считать нельзя. Однако работу он может выполнять, что рассчитывается по такой формуле:

A = M*θ.

Где θ – центральный угол в радианах, на который система повернулась за известное время t.

Работа при вращательном движении. Момент силы

Рассмотрим работу, совершаемую при вращении материальной точки по окружности под действием проекции действующей силы на перемещение (тангенциальной составляющей силы). В соответствии с (3.1) и рис. 4.4, перейдя от параметров поступательного движения к параметрам вращательного движения (dS = R dcp)

Здесь введено понятие момента силы относительно оси вращения OOi как произведение силы F_s на плечо силы R:

Как видно из соотношения (4.8), момент силы во вращательном движении является аналогом силы в поступательном движении, поскольку оба параметра при умножении на аналоги dcp и dS дают работу. Очевидно, момент силы тоже должен задаваться векторно, причем относительно точки О его определение дается через векторное произведение и имеет вид

Окончательно: работа при вращательном движении равна скалярному произведению момента силы на угловое перемещение:

Кинетическая энергия при вращательном движении. Момент инерции

Рассмотрим абсолютно твердое тело, вращающееся относительно неподвижной оси. Мысленно разобьем это тело на бесконечно малые кусочки с бесконечно малыми размерами и массами mi, m2, Шз . находящиеся на расстоянии R_b R₂, R3 . от оси. Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его малых частей

где У— момент инерции твердого тела, относительно данной оси OOj.

Из сопоставления формул кинетической энергии поступательного и вращательного движений видно, что момент инерции во вращательном движении является аналогом массы в поступательном движении. Формула (4.12) удобна для расчета момента инерции систем, состоящих из отдельных материальных точек. Для расчета момента инерции сплошных тел, воспользовавшись определением интеграла, можно преобразовать (4.12) к виду

Несложно заметить, что момент инерции зависит от выбора оси и меняется при ее параллельном переносе и повороте. Приведем значения моментов инерции для некоторых однородных тел.

Из (4.12) видно, что момент инерции материальной точки равен

где т — масса точки;

R — расстояние до оси вращения.

Несложно вычислить момент инерции и для полого тонкостенного цилиндра (или частного случая цилиндра с малой высотой — тонкого кольца) радиуса R относительно оси симметрии. Расстояние до оси вращения всех точек для такого тела одинаково, равно радиусу и может быть вынесено из-под знака суммы (4.12):

Сплошной цилиндр (или частный случай цилиндра с малой высотой — диск) радиуса R для расчета момента инерции относительно оси симметрии требует вычисления интеграла (4.13). Масса в этом случае в среднем сосредоточена несколько ближе, чем в случае полого цилиндра, и формула будет похожа на (4.15), но в ней появится коэффициент меньше единицы. Найдем этот коэффициент.

Пусть сплошной цилиндр имеет плотность р и высоту h. Разобьем его на

полые цилиндры (тонкие цилиндрические поверхности) толщиной dr (рис. 4.5) показывает проекцию, перпендикулярную оси симметрии). Объем такого полого цилиндра радиуса г равен площади поверхности, умноженной на толщину: масса: а момент

инерции в соответствии с (4.15): Полный момент

инерции сплошного цилиндра получается интегрированием(суммированием) моментов инерции полых цилиндров:

. С учетом того, что масса сплошного цилиндра связана с

плотностью формулой т = 7iR 2 hp имеем окончательно момент инерции сплошного цилиндра:

Аналогично ищется момент инерции тонкого стержня длины L и массы т, если ось вращения перпендикулярна стержню и проходит через его середину. Разобьем такой стержень в соответствии с рис. 4.6

на кусочки толщиной dl. Масса такого кусочка равна dm=m dl/L, а момент инерции в соответствии с Пол

ный момент инерции тонкого стержня получается интегрированием (суммированием) моментов инерции кусочков:

Взятие элементарного интеграла дает момент инерции тонкого стержня длины L и массы т:

Несколько сложней берется интеграл при поиске момента инерции однородного шара радиуса R и массы т относительно оси симметрии. Пусть сплошной шар имеет плотность р. Разобьем его в соответствии с рис. 4.7 на полые тонкие цилиндры толщиной dr, ось симметрии которых совпадает с осью вращения шара. Объем такого полого цилиндра радиуса г равен площади поверхности, умноженной на толщину, , где высота цилиндра h

найдена с использованием теоремы Пифагора: Тогда несложно найти массу полого цилиндра , а также

момент инерции в соответствии с (4.15):

Полный момент инерции сплошного шара получается интегрированием (суммированием) моментов инерции полых цилиндров:

С учетомтого, что масса сплошного шара связана с плотностью формулой , имеем окончательно момент инерции относительно оси симметрии однородного шара радиуса R массы т:

Работа и мощность при вращательном движении

Работа. Вращательное движение обеспечивается приложенным к телу вращательным моментом относительно оси, который создаётся парой сил РР (рис. 38) и определяется по формуле

Рис. 38 Вращательный момент

При повороте тела на угол ср, работа А совершается силой Р, перемещённой из точки С в точку Ci. Полное перемещение точки приложения силы S равно длине дуги радиусом R_y то есть

Поскольку сила Р всегда направлена по касательной к перемещению 5, то совершаемая работа будет

Сила Р приложенная в неподвижной точке О работы не совершает.

Учитывая, что , окончательно находим:

Работа постоянной силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угол поворота.

Мощность. Если работа совершается силой, приложенной к вращающемуся телу, и притом равномерно, то мощность в этом случае определяют по формуле

Таким образом, мощность силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угловую скорость.

Подставив в выражение мощности значение угловой скорости, получим

Если крутящий момент выражается в Н м, а частота вращения в оборотах в минуту, то мощность выражается в ваттах (Вт).

Вращательное движение тела в физике – виды, формулы и определения с примерами

Содержание:

Вращательное движение тела:

До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18).

Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.

Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.

Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги

где — скорость движения тела по окружности; — пройденный телом путь (длина дуги); — время движения тела.

Направление скорости проще всего определить на опыте.

Опыт:

К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).

Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.

Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22).

Опыт:

Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.

Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.

Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.

Период обращения – это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.

Обозначается период обращения большой латинской буквой Т.

Если за время материальная точка при равномерном движении по окружности совершает N оборотов, то период обращения определяется формулой:

Единицей периода обращения в СИ является одна секунда (1 с).

Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.

Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности

Обозначается частота обращения малой латинской буквой .

* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой (ню).

Если за время материальная точка совершила N оборотов, то, чтобы определить частоту обращения , нужно N поделить на , т. е.:
а так как = ТN , то .
Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.

Единицей частоты обращения в СИ является единица, разделённая на секунду . это частота обращения, при котором за 1 с материальная точка совершает 1 полный оборот, двигаясь равномерно по окружности. В технике такую единицу иногда называют одним оборотом в секунду , часто применяют также единицу один оборот в минуту .

Движение точки по окружности

Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.

Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.

Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время переходит из точки А в точку В. При этом отрезок OA поворачивается на угол – угловое перемещение точки. Такое движение можно характеризовать угловой скоростью:

где (греческая буква «омега») – угловая скорость; (греческая буква «фи») – угловое перемещение.

Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки – длина дуги окружности АВ – равна длине радиуса R.

Единицей угловой скорости является радиан в секунду (рад/с).

1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.

При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).

Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.

Период вращения (Т) – это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:

где t — время вращения, N — количество выполненных оборотов.

Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):

где N — количество совершенных оборотов за время t .

Частота вращения измеряется в оборотах за секунду (об/с).

Частота вращения определяет количество оборотов точки (тела) вокруг центра (оси вращения) за 1 с.

Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой («пи»).

Таким образом, длина окружности

За один оборот материальная точка осуществляет угловое перемещение 2 рад.

Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь то линейная скорость равномерного движения точки по окружности или

Вращение твердого тела

Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.

Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.

В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?

Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.

Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния – чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение всех точек одинаково. Следовательно, и угловая скорость для всех точек данного тела также будет одинаковой.

Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т – время одного полного вращения; вращательная частота (частота вращения) — количество полных вращений за единицу времени; угловая скорость со. Кроме основной единицы частоты вращения об/с, используют об/мин, об/ч и т. п.

Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.

Динамика вращательного движения

При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.

Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:

По третьему закону Ньютона:

и при вращении появляется также центробежная сила.
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.

На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом . В точке 1, из-за того что центробежная сила направлена противоположно силе тяжести , вес тела уменьшается:

В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:

Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения.
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.

Пример

При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки . Скорость тела в точке равна 30 м/с.
Дано:

Чтобы тело не упало из точки должно выполняться следующее условие:

Ответ: 90 м.

Кинематика вращательного движения

При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.

Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.

Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.

Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота (рис. 25)

радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:

По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению

Скорость с которой материальная точка движется по окружности, называется линейной скоростью (рис. 26).

Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения

Модуль угловой скорости — это отношение угла поворота к промежутку времени за который этот поворот произошел:

Угловая скорость со является величиной векторной. Она направлена вдоль оси вращения материальной точки, и ее направление определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения конца буравчика, рукоятка которого вращается в том же направлении, что и тело (рис. 27).

Единица угловой скорости в СИ — радиан в секунду

При движении по окружности с постоянной по модулю скоростью v угловая скорость является величиной постоянной и ее модуль равен отношению угла поворота к промежутку времени за который этот поворот произошел:

Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:

Единица частоты вращения в СИ — секунда в минус первой степени Время совершения одного оборота называется периодом вращения Т.

В СИ период измеряется в секундах (1с).

При совершении полного оборота период определяется по формуле

Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле

Проекции скорости (см. рис. 25) с течением времени изменяются по закону

Модуль угловой скорости определяется соотношением

Следовательно, соотношение между модулями линейной и угловой скорости имеет вид

Поскольку (докажите самостоятельно), где — угол поворота радиус-вектора в момент начала движения, то кинематический закон движения МТ но окружности имеет вид

При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным или нормальным Ускорение направлено по радиусу к центру окружности и характеризует быстроту изменения направления скорости с течением (см. рис. 26). Его модуль определяется формулой

Нормальное ускорение в любой момент времени перпендикулярно скорости

Как и при прямолинейном равноускоренном движении, ускорение называемое тангенциальным (касательным), совпадает с направлением скорости или направлено противоположно ей и поэтому изменяет только модуль скорости. Следовательно, при движении по окружности с непостоянной по модулю скоростью (например, математический маятник) или при любом криволинейном движении полное ускорение можно представить в виде векторной суммы нормального ускорения и тангенциального ускорения направленного по касательной к окружности в данной точке (рис. 28):

Полное ускорение всегда направлено в сторону вогнутости траектории (см. рис. 28).

Модуль полного ускорения находится по теореме Пифагора:

где – нормальное ускорение, с которым точка двигалась бы по дуге
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Равномерное движение материальной точки по окружности
• Колебательное движение
• Физический и математический маятники
• Пружинные и математические маятники
• Поступательное движение
• Равномерное и неравномерное движение
• Равномерное движение
• Неравномерное движение

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

[spoiler title=”источники:”]

http://studme.org/187786/tehnika/rabota_moschnost_vraschatelnom_dvizhenii

http://www.evkova.org/vraschatelnoe-dvizhenie-tela-v-fizike

[/spoiler]