В этой заметке рассмотрим как можно вычислить работу идеального газа при различных изо-процессах. Это будет полезно тем, кто только начинает изучать термодинамику и МКТ. Для простоты изображения всех процессов возьмем самые популярные P-V диаграммы.
Есть такое понятие как термодинамический процесс. Изменение любого параметра термодинамической системы (к параметрам можно отнести температуру T, давление p, объем V, энтропию S). Но так как все параметры термодинамической системы взаимосвязаны, то частенько, когда изменяется один параметр, то и изменяются другие параметры.
Если термодинамические процессы не протекают, то система находится в равновесном состоянии. То есть равновесное состояние — такое абстрактное состояние системы, при котором все термодинамические параметры системы остаются сколь угодно долго неизменными, если над системой не совершают никаких внешних воздействий. То есть система предоставлена сама себе. Почему же это состояние абстрактно? Потому что в реальной жизни очень тяжело изолировать систему от внешнего влияния окружающего мира. Таким образом, в каждый момент времени протекают какие-то термодинамические процессы.
Однако, процессы могут протекать настолько медленно, что система изменяется почти незаметно. Иногда это дает возможность рассматривать состояние системы из последовательных равновесных состояний. Такие процессы еще называются квазистатическими. Под квазистатичностью можно понимать что-то ооочень медленное, настолько медленной, что оно длится намного дольше, чем время релаксации (время, за которое амплитудное значение внешнего возмущения, которое начало менять систему, уменьшилось в e раз).
Еще система может постоянно возвращаться к исходному состоянию. Такой круговой процесс называется циклом (примерно по таким процессам работают тепловые машины и ДВС).
Что нужно чтобы изучить какую-либо термодинамическую систему?
1. Определить работу, совершаемую в данном процессе
2. Определить изменение внутренней энергии системы
3. Определить количество теплоты, которое вошло в систему или которое отдала система.
4. Установить связи между отдельными величинами, которые характеризуют состояние рабочего тела (газа)
Основные термодинамические процессы: изохорный, изобарный, изотермический, адиабатный и политропный.
И далее мы с вами выведем работы в этих основных процессах.
1. Изохорный процесс
Изохорным процесс — термодинамический процесс, который протекает при постоянном объеме. Такой процесс может совершаться при нагревании газа, помещенного в закрытый сосуд. Газ в результате подвода теплоты нагревается, и его давление возрастает.
2. Изотермический процесс
Изотермический процесс — термодинамический процесс, который протекает при постоянной температуре. На практике очень сложно осуществить этот процесс. Потому что при сжатии или расширении газа, нужны условия, при которых газ будет успевать обмениваться температурой с внешней средой, чтобы поддерживать свою температуру неизменной.
3. Изобарный процесс
Изобарный процесс — термодинамический процесс, который протекает при постоянном давлении. Помещение газа в плотный цилиндр с подвижным поршнем, на который действует постоянная сила ( например сила тяжести со стороны груза ) при отводе и подводе теплоты, может смоделировать такой процесс.
4. Адиабатный процесс
Адиабатный процесс — термодинамический процесс, который протекает без теплообмена (Q = 0) рабочего тела (газа) с окружающей средой. Также сложно осуществимый процесс. Примерная модель: газ помещают в цилиндр с подвижным поршнем. При этом цилиндр и поршень выполнены из высококачественного теплоизолирующего материала.
5. Политропный процесс (p∙Vⁿ = const )
Этот процесс является обобщением всех предыдущих. Все параметры в этом процессе могут меняться. А процессы выше являются его частными случаями. n – показатель политропы, некоторая постоянная, которая может принимать любые значения от -∞ до +∞.
n = 0 – изобарный процесс p = const
n = 0 – изотермический процесс T = const
n = γ – адиабатный процесс p∙Vⁿ = const
n = +∞ или n = -∞ – изохорный процесс V = const
Любые формулы для этого процесса аналогичны адиабатному процессу. При этом работа выводится точно также. Только коэффициент адиабаты (γ) в общем случае заменяется на коэффициент политропы (n).
Понравился разбор задачи ? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
№20456
Экзамены с этой задачей:
Предмет и тема: Физика, Молекулярная физика и термодинамика, Термодинамика, Цикл Карно,
Задача в следующих классах: 10 класс 11 класс
Сложность задачи : 2
Задача встречается в следующей книге: Турчина Н. В. и др. Физика: 3800 задач для школьников и поступающих в вузы //М.: Дрофа. – 2000. – Т. 3.
Условие
Найти работу на участке изотермического расширения рабочего тела теплового двигателя, работающего по циклу Карно, если коэффициент полезного действия равен (eta =80) %, а количество теплоты, отдаваемое за цикл холодильнику, (Q=2) Дж. Ответ дать в Дж и округлить до целых.
Ответ
5
Решение № 20447:
(A_{12}=Q_{1}=frac{Q_{2}}{1-eta })
Изменение
объема газа, т.е. его расширение или
сжатие, можно произвести так, чтобы
температура газа оставалась постоянной.
Такой процесс изменения состояния газа
или другой системы, который проходит
при постоянной температуре, называется
изотермическим. Для того чтобы процесс
в системе мог протекать изотермически,
она должна быть помещена в среду с
постоянной температурой, к примеру, в
термостат — аппарат, в котором специальное
устройство — терморегулятор —
автоматически поддерживает температуру
постоянной. Расширяясь в термостате,
т.е. при T=const,
система производит некоторую работу,
которая по первому началу термодинамики
равна:
|
(109) |
![]()
где
![]()
― количество теплоты, поглощенной
системой от термостата, а
![]()
― изменение ее внутренней энергии.
В
случае идеального газа внутренняя
энергия зависит только от температуры
и не зависит от занимаемого им объема.
Поэтому при изотермическом расширении
или сжатии идеального газа его внутренняя
энергия остается неизменной при
![]()
и
![]()
.
Первое начало термодинамики (109) в этом
случае принимает вид:
|
(110) |
![]()
|
(111) |
A=Q
Это
равенство показывает, что при изотермическом
расширении объема идеального газа
работа
![]()
может производится только за счет
поглощаемого им тепла
.
Если газ изотермически расширяется
(![]()
),
то он совершает положительную работу
(![]()
)
и согласно равенству (110) получает извне
(от среды термостата) такое же количество
тепла (![]()
).
Если же внешние силы совершают над газом
работу при его изотермическом сжатии
(![]()
,![]()
),
то он отдает такое же количество тепла
(![]()
).
Таким образом, в случае изотермического
расширения газ полностью преобразует
подводимое к нему тепло в совершаемую
работу. Наоборот, при изотермическом
сжатии работа, затраченная на сжатие,
полностью преобразуется в отдаваемое
газом внешней среде (среде термостата)
тепло. Именно по этой причине внутренняя
энергия и температура газа остаются
неизменными. Газ при изотермическом
процессе ведет себя как тело с бесконечно
большой теплоемкостью. Математически
это следует из общего определения
теплоемкости; обозначив изотермическую
теплоемкость через СТ,
получаем
![]()
,
т. к.
![]()
,
![]()
Из
сказанного выше ясно, что для того, чтобы
расширение газа могло происходить
изотермически, ему необходимо непрерывно
передавать тепло извне. Наоборот, чтобы
сжатие газа протекало изотермически,
от него необходимо непрерывно отбирать
тепло. Изотермический процесс,
следовательно, возможен лишь при идеально
хорошем обмене теплом между газом и
внешней средой (средой термостата).
Практически приблизиться к изотермическому
процессу можно, заставляя протекать
его настолько медленно, чтобы температура
газа все время успевала выравниваться
с температурой окружающей среды.
Вычислим
работу, совершаемую идеальным газом
при изотермическом изменении его объема
от V1
до V2.
Работа, производимая любой системой
при изменении ее объема, как мы видели,
определяется интегралом
|
(112) |
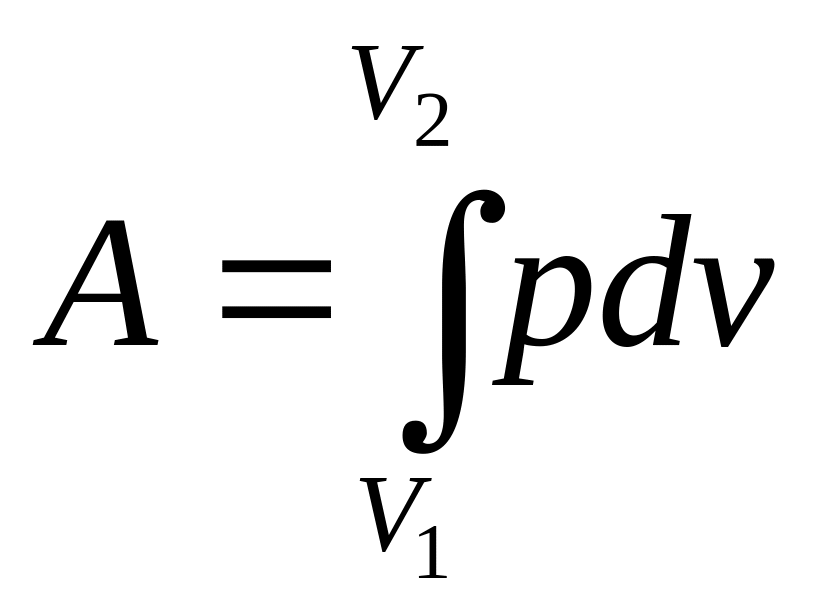
Чтобы
произвести интегрирование, нужно знать,
как при рассматриваемом процессе
давление p
связано с объемом V,
т.е. необходимо знать уравнение процесса
в переменных p,
V.
Уравнение изотермического процесса
для идеального газа получается
непосредственно из его уравнения
состояния
|
(113) |
![]()
Так
как при изотермическом процессе T=const,
то для данной массы газа
![]()
и, следовательно,
|
(114) |
![]()
![]()
где
p1
и V1
― значения давления и объема газа в
начальном состоянии. Таким образом, при
изотермическом процессе давление и
объем идеального газа связаны между
собой законом Бойля-Мариотта. Выражая
из (114) давление газа через объем и
значение параметров в начальном состоянии
|
(115) |
![]()
и
подставляя полученное выражение в
(112), находим
|
(116) |
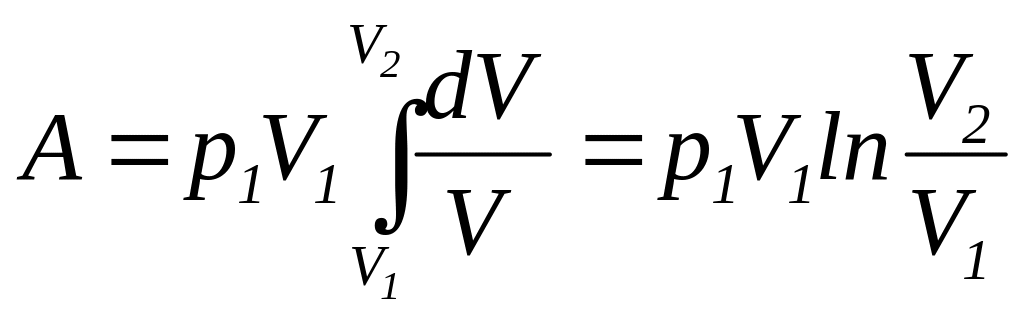
Так
как
![]()
,
то формулу для работы идеального газа
при изотермическом изменении его объема
можно представить в виде
|
(117) |
![]()
Из
(116) и (117) видно, что работа идеального
газа при изотермическом процессе
изменения объема зависит не от разности
объемов как для изобарического процесса,
между которыми происходит расширение
или сжатие, а от их отношения (т. е. степени
расширения или сжатия газа).
Так
как при изотермическом процессе работа
A
производится идеальным газом за счет
передаваемого ему извне тепла, то
полученные выше формулы могут в равной
мере служить как для определения
совершаемой газом изотермической
работы, так и для расчета количества
теплоты Q,
необходимой для его изотермического
расширения или сжатия
|
(118) |
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как определить работу при изотермическом процессе
При изотермическом процессе, который протекает при постоянной температуре, газ выполняет работу за счет расширения. Расширение газа характеризуется его объемом, который изменяется в зависимости от изменения давления газа, обусловленного внешними воздействиями.
Вам понадобится
- – герметичный сосуд с поршнем;
- – весы;
- – термометр;
- – линейка.
Инструкция
Рассчитайте работу газа при постоянной температуре. Для этого определите, какой газ выполняет работу, и рассчитайте его молярную массу. С помощью периодической таблицы найдите молекулярную массу, которая численно равна молярной массе, измеренной в г/моль.
Найдите массу газа. Для этого откачайте воздух из герметичного сосуда и взвесьте его на весах. После этого закачайте газ, работа которого определяется, и снова взвесьте сосуд. Разность масс пустого и заполненного сосудов и будет равна массе газа. Измеряйте ее в граммах.
Измерьте при помощи термометра температуру газа. При изотермическом процессе она будет постоянна. Если измерение производится при комнатной температуре, достаточно измерить температуру окружающего воздуха. Измерения произведите в Кельвинах. Для этого к температуре, измеренной в градусах Цельсия, прибавьте число 273.
Определите начальный и конечный объем газа при выполнении работы. Для этого сосуд берите с подвижным поршнем, и, вычисляя уровень его подъема, рассчитайте первичный и вторичный объем геометрическими методами. Для этого используйте формулу для объема цилиндра V=π•R²•h, где π≈3,14, R – радиус цилиндра, h его высота.
Рассчитайте работу газа при изотермическом процессе. Для этого поделите массу газа m на его молярную массу M. Полеченный результат умножьте на универсальную газовую постоянную R=8,31 и значение температуры Т в Кельвинах. Полученный результат умножьте на натуральный логарифм из отношения конечного и начального объемов V2 и V1, A = m/M•R•T•ln(V2/V1).
В том случае, когда известно количество теплоты Q, которое получило тело при изотермическом процессе, используйте второе начало термодинамики Q = ∆U + A. Где A – работа газа, а ΔU – изменение его внутренней энергии. Поскольку изменение внутренней энергии зависит от температуры, а при изотермическом процессе она остается постоянной, то ΔU=0. В этом случае работа газа равна теплоте, переданной ему Q = A.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Блог об энергетике
энергетика простыми словами
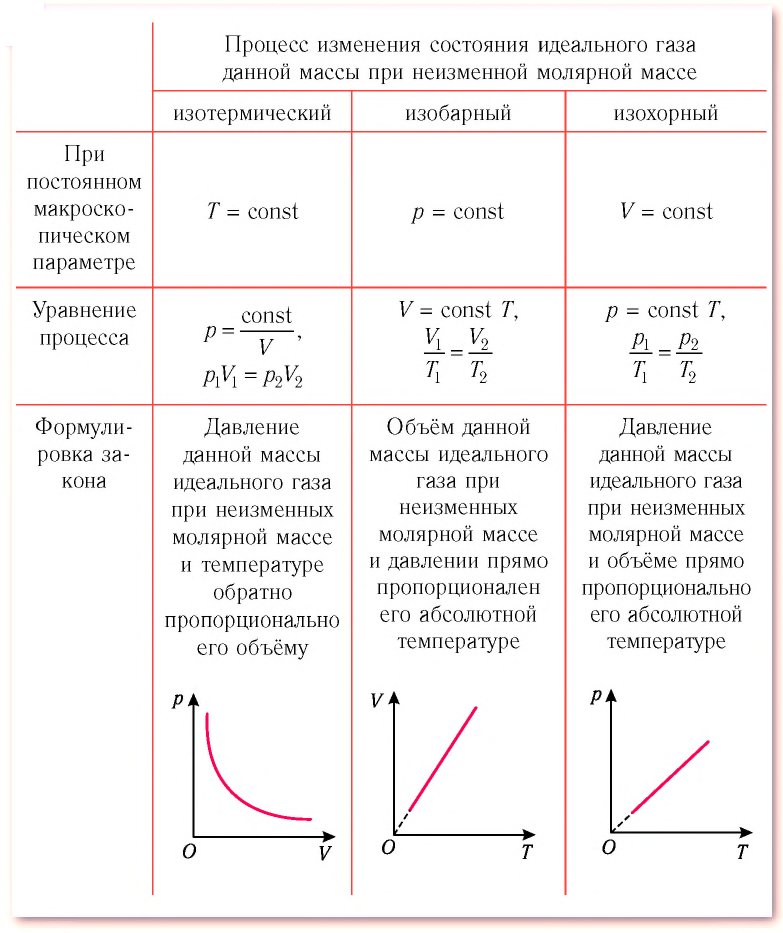
Основные термодинамические процессы
Основными процессами в термодинамике являются:
- изохорный, протекающий при постоянном объеме;
- изобарный, протекающий при постоянном давлении;
- изотермический, происходящий при постоянной температуре;
- адиабатный, при котором теплообмен с окружающей средой отсутствует;
- политропный, удовлетворяющий уравнению pv n = const.
Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.
При исследовании термодинамических процессов определяют:
- уравнение процесса в p—v иT—s координатах;
- связь между параметрами состояния газа;
- изменение внутренней энергии;
- величину внешней работы;
- количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.
Изохорный процесс



При изохорном процессе выполняется условие v = const.
Из уравнения состояния идеального газа (pv = RT) следует:
т. е. давление газа прямо пропорционально его абсолютной температуре:
Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).
Количество теплоты, подведенной к рабочему телу в процессе 1-2 при cv = const определяется по формуле:
Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:
Изменение энтропии в изохорном процессе определяется по формуле:
Изобарный процесс



Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:
т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.
Работа будет равна:
Количество теплоты при cp = const определяется по формуле:
Изменение энтропии будет равно:
Изотермический процесс



При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:
т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.
Работа процесса будет равна:
Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:
При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.
Изменение энтропии равно:
Адиабатный процесс



Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:
В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.
Обозначим теплоемкость в адиабатном процессе через cад, и условие dq = 0 выразим следующим образом:
Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (cад = 0).
и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:
В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).
kвыхлопных газов ДВС = 1,33
Из предыдущих формул следует:
Техническая работа адиабатного процесса (lтехн) равна разности энтальпий начала и конца процесса (i1 – i2).
Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.
Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.
Политропный процесс
Политропным называется процесс, который описывается уравнением:
Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.
Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:
Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

представляет собой теплоемкость идеального газа в политропном процессе.
При cv, k и n = const cn = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.
Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.
Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv 0 = const (n = 0) – изобара;
pv = const (n = 1) – изотерма;
p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;
n > 0 – гиперболические кривые,
n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.
Изопроцессы в физике – формулы и определение с примерами
Содержание:
Изотермический, изобарный и изохорный процессы:
Свойство газов существенно изменять предоставленный им объём широко используют в тепловых двигателях. Анализируя процессы, происходящие с газом в этих устройствах, важно знать, каким законам подчиняются газы и каковы условия применимости этих законов.
Процессы в газах часто происходят так, что изменяются только два параметра из пяти 
Изотермический процесс
Процесс изменения состояния физической системы при постоянной температуре 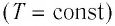 называют изотермическим.
называют изотермическим.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то из уравнения Клапейрона—Менделеева следует: 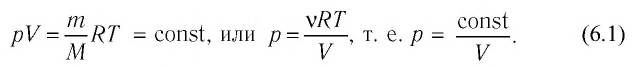
Давление данной массы газа при постоянных молярной массе и температуре обратно пропорционально его объёму.
Это утверждение называют законом Бойля—Мариотта.
Справедливость закона Бойля—Мариотта можно продемонстрировать экспериментально, используя установку, представленную на рисунке 18 в § 5.
Если медленно изменять объём газа, находящегося в сосуде, то вследствие теплообмена с окружающей средой можно поддерживать температуру газа в сосуде практически постоянной. При этом уменьшение объёма газа при вращении винта 3 повлечёт за собой увеличение его давления и некоторое незначительное увеличение температуры. И наоборот, увеличение объёма приведёт к уменьшению давления и некоторому незначительному уменьшению температуры газа*.
* Незначительное изменение температуры газа принципиально необходимо для теплообмена с термостатом — передача тепла возможна только при разных температурах тел.
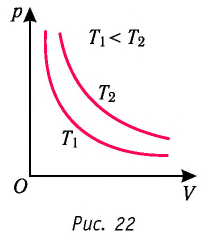
График изотермического процесса, совершаемого идеальным газом, в координатах  представляет собой гиперболу (рис. 22). В физике такую кривую называют изотермой. Разным значениям температуры газа соответствуют разные изотермы. Согласно соотношениям (6.1) для одинаковых объёмов газов с одинаковыми количествами вещества и разными температурами чем больше давление, тем выше температура (рис. 22).
представляет собой гиперболу (рис. 22). В физике такую кривую называют изотермой. Разным значениям температуры газа соответствуют разные изотермы. Согласно соотношениям (6.1) для одинаковых объёмов газов с одинаковыми количествами вещества и разными температурами чем больше давление, тем выше температура (рис. 22).
Многочисленные опыты показали, что исследованные газы подчиняются закону Бойля —Мариотта тем точнее, чем меньше их плотность. При значительном увеличении давления газа этот закон перестаёт выполняться.
Интересно знать:
Лёгкие расположены в грудной клетке, объём которой при дыхании периодически изменяется благодаря работе межрёберных мышц и диафрагмы. Когда грудная клетка расширяется, давление воздуха в лёгких становится меньше атмосферного, и воздух через воздухоносные пути устремляется в лёгкие — происходит вдох. При выдохе объём грудной клетки уменьшается, что вызывает уменьшение объёма лёгких. Давление воздуха в них становится выше атмосферного, и воздух из лёгких устремляется в окружающую среду.
Изобарный процесс
Процесс изменения состояния газа при постоянном давлении (р = const) называют изобарным.
В 1802 г. французский учёный Жозеф Гей-Люссак (1778-1850) рассмотрел этот процесс для воздуха, водорода, кислорода и азота.
Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются, то объём газа, как следует из уравнения Клапейрона—Менделеева:
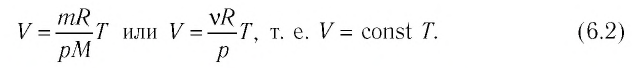
Объём данной массы газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре.
Это утверждение называют законом Гей-Люссака.
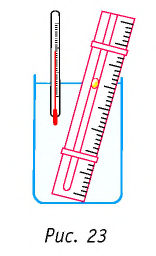
Справедливость закона Гей-Люссака можно продемонстрировать экспериментально, используя установку, представленную на рисунке 23. Жидкость в сосуде находится в тепловом равновесии с тонкой трубкой, заполненной воздухом, запертым капелькой масла. При увеличении температуры жидкости объём воздуха, находящегося в трубке под капелькой масла, возрастает и капелька движется вверх. При уменьшении температуры объём воздуха уменьшается — и капелька движется вниз.
Поскольку 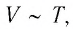 то в координатах
то в координатах 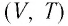 график изобарного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 24). Эту линию называют изобарой.
график изобарного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 24). Эту линию называют изобарой.
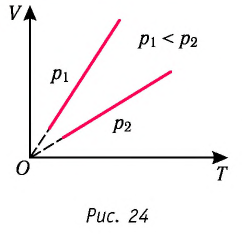
Изобара реальных газов не может быть продлена до нулевого значения температуры (на графике пунктирная линия), потому что при низких температурах все газы существенно отличаются от модели «идеальный газ» и при дальнейшем уменьшении температуры превращаются в жидкости.
В одних и тех же координатах  можно построить несколько изобар, которые соответствуют разным давлениям данной массы идеального газа при неизменной молярной массе. Анализ соотношений (6.2) позволяет сделать вывод, что большему давлению соответствует меньший наклон изобары к оси температур (см. рис. 24).
можно построить несколько изобар, которые соответствуют разным давлениям данной массы идеального газа при неизменной молярной массе. Анализ соотношений (6.2) позволяет сделать вывод, что большему давлению соответствует меньший наклон изобары к оси температур (см. рис. 24).
Изохорный процесс
Процесс изменения состояния газа при постоянном объёме (V = const) называют изохорным.
Впервые этот процесс рассмотрел в 1787 г. французский учёный Жак Шарль (1746-1823)*.
* Несмотря на то что Шарль не опубликовал результаты своих исследований, история физики отдаёт приоритет открытия ему.
Если при переходе из начального состояния в конечное масса и молярная масса идеального газа не изменяются, то давление газа, как следует из уравнения Клапейрона—Менделеева:
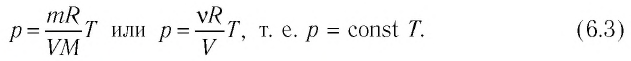
Давление данной массы газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре.
Это утверждение называют законом Шарля.
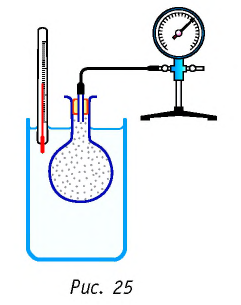
Справедливость закона Шарля можно продемонстрировать экспериментально, используя установку, представленную на рисунке 25. Колба, наполненная воздухом и соединённая с манометром, находится в тепловом равновесии с жидкостью в сосуде. При увеличении температуры жидкости давление воздуха в колбе возрастает, а при уменьшении температуры — давление воздуха уменьшается.
В координатах 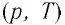 график изохорного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 26). Эту линию называют изохорой.
график изохорного процесса, совершаемого идеальным газом, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 26). Эту линию называют изохорой.
Как и в случае изобарного процесса, изохора реальных газов не может быть продлена до нулевого значения температуры.
В одних и тех же координатах  можно построить несколько изохор, соответствующих разным объёмам данной массы газа при неизменной моляр- О ной массе. Анализ соотношений (6.3) показывает, что большему объёму соответствует меньший наклон изохоры к оси температур (см. рис. 26).
можно построить несколько изохор, соответствующих разным объёмам данной массы газа при неизменной моляр- О ной массе. Анализ соотношений (6.3) показывает, что большему объёму соответствует меньший наклон изохоры к оси температур (см. рис. 26).
На рисунке 28 представлен график трёх процессов изменения состояния некоторой массы идеального газа. Как изменялись параметры газа на участках 
 Изобразите эти процессы в координатах
Изобразите эти процессы в координатах 
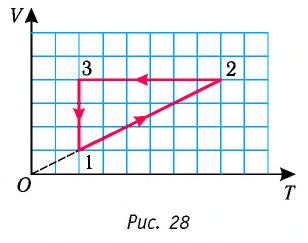
Решение. На участке 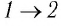 объём газа прямо пропорционален абсолютной температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика следует, что в состоянии 2 температура и объём газа больше в 4 раза, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом:
объём газа прямо пропорционален абсолютной температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика следует, что в состоянии 2 температура и объём газа больше в 4 раза, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом:
переход 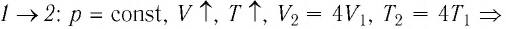
происходит изобарное нагревание газа.
В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается в 4 раза. Из соотношения (6.3) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его абсолютной температуре. Поэтому можно записать:
переход 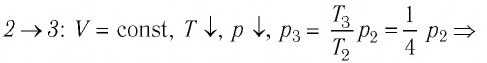
происходит изохорное охлаждение газа.
Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается в 4 раза, что влечёт за собой, согласно закону Бойля—Мариотта, увеличение давления газа в 4 раза:
- переход
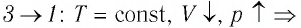 происходит изотермическое сжатие газа.
происходит изотермическое сжатие газа.
Опираясь на сделанные выводы, представим все три процесса в координатах 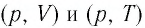 (рис. 29, а, б).
(рис. 29, а, б). 
При изотермическом расширении идеального газа определённой массы его объём увеличился от 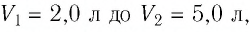 а давление уменьшилось на
а давление уменьшилось на 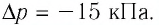 Определите первоначальное давление газа.
Определите первоначальное давление газа.
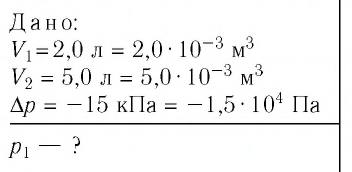
Решение. Так как температура и масса газа не изменяются, то его начальное и конечное состояния связаны законом Бойля—Мариотта, т. е. 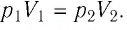 С учётом того, что
С учётом того, что 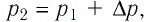 получим:
получим:
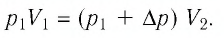
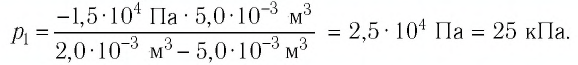
Ответ: 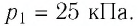
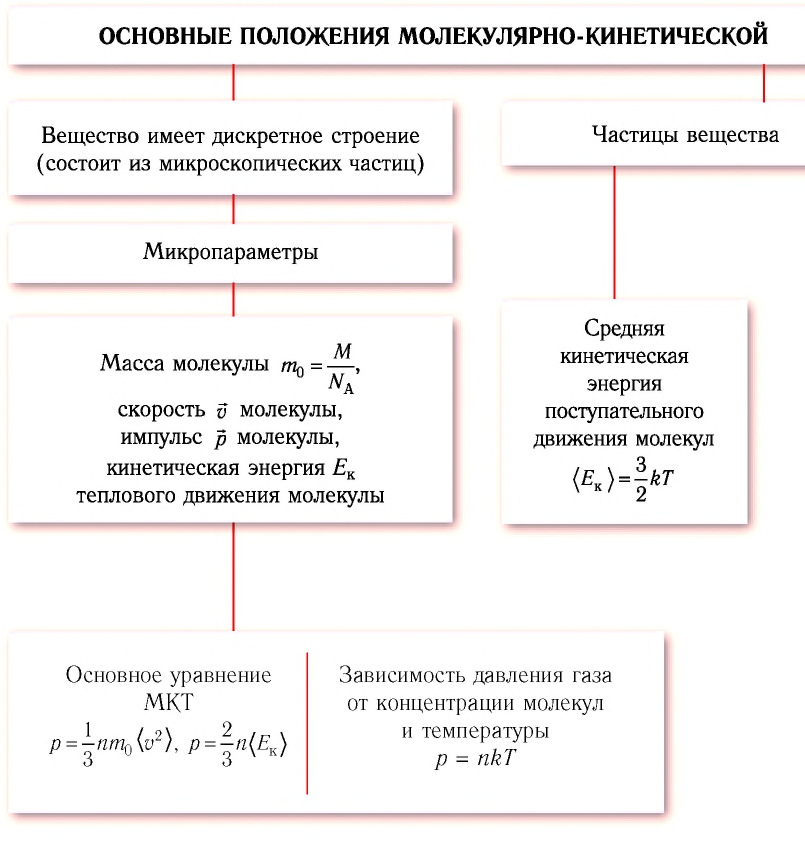
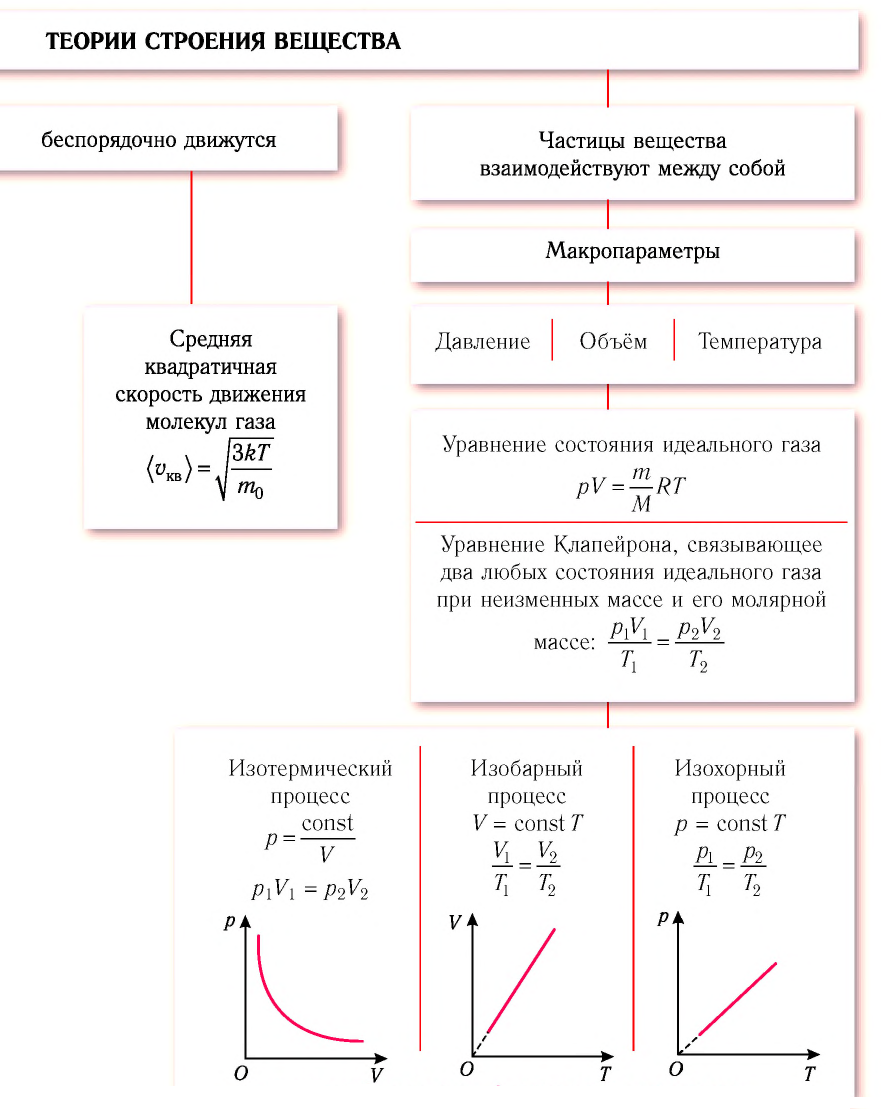
Обобщение и систематизация определений:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Твердые тела и их свойства в физике
- Строение и свойства жидкостей в физике
- Испарение и конденсация в физике
- Влажность воздуха в физике
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Изотермический процесс | Это все важные факты с 13 часто задаваемыми вопросами
Content
- Изотермическое определение
- Изотермическое расширение
- Изотермическое сжатие
- Изотермический против адиабатического
- Изотермическая калориметрия
- Изотермическое усиление
- Изотермическая амплификация нуклеиновых кислот
- Диаграмма изотермического превращения
- Изотермическая фотоэлектрическая диаграмма
- Пример изотермического процесса
- Изотермические работы
- Изотермический слой
- Изотермическая ПЦР
- Уравнение изотермического процесса
- Изотермическое расширение идеального газа
- Изотермическое обратимое расширение
- Изотермическая реакция
- Изотермическое необратимое расширение
- Изотермическая система
- Изотермический объемный модуль
- Изотермическая внутренняя энергия
- Коэффициент изотермической сжимаемости
- Изотермический теплообмен
- Изотермическая атмосфера
- Изотермическая поверхность
- Изотермические условия
- Изотермическая зона
- Изотермические линии
- Изотермический пояс
- Изотермический против изобарического
- Изотермический или изоэнтропический
Изотермическое определение
Изотермический процесс – это термодинамический процесс. В этом изотермическом процессе температура системы остается постоянной на протяжении всего процесса. Если рассматривать температуру как T. Изменение температуры составляет ΔT.
Для изотермического процесса можно сказать, что ΔT = 0
Изотермическое расширение
Изотермическое расширение – это увеличение объема при постоянной температуре системы.
Изотермический – температурная постоянная
Расширение – Увеличение громкости
Давайте рассмотрим устройство поршень-цилиндр, чтобы понять, движется ли поршень из НМТ (нижней мертвой точки) в ВМТ (верхней мертвой точки) с постоянной температурой газа. Этот изотермический процесс считается изотермическим расширением.
Изотермическое сжатие
Изотермическое сжатие – это уменьшение объема при постоянной температуре системы.
Изотермический – температурная постоянная
Сжатие – уменьшение громкости
Рассмотрим еще одно условие, если поршень движется из ВМТ в НМТ (нижнюю мертвую точку) с постоянной температурой газа. Этот изотермический процесс считается изотермическим сжатием.
Изотермический против адиабатического
Изотермический означает постоянную температуру.
Адиабатика означает постоянную тепловую энергию.
Некоторые условия изотермического процесса:
- Температура должна оставаться постоянной.
- Изменение должно происходить медленно.
- Удельная теплоемкость газа бесконечна.
Ниже приведены некоторые основные условия адиабатики:
- В адиабатическом режиме теплообмен не происходит.
- Изменение должно происходить очень быстро.
- Удельная теплоемкость газа равна 0 (ноль).
Изотермическая калориметрия
Это один из методов определения взаимодействия термодинамических параметров в химическом растворе. Используя изотермическую калориметрию, можно определить сродство связывания, стехиометрию связывания и изменения энтальпии между двумя или более взаимодействиями молекул.
Изотермическое усиление
Это один из методов, используемых для мониторинга патогенов. В этих методах ДНК амплифицируется с сохранением более высокой чувствительности, чем эталонная полимеразная цепная реакция (ПЦР).
Изотермическая амплификация нуклеиновых кислот
Изотермическая амплификация нуклеиновых кислот – это метод, который позволяет эффективно и быстрее накапливать нуклеиновую кислоту в изотермическом процессе. Это простой и эффективный процесс. С тех пор, примерно в 1990 году, многие процессы изотермической амплификации были разработаны в качестве альтернативы полимеразной цепной реакции (ПЦР).
Диаграмма изотермического превращения
Диаграмма изотермического превращения используется для понимания кинетики стали. Она также известна как диаграмма преобразования время-температура.
Это связано с механическими свойствами, микрокомпонентами / микроструктурами и термообработкой углеродистых сталей.
Изотермическая фотоэлектрическая диаграмма
Пример изотермического процесса
Изотермический – это процесс, при котором температура системы остается неизменной или постоянной.
Возьмем, к примеру, холодильник и тепловой насос. Здесь в обоих случаях тепловая энергия снимается и добавляется, но температура системы остается постоянной.
Примеры: холодильник, тепловой насос.
Изотермические работы
Мы использовали фотоэлектрическую диаграмму выше. Если мы хотим написать для него формулу проделанной работы. Мы должны рассмотреть площадь под кривой AB-VA-VB. Работа, проделанная для этого интеграла, может быть представлена как,
Здесь в уравнении
n – количество молей
R – газовая постоянная
T – температура в кельвинах
Изотермический слой
Термин изотермический слой используется в науке об атмосфере. Он определяется как вертикальный слой воздуха или газа с постоянной температурой по всей высоте. Эта ситуация происходит на нижнем уровне тропосферы в различных ситуациях адвекции.
Изотермическая ПЦР
Полная форма ПЦР – это полимеразная цепная реакция. Эта реакция используется в методах изотермической амплификации для амплификации ДНК.
Уравнение изотермического процесса
Если мы рассмотрим универсальный газовый закон, то уравнение будет выглядеть следующим образом:
Теперь, здесь это изотермический процесс, поэтому T = Constant,
Вышеприведенное уравнение справедливо для замкнутой системы, содержащей идеальный газ.
Мы обсуждали проделанную ранее работу. Мы можем рассматривать это уравнение для изотермического процесса. Как мы знаем из рисунка Vb – это конечный объем, а Va – начальный объем.
Изотермическое расширение идеального газа
- изотермический – температура постоянная.
- расширение – громкость увеличивается.
Это означает, что изотермическое расширение увеличивает объем при постоянной температуре системы.
В этом состоянии газ делает Работа, поэтому работа будет отрицательной, потому что газ применяет энергию для увеличения объема.
Изменение внутренней энергии также равно нулю ΔU = 0 (идеальный газ, постоянная температура)
Изотермическое обратимое расширение
Эта тема раскрывается при объяснении изотермического расширения идеального газа.
Изотермическая реакция
Химическая реакция, протекающая при одной температуре или, можно сказать, при постоянной температуре, является изотермической реакцией. Нет необходимости в изменении температуры для продолжения реакции до ее завершения.
Изотермическое необратимое расширение
Необратимый процесс – это реальный процесс, с которым мы сталкиваемся в реальности почти все время. Систему и ее окружение невозможно вернуть в исходное состояние.
Изотермическая система
Мы обсудили изотермическую систему при расширении и сжатии, если взять конструкцию поршень-цилиндр.
Есть некоторые предположения для этой системы, например,
- Нет трения между поршнем и цилиндром
- Отсутствие потери тепла или работы в системе
- Внутренняя энергия системы должна быть постоянной на протяжении всего изотермического процесса.
Если мы подаем тепло в нижнюю часть цилиндра, то поршень переместится из НМТ в ВМТ, как показано на рисунке. Это изотермическое расширение. Точно так же при изотермическом сжатии обратное, как мы объясняли ранее. Эта полная система изотермична.
Изотермический объемный модуль
Объемный модуль упругости обратен сжимаемости.
Здесь термин представляет собой изотермический модуль объемной упругости. Его можно определить как отношение изменения давления к изменению объема при постоянной температуре. Оно равно P (давление), если мы решим вышеуказанное уравнение.
Изотермическая внутренняя энергия
Ранее мы обсуждали, что внутренняя энергия процесса при постоянной температуре остается постоянной.
Коэффициент изотермической сжимаемости
Коэффициент изотермической сжимаемости можно принять как изменение объема на единицу изменения давления. Это также известно как сжимаемость масла. Он широко используется при оценке ресурсов нефти или газа при изучении нефтяных месторождений.
Изотермический теплообмен
Процесс расширения и сжатия при постоянной температуре работает по принципу нулевой энергии разложения. Если температура постоянна, то изменение внутренней энергии и изменение энтальпии равны нулю. Итак, теплопередача такая же, как и передача работы.
Если нагреть газ в каком-либо баллоне, то температура газа повысится. Нам нужна система с постоянной температурой, поэтому мы должны установить одну раковину (источник холода), чтобы не допустить повышения температуры.
Предположим, мы рассматриваем цилиндр с поршнем. Газ будет расширяться в цилиндре, и поршень дает рабочий объем из-за нагревания. В этом случае температура также будет оставаться постоянной.
Изотермическая атмосфера
Его можно определить как отсутствие изменения температуры с высотой в атмосфере, а давление экспоненциально снижается по мере продвижения вверх. Это также известно как экспоненциальная атмосфера. Можно сказать, что атмосфера находится в гидростатическом равновесии.
В атмосфере этого типа мы можем рассчитать толщину между двумя соседними высотами с помощью уравнения, приведенного ниже:
Z1 и Z2 – две разные высоты,
P1 и P2 – давления в точках Z1 и Z2 соответственно,
R – газовая постоянная для сухого воздуха,
T – виртуальная температура в K,
g – ускорение свободного падения в м / с 2
Изотермическая поверхность
Предположим, мы рассматриваем любую поверхность плоской, круглой или кривизной и т. Д. Если все точки на этой поверхности имеют одинаковую температуру, то мы можем сказать, что поверхность изотермическая.
Изотермические условия
К слову сказать, мы знаем, что температура системы должна оставаться постоянной в этом изотермическом процессе. Чтобы поддерживать постоянную температуру, система может изменять другие параметры, такие как давление, объем и т. Д. Во время этого процесса также возможно изменение рабочей энергии и тепловой энергии, но температура остается неизменной.
Изотермическая зона
Это слово обычно используется в атмосферных науках. Это зона в атмосфере, где относительная температура постоянна на высоте нескольких километров. Обычно это нижняя часть стратосферы. Эта зона обеспечивает удобные условия для самолетов благодаря постоянной температуре, общему доступу к облакам и дождям и т. Д.
Изотермические линии
Это слово используется в географии. Предположим, мы проводим линию на карте земли, соединяющую разные места с одинаковой или близкой температурой. В общем, она известна как изотермическая линия.
Здесь каждая точка отражает конкретную температуру для считывания за определенный период времени.
Изотермический пояс
В 1858 Сайлас Макдауэлл Франклина, получившего это название от западных стран Северной Каролины, Резерфорда и Полка. Этот термин используется для обозначения сезона в этих зонах, когда можно легко выращивать фрукты, овощи и т. Д. Из-за постоянной температуры.
Изотермический против изобарического
Изотермический – температурная постоянная
Изобарический – постоянное давление
Сравним оба процесса по проделанной работе. По рисунку можно заметить оба процесса. Как известно, эта проделанная работа находится под интегралом. На рисунке мы легко можем видеть, что область изобарического процесса более очевидна, работа выполняется в большей степени в изобарической области. Для этого есть какое-то условие. Начальное давление и объем должны быть одинаковыми. Это неверно, потому что мы никогда не получаем работы во время изобарического цикла ни в одном из термодинамических циклов. Эта тема логична.
Правильный ответ зависит от типа условия, при котором объем увеличивается или уменьшается в процессе.
Изотермический или изоэнтропический
Изотермический – температурная постоянная
Isentropic – константа энтропии
Давайте рассмотрим процесс сжатия, чтобы понять это,
При изотермическом сжатии поршень очень медленно сжимает газ. Так же медленно, чтобы поддерживать постоянную температуру системы.
Тогда как в случае изоэнтропии не должно быть возможности передачи тепла между системой и окружающей средой. Изэнтропическое сжатие будет происходить без теплопередачи с постоянной энтропией.
Изэнтропический процесс аналогичен адиабатическому, когда теплообмен отсутствует. Система для изоэнтропического процесса должна быть хорошо изолирована от потерь тепла. Процесс изэнтропического сжатия всегда дает больше работы из-за отсутствия потерь тепла.
Часто задаваемые вопросы
Есть ли теплообмен в изотермическом процессе?
Ответ: Да, теперь вопрос в том, почему и как?
Давайте рассмотрим пример поршневой цилиндр, чтобы понять это,
Если тепло подводится ко дну баллона. Температура будет поддерживаться постоянной, и поршень будет двигаться. Либо процесс расширения, либо сжатия. Тепло передается, но температура системы остается прежней. Вот почему во время цикла Карно добавляется тепло при постоянной температуре.
Почему изотермический процесс идет очень медленно?
Необходимо, чтобы изотермический процесс происходил медленно. Теперь посмотрите, передача тепла возможна при поддержании постоянной температуры системы. Это означает, что существует тепловое равновесие системы с телом. Время процесса медленное, чтобы поддерживать это тепловое равновесие и постоянную температуру. Время, необходимое для эффективной теплопередачи, будет больше, что замедлит процесс.
Примеры проблем изотермического процесса
В повседневной жизни есть много применений с постоянной температурой. Некоторые из них описаны ниже:
- Температура внутри холодильника поддерживается
- Можно растопить лед, поддерживая постоянную температуру на уровне 0 ° C.
- Процесс фазового перехода происходит при постоянной температуре, испарении и конденсации.
- Тепловой насос, работающий в отличие от охлаждения
Каковы реальные примеры изотермического процесса? ?
По этому вопросу можно привести огромное количество примеров. Пожалуйста, обратитесь к приведенным выше вопросам.
Любой процесс фазового перехода, происходящий при постоянной температуре, является примером изотермического процесса.
Испарение воды из моря и реки,
Замерзание воды и таяние льда.
Почему изотермический процесс более эффективен, чем адиабатический?
Рассмотрим обратимый процесс. Если процесс является расширением, то работа изотермического процесса более чем адиабатическая. Вы можете заметить это по диаграмме. Проделанная работа – это область под кривой.
Предположим, что процесс сжатия, тогда противоположный приведенному выше предложению. В адиабатическом процессе работы больше.
Судить об этом вопросе зависит от каждого условия. Согласно вышеуказанному условию изотермический процесс более эффективен, чем адиабатический.
Какой будет удельная теплоемкость изотермического процесса адиабатического процесса и почему?
Удельную теплоемкость можно определить как количество тепла, необходимое для повышения температуры вещества на 1 градус.
Если процесс является постоянной температурой, ΔT = 0, поэтому удельная теплоемкость не определена или бесконечна.
Cp = бесконечное (если температура постоянная)
Для адиабатического процесса передача тепла невозможна, Q = 0
Cp = 0 (теплопередача равна 0)
В изотермическом процессе изменение внутренней энергии равно 0 Почему??
Внутренняя энергия – это функция кинетической энергии молекул.
Температура указывает среднюю кинетическую энергию молекул, связанных с системой.
Если температура остается постоянной, кинетическая энергия не изменяется. Следовательно, внутренняя энергия остается постоянной. Изменение внутренней энергии равно нулю.
Что более эффективно изотермическое сжатие или изоэнтропическое сжатие и почему??
Изэнтропический процесс происходит при постоянной энтропии без теплопередачи. Этот процесс всегда идеален и обратим. В процессе изоэнтропического сжатия внутренняя энергия системы увеличивается, поскольку отсутствует возможность передачи тепла между системой и окружающей средой.
При изотермическом сжатии процесс происходит очень медленно, поскольку температура и внутренняя энергия остаются постоянными. Между системой и окружающей средой происходит теплопередача.
Вот почему процесс изэнтропического сжатия более эффективен.
Есть ли у изотермического процесса изменение энтальпии?
Мы можем ясно понять это с помощью уравнения энтальпии.
Энтальпия H приведена ниже,
Изменение энтальпии = изменение внутренней энергии + изменение PV
Для процесса с постоянной температурой,
Изменение внутренней энергии = 0,
Изменение PV = 0.
Поэтому изменить энтальпию = 0
Почему адиабатическая кривая круче изотермической кривой?
В адиабатическом процессе температура системы увеличивается во время сжатия. Он уменьшается при расширении. Благодаря этому эта кривая пересекает изотермическую кривую в определенной точке на диаграмме.
В изотермическом режиме изменения температуры нет. Кривая не станет круче адиабатической.
Что произойдет, если я увеличу объем системы в изотермическом процессе с помощью внешней энергии?
Допустим, вы увеличиваете громкость системы. Вы хотите, чтобы система была изотермической. Вы должны сделать другое устройство для поддержания температуры. Увеличение объема снижает давление.
Что такого особенного в слове «обратимый» в изотермическом или адиабатическом процессе?
Первый закон термодинамики гласит, что оба процесса, изображенные на фотоэлектрической диаграмме, являются обратимыми средними. Система перейдет на начальную стадию, чтобы оставаться в равновесии.
Почему в двигателе Карно изотермический и адиабатический?
Цикл Карно является наиболее эффективным в термодинамике. Причина в том, что весь процесс в цикле обратим.
Карно пытался передавать энергию между двумя источниками при постоянной температуре (изотермической).
Он попытался максимизировать работу по расширению и минимизировать необходимое сжатие. Он выбрал для этого адиабатический процесс.
[spoiler title=”источники:”]
http://www.evkova.org/izoprotsessyi-v-fizike
http://ru.lambdageeks.com/isothermal-process/
[/spoiler]
