Как найти работу одноатомного газа за цикл

Речь в статье пойдет о КПД различных циклов, проводимых с газом. При этом давайте помнить, что внутренняя энергия изменяется тогда, когда изменяется температура, а в адиабатном процессе передачи тепла не происходит, то есть для совершения работы в таком процессе газ “изыскивает внутренние резервы”. Кроме того, работа численно равна площади под кривой процесса, а работа за цикл – площади внутри цикла.

Задача 1.

На рисунке представлена диаграмма цикла с одноатомным идеальным газом. Участки и – адиабаты.  Вычислите КПД данной тепловой машины и максимально возможный КПД .

КПД тепловой машины можно вычислить как

Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:

Работа численно равна площади, ограниченной циклом. Поэтому

Участк и по условию – адиабаты, то есть передачи тепла газу на этих участках не происходит, следовательно, работа будет совершена за счет «внутренних резервов» – то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.

Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и , и , это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать . Но, так как , а ,то изменение внутренней энергии будет равно

Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке :

Ответ: , .

Задача 2.

Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж.  В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу кДж. Найдите КПД данной тепловой машины.

Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.

Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД

Ответ: .

Задача 3.

КПД  тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе кДж. Найдите разность максимальной и минимальной  температур  газа в цикле.

Полная площадь под кривой процесса 1-2 равна кДж. При этом, так как КПД машины 25%, то площадь внутри цикла равна , а под кривой 3-1  – .  В процессе 1-2 изменения внутренней энергии не было, так как температура не менялась, а в процессе 3-1 газу не передавали тепло, следовательно, работа совершена за счет внутренней энергии. Т.е.

Ответ: 500 K.

Условие задачи:

Определите работу, совершаемую одним молем газа за цикл, если (frac{p_2}{p_1}=2), (T_1=280) К, (T_2=360) К (схема к условию приведена справа).

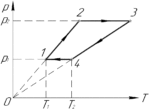
Задача №5.4.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(nu=1) моль, (frac{p_2}{p_1}=2), (T_1=280) К, (T_2=360) К, (A-?)

Решение задачи:

Приведённый в условии график для нахождения работы газа в цикле (A) перестроим в координатах p-V. Для этого нужно произвести анализ каждого из процессов.

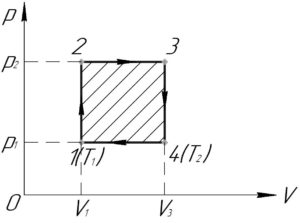
Итак, начнём. Процесс 1-2 – изохорный ((V=const)), поскольку график этого процесса в координатах p-T лежит на прямой, проходящей через начало координат. Так как температура газа в процессе увеличивается, то по закону Шарля давление растёт (хотя это итак понятно из исходного графика). Аналогично, изохорным является процесс 3-4, но так как температура газа в этом процессе уменьшается, то будет уменьшаться и давление.

Процесс 2-3 – изобарный ((p=const)). Температура газа в процессе растёт, поэтому по закону Гей-Люссака будет увеличиваться и объем. Также изобарным является процесс 4-1. Объем газа в этом процессе уменьшается, так как уменьшается температура.

С учётом всего вышесказанного получим следующий график (смотрите схему к решению).

Работа газа в цикле (A) равна площади этого цикла в координатах p-V. Если цикл обходится по часовой стрелке, то работа положительна (что имеет место в нашем случае), иначе – отрицательна. Тогда:

[A = left( {{p_2} – {p_1}} right)left( {{V_3} – {V_1}} right);;;;(1)]

Запишем закон Гей-Люссака для изобарного процесса 4-1:

[frac{{{V_3}}}{{{T_2}}} = frac{{{V_1}}}{{{T_1}}}]

[{V_3} = {V_1}frac{{{T_2}}}{{{T_1}}};;;;(2)]

Учитывая выражение (2) и то, что по условию (frac{p_2}{p_1}=2), формула (1) примет вид:

[A = left( {2{p_1} – {p_1}} right)left( {{V_1}frac{{{T_2}}}{{{T_1}}} – {V_1}} right) = {p_1}{V_1}left( {frac{{{T_2}}}{{{T_1}}} – 1} right)]

Теперь запишем уравнение Клапейрона-Менделеева для состояния газа в точке 1:

[{p_1}{V_1} = nu R{T_1}]

Тогда:

[A = nu R{T_1}left( {frac{{{T_2}}}{{{T_1}}} – 1} right)]

[A = nu Rleft( {{T_2} – {T_1}} right)]

Посчитаем ответ:

[A = 1 cdot 8,31 cdot left( {360 – 280} right) = 664,8;Дж]

Ответ: 664,8 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

5.4.33 Газообразный водород массой 1 кг при начальной температуре 300 К охлаждают
5.4.35 В сосуде объемом 2 л находится гелий при давлении 100 кПа и температуре 200 К
5.4.36 Два одинаковых сосуда, содержащих одинаковое число молекул азота, соединены

На этой странице вы узнаете

• В чем прелесть фазовых переходов?
• Что лучше выбрать: Mercedes или BMW?

Люди научились летать в космос, покорять недра Земли и погружаться в глубины океана. Эти и другие достижения возможны благодаря способности извлекать максимум пользы из имеющихся ресурсов,а именно получать тепловую энергию различными доступными способами. Сегодня мы разберем задачи, которые заставят тепловые процессы играть на нашей стороне. 

Тепловые машины и их КПД

Рекомендация: перед тем как приступить к выполнению задач неплохо было бы повторить тему «Уравнение состояния идеального газа» . Но ключевую теорию, на которой основано решение задач, сейчас разберем вместе.

Мы не почувствуем, как испарится капелька у нас на руке, потому что это не требует много тепла от нашего тела. Но мы можем наблюдать, как горят дрова в мангале, когда мы жарим шашлык, потому что выделяется огромное количество теплоты. А зачем мы вообще рассматриваем эти фазовые переходы? Все дело в том, что именно фазовые переходы являются ключевым звеном во всех процессах, где нас просят посчитать КПД, от них нашему рабочему телу и подводится теплота нагревателя.

Человечество придумало такие устройства, которые могут переработать тепловую энергию в механическую.

Тепловые двигатели, или тепловые машины, — устройства, способные преобразовывать внутреннюю энергию в механическую. 

Их устройство довольно просто: они на входе получают какую-то энергию (в основном — энергию сгорания топлива), а затем часть этой теплоты расходуется на совершение работы механизмом. Например, в автомобилях часть энергии от сгоревшего бензина идет на движение. Схематично можно изобразить так:

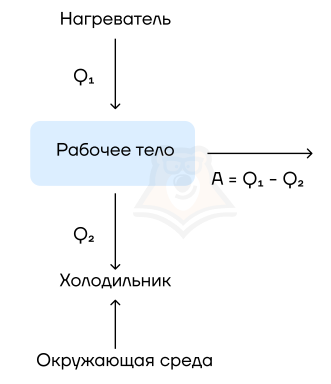
Рабочее тело — то, что совершает работу — принимает от нагревателя количество теплоты Q₁, из которой A уходит на работу механизма. Остаток теплоты Q₂ рабочее тело отдает холодильнику, по сути — это потеря энергии.

Физика не была бы такой загадочной, если б все в ней было идеально. Как и в любом процессе или преобразовании, здесь возможны потери, зачастую очень большие. Поэтому «индикатором качества» машины является КПД, с которым мы уже сталкивались в механике:

Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.

Мы должны понимать, что КПД на практике никогда не получится больше 1, поскольку всегда будут тепловые потери. 

Полезную работу можно расписать как Q₁ — Q₂ (по закону сохранения энергии). Тогда формула примет вид:

(eta = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})

Цикл Карно

Мы знаем, что потери — это плохо, поэтому должны предотвращать их. Как это сделать? Нам ничего делать не нужно, за нас уже все сделал Сади Карно, французский физик, разработавший цикл, в котором машины достигают наивысшего КПД. Этот цикл носит его имя и состоит из двух изотерм и двух адиабат. Рассмотрим, как этот цикл выглядит в координатах p(V).

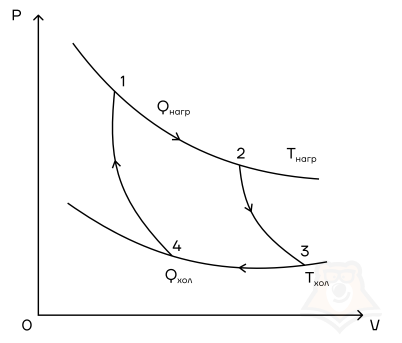
• Температура верхней изотермы 1-2 — температура нагревателя (так как теплота в данном процессе подводится).
• Температура нижней изотермы 3-4 — температура холодильника (так как теплота в данном процессе отводится).
• 2-3 и 4-1 — это адиабатические расширение и сжатие соответственно, в них газ не обменивается теплом с окружающей средой.

Цикл Карно — цикл идеальной тепловой машины, которая достигает наивысшего КПД. 

Формула, по которой можно рассчитать ее КПД выражается через температуры:

Приступим к задачам

Задачи на данную тему достаточно часто встречаются в задании 27 из КИМа ЕГЭ. Давайте разберем некоторые примеры.

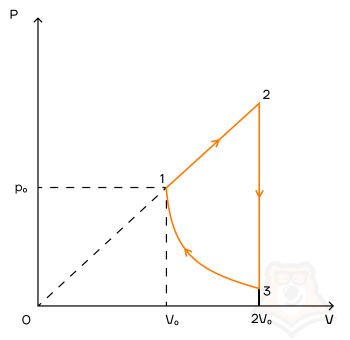
Задание 1. Одноатомный газ совершает циклический процесс, как показано на рисунке. На участке 1–2 газ совершает работу A₁₂ = 1520 Дж. Участок 3–1 представляет собой адиабатный процесс. Количество теплоты, отданное газом за цикл холодильнику, равно |Q_хол| = 4780 Дж. Найдите работу газа |A₁₃| на адиабате, если количество вещества постоянно.

Решение:

Шаг 1. Первое, с чего лучше начинать задачи по термодинамике — исследование процессов. 

Посмотрим на участок 1-2 графика: продолжение прямой проходит через начало координат, поэтому график функционально можно записать, как p = aV, где a — какое-то число, константа. Графиком является не изотерма, поскольку график изотермы в координатах p-V — гипербола. Из уравнения Менделеева-Клапейрона следует: (frac{pV}{T} = const). Отсюда можно сделать вывод, что возрастает температура, так как растут давление и объем.  Температура и объем растут, значит, увеличивается и внутренняя энергия и объем соответственно.

Участок 2-3: процесс изохорный, поскольку объем постоянен, следовательно, работа газом не совершается. Рассмотрим закон Шарля: (frac{p}{T} = const). Давление в этом процессе растет, тогда растет и температура, поскольку дробь не должна менять свое значение. Делаем вывод, что внутренняя энергия тоже увеличивается.

Участок 3-1: адиабата по условию, то есть количество теплоты в этом переходе равна нулю из определения адиабатного процесса. Работа газа отрицательна, так как газ уменьшает объем. 

Оформим все данные в таблицу. 

Определим знаки Q, используя первый закон термодинамики: Q = ΔU + A.

Из этих данных сразу видно, что количество теплоты, отданное холодильнику — это количество теплоты в процессе 2-3.

Шаг 2. Первый закон термодинамики для процесса 1-2 запишется в виде: 

Q₁₂ = ΔU₁₂ + A₁₂. 

Работа A12 — площадь фигуры под графиком процесса, то есть площадь трапеции: 

(A_{12} = frac{p_0 + 2p_0}{2} * V0 =frac{3p_0V_0}{2}). 

Запишем изменение внутренней энергии для этого процесса через давление и объем. Мы выводили эту формулу в статье «Первое начало термодинамики»:

(Delta U_{12} = frac{3}{2}(2p_0 * 2V_0 — p_0V_0) = frac{9p_0V_0}{2}). 

Заметим, что это в 3 раза больше работы газа на этом участке: 

(Delta U_{12} = 3A_{12} rightarrow Q_{12} = 4A_{12}).

Шаг 3. Работа цикла — площадь фигуры, которую замыкает график, тогда . A = A₁₂ — |A₃₁|. С другой стороны, работа цикла вычисляется как разность между энергиями нагревателя и холодильника: A = Q₁₂ — |Q₃₁|.

 Сравним эти формулы:

Q₁₂ -|Q₃₁| = A₁₂ — |A₃₁|,

подставим выражения из предыдущего пункта:

4A₁₂ — |Q₃₁| = A₁₂ — |A₃₁| (rightarrow) |A₃₁| = -3A₁₂ + |Q₃₁| = -31520 + 4780 = 220 Дж.

Ответ: 220 Дж

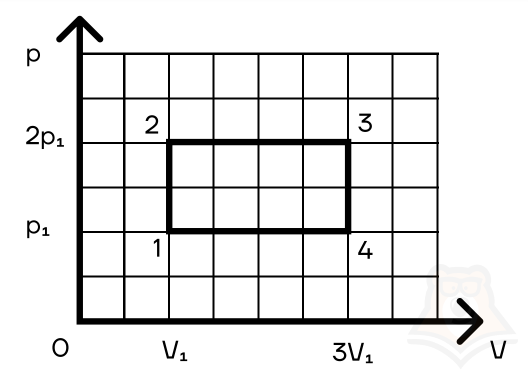
Задание 2. Найти КПД цикла для идеального одноатомного газа.

Решение:

Шаг 1. КПД цикла определим по формуле: (eta = frac{A}{Q}), где Q — количество теплоты от нагревателя, а А — работа газа за цикл. Найдем А как площадь замкнутой фигуры: A = (2p₁ — p₁)(3V₁ — V₁) = 2p₁V₁.

Шаг 2. Найдем процесс, который соответствует получению тепла от нагревателя. Воспользуемся теми же приемами, что и в прошлой задаче:

Посмотрим на участок 1-2 графика: давление растет, объем не меняется. По закону Шарля (frac{p}{T} = const) температура тоже растет. Работа газа равна 0 при изохорном процессе, а изменение внутренней энергии положительное.

2-3: давление не меняется, растет объем, а значит, работа газа положительна. По закону Гей-Люссака (frac{V}{T} = const) температура тоже растет, растет и внутренняя энергия.

3-4: давление уменьшается, следовательно, и температура уменьшается. При этом процесс изохорный и работа газа равна 0.

4-1: давление не меняется, объем и температура уменьшаются — работа газа отрицательна и внутренняя энергия уменьшается.

Оформим данные в таблицу: 

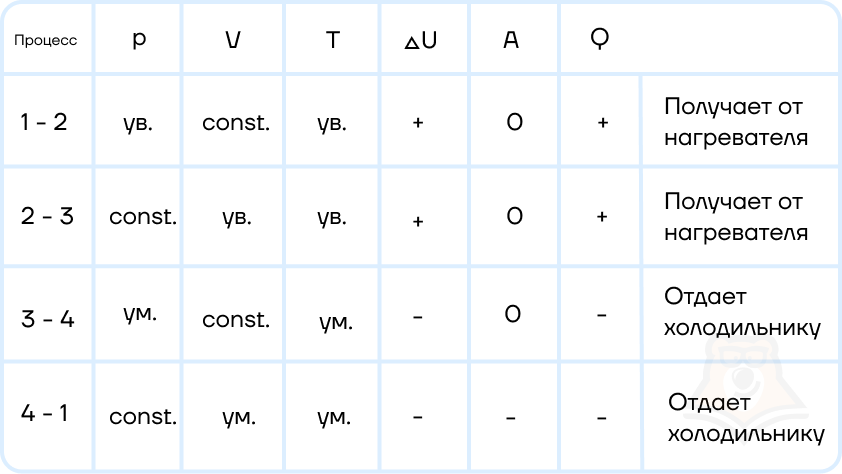
Отметим, что  необходимое Q = Q₁₂ + Q₂₃.

Шаг 3. Запишем первый закон термодинамики для процессов 1-2 и 2-3:

(Q_{12} = U_{12} + A_{12} = Delta U_{12} = frac{3}{2}(2p_1V_1 -p_1V_1) = frac{3}{2}p_1V_1).
(Q_{23} = Delta U_{23} + A_{23}), работу газа найдем как площадь под графиком: A₂₃ = 2p₁(3V₁ — V₁) = 4p₁V₁.
(Delta U_{12} = frac{3}{2}(2p_1 * 3V_1 — 2p_1V_1) = 6p_1V_1).
(Q_{23} = Delta U_{23} + A_{23} = 10p_1V_1).

Шаг 4. Мы готовы считать КПД: (eta = frac{A}{Q} = frac{A}{Q_{12} + Q_{23}} = frac{2p_1V_1}{frac{3}{2}p_1V_1 + 10p_1V_1} = frac{4}{23} approx 0,17).

Ответ: 17%

Теперь вас не должно настораживать наличие графиков в условиях задач на расчет КПД тепловых машин. Продолжить обучение решению задач экзамена вы можете в статьях «Применение законов Ньютона» и «Движение точки по окружности».

Фактчек

• Тепловые двигатели — устройства, способные преобразовывать внутреннюю энергию в механическую. 
• Тепловая машина принимает тепло от нагревателя, отдает холодильнику, а рабочим телом совершает работу.
• Коэффициент полезного действия (КПД) тепловой машины — это отношение полезной работы двигателя к энергии, полученной от нагревателя.
  (eta = frac{A}{Q_1} = frac{Q_1 — Q_2}{Q_1} = 1 — frac{Q_2}{Q_1})  
• Цикл Карно — цикл с максимально возможным КПД: (eta = frac{T_1 — T_2}{T_1} = 1 — frac{T_2}{T_1})
• Не забываем, что работа считается, как площадь фигуры под графиком.

Проверь себя

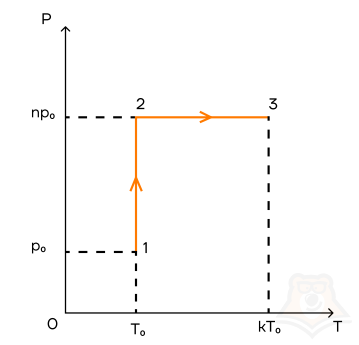
Задание 1. 
1 моль идеального газа переходит из состояния 1 в состояние 2, а потом — в состояние 3 так, как это показано графике. Начальная температура газа равна T₀ = 350 К. Определите работу газа при переходе из состояния 2 в состояние 3, если k = 3, а n = 2.

1. 5672 Дж
2. 4731 Дж
3. 5817 Дж
4. 6393 Дж

Задание 2. 
1 моль идеального одноатомного газа совершает цикл, который изображен на pV-диаграмме и состоит из двух адиабат, изохоры, изобары. Модуль отношения изменения температуры газа при изобарном процессе ΔT₁₂ к изменению его температуры ΔT₃₄ при изохорном процессе равен 1,5. Определите КПД цикла.

1. 0,6
2. 0,5
3. 0,8
4. 1

Задание 3.
В топке паровой машины сгорело 50 кг каменного угля, удельная теплота сгорания которого равна 30 МДж/кг. При этом машиной была совершена полезная механическая работа 135 МДж. Чему равен КПД этой тепловой машины? Ответ дайте в процентах.

1. 6%
2. 100%
3. 22%
4. 9%

Задание 4.
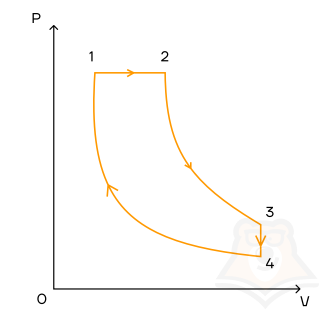
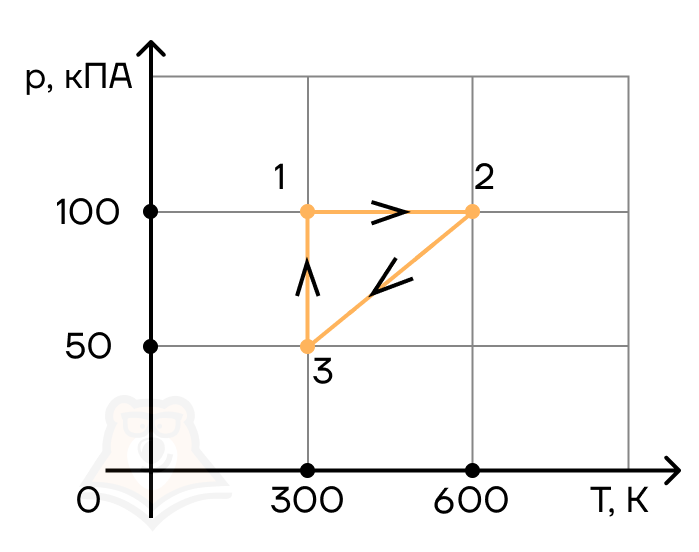
С двумя молями одноатомного идеального газа совершают циклический процесс 1–2–3–1 (см. рис.). Чему равна работа, совершаемая газом на участке 1–2 в этом циклическом процессе?

1. 4444 Дж
2. 2891 Дж
3. 4986 Дж
4. 9355 Дж

Ответы:1 — 3; 2 — 1; 3 — 4; 4 — 3.

Полное условие задачи

Одноатомный идеальный газ совершает циклический процесс, показанный на рисунке. За цикл от нагревателя газ получает количество теплоты 8 кДж. Чему равна работа газа за цикл? Масса газа в ходе процесса не изменяется.

Краткое условие задачи

Решение задачи:

Определим количество теплоты, полученное газом от нагревателя за цикл. Для этого выясним, в каких процессах газ получает теплоту. Процесс 1 – 2 изобарный, газ нагревается:

и совершает работу:

Такое возможно, если газ получает теплоту.

Процесс 2 – 3 не является изопроцессом, газ в этом процессе охлаждается:

и над ним совершают работу сторонние силы:

Такое возможно, если газ отдает теплоту.

Процесс 3 – 1 является изохорным, газ нагревается:

и газ не совершает работы, и над ним не совершают работу:

Такое возможно, если газ получает теплоту.

Таким образом, теплота, полученная газом от нагревателя за цикл, равна сумме теплот, полученных в процессах 1 – 2 и 3 – 1:

Распишем эти теплоты, используя первое начало термодинамики:

Подставим выражения (8) и (9) в равенство (7):

Запишем формулы для внутренних энергий:

Для определения температур запишем уравнение состояния идеального газа для состояний 2 и 3:

Выразим температуры:

Из графика видно, что:

Тогда получаем:

Подставляем (21) в (11), а (22) в (12):

Определим теперь работу газа в процессе 1 – 2. Используем для этого геометрический смысл термодинамической работы, который заключатся в следующем: работа, совершаемая газом в процессе его расширения (или сжатия), при любом термодинамическом процессе, численно равна площади под кривой, изображающей изменение состояния газа на диаграмме (p,V). Эта площадь показана на рисунке штриховкой:

Получаем:

Подставляем (23), (24) и (25) в (10):

Отсюда получаем:

Найдем теперь работу за цикл. Используем для этого геометрический смысл работы за цикл, который заключается в том, что она численно равна площади фигуры, ограниченной кривыми, изображающими изменение состояния газа. Эта площадь показана на рисунке штриховкой:

Получаем:

Подставим в выражение (28) равенство (27):

Подставляем данные и находим численный результат:

Ответ: 0,7 кДж.

Ранее мы достаточно плотно познакомились с процессами и методами работы с ними. Среди часто используемых способов работы с процессами выделяются два: уравнение Менделеева-Клапейрона (для описания состояния идеального газа) и первое начало термодинамики. Из нескольких друг за другом идущих разных процессов можно составить общий циклический процесс.

Круговой процесс (цикл) – составной термодинамический процесс, в результате совершения которого рабочее тело (газ) возвращается в исходное состояние. Таким образом, начальное и конечное состояние газа (давление газа , объём газа  и температура газа ) одинаковы. Попробуем изобразить такой процесс в координатах  (рис. 1).

Например, наш циклический процесс 1.1 состоит из двух изохор, двух изотерм, а процесс 1.2 — из двух изобар и двух изохор. Таким образом, исходя из текстовых условий любой задачи и знания общего вида изопроцессов (именно из них чаще всего составляется цикл), можно нарисовать рисунок.

Для энергетического описания процесса (или цикла) через первое начало термодинамики необходимо обдумать два вопроса:

1. как изменяется внутренняя энергия газа ()
2. чему равна работа газа ()

• где

Для циклов есть небольшие фишки, которые удобно использовать для убыстрения задачи.

Так, изменение внутренней энергии газа зависит только от изменения температуры, а т.к. в цикле начальное и конечное состояние газа одинаково, то изменение внутренней энергии идеального газа за цикл равно 0 ().

Поиск работы для газа также можно несколько упростить. Попробуем в координатах  нарисовать график изобарического процесса и найти работу газа (рис. 2). Пусть газ находится в состоянии (давление  и объём ), далее газ изобарически перевели в состояние 2 (давление  и объём ). Тогда по определению работы газа:

(1)

Геометрически (рис. 2), произведение давления на разность объёмов численно равна площади прямоугольника, ограниченного сверху прямой (процессом), а снизу осью. В целом, эту логику можно расширить на любые процессы, тогда работа газа численно равна площади под кривой в координатах .

Также в рамках школьной физики присутствует условное деление циклов на прямые и обратные:

Прямой цикл – круговой, в котором рабочее тело совершает положительную работу за счёт сообщённой ему теплоты.

Обратный цикл — круговой, в котором рабочее тело совершает отрицательную работу.

Анализируя (1) вопрос о положительной и отрицательной работе, сводится к вопросу о соотношении между начальным и конечным объёмами, если:

• — газ расширяется, работа положительна,
• — газ сжимается, работа отрицательна.

Для графиков можно использовать следующую логику: в случае, если площадь под графиком расширения газа больше соответствующей площади для сжатия, значит цикл — прямой (рис. 3), если наоборот — обратный (рис. 4).

Таким образом, разница в прямом и обратном цикле может быть в очерёдности процессов. Так, прямой процесс, в нашем примере, — это 1-2-3-4-1, а обратный — 1-4-3-2-1.

Вывод: в задачах на циклические процессы нужно быть очень внимательным при прочтении, т.к. часть слов будет иметь глубокий физический смысл. Лучше всего процессы в таких задачах прорисовывать на графиках в координатах . Если график уже есть, то это к лучшему. Определяемся с конкретными изопроцессами, заданными в задаче, и используем это знание или через уравнение Менделеева-Клапейрона, или через первое начало термодинамики.