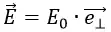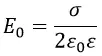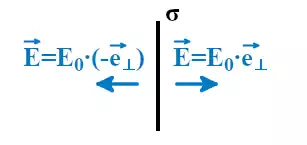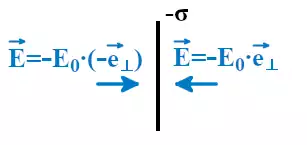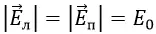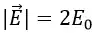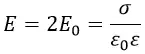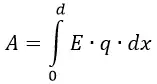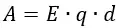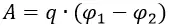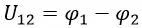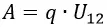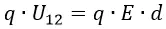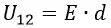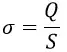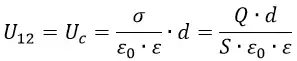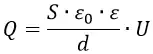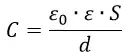Как найти работу плоского конденсатора

Условие задачи:

Определить работу, которую необходимо совершить, чтобы увеличить расстояние между пластинами плоского конденсатора на 3 см. Площадь пластины 200 см², заряд составляет 0,2 мкКл.

Задача №6.4.55 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(Delta d=3) см, (S=200) см², (q=0,2) мкКл, (A-?)

Решение задачи:

Работу (A) внешней силы, которую нужно совершить, чтобы увеличить расстояние между пластинами конденсатора, можно найти как разность конечной (W_2) и начальной (W_1) энергии конденсатора, то есть:

[A = {W_2} – {W_1};;;;(1)]

Начальную (W_1) и конечную (W_2) энергии конденсатора целесообразно находить по следующим формулам:

[left{ begin{gathered}
{W_1} = frac{{{q^2}}}{{2{C_1}}} hfill \
{W_2} = frac{{{q^2}}}{{2{C_2}}} hfill \
end{gathered} right.]

Начальную (C_1) и конечную (C_2) электроемкости плоского конденсатора легко найти таким образом:

[left{ begin{gathered}
{C_1} = frac{{{varepsilon _0}S}}{d} hfill \
{C_2} = frac{{{varepsilon _0}S}}{{d + Delta d}} hfill \
end{gathered} right.]

Электрическая постоянная (varepsilon _0) равна 8,85·10^-12 Ф/м.

Тогда:

[left{ begin{gathered}
{W_1} = frac{{{q^2}d}}{{2{varepsilon _0}S}} hfill \
{W_2} = frac{{{q^2}left( {d + Delta d} right)}}{{2{varepsilon _0}S}} hfill \
end{gathered} right.]

Полученные выражения подставим в формулу (1):

[A = frac{{{q^2}left( {d + Delta d} right)}}{{2{varepsilon _0}S}} – frac{{{q^2}d}}{{2{varepsilon _0}S}}]

В итоге решение задачи в общем виде выглядит так:

[A = frac{{{q^2}Delta d}}{{2{varepsilon _0}S}}]

Посчитаем численный ответ:

[A = frac{{{{left( {0,2 cdot {{10}^{ – 6}}} right)}^2} cdot 3 cdot {{10}^{ – 2}}}}{{2 cdot 8,85 cdot {{10}^{ – 12}} cdot 200 cdot {{10}^{ – 4}}}} = 3,4 cdot {10^{ – 3}};Дж = 3,4;мДж]

Ответ: 3,4 мДж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.4.54 Напряженность электрического поля конденсатора электроемкостью 0,8 мкФ равна 1 кВ/м
6.4.56 Парафиновая пластинка заполняет все пространство между обкладками плоского конденсатора
6.4.57 Определить количество электрической энергии, перешедшей в тепло при соединении одноименно

В статье поле плоской пластины была выведена формула напряжённости электрического поля бесконечной плоской пластины. Если эту пластину рассмотреть в разрезе и ввести понятие поверхностной плотности заряда σ, то согласно указанной статьи в любой точке пространства напряжённость электрического поля направлена перпендикулярно плоскости пластины и по величине равно:

E₀ здесь жёстко определяется поверхностной плотностью заряда σ:

где σ – поверхностная плотность заряда;
ε₀ – диэлектрическая проницаемость для вакуума;
ε – относительная диэлектрическая проницаемость для вещества, которая для вакуума равна 1.

Формулы показывают, что величина напряжённости электрического поля плоской пластины, имеющей бесконечные размеры, не зависит от расстояния до неё.

Если σ положительная, то напряжённость электрического поля будет направлена от пластины и поле отталкивает положительные заряды.

Если σ отрицательная, то напряжённость электрического поля направлена к пластине и поле притягивает положительные заряды.

Плоским конденсатором будем называть пару параллельных плоских пластин с плотностью заряда одинаковой по модулю, но противоположной по знаку.

Расчёт и вывод формулы ёмкости плоского конденсатора

Напряжённость электрического поля конденсатора

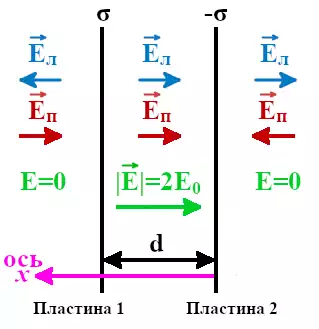
Для расчёта плоского конденсатора расположим две пластины бесконечных размеров параллельно друг другу на некотором расстоянии d. Пусть одна пластина будет иметь поверхностную плотность заряда σ, а другая -σ. По модулю величины поверхностных плотностей зарядов будут равны. В такой ситуации общее поле плоского конденсатора по принципу суперпозиции равно сумме полей.

Обозначим напряжённости электрического поля от левой пластины плоского конденсатора как E_л, при этом положительные заряды будут отталкиваться от пластины.

Напряжённость электрического поля от правой пластины плоского конденсатора обозначим как E_п, при этом поле пластины будет притягивать к себе положительные заряды.

При равной плотности заряда напряжённость поля во всех точках пространства и от левой, и от правой пластин конденсатора будут равны по модулю. Это приведёт к тому, что слева и справа от пары пластин поля взаимно компенсируются и их сумма будет равна нулю. При этом поля между пластинами плоского конденсатора будут складываться.

где E₀ – напряжённость поля при положительной σ.

Суммарная напряжённость электрического поля плоского конденсатора будет направлена от пластины с положительной σ к пластине с отрицательной σ.

Электрическая энергия плоского конденсатора отсутствует вне его пластин и вся накоплена в пространстве между пластинами.

Работа по перемещению заряда

Для перемещения заряда от отрицательно заряженной пластины в направлении к положительно заряженной придётся совершить работу против электрической силы:

При вычислении этой работы видно, что величина заряда q и напряжённость поля E постоянны, поэтому формула примет вид:

В электрическом поле можно ввести понятие потенциала ϕ и выразить работу по перемещению заряда в точку 2 из точки 1 через разность потенциалов ϕ₁-ϕ₂.

Напряжение между пластинами плоского конденсатора

Разность электрических потенциалов между двумя точками называют напряжением и обозначают U₁₂:

Таким образом, сравнивая две формулы для работы мы получим:

В реальном конденсаторе площадь пластин ограничена по естественным причинам, поэтому, как правило, мы не имеем возможности знать плотность заряда, а знаем только заряд пластины. В этом случае плотность заряда σ мы можем вычислить по формуле:

где Q – заряд пластины;
S – площадь пластины.

Если пластины плоского конденсатора находятся достаточно близко друг к другу, то краевыми эффектами можно пренебречь и считать, что поле внутри конденсатора реальных размеров подобно полю внутри конденсатора с пластинами бесконечных размеров.

В таком случае имеем следующее выражение:

Напряжение между пластинами пропорционально полному заряду этих пластин:

Электрическая ёмкость плоского конденсатора

Коэффициент пропорциональности между зарядом на обкладках плоского конденсатора и напряжением между ними носит название ёмкости плоского конденсатора и обозначается буквой C:

Подробности венецианская штукатурка для внутренней отделки цена на сайте.

Плоский конденсатор

Конденсаторы наравне с резисторами являются наиболее используемыми электронными компонентами. Самым интересным случаем является тот, когда заряды пластин плоского конденсатора противоположны по знаку и одинаковы по модулю, как представлено на рисунке ниже.

На пластинах сосредоточен заряд – между ними возникает электрическое поле. У плоского конденсатора электрическое поле в основном сосредоточено между его обкладками, но в окружающем пространстве также имеет место быть электрическое поле, которое называется полем рассеяния. При решении задач им, в большинстве случаев, пренебрегают. Чтобы определить величины данного поля, необходимо рассмотреть схематическое изображение плоского конденсатора, которое представлено на рисунке ниже.

Каждой пластиной конденсатора создается электрическое поле:

1. положительно заряженная частица +q создающая электрическое поле напряженностью Е+;
2. отрицательно заряженная частица -q создающая электрическое поле напряженностью Е-.

Формула для расчета напряженности поля для равномерно заряженной пластины выглядит следующим образом:

$Епл = j / (2*e¬_0*e)$

где: j – поверхностная плотность заряда; е – диэлектрическая проницаемость диэлектрического слоя между обкладками конденсатора.

Так как площадь пластин у рассматриваемого конденсатора одинакова, то модули напряженности равны между собой:

$Е+ = Е- = q / (2*e_0*e*S)$

где S – площадь пластин.

Однако направление векторов разные, то есть внутри конденсатора векторы направлены в одну сторону, а вне его в противоположные. Поэтому внутри пластин результирующее поле определяется следующим образом:

$Е = Е+ + Е- = (q / (2*e_0*e*S)) + (q / (2*e_0*e*S)) = q / (e_0*e*S)$

Таким образом вне плоского конденсатора электрические поля обкладок компенсируют друг друга – результирующая напряженность равна 0.

Примеры решения задач

Предположим, что необходимо рассчитать расстояние между пластинами плоского конденсатора при следующих условиях: разность потенциалов равняется 150 вольт, заряд на обкладке конденсатора равняется $10^{-8}$ кулон, площадь пластин 10^{-2}$ метра диэлектрический слой сделан из слюд, диэлектрическая проницаемость которой равняется 7. метра диэлектрический слой сделан из слюд, диэлектрическая проницаемость которой равняется 7.

Емкость конденсатора рассчитывается по следующей формуле:

$С = (е*е_0*S) / d$

где: е – диэлектрическая проницаемость слюды; е0 – диэлектрическая проницаемость вакуума; S – площадь пластин; d – расстояние между пластинами.

Из представленной выше формулы можно вывести формулу для расчета расстояния между пластинами:

$d = (е*е_0*S) / С$

Емкость любого конденсатора может быть рассчитана по формуле:

$С = q/U$

где q – заряд на обкладке конденсатора; U – разность потенциалов.

Таким образом получается следующая формула для расчета расстояния между пластинами:

$d = (U*e*e_0*S) / q = (150*7*8.85*10^{-12}*10^{-2}) / 10^{-8} = 9.3 * 10^{-3}$

Предположим, что необходимо рассчитать первоначальную энергию плоского воздушного конденсатора и его энергию, если пластины раздвинуть до расстояния $1,5*10^{-2}$ при следующих исходных данных: первоначальная разность потенциалов 500 вольт, площадь пластин $2*10^{-2}$ метра, первоначальное расстояние между обкладками конденсатора $1,5-10^{-3}$, а источник напряжения в случае раздвижения пластин не отключается.

Энергия электрического поля конденсатора можно рассчитать по следующей формуле:

$W = (C*U^2) / 2$

где С – электрическая емкость конденсатора; U – разность потенциалов.

Электрическая емкость плоского конденсатора рассчитывается по формуле:

$С = (е*е_0*S) / d$

Если учесть, что рассматриваемый конденсатор воздушный, то первоначальная емкость может быть рассчитана – электрическая проницаемость воздуха равняется 1, по формуле:

$С_1 = (е_0*S) / d_1$

где, $d_1$ – первоначальная емкость конденсатора.

В таком случае первоначальная энергия конденсатора рассчитывается по формуле:

$W_1 = ((е_0*S) / d_1) * ((C*U^2) / 2) = (8.85 * 10 ^{-12}*2*10^{-2}*500^2) / (2*1.5*10^{-3}) = 14.8 * 10^{-6}$

При изменении расстоянии между обкладками конденсатора и не выключенном источнике напряжения разность потенциалов не меняется и, следовательно, формула для расчета энергии конденсатора при именном расстоянии между пластинами имеет следующий вид:

$W_2 = ((е_0*S)/d_2) * (U^2/2) = W_1*(d_1/d_2) = 14.8*10^{-6} * (1.5*10^{-3} / 1.5*10^{-2}) = 1.5 * 10^{-6}$