Содержание
- Плоский конденсатор: примеры решения задач
- Плоский конденсатор
- Готовые работы на аналогичную тему
- Примеры решения задач
- Плоский конденсатор. Заряд и емкость конденсатора.
- Плоский конденсатор.
- Процессы зарядки и разрядки конденсаторов.
- Емкость и энергия конденсатора.
- Конденсаторы
- Содержание
- Простейший конденсатор и его устройство
- Зарядка конденсатора и его способность накапливать заряды
- Электроемкость конденсатора
- Единицы измерения электроемкости
- Зависимость электроемкости от площади пластин конденсатора
- Зависимость электроемкости от расстояния между пластинами конденсатора
- Зависимость электроемкости от диэлектрика
- Виды конденсаторов
- Энергия конденсатора и работа его электрического поля
- Последовательное соединение конденсаторов
- Параллельное соединение конденсаторов
- Первый конденсатор — лейденская банка
- Упражнения
- Упражнение №1
- Упражнение №2
Плоский конденсатор: примеры решения задач
Вы будете перенаправлены на Автор24
- Telegram
- Вконтакте
- Одноклассники
Плоский конденсатор
Плоский конденсатор – это самый простой конденсатор, который представляет собой две плоские проводящие пластины, называемые обкладками, расположенные параллельно друг другу, разделенные диэлектриком, причем расстояние между пластинами должно быть намного меньше, чем размеры пластин.
Конденсаторы наравне с резисторами являются наиболее используемыми электронными компонентами. Самым интересным случаем является тот, когда заряды пластин плоского конденсатора противоположны по знаку и одинаковы по модулю, как представлено на рисунке ниже.
Рисунок 1. Конденсатор. Автор24 — интернет-биржа студенческих работ
На пластинах сосредоточен заряд — между ними возникает электрическое поле. У плоского конденсатора электрическое поле в основном сосредоточено между его обкладками, но в окружающем пространстве также имеет место быть электрическое поле, которое называется полем рассеяния. При решении задач им, в большинстве случаев, пренебрегают. Чтобы определить величины данного поля, необходимо рассмотреть схематическое изображение плоского конденсатора, которое представлено на рисунке ниже.
Рисунок 2. Плоский конденсатор. Автор24 — интернет-биржа студенческих работ
Каждой пластиной конденсатора создается электрическое поле:
- положительно заряженная частица +q создающая электрическое поле напряженностью Е+;
- отрицательно заряженная частица -q создающая электрическое поле напряженностью Е-.
Готовые работы на аналогичную тему
Формула для расчета напряженности поля для равномерно заряженной пластины выглядит следующим образом:
где: j — поверхностная плотность заряда; е — диэлектрическая проницаемость диэлектрического слоя между обкладками конденсатора.
Плотность заряда – это величина электрического заряда, который приходится на одну единицу объема, площади или длины, измеряющаяся в кулонах на метр.
Так как площадь пластин у рассматриваемого конденсатора одинакова, то модули напряженности равны между собой:
$Е+ = Е- = q / (2*e_0*e*S)$
где S — площадь пластин.
Однако направление векторов разные, то есть внутри конденсатора векторы направлены в одну сторону, а вне его в противоположные. Поэтому внутри пластин результирующее поле определяется следующим образом:
$Е = Е+ + Е- = (q / (2*e_0*e*S)) + (q / (2*e_0*e*S)) = q / (e_0*e*S)$
Таким образом вне плоского конденсатора электрические поля обкладок компенсируют друг друга — результирующая напряженность равна 0.
Примеры решения задач
Предположим, что необходимо рассчитать расстояние между пластинами плоского конденсатора при следующих условиях: разность потенциалов равняется 150 вольт, заряд на обкладке конденсатора равняется $10^<-8>$ кулон, площадь пластин 10^<-2>$ метра диэлектрический слой сделан из слюд, диэлектрическая проницаемость которой равняется 7. метра диэлектрический слой сделан из слюд, диэлектрическая проницаемость которой равняется 7.
Емкость конденсатора рассчитывается по следующей формуле:
где: е — диэлектрическая проницаемость слюды; е0 — диэлектрическая проницаемость вакуума; S — площадь пластин; d — расстояние между пластинами.
Диэлектрическая проницаемость – это коэффициент, который входит в математическую запись закона Кулона для силы взаимодействия между точечными зарядами, находящимися в однородной диэлектрической (изолирующей) среде на определенном расстоянии друг от друга.
Из представленной выше формулы можно вывести формулу для расчета расстояния между пластинами:
Емкость любого конденсатора может быть рассчитана по формуле:
где q — заряд на обкладке конденсатора; U — разность потенциалов.
Таким образом получается следующая формула для расчета расстояния между пластинами:
$d = (U*e*e_0*S) / q = (150*7*8.85*10^<-12>*10^<-2>) / 10^ <-8>= 9.3 * 10^<-3>$
Предположим, что необходимо рассчитать первоначальную энергию плоского воздушного конденсатора и его энергию, если пластины раздвинуть до расстояния $1,5*10^<-2>$ при следующих исходных данных: первоначальная разность потенциалов 500 вольт, площадь пластин $2*10^<-2>$ метра, первоначальное расстояние между обкладками конденсатора $1,5-10^<-3>$, а источник напряжения в случае раздвижения пластин не отключается.
Энергия электрического поля конденсатора можно рассчитать по следующей формуле:
где С — электрическая емкость конденсатора; U — разность потенциалов.
Электрическая емкость плоского конденсатора рассчитывается по формуле:
Если учесть, что рассматриваемый конденсатор воздушный, то первоначальная емкость может быть рассчитана — электрическая проницаемость воздуха равняется 1, по формуле:
где, $d_1$ — первоначальная емкость конденсатора.
В таком случае первоначальная энергия конденсатора рассчитывается по формуле:
$W_1 = ((е_0*S) / d_1) * ((C*U^2) / 2) = (8.85 * 10 ^<-12>*2*10^<-2>*500^2) / (2*1.5*10^<-3>) = 14.8 * 10^<-6>$
При изменении расстоянии между обкладками конденсатора и не выключенном источнике напряжения разность потенциалов не меняется и, следовательно, формула для расчета энергии конденсатора при именном расстоянии между пластинами имеет следующий вид:
$W_2 = ((е_0*S)/d_2) * (U^2/2) = W_1*(d_1/d_2) = 14.8*10^ <-6>* (1.5*10^ <-3>/ 1.5*10^<-2>) = 1.5 * 10^<-6>$
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 03.05.2022
![]()
Эксперт по предмету «Электроника, электротехника, радиотехника» , преподавательский стаж — 5 лет
Источник
Плоский конденсатор. Заряд и емкость конденсатора.
![]()

Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются 👍 В первую очередь, рассмотрим устройство и принцип работы, а затем плавно перейдем к основным свойствам и характеристикам — заряду, энергии и, конечно же, емкости конденсатора.
Плоский конденсатор.
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:
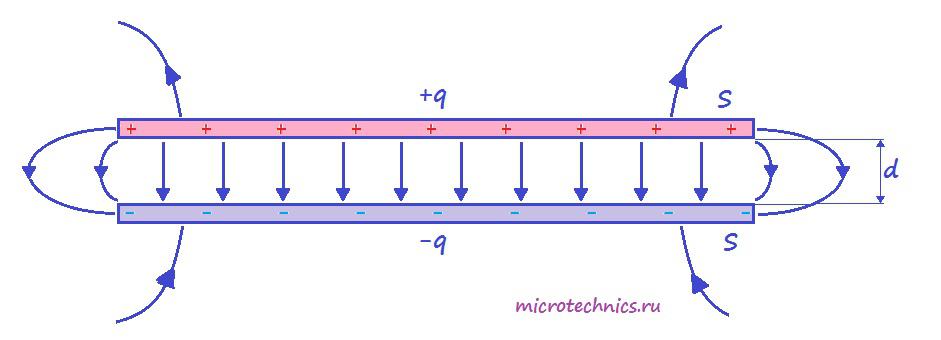
Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:
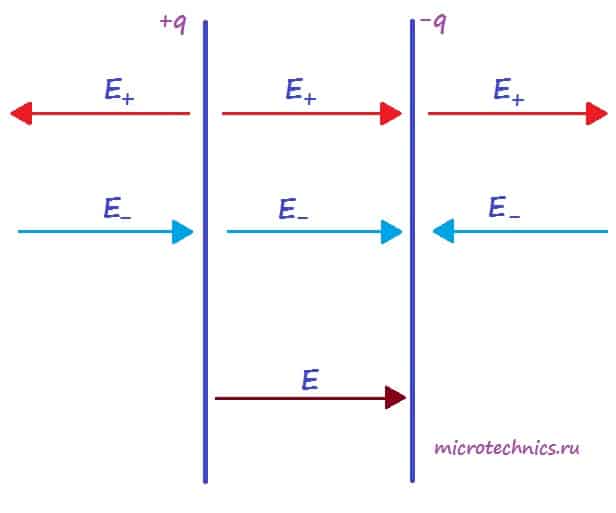
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина ( +q ) создает поле, напряженность которого равна E_
- отрицательно заряженная пластина ( -q ) создает поле, напряженность которого равна E_
Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:
Здесь sigma — это поверхностная плотность заряда: sigma = frac
, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:
Соответственно, вне конденсатора (слева и справа от обкладок) поля пластин компенсируют друг друга и результирующая напряженность равна 0.
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
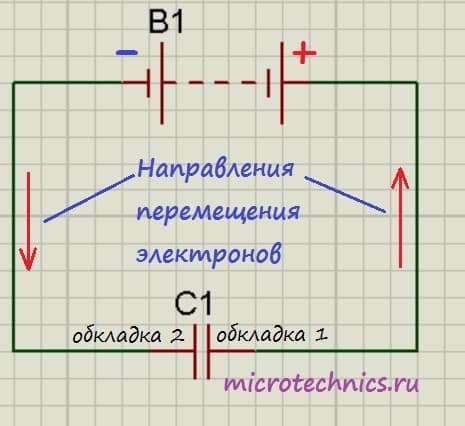
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной.
Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
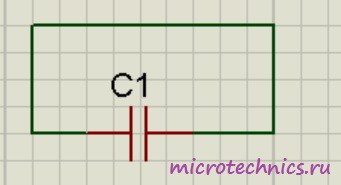
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Именно так происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию. Как видите, здесь нет ничего сложного.
Емкость и энергия конденсатора.
Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда q одного из проводников к разности потенциалов между проводниками:
Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является неимоверно большой, поэтому чаще всего используются микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:
Здесь у нас d — это расстояние между пластинами конденсатора, а q — заряд конденсатора. Подставим эту формулу в выражение для емкости:
Если в качестве диэлектрика выступает воздух, то во всех формулах можно подставить varepsilon = 1 . Для запасенной же энергии конденсатора справедливы следующие выражения:
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Итак, резюмируем — сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку.
Источник
Конденсаторы
Содержание
Если тело обладает некоторым электрическим зарядом, то вокруг него обязательно присутствует электрическое поле. Это поле обладает некоторой энергией — может совершить какую-то работу.
Можно ли как-то накопить эту энергию? Да, такая возможность существует. Для этого используют специальный прибор — конденсатор.
Конденсатор — это устройство, позволяющее накапливать электрические заряды и, соответственно, энергию электрического поля.
На данном уроке вы познакомитесь с устройством этого прибора, его характеристиками и свойствами.
Простейший конденсатор и его устройство
Устройство простейшего конденсатора представлено на рисунке 1. Он состоит из двух одинаковых металлический пластин. Эти пластины называются обкладками конденсатора.
Обкладки расположены на небольшом расстоянии друг от друга. Этот промежуток между ними обязательно должен быть заполнен слоем диэлектрика. В нашем случае таким диэлектриком является обычный воздух.
Такой конденсатор называется плоским (по форме обкладок).
Конденсатор имеет свой условный знак для обозначения на схеме электрической цепи (рисунок 2).
Зарядка конденсатора и его способность накапливать заряды
Теперь разберемся, каким же образом мы можем накапливать заряды с помощью конденсатора.
Рассмотрим простой опыт. Возьмем конденсатор, состоящий из двух металлических пластин, расположенных параллельно друг другу, и заряженный аккумулятор.
Две обкладки конденсатора подключим к разным полюсам аккумулятора. На обкладках начнут образовываться электрические заряды (рисунок 3). Они будут равны друг другу, но иметь противоположные знаки.
Эти заряды образуют электрическое поле конденсатора. Оно будет сосредоточено между обкладками.
Отключим аккумулятор от конденсатора. Что мы увидим? Заряды, образованные на обкладках, никуда не деваются. Они сохраняются, как и электрическое поле между пластин. Конденсатор заряжен.
Если мы соединим проводником обкладки конденсатора, то увидим, что по нему некоторое время будет течь ток. Значит, заряженный конденсатор является источником тока в электрической цепи.
Электроемкость конденсатора
Логично предположить, что разные конденсаторы по-разному будут накапливать заряд. Как охарактеризовать эту способность прибора? Для этого существует специальная величина — электроемкость (или просто емкость) конденсатора.
Чтобы понять смысл этой величины, рассмотрим опыт. Возьмем две металлические пластины и установим их на изолированных подставках друг напротив друга.
Подключим к пластинам электрометр. Этот прибор (рисунок 4) по своему устройству и принципу действия схож с электроскопом. Он позволит нам зафиксировать значения напряжения, которое возникнет между пластинами.
Итак, одну из пластин (A) мы соединим проводом со стержнем электрометра, а другую (B) соединим с корпусом прибора (заземлим). Коснемся положительно наэлектризованной стеклянной палочкой внешней стороны пластины A (рисунок 5).
Мы сообщили пластине A положительный заряд $+q$. Вокруг этого заряда (пластины A) теперь существует электрическое поле. Под его действием произойдет перераспределение зарядов в пластине B. Отрицательные заряды перейдут на внутреннюю сторону пластины, а положительные — на внешнюю.
Помните, что мы заземлили пластину B? За счет этого на пластину пойдут свободные электроны с земли. Они нейтрализуют положительный заряд на внешней стороне пластины. Таким образом, мы получили на пластине B отрицательный заряд $-q$ (рисунок 6). По величине он равен заряду на другой пластине.
Стрелка электрометра отклонилась. Зафиксируем это значение напряжения между пластинами. Далее мы снова сообщим заряд пластине B, равный по величине первому сообщаемому заряду. Потом сообщим третий и четвертый такие же заряды, наблюдая за стрелкой электрометра.
Вы увидите, что при увеличении заряда в 2, 3, 4 раза, соответственно, в 2, 3, 4 раза увеличиваются показания электрометра — напряжение между пластинами. Важно отметить, что отношение заряда к напряжению при этом будет постоянно:
$frac = frac<2q> <2u>= frac<3q> <3u>= frac<4q> <4u>= const$.
Теперь мы можем дать определение электроемкости конденсатора.
Электроемкость конденсатора — это величина, измеряемая отношением заряда на одной из пластин конденсатора к напряжению между пластинами:
$C = frac$.
Единицы измерения электроемкости
В СИ электроемкость измеряется в фарадах ($Ф$).
Электроемкость конденсатора равна единице, если при сообщении ему заряда в $1 space Кл$ возникает напряжение, равное $1 space В$ (рисунок 7):
$1 space Ф = frac<1 space Кл><1 space В>$.
Эта единица измерения названа в честь английского физика Майкла Фарадея (рисунок 8).
Емкость в $1 space Ф$ является очень большой, поэтому на практике часто используют дольные единицы: микрофарад ($мкФ$) и пикофарад ($пФ$).
Зависимость электроемкости от площади пластин конденсатора
От чего зависит электроемкость? Начнем с размера пластин.
Зафиксируем полученное в первом опыте с электрометром и конденсатором значение напряжения $U_1$. Теперь возьмем пластины, имеющие большую площадь. Сообщим им точно такой же заряд $q$ (рисунок 9).
Мы увидим, что стрелка электрометра отклоняется меньше. Это означает, что напряжение между этими пластинами меньше напряжения между пластинами меньшей площади ($U_1 > U_2$).
Из определения электроемкости:
$C_1 = frac$,
$C_2 = frac$,
$C_2 > C_1$.
Чем больше площадь пластин, тем больше электроемкость конденсатора.
Зависимость электроемкости от расстояния между пластинами конденсатора
Снова обратимся к опыту. Теперь изменим расстояние между пластинами — уменьшим его (рисунок 10).
Мы увидим, что напряжение между пластинами уменьшилось: $U_2 C_1$.
При уменьшении расстояния между пластинами конденсатора и при неизменном заряде электроемкость конденсатора увеличивается.
Зависимость электроемкости от диэлектрика
Проведем еще один опыт. Зафиксируем значение напряжения между пластинами конденсатора. Затем внесем между ними лист из оргстекла (рисунок 11). Он является диэлектриком.
Если раньше диэлектриком между пластинами являлся только воздух, то теперь это и воздух, и лист оргстекла. Напряжение между пластинами уменьшилось: $U_1 > U_2$. Значит,
$C_1 = frac$,
$C_2 = frac$,
$C_2 > C_1$.
При внесении диэлектрика электроемкость конденсатора увеличивается.
Виды конденсаторов
Между обкладками конденсатора могут быть помещены разнообразные диэлектрики. В зависимости от природы этого диэлектрика конденсаторы разделяют на несколько видов: с твердым, жидким и газообразным диэлектриком.
Также существует классификация и по форме обкладок. Конденсаторы бывают плоские, цилиндрические, сферические (рисунок 12) и др.
Конденсаторы бывают с постоянной емкостью и с переменной емкостью. В последних можно регулировать параметры, от которых зависит емкость — ширину пластин и расстояние между ними.
На данный момент существует огромное разнообразие конденсаторов (рисунок 13). Многие из них носят названия, происходящие от названий материалов, составляющих их: слюдяные, керамические, алюминиевые электролитические, танталовые электролитические, конденсаторы на полимерной пленке.
ЧЕМ ОТЛИЧАЮТСЯ КОНДЕНСАТОРЫ РАЗНЫХ ТИПОВ | Можно ли заменить один тип на другой?
Энергия конденсатора и работа его электрического поля
Заряженный конденсатор обладает некоторой энергией. Это легко проверить на опыте. Если мы подключим к конденсатору электрическую лампочку, то она она ярко вспыхнет (рисунок 14). Энергия конденсатора превратилась во внутреннюю энергию нити накаливания лампы и соединительных проводов.
Откуда взялась эта энергия? Конденсатор получает ее при зарядке.
Для того, чтобы зарядить конденсатор, нужно совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии совершенная работа A и будет равна энергии конденсатора E:
$A = E$.
Для расчета такой работы электрического поля конденсатора существует специальная формула.
В процессе разрядки напряжение постоянно падает, поэтому нам и необходимо знать для расчетов его среднее значение:
$U_ <ср>= frac<2>$.
Из формулы для электроемкости:
$C = frac$,
$q = CU$.
Подставим в формулу для работы:
$A = frac <2>= frac <2>= frac<2>$.
По закону сохранения энергия эта работа и будет равна энергии конденсатора $W$.
Накапливание конденсатором энергии часто происходит достаточно длительное время. При разрядке эта энергия отдается почти мгновенно.
Это свойство (накопление энергии и ее быстрая отдача) широко применяется в различных электронных устройствах, в медицинской технике (рентген, устройства для электротерапии), при изготовлении дозиметров, фотосъемке.
Последовательное соединение конденсаторов
В электрической цепи может быть не один, а сразу несколько конденсаторов. Они могут быть соединены как последовательно, так и параллельно.
Рассмотрим первый тип соединения — последовательный (рисунок 15).
Обкладки 2 и 3, принадлежащие разным конденсаторам, будут являться отдельной деталью. По закону сохранения заряда, заряды на обкладках 2 и 3 будут равны друг другу по модулю, но противоположны по знаку. Из этого следует, что общий заряд конденсаторов численно будет равен заряду на любой из обкладок конденсаторов.
Напряжение на концах участка цепи с последовательно соединенными конденсаторами будет складываться из значения напряжений на каждом конденсаторе.
Чтобы получить формулу для общей емкости конденсаторов, последнее равенство нужно разделить на заряд q (любой, так как они равны).
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов показано на рисунке 16.
В этом случае выходы от источника питания будут соединены с каждой обкладкой конденсаторов. Поэтому напряжение на концах такого участка цепи будет равно напряжению между обкладками любого из конденсаторов.
Заряды на обкладках будут суммироваться.
Разделим это равенство на значение напряжения и получим формулу для электроемкости параллельно соединенных конденсаторов.
$C = C_1 + C_2 + … + C_n$
Первый конденсатор — лейденская банка
Лейденская банка официально является первым конденсатором. Изобретение ее относится к 1745 году. Существует множество версий о том, кто же именно должен считаться изобретателем этого прибора, но официально авторство принадлежит Питеру ван Мушенбруку и его студенту Андреасу Кунэусу.
В ранней версии лейденская банка была на часть заполнена водой, которая выступала в роли обкладки (рисунок 17). Второй обкладкой являлась рука, держащая банку. После зарядки этого приспособления Андреас Кунэус испытал сильный удар током, коснувшись до верха металлического стержня.
Более поздняя и более распространенная версия этого незамысловатого прибора представляет собой сосуд из стекла с широким горлом, снаружи покрытый листом из фольги (рисунок 18). Фольга также находится и внутри банки. Через пробку в этот сосуд вставляется металлический стержень. Он должен касаться фольги внутри банки.
Таким образом, фольга внутри и фольга снаружи становятся своеобразными обкладками. При подключении к источнику тока на них накапливается электрический заряд.
Внимание! Лейденская банка не является безопасным инструментом в электротехнике! Разряд такого конденсатора может оказаться смертельным или привести к серьезным физическим повреждениям. Будьте аккуратны при использовании данного прибора: не следует пытаться разрядить лейденскую банку, взявшись за нее голыми руками.
Как изготовить лейденскую банку своими руками? Возьмите пластиковую банку с крышкой (из-под кофе, витаминов). Внешнюю сторону банки на $frac<2><3>$ обклейте фольгой. Далее или налейте в банку соленую воду, или обклейте изнутри фольгой. Затем закройте крышку и проткните ее достаточно длинным гвоздем, чтобы он касался внутренней обкладки (воды или фольги). После зарядки такая банка представляет собой заряженный конденсатор.
Упражнения
Упражнение №1
Пластины плоского конденсатора подсоединяют к источнику напряжения в $220 space В$. Емкость конденсатора равна $1.5 cdot 10^ <-4>space мкФ$. Чему будет равен заряд конденсатора?
Дано:
$C = 1.5 cdot 10^ <-4>space мкФ$
$U = 220 space В$
СИ:
$С = 1.5 cdot 10^ <-10>space Ф$
Посмотреть решение и ответ
Решение:
Формула для расчета электроемкости конденсатора:
$C = frac$.
Выразим отсюда заряд конденсатора и рассчитаем его:
$q = CU$,
$q = 1.5 cdot 10^ <-10>space Ф cdot 220 space В = 33 cdot 10^ <-9>space Кл$.
Ответ: $q = 33 cdot 10^ <-9>space Кл$.
Упражнение №2
Заряд плоского конденсатора равен $2.7 cdot 10^ <-2>space Кл$, его емкость составляет $0.01 space мкФ$. Найдите напряжение между обкладками конденсатора.
Дано:
$C = 0.01 space мкФ$
$q = 2.7 cdot 10^ <-2>space Кл$
СИ:
$C = 10^ <-8>space Ф$
Показать решение и ответ
Решение:
Формула для расчета электроемкости конденсатора:
$C = frac$.
Выразим отсюда напряжение между обкладками конденсатора и рассчитаем его:
$U = frac$,
$U = frac <2.7 cdot 10^<-2>space Кл> <10^<-8>space Ф> = 2.7 cdot 10^6 space В$.
Ответ: $U = 2.7 cdot 10^6 space В$.
Источник
Интегралы, которые
мы рассматривали до сих пор, имели своими
областями либо отрезки на прямой, либо
некоторые области на плоскости и в
пространстве.
Теперь рассмотрим
случай, когда областью интегрирования
является кривая, расположенная в
плоскости. Затем все рассуждения можно
перенести на случай кривой в пространстве.
Рассмотрение
криволинейных интегралов расширяет
возможности приложений математического
анализа и решения задач физики и техники
(и в самой математике – в теории поля и
в ТФКП).
Существует два
типа криволинейных интегралов. Мы
рассмотрим только криволинейные
интегралы второго типа.
Криволинейные интегралы II типа
1. Задача о работе плоского силового поля
Пусть материальная
точка М,
двигаясь прямолинейно под действием
постоянной силы
![]() совершает перемещение
совершает перемещение![]() .
.
РаботойА,
производимой этой силой, называется
скалярное произведение вектора силы
![]() на вектор перемещения
на вектор перемещения![]() :
:
![]() .
.
Если в каждой точке
М
области (P)
определена сила, величина и направление
которой зависят только от приложения
точки М,
то говорят, что на области (P)
задано силовое поле.
Пусть материальная
точка М
движется по кривой ВС,
лежащей в области (P)
под действием силового поля.
Задача.
Определить
работу А
силового поля при перемещении материальной
точки из точки В
в точку С
по кривой.
Разобьем кривую
ВС
произвольными точками
![]() ,
,
взятыми по направлению отВ
к С,
на n
частичных дуг. На каждой частичной дуге
![]() выберем
выберем
произвольно точки
![]() .
.
На частичной дуге
![]() заменим
заменим
приближенно
переменную силу
![]() постоянной силой
постоянной силой![]() ,
,
равной вектору силы![]() в точке
в точке![]() .
.
А движение материальной точки по этой
дуге заменим ее движением по хорде
![]() этой дуги.
этой дуги.
Выполним
это все
![]() .
.
В результате приближенных замен имеем:
1 )
)
материальная точка движется по ломаной,
вписанной в кривуюВС;
2) на каждом звене
ломаной на материальную точку действует
постоянная сила.
Работа силы
![]() на хорде
на хорде![]() равна
равна
![]() .
.
Суммируя по
![]() ,
,
получим
 ,
,
(1)
![]() – работа ступенчатой
– работа ступенчатой
силы при движении материальной точки
по ломаной
![]() ,
,
вписанной в кривуюВС.
Эту работу считают приближением искомой
работы А
силы
![]() при перемещении материальной точки по
при перемещении материальной точки по
кривойВС:
![]() .
.
Пусть ![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
Тогда
 . (2)
. (2)
Пусть
![]() – длина
– длина
![]() ,
,
![]() .
.
Переходя в (2) к![]() ,
,
получим точное равенство:
 (3).
(3).
2. Определение криволинейного интеграла II типа
Пусть в плоскости
![]() задана спрямляемая кривая
задана спрямляемая кривая![]() и вдоль нее определена функцияf(x;y).
и вдоль нее определена функцияf(x;y).
Кривую
![]() разобьем произвольно на
разобьем произвольно на![]() частей точками
частей точками![]() ,
,![]() .
.
На каждой частичной дуге
![]() выберем произвольную точку
выберем произвольную точку![]() .
.
Обозначим черезxk
и уk
проекции дуги
![]() на оси координат,xk=xk–xk-1,
на оси координат,xk=xk–xk-1,
yk=yk–yk-1.
Разбиение обозначим через
![]() .
.
Составим сумму
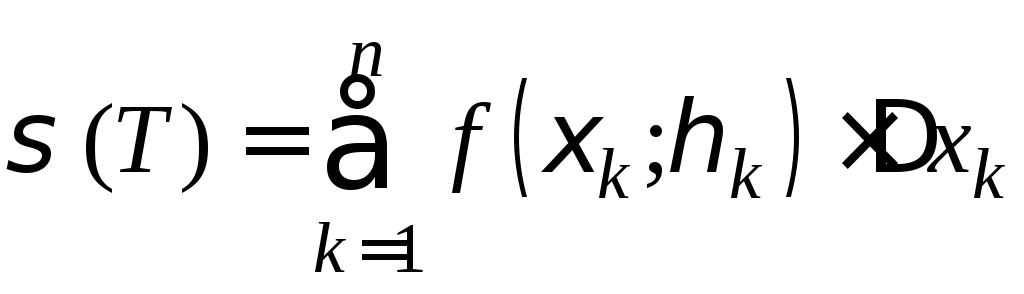 (4).
(4).
(4) – интегральная
сумма для функции f(x;y)
на кривой AB
по координате x.
Пусть
![]() ,
,![]() – длина частичной дуги
– длина частичной дуги![]() .
.
Определение 1.
Число I
называется пределом
интегральной суммы
![]() при
при
![]() ,
,
если![]() выполнено
выполнено![]() .
.
Обозначается:![]() .
.
Определение 2.
Если существует
конечный предел интегральной суммы
![]() при
при![]() ,
,
не зависящий ни от способа разбиения
кривойАВ,
ни от выбора точек ![]() ,
,
то он называется криволинейным
интегралом по координате х от
функции f(x;y),
взятым по кривой AB.
Функция называется интегрируемой
вдоль кривой AB
по координате
х,
если для нее
вдоль этой кривой существует криволинейный
интеграл по x.
Обозначается:
![]() .
.
Таким образом, 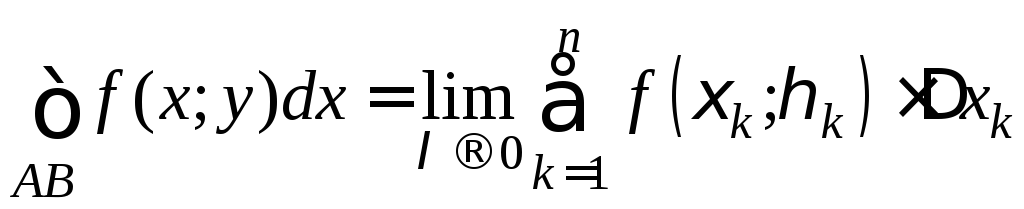 .
.
Аналогично
определяется криволинейный интеграл
от функции f(x;y)
по координате y,
взятый по кривой AB:
 .
.
Криволинейные
интегралы по координатам x
и y
называются криволинейными
интегралами II
типа.
Если вдоль кривой
AB
две функции P(x;y)
и Q(x;y),
и существуют
![]() ,
,![]() ,
,
то сумма этих интегралов также называется
криволинейным интеграломII
типа (общего вида) и обозначается:
![]() .
.
Физический смысл
криволинейного интеграла II
типа
Из
задачи о работе плоского силового поля
и определения криволинейного интеграла
II
типа следует, что криволинейный интеграл
II
типа общего вида
![]() ,
,
то есть выражает
работу силы
![]() по перемещению материальной точки по
по перемещению материальной точки по
кривой из точкиА
в точку В.
Замечание 1.
Определенный
интеграл является частным случаем
криволинейного интеграла II
типа. Пусть кривая АВ
– это отрезок AB=[a;b]
оси Ox.
Тогда f(x;y)=f(x;0)=F(x).
Поэтому на [a;b]
 .
.
В правой части –
обыкновенная интегральная сумма для
функции F(x)
на [a;b].
Переходя к
![]() ,
,
получим
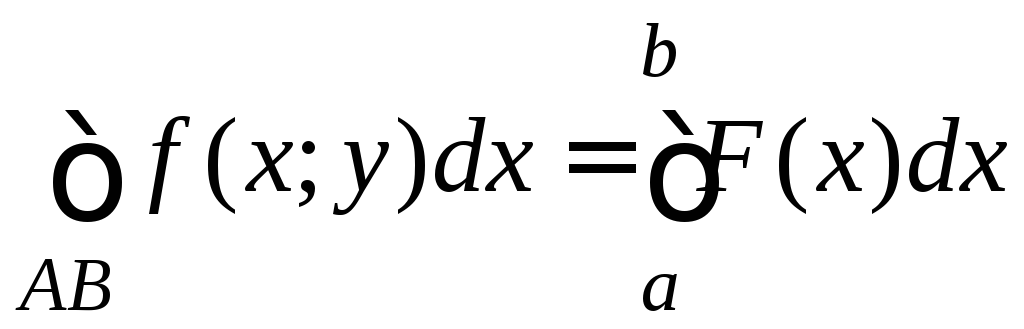 .
.
Аналогично, если
кривая AB
является некоторым отрезком [c;d]
оси Oy,
то
 ,
,
где(y)=f(0;y),
y[c;d].
Замечание 2.
Если на кривой AB
поменять направление интегрирования
на противоположное, то и знак криволинейного
интеграла II
типа изменится на противоположный. Это
происходит потому, что в интегральных
суммах
 изменяется знак
изменяется знак![]() .
.
Таким образом, криволинейные интегралыII
типа от одной и той же функции f(x;y),
взятые по одной и той же кривой АВ,
но в противоположных направлениях,
равны по модулю, но противоположны по
знаку:
![]() ,
,
![]() .
.
С ледовательно,
ледовательно,
при вычислении криволинейных интеграловII
типа необходимо учитывать направление
интегрирования. Из двух направлений на
кривой одно считают положительным, а
другое – отрицательным.
Если кривая замкнута
и представляет собой контур, ограничивающий
некоторую область на плоскости (это
будет в случае, если замкнутая кривая
не имеет кратных точек), то за положительное
направление принимают обычно направление
против хода часовой стрелки, а за
отрицательное – по ходу часовой стрелки.
Но для некоторых областей такой способ
задания направления непригоден. В этом
случае положительным направлением
считают такое направление обхода
контура, когда ограниченная им область
(Р)
остается все время слева. Интеграл по
замкнутому контуру L
обозначается:
![]() .
.
Иногда с помощью стрелки указывают
направление обхода:![]() или
или![]() .
.
Соседние файлы в папке лекции_3
- #
- #
- #
- #
- #
- #
Вычисление работы силового поля по перемещению материальной точки не обходится без применения криволинейного интеграла ІІ рода. Чтобы не повторять в каждой новой статье для криволинейных интегралов те же формулы сразу переходим к анализу готовых примеров.
Вычисление работы силового поля с помощью криволинейного интегралу ІІ рода
ЗАДАНИЕ 3.5 Вычислить работу силового поля 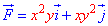 при перемещению материальной точки вдоль линии L:
при перемещению материальной точки вдоль линии L:
x2+y2=4 от точки A(2;0) к точке B(0;2).
Решение: Построим в декартовых координатах траекторию материальной точки вдоль круга L: x2+y2=4.
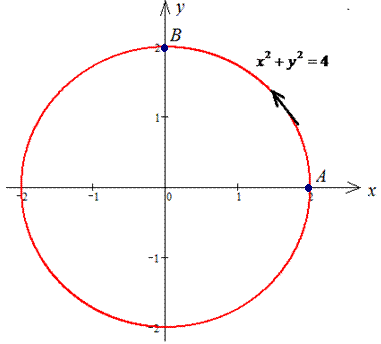
Уравнение верхней части полукруга и ее производной равны
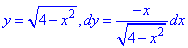
В соответствии с точками A(2;0), B(0;2) пределы интегрирования изменяются от 2 до 0.
Не удивляйтесь, что не в обратном порядке. Их всегда нужно выписывать в порядке обхода контуру от точки A к B.
Робота силового поля F по перемещения материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода :
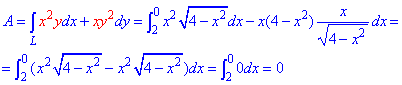
Внимательно пересмотрите уравнение силового поля и подинтегральную функцию и Вам станет понятно, что и откуда берется. Как вычислить криволинейный интеграл детально расписано в предыдущих статьях (меняем y, dy на ф-и от “х” под интегралом).
ЗАДАНИЕ 3.10 Найти работу силового поля 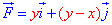 по перемещению материальной точки вдоль линии L:
по перемещению материальной точки вдоль линии L:
y=a-x2/a от точки A(-a;0) к точке B(0;a).
Решение: Имеем y=a-x2/a – уравнение параболы, находим дифференциал dy=-2x/a*dx и пределы изменения переменной
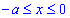
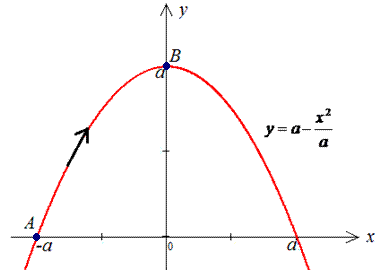
Вычисляем работу силового поля F, потраченную на перемещению материальной точки вдоль вдоль линии L 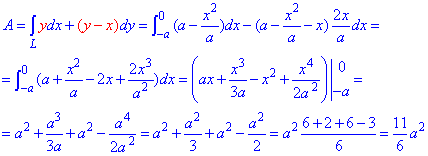
Криволинейный интеграл ІІ рода находим за первой формулой интегрирования.
ЗАДАНИЕ 3.12 Вычислить работу силового поля 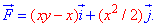 по перемещению материальной точки вдоль линии L:
по перемещению материальной точки вдоль линии L: 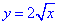 от точки A(0;0) к точке B(1;2). .
от точки A(0;0) к точке B(1;2). .
Решение: Строим траекторию материальной точки вдоль корневой функции L: 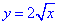 .
.
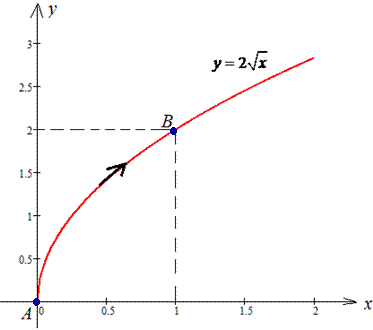
Записываем производную 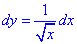 и промежуток интегрирования [0;1].
и промежуток интегрирования [0;1].
Находим роботу A силового поля F : 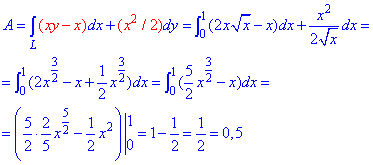
Перед интегрированием превращаем корни к показательной форме записи, а дальше вычисляем за табличными формулами интеграл.
ЗАДАНИЕ 3.14 Вычислить работу силового поля 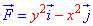 по перемещению материальной точки вдоль линии L:
по перемещению материальной точки вдоль линии L:
x2+y2=9.
Решение: Наведем траекторию движения материальной точки по кругу L: x2+y2=9.
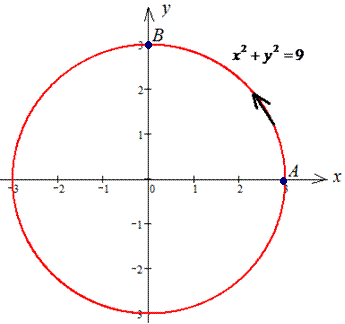
Верхняя ветка ограничена функцией
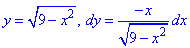
Аргумент изменяется от 3 до 0 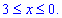
Работа А силового поля F при перемещению материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода : 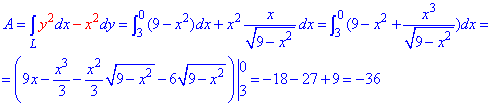
Интегрирование само по себе тяжелое, главное правильно найти дифференциал функции и не ошибиться с пределами интегрирования.
ЗАДАНИЕ 3.19 Вычислить работу силового поля 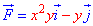 по перемещения материальной точки вдоль линии L:
по перемещения материальной точки вдоль линии L:
прямая от точки A(-1;0) к точке B(0;1).
Решение: Запишем уравнение прямой, которая проходит через две точки A(-1;0) и B(0;1):
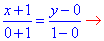
отсюда y=x+1.
Таким образом, имеем дифференциал дуги dy=dx плюс интервал интегрирования [- 1;0].
График прямой приведен на рисунку ниже
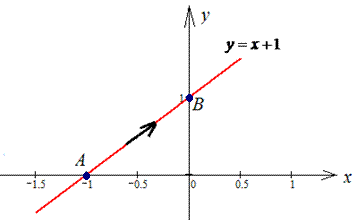 Подсчитываем работу силового поля F по перемещения материальной точки вдоль линии L:
Подсчитываем работу силового поля F по перемещения материальной точки вдоль линии L: 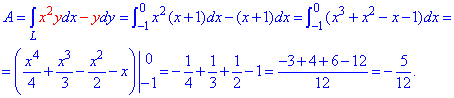
Криволинейный интеграл 2 рода легко сводим к определенному и находим результирующее значение работы.
ЗАДАНИЕ 3.20 Вычислить работу силового поля 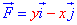 по перемещению материальной точки вдоль линии L:
по перемещению материальной точки вдоль линии L:
x2+y2=1 от точки A (1;0) к точке B (- 1;0).
Решение: Построим траекторию материальной точки против движения часовой стрелки по кругу L: x2+y2=9.
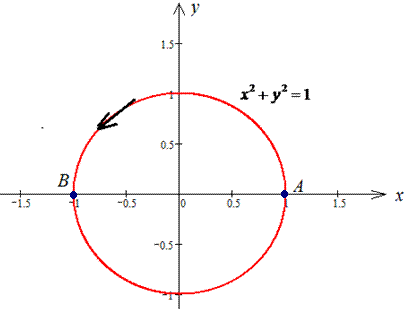
Верхнюю его дуга предствим корневой зависимостью
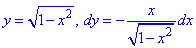
Аргумент при этом изменяется от 1 к -1.
Работа силового поля потрачена на перемещение материальной точки вдоль дуги круга равна интегралу: 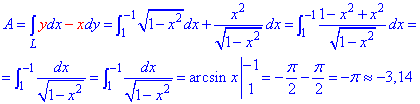
Во время интегрирования получим арксинус, который на границах дает число Pi/2.
Еще один раздел где можно применить криволинейный интеграл ІІ рода теперь доступный и известный Вам.
Будьте внимательные в вычислениях и успешной Вам учебы!
Примеры решений задач по теории поля
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Лучшее спасибо – порекомендовать эту страницу
Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline{a}=(3x-y) overline{i}+(6z+5x) overline{k}$
Задача 3. Дано скалярное поле $u(x,y,z)$ и векторное поле $overline{a}(x,y,z)$. Найти $grad u$, $div overline{a}$, $rot overline{a}$ в точке $M(1;5;-2)$.
$$u=frac{sqrt{x}}{y}-frac{yz}{x+sqrt{y}}, quad
overline{a}=yzoverline{i} +xzoverline{j} +xyoverline{k}$$
Задача 4. Вычислить потенциальную функцию векторного поля
$$overline{a}=left( frac{x}{y}+ycos x right)overline{i} +left(-frac{x^2}{2y^2}+sin xright)overline{j}.$$
Поток поля через поверхность
Задача 5. Найти поток векторного поля $overline{a}=2x overline{i}+y overline{j}-2z overline{k}$ через часть плоскости $P: 2x+y/2+z=1$, расположенную в первом октанте (нормаль образует острый угол с осью $Oz$).
Задача 6. Найти поток векторного поля $overline{a}$ через часть поверхности $S$, вырезаемую плоскостями $P_1, P_2$ (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
$$ overline{a}=(x^3+xy^2)overline{i}+(y^3+x^2y)overline{j}+z^2overline{k},\
S: x^2+y^2=1, P_1^ z=0; P_2: z=3$$
Задача 7. Найти поток векторного поля $overline{a}$ через замкнутую поверхность $S$ (нормаль внешняя).
$$ overline{a}=xoverline{i}+zoverline{j}-yoverline{k},\
S: z=4-2(x^2+y^2), z=2(x^2+y^2).$$
Задача 8. Найти поток векторного поля $overline{a}=x^3overline{i}+y^3overline{j}+z^3overline{k}$ через замкнутую поверхность $S: x^2+y^2+z^2=1$ (нормаль внешняя).
Задача 9. Найти поток векторного поля $overline{a}$ через часть плоскости $S$, вырезанную плоскостью $P: z=1$ непосредственно и с помощью формулы Гаусса-Остроградского (нормаль внешняя к замкнутой поверхности).
$$overline{a}=(x+xy^2) overline{i} + (y-yx^2)overline{j}+(z-3)overline{k}, quad S: x^2+y^2=z^2 (z geq 0).$$
Циркуляция векторного поля
Задача 10. Найти модуль циркуляции векторного поля $overline{a}=xyoverline{i}+yzoverline{j}+zxoverline{k}$ вдоль контура
$$x^2+y^2=9, x+y+z=1.$$
Задача 11. Найдите циркуляцию вектора $overline{a}=(x^2-y) overline{i}+ xoverline{j}+ overline{k}$ по контуру
$$x^2+y^2=1;\
z=1$$
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$.
$$ overline{F} = (3x-1) overline{i}+ (y-x+z)overline{j}+4z overline{k}, $$
$L$ – контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline{F} = xz overline{i} -overline{j}+y overline{k}$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline{F} = z overline{i}+ (x+y)overline{j}+y overline{k}, quad (p): 2x+y+2z=2. $$
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей, оформление производится в Word, срок от 1 дня.
Проконсультируем по задачам теории поля
Полезные ссылки
- Учебник с примерами онлайн по теории поля
- Функции нескольких переменных – задачи с решениями
Сообщения без ответов | Активные темы
Найти работу силового поля вдоль дуги плоской кривой
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
botanik007 |
|
||
|
Подскажите, как такие решать, особенно второй. 1. Найти работу силового поля [math]mathbf{F}(x,y)=x^2mathbf{i}+frac{1}{y^2}mathbf{j}[/math] вдоль дуги плоской кривой [math]xy=1[/math] заключенной между точками (1;1) и (4;1/4) Напишите, пожалуйста, алгоритм и по возможности решение.
|
||
| Вернуться к началу |
|
||
|
botanik007 |
|
||
|
спасибо )
|
|||
| Вернуться к началу |
|
||
|
mad_math |
|
||
|
1. [math]P(x,y)=x^2,Q(x,y)=frac{1}{y^2},AB:y=frac{1}{x},1leq xleq 4[/math]
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю mad_math “Спасибо” сказали: Medvedo |
|||
|
botanik007 |
|
||
|
спасибо
|
|||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти работу поля F вдоль дуги AB кривой Г, если
в форуме Интегральное исчисление |
haykaz1898 |
3 |
769 |
25 апр 2018, 12:52 |
|
Найти работу силового поля
в форуме Интегральное исчисление |
Ryslannn |
11 |
1598 |
29 ноя 2017, 16:32 |
|
Вычислить работу силового поля
в форуме Векторный анализ и Теория поля |
meidina |
1 |
645 |
22 май 2013, 19:20 |
|
Вычислить работу силового поля
в форуме Интегральное исчисление |
kicultanya |
0 |
315 |
05 окт 2018, 20:04 |
|
Найти работу поля вдоль винтовой линии
в форуме Векторный анализ и Теория поля |
DIDG |
0 |
690 |
21 фев 2014, 14:43 |
|
Найти длину дуги плоской кривой ау^2=х^3 0<=x<=5a
в форуме Интегральное исчисление |
karinakarina |
1 |
326 |
13 дек 2016, 21:02 |
|
Длина дуги плоской кривой
в форуме Интегральное исчисление |
kusya |
1 |
205 |
27 ноя 2016, 14:32 |
|
Площадь плоской фигуры и длина дуги кривой
в форуме Интегральное исчисление |
IvanKnyshov1996 |
2 |
485 |
26 апр 2015, 21:57 |
|
Работа силового поля
в форуме Интегральное исчисление |
paul_woker |
4 |
250 |
02 май 2020, 19:58 |
|
Работа силового поля
в форуме Интегральное исчисление |
Ryslannn |
8 |
410 |
30 ноя 2017, 15:09 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB





