Как найти работу по индукции магнитного поля

• Работа по перемещению замкнутого
контура с током в маг­нитном поле

A=IФ,

где Ф— изменение
магнитного потока, пронизывающего
поверх­ность, ограниченную контуром;I— сила тока в контуре.

•
Основной
закон электромагнитной индукции (закон
Фарадея — Максвелла)

где
— электродвижущая сила индукции;N —число витков кон­тура;— потокосцепление.

Частные случаи применения основного
закона электромагнитной индукции:

а) разность потенциалов Uна концах проводника длинойI,
движущегося со скоростьюв однородном магнитном поле,

U=Blsin,

где — угол между
направлениями векторов скоростии магнит­ной индукции В;

б) электродвижущая сила индукции
,
возникающая в рамке, содержащейNвитков, площадьюS,при вращении рамки с угловой скоростью
со в однородном магнитном поле с индукциейВ

где t— мгновенное значение угла между
векторомВи вектором нормалиnк плоскости рамки.

• Количество электричества Q,
протекающего в контуре,

где R —сопротивление
контура;—
изменение потокосцепления.

•Электродвижущая сила самоиндукции

возникающая в замкнутом контуре при
изменении силы тока в нем,

где L —индуктивность
контура.

• Потокосцепление контура =LI,
гдеL —индуктивность контура.

• Индуктивность соленоида (тороида)

Во всех случаях вычисления индуктивности
соленоида (тороида) с сердечником по
приведенной формуле для определения
магнит­ной проницаемости следует
пользоваться графиком зависимости В
отН(см. рис. 24.1), а затем формулой

• Мгновенное значение силы тока Iв цепи, обладающей актив­ным
сопротивлениемRи индуктивностьюL:

а) после замыкания цепи

—ЭДС
источника тока;t—время,
прошедшее после замы­кания цепи;

б) после размыкания цепи

гдеl₀— сила тока в цепи приt=0,
t—время,
прошедшее с момен­та размыкания цепи.

Примеры решения задач

Пример 1.Виток, по которому течет
токI=20 А, свободно уста­новится в
однородном магнитном полеВ=16 мТл.
Диаметрdвитка равен
10 см. Какую работу нужно совершать, чтобы
медленно по­вернуть виток на угол=/2
относительно оси, совпадающей с
диа­метром?

Решение.При
медленном повороте контура в магнитном
поле индукционными токами можно
пренебречь и считать ток в контуре

неизменным. Работа сил поля в этом случае
определяется выраже­нием

где Ф₁и Ф₂— магнитные
потоки, пронизывающие контур в началь­ном
и конечном положениях.

Работа внешних сил будет равна модулю
работе сил поля и про­тивоположна ей
по знаку, т. е.

(1)

Так как в
начальном положении контур установился
свободно (по­ложение устойчивого
равновесия), то момент внешних сил,
действующий
на контур, равен нулю. В этом положении
вектор магнитного мо­ментаp_mконтура сонаправлен с векторомВ(рис. 25.1, а) и магнит­ный поток Ф₁максима­лен (=0,cos=1),
т. е. Ф₁=ВS(гдеS— площадь контура). В ко­нечном
положении (рис. 25.1,б)векторp_mперпендикулярен векторуB
(=/2,cos=0)
и маг­нитный поток Ф₂=0. Перепишем
выражение (1) с учетом сделан­ных
замечаний:

Так как площадь
контура S=d²/4.то работа

Убедимся в том, что правая часть равенства
дает единицу работы (Дж):

Произведем вычисления:

Пример 2.В однородном магнитном
поле с индукциейB=0,1 Тл равномерно
вращается рамка, содержащаяN=1000 витков, с часто­тойn=l0c^-1. ПлощадьSрамки равна 150 см². Определить
мгновен­ное значение ЭДС,
соответствующее углу поворота рамки
30°.

Решение.Мгновенное значение ЭДС индукции,
определя­ется основным уравнением
электромагнитной индукции Фарадея —
Максвелла:

Потокосцепление =NФ,
гдеN —число витков, пронизывае­мых
магнитным потоком Ф. Подставив выражениев формулу (1),

получим

(2)

При вращении рамки магнитный поток Ф,
пронизывающий рам­ку в момент времени
t,изменяется по
законуФ=ВScost,гдеВ — магнитная
индукция;S— площадь
рамки;— угловая
частота. Подставив в формулу (2) выражение
Ф и продифференцировав по времени,
найдем мгновенное значение ЭДС индукции:

(3)

Угловая частота со связана с частотой
пвращения соотношением=2п.Подставив выражение со в формулу (3) и
заменивtна угол, получим

(4)

Убедимся в том, что правая часть
полученного равенства дает единицу ЭДС
(В). Учтя, что 2 ,Nиsint
—величины безразмер­ные и
неименованные, получим

Произведя вычисления по формуле (4),
найдем

Пример. 3По соленоиду течет токI=2
А. Магнитный поток Ф, пронизывающий
поперечное сечение соленоида, равен 4
мкВб. Оп­ределить индуктивностьLсоленоида, если он имеетN=800витков.

Решение.ИндуктивностьLсоленоида связана
с потокосцеплениемсоотношением=LI,
откудаL=/I.Заменив здесь потокосцеплениеего выражением через магнитный поток
Ф и число витковNсоленоида (=ФN),
получим

(1)

Произведя вычисления по формуле (1),
получим

L == 1,6 мГн.

Пример 4.При скорости изменения
силы токаI/tв соле­ноиде, равной 50 А/с, на его концах
возникает ЭДС самоиндук­ции=0,08
В. Определить индуктивностьLсоленоида.

Решение.Индуктивность соленоида связана с ЭДС
само­индукции и скоростью изменения
силы тока в его обмотке соотноше­нием
*

*Сравните с предыдущим
примером

Вынося постоянную величину Lза знак
приращения, получим

Опустив знак минус в этом равенстве
(направление ЭДС в данном случае
несущественно) и выразив интересующую
нас величину — индуктивность, получим

Сделав вычисления по этой формуле,
найдем

L=1,6 мГн.

Пример 5.Обмотка соленоида состоит
из одного слоя плотно прилегающих друг
к другу витков медного провода диаметромd=0,2мм. ДиаметрDсоленоида равен 5 см. По соленоиду течет
токI=1 А. Определить количество
электричестваQ, протекающее
через обмотку, если концы ее замкнуть
накоротко. Толщиной изо­ляции
пренебречь.

Решение.Возможны два способа решения,1-й
способ.Ко­личество электричестваdQ, которое протекает
по проводнику за времяdtпри силе токаI, определяется
равенством

(1)

Полное количество электричества,
протекающее через проводник за время
t, будет.
Сила тока в данном случае убывает
экспоненциально со временем и выражается
формулой

Внося выражение силы тока Iпод знак
интеграла и интегрируя от 0 до(приtI0),получим

Подставим пределы интегрирования и
определим количество электричества,
протекающее через обмотку:

(2)

2-й способ.Подставив в формулу (1)
вместо силы токаIвыраже­ние ее
через ЭДС индукции,и сопротивлениеRсоленоида, т. е.

Но
связана со скоростью изменения
потокосцепленияпо закону Фарадея —Максвелла:=-d/dt,
тогда

Интегрируя, получаем

(3)

Потокосцепление пропорционально силе тока в соленоиде.
Следовательно,₁=LI₀;₂=0, так как₂соответствует тому мо­менту, когда
ток в цепи обратится в нуль. Подставив
выражения₁и₂в формулу
(3), получимQ=₁/R,
или

что совпадает
с формулой (2). Для определения заряда,
протекающего через обмотку соленои­да,
следует найти индуктивность Lсоленоида и сопротивлениеR
обмотки соленоида, которые выражаются
формулами

где ₀
— магнитная постоянная;N —число витков;l₁
—длина соленоида;S₁— площадь сечения соленоида;— удельное сопро­тивление провода;l—длина провода;S—площадь
сечения про­вода;d—диаметр
провода;d₁—диаметр
соленоида.

Подставив
найденные выражения LиRв формулу (2), получим

Заметим, что длина провода lможет
быть выражена через диа­метрd₁соленоида соотношениемl=d₁
N,гдеN —число витков, тогда формуле (4) можно
придать вид

Но l₁/Nесть диаметр провода, так как витки
плотно прилегают друг к другу.
Следовательно,

Произведя вычисления по формуле (5),
получим

Q=363 мкКл.

Задачи

Работа
по перемещению проводника * в магнитном
поле

25.1.В однородном магнитном поле
с индукциейB=0,01 Тл находится прямой
провод длинойl=8см, расположенный
перпен­дикулярно линиям индукции. По
проводу течет токI=2 А. Под действием
сил поля провод переместился на расстояниеs=5 см. Найти работуAсил поля.

25.2.Плоский контур, площадьS которого
равна 300 см², на­ходится в
однородном магнитном поле с индукциейВ=0,01 Тл. Плоскость контура
перпендикулярна линиям индукции. В
контуре поддерживается неизменный токI=10 А. Определить работуА внешних
сил по перемещению контура с током в
область пространст­ва, магнитное поле
в которой отсутствует.

25.3.По
проводу, согнутому в виде квадрата со
стороной дли­нойа=10 см, течет токI=20 А, сила которого поддерживается
не­изменной. Плоскость квадрата
составляет угол=20°
с линиями индукции однородного магнитного
поля(В=0,1 Тл). Вычислить работуA,
которую необходимо совершить для того,
чтобы удалить провод за пределы поля.

25.4.По
кольцу, сделанному из тонкого гибкого
провода радиу­сомR=10 см, течет токI=100 А. Перпендикулярно плоскости
коль­ца возбуждено магнитное поле с
индукциейB=0,1 Тл, по направле­нию
совпадающей с индукциейB₁собственного магнитного поля кольца.
Определить работуАвнешних сил,
которые, действуя на провод, деформировали
его и придали ему форму квадрата. Сила
тока при этом поддерживалась неизменной.
Работой против упру­гих сил пренебречь.

*
Перемещение проводника или контура с
током в магнитном поле счи­тать
настолько медленным, что возникающими
индукционными токами можно пренебречь.

25.5(1).Виток, по которому течет токI=20 А, свободно устано­вился в
однородном магнитном поле с индукциейВ=0,016 Тл. Диа­метрdвитка равен 10 см. Определить работуA,
которую нужно совершить, чтобы повернуть
виток на угол=/2
относительно оси, совпадающей с диаметром.
То же, если угол=2.

25.5(2).Квадратная рамка со стороной
а=10см, по которой течет токI=200 А,
свободно установилась в однородном
магнитном поле (B=0,2 Тл). Определить
работу, которую необходимо совер­шить
при повороте рамки вокруг оси, лежащей
в плоскости рамки и перпендикулярной
линиям магнитной индукции, на угол=2/з.

Электродвижущая
сила индукции

25.6.Магнитный поток Ф=40 мВб
пронизывает замкнутый контур. Определить
среднее значение ЭДС индукции <>,
возни­кающей в контуре, если магнитный
поток изменится до нуля за времяt=2
мс.

25.7.Прямой провод длинойl=40
см движется в однородном магнитном поле
со скоростью=5м/с перпендикулярно линиям индукции.
Разность потенциаловUмежду концами провода равна 0,6 В. Вычислить
индукциюВмагнитного поля.

25.8.В однородном магнитном поле с
индукциейВ=1Тл нахо­дится прямой
провод длинойl=20 см, концы которого
замкнуты вне поля. СопротивлениеRвсей цепи равно 0,1 Ом. Найти силуF,
которую нужно приложить к проводу,
чтобы перемещать его пер­пендикулярно
линиям индукции со скоростью=2,5
м/с.

25.9.Прямой провод длинойl=10 см
помещен в однородном маг­нитном поле
с индукциейВ=1 Тл. Концы его замкнуты
гибким про­водом, находящимся вне
поля. СопротивлениеRвсей цепи равно
0,4 Ом. Какая мощностьРпотребуется
для того, чтобы двигать про­вод
перпендикулярно линиям индукции со
скоростью=20 м/с?

25.10.К
источнику тока с ЭДС=0,5
В и ничтожно малым внут­ренним
сопротивлением присоединены два
металлических стержня, расположенные
горизонтально и параллельно друг другу.
Рас­стояниеlмежду стержнями
равно 20 см. Стержни находятся в однородном
магнитном поле, направленном вертикально.
Магнит­ная индукцияВ=1,5 Тл. По
стержням под действием сил поля сколь­зит
со скоростью=lм/с прямолинейный провод сопротивлениемR=0,02 Ом. Сопротивление стержней
пренебрежимо мало. Опреде­лить: 1) ЭДС
индукции2) силуF, действующую на
провод со стороны поля; 3) силу токаIв цепи; 4) мощностьP₁,
расходуемую на движение провода; 5)
мощность Р₂, расходуемую на
нагревание провода; 6) мощность Р₃,
отдаваемую в цепь источника тока.

25.11.В
однородном магнитном поле с индукциейB=0,4 Тл в плоскости,
перпендикулярной линиям индукции поля,
вращается

стержень
длиной l=10 см. Ось
вращения проходит через один из концов
стержня. Определить разность потенциаловUна концах стержня
при частоте вращенияn=16
с^-1.

25.12.Рамка площадьюS=200
см²равномерно вращается с частотойn=10 с^-1относительно
оси, лежащей в плоскости рамки и
перпендикулярно линиям индукции
однородного магнитного поля (B=0,2
Тл). Каково среднее значение ЭДС индукции
<_i>
за время, в течение которого магнитный
поток, пронизывающий рамку, из­менится
от нуля до максимального значения?

25.13.В однородном магнитном поле с
индукциейB=0,35 Тл
равномерно с частотойn=480
мин^-1вращается рамка, содержащаяN=500витков площадьюS=50
см². Ось вращения лежит в плос­кости
рамки и перпендикулярна линиям индукции.
Определить максимальную ЭДС индукции
ε_max, возникающую в
рамке.

25.14.Рамка площадьюS=100
см²содержитN=10³витков провода сопротивлениемR₁=l2
Ом. К концам обмотки подключено внешнее
сопротивлениеR₂=20
Ом. Рамка равномерно вращается в
однородном магнитном поле (B=0,1
Тл) с частотойn=8 с^-1.
Оп­ределить максимальную мощностьP_maxпеременного тока в цепи.

25.15.Магнитная индукцияBполя между полюсами двухполюс­ного
генератора равна 0,8 Тл. Ротор имеетN=100
витков площадьюS=400
см². Определить частотупвращения якоря, если максималь­ное
значение ЭДС индукции_i=200 В.

25.16.Короткая катушка, содержащаяN=1000 витков, рав­номерно
вращается в однородном магнитном поле
с индукциейB=0,04 Тл с
угловой скоростью ω=5 рад/с относительно
оси, совпа­дающей с диаметром катушки
и перпендикулярной линиям индук­ции
поля. Определить мгновенное значение
ЭДС индукции_iдля тех моментов времени, когда плоскость
катушки составляет уголα=60°
линиями индукции поля. ПлощадьSкатушки равна 100 см².

Количество
электричества, протекающее в контуре
при изменении магнитного потока^*

25.17.Проволочный виток радиусомr=4
см, имеющий сопротив­лениеR=0,01
Ом, находится в однородном магнитном
поле с ин­дукциейB=0,04
Тл. Плоскость рамки составляет уголα=30° с линиями индукции
поля. Какое количество электричестваQпроте­чет по витку,
если магнитное поле исчезнет?

25.18.Проволочное кольцо радиусомr=10 см лежит на столе.
Какое количество электричестваQпротечет по кольцу, если его повернуть
с одной стороны на другую? СопротивлениеRкольца равно 1 Ом.
Вертикальная составляющая индукцииВмагнитного поля Земли равна 50 мкТл.

25.19.В проволочное кольцо, присоединенное
к баллистическому гальванометру,
вставили прямой магнит. По цепи протекло
количество электричестваQ=10
мкКл. Определить магнитный поток Ф,
пересеченный кольцом, если сопротивлениеRцепи гальванометра
равно 30 Ом.

25.20.Между полюсами электромагнита
помещена катушка, сое­диненная с
баллистическим гальванометром. Ось
катушки парал­лельна линиям индукции.
Катушка сопротивлениемR₁=4
Ом име­етN=15 витков
площадьюS=2 см².
СопротивлениеR₂гальвано­метра равно 46 Ом. Когда ток
в обмотке электромагнита выключи­ли,
по цепи гальванометра протекло количество
электричестваQ=90
мкКл. Вычислить магнитную индукциюВполя электромаг­нита.

25.21.Рамка из провода сопротивлениемR=0,01 Ом равномер­но
вращается в однородном магнитном поле
с индукциейB=0,05 Тл.
Ось вращения лежит в плоскости рамки и
перпендикулярна линиям индукции. ПлощадьSрамки равна 100 см².
Найти, какое количест­во электричестваQ протечет через
рамку за время поворота ее на угол α=30°
в следующих трех случаях: 1) от α₀=0
до α₁=30°; 2) от α₁до α₂=60°;
3) от α₃=90°.

25.22.Тонкий медный провод массойт=1г согнут в виде квад­рата, и
концы его замкнуты. Квадрат помещен в
однородное маг­нитное поле (B=0,1
Тл) так, что плоскость его перпендикулярна
линиям индукции поля. Определить
количество электричества Q, которое
протечет по проводнику, если квадрат,
потянув за противо­положные вершины,
вытянуть в линию.

25.23.На расстоянииа= 1 м от длинного
прямого провода с то­комI=кА
находится кольцо радиусомr=1
см. Кольцо расположе­но так, что
поток, пронизывающий его, максимален.
Определить количество электричестваQ, которое протечет по кольцу, когда
ток в проводнике будет выключен.
СопротивлениеRкольца 10 Ом.

Указание.
Поле в пределах кольца считать однородным.

25.24.По длинному прямому проводу
течет ток. Вблизи провода расположена
квадратная рамка из тонкого провода
сопротивле­ниемR=0,02
Ом. Провод лежит в плоскости рамки и
параллелен двум ее сторонам, расстояния
до которых от провода соответствен­но
равныa₁=10
см,a₂=20 см.
Найти силу токаIв
проводе, если при его включении через
рамку протекло количество электричест­ваQ=693 мкКл.

Тема: Магнитный поток.

Работа по перемещению

проводника с током

в магнитном поле.

Цель:

• сформулировать понятие магнитный поток, показать от чего он зависит, и записать формулу для его вычисления;
• показать, какая работа совершается магнитным полем при перемещении проводника с током;
• научить решать задачи по данной теме.

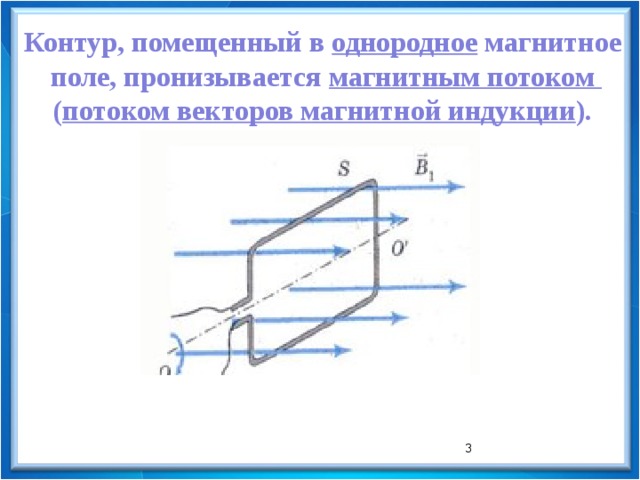
Контур, помещенный в однородное магнитное

поле, пронизывается магнитным потоком

( потоком векторов магнитной индукции ).

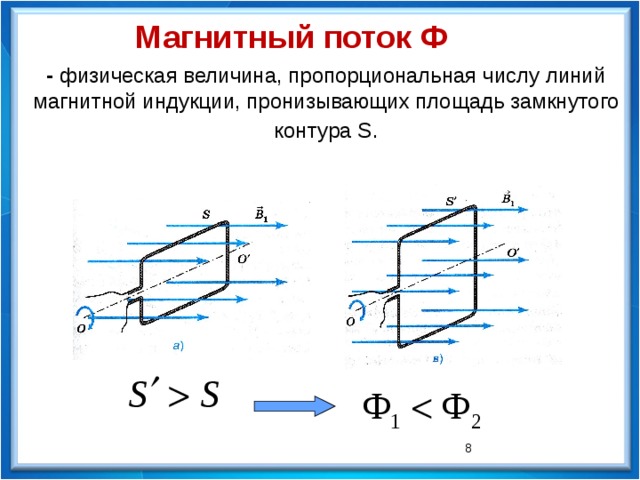
Магнитный поток ─ это физическая величина,

пропорциональная числу линий магнитной

индукции, пронизывающих площадь замкнутого

контура S.

Магнитный поток обозначается (Ф)

Единица магнитного потока в СИ –

вебер (Вб)

Магнитный поток Ф

характеризует магнитное поле, пронизывающее поверхность S

Ф – магнитный поток , пронизывающий площадь

контура, зависит от величины вектора магнитной

индукции , площади контура и его ориентации

относительно линий индукции магнитного поля .

Если вектор магнитной индукции перпендикулярен площади контура, то магнитный поток максимальный.

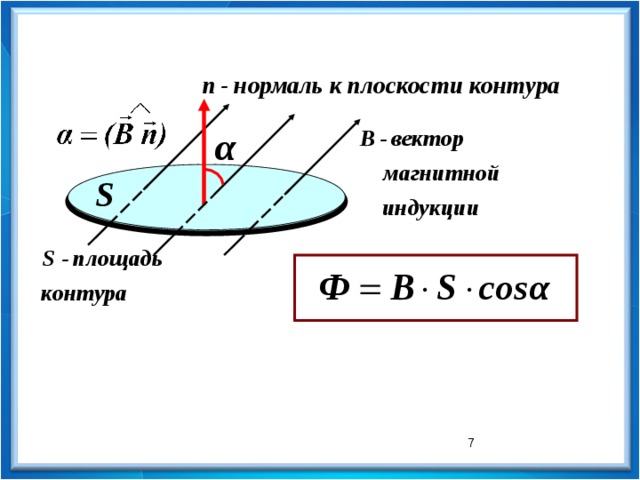
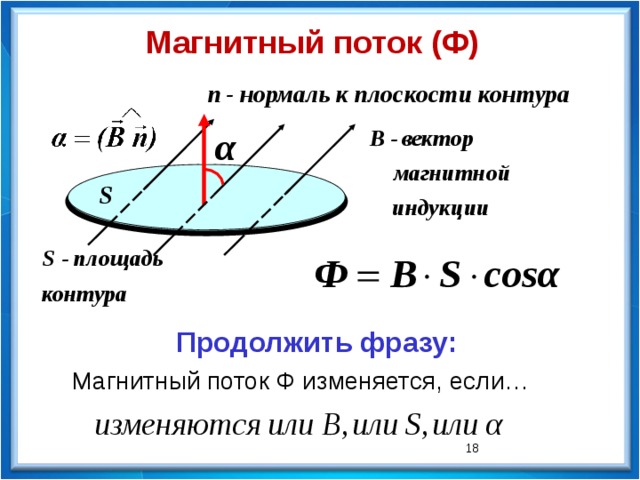
Магнитный поток Ф – физическая величина,

численно равная произведению модуля магнитной

индукции на площадь контура и на косинус угла

между нормалью к контуру и вектором магнитной

индукции.

Магнитный поток через контур равен нулю, если контур

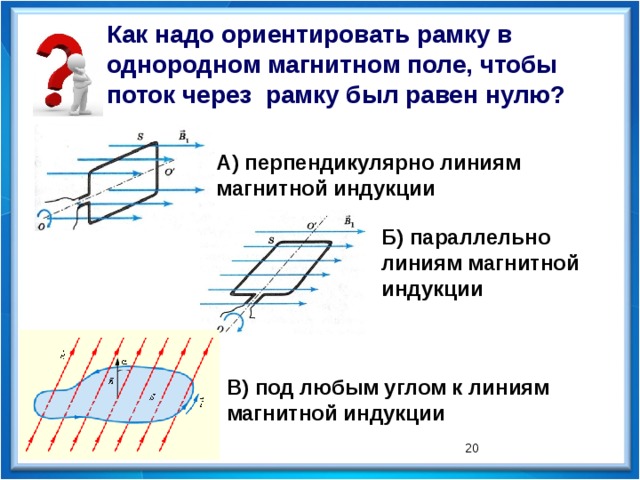
располагается параллельно магнитному полю.

Магнитный поток Ф

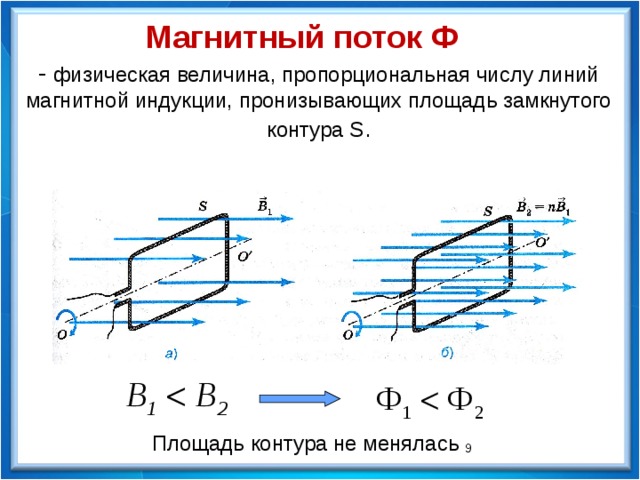
– физическая величина, пропорциональная числу линий магнитной индукции, пронизывающих площадь замкнутого контура S .

Магнитный поток Ф

– физическая величина, пропорциональная числу линий магнитной индукции, пронизывающих площадь замкнутого контура S .

Площадь контура не менялась

Работа по перемещению проводника с током в магнитном поле

Сила Ампера:

При перемещении проводника под действием F A на расстояние dx совершается работа:

Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.

Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.

Физкультминутка

• Колебательные движения головы
• Колебательные движения головы

влево – вправо (5 раз)

2.Вращательное движение головы,

подбородком касаясь груди

влево – вправо (5 раз)

3.Наклоны влево – вправо (5 раз)

Чему равен магнитный поток, пронизывающий контур, площадь которого 60см 2 ? Модуль вектора магнитной индукции однородного магнитного поля равен 50мТл. Контур расположен перпендикулярно линиям магнитной индукции.

Магнитный поток через квадратную проволочную рамку со стороной 20см, плоскость которой перпендикулярна линиям магнитной индукции однородного магнитного поля, равен 0,1мВб. Каков модуль вектора магнитной индукции поля? Ответ в мТл.

Прямой проводник длиной 15см помещён в однородное магнитное поле с индукцией 0,4Тл, направленной перпендикулярно направлению тока. Сила тока, протекающего по проводнику, равна 6А. Найдите силу Ампера, действующую на проводник.

В проводнике с длиной активной части 8см сила тока равна 50А. Он находится в однородном магнитном поле с индукцией 20мТл. Какую работу совершил источник тока, если проводник переместился на 10см перпендикулярно линиям индукции?

Индукция однородного магнитного поля В=0,3Тл направлена в положительном направлении оси Х. Найдите модуль и направление силы Лоренца, действующей на протон, движущийся в положительном направлении оси Y со скоростью ʋ=5∙10 6 м/с.

Магнитный поток (Ф)

Продолжить фразу:

Магнитный поток Ф изменяется, если…

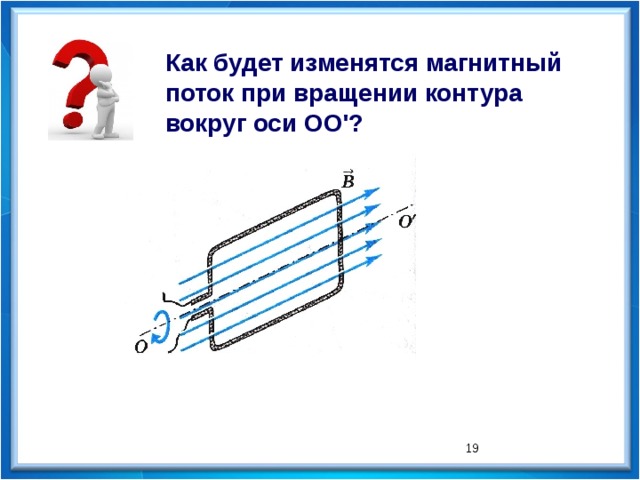
Как будет изменятся магнитный поток при вращении контура вокруг оси ОО ‘?

Как надо ориентировать рамку в однородном магнитном поле, чтобы поток через рамку был равен нулю?

А) перпендикулярно линиям магнитной индукции

Б) параллельно линиям магнитной индукции

В) под любым углом к линиям магнитной индукции

Домашнее задание:

§153, §154 повторить

§155 и §156 законспектировать

Подготовиться к физ. диктанту

Решить задачи 17.62, 17.63

Рефлексия:

• Довольны ли вы тем , как прошло занятие?
• Было ли вам интересно?
• Что больше всего вам понравилось на уроке?
• Сумели ли вы закрепить свои знания?
• Сумели ли вы показать свои знания?
• Были ли вы активны на уроке?
• Преподаватель был внимателен к вам?

Спасибо за внимание!

Как и любая другая сила, сила Ампера имеет возможность совершить работу. По определению механической работы:

(1)

Рис. 1. Работа силы Ампера

Пусть в нашей системе проводник длиной , находящийся в однородном магнитном поле индукции , по которому течёт ток , движется под действием силы Ампера и перемещается на расстояние  (рис. 1). Тогда, при условии, что сила Ампера равна , получим:

(2)

Пометим  — площадь, «заметаемая» при движении проводника. Т.е. площадь, которую «прошёл» проводник во время движения. Тогда, в общем случае:

(3)

Соотношение (3) указывает на работу сил Ампера. Однако, если использовать определение изменения потока магнитного поля:

Ф (4)

получим:

Ф (5)

• где

Электромагнитная индукция

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​( S )​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​( B )​, площади поверхности ​( S )​, пронизываемой данным потоком, и косинуса угла ​( alpha )​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​( Phi )​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​( alpha )​ магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​( N )​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​( R )​:

При движении проводника длиной ​( l )​ со скоростью ​( v )​ в постоянном однородном магнитном поле с индукцией ​( vec{B} )​ ЭДС электромагнитной индукции равна:

где ​( alpha )​ – угол между векторами ​( vec{B} )​ и ( vec{v} ).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​( varepsilon_{is} )​, возникающая в катушке с индуктивностью ​( L )​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​( Phi )​ через контур из этого проводника пропорционален модулю индукции ​( vec{B} )​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​( L )​ между силой тока ​( I )​ в контуре и магнитным потоком ​( Phi )​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.

Содержание:

1. Электромагнитная индукция
2. Потокосцепление и индуктивность
3. Явление электромагнитной индукции
4. ЭДС индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки
5. Опыты Фарадея
6. Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений
7. Величина ЭДС индукции
8. Вихревое электрическое поле и его связь с магнитным полем
9. Вихревые токи
10. Роль магнитных полей в явлениях, происходящих на Солнце и в космосе
11. Явление самоиндукции ЭДС самоиндукции
12. Энергия магнитного поля

Электромагнитная индукция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении магнитного поля во времени или при движении материальной среды в магнитном поле. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Электромагнитная индукция

Электромагнитная индукция – это явление возникновения тока в замкнутом проводнике при прохождении через него магнитного потока, изменяющегося со временем.

Потокосцепление и индуктивность

Была приведена формула (22.10), которую можно использовать для вычисления работы при повороте контура с током во внешнем магнитном поле. Выясним теперь, как подсчитать работу при повороте соленоида во внешнем магнитном поле, если он имеет  витков.

Поскольку работа при повороте одного витка равна а в рассматриваемом случае магнитный поток пронизывает витков, то работа при повороте соленоида выразится формулой

Если обозначить произведение через  (греч. «пси»), то для работы получим формулу

или     (23.1)

Величину характеризующую связь («сцепление») магнитного потока с замкнутой цепью, сквозь которую он проходит, называют потокосцеплением. Если магнитный поток Ф пронизывает катушку с числом витков то потокосцепление равно произведению числа витков на магнитный поток:

   (23.2)

(Покажите, что единицей потокосцепления в СИ является вебер; §22.12.)

Теперь представим себе любую замкнутую цепь, по которой течет ток I. Этот ток создает свое собственное магнитное поле вокруг цепи. Пусть сквозь поверхность, охваченную проводниками замкнутой цепи, проходит собственный поток Ф. Если эта цепь представляет собой один плоский контур, то равно Ф. Если же проводники цепи образуют катушку с витками, то  Таким образом, собственное потокосцепление цепи зависит от ее конфигурации, т. е. от расположения проводников в пространстве.

Опыт показал, что когда в замкнутой цепи нет ферромагнетиков, то собственное потокосцепление этой цепи изменяется прямо пропорционально силе тока I в ней:

    (23.3)

Коэффициент пропорциональности L остается постоянным только при неизменной конфигурации проводов замкнутой цепи и неизменной окружающей среде. Коэффициент L, характеризующий зависимость собственного потокосцепления замкнутой цепи от ее формы и от окружающей среды, называется индуктивностью цепи.

Выведем единицу индуктивности L в СИ:

За единицу индуктивности в СИ принимают генри (Гн). Генри называют индуктивность такой цепи, в которой возникает потокосцепление в 1 Вб при токе в 1 А.

Вспомним, что единица магнитной проницаемости в СИ имеет наименование (§22.8) или (§22.14). Так как (§22.12), то Обычно используют последнее наименование — генри на метр.

В качестве примера определим индуктивность соленоида L_coл. Из (23.3) имеем

Так как Ф_сол определяется соотношением (22.15), то

    (23.4)

Таким образом, индуктивность соленоида определяется средой, размерами и числом витков соленоида.

Явление электромагнитной индукции

Было установлено, что электрический ток и его магнитное поле всегда существуют одновременно. Фарадей, зная о тесной связи между током и магнитным полем, был уверен, что с помощью магнитного поля можно создать в замкнутом проводнике электрический ток. Он провел многочисленные опыты и доказал это, открыв в 1831 г. явление электромагнитной индукции.

Возникновение в замкнутом проводнике электрического тока, обусловленное изменением магнитного поля, называют явлением электромагнитной индукции. Полученный таким способом ток называют индукционным (наведенным), а создающую его э. д. с. называют э. д. с. индукции.

Всесторонние исследования явления электромагнитной индукции показали, что с помощью этого явления можно получить электрический ток практически любой мощности, что позволяет широко использовать электрическую энергию в промышленности. В настоящее время почти вся электрическая энергия, используемая на производстве, получается с помощью индукционных генераторов, принцип работы которых основан на явлении электромагнитной индукции. Поэтому Фарадей по праву считается одним из основателей электротехники.

Рассмотрим подробнее явление электромагнитной индукции.

ЭДС индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки

Пусть в однородном магнитном поле с индукцией В находится прямолинейный металлический проводник длиной l (рис. 23.1). Если этот проводник привести в движение со скоростью  так, чтобы угол  между векторами В и составлял 90°, то вместе с проводником будут направленно двигаться и его собственные электроны. Так как их движение происходит в магнитном поле, то на них должна действовать сила Лоренца.

Рис. 23.1.

С помощью правила левой руки можно установить, что свободные электроны будут смещаться к концу провода А. Напряжение U, которое при этом возникает между концами провода A и В, создаст в нем электрическую силу которая уравновесит силу Лоренца Итак, смещение электронов к концу А прекратится при Поскольку a  имеем откуда

Так как напряжение на полюсах при разомкнутой цепи равно э. д. с., то э. д. с. индукции, возникающая в проводнике при его движении в магнитном поле, выражается формулой

   (23.5)

Заметим, что сторонними силами, создающими э. д. с., здесь являются магнитные силы, действующие на свободные электроны в проводнике. Если этот проводник включить в цепь, то в ней возникнет индукционный ток; это можно установить по показанию гальванометра G.

Направление индукционного тока, возникающего в прямолинейном проводнике при его движении в магнитном поле, определяется по правилу правой руки (рис. 23.2): если правую руку расположить вдоль проводника так, чтобы линии магнитной индукции входили в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца укажут направление индукционного тока в проводнике.

Рис. 23.2.

Опыты Фарадея

Рассмотрим опыты Фарадея, с помощью которых он открыл явление электромагнитной индукции.

1. Возьмем соленоид, соединенный с гальванометром (рис. 23.3), и будем вдвигать в него постоянный магнит. Оказывается, что при движении магнита стрелка гальванометра отклоняется. Если же магнит останавливается, то стрелка гальванометра возвращается в нулевое положение. То же самое получается при выдвижении магнита из соленоида или при надевании соленоида на неподвижный магнит. Такие опыты показывают, что индукционный ток возникает в соленоиде только при относительном’ перемещении соленоида и магнита.

Рис. 23.3. 

2. Будем опускать в соленоид В катушку с током А (рис. 23.4). Оказывается, что и в этом случае в соленоиде В возникает индукционный ток только при относительном перемещении соленоида В и катушки А.

Рис. 23.4.

3. Вставим катушку А в соленоид В и закрепим их неподвижно (рис. 23.5). При этом тока в соленоиде нет. Но в моменты замыкания или размыкания цепи катушки А в соленоиде В появляется индукционный ток. То же самое получается в моменты усиления или ослабления тока в катушке А с помощью изменения сопротивления R.

Рис. 23.5.

В дальнейшем цепь катушки А, соединенную с источником электрической энергии, будем называть первичной, а цепь соленоида В, в которой возникает индукционный ток, — вторичной. Эти же названия будем применять и к самим катушкам.

4. Включим первичную катушку в сеть переменного тока, а вторичную катушку соединим с лампой накаливания (рис. 23.6). Оказывается, лампа непрерывно горит, пока в первичной катушке течет переменный ток.

Рис. 23.6.

Нетрудно заметить, что общим для всех описанных опытов является изменение магнитного поля в соленоиде, которое и создает в нем индукционный ток.

Выясним теперь, всякое ли изменение магнитного поля вокруг замкнутого контура наводит в нем индукционный ток. Возьмем плоский контур в виде рамки, соединенной с гальванометром. Поместим рядом с рамкой магнит так, чтобы его линии индукции не проходили внутри рамки, а находились в ее плоскости (рис. 23.7, а).

Рис. 23.7.

Оказывается, что при перемещении рамки или магнита вдоль плоскости рисунка .стрелка гальванометра не отклоняется. Если же рамку поворачивать вокруг оси 00′ (рис. 23.7, б), то в ней возникает индукционный ток.

На основании описанных опытов можно сделать следующий вывод: индукционный ток (и э. д. с. индукции) в замкнутом контуре появляется только в том случае, когда изменяется магнитный поток, который проходит через площадь, охваченную контуром.

Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений

Индукционный ток создает собственное магнитное поле. Связь между направлением индукционного тока в контуре и индуцирующим магнитным полем была установлена Ленцем.

В опыте, изображенном, на рис. 23.3, индукционный ток в соленоиде создает магнитное поле, полюсы которого указаны в отверстии соленоида. Проследив взаимодействие между магнитными полюсами соленоида и магнита во всех четырех случаях, приведенных на рисунке, и сравнив его с направлением движения магнита, можно видеть, что взаимодействие между полюсами всегда препятствует движению магнита. Ленцу удалось обобщить эту закономерность на все случаи электромагнитной индукций. Найденную им связь называют законом (правилом) Ленца для электромагнитной индукции: э. д. с. индукции создает в замкнутом контуре такой индукционный ток, который своим магнитным полем препятствует причине, вызывающей появление этой э. д. с.

Используя закон Ленца для определения направления индукционного тока, следует поступать следующим образом:

1)  найти причину, создающую индукционный ток;

2)  считая, что индукционный, ток противодействует этой причине, найти направление его магнитного поля;

3)  определить направление индукционного тока по направлению его магнитного поля.

Приведем пример. Причиной, вызывающей появление индукционного тока во вторичной катушке при размыкании цепи первичной катушки (рис. 23.5), является исчезновение поля первичной катушки. Мешая этому исчезновению, индукционный ток во_вторичной катушке должен создавать магнитное поле такого же направления, как у поля первичной катушки. Следовательно, направление индукционного тока во вторичной катушке будет совпадать с направлением тока, который протекал в первичной катушке до размыкания. (Покажите, что при замыкании цепи первичной катушки во вторичной возникает ток обратного направления.)

Из закона Ленца можно установить, что энергия индукционного тока в проводнике получается за счет той энергии, которая затрачивается на преодоление противодействия магнитного поля индукционного тока. Например, если разомкнуть цепь катушки, изображенной на рис. 23.3, и подсчитать работу, нужную для того, чтобы вставить в нее и вынуть магнит определенное число раз, а затем повторить этот опыт при замкнутой цепи, то во втором случае работа будет заметно больше, чем в первом. Это объясняется тем, что в первом случае собственного магнитного поля вокруг катушки нет, так как в ней нет тока, а во втором случае поле есть. Лишняя работа во втором случае идет на преодоление противодействия этого поля и равна энергии индукционного тока в катушке. Нетрудно видеть, что с помощью явления электромагнитной индукции можно превращать механическую энергию в электрическую, а также передавать электрическую энергию из одной цепи в другую.

Когда индукционный ток возникает вследствие какого-либо механического движения, то электрическая энергия получается за счет механической. Такое превращение энергии происходит в индукционных генераторах, установленных на электростанциях. Когда же индукционный ток возникает при отсутствии механического движения, то электрическая энергия переходит из одной цепи в другую. Такая передача энергии происходит в трансформаторах (§ 26.5).

Явлением электромагнитной индукции объясняют диамагнитный эффект. Когда вещество попадает в магнитное поле, на каждый движущийся по орбите электрон начинает действовать сила Лоренца, которая увеличивает или уменьшает (в зависимости от направления вращения электрона) центростремительную силу, действующую на электрон. Это приводит к изменению орбиты и частоты обращения электрона, что равносильно уменьшению или увеличению кругового тока, соответствующего движению электрона по орбите, причем получается, что круговые токи электронов усиливаются, если их магнитные поля направлены против внешнего поля, и уменьшаются, если они направлены по полю.

Таким образом, если в отсутствие внешнего поля круговые токи электронов в молекуле диамагнетика уравновешивают друг друга и молекула не имеет магнитного момента, то во внешнем поле это равновесие нарушается и возникает результирующий магнитный момент молекулы, направленный против внешнего поля. Этот результат, вообще говоря, прямо следует и из закона Ленца: изменение круговых токов в молекуле является индукционным током, и его магнитное поле должно быть направлено против вызвавшего его внешнего поля.

Диамагнитный эффект возникает во всех веществах, но если молекулы вещества имеют собственные магнитные моменты, которые ориентируются по направлению внешнего магнитного поля и усиливают его, то диамагнитный эффект перекрывается более сильным парамагнитным эффектом и вещество оказывается парамагнетиком.

Сильный диамагнитный эффект наблюдается при сверхпроводимости. Когда сверхпроводник попадает в магнитное поле, в нем, как и в обычном проводнике, наводятся индукционные токи, но, в отличие от молекулярных индукционных токов, их образуют свободные электроны. В сверхпроводнике эти индукционные токи не встречают сопротивления и циркулируют, пока существует внешнее магнитное поле, противодействуя его проникновению внутрь сверхпроводника. Сверхпроводники, как и все диамагнетики, выталкиваются из магнитного поля.

Величина ЭДС индукции

При выполнении опытов Фарадея можно видеть, что стрелка гальванометра отклоняется тем дальше, чем быстрее вдвигается в соленоид магнит или катушка с током (§ 23.4). То же самое получится, если усилить магнитное поле первичной катушки, увеличив в ней ток. Подробное изучение этого явления показало, что э. д. с. индукции, возникающая в какой-либо цепи, прямо пропорциональна скорости изменения потокосцепления магнитного поля с этой цепью:

   (23.6)

Отметим, что когда цепь состоит из одного витка, т. е. является простым контуром, то формула (23.6) принимает вид

    (23.6а)

В этих формулах  — время, за которое происходит изменение потокосцепления на Если очень мало, то формулы (23.6) дают мгновенное значение э. д. с. индукции. Если же велико, то при подсчете по этим формулам получается среднее значение э. д. с. индукции.

Знак минус в формулах показывает, что, когда потокосцепление уменьшается ( отрицательно), э. д. с. создает индукционный ток, увеличивающий потокосцепление, и наоборот. Таким образом, знак минус показывает, что в соответствии с законом Ленца э. д. с. индукции должна препятствовать причине, вызывающей ее появление.

Из формулы (23.6а) видно, что единицу магнитного потока в СИ можно назвать вольт-секундой, так как

Вихревое электрическое поле и его связь с магнитным полем

Появление э. д. с. индукции в прямолинейном проводнике, движущемся в магнитном поле, было объяснено действием силы Лоренца на подвижные носители зарядов. Однако объяснить таким способом появление э. д. с. индукции во вторичной цепи при неподвижной относительно нее первичной цепи (четвертый опыт в § 23.4) оказалось невозможным, поскольку магнитное поле не действует на покоящиеся заряды.

Вспомним, что на покоящиеся заряды действует электрическое поле. Не оно ли создает индукционный ток во вторичной цепи? Если это так, то откуда это электрическое поле берется? Объяснить это можно тем, что переменное магнитное поле может создавать электрическое поле, которое уже и возбуждает в замкнутом проводнике индукционный ток.

Такое объяснение явления электромагнитной индукции впервые дал Д. Максвелл. Развивая эту идею, он создал теорию электромагнитного поля, которая была подтверждена многими опытами. По теории Максвелла в пространстве, в котором изменяется магнитное поле, обязательно возникает электрическое поле с замкнутыми линиями напряженности, независимо от присутствия вещества.

На рис. 23.8 прямые линии изображают изменяющееся магнитное поле с индукцией В, возрастающей (а) и убывающей (б), а замкнутые линии — возникшее электрическое поле, напряженность которого Е. Если в этом пространстве окажется проводник, то в нем возникнет индукционный ток. Например, при выдвижении магнита из катушки на рис. 23.3, г возникает электрическое поле, изображенное на рис. 23.8, б, которое и создает ток в соленоиде. (Объясните, как возникает ток в других случаях, показанных на рис. 23.3.)

Рис. 23.8.

На рис. 23.8 видно, что линии электрического и магнитного полей расположены во взаимно перпендикулярных плоскостях. Исследования показали, что вектор напряженности (индукции) магнитного поля в каждой точке пространства перпендикулярен вектору напряженности созданного им электрического поля. Именно поэтому наибольшая э. д. с. индукции в прямолинейном проводнике возникает тогда, когда он движется перпендикулярно к линиям индукции магнитного поля.

Вихревые токи

Возьмем катушку с выступающим сердечником из мягкого ферромагнетика и положим на его конец металлический предмет. Если катушку включить в сеть переменного тока, то предмет быстро и сильно нагревается.

Заменим предмет алюминиевым кольцом К, надетым на сердечник (рис. 23.9), и снова включим катушку в сеть. Если кольцо держать, то оно сильно нагревается, а если не держать, то при включении катушки в сеть оно соскакивает с сердечника. Описанные явления объясняются тем, что изменяющееся магнитное поле вокруг сердечника создает электрическое поле, поэтому в теле и в кольце возникают сильные индукционные токи, так как сопротивление тела и кольца очень маленькое. Эти токи и нагревают их. Соскакивает кольцо потому, что индукционный ток в кольце направлен противоположно току в катушке, а такие токи отталкиваются друг от друга.

Рис. 23.9.

Индукционные токи, которые возникают в сплошных металлических телах, находящихся в переменном магнитном поле, и замыкаются внутри этих тел, называют вихревыми токами или токами Фуко (в честь французского ученого Ж. Фуко, который их исследовал).

Якорь электродвигателя и сердечник трансформатора по условиям

своей работы находятся в переменном магнитном поле, поэтому в них должны циркулировать вихревые токи. Энергия, затраченная на создание вихревых токов, превращается во внутреннюю энергию якоря и сердечника, т. е. идет на их нагревание (кроме потерь энергии на нагревание вихревыми токами, в них возникают еще и потери, обусловленные гистерезисом). Для ослабления вредного действия вихревых токов тела, которые должны находиться в переменном магнитном поле, делают из отдельных листов, изолированных друг от друга (рис. 23.10).

Рис. 23.10.

Заметим, что ферриты имеют очень большое удельное сопротивление, поэтому вихревые токи в них практически не возникают, и это значительно уменьшает потери энергии в них. Поскольку потери энергии, вызванные гистерезисом, в ферритах тоже очень малы, их применение заметно повышает к. п. д. приборов, например трансформаторов.

Если вихревой ток вызывается движением тела в магнитном поле, то согласно закону Ленца этот ток должен тормозить движение тела. Тормозящее действие вихревых токов можно проиллюстрировать с помощью следующего опыта.

Если медную пластинку Р (рис. 23.11) заставить колебаться при выключенном токе в электромагните М, а затем при включенном токе в нем, то будет видно, что во втором случае колебания прекращаются почти мгновенно. Внешне кажется, что в этом случае пластинка как бы вязнет в густой жидкости. Тормозящее действие вихревых токов используется в измерительных приборах для успокоения колебаний стрелки измерительного механизма.

Рис. 23.11.

В современной технике нагревание вихревыми токами используется для закалки деталей и для изготовления сплавов в индукционных печах.

Роль магнитных полей в явлениях, происходящих на Солнце и в космосе

Изучение Солнца показало, что оно имеет магнитное поле, напряженность которого примерно в два раза выше, чем у поля Земли. Многие явления, происходящие в атмосфере Солнца (образование темных пятен, факелов и др.), тесно связаны с возникновением и развитием в отдельных областях сильных местных магнитных полей. Эти области получили название активных.

Как отмечалось выше, в слое, лежащем под фотосферой, происходит интенсивное перемешивание газа — конвекция. Исследования показали, что в области пятна всегда существует сильное магнитное поле, напряженность которого в тысячу раз больше, чем в других, невозмущенных областях. Это поле отклоняет заряженные частицы плазмы и препятствует образованию конвекционных потоков. В этой области подъем горячего газа из глубины прекращается, и газ в пятне сильно охлаждается.

В области факела магнитное ноле далеко не такое сильное, чтобы остановить вертикальные конвекционные потоки плазмы. Однако оно подавляет беспорядочные движения плазмы в потоке и уменьшает внутреннее трение. Таким образом, создается устойчивый восходящий поток горячего газа — факел.

Многие явления, наблюдаемые в атмосфере Солнца, связаны с изменяющимися магнитными полями. Как было показано выше, при движении заряженной частицы в постоянном магнитном поле изменяется только направление скорости ее движения. Оказывается, что изменяющееся во времени магнитное поле, пронизывающее плазму, изменяет не только направление, но и величину скорости заряженных частиц и может создавать направленное движение плазмы. Так иногда образуются мощные потоки плазмы, которые выбрасывают огромные массы газа в корону и образуют протуберанцы — гигантские облака газа, простирающиеся далеко в корону (рис. 6.4).

Сильное магнитное поле, изменяющееся при развитии группы пятен, оказывает давление на плазму, и в хромосфере над областью пятен иногда происходит резкое сжатие плазмы, вызывающее сильное повышение температуры газа. В этой зоне хромосферы наблюдается внезапное резкое усиление свечения газа, называемое хромосферной вспышкой.

Изменяющееся магнитное поле выбрасывает в космическое пространство потоки частиц плазмы, движущихся со скоростью около 1000 км/с, которые называют корпускулярными потоками. Некоторые частицы разгоняются до огромных скоростей (сравнимых со скоростью света), образуя солнечные космические лучи.

Многолетние наблюдения показали, что число и общая площадь пятен периодически изменяются, достигая максимума в среднем через каждые 11 лет. В это время увеличивается число факелов, количество протуберанцев, чаще, чем обычно, наблюдаются вспышки, в десятки раз возрастает интенсивность корпускулярного излучения. Все эти явления объединяются под общим названием — солнечная активность.

Потоки выброшенных Солнцем заряженных частиц, долетая до Земли, отклоняются ее магнитным полем и в свою очередь воздействуют на магнитное поле Земли. В периоды максимума солнечной активности наблюдаются сильные возмущения магнитного поля Земли — магнитные бури, вызывающие беспорядочные колебания стрелки компаса. Часть заряженных частиц проникает в магнитное поле Земли и, двигаясь по спиралям вдоль силовых линий, оказывается как бы в ловушке. Скапливаясь в кольцевых зонах вокруг Земли, заряженные частицы образуют радиационные пояса, обнаруженные с помощью спутников. В области полюсов космические частицы легко проникают в атмосферу, вызывая полярные сияния.

Магнитные поля существуют и в межзвездном пространстве. Они в десятки тысяч раз слабее земного магнитного поля, но обладают огромной протяженностью и поэтому оказывают большое влияние на характер движения заряженных частиц в межзвездном пространстве.

Явление самоиндукции ЭДС самоиндукции

Вспомним, что собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания и размыкания цепи, а также при изменении в ней силы тока. Это означает, что в указанные моменты в такой цепи должна возникать э. д. с. индукции. Возникновение э. д. с. индукции в цепи, которое вызвано изменением магнитного поля тока, текущего в этой же цепи, называют явлением самоиндукции, а появляющуюся электродвижущую силу — э. д. с. самоиндукции.

Выясним подробнее, что происходит при замыкании цепи. Пусть имеется разомкнутая цепь (рис. 23.12), состоящая из источника электрической энергии Б и последовательно соединенных ключа К, лампочки М и катушки с сердечником из ферромагнетика S. При замыкании цепи лампочка загорается с некоторым запозданием. Это объясняется возникновением в катушке значительной э. д. с. самоиндукции, которая согласно закону Ленца мешает быстрому нарастанию тока в цепи (см. рис. 23.13; I₀ — сила постоянного тока в цепи).

Рис. 23.12.

Рис. 23.13.

Заметим, что энергия источника, затраченная на преодоление противодействия э. д. с. самоиндукции, накапливается в магнитном поле этой цепи, главным образом внутри катушки с сердечником S. (Почему?) Когда сила тока в цепи становится постоянной, то и энергия магнитного поля цепи не изменяется. Энергия магнитного поля цепи зависит не только от силы тока, но и от вида цепи, т. е. от ее индуктивности L. В сильных электромагнитах магнитная энергия особенно велика.

Для наблюдения явления самоиндукции при размыкании составляют цепь, показанную на рис. 23.14. При размыкании этой цепи ключом К остается замкнутой цепь катушки S и лампочки М. Так как ток в катушке начинает быстро спадать (рис. 23.15), то в ней создается э. д. с. самоиндукции, которая замедляет спад тока. При этом катушка на короткое время становится источником энергии, который создает ток в лампочке М. В момент размыкания цепи ток в лампе спадает до нуля и, изменив направление, скачком увеличивается до такой величины, которая может быть значительно больше, чем сила тока в лампе до размыкания. Поэтому лампа в момент размыкания может ярко вспыхнуть и даже перегореть.

Рис. 23.14.

Рис. 23.15.

Явление самоиндукции создает искру в том месте, где происходит размыкание цепи. Если в цепи имеются мощные электромагниты, в которых запасена большая магнитная энергия, то искра может перейти в дуговой разряд и испортить выключатель. Для размыкания таких цепей на электростанциях пользуются масляными выключателями и применяются другие меры предосторожности.

Выведем формулу для вычисления э. д. с. самоиндукции. Так как всякая э. д. с. индукции может быть найдена по формуле (23.6)  а то откуда

 (23.7)

Э. д. с. самоиндукции в цепи пряно пропорциональна скорости изменения силы тока в этой цепи.

Энергия магнитного поля

В предыдущем параграфе говорилось, что энергия магнитного поля цепи зависит от силы тока в ней и от ее формы. Уточним эту зависимость. Вспомним, что энергия магнитного поля цепи равна работе, которая затрачивается на преодоление э. д. с. самоиндукции, возникающей при замыкании цепи. Если среднее значение э. д. с. самоиндукции при этом равно а по цепи за время нарастания тока в ней прошел заряд q, то работа по преодолению э. д. с. самоиндукции равна Тогда

Знак минус означает, что заряды при этом движутся против э. д. с. самоиндукции. Так как — то

Поскольку ток в цепи возрастает от 0 до получаем, что a есть средняя сила тока за время его нарастания. Приняв среднюю силу тока за  и подставляя значения и в приведенное выше соотношение, найдем формулу для вычисления энергии магнитного поля цепи, в которой идет.ток

    (23.8)

Энергия магнитного поля цепи прямо пропорциональна квадрату величины тока в ней и зависит от ее индуктивности L. Поскольку индуктивность соленоида с сердечником из ферромагнетика особенно велика, большая магнитная энергия получается в цепи, содержащей электромагниты.

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Масса
7. Взаимодействия тел
8. Механическая энергия
9. Импульс
10. Вращение твердого тела
11. Криволинейное движение тел
12. Колебания
13. Колебания и волны
14. Механические колебания и волны
15. Бегущая волна
16. Стоячие волны
17. Акустика
18. Звук
19. Звук и ультразвук
20. Движение жидкости и газа
21. Молекулярно-кинетическая теория
22. Молекулярно-кинетическая теория строения вещества
23. Молекулярно – кинетическая теория газообразного состояния вещества
24. Теплота и работа
25. Температура и теплота
26. Термодинамические процессы
27. Идеальный газ
28. Уравнение состояния идеального газа
29. Изменение внутренней энергии
30. Переход вещества из жидкого состояния в газообразное и обратно
31. Кипение, свойства паров, критическое состояние вещества
32. Водяной пар в атмосфере
33. Плавление и кристаллизация
34. Тепловое расширение тел
35. Энтропия
36. Процессы перехода из одного агрегатного состояния в другое
37. Тепловое расширение твердых и жидких тел
38. Свойства газов
39. Свойства жидкостей
40. Свойства твёрдых тел
41. Изменение агрегатного состояния вещества
42. Тепловые двигатели
43. Электрическое поле
44. Постоянный ток
45. Переменный ток
46. Магнитное поле
47. Электромагнитное поле
48. Электромагнитное излучение
49. Электрический заряд (Закон Кулона)
50. Электрический ток в металлах
51. Электрический ток в электролитах
52. Электрический ток в газах и в вакууме
53. Электрический ток в полупроводниках
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома