Как найти работу поля через потенциал

Работа сил электростатического поля. Понятие потенциала

Когда пробный заряд q перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения ∆l→ формулу работы можно записать так: ∆A=F·∆l·cos α=Eq∆lcos α=Elq∆l.

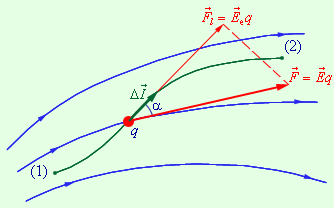
Рисунок 1.4.1. Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.

Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.

При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.

У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.

Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:

Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна 0. Поле, обладающее таким свойством, называется консервативным, или потенциальным.

Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом Q, а также две траектории перемещения пробного заряда q в другую точку. Символом ∆l→  на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:

∆A=F∆lcos α=Eq∆r=14πε0Qqr2∆r.

Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением Δr. Проинтегрируем данное выражение на интервале от r=r1 до r=r2 и получим следующее:

A=∫r1r2E·q·dr=Qq4πε01r1-1r2.

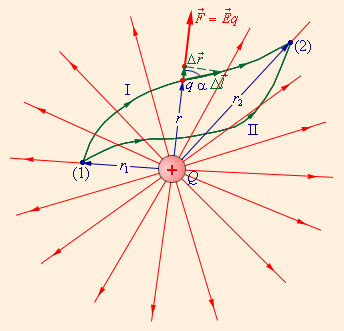
Рисунок 1.4.2. Траектории перемещения заряда и работа кулоновских сил. Зависимость от расстояния между начальной и конечной точкой траектории.

Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны. Если же мы изменим направление на противоположное, то и работа также поменяет знак. А если траектории будут соединены, т.е. заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.

Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов. Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле. Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.

Поскольку у электростатического поля есть свойство потенциальности, мы можем добавить новое понятие – потенциальная энергия заряда в электрическом поле. Выберем какую-либо точку, поместим в нее разряд и примем его потенциальную энергию за 0.

Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.

Обозначив энергию как W, а работу, совершаемую зарядом, как A10, запишем следующую формулу:

Wp1=A10.

Обратите внимание, что энергия обозначается именно буквой W, а не E, поскольку в электростатике E – это напряженность поля.

Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки). На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет. Важна лишь разность ее значений в начальной и конечной точке пространства.

Чтобы вычислить работу, которая совершается электростатическим полем при перемещении точечного заряда из точки 1 в точку 2, нужно найти разность значений потенциальной энергии в них. Путь перемещения и выбор нулевой точки значения при этом не имеют.

A12=A10+ A02= A10 – A20 =Wp1 – Wp2.

Если мы поместим заряд q в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.

Понятие потенциала электрического поля

Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.

Он обозначается буквой φ. Это важная энергетическая характеристика электростатического поля.

φ=Wpq.

Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.

A12=Wp1–Wp2=qφ1–qφ2=q(φ1 – φ2).

Потенциал электрического поля измеряется в вольтах (В).

1 В=1 Дж1 Кл.

Разность потенциалов в формулах обычно обозначается Δφ.

Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:

Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.

φ∞=A∞q.

Чтобы вычислить потенциал точечного заряда на расстоянии r, на котором размещается бесконечно удаленная точка, нужно использовать следующую формулу:

φ=φ∞=1q∫r∞Edr=Q4πε0∫r∞drr2=14πε0Qr

С помощью нее мы также можем найти потенциал поля однородно заряженной сферы или шара при r≥R, что следует из теоремы Гаусса.

Изображение электрических полей с помощью эквипотенциальных поверхностей

Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.

Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.

Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.

Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.

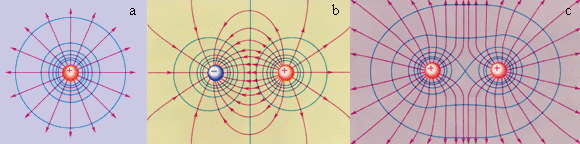
Рисунок 1.4.3. Красным показаны силовые линии, а синим – эквипотенциальные поверхности простого электрического поля. На первом рисунке изображен точечный заряд, на втором –электрический диполь, на третьем – два равных положительных заряда.

Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.

В случае малого перемещения пробного заряда q вдоль силовой линии из начальной точки 1 в конечную точку 2 мы можем записать такую формулу:

ΔA12=qEΔl=q(φ1–φ2)=–qΔφ,

где Δφ=φ1-φ2 – изменение потенциала. Отсюда выводится, что: 

E=-∆φ∆l, (∆l→0) или E=-dφdl.

Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой l обозначена координата, которую следует отсчитывать вдоль силовой линии.

Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:

φ=φ1+φ2+φ3+…

§
15. ПОТЕНЦИАЛ. ЭНЕРГИЯ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ
ЗАРЯДОВ. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА
В ПОЛЕ

Основные
формулы

 Потенциал
электрического поля есть величина,
равная отношению потенциальной энергии
точечного положительного заряда,
помещенную в данную точку поля, к этому
заряду;

=П/Q,

или
потенциал электрического поля есть
величина, равная отношению работы сил
поля по перемещению точечного
положительного заряда из данной точки
поля в бесконечность к этому заряду:

=A/Q.

Потенциал
электрического поля в бесконечности
условно принят равным нулю.

Отметим, что при
перемещении заряда в электрическом
поле работа A_в.с
внешних сил равна по модулю работе A_с.п
сил поля и противоположна ей по знаку:

A_в.с=
– A_с.п.

 Потенциал
электрического поля, создаваемый
точечным зарядом Q на
расстоянии r от заряда,

.

 Потенциал
электрического поля, создаваемого
металлической, несущей заряд Q сферой
радиусом R, на расстоянии
гот центра сферы:

внутри сферы
(r<R) ;

на поверхности
сферы (r=R)

;

вне сферы (r>R) .

Во всех приведенных
для потенциала заряженной сферы формулах
 есть диэлектрическая
проницаемость однородного безграничного
диэлектрика, окружающего сферу.

 Потенциал
электрического поля, созданного системой
п точечных зарядов, в данной точке
в соответствии с принципом суперпозиции
электрических полей равен алгебраической
сумме потенциалов ₁,
₂, … , _n,
создаваемых отдельными точечными
зарядами Q₁,
Q₂, …, Q_n:

 Энергия W
взаимодействия системы точечных зарядов
Q₁, Q₂,
…, Q_n
определяется работой, которую эта
система зарядов может совершить при
удалении их относительно друг друга
в бесконечность, и выражается формулой

,

где _i
— потенциал поля, создаваемого всеми
п–1 зарядами (за исключением 1-го) в
точке, где расположен заряд Q_i.

 Потенциал связан
с напряженностью электрического поля
соотношением

Е= –grad.

В случае электрического
поля, обладающего сферической симметрией,
эта связь выражается формулой

,

или в скалярной
форме

,

а
в случае однородного поля, т. е. поля,
напряженность которого в каждой точке
его одинакова как по модулю, так и по
направлению,

E=(₁–₂,)/d,

где ₁
и ₂
— потенциалы точек двух эквипотенциальных
поверхностей; d —
расстояние между этими поверхностями
вдоль электрической силовой линии.

 Работа, совершаемая
электрическим полем при перемещении
точечного заряда Q из
одной точки поля, имеющей потенциал ₁,
в другую, имеющую потенциал ₂,

A=Q(₁—₂),
или
,

где E_l
— проекция вектора напряженности Е
на направление перемещения; dl
— перемещение.

В случае однородного
поля последняя формула принимает вид

A=QElcos,

где l
— перемещение;  —
угол между направлениями вектора Е
и перемещения l.

Примеры
решения задач

Пример 1.
Положительные заряды Q₁=3
мкКл и Q₂=20
нКл находятся в вакууме на расстоянии
r₁=l,5
м друг от друга. Определить работу A,
которую надо совершить, чтобы сблизить
заряды до расстояния r₂=1
м.

Решение.
Положим, что первый заряд Q₁
остается неподвижным, а второй Q₂
под действием внешних сил перемещается
в поле, созданном зарядом Q₁,
приближаясь к нему с расстояния r₁=t,5
м до r₂=1 м.

Работа А’
внешней силы по перемещению заряда Q
из одной точки поля с потенциалом
₁
в другую, потенциал которой ₂,
равна по модулю и противоположна по
знаку работе А сил поля по перемещению
заряда между теми же точками:

А’= —А.

Работа А сил
поля по перемещению заряда A=Q(₁—₂).
Тогда работа А’ внешних сил может
быть записана в виде

A‘=
–Q(₁—₂)=Q(₂—₁). (1)

Потенциалы точек
начала и конца пути выразятся формулами

;

.

Подставляя выражения
₁
и ₂ в
формулу (1) и учитывая, что для данного
случая переносимый заряд Q=Q₂,
получим

. (2)

Если
учесть, что 1/(4₀)=910⁹
м/Ф, то после подстановки значений
величин в формулу (2) и вычисления найдем

A‘=180 мкДж.

Пример 2. Найти
работу А поля по перемещению заряда
Q=10 нКл из точки 1
в точку 2 (рис. 15.1), находящиеся между
двумя разноименно заряженными с
поверхностной плотностью =0,4
мкКл/м² бесконечными параллельными
плоскостями, расстояние l
между которыми равно 3 см.

Решение.
Возможны два способа решения задачи.

1-й способ.
Работу сил поля по перемещению заряда
Q из точки 1 поля с потенциалом ₁
в точку 2 поля с потенциалом ₂
найдем по формуле

A=Q(₁—₂). (1)

Для определения
потенциалов в точках 1 и 2 проведем
через эти точки эквипотенциальные
поверхности I и II.
Эти поверхности будут плоскостями, так
как поле между двумя равномерно
заряженными бесконечными параллельными
плоскостями однородно. Для такого поля
справедливо соотношение

₁—₂=El, (2)

где Е —
напряженность поля; l
— расстояние между эквипотенциальными
поверхностями.

Напряженность
поля между параллельными бесконечными
разноименно заряженными плоскостями
E=/₀.
Подставив это выражение Е в формулу
(2) и затем выражение ₁—₂
в формулу (1), получим

A=Q(/₀)l.

2-й способ. Так
как поле однородно, то сила, действующая
на заряд Q, при его перемещении
постоянна. Поэтому работу перемещения
заряда из точки 1 в точку 2 можно
подсчитать по формуле

A=Fr
cos, (3)

где F
— сила, действующая на заряд; r
— модуль перемещения заряда Q
из точки 1 в точку 2; 
— угол между направлениями перемещения
и силы. Но F=QE=Q(/₀).
Подставив это выражение F в равенство
(3), а также заметив, что rcos=l,
получим

A=Q(/₀)l. (4)

Таким образом, оба
решения приводят к одному и тому же
результату.

Подставив в
выражение (4) значение величин Q,
, ₀
и l, найдем

A=13,6
мкДж.

Пример 3. По
тонкой нити, изогнутой по дуге окружности
радиусом R,
равномерно распределен заряд с линейной
плотностью =10 нКл/м.
Определить напряженность Е и
потенциал 
электрического поля, создаваемого таким
распределенным
зарядом в точке О, совпадающей с
центром кривизны дуги. Длина l
нити составляет 1/3 длины окружности и
равна 15 см.

Решение. Выберем
оси координат так, чтобы начало координат
совпадало с центром кривизны дуги, а
ось у была симметрично расположена
относительно концов дуги (рис. 15.2). На
нити выделим элемент длины dl.
Заряд dQ=dl,
находящийся на выделенном участке,
можно считать точечным.

Определим
напряженность электрического поля в
точке О. Для этого найдем сначала
напряженность dE
поля, создаваемого зарядом dQ:

,

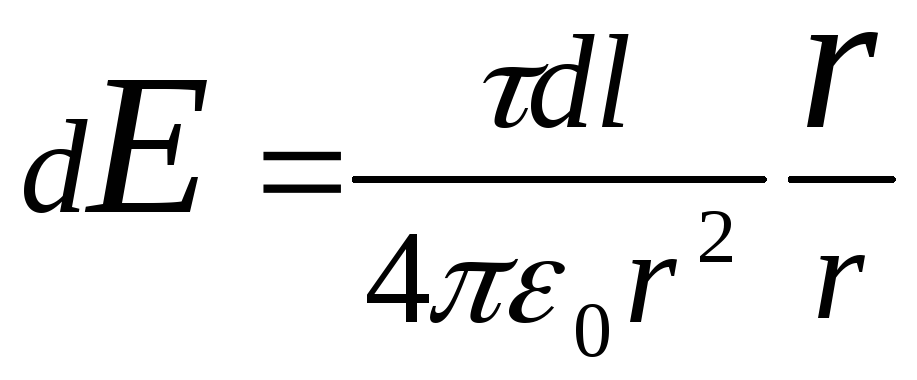где r
—радиус-вектор, направленный от элемента
dl к
точке, напряженность в которой вычисляется.
Выразим вектор dE через проекции dE_x
c и dE_y
на оси координат:

,

где i
и j — единичные векторы
направлений (орты).

Напряженность Е
найдем интегрированием:

.

Интегрирование
ведется вдоль дуги длины l.
В силу симметрии интеграл

равен нулю. Тогда

, (1)

где
.
Так как r=R=const
и dl=Rd.
то

Подставим найденное
выражение dE_y
в (1) и, приняв во внимание симметричное
расположение дуги относительно оси Оу,
пределы интегрирования возьмем от 0 до
/3, а результат
удвоим;

.

Подставив указанные
пределы и выразив R
через длину дуги (3l=2r),
получим

.

Из этой формулы
видно, что вектор Е совпадает с
положительным направлением оси Оу
Подставив значение 
и l в последнюю формулу и сделав
вычисления, найдем

E=2,18
кВ/м.

Определим потенциал
электрического поля в точке О. Найдем
сначала потенциал d,
создаваемый точечным зарядом dQ
в точке О:

Заменим r
на R и произведем
интегрирование:

.Так
как l=2R/3,
то

=/(6₀).

Произведя вычисления
по этой формуле, получим

=188 В.

Пример 4.
Электрическое поле создана длинным
цилиндром радиусом R=1
см, равномерно заряженным с
линейной плотностью =20
нКл/м. Определить разность потенциалов
двух точек этого поля, находящихся на
расстояниях a₁=0,5
см и а₂=2 см от поверхности
цилиндра, в средней его части.

Решение. Для
определения разности потенциалов
воспользуемся соотношением между
напряженностью поля и изменением
потенциала Е= —grad.
Для поля с осевой симметрией, каким
является поле цилиндра, это соотношение
можно записать в виде

Е= –(d/dr),
или d=
—Еdr.

Интегрируя последнее
выражение, найдем разность потенциалов
двух точек, отстоящих на r₁
и r₂ от оси
цилиндра;

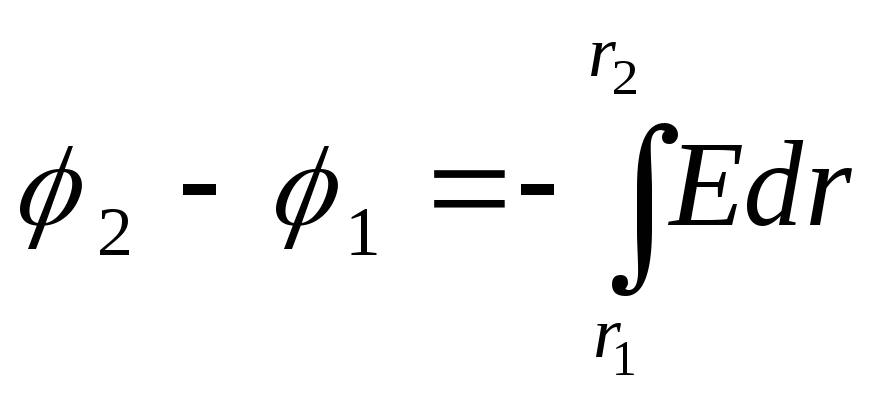. (1)

Так как цилиндр
длинный и точки взяты вблизи его средней
части, то для выражения напряженности
поля можно воспользоваться формулой
.
Подставив это выражение Е в равенство
(1), получим

(2)

Так как величины
r₂ и r₁
входят в формулу в виде отношения, то
их можно выразить в любых, но только
одинаковых единицах:

r₁=R+a₁=1,5
см; r₂=R+a₂=3
см.

Подставив значения
величия , ₀,
r₁ и r₂
в формулу (2) и вычислив, найдем

₁—₂=250
В.

Пример 5.
Электрическое поле создано тонким
стержнем, несущим равномерно распределенный
по длине заряд =0,1
мкКл/м. Определить потенциал 
поля в точке, удаленной от концов стержня
на расстояние, равное длине стержня.

Решение. Заряд,
находящийся на стержне, нельзя считать
точечным, поэтому непосредственно
применить для вычисления потенциала
формулу

, (1)

справедливую
только для точечных зарядов, нельзя. Но
если разбить стержень на элементарные
отрезки dl,
то заряд dl,
находящийся на каждом из них, можно
рассматривать как точечный и тогда
формула (1) будет справедлива. Применив
эту формулу, получим

, (2)

где r
— расстояние точки, в которой
определяется потенциал, до элемента
стержня.

Из рис. 15.3 следует,
что dl=(rd/cos).
Подставив это выражение dl
в формулу (2), найдем.

Интегрируя
полученное выражение в пределах от ₁
да ₂,
получим потенциал, создаваемый всем
зарядом, распределенным на стержне:.

В
силу симметрии расположения точки А
относительно концов стержня имеем ₂=₁
и поэтому.

Следовательно,

.Так
как

Рис 15.3

(см. табл. 2), то.

Подставляя пределы
интегрирования, получим

Сделав вычисления
по этой формуле, найдем

=990 В.

Пример 6.
Электрон со скоростью v=1,8310⁶
м/с влетел в однородное электрическое
поле в направлении, противоположном
вектору напряженности поля. Какую
разность потенциалов U
должен пройти электрон, чтобы обладать
энергией E_i=13,6
эВ*? (Обладая такой энергией, электрон
при столкновении с атомом водорода
может ионизировать его. Энергия 13,6 эВ
называется энергией ионизации водорода.)

Решение.
Электрон должен пройти такую разность
потенциалов U, чтобы приобретенная
при этом энергия W в
сумме с кинетической энергией T,
которой обладал электрон перед вхождением
в поле, составила энергию, равную энергии
ионизации E_i,
т. е. W+T=E_i.
Выразив в этой формуле W=eU
и Т =(mv²/2),
получим eU+(mv²/2)=E_i.
Отсюда.

___________________

* Электрон-вольт
(эВ) — энергия, которую приобретает
частица, имеющая заряд, равный заряду
электрона, прошедшая разность потенциалов
1 В. Эта внесистемная единица энергии в
настоящее время допущена к применению
в физике.

Произведем
вычисления в единицах СИ:

U=4,15 В.

Пример 7. Определить
начальную скорость υ₀
сближения про­тонов, нахо­дя­щихся
на достаточно большом расстоянии друг
от друга, если минимальное расстояние
r_min, на которое
они могут сблизиться, равно 10^-11
см.

Р е ш е н и е. Между
двумя протонами действуют силы
оттал­кивания, вслед­ствие чего
движение протонов будет замедленным.
Поэтому задачу можно ре­шить как в
инерциальной системе коор­динат
(связанной с центром масс двух протонов),
так и в неинер­циальной (связанной с
одним из ускоренно движу­щихся
протонов). Во втором случае законы
Ньютона не имеют места. Примене­ние
же принципа Даламбера затруднительно
из-за того, что ускорение системы будет
переменным. Поэтому удобно рассмотреть
задачу в инерциальной сис­теме отсчета.

Поместим начало
координат в центр масс двух протонов.
По­скольку мы имеем дело с одинаковыми
частицами, то центр масс будет находиться
в точке, делящей пополам отрезок,
соединяющий частицы. Относительно
центра масс частицы будут иметь в любой
момент времени одинаковые по модулю
скоро­сти. Когда частицы находятся
на достаточно большом расстоянии друг
от друга, скорость υ₁ каждой
частицы равна половине υ₀,
т. е. υ₁ =υ₀/2.

Для решения задачи
применим закон сохранения энергии,
со­гласно кото­рому полная механическая
энергия Е изолированной системы
постоянна, т. е.

Е=Т+П,

где Т – сумма
кинетических энергий обоих протонов
относительно центра масс; П – потенциальная
энергия системы зарядов.

Выразим потенциальную
энергию в начальный П₁ и конечный
П₂ моменты движения.

В начальный момент,
согласно условию задачи, протоны
нахо­дились на большом расстоянии,
поэтому потенциальной энергией можно
пренебречь (П₁=0). Следовательно,
для начального момента полная энергия
будет равна кинетической энергии T₁
протонов, т. е.

E=T_l.
(1)

В конечный момент,
когда протоны максимально сблизятся,
скорость и кинети­ческая энергия
равны нулю, а полная энергия будет равна
потенциальной энер­гии П₂, т. е.

Е=П₂.
(2)

Прирав­няв правые
части равенств (1) и (2), получим

T₁=П₂.
(3)

Кинети­ческая
энергия равна сумме кинетических энергий
про­тонов:

(4)

Потенциальная
энергия системы двух зарядов Q₁
и Q₂, находя­щихся
в вакууме, определяется по формуле
,
где r – расстоя­ние
между зарядами. Воспользовавшись этой
формулой, полу­чим

(5)

С учетом равенств
(4) и (5) формула (3) примет вид

откуда

Выполнив вычисления
по полученной формуле, найдем υ₀=2,35
Мм/с.

Пример
8. Электрон без на­чальной скорости
прошел разность потен­циалов U₀=10
кВ и влетел в пространство между
пластинами плоского конденсатора,
заряжен­ного до разности потенциалов
U_l=100 В, по ли­нии АВ,
парал­лельной пластинам (рис. 15.4).
Рас­стояние d между пла­стинами
равно 2 см. Длина l₁
­пластин конденсатора в нап­равлении
по­лета элек­трона, равна 20 cм.
Определить рас­стояние ВС на
экране Р, от­стоящем от конденсатора
на l₂=1 м.

Р е ш е н и е. Движение
электрона внутри конденсато­ра
складыва­ется из двух дви­жений: 1)
по инерции вдоль линии АВ с постоянной
скоро­стью υ₀, приобретенной
под действием разности потенциалов U₀,
кото­рую электрон прошел до
конденсатора; 2) равномерно ускоренного
дви­жения в вертикальном направлении
к положительно заряженной пла­стине
под действием постоянной силы поля
конденсатора. По вы­ходе из конденсатора
электрон будет двигаться равномерно
со скоро­стью υ, которую он имел
в точке М в момент вылета из
кон­денсатора.

Из рис. 15.4 видно,
что искомое расстояние |BC|=h₁+h₂,
где с h₁ – рас­стояние, на
которое сместится электрон в вертикальном
направлении во время движения в
конденсаторе; h₂ – расстояние
между точкой D на эк­ране, в которую
электрон попал бы, двигаясь по выходе
из конденса­тора по направлению
начальной скорости υ₀, и точкой
С, в которую электрон попадет в
действительности.

Выразим отдельно
h₁ и h₂. Пользуясь
формулой длины пути равно­мерно
ускоренного движе­ния, найдем

.
(1)

где а – ускорение,
полученное электроном под действием
поля конден­сатора; t- время полета
электрона внутри конденсатора.

По второму закону
Ньютона a=F/m, где F – сила, с которой
поле дей­ствует на электрон; т- его
масса. В свою очередь, F
=eE=eU₁/d, где е – заряд
электрона; U₁ – разность
потенциалов между пластинами конден­сатора;
d – расстояние между ними. Время
полета электрона внутри конденсатора
найдем из фор­мулы пути равномерного
движения
,
откуда

где l₁
– длина конденсатора в направлении
полета электрона. Выраже­ние скорости
найдем из условия равенства работы,
совер­шенной полем при перемещении
электрона, и приобретенной им кинетической
энер­гии:.
Отсюда

(2)

Подставляя в
формулу (1) последовательно значения а,
F, t и υ₀²
из со­ответствующих выражений,
получим

Длину отрезка h₂
найдем из подобия треугольников MDC
и век­тор­ного:

(3)

где υ₁
– скорость электрона в вертикальном
направлении в точке М; l₂–
расстояние от конденсатора до экрана.

Скорость υ₁
найдем по формуле υ₁=at, которая
с учетом выра­жений для а, F и t
примет вид

Подставив выражение
υ₁ в формулу (3), получим
,
или, заменив υ₀² по
формуле (3), найдем

Окончательно для
искомого расстояния |BC|
будем иметь

|BC|=­

­Подставив
значения величин U₁, U₀,
d, l₁ и l₂
в последнее выражение и произведя
вычисления, получим |BC|=5,5cм.

Задачи

Потенциальная
энергия и потенциал поля точечных
зарядов

15.1. Точечный
заряд Q = 10 нКл, находясь в некоторой
точке поля, обладает потенциальной
энергией П = 10 мкДж. Найти потенциал φ
этой точки поля.

5.2. При перемещении
заряда Q=20 нКл между двумя точками
поля внеш­ними силами была совершена
работа А=4 мкДж. Определить работу
A₁ сил поля и разность Δφ
потенциалов этих точек поля.

15.3. Электрическое
поле создано точечным положительным
заря­дом Q₁=6 нКл. Положительный
заряд Q₂ переносится из точки
А этого поля в точку В (рис. 15.5).
Каково изменение потенциаль­ной
энергии ΔП, приходящееся на единицу
переносимого заряда, если r₁=20
см и r₂=50 см?

15.4. Электриче­ское
поле создано точечным зарядом Q_l=50
нКл. Не пользуясь понятием потенциала,
вычислить работу А в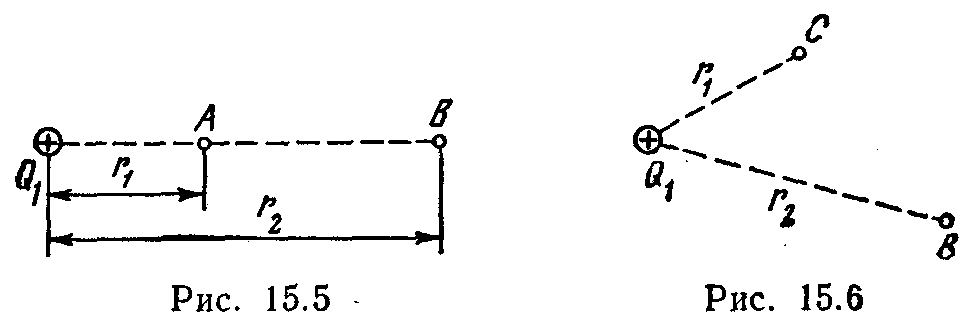
нешних
сил по пе­ремещению точечного заряда
Q₂= -2 нКл из точки С в точку
В

(рис. 15.6), если r₁=10
см, r₂=20 см.
Определить также измене­ние ΔП
потенциальной энергии сис­темы
зарядов.

15.5. Поле создано
точечным зарядом Q=1 нКл. Определить
потен­циал φ поля в точке, удаленной
от заряда на расстояние r=20
см.

15.6. Определить
потенциал φ электрического поля в точке,
,удаленной от зарядов Q₁= -0,2
мкКл и Q₂=0,5 мкКл соответственно
на r₁=15 см и r₂=25
см. Определить также минимальное и
мак­симальное расстояния между
зарядами, при которых возможно решение.

15.7. Заряды Q₁=1
мкКл и Q₂= -1 мкКл находятся
на рас­стоянии d=10 см. Определить
напряженность Е и потенциал φ поля
в точке, уда­ленной на рас­стояние
r= 10 см от первого
заряда и лежащей на линии, проходящей
через первый заряд перпенди­кулярно
направлению от Q₁ к Q₂.

15.8. Вычислить
потенциальную энергию П системы двух
точеч­ных зарядов Q₁=100 нКл
и Q₂=10 нКл, находящихся на
рас­стоянии d=10 см друг от друга.

15.9. Найти
потенциальную энергию П системы трех
точечных за­рядов Q₁=10 нКл,
Q₂=20 нКл и Q₃= -30
нКл, расположенных в вершинах
равностороннего треугольника со стороной
длиной a=10 см.

15.10. Какова
потенциальная энергия П системы четырех
одинако­вых то­чечных зарядов Q=10
нКл, расположенных в верши­нах квадрата
со стороной дли­ной а=10 см? .

15.11. Определить
потенциальную энергию П системы четырех
то­чечных зарядов, расположенных в
вершинах квадрата со стороной дли­ной
a=10 см. За­ряды одинаковы по модулю
Q=10 нКл,но два из них отрицательны.
Рассмотреть два возможных случая
расположения зарядов.

15.12.
Поле создано двумя точечными зарядами
+2Q и -Q, находящимися на
расстоянии d=12 см друг от друга.
Определить геометрическое место точек
на плоскости, для которых потенциал
равен нулю (написать уравнение линии
нулевого потенциала).

5.13. Система
состоит из трех зарядов – двух одинаковых
по величине Q₁=|Q₂|=1
мкКл и противоположных по знаку и заряда
Q=20 нКл, расположенного точке 1
посередине между двумя другими зарядами
системы (рис. 15.7). Определить изменение
потенциальной энергии ΔП системы при
переносе заряда Q из точ­ки 1 в
точку 2. Эти точки удалены от отрицательного
заряда Q₁ на расстояние а=0,2
м.

Где находится электростатическое поле?

Однородное электрическое поле сосредоточено между разноименно заряженными пластинами (обкладками конденсатора).

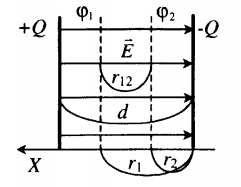
Характеристики однородного электростатического поля

Силовые линии	Начинаются на положительно заряженной пластине, а заканчиваются на отрицательно заряженной. Силовые линии параллельны друг другу, т. е. поле однородно.
Напряженность	−E
Потенциал	φ=Er
Разность потенциалов	φ1−φ2=Er12
Напряжение между пластинами	U=Ed d — расстояние между заряженными пластинами.
Эквипотенциальные поверхности	Плоскости, параллельные заряженным пластинам.
Закон Кулона	FK=qE=qUd
Ускорение силы Кулона (следует из второго закона Ньютона)	a=FKm=qEm=qUmd

Подсказки к решению задач:

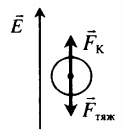	Равновесие заряженного тела в электростатическом поле: Fтяж=FK Сила тяжести равна произведению массы заряженного тела на ускорение свободного падения: Fтяж=mg Сила Кулона равна: FK=qE=qUd
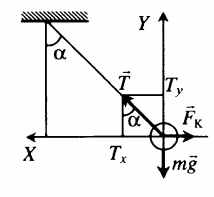	Отклонение от вертикали нити с заряженным телом в горизонтальном электростатическом поле. Второй закон Ньютона в векторной форме: −FK+m−g+−T=m−a Проекции на оси: OX:Tsinα−FK=0 OY:Tcosα−mg=0 Отсюда сила Кулона равна: FK=mgtanα FK=qE=qUd
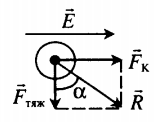	Направление траектории полого шарика массой m и зарядом q, который движется в горизонтальном электрическом поле напряженностью −E. Важно! Направление траектории совпадает с направлением равнодействующей силы. Равнодействующая силы находится по второму закону Ньютона: −R=−FK+m−g Из рисунка видно, что: tanα=FKFтяж=qEmg

Пример №1. Полый шарик массой m = 0,4 г с зарядом q = 8 нКл движется в горизонтальном однородном электрическом поле, напряженность которого E = 500 кВ/м. Какой угол α образует с вертикалью траектория шарика, если его начальная скорость равна нулю?

0,4 г = 0,4∙10^–3 кг

8 нКл = 8∙10^–9 Кл

500 кВ/м = 5∙10⁵ В/м

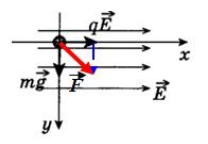
При движении в электрическом поле на заряженную частицу действует сила тяжести:

−Fтяж=m−g

На нее также действует сила Кулона со стороны электрического поля:

−FK=q−E

В инерциальной система отсчета, связанной с Землей, в соответствии со вторым законом Ньютона:

−FK+m−g=m−a

При движении из состояния покоя с постоянным ускорением тело движется по прямой в направлении вектора ускорения, т. е. в направлении равнодействующей приложенных сил. Прямая, вдоль которой направлен вектор ускорения, образует угол с вертикалью, равный:

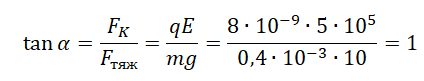
Тангенс, равный единице, соответствует углу, равному 45 градусам.

Работа однородного электрического поля

Из курса механики вспомним, что работа определяется произведением силы, действующей на тело, на его перемещение и косинус угла между векторами силы и этого перемещения:

A=Fscosα

Эту же формулу можно использовать для нахождения работы однородного электрического поля. В качестве силы в данном случае выступает сила Кулона:

FK=qE=qUd

А произведение перемещения на косинус угла между силой и перемещением в этом случае равно разности начального и конечного положения заряда:

scosα=r0−r

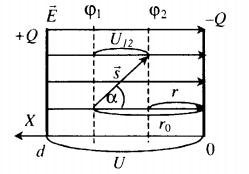
Отсюда работа однородного электрического поля равна:

Формулы работы электрического поля

A=±qE(r0−r)=±qUd(r0−r)

или

A=FKscosα=±qEscosα=±qUdscosα

• E (В/м или Н/Кл) — модуль напряженности электрического поля;
• U (В) — разность потенциалов (напряжение) между пластинами;
• d (м) — расстояние между пластинами;
• ±q — заряд, переносимый полем;
• s (м) — модуль перемещения заряда;
• α — угол между силой Кулона и перемещением;
• r0 (м) — начальное положение заряда;
• r (м) — конечное положение заряда.

Работу также можно выразить через разность потенциалов:

A=±q(φ1−φ2)=±qU12

• φ1 — начальный потенциал;
• φ2 — конечный потенциал;
• U12 — напряжение между начальным и конечным положением заряда.

Внимание! Работа электростатического поля не зависит от вида траектории.

Работа и изменение кинетической энергии:

A=mv22−mv202=ΔEk

Работа и изменение потенциальной энергии:

A=−(qEr−qEr0)=−ΔWp

Пример №2. В точке А потенциал электрического поля равен 200 В. Потенциал в точке В равен 100В. Какую работу совершают силы электростатического поля при перемещении заряда 5 мКл из точки А в точку В?

5 мКл = 5∙10^–3 Кл

A=±q(φ1−φ2)=5·10−3(200−100)=0,5 (Дж)

Задание EF17633

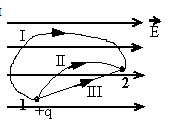Положительный заряд перемещается в однородном электростатическом поле из точки 1 в точку 2 по разным траекториям. Работа сил электростатического поля

Ответ:

а) максимальна в случае перемещения по траектории I

б) не совершается в случае перемещения по траектории II

в) минимальна в случае перемещения по траектории III

г) одинакова при перемещении по всем траекториям

---

Алгоритм решения

1. Установить, от чего зависит работа электростатического поля, затрачиваемая на перемещение в нем заряженной частицы.
2. Определить, какую работу совершает поле при движении заряда по каждой из траекторий.

Решение

Кулоновская сила — это потенциальная сила. Поэтому работа, которую она совершает, не зависит от вида траектории. Учитываться будет только перемещение, равное кратчайшему расстоянию между точками 1 и 2. Следовательно, работа будет одинаковой при перемещении положительного заряда по всем траекториям.

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18815

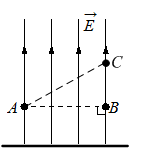Однородное электростатическое поле создано равномерно заряженной протяжённой горизонтальной пластиной. Линии напряжённости поля направлены вертикально вверх (см. рисунок).

Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.

Ответ:

1) Пластина имеет отрицательный заряд.

2) Потенциал электростатического поля в точке В ниже, чем в точке С.

3) Работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю.

4) Если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз.

5) Напряжённость поля в точке А меньше, чем в точке С.

---

Алгоритм решения

1.Проанализировать каждое из утверждений.

2.Установить, какие из утверждений являются истинными.

3.Записать номера верных утверждений.

Решение

Согласно утверждению 1, пластина имеет отрицательный заряд. Известно, что векторы напряженности поля, создаваемого отрицательным зарядом, направляются в сторону этого заряда. Но мы видим, что векторы направляются от заряда. Следовательно, пластина заряжена положительно, а утверждение 1 неверно.

Согласно утверждению 2, потенциал электростатического поля в точке В ниже, чем в точке С. Известно, что потенциал зависит от расстояния до отрицательно пластины. Поскольку в нашем случае пластина заряжена положительно, с увеличением расстояния от нее потенциал уменьшается. Поэтому потенциал в точке С меньше потенциала в точке В, а утверждение 2 неверно.

Согласно утверждению 3, работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю. Работа определяется формулой:

A=FKscosα=±qEscosα

Видно, что работа зависит от перемещения относительно заряженной пластины. Но точки А и В находятся от пластины на одинаковом расстоянии. Следовательно, перемещение относительно нее равно 0. Поэтому работа по перемещению заряда тоже будет нулевой, и утверждение 3 верно.

Согласно утверждению 4, если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз. Это действительно так. Мы выяснили, что пластина заряжена положительно. Следовательно, отрицательный заряд будет притягиваться к ней, и утверждение 4 верно.

Согласно утверждению 5, напряжённость поля в точке А меньше, чем в точке С. Это не так, потому что речь идет об однородном поле. Напряженность однородного поля одинакова во всех точках, и утверждение 5 неверно.

Верные утверждения: 3 и 4.

Ответ: 34

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 3.6k

Содержание:

Работа по перемещению заряда в электростатическом поле:

В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.

Работа по перемещению заряда в однородном электростатическом поле

Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.

Пусть в однородном электростатическом поле напряженностью

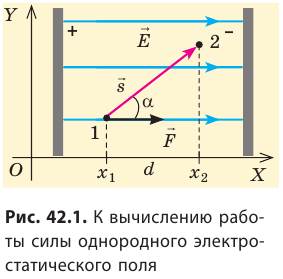
Вычислим работу А, которую совершает сила 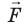, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.

Поле однородное, поэтому сила 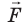постоянна, ее модуль равен: F=qE, а scosα=d=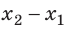является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( 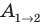) равна:

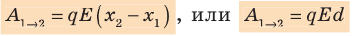
Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.

Обратите внимание! Формула 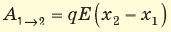будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.

Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:

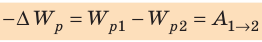
Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:

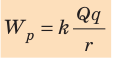
Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( < 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.

Что называют потенциалом электростатического поля

Потенциал 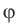электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к значению q этого заряда:

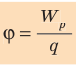
Единица потенциала в Си — вольт: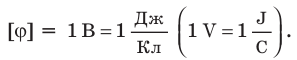

Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле: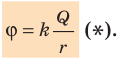

Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.

Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 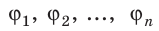полей, созданных каждым зарядом:

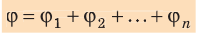
Как определяют разность потенциалов

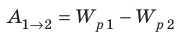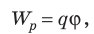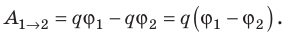Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: . Поскольку то Выражение 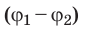называют разностью потенциалов, где 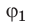— значение потенциала в начальной точке траектории движения заряда, 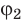— значение потенциала в ее конечной точке.

Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:

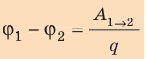
Единица разности потенциалов в Си — вольт: 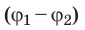= 1 В (V).

Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов 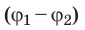− также называют напряжением (U). Важно не путать изменение потенциала 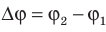и разность потенциалов (напряжение) .

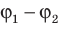Как связаны напряженность однородного электростатического поля и разность потенциалов

Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).

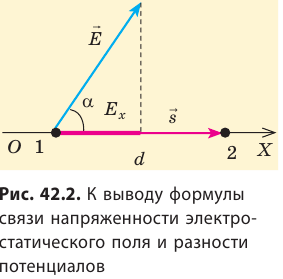
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: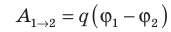; 2) через напряженность поля: 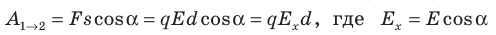— проекция вектора 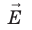на ось Ох, проведенную через точки 1 и 2.

Приравняв оба выражения для работы, получим: 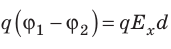, откуда: 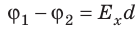, или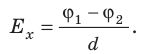

Если заряд перемещается в направлении напряженности электрического поля () , последняя формула примет вид:

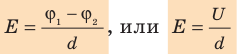
Из последней формулы следует единица напряженности в Си — вольт на метр:

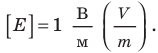
Какие поверхности называют эквипотенциальными

Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.

Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.

Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).

Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( 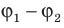), а на эквипотенциальной поверхности .

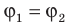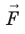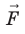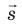Работу электростатического поля также можно представить через силу , действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами и . Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы 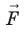, а следовательно, и вектор напряженности 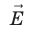поля в любой точке перпендикулярны вектору перемещения .

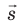Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).

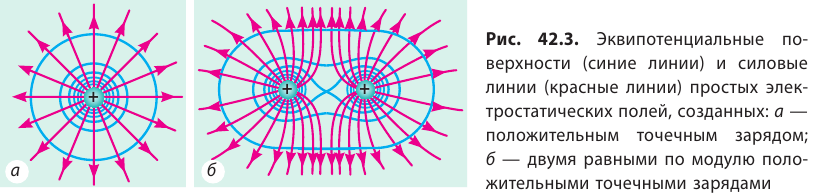
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.

• Заказать решение задач по физике

Пример решения задачи

Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона 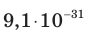кг, заряд 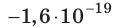Кл.

Заряд электрона — отрицательный, его начальная скорость 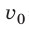= 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.

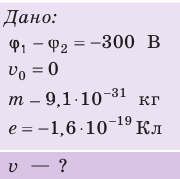
Решение:

Поиск математической модели, решение Согласно теореме о кинетической энергии:

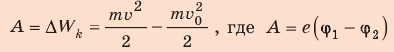— работа сил поля.

Таким образом, 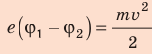, отсюда .

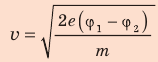Проверим единицу, найдем значение искомой величины:

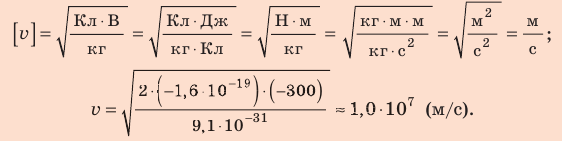
Ответ: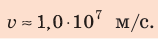

Выводы:

Часть задач школьного уровня связана с поиском работы и энергии в электростатическом поле.

Работа по перемещению заряда в электростатическом поле.

• Поле однородно

Однородным называется поле, напряжённость которого во всех точках одинакова (). Поместим в данное поле заряд . Тогда, исходя из определения напряжённости электростатического поля, модуль силы, действующей на заряд:

(1)

• где

Вспомним определение механической работы:

(2)

Подставим (1) в (2):

(3)

Соотношение (3) удобно для поиска работы, в случае заряда в однородном электростатическом поле.

Важно: в задачах однородное поле должно быть задано самим выражением «считать поле однородным», также электростатическое поле плоского конденсатора можно считать однородным.

• Поле неоднородно

Неоднородным называется поле, напряжённость которого непостоянно в различных точках пространства. В случае неоднородности поля, воспользуемся выражением (3):

=  =  (4)

Мы воспользовались определением перемещения: разность конечного () и начального () положения тела.

Исходя из определения потенциала:

=  =  (5)

Тогда, если ввести и , получим:

(6)

Т.е. в неоднородном электростатическом поле (а на самом деле, в любом), работа по переносу заряда численно равна переносимому заряду, умноженному на разность потенциалов между точками переноса.

Важно: неоднородное поле в задаче вводится через саму фразу «поле неоднородное» и через источники: точечный заряд, шар, которые также создают неоднородные поля.

Вывод: в задачах на нахождение работы по переносу заряда необходимо выяснить характер поля (однородное или неоднородное) и применить соответствующее выражение (3) или (6).

Энергия взаимодействия зарядов

А теперь обсудим энергию взаимодействия зарядов. Энергия взаимодействие зарядов на школьном уровне даётся без вывода, поэтому мы тоже ещё просто зафиксируем:

(7)

• где