Дадим физическую
интерпретацию криволинейного интеграла
второго рода. Если в некоторой области
![]() задано непрерывное силовое поле
задано непрерывное силовое поле![]() ,
,
то при перемещении материальной точки
вдоль гладкой ориентированной кривойL
поле совершает некоторую работу А.
Для её определения разобьём линию L
на
![]() дуг точками
дуг точками![]() ,
,![]() ,
,
…,![]() (рис. 16). Пусть
(рис. 16). Пусть![]() произвольная точка дуги
произвольная точка дуги![]() .
.
Обозначим![]() – единичный вектор касательнойL
– единичный вектор касательнойL
в этой точке и
![]() – длину дуги
– длину дуги![]() .
.
Р

Рис.5
аботу на дуге![]() можно приближённо вычислить с помощью
можно приближённо вычислить с помощью
скалярного произведения![]() .
.
Тогда приближённо работа есть![]() .
.
За работу А
на всей кривой L
естественно принять предел
![]() .
.
Если этот предел
существует, то он является криволинейным
интегралом I
рода от скалярной функции
![]() ,
,
т.е. это криволинейный интегралII
рода. Таким образом, работа А
по перемещению материальной точки в
непрерывном силовом поле выражается
криволинейным интегралом II
рода:
![]() .
.
(2)
Покажем, что работа
поля
![]() вдоль любой векторной линии этого поля
вдоль любой векторной линии этого поля
отлична от нуля. ПустьL
– векторная линия, тогда
![]() вектор
вектор![]() параллелен
параллелен![]() .
.
Тогда скалярное произведение![]() ,
,
тогда![]() ,
,
причём кривая может быть замкнутой.
Определение 1.
Работа векторного поля
![]() вдоль замкнутой кривойL
вдоль замкнутой кривойL
называется
циркуляцией
этого поля:
![]() .
.
Ф
Рис.6
изически её можно интерпретировать
следующим образом. Пусть![]() – поле скоростей
– поле скоростей![]() текущей жидкости. Поместим в это поле
текущей жидкости. Поместим в это поле
колёсико с лопастями, расположенными
по окружностиL
этого колеса (рис.6). Частицы жидкости,
действуя на эти лопасти, будут создавать
вращательные моменты, суммарное действие
которых приводит колесо в движение –
вращение вокруг своей оси. Вращательное
действие поля
![]() в каждой точке будет характеризоваться
в каждой точке будет характеризоваться
проекцией![]() на касательную
на касательную![]() ,
,
т.е. скалярным произведением![]() .
.
Суммирование вращательных действий
жидкости по всему контуру колёсика
приводит к понятию циркуляции вектора![]() .
.
Ф
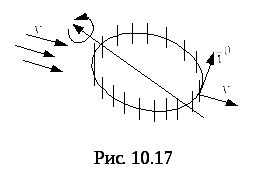
изический смысл циркуляции:
циркуляция векторного поля
![]() определяет его вращательную способность
определяет его вращательную способность
в данном направлении и характеризует
завихрённость поля в этом направлении.
Чем меньше угол между касательной и
вектором поля, тем большеС,
а следовательно и завихрённость.
Пример 2.
Вычислить циркуляцию векторного поля
![]() вдоль замкнутого контура
вдоль замкнутого контура![]() ,
,
являющегося границей части сферы![]() ,
,
расположенной в первом октанте:![]() ,
,![]() ,
,![]() ,
,
причем направление обхода контура
таково, что в плоскостиОху
движение происходит от точки
![]() к
к![]() .
.
Решение.
Контур
![]() состоит из трех кривых
состоит из трех кривых![]() ,
,
каждая из которых является дугой
единичной окружности, лежащей
соответственно в координатной плоскостиОху,
Оуz,
Oxz.
Поэтому
![]() ,
,
![]() .
.
Найдем интеграл
![]() по кривой
по кривой![]() .
.
Так как кривая![]() лежит в плоскостиОху,
лежит в плоскостиОху,
то
![]() ,
,![]() и
и![]() ,
,
где![]() ,
,![]() ,
,![]() .
.
Запишем параметрическое уравнение![]() :
:![]() ,
,![]() ,
,![]() .
.
Получаем
![]()
![]() .
.
Точно так же
вычисляются интегралы
![]() и
и![]() .
.
При этом![]() .
.
Следовательно,![]() .
.
10.3. Потенциальное векторное поле
Определение 2.
Векторное поле
![]() называетсяпотенциальным
называетсяпотенциальным
в области
![]() ,
,
если существует такое скалярное поле![]() ,
,
что для всех точек этой области
вектор-функция![]() является градиентом этого скалярного
является градиентом этого скалярного
поля![]() :
:
![]() .
.
Скалярное поле
![]() называетсяпотенциалом
называетсяпотенциалом
векторного поля
![]() .
.
Потенциальное поле является одним из
наиболее простых полей, так как
определяется одной скалярной функцией![]() ,
,
в то время как произвольное векторное
поле – тремя скалярными функциями![]() .
.
Теорема 1. Если
поле
![]() потенциально, то его потенциал определяется
потенциально, то его потенциал определяется
однозначно с точностью до произвольного
постоянного слагаемого.
Пусть поле
![]() имеет два потенциала
имеет два потенциала![]() и
и![]() ,
,
т.е.![]() и
и![]() .
.
Тогда![]() и, следовательно,
и, следовательно,![]() .
.
Таким образом, получаем, что![]() .<
.<
Теорема 2. Если
поле
![]() потенциально в областиV,
потенциально в областиV,
то работа этого поля (криволинейный
интеграл второго рода) не зависит от
формы пути, соединяющий две любые точки
из V.
Потенциал
![]() с точностью до произвольной постоянной
с точностью до произвольной постоянной
определяется криволинейным интегралом
второго рода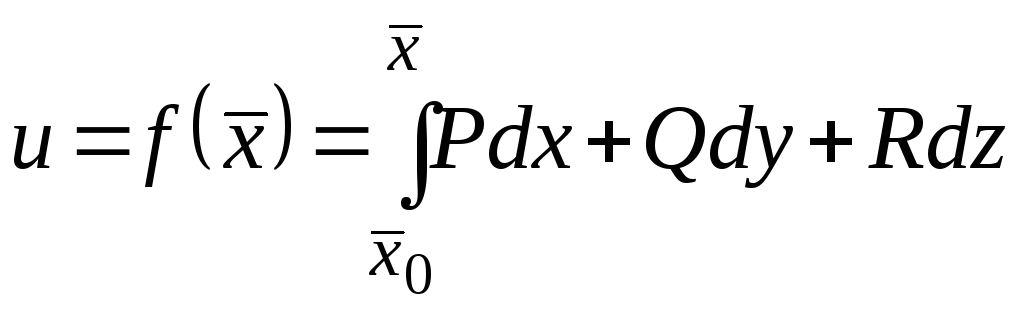 ,
,
взятому по произвольной кривой![]() ,
,
соединяющей точки![]() и
и![]() ,
,
где![]() – фиксированная точка, а
– фиксированная точка, а![]() – текущая точка.
– текущая точка.
Работа А
поля
![]() по некоторому путиL,
по некоторому путиL,
соединяющему точки
![]() и
и![]() ,
,
вычисляется по формуле (11):
![]() .
.
Поле
![]() потенциально, тогда существует потенциал
потенциально, тогда существует потенциал![]() ,
,
причем![]() .
.
Тогда скалярное произведение
![]() ,
,
Для простоты
преобразований пусть
![]() плоская кривая, заданная параметрическими
плоская кривая, заданная параметрическими
уравнениями![]() ,
,![]() ,
,![]() ,
,
причем начало в точке![]() ,
,
которой соответствует значение параметра![]() ,
,
а конечной точки![]() соответствует значение параметра
соответствует значение параметра![]() ,
,
т.е.![]() ,
,![]() .
.
Тогда
![]()
=![]()
![]()
![]() .
.
Т.е потенциал
![]() определяется по формуле
определяется по формуле
![]() (3)
(3)
Откуда следует,
что работа не зависит от формы пути, а
зависит от положения начальной
![]() и конечной
и конечной![]() точек.<
точек.<
Задача отыскания
потенциала
![]() поля
поля![]() тесно связано с задачей восстановления
тесно связано с задачей восстановления
функции трёх переменных по её полному
дифференциалу.
Теорема 3.
Пусть векторное поле задано функцией
![]() ,
,
которая непрерывно дифференцируема в
области![]() .
.
Для того, чтобы выражение
![]() (4)
(4)
было полным
дифференциалом некоторой функции
![]() ,
,
необходимо и достаточно, чтобы поле![]() было потенциальным.
было потенциальным.
Необходимость.
Пусть (4) есть полный дифференциал
![]() ,
,
то с одной стороны по определению![]() ,
,
а с другой стороны![]() ,
,
откуда![]() .
.
Т.е.![]() ,
,
а, следовательно,![]() – потенциальное поле.
– потенциальное поле.
Достаточность.
Пусть
![]() – потенциально, тогда существует функция
– потенциально, тогда существует функция![]() ,
,
такая, что![]() .
.
По определению градиента![]() ,
,![]() ,
,![]() ,
,
тогда получаем![]() .<
.<
Для того,
чтобы найти функцию
![]() по её полному дифференциалу необходимо
по её полному дифференциалу необходимо
применить формулу (3), т.е. с точностью
до произвольного постоянного слагаемого
вычислить криволинейный интеграл по
любой кривой, соединяющей две точки![]() и
и![]()
т.е.
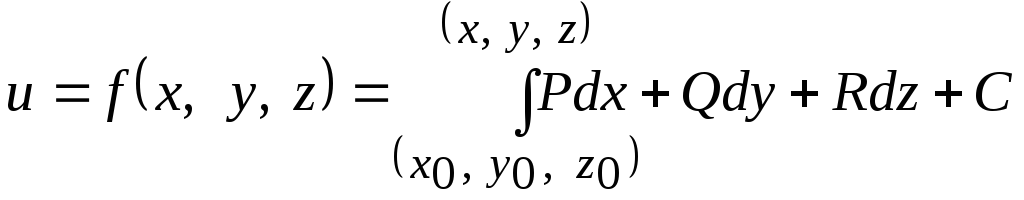 .
.
Теперь естественно
возникает вопрос: когда, при каких
условиях векторное поле является
потенциальным?
Теорема 4.
Для того чтобы работа векторного поля
![]() не
не
зависела от формы пути, соединяющего
две точки в области, необходимо и
достаточно, чтобы циркуляция по любому
замкнутому контуру, лежащему в этой
области, была равна нулю.
Необходимость.
Пусть работа не зависит от пути. Возьмём
контур ![]()
(рис. 10.18).
![]()
Рис.7
,
![]()
Рис.18
.
Достаточность.
Пусть ![]() ,
,
тогда ![]() .
.
Получаем
![]() ,
,
т.е. работа не
зависит от пути.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление работы силового поля по перемещению материальной точки не обходится без применения криволинейного интеграла ІІ рода. Чтобы не повторять в каждой новой статье для криволинейных интегралов те же формулы сразу переходим к анализу готовых примеров.
Вычисление работы силового поля с помощью криволинейного интегралу ІІ рода
ЗАДАНИЕ 3.5 Вычислить работу силового поля 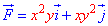 при перемещению материальной точки вдоль линии L:
при перемещению материальной точки вдоль линии L:
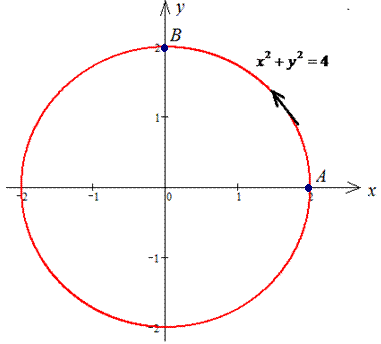
x2+y2=4 от точки A(2;0) к точке B(0;2).
Решение: Построим в декартовых координатах траекторию материальной точки вдоль круга L: x2+y2=4.
Уравнение верхней части полукруга и ее производной равны
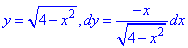
В соответствии с точками A(2;0), B(0;2) пределы интегрирования изменяются от 2 до 0.
Не удивляйтесь, что не в обратном порядке. Их всегда нужно выписывать в порядке обхода контуру от точки A к B.
Робота силового поля F по перемещения материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода :
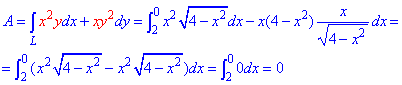
Внимательно пересмотрите уравнение силового поля и подинтегральную функцию и Вам станет понятно, что и откуда берется. Как вычислить криволинейный интеграл детально расписано в предыдущих статьях (меняем y, dy на ф-и от “х” под интегралом).
ЗАДАНИЕ 3.10 Найти работу силового поля 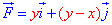 по перемещению материальной точки вдоль линии L:
по перемещению материальной точки вдоль линии L:
y=a-x2/a от точки A(-a;0) к точке B(0;a).
Решение: Имеем y=a-x2/a – уравнение параболы, находим дифференциал dy=-2x/a*dx и пределы изменения переменной
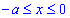
Вычисляем работу силового поля F, потраченную на перемещению материальной точки вдоль вдоль линии L 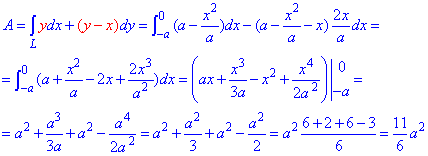
Криволинейный интеграл ІІ рода находим за первой формулой интегрирования.
ЗАДАНИЕ 3.12 Вычислить работу силового поля 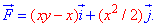 по перемещению материальной точки вдоль линии L:
по перемещению материальной точки вдоль линии L: 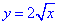 от точки A(0;0) к точке B(1;2). .
от точки A(0;0) к точке B(1;2). .
Решение: Строим траекторию материальной точки вдоль корневой функции L: 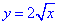 .
.
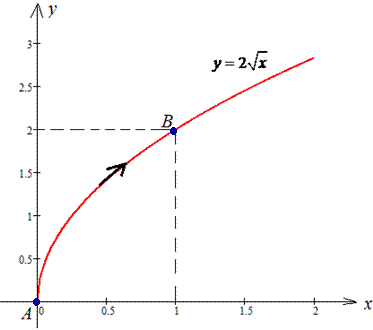
Записываем производную 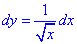 и промежуток интегрирования [0;1].
и промежуток интегрирования [0;1].
Находим роботу A силового поля F : 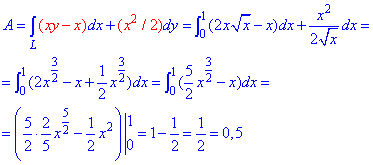
Перед интегрированием превращаем корни к показательной форме записи, а дальше вычисляем за табличными формулами интеграл.
ЗАДАНИЕ 3.14 Вычислить работу силового поля 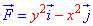 по перемещению материальной точки вдоль линии L:
по перемещению материальной точки вдоль линии L:
x2+y2=9.
Решение: Наведем траекторию движения материальной точки по кругу L: x2+y2=9.
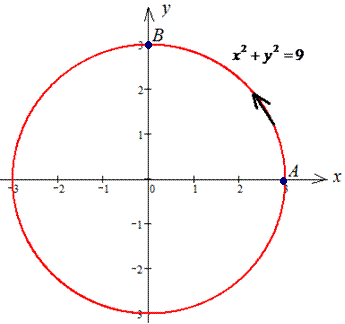
Верхняя ветка ограничена функцией
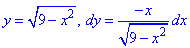
Аргумент изменяется от 3 до 0 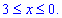
Работа А силового поля F при перемещению материальной точки вдоль линии L вычисляется с помощью криволинейного интеграла ІІ рода : 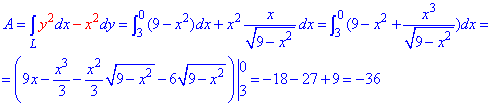
Интегрирование само по себе тяжелое, главное правильно найти дифференциал функции и не ошибиться с пределами интегрирования.
ЗАДАНИЕ 3.19 Вычислить работу силового поля 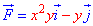 по перемещения материальной точки вдоль линии L:
по перемещения материальной точки вдоль линии L:
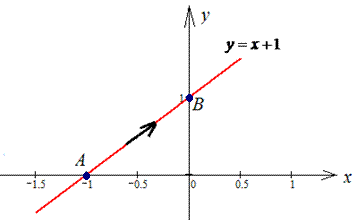
прямая от точки A(-1;0) к точке B(0;1).
Решение: Запишем уравнение прямой, которая проходит через две точки A(-1;0) и B(0;1):
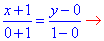
отсюда y=x+1.
Таким образом, имеем дифференциал дуги dy=dx плюс интервал интегрирования [- 1;0].
График прямой приведен на рисунку ниже
 Подсчитываем работу силового поля F по перемещения материальной точки вдоль линии L:
Подсчитываем работу силового поля F по перемещения материальной точки вдоль линии L: 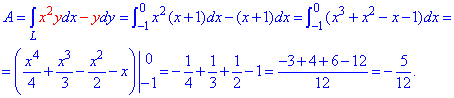
Криволинейный интеграл 2 рода легко сводим к определенному и находим результирующее значение работы.
ЗАДАНИЕ 3.20 Вычислить работу силового поля 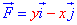 по перемещению материальной точки вдоль линии L:
по перемещению материальной точки вдоль линии L:
x2+y2=1 от точки A (1;0) к точке B (- 1;0).
Решение: Построим траекторию материальной точки против движения часовой стрелки по кругу L: x2+y2=9.
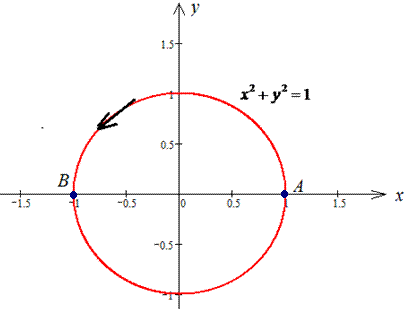
Верхнюю его дуга предствим корневой зависимостью
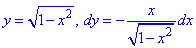
Аргумент при этом изменяется от 1 к -1.
Работа силового поля потрачена на перемещение материальной точки вдоль дуги круга равна интегралу: 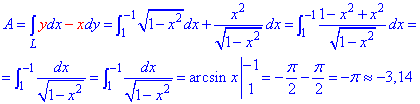
Во время интегрирования получим арксинус, который на границах дает число Pi/2.
Еще один раздел где можно применить криволинейный интеграл ІІ рода теперь доступный и известный Вам.
Будьте внимательные в вычислениях и успешной Вам учебы!
Примеры решений задач по теории поля
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Полезная страница? Сохрани или расскажи друзьям
Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline{a}=(3x-y) overline{i}+(6z+5x) overline{k}$
Задача 3. Дано скалярное поле $u(x,y,z)$ и векторное поле $overline{a}(x,y,z)$. Найти $grad u$, $div overline{a}$, $rot overline{a}$ в точке $M(1;5;-2)$.
$$u=frac{sqrt{x}}{y}-frac{yz}{x+sqrt{y}}, quad
overline{a}=yzoverline{i} +xzoverline{j} +xyoverline{k}$$
Задача 4. Вычислить потенциальную функцию векторного поля
$$overline{a}=left( frac{x}{y}+ycos x right)overline{i} +left(-frac{x^2}{2y^2}+sin xright)overline{j}.$$
Поток поля через поверхность
Задача 5. Найти поток векторного поля $overline{a}=2x overline{i}+y overline{j}-2z overline{k}$ через часть плоскости $P: 2x+y/2+z=1$, расположенную в первом октанте (нормаль образует острый угол с осью $Oz$).
Задача 6. Найти поток векторного поля $overline{a}$ через часть поверхности $S$, вырезаемую плоскостями $P_1, P_2$ (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
$$ overline{a}=(x^3+xy^2)overline{i}+(y^3+x^2y)overline{j}+z^2overline{k},\
S: x^2+y^2=1, P_1^ z=0; P_2: z=3$$
Задача 7. Найти поток векторного поля $overline{a}$ через замкнутую поверхность $S$ (нормаль внешняя).
$$ overline{a}=xoverline{i}+zoverline{j}-yoverline{k},\
S: z=4-2(x^2+y^2), z=2(x^2+y^2).$$
Задача 8. Найти поток векторного поля $overline{a}=x^3overline{i}+y^3overline{j}+z^3overline{k}$ через замкнутую поверхность $S: x^2+y^2+z^2=1$ (нормаль внешняя).
Задача 9. Найти поток векторного поля $overline{a}$ через часть плоскости $S$, вырезанную плоскостью $P: z=1$ непосредственно и с помощью формулы Гаусса-Остроградского (нормаль внешняя к замкнутой поверхности).
$$overline{a}=(x+xy^2) overline{i} + (y-yx^2)overline{j}+(z-3)overline{k}, quad S: x^2+y^2=z^2 (z geq 0).$$
Циркуляция векторного поля
Задача 10. Найти модуль циркуляции векторного поля $overline{a}=xyoverline{i}+yzoverline{j}+zxoverline{k}$ вдоль контура
$$x^2+y^2=9, x+y+z=1.$$
Задача 11. Найдите циркуляцию вектора $overline{a}=(x^2-y) overline{i}+ xoverline{j}+ overline{k}$ по контуру
$$x^2+y^2=1;\
z=1$$
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$.
$$ overline{F} = (3x-1) overline{i}+ (y-x+z)overline{j}+4z overline{k}, $$
$L$ – контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline{F} = xz overline{i} -overline{j}+y overline{k}$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline{F} = z overline{i}+ (x+y)overline{j}+y overline{k}, quad (p): 2x+y+2z=2. $$
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей, оформление производится в Word, срок от 1 дня.
Проконсультируем по задачам теории поля
Полезные ссылки
- Учебник с примерами онлайн по теории поля
- Функции нескольких переменных – задачи с решениями
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.
Работа вектора вдоль кривой
Работа вектора вдоль кривой
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты

Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Геометрические и физические приложения
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
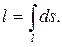 (39)
(39)
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
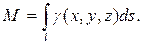 (40)
(40)
Пример 6.
Найти массу кривой с линейной плотностью 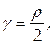 заданной в полярных координатах уравнением ρ =4φ, где
заданной в полярных координатах уравнением ρ =4φ, где 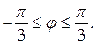
Используем формулу (40) с учетом того, что кривая задана в полярных координатах:
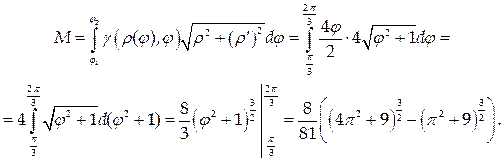
3) Моменты кривой l:
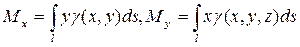 — (41)
— (41)
— статические моменты плоской кривой l относительно осей Ох и Оу;
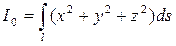 — (42)
— (42)
— момент инерции пространственной кривой относительно начала координат;
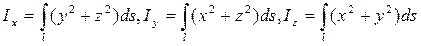 — (43)
— (43)
— моменты инерции кривой относительно координатных осей.
4) Координаты центра масс кривой вычисляются по формулам
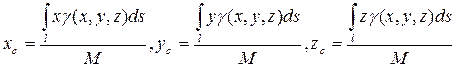 . (44)
. (44)
5) Работа силы 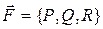 , действующей на точку, движущуюся по кривой (АВ):
, действующей на точку, движущуюся по кривой (АВ):
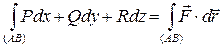 , (45)
, (45)
Пример 7.
Вычислить работу векторного поля 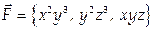 вдоль отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).
вдоль отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).
Найдем канонические и параметрические уравнения прямой АВ:
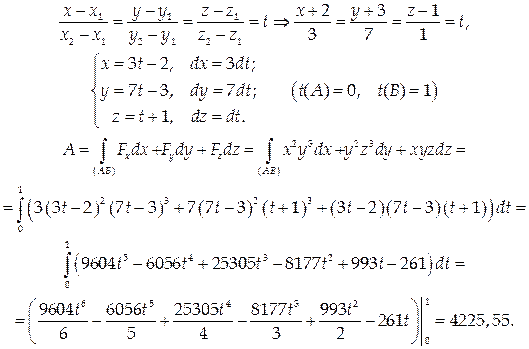
6) Площадь криволинейной поверхности, уравнение которой
z = f(x, y), можно найти в виде:
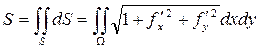 (46)
(46)
(Ω – проекция S на плоскость Оху).
7) Масса поверхности
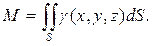 (47)
(47)
Пример 8.
Найти массу поверхности 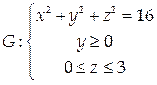 с поверхностной плотностью γ = 2z 2 + 3.
с поверхностной плотностью γ = 2z 2 + 3.

На рассматриваемой поверхности 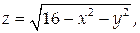
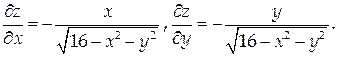 Тогда
Тогда
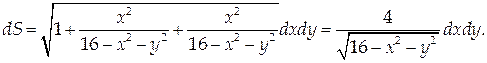
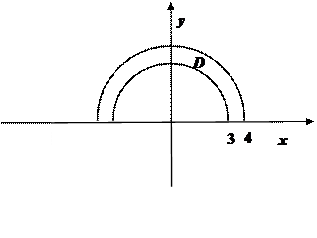
Проекцией D этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.
Применяя формулу (47) и переходя к полярным координатам, получим:
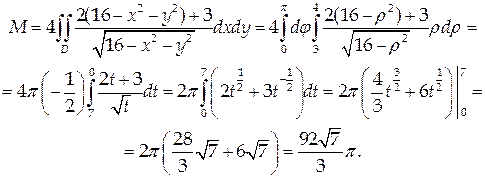
8) Моменты поверхности:
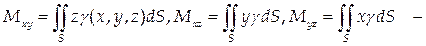 (48) статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;
(48) статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;
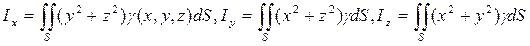
— моменты инерции поверхности относительно координатных осей;
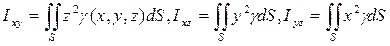 — (50)
— (50)
— моменты инерции поверхности относительно координатных плоскостей;
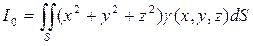 — (51)
— (51)
— момент инерции поверхности относительно начала координат.
9) Координаты центра масс поверхности:
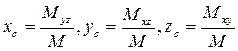 . (52)
. (52)
III. Теория поля
Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярноеили векторное).
Если в некоторой области задано скалярное поле U(x,y,z), то вектор
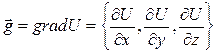 (53)
(53)
называется градиентомвеличины U в соответствующей точке.
Пусть дано векторное поле 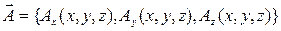 . Интеграл
. Интеграл
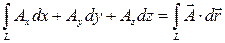 (54)
(54)
называется линейным интегралом от вектора 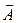 вдоль кривой L. Если кривая L замкнута, то этот интеграл называют циркуляцией вектора
вдоль кривой L. Если кривая L замкнута, то этот интеграл называют циркуляцией вектора 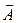 вдоль кривой L.
вдоль кривой L.
Пример 9.
Вычислить циркуляцию векторного поля 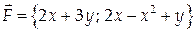 по контуру Г, состоящему из частей линий
по контуру Г, состоящему из частей линий 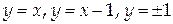 (направление обхода положительно).
(направление обхода положительно).

Воспользуемся формулой Грина:
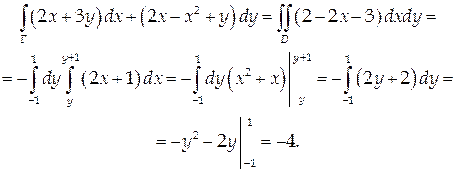
Ротором или вектором вихрявекторного поля A = , где Ax, Ay, Az – функции от x, y, z, называется вектор, определяемый следующим образом:
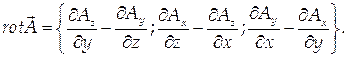 (55)
(55)
Рассмотрим векторное поле А(М), определенное в пространственной области G, ориентированную гладкую поверхность S 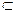 G и поле единичных нормалей п(М) на выбранной стороне поверхности S.
G и поле единичных нормалей п(М) на выбранной стороне поверхности S.
Поверхностный интеграл 1-го рода
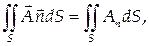 (56)
(56)
где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.
Пример 10.
Найти поток векторного поля 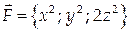 через часть плоскости
через часть плоскости 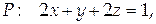 ограниченную координатными плоскостями (нормаль к плоскости образует острый угол с осью Oz).
ограниченную координатными плоскостями (нормаль к плоскости образует острый угол с осью Oz).
Проекцией данной поверхности на координатную плоскость Оху является треугольник с вершинами в точках А(0;0), В(0;1), С(½; 0). Найдем координаты единичной нормали к плоскости:
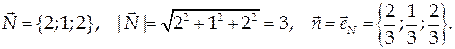
Вычислим соответствующий поверхностный интеграл (формула (56)):
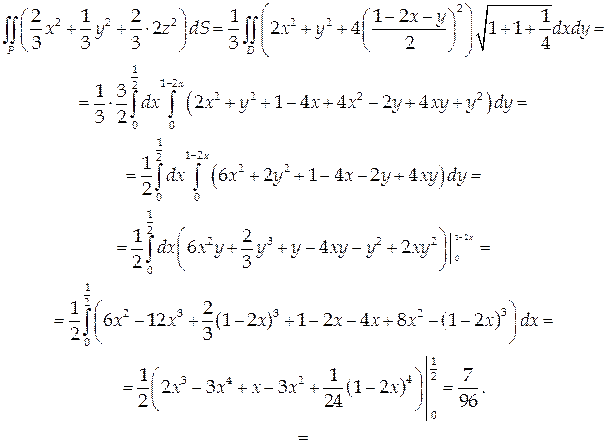
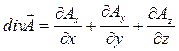 . (57)
. (57)
Пример 11.
Найти дивергенцию и ротор векторного поля 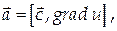 где
где 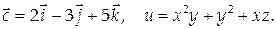
Найдем координаты вектора а:
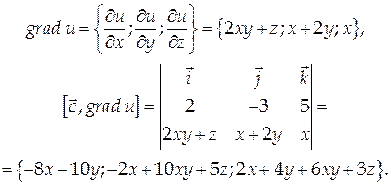
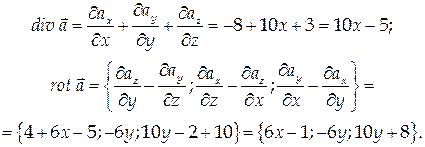
Векторное поле A = называется потенциальным, если вектор А является градиентом некоторой скалярной функции u = u(x, y, z):
A = grad u = 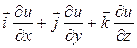 . (58)
. (58)
При этом функция и называется потенциалом данного векторного поля.
Пример 12.
потенциальным, и в случае положительного ответа найти потенциал и, считая, что в начале координат он равен нулю.
Следовательно, поле  потенциальное. Найдем его потенциал и, считая, что и(0;0;0) = 0:
потенциальное. Найдем его потенциал и, считая, что и(0;0;0) = 0:
Векторное поле A = называется соленоидальным в области D, если в каждой точке этой области
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline=(3x-y) overline+(6z+5x) overline $
Однородное электрическое поле сосредоточено между разноименно заряженными пластинами (обкладками конденсатора).
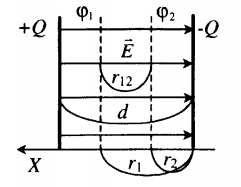
Характеристики однородного электростатического поля
| Силовые линии | Начинаются на положительно заряженной пластине, а заканчиваются на отрицательно заряженной. Силовые линии параллельны друг другу, т. е. поле однородно. |
| Напряженность |
−E |
| Потенциал |
φ=Er |
| Разность потенциалов |
φ1−φ2=Er12 |
| Напряжение между пластинами |
U=Ed d — расстояние между заряженными пластинами. |
| Эквипотенциальные поверхности | Плоскости, параллельные заряженным пластинам. |
| Закон Кулона |
FK=qE=qUd |
| Ускорение силы Кулона (следует из второго закона Ньютона) |
a=FKm=qEm=qUmd |
Подсказки к решению задач:
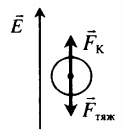 |
Равновесие заряженного тела в электростатическом поле:
Fтяж=FK Сила тяжести равна произведению массы заряженного тела на ускорение свободного падения: Fтяж=mg Сила Кулона равна: FK=qE=qUd |
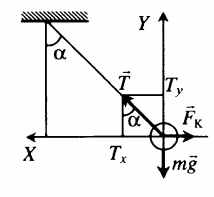 |
Отклонение от вертикали нити с заряженным телом в горизонтальном электростатическом поле.
Второй закон Ньютона в векторной форме: −FK+m−g+−T=m−a Проекции на оси: OX:Tsinα−FK=0 OY:Tcosα−mg=0 Отсюда сила Кулона равна: FK=mgtanα FK=qE=qUd |
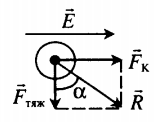 |
Направление траектории полого шарика массой m и зарядом q, который движется в горизонтальном электрическом поле напряженностью −E. Важно! Направление траектории совпадает с направлением равнодействующей силы. Равнодействующая силы находится по второму закону Ньютона: −R=−FK+m−g Из рисунка видно, что: tanα=FKFтяж=qEmg |
Пример №1. Полый шарик массой m = 0,4 г с зарядом q = 8 нКл движется в горизонтальном однородном электрическом поле, напряженность которого E = 500 кВ/м. Какой угол α образует с вертикалью траектория шарика, если его начальная скорость равна нулю?
0,4 г = 0,4∙10–3 кг
8 нКл = 8∙10–9 Кл
500 кВ/м = 5∙105 В/м
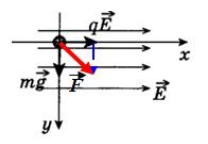
При движении в электрическом поле на заряженную частицу действует сила тяжести:
−Fтяж=m−g
На нее также действует сила Кулона со стороны электрического поля:
−FK=q−E
В инерциальной система отсчета, связанной с Землей, в соответствии со вторым законом Ньютона:
−FK+m−g=m−a
При движении из состояния покоя с постоянным ускорением тело движется по прямой в направлении вектора ускорения, т. е. в направлении равнодействующей приложенных сил. Прямая, вдоль которой направлен вектор ускорения, образует угол с вертикалью, равный:
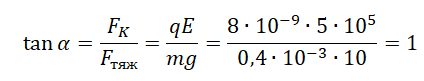
Тангенс, равный единице, соответствует углу, равному 45 градусам.
Работа однородного электрического поля
Из курса механики вспомним, что работа определяется произведением силы, действующей на тело, на его перемещение и косинус угла между векторами силы и этого перемещения:
A=Fscosα
Эту же формулу можно использовать для нахождения работы однородного электрического поля. В качестве силы в данном случае выступает сила Кулона:
FK=qE=qUd
А произведение перемещения на косинус угла между силой и перемещением в этом случае равно разности начального и конечного положения заряда:
scosα=r0−r
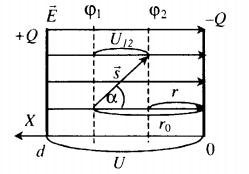
Отсюда работа однородного электрического поля равна:
Формулы работы электрического поля
A=±qE(r0−r)=±qUd(r0−r)
или
A=FKscosα=±qEscosα=±qUdscosα
- E (В/м или Н/Кл) — модуль напряженности электрического поля;
- U (В) — разность потенциалов (напряжение) между пластинами;
- d (м) — расстояние между пластинами;
- ±q — заряд, переносимый полем;
- s (м) — модуль перемещения заряда;
- α — угол между силой Кулона и перемещением;
- r0 (м) — начальное положение заряда;
- r (м) — конечное положение заряда.
Работу также можно выразить через разность потенциалов:
A=±q(φ1−φ2)=±qU12
- φ1 — начальный потенциал;
- φ2 — конечный потенциал;
- U12 — напряжение между начальным и конечным положением заряда.
Внимание! Работа электростатического поля не зависит от вида траектории.
Работа и изменение кинетической энергии:
A=mv22−mv202=ΔEk
Работа и изменение потенциальной энергии:
A=−(qEr−qEr0)=−ΔWp
Пример №2. В точке А потенциал электрического поля равен 200 В. Потенциал в точке В равен 100В. Какую работу совершают силы электростатического поля при перемещении заряда 5 мКл из точки А в точку В?
5 мКл = 5∙10–3 Кл
A=±q(φ1−φ2)=5·10−3(200−100)=0,5 (Дж)
Задание EF17633
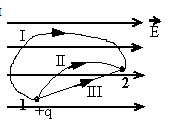 Положительный заряд перемещается в однородном электростатическом поле из точки 1 в точку 2 по разным траекториям. Работа сил электростатического поля
Положительный заряд перемещается в однородном электростатическом поле из точки 1 в точку 2 по разным траекториям. Работа сил электростатического поля
Ответ:
а) максимальна в случае перемещения по траектории I
б) не совершается в случае перемещения по траектории II
в) минимальна в случае перемещения по траектории III
г) одинакова при перемещении по всем траекториям
Алгоритм решения
- Установить, от чего зависит работа электростатического поля, затрачиваемая на перемещение в нем заряженной частицы.
- Определить, какую работу совершает поле при движении заряда по каждой из траекторий.
Решение
Кулоновская сила — это потенциальная сила. Поэтому работа, которую она совершает, не зависит от вида траектории. Учитываться будет только перемещение, равное кратчайшему расстоянию между точками 1 и 2. Следовательно, работа будет одинаковой при перемещении положительного заряда по всем траекториям.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18815
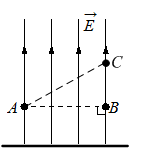 Однородное электростатическое поле создано равномерно заряженной протяжённой горизонтальной пластиной. Линии напряжённости поля направлены вертикально вверх (см. рисунок).
Однородное электростатическое поле создано равномерно заряженной протяжённой горизонтальной пластиной. Линии напряжённости поля направлены вертикально вверх (см. рисунок).
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
Ответ:
1) Пластина имеет отрицательный заряд.
2) Потенциал электростатического поля в точке В ниже, чем в точке С.
3) Работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю.
4) Если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз.
5) Напряжённость поля в точке А меньше, чем в точке С.
Алгоритм решения
1.Проанализировать каждое из утверждений.
2.Установить, какие из утверждений являются истинными.
3.Записать номера верных утверждений.
Решение
Согласно утверждению 1, пластина имеет отрицательный заряд. Известно, что векторы напряженности поля, создаваемого отрицательным зарядом, направляются в сторону этого заряда. Но мы видим, что векторы направляются от заряда. Следовательно, пластина заряжена положительно, а утверждение 1 неверно.
Согласно утверждению 2, потенциал электростатического поля в точке В ниже, чем в точке С. Известно, что потенциал зависит от расстояния до отрицательно пластины. Поскольку в нашем случае пластина заряжена положительно, с увеличением расстояния от нее потенциал уменьшается. Поэтому потенциал в точке С меньше потенциала в точке В, а утверждение 2 неверно.
Согласно утверждению 3, работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю. Работа определяется формулой:
A=FKscosα=±qEscosα
Видно, что работа зависит от перемещения относительно заряженной пластины. Но точки А и В находятся от пластины на одинаковом расстоянии. Следовательно, перемещение относительно нее равно 0. Поэтому работа по перемещению заряда тоже будет нулевой, и утверждение 3 верно.
Согласно утверждению 4, если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз. Это действительно так. Мы выяснили, что пластина заряжена положительно. Следовательно, отрицательный заряд будет притягиваться к ней, и утверждение 4 верно.
Согласно утверждению 5, напряжённость поля в точке А меньше, чем в точке С. Это не так, потому что речь идет об однородном поле. Напряженность однородного поля одинакова во всех точках, и утверждение 5 неверно.
Верные утверждения: 3 и 4.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.6k
