Работа сил электростатического поля. Понятие потенциала
Когда пробный заряд q перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения ∆l→ формулу работы можно записать так: ∆A=F·∆l·cos α=Eq∆lcos α=Elq∆l.
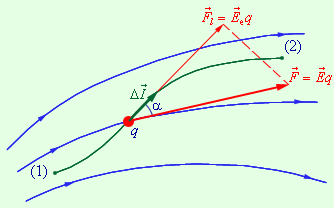
Рисунок 1.4.1. Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.
Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.
При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.
У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.
Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:
Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна 0. Поле, обладающее таким свойством, называется консервативным, или потенциальным.
Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом Q, а также две траектории перемещения пробного заряда q в другую точку. Символом ∆l→ на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:
∆A=F∆lcos α=Eq∆r=14πε0Qqr2∆r.
Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением Δr. Проинтегрируем данное выражение на интервале от r=r1 до r=r2 и получим следующее:
A=∫r1r2E·q·dr=Qq4πε01r1-1r2.
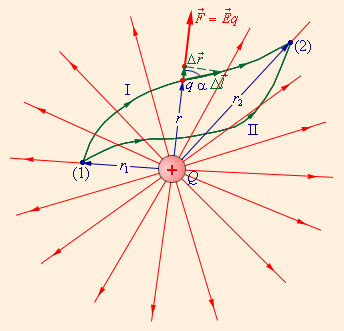
Рисунок 1.4.2. Траектории перемещения заряда и работа кулоновских сил. Зависимость от расстояния между начальной и конечной точкой траектории.
Результат применения данной формулы не будет зависеть от траектории. Для двух различных траекторий перемещения заряда, указанных на изображении, работы кулоновских сил будут равны. Если же мы изменим направление на противоположное, то и работа также поменяет знак. А если траектории будут соединены, т.е. заряд будет перемещаться по замкнутой траектории, то работа кулоновских сил будет нулевой.
Вспомним, как именно создается электростатическое поле. Оно представляет собой сочетание точечных разрядов. Значит, согласно принципу суперпозиции, работа результирующего поля, совершаемая при перемещении пробного заряда, будет равна сумме работ кулоновских полей тех зарядов, из которых состоит электростатическое поле. Соответственно, величина работы каждого заряда не будет зависеть от того, какой формы траектория. Значит, и полная работа не будет зависеть от пути – важно лишь местоположение начальной и конечной точки.
Поскольку у электростатического поля есть свойство потенциальности, мы можем добавить новое понятие – потенциальная энергия заряда в электрическом поле. Выберем какую-либо точку, поместим в нее разряд и примем его потенциальную энергию за 0.
Потенциальная энергия заряда, помещенного в любую точку пространства относительно нулевой точки, будет равна той работе, которая совершается электростатическим полем при перемещении заряда из этой точки в нулевую.
Обозначив энергию как W, а работу, совершаемую зарядом, как A10, запишем следующую формулу:
Wp1=A10.
Обратите внимание, что энергия обозначается именно буквой W, а не E, поскольку в электростатике E – это напряженность поля.
Потенциальная энергия электрического поля является определенной величиной, которая зависит от выбора точки отсчета (нулевой точки). На первый взгляд в таком определении есть заметная неоднозначность, однако на практике она, как правило, не вызывает недоразумений, поскольку сама по себе потенциальная энергия физического смысла не имеет. Важна лишь разность ее значений в начальной и конечной точке пространства.
Чтобы вычислить работу, которая совершается электростатическим полем при перемещении точечного заряда из точки 1 в точку 2, нужно найти разность значений потенциальной энергии в них. Путь перемещения и выбор нулевой точки значения при этом не имеют.
A12=A10+ A02= A10 – A20 =Wp1 – Wp2.
Если мы поместим заряд q в электростатическое поле, то его потенциальная энергия будет прямо пропорциональна его величине.
Понятие потенциала электрического поля
Потенциал электрического поля – это физическая величина, значение которой можно найти, разделив величину потенциальной энергии электрического заряда в электростатическом поле на величину этого заряда.
Он обозначается буквой φ. Это важная энергетическая характеристика электростатического поля.
φ=Wpq.
Если мы умножим величину заряда на разность потенциалов начальной и конечной точки перемещения, то мы получим работу, совершаемую при этом перемещении.
A12=Wp1–Wp2=qφ1–qφ2=q(φ1 – φ2).
Потенциал электрического поля измеряется в вольтах (В).
1 В=1 Дж1 Кл.
Разность потенциалов в формулах обычно обозначается Δφ.
Чаще всего при решении задач на электростатику в качестве нулевой берется некая бесконечно удаленная точка. Учитывая это, мы можем переформулировать определение потенциала так:
Потенциал электростатического поля точечного заряда в некоторой точке пространства будет равен той работе, которая совершается электрическими силами тогда, когда единичный положительный заряд удаляется из этой точки в бесконечность.
φ∞=A∞q.
Чтобы вычислить потенциал точечного заряда на расстоянии r, на котором размещается бесконечно удаленная точка, нужно использовать следующую формулу:
φ=φ∞=1q∫r∞Edr=Q4πε0∫r∞drr2=14πε0Qr
С помощью нее мы также можем найти потенциал поля однородно заряженной сферы или шара при r≥R, что следует из теоремы Гаусса.
Изображение электрических полей с помощью эквипотенциальных поверхностей
Чтобы наглядно изобразить электростатические поля, кроме силовых линий используются поверхности, называемые эквипотенциальными.
Эквипотенциальная поверхность (поверхность равного потенциала) – это такая поверхность, у которой во всех точкам потенциал электрического поля одинаков.
Эквипотенциальные поверхности и силовые линии на изображении всегда находятся перпендикулярно друг другу.
Если мы имеем дело с точечным зарядом в кулоновском поле, то эквипотенциальные поверхности в данном случае являются концентрическими сферами. На изображениях ниже показаны простые электростатические поля.
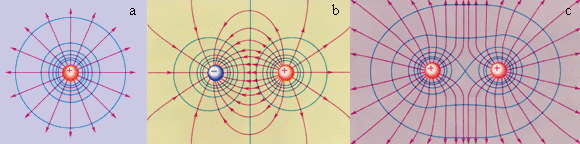
Рисунок 1.4.3. Красным показаны силовые линии, а синим – эквипотенциальные поверхности простого электрического поля. На первом рисунке изображен точечный заряд, на втором –электрический диполь, на третьем – два равных положительных заряда.
Если поле однородное, то его эквипотенциальные поверхности являются параллельными плоскостями.
В случае малого перемещения пробного заряда q вдоль силовой линии из начальной точки 1 в конечную точку 2 мы можем записать такую формулу:
ΔA12=qEΔl=q(φ1–φ2)=–qΔφ,
где Δφ=φ1-φ2 – изменение потенциала. Отсюда выводится, что:
E=-∆φ∆l, (∆l→0) или E=-dφdl.
Это соотношение передает связь между потенциалом поля и его напряженностью. Буквой l обозначена координата, которую следует отсчитывать вдоль силовой линии.
Зная принцип суперпозиции напряженности полей, которые создаются электрическими разрядами, мы можем вывести принцип суперпозиции для потенциалов:
φ=φ1+φ2+φ3+…
From Wikipedia, the free encyclopedia
For other examples of “work” in physics, see Work (physics).
Electric field work is the work performed by an electric field on a charged particle in its vicinity. The particle located experiences an interaction with the electric field. The work per unit of charge is defined by moving a negligible test charge between two points, and is expressed as the difference in electric potential at those points. The work can be done, for example, by electrochemical devices (electrochemical cells) or different metals junctions[clarification needed] generating an electromotive force.
Electric field work is formally equivalent to work by other force fields in physics,[1] and the formalism for electrical work is identical to that of mechanical work.
Physical process[edit]
Particles that are free to move, if positively charged, normally tend towards regions of lower electric potential (net negative charge), while negatively charged particles tend to shift towards regions of higher potential (net positive charge).
Any movement of a positive charge into a region of higher potential requires external work to be done against the electric field, which is equal to the work that the electric field would do in moving that positive charge the same distance in the opposite direction. Similarly, it requires positive external work to transfer a negatively charged particle from a region of higher potential to a region of lower potential.
Kirchhoff’s voltage law, one of the most fundamental laws governing electrical and electronic circuits, tells us that the voltage gains and the drops in any electrical circuit always sum to zero.
The formalism for electric work has an equivalent format to that of mechanical work. The work per unit of charge, when moving a negligible test charge between two points, is defined as the voltage between those points.
where
- Q is the electric charge of the particle
- E is the electric field, which at a location is the force at that location divided by a unit (‘test’) charge
- FE is the Coulomb (electric) force
- r is the displacement
is the dot product operator
Mathematical description[edit]
Given a charged object in empty space, Q+. To move q+ closer to Q+ (starting from 
Where U(r) is the potential energy of q+ at a distance r from the source Q. So, integrating and using Coulomb’s Law for the force:
Now, use the relationship
To show that the external work done to move a point charge q+ from infinity to a distance r is:
This could have been obtained equally by using the definition of W and integrating F with respect to r, which will prove the above relationship.
In the example both charges are positive; this equation is applicable to any charge configuration (as the product of the charges will be either positive or negative according to their (dis)similarity).
If one of the charges were to be negative in the earlier example, the work taken to wrench that charge away to infinity would be exactly the same as the work needed in the earlier example to push that charge back to that same position.
This is easy to see mathematically, as reversing the boundaries of integration reverses the sign.
Uniform electric field[edit]
Where the electric field is constant (i.e. not a function of displacement, r), the work equation simplifies to:
or ‘force times distance’ (times the cosine of the angle between them).
Electric power[edit]
The electric power is the rate of energy transferred in an electric circuit. As a partial derivative, it is expressed as the change of work over time:
,
where V is the voltage. Work is defined by:
Therefore
References[edit]
- ^ Debora M. Katz (1 January 2016). Physics for Scientists and Engineers: Foundations and Connections. Cengage Learning. pp. 1088–. ISBN 978-1-337-02634-5.
Содержание:
Работа по перемещению заряда в электростатическом поле:
В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.
Работа по перемещению заряда в однородном электростатическом поле
Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.
Пусть в однородном электростатическом поле напряженностью 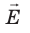
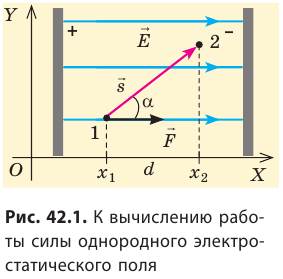
Вычислим работу А, которую совершает сила 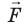 , действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.
, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.
Поле однородное, поэтому сила 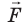 постоянна, ее модуль равен: F=qE, а scosα=d=
постоянна, ее модуль равен: F=qE, а scosα=d=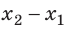 является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 (
является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( 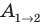 ) равна:
) равна:
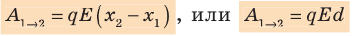
Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.
Обратите внимание! Формула 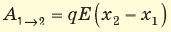 будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.
будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.
Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.
Потенциальная энергия заряженного тела в поле, созданном точечным зарядом
Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом  . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:
. Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:
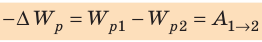
Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:
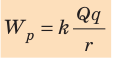
Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна (
> 0), если заряды одноименные, и отрицательна ( < 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то
< 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то  = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.
= 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.
Что называют потенциалом электростатического поля
Потенциал 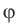 электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии
электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии  электрического заряда, помещенного в данную точку поля, к значению q этого заряда:
электрического заряда, помещенного в данную точку поля, к значению q этого заряда:
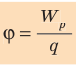
Единица потенциала в Си — вольт: 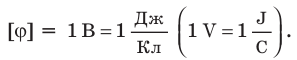
Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле: 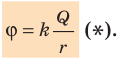
Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.
Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 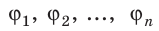 полей, созданных каждым зарядом:
полей, созданных каждым зарядом:
Как определяют разность потенциалов
Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: 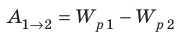 . Поскольку
. Поскольку 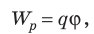 то
то 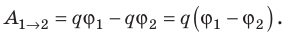 Выражение
Выражение 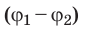 называют разностью потенциалов, где
называют разностью потенциалов, где 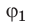 — значение потенциала в начальной точке траектории движения заряда,
— значение потенциала в начальной точке траектории движения заряда, 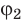 — значение потенциала в ее конечной точке.
— значение потенциала в ее конечной точке.
Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:
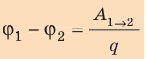
Единица разности потенциалов в Си — вольт: 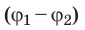 = 1 В (V).
= 1 В (V).
Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов 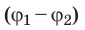 − также называют напряжением (U). Важно не путать изменение потенциала
− также называют напряжением (U). Важно не путать изменение потенциала 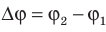 и разность потенциалов (напряжение)
и разность потенциалов (напряжение) 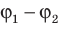 .
.
Как связаны напряженность однородного электростатического поля и разность потенциалов
Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).
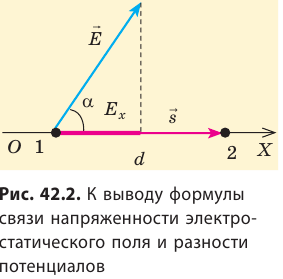
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: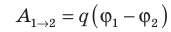 ; 2) через напряженность поля:
; 2) через напряженность поля: 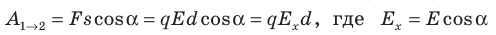 — проекция вектора
— проекция вектора 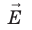 на ось Ох, проведенную через точки 1 и 2.
на ось Ох, проведенную через точки 1 и 2.
Приравняв оба выражения для работы, получим: 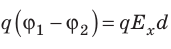 , откуда:
, откуда: 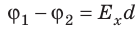 , или
, или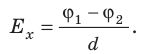
Если заряд перемещается в направлении напряженности электрического поля ( ) , последняя формула примет вид:
) , последняя формула примет вид:
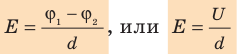
Из последней формулы следует единица напряженности в Си — вольт на метр:
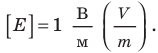
Какие поверхности называют эквипотенциальными
Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.
Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.
Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).
Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( 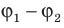 ), а на эквипотенциальной поверхности
), а на эквипотенциальной поверхности 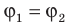 .
.
Работу электростатического поля также можно представить через силу 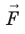 , действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами
, действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами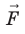 и
и 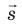 . Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы
. Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы 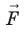 , а следовательно, и вектор напряженности
, а следовательно, и вектор напряженности 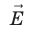 поля в любой точке перпендикулярны вектору перемещения
поля в любой точке перпендикулярны вектору перемещения 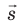 .
.
Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).
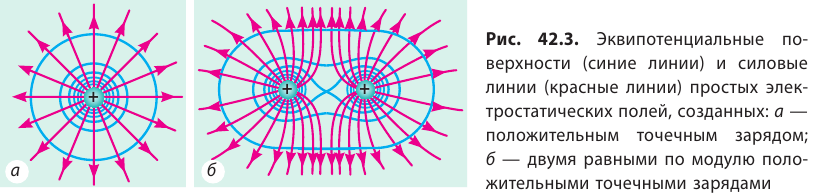
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.
- Заказать решение задач по физике
Пример решения задачи
Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона 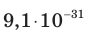 кг, заряд
кг, заряд 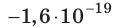 Кл.
Кл.
Заряд электрона — отрицательный, его начальная скорость 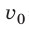 = 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.
= 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.
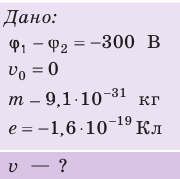
Решение:
Поиск математической модели, решение Согласно теореме о кинетической энергии:
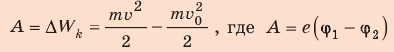 — работа сил поля.
— работа сил поля.
Таким образом, 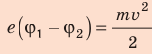 , отсюда
, отсюда 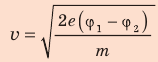 .
.
Проверим единицу, найдем значение искомой величины:
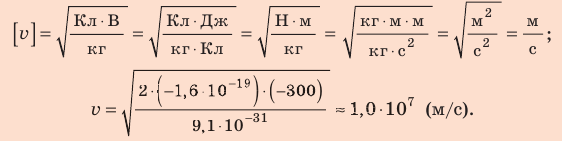
Ответ: 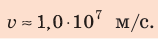
Выводы:
- Закон Ома для однородного участка электрической цепи
- Закон Ома для полной цепи
- Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
- Сила и закон Ампера
- Волновое движение в физике
- Продольные и поперечные волны в физике
- Звуковые волны в физике
- Электрическое поле в физике
Работа сил электрического поля. Напряжение
План урока
- Работа электрического поля
- Напряжение
Цели урока
- Знать: формулы для расчета работы электрического поля; понятие напряжения; формулу напряжения; связь между работой электрических сил и напряжением
- Уметь: проводить аналогию между работой силы тяжести и работой электрической силы; выводить формулу для расчета работы однородного электрического поля
Разминка
- По какой формуле рассчитывается работа в механике?
- Может ли электрическое поле совершить механическую работу?
- Что общего между гравитационным полем Земли и электрическим полем?
Работа электрического поля
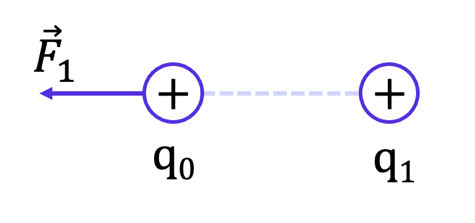
Рис. 1. Взаимодействие двух положительных зарядов
Рассмотрим систему, состоящую из двух положительных зарядов q0 и q1 (рис. 1). Нам уже известно, что сила Кулона, действующая на заряд q0, будет направлена от заряда q1, в нашем случае – влево.
Из механики нам известно, что работу можно найти по следующей формуле:
A=F·∆x,
где F – модуль постоянной силы, действующей на тело, ∆x – перемещение тела.
Если направления движения тела и действующей на него силы совпадают, то работа такой силы положительна.
Если же направления приложенной силы и движения тела противоположны, то работа такой силы отрицательна.
Соответственно, если заряд q0 перемещается влево, по направлению силы, то электрическая сила Fэл→ совершает положительную работу. Потенциальная энергия такой системы уменьшается.
В противном случае, если заряд q0 перемещается вправо, против направления действия силы, то электрическая сила совершает отрицательную работу.
Потенциальная энергия системы увеличивается, подобно энергии сжатой пружины.
Формула подразумевает действие постоянной силы, в приведенном примере сила, равная Fэл=E·q0 будет уменьшаться по мере удаления от заряда q1 вместе с модулем напряженности. Расчет работы электрического поля в данном случае будет очень трудоемок, поэтому мы рассмотрим работу однородного поля, в котором вектор напряженности не меняется E=const, следовательно, и значение силы также не будет меняться с течением времени.
Как вы уже знаете, однородное электрическое поле существует между двумя разноименно заряженными пластинами. В этом случае силу, действующую на пробный заряд q0, можно найти по формуле:
Fэл→=E→·q0.
Проведем аналогию между однородным электрическим полем и гравитационным полем Земли. Известно, что сила тяжести находится по следующей формуле:
Fтяж→=m·g→.
Сила тяжести прямо пропорциональная массе тела m и сонаправлена с вектором ускорения свободного падения g→; электрическая сила прямо пропорциональна величине пробного заряда q и сонаправлена с вектором напряженности E→.
Сравним работу силы тяжести и работу электрической силы в случае, когда вектор напряженности направлен вертикально вниз (рис. 2).
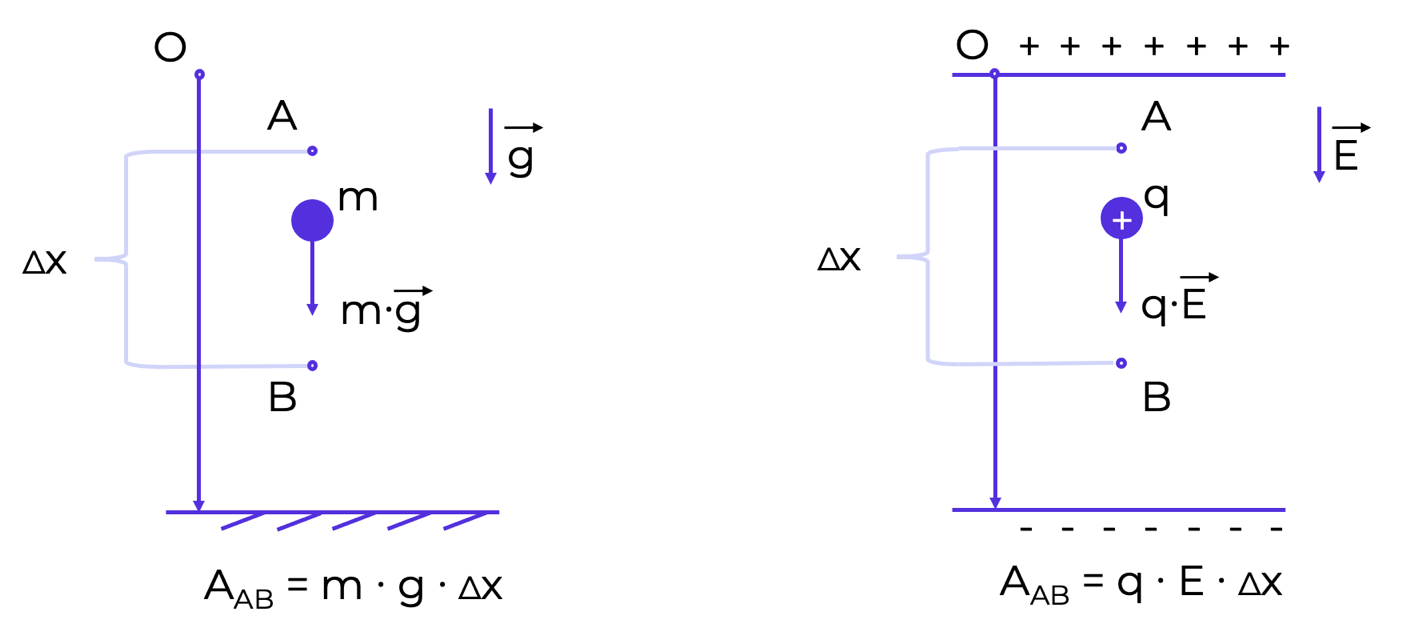
Рис. 2. Сравнение работы силы тяжести и работы электрической силы при перемещении положительного заряда
Пусть тело массой m под действием силы тяжести перемещается из точки A в точку B. Тогда перемещение этого тела равно:
∆x=xB-xA.
В соответствии с формулами выше работа силы тяжести будет равна:
A=m·g·∆x.
Пусть теперь точечный положительный заряд q перемещается из точки A в точку B вдоль силовой линии электрического поля, то есть по направлению действия силы Fэл=q·E.
A=Fэл·∆x=E·q·∆x.
Если вместо положительного заряда q перемещается отрицательный заряд -q, то действующая на него электрическая сила будет направлена в сторону, противоположную перемещению. Поэтому работа электрической силы в этом случае будет отрицательна:
A=Fэл·∆x=-E·q·∆x.
Напряжение
Из последнего выражения видно, что работа электрического поля прямо пропорциональна величине заряда q. Отношение работы электрической силы к величине заряда называется напряжением:
U=Aq,
где U [В] – напряжение;
A [Дж] – работа электрического поля по перемещению заряда q0;
q [Кл] – величина заряда.
Напряжение
– скалярная физическая величина, равная отношению работы сил электрического поля по перемещению точечного заряда q к величине этого заряда:
U=Aq.
В СИ единица измерения напряжения – вольт (В).
Если напряженность – силовая характеристика поля, то напряжение – это энергетическая характеристика электрического поля.
С одной стороны, при перемещении положительного заряда q по линии напряженности однородного поля на расстояние ∆x электрическая сила Fэл→ совершает работу, равную
A=Fэл·∆x=E·q·∆x.
С другой стороны, работа электрической силы поля может быть найдена по известному напряжению U между начальной и конечной точками перемещения:
A=q·U.
Приравнивая правые части выражений для работы, получаем, что напряжение U между двумя точками в однородном электрическом поле, расположенными на одной линии напряженности, равно произведению модуля вектора напряженности E→ поля на расстояние ∆x между этими точками:
U=E·∆x.
Отсюда для напряженности однородного электрического поля получаем выражение
E=U∆x.
Таким образом единицей измерения напряженности, кроме Н/Кл, также справедливо называть В/м.
Пример 1
Тело, двигаясь равномерно прямолинейно вдоль направления электрического поля со скоростью v = 15 м/с в течение 2 минут, совершило работу 7,2 кДж. Определить модуль вектора напряжённости электрического поля E, если заряд тела равен 4 Кл.
Решение
1. Запишем исходные данные:
v = 15 м/с; t = 2 мин = 120 с; A = 3,6 кДж = 3600 Дж; q = 4 Кл.
2. Запишем выражение для работы электрической силы:
A=E·q·∆x.
3. Поскольку заряд двигается вдоль направления электрического поля E→, то знак работы электрической силы будет иметь положительное значение.
4. Заряд двигался равномерно, значит его перемещение равно ∆x=v·t. Теперь перепишем формулу для работы электрического поля:
A=E·q·v·t.
5. Выразим напряжённость электрического поля из уравнения выше:
E=Aq·v·t=36004·15·120=0,5 Вм.
Ответ: E=0,5 Вм.
Итоги
- Работу электрического поля напряженностью E по перемещению заряда q можно найти по следующей формуле: A=E·q·∆x.
Напряжение
– скалярная физическая величина, равная отношению работы сил электрического поля по перемещению точечного заряда q к величине этого заряда: U=Aq=E·∆x.- Напряжение не зависит от величины перемещаемого заряда q.
- Напряжение – это энергетическая характеристика электрического поля.
Контрольные вопросы
1. Приведите пример, когда электрическое поле совершает отрицательную работу.
2. Как найти работу электрической силы?
3. От каких физических величин зависит напряжение?
Электрическое поле

Электродинамика – раздел физики, изучающий свойства и взаимодействия электрических зарядов, осуществляемые посредством электромагнитного поля.
Электростатикой называется раздел электродинамики, в котором рассматриваются свойства и взаимодействия неподвижных электрически заряженных тел или частиц.
Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макротелами.
Точечный заряд – заряженное тело, размер которого мал по сравнению с расстоянием, на котором оценивается его действие.
Содержание
- Электризация тел
- Взаимодействие зарядов. Два вида зарядов
- Закон сохранения электрического заряда
- Закон Кулона
- Действие электрического поля на электрические заряды
- Напряженность электрического поля
- Принцип суперпозиции электрических полей
- Потенциальность электростатического поля
- Потенциал электрического поля. Разность потенциалов
- Проводники в электрическом поле
- Диэлектрики в электрическом поле
- Электрическая емкость. Конденсатор
- Энергия электрического поля конденсатора
- Основные формулы раздела «Электрическое поле»
Электризация тел
Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.
Способы электризации:
- трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
- через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
- при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
- при ударе;
- под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.
Взаимодействие зарядов. Два вида зарядов
Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.
Обозначение – ( q ), единица измерения в СИ – кулон (Кл).
Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10-19 Кл), наименьший положительный заряд (1,6·10-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.
Величина заряда тела будет равна
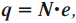
где ( N ) — число избыточных или недостающих электронов;
( e ) — элементарный заряд, равный 1,6·10-19 Кл.
Важно!
Частица может не иметь заряда, но заряд без частицы не существует.
Электрические заряды взаимодействуют:
- заряды одного знака отталкиваются:
- заряды противоположных знаков притягиваются:

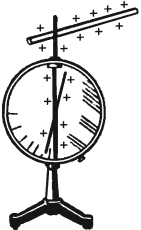
Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.
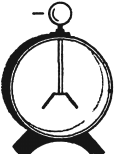
Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.
Закон сохранения электрического заряда
Систему называют замкнутой (электрически изолированной), если в ней не происходит обмена зарядами с окружающей средой.
В любой замкнутой (электрически изолированной) системе сумма электрических зарядов остается постоянной при любых взаимодействиях внутри нее.
Полный электрический заряд ( (q) ) системы равен алгебраической сумме ее положительных и отрицательных зарядов ( (q_1, q_2 … q_N) ):
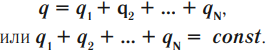
Важно!
В природе не возникают и не исчезают заряды одного знака: положительный и отрицательный заряды могут взаимно нейтрализовать друг друга, если они равны по модулю.
Закон Кулона
Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.
Закон Кулона формулируется так:
сила взаимодействия ( F ) двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям ( q_1 ) и ( q_2 ) и обратно пропорциональна квадрату расстояния между ними ( r ):
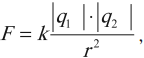
где ( k=frac{1}{4pivarepsilon_0}=9cdot10^9 ) (Н·м2)/Кл2 – коэффициент пропорциональности,
( varepsilon_0=8.85cdot10^{-12} ) Кл2/(Н·м2) – электрическая постоянная.
Коэффициент ( k ) численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.
Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.
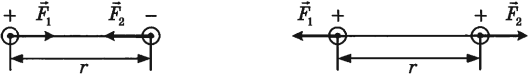
Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:
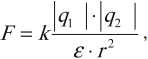
где ( varepsilon ) – диэлектрическая проницаемость среды.
Закон Кулона применим к взаимодействию
- неподвижных точечных зарядов;
- равномерно заряженных тел сферической формы.
В этом случае ( r ) – расстояние между центрами сферических поверхностей.
Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции).
Действие электрического поля на электрические заряды
Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.
Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.
Свойства электрического поля заключаются в том, что оно:
- материально;
- создается зарядом;
- обнаруживается по действию на заряд;
- непрерывно распределено в пространстве;
- ослабевает с увеличением расстояния от заряда.
Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.
Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:
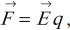
где ( vec{E} ) – напряженность электрического поля, ( q ) – заряд.
Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.
Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:
- сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
- записать для заряда условие равновесия или основное уравнение динамики материальной точки;
- выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
- если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
- записать математически все вспомогательные условия;
- решить полученную систему уравнений относительно неизвестной величины;
- проверить решение
Напряженность электрического поля
Напряженность электрического поля ( vec{E} ) – векторная физическая величина, равная отношению силы ( F ), действующей на пробный точечный заряд, к величине этого заряда ( q ):
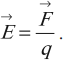
Обозначение – ( vec{E} ), единица измерения в СИ – Н/Кл или В/м.
Напряженность поля точечного заряда в вакууме вычисляется по формуле:
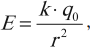
где ( k=frac{1}{4pivarepsilon_0}=9cdot10^9 ) (Н·м2)/Кл2,
( q_0 ) – заряд, создающий поле,
( r ) – расстояние от заряда, создающего поле, до данной точки.
Напряженность поля точечного заряда в среде вычисляется по формуле:
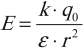
где ( varepsilon ) – диэлектрическая проницаемость среды.
Важно!
Напряженность электрического поля не зависит от величины пробного заряда, она определяется величиной заряда, создающего поле.
Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку.
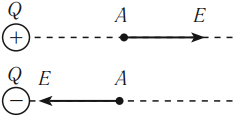
Линией напряженности электрического поля называется линия, касательная к которой в каждой точке направлена вдоль вектора напряженности ( vec{E} ).
Линии напряженности электростатического поля начинаются на положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность от положительного заряда и приходят из бесконечности к отрицательному заряду.
Распределение линий напряженности вокруг положительного и отрицательного точечных зарядов показано на рисунке.
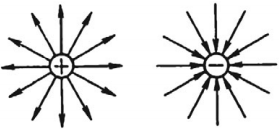
Определяя направление вектора ( vec{E} ) в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.
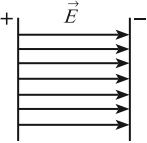
Поле, в котором напряженность одинакова по модулю и направлению в любой точке, называется однородным электрическим полем. Однородным можно считать электрическое поле между двумя разноименно заряженными металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу.
Принцип суперпозиции электрических полей
Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов.
Принцип суперпозиции электрических полей: напряженность электрического поля системы ( N ) зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности:
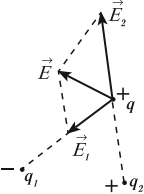
Электрические поля от разных источников существуют в одной точке пространства и действуют на заряд независимо друг от друга.
Потенциальность электростатического поля
Электрическое поле с напряженностью ( vec{E} ) при перемещении заряда ( q ) совершает работу. Работа ( A ) электростатического поля вычисляется по формуле:
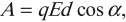
где ( d ) – расстояние, на которое перемещается заряд,
( alpha ) – угол между векторами напряженности электрического поля и перемещения заряда.
Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле.
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.
Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.
Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным.
Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ( W ), так как буквой ( E ) обозначают напряженность поля:
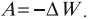
Потенциальная энергия заряда ( q ), помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.
Потенциал электрического поля. Разность потенциалов
Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.
Обозначение – ( varphi ), единица измерения в СИ – вольт (В).
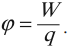
Потенциал ( varphi ) является энергетической характеристикой электростатического поля.
Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:
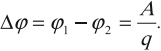
Обозначение – ( Deltavarphi ), единица измерения в СИ – вольт (В).
Иногда разность потенциалов обозначают буквой ( U ) и называют напряжением.
Важно!
Разность потенциалов ( Deltavarphi=varphi_1-varphi_2 ), а не изменение потенциала ( Deltavarphi=varphi_2-varphi_1 ). Тогда работа электростатического поля равна:
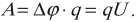
Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле.
В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал поля точечного заряда ( q ) в точке, удаленной от него на расстояние ( r ), вычисляется по формуле:
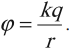
Для наглядного представления электрического поля используют эквипотенциальные поверхности.
Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (( r =R ), где ( R ) – радиус шара). Напряженность поля внутри шара равна нулю.
Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.
Свойства эквипотенциальных поверхностей
- Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
- Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.
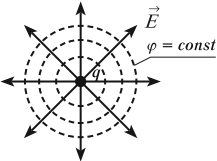
Разность потенциалов и напряженность связаны формулой:
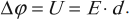
Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:
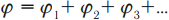
Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.
Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов.
Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.
Алгоритм решения таких задач:
- установить характер и особенности электростатических взаимодействий объектов системы;
- ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
- записать законы сохранения и движения для объектов;
- выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
- составить систему уравнений и решить ее относительно искомой величины;
- проверить решение.
Проводники в электрическом поле
Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.
Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.
Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.
Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.
Важно!
Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей. На этом основана электростатическая защита.
Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.
Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.
Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны).
Диэлектрики в электрическом поле
Диэлектриками называют вещества, не проводящие электрический ток. Диэлектриками являются стекло, фарфор, резина, дистиллированная вода, газы.
В диэлектриках нет свободных зарядов, все заряды связаны. В молекуле диэлектрика суммарный отрицательный заряд электронов равен положительному заряду ядра. Различают полярные и неполярные диэлектрики.
В молекулах полярных диэлектриков ядра и электроны расположены так, что центры масс положительных и отрицательных зарядов не совпадают и находятся на некотором расстоянии друг от друга. То есть молекулы представляют собой диполи независимо от наличия внешнего электрического поля. В отсутствие внешнего электрического поля из-за теплового движения молекул диполи расположены хаотично, поэтому суммарная напряженность поля всех диполей диэлектрика равна нулю.
Если в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов в молекуле диэлектрика совпадают, то он называется неполярным. Пример такого диэлектрика – молекула водорода. Если такой диэлектрик поместить во внешнее электрическое поле, то направления векторов сил, действующих на положительные и отрицательные заряды, будут противоположными. В результате молекула деформируется и превращается в диполь. При внесении диэлектрика в электрическое поле происходит его поляризация.
Поляризация диэлектрика – процесс смещения в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества в электрическом поле.
Если диэлектрик неполярный, то в его молекулах происходит смещение положительных и отрицательных зарядов. На поверхности диэлектрика появятся поверхностные связанные заряды. Связанными эти заряды называют потому, что они не могут свободно перемещаться отдельно друг от друга.
Внутри диэлектрика суммарный заряд равен нулю, а на поверхностях заряды не скомпенсированы и создают внутри диэлектрика поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Это значит, что внутри диэлектрика поле имеет меньшую напряженность, чем в вакууме.
Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:
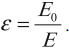
В полярном диэлектрике во внешнем электрическом поле происходит поворот диполей, и они выстраиваются вдоль линий напряженности.
Если внесенный в электрическое поле диэлектрик разрезать, то его части будут электрически нейтральны.
Электрическая емкость. Конденсатор
Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.
Обозначение – ( C ), единица измерения в СИ – фарад (Ф).
Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.
Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:
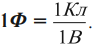
Формула для вычисления электроемкости:
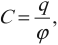
где ( q ) – заряд проводника, ( varphi ) – его потенциал.
Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.
Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.
Электроемкость конденсатора рассчитывается по формуле:
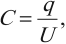
где ( q ) – модуль заряда одной из обкладок,
( U ) – разность потенциалов между обкладками.
Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.
Плоский конденсатор представляет две параллельные пластины площадью ( S ), находящиеся на расстоянии ( d ) друг от друга.
Электроемкость плоского конденсатора:
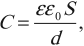
где ( varepsilon ) – диэлектрическая проницаемость вещества между обкладками,
( varepsilon_0 ) – электрическая постоянная.
На электрической схеме конденсатор обозначается:
Виды конденсаторов:
- по типу диэлектрика – воздушный, бумажный и т. д.;
- по форме – плоский, цилиндрический, сферический;
- по электроемкости – постоянной и переменной емкости.
Конденсаторы можно соединять между собой.
Параллельное соединение конденсаторов
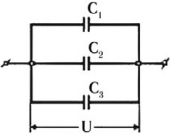
При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:
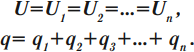
Общая емкость:
Последовательное соединение конденсаторов
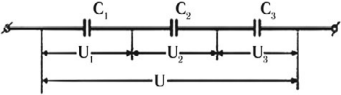
При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.
Заряды конденсаторов при таком соединении равны:
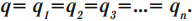
Общее напряжение:
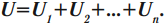
Величина, обратная общей емкости:
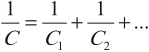
При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.
Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости.
Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.
Энергия электрического поля конденсатора
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:
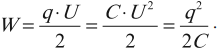
Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.
Плотность энергии электрического поля:
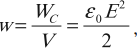
где ( V ) – объем пространства между обкладками конденсатора.
Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.
Основные формулы раздела «Электрическое поле»



Электрическое поле
2.9 (58.76%) 129 votes








