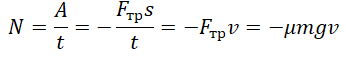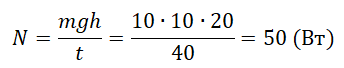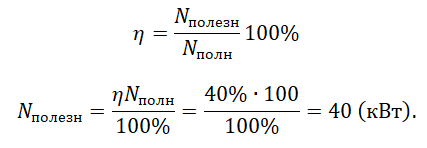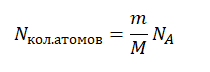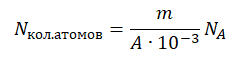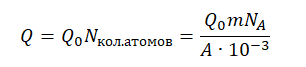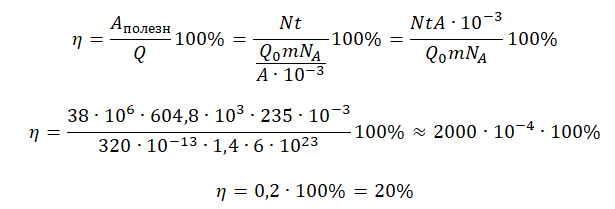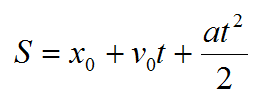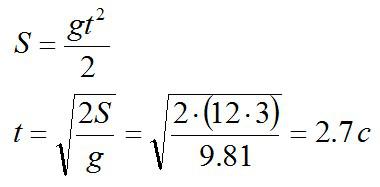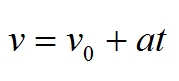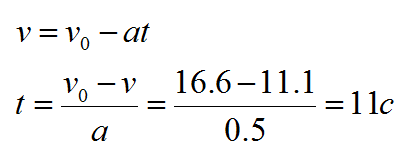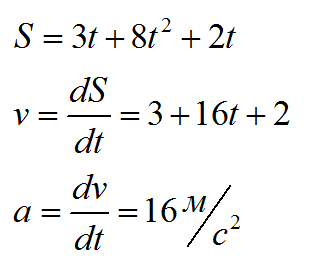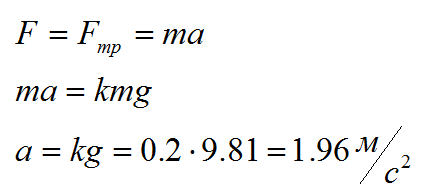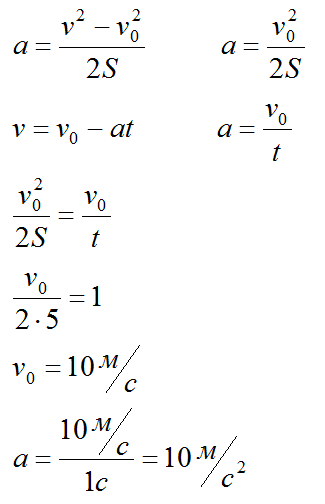Тема: Найти работу, совершаемую при равноускоренном движение груза массой 10 кг по нак (Прочитано 24911 раз)
0 Пользователей и 1 Гость просматривают эту тему.
roma
Найти работу, совершаемую при равноускоренном подъёме груза массой 10 кг по наклонной плоскости с углом наклона 45 градусов на расстояние 4 метра, если время подъёма 2 с, а коэффициент трения 0,1.
Записан
djeki
Работа равна произведению силы тяги F на пройденный путь S в направлении действия силы.
A = F ·S.
На тело действуют: mg – сила тяжести,Ftr = μ·N – сила трения,F – сила тяги, N – сила нормальной реакции опоры. Запишем второй закон ньютона применительно к нашему случаю и спроецируем уравнения на систему координат
[ begin{align}
& {{{vec{F}}}_{tr}}+vec{N}+mvec{g}+vec{F}=mvec{a}; \
& OX:-{{F}_{tr}}-mcdot gcdot sin alpha +F=mcdot a; \
& OY:N-mcdot gcdot cos alpha =0; \
& F=mcdot a+{{F}_{tr}}+mcdot gcdot sin alpha ; \
& F=mcdot a+mu cdot mcdot gcdot cos alpha +mcdot gcdot sin alpha ; \
& F=mcdot (a+mu cdot gcdot cos alpha +gcdot sin alpha ); \
end{align}
]
Для нахождения ускорения воспользуемся формулой для определения пройденного пути при равноускоренном движении, считая, что тело двигалось из состояния покоя
[ S=frac{acdot {{t}^{2}}}{2};a=frac{2cdot S}{{{t}^{2}}} ]
Тогда
[ A=Fcdot S=mcdot left( frac{2cdot S}{{{t}^{2}}}+mu cdot gcdot cos alpha +gcdot sin alpha right)cdot S ]
А = 390.2 Дж
« Последнее редактирование: 01 Октября 2012, 23:02 от djeki »
Записан
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости: |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна: |
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому: |
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость: |
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения: |
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
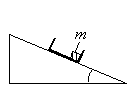
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 11.8k
m = 200 кг.
g = 9,8 м/с2.
h = 30 м.
t = 16 с.
A – ?
Работа силы А определяется формулой: А = F * S * сosα.
Так как груз опускается из состояния покоя, то найдём его ускорение а из формулы: h = а * t2 /2.
а = 2 * h / t2.
а = 2 * 30 м / (16 с)2 = 0,23 м/с2.
m * a = F – m * g.
На груз действует сила F, направленная вертикально вверх, определяется формулой: F = m * (a + g).
∠α = 180°, сos180° = -1.
А = – m * (a + g) * h.
А = – 200 кг * (0,23 м/с2 + 9,8 м/с2) * 30 м = – 60180 Дж.
Работу силы тяжести Ат выразим формулой: Ат = m * g * h.
Ат = 200 кг * 9,8 м/с2 * 30 м = 58800 Дж.
Ответ: при равноускоренном опускании сила тяжести выполняет работу Ат = 58800 Дж, сила, с которой тянут за веревку, выполняет работу А = – 60180 Дж.
При решении задач на равноускоренное движение не обойтись без формул кинематики и второго закона Ньютона. Рекомендуем сначала изучить теорию по этим разделам, а уже потом приступать к практике.
Больше полезных сведений и ежедневная интересная рассылка – на нашем телеграм-канале, присоединяйтесь!
Равноускоренное движение: определение и примеры
Равноускоренное движение – это движение с меняющейся скоростью, но постоянным ускорением (a=const).
Самый простой случай такого движения – равноускоренное прямолинейное движение.
Вот типичные примеры равноускоренного движения:
- рояль падает с 12-го этажа с ускоренинием свободного падения g;
- автомобиль разгоняется со светофора от 0 до 60 км/ч с ускорением равным 1 метр на секунду в квадрате;
- автобус плавно тормозит перед светофором. Это также равноускоренное движение, только векторы скорости и ускорения направлены в разные стороны.
Вопросы с ответами на равноускоренное движение
Вопрос 1. График движения представляет собой прямую линию. Является ли движение тела равноускоренным?
Ответ: да. Если график представляет собой кривую, то ускорение тела меняется со временем. Равномерное движение, которое также описывается прямой – частный случай равноускоренного движения с нулевым ускорением. Перемещение при равноускоренном движении численно равно площади трапеции, ограниченной осями координат и графиком.
Вопрос 2. Тело равномерно движется по окружности. Как направлено ускорение?
Ответ: перпендикулярно телу. В общем случае при криволинейном движении ускорение имеет две составляющие: нормальную (центростремительное ускорение) и тангенциальную, направленную по касательной к скорости. Тангенциальное ускорение при равномерном движении по окружности равно нулю.
Вопрос 3. Является ли ускорение свободного падения постоянным ускорением?
Ответ: да, является.
Вопрос 4. Может ли тело иметь нулевую скорость и ненулевое ускорение?
Ответ: да, может. После того, как скорость станет равна нулю, тело начнет двигаться в другом направлении.
Вопрос 5. Что такое ускорение?
Ответ: Векторная физическая величина, характеризующая изменение скорости за единицу времени. При равноускоренном движении скорость меняется одинаково за равные промежутки времени.
Задачи на равноускоренное движение
Сначала обратимся к уже приведенным примерам.
Задача №1. Равноускоренное движение
Условие
Рояль роняют с 12 этажа с нулевой начальной скоростью. За какое время он долетит до земли? Один этаж имеет высоту 3 метра, сопротивлением воздуха принебречь.
Решение
Известно, что рояль движется с ускорением свободного падения g. Применим формулу для пути из кинематики:
Начальная скорость равна нулю, а за точку отсчета примем то место, откуда рояль начал движение вниз.
Ответ: 2.7 секунды.
Скорость свободно падающих тел не зависит от их массы. Любое тело в поле силы тяжести Земли будет падать с одинаковым ускорением. Этот факт был экспериментально установлен Галилео Галилеем в его знаменитых экспериментах со сбрасыванием предметов с Пизанской башни.
Задача №2. Равноускоренное движение
Условие
Автобус ехал со скоростью 60 км/ч и начал тормозить на светофоре с ускорением 0,5 метра на секунду в квадрате. Через сколько секунд его скорость станет равной 40 км/ч?
Решение
Вспоминаем формулу для скорости:
Начальная скорость дана в условии, но автобус тормозит, а значит, векторы скорости и ускорения направлены в противоположные стороны. В проекции на горизонтальную ось ускорение будем записывать со знаком минус:
Ответ: 11 секунд.
Обязательно переводите величины в систему СИ.Чтобы перевести километры в час в метры в секунду нужно значение скорости в километрах в час сначала умножить на 1000, а потом разделить на 3600.
Задача №3. Нахождение ускорения
Условие
Тело движется по закону S(t)=3t+8t^2+2t. Каково ускорение тела?
Решение
Вспоминаем, что скорость – это производная пути по времени, а ускорение – производная скорости:
Ответ: 16 метров на секунду в квадрате.
При решении физических задач не обойтись без знания производной.
Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задача №4. Нахождение ускорения при равноускоренном движении
Условие
Грузовик разгоняется на дороге, а в кузове лежит незакрепленный груз. С каким максимальным ускорением должен разгоняться грузовик, чтобы груз не начал смещаться к заднему борту? Коэффициент трения груза о дно кузова k=0.2, g=10 м/c2
Решение
Для решения этой задачи нужно использовать второй закон Ньютона. Сила трения в данном случае равна F=kmg.
Ответ: 2 метра на секунду в квадрате.
Задача №5. Нахождение ускорения и скорости при равноускоренном движении
Условие
За пятую секунду прямолинейного движения с постоянным ускорением тело проходит путь 5 м и останавливается. Найти ускорение тела.
Решение
Конечная скорость тела v равна 0, v нулевое – скорость в конце 4-й секунды.
Ответ: 10 метров на секунду в квадрате.
Нужна помощь в решении задач? Обращайтесь в профессиональный студенческий сервис в любое время.
Равноускоренное движение
Равноускоренное движение – это движение, при котором вектор ускорения не меняется по модулю и направлению (в случае равнозамедленного движения модуль скорости равномерно меняется). Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение, в отличие от неравномерного, – частный случай ускоренного в равной степени движения с ускорением, равным нулю.
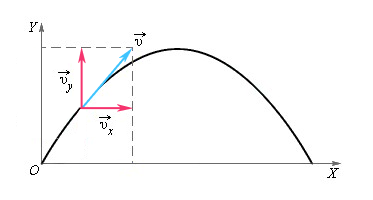
Рассмотрим случай свободного падения (тело брошено под углом к горизонту) более подробно с вычислением. Такое движение можно рассчитать и представить в виде суммы движений относительно вертикальной и горизонтальной осей.
Как найти ускорение в физике? Нахождение ускорения в физике происходит с учетом того, что в любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону.
Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y – движение равноускоренное и прямолинейное. Будем рассматривать определенные проекции векторов скорости и ускорения на оси.
Формулы для равноускоренного движения
Формула для скорости (формула ускорения) при равноускоренном движении:
v=v0+at.
Здесь v0 – начальная скорость тела, a=const – ускорение.
Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии. Вот небольшой тест.
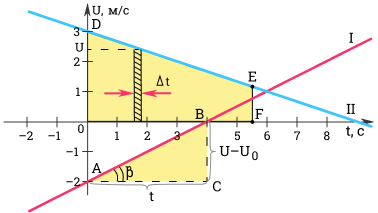
Как найти ускорение? Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC. Вот как выглядит формула ускорения в физике.
a=v-v0t=BCAC
Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.
Для первого графика: v0=-2 мс; a=0,5 мс2.
Для второго графика: v0=3 мс; a=-13 мс2.
По данному графику физик может также вычислить (произвести определение) перемещение тела за время t. Как это сделать?
Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.
Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.
s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.
Мы знаем, что v-v0=at, поэтому окончательная формула или расчет для перемещения тела примет вид:
s=v0t+at22
Для того чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение (расстояние). Изменение координаты в зависимости от времени выражает закон равноускоренного движения.
Какова будет формула пути при равноускоренном движении? В этом случае путь изменяется согласно квадратной зависимости: 8=v0t + at²/2.
Закон равноускоренного движения
y=y0+v0t+at22.
Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения – находить координаты при заданных значениях начальной и конечной скоростей и ускорения.
Исключая из записанных выше уравнений t и решая их, получаем:
s=v2-v022a.
По известным начальной скорости, ускорению и перемещению может находиться конечная скорость тела:
v=v02+2as.
При v0=0 s=v22a и v=2as
Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. Они могут принимать как положительные, так и отрицательные значения – это будет зависеть от характера движения и направления координатных осей в условиях конкретной задачи.