Как найти работу пули

баллистического маятника

Цель работы: Определение скорости
пули с помощью баллистического маятника с использованием законов сохранения
импульса и энергии.

Приборы и принадлежности: баллистический маятник,
шкала, пружинный пистолет, линейка и пули.

Теоретическое введение

Из
практики известно, что скорость полета пули достигает значительной величины.
Поэтому прямое измерение скорости, т.е. определение времени, за которое пуля
проходит известное расстояние, требует специальной аппаратуры. Много проще
измерять скорость пули косвенными методами, среди которых широко
распространены методы, использующие неупругие соударения, т.е. соударения, в
результате которых столкнувшиеся тела соединяются вместе и продолжают
движение как одно целое.

Пусть летящая пуля испытывает неупругий удар со свободным неподвижным
телом значительно большей массы. После удара тело начинает двигаться, причем
скорость его во столько раз меньше скорости пули, во сколько раз масса пули
меньше массы тела. (Этот результат можно получить с помощью закона сохранения
импульса). Если теперь измерить сравнительно небольшую скорость тела, то
легко можно вычислить и скорость полета пули.

К числу методов, основанных на этой идее, относится и метод
баллистического маятника. В данной работе для определения скорости пули
использованы законы сохранения импульса и полной механической энергии.

Описание рабочей установки и
метода измерений

Баллистический
маятник представляет собой тяжелое тело массой М, подвешенное на двойном бифилярном подвесе (рис.1). Когда после
выстрела пуля попадает в это тело, то оно отклоняется от положения
равновесия.

Пренебрегая сопротивлением воздуха, к системе «маятник-пуля» можно
применить закон сохранения импульса, который в проекции на ось x запишется

где mυ – проекция импульса на
ось x до взаимодействия;

(М+m)U –проекция
импульса системы (пуля +маятник) на ось x неупругого удара.

Закон сохранения
импульса: в изолированной системе тел 
сумма импульсов взаимодействующих тел остается постоянной во времени,
т.е. .

Закон сохранения механической энергии: в изолированной системе тел,
где действуют только консервативные силы, полная механическая энергия
(кинетическая плюс полная потенциальная энергии) остается постоянной, т.е. Е=Е_к+Е_п=const.

При ударе пули маятник вместе с пулей приобретает кинематическую
энергию, равную после соударения

Маятник с пулей приходит в движение, отклоняется на некоторый угол от
вертикали, и центр масс системы «маятник-пуля» поднимается на некоторую
высоту h
(рис.2).

Если
пренебречь трением в подвесе маятника и сопротивлением воздуха, то можно
рассматривать систему «маятник-пуля» как изолированную, консервативную и
применять к ней закон сохранения полной механической энергии.

В
момент наибольшего отклонения маятника его кинетическая энергия Е_к
полностью превратится в потенциальную энергию силы тяжести

где g
– ускорение свободного падения тела.

Тогда

Подставив (5) в (2), найдем выражение для скорости пули

Следовательно, скорость пули можно вычислить, если измерить высоту
подъема h
центра масс маятника. Однако измерение h довольно сложно. Его можно
заменить более простым измерением горизонтального перемещения S, которое определяют по неподвижной
шкале.

Если после соударения маятник отклонился на небольшой угол (рис.2), то
можно считать, что центр масс маятника перемещается вдоль хорды АВ. Тогда из подобия треугольников АКВ и ОАС можно записать отношение

где ВК = S– горизонтальное
смещение маятника; АК = h, ОС^АВ.

При малом отклонении S и
достаточной длине подвеса l (S<<l) можно положить, что

 и

Тогда соотношение (6) можно записать в виде

 или

Поставив (7) в (5), получим формулу для скорости пули:

Формула (8) является расчетной. Определяя величины M,
m, S, l,
экспериментально, по формуле (7) можно определить скорость пули υ.

Ход работы

1.     
Привести маятник в состояние равновесия и подвесить шкалу под
указатель маятника.

2.     
Произвести 5 – 6 выстрелов, каждый раз отмечая смещения указателя по
шкале. Результаты измерений записать в таблицу.

3.     
Вычислить скорость пули по формуле (8).

4.     
Вычислить абсолютную погрешность измерения S по формуле:

где t_p(n)– коэффициент Стьюдента для доверительной
вероятности p
= 0,95 и числа измерений n.

5.     
Вычислить относительную погрешность измерения скорости

6.     
Найти абсолютную погрешность

7.     
Результаты измерения записать в виде

– средние величины.

m = 9,6 г; М =296 г; l = 193 см.

Таблица

Вопросы для допуска

1.     
Изложите цель работы, назначение приборов и принадлежностей.

2.     
Опишите рабочую установку и ход эксперимента.

3.     
Какие допущения возможны, если рассматривать систему «маятник-пуля»
как замкнутую?

4.     
Напишите рабочую формулу, примененную в данной работе.

5.     
Какие законы Вы использовали для получения расчетной формулы для
скорости пули?

6.     
Оцените погрешность метода измерений.

7.     
Как в установке обеспечить условия, при которых удар пули в маятник
можно считать неупругим, центральным и прямым?

8.     
Какие допущения делаете, используя закон сохранения механической
энергии в форме, выраженной формулой (9)?

Вопросы для защиты работы

1.     
Что называется импульсом тела (количеством движения) и в каких
единицах он измеряется в системе СИ?

2.     
При каком условии систему «маятник-пуля» можно рассматривать как
изолированную?

3.     
В чем состоит закон сохранения импульса? К каким системам он применим?
Дайте вывод этого закона и приведите примеры его проявления (его действия).

4.     
Как найти изменение импульса неизолированной системы?

5.     
Какие существуют виды механической энергии. Дайте их определения.

6.     
Для каких систем справедлив закон сохранения механической энергии и
как он формулируется?

7.     
Выведите формулу кинетической энергии.

8.     
Выведите расчетную формулу.

9.     
Какой удар называют абсолютно упругим и какой
неупругим?

10.  Объяснить происхождение
систематических и случайных ошибок, встречающихся в данной работе.

Перейти к контенту

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ «МАМИ»

Кафедра
физики

ЛАБОРАТОРНАЯ
РАБОТА 1.07

ОПРЕДЕЛЕНИЕ
СКОРОСТИ ПОЛЕТА ПУЛИ С ПОМОЩЬЮ КРУТИЛЬНОГО
МАЯТНИКА

Москва
2005 г.

Лабораторная
работа N 107

ОПРЕДЕЛЕНИЕ
СКОРОСТИ ПОЛЕТА ПУЛИ С ПОМОЩЬЮ КРУТИЛЬНОГО
МАЯТНИКА

Цель работы:
определение скорости пули при
помощи крутильно­го маятника.

ВВЕДЕНИЕ

Скорость
полета пули определяется в данной работе
при помощи крутильного маятника,
изображенного на рис.1. Пуля массой m,
летя­щая со скоростью v
попада­ет
в лопатку крутильного маятника (1)
и застревает
в ней (происходит неупругий удар). После
удара маятник отклоняется от положения
равновесия на угол φ. Скорость полета
пули можно определить, пользуясь законами
сохра­нения момента импульса и
механической энергии.

Моментом
импульса

материальной точ­ки m
относительно точки О,
называется векторная величина,
определяемая вектор­ным произведением
радиуса вектора
,
материальной
точки на ее импульс
,
то есть
.

Численное значение
момента
.
Направление вектора

у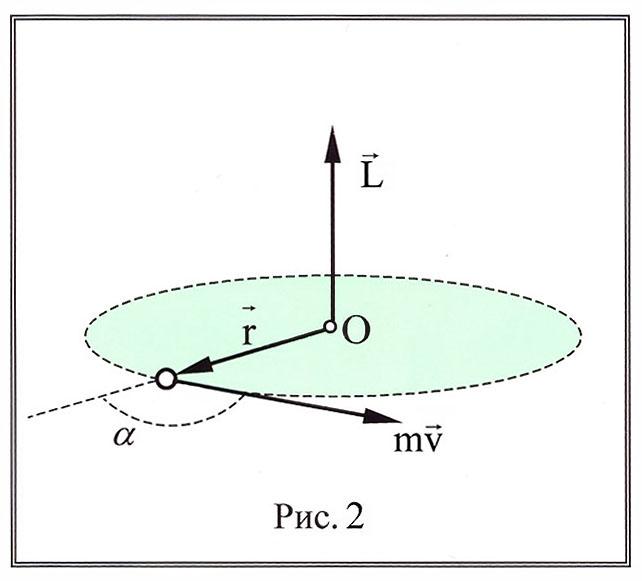казано
на рис.2.

Моментом импульса
тела относительно оси вращения называется
величина
,
где

момент инерции тела относи­тельно
этой оси,


угловая скорость вращения тела.

В замкнутой системе
тел момент импульса есть величина
посто­янная (закон сохранения момента
импульса), то есть
,
если
,
где

момент внешних сил.

Систему, состоящую
из крутильного маятника и пули, в момент
удара можно считать замкнутой, так как
при соударении возникают такие большие
силы взаимодействия, что внешними силами
можно пре­небречь. Поэтому можно
применить закон сохранения момента
импуль­са. Момент импульса пули

2

непосредственно
до удара ()
и момент импульса пули и маятника после
удара

равны:

(1)

где J

момент инерции маятника относительно
оси вращения,

момент инерции
пули относительно этой же оси,


угловая скорость маятника непосредственно
после удара пули,

расстояние от оси
вращения маятника до точки, в которую
попадает пуля.

Так как масса пули
мала по сравнению с массой маятника
,
из уравнения (1) имеем:

.

(2)

m
и r
могут быть непосредственно измерены.
Поэтому для опре­деления скорости
полета пули необходимо найти угловую
скорость вращения после удара

и момент инерции крутильного маятника
J.

Угловую скорость

найдем, пользуясь законом сохранения
механической энергии.

Если силами трения,
возникающими при движении маятника
пре­небречь, то при отклонении
маятника из положения равновесия на
угол

кинетическая энергия его вращения
переходит
в потенциальную энергию
упругой
деформации нити, где k

коэффициент, зависящий от размеров,
формы и материала прово­локи.

То есть

(3)

(закон сохранения
механической энергии), откуда

(4)

По основному закону
динамики вращательного движения

(5)

При повороте
маятника на небольшой угол

деформация прово­локи является упругой
и возвращающий момент M
пропорционален углу поворота
,
то есть

(6)

Угловое ускорение

,
является второй производной от угла
поворота

по времени

(7)

3

С учетом (6) и (7)
уравнение (5) принимает вид

Разделив на J
и обозначив

,
получим

Решение этого
уравнения имеет вид
,
(8)

где

амплитуда,

начальная фаза колебаний.

Формула (8) описывает
гармонические колебания. Циклическая
частота таких колебаний

.

Учитывая, что
циклическая частота
,
где Т
– период
колебаний,
получим

,
(9)

то есть период
колебаний крутильного маятника Т
зависит от его момента инерции J.
Из (8) следует,
что
.
(10)

Подставляя формулы
(4) и (10) в
формулу (3), для скорости полета пули
получим


, (11)

где
Т

период колебаний крутильного маятника,


максимальный
угол его
поворота после попадания пули массой
m,
r

расстояние
от
оси вращения
маятника до точки лопатки, в которую
попадает пуля, k

коэффициент, зависящий от размера,
формы и
материала проволоки.

ОПИСАНИЕ
УСТАНОВКИ

О

Рис. 3

бщий вид установки представлен на
рис. 3. На основании смонтирована
колонка, на которой зак­реплены три
кронштейна. К среднему кронштейну
прик­реплено стреляющее уст­ройство
(1), а также прозрачный экран
цилинд­рической формы с нанесен­ной
на него шкалой для измерения углов
отклоне­ния маятника (2). Верхний и
нижний кронштейны имеют зажимы, служащие
для зак­репления

4

стальной
прово­локи, на которой подвешен
маятник, состоящий из стержня, двух
лопаток и двух грузов.

ПОРЯДОК
ВЫПОЛНЕНИЯ РАБОТЫ

1. Нажать клавишу
   «сеть».

2. Отклонить
   маятник на небольшой угол (10-15 градусов).

1. Нажать клавишу
   «сброс». При этом на световом табло
   высве­чиваются нули.

2. Отпустить маятник.
   После подсчета измерителем числа
   коле­баний времени 9 полных колебаний
   нажать клавишу «стоп». При этом прибор
   автоматически совершит отсчет времени
   10 полных колебаний.

3. Результаты
   измерений числа колебаний n
   и времени
   колебаний t
   занести в
   таблицу 1.

4. Измерения повторить
   3 раза.

5. Установить маятник
   так, чтобы черта на одной из лопаток
   совпадала с нулевой отметкой шкалы для
   измерения углов поворота маятника.

6. Выпустить пулю
   из стреляющего устройства. Определить
   угол
   максимального отклонения маятника
   .
   Его значение
   занести в таблицу.

7. Измерить расстояние
   r
   от оси вращения маятника до точки
   лопатки, в которую попадает пуля.
   Результаты измерения r
   за­нести
   в таблицу.

8. Занести в таблицу
   значения массы пули
   m
   и
   коэффициента
   k.

Таблица 1.

5

ОБРАБОТКА
РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1. Найти
   среднее значение времени 10 колебаний

   .

2. По
   формуле
   
   найти среднее значение периода колебаний
   крутильного маятника.

3.
По формуле

определить среднюю скорость полета
тела

Значение

подставить в радианах

4. Определить
относительную ошибку в определении
скорости

полета тела по
формуле

.

5. Определить
абсолютную ошибку
.

КОНТРОЛЬНЫЕ
ВОПРОСЫ

1. Что называется
   моментом импульса материальной точки,
   мо­ментом импульса тела?

2. Сформулируйте
   закон сохранения момента импульса.
   Запишите его применительно к данной
   лабораторной работе.

3. Почему систему
   тел в момент удара можно считать
   замкнутой?

4. Выведите формулу
   (9) для определения
   периода колебаний крутильного маятника.

5. Сформулируйте
   закон сохранения механической энергии.
   За­пишите его применительно к данной
   лабораторной работе.

6. Выведите расчетную
   формулу (11) для определения скорости
   полета пули.

ЛИТЕРАТУРА

1. Детлаф
   А.А., Яворский Б.М. Курс физики. М.: «Высшая
   школа».1999 г.

1. Трофимова
   Т.И. Курс физики. М.: «Высшая школа».
   2003г.

1. Савельев
   И.В. Курс общей физики. М.: «Наука».2001 г.
   Книги 1,4.

1. Сивухин
   Д.В. Общий курс физики. М.: «Наука».2003.
   Т.I.

Соседние файлы в папке 001_MEHANIKA

• #
• #
• #
• #
• #
• #
• #
• #