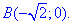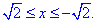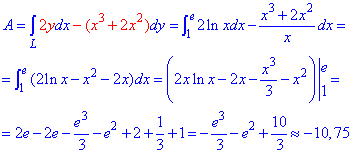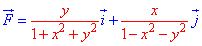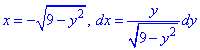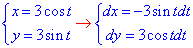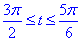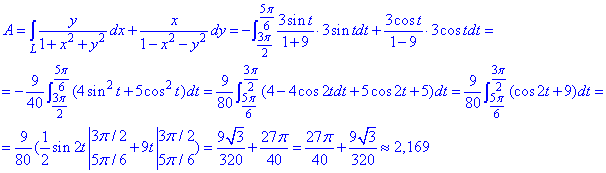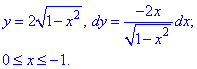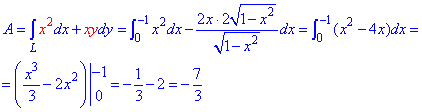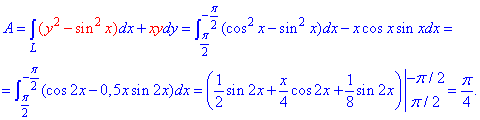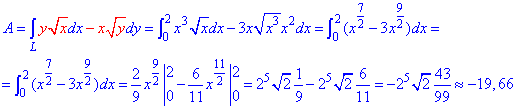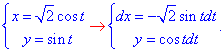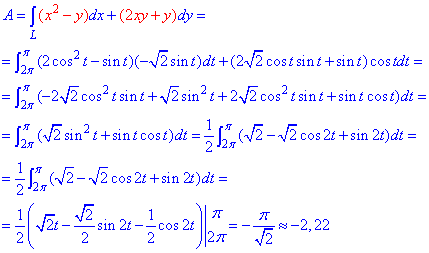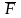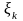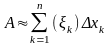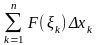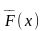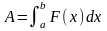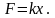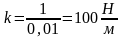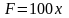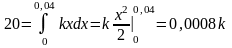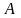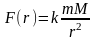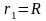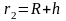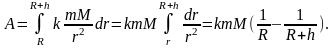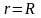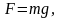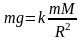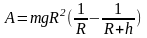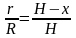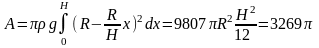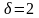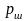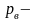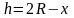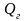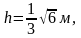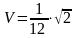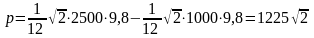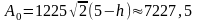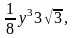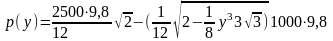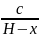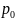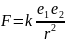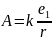На материальную точку $Tleft(x,yright)$ действует переменная сила $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$. Под действием этой силы материальная точка перемещается на отрезке $left[6;15right]$ от точки $M$ до точки $N$ вдоль синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$. Найти работу переменной силы $overline{F}$ на криволинейном пути от точки $M$ до точки $N$. Построить графическое изображение пути от точки $M$ до точки $N$, а также векторы переменной сили $overline{F}$ в этих точках.
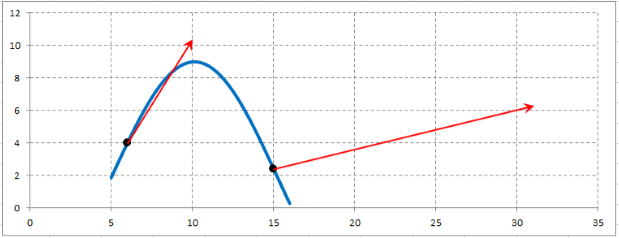
Выполняем графическое изображение синусоидальной кривой $y=7cdot sin left(0,31cdot x-1,57right)+2$ на отрезке $left[6;15right]$.
Находим значения синусоиды в точках $x_{M} =6$ и $x_{N} =15$:
- $y_{M} =7cdot sin left(0,31cdot 6-1,57right)+2approx 4$;
- $y_{N} =7cdot sin left(0,31cdot 15-1,57right)+2approx 2,43$.
Выполняем графические изображения векторов переменной силы $overline{F}=left(3cdot x-2cdot yright)cdot overline{i}+4cdot ycdot overline{j}$, значения которого в точках $M$ и $N$ соответственно равны $overline{F}_{M} =left(3cdot 6-2cdot 4right)cdot overline{i}+4cdot 4cdot overline{j}=10cdot overline{i}+16cdot overline{j}$ и $bar{F}_{N} =left(3cdot 15-2cdot 2,43right)cdot overline{i}+4cdot 2,43cdot overline{j}=40,14cdot overline{i}+9,72cdot overline{j}$.
Работу данной силы на данном участке кривой $MN$ вычисляем по формуле $A=int limits _{a}^{b}Pleft(x,yleft(xright)right)cdot dx +int limits _{a}^{b}Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
Здесь участок кривой $MN$ задан на отрезке $left[x_{M} ,; x_{N} right]$, поэтому формула для работы приобретает вид: $A=int limits _{x_{M} }^{x_{N} }Pleft(x,yleft(xright)right)cdot dx +int limits _{x_{M} }^{x_{N} }Qleft(x,yleft(xright)right)cdot y’left(xright)cdot dx $.
В этой формуле первый интеграл дает значение работы силы $F$ вдоль оси $Ox$, второй интеграл — вдоль оси $Oy$.
Находим работу силы вдоль оси $Ox$: $A_{x} =int limits _{6}^{15}Pleft(x,yleft(xright)right)cdot dx $.
Согласно условию задачи имеем:
[Pleft(x,yright)=3cdot x-2cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2.]
Поэтому:
[Pleft(x,yleft(xright)right)=3cdot x-2cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=]
[=3cdot x-14cdot sin left(0,31cdot x-1,57right)-4.]
Далее получаем:
[A_{x} =int limits _{6}^{15}left(3cdot x-14cdot sin left(0,31cdot x-1,57right)-4right)cdot dx =]
[=int limits _{6}^{15}3cdot xcdot dx +int limits _{6}^{15}left(-14cdot sin left(0,31cdot x-1,57right)right)cdot dx +int limits _{6}^{15}left(-4right)cdot dx =]
[=3cdot int limits _{6}^{15}xcdot dx -14cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dx -4cdot int limits _{6}^{15}dx =]
[=3cdot left[frac{x^{2} }{2} right]_{6}^{15} -14cdot left[-frac{1}{0,31} cdot cos left(0,31cdot x-1,57right)right]_{6}^{15} -4cdot left[xright]_{6}^{15} =]
[=1,5cdot left(15^{2} -6^{2} right)+frac{14}{0,31} cdot left(cos left(0,31cdot 15-1,57right)-cos left(0,31cdot 6-1,57right)right)-]
[-4cdot left(15-6right)=135,15.]
Находим работу силы вдоль оси $Oy$: $A_{y} =int limits _{6}^{15}Qleft(x,yleft(xright)right)cdot y’cdot dx $.
Согласно условию задачи имеем:
[Qleft(x,yright)=4cdot y; y=7cdot sin left(0,31cdot x-1,57right)+2. ]
Поэтому:
[Qleft(x,yleft(xright)right)=4cdot left(7cdot sin left(0,31cdot x-1,57right)+2right)=28cdot sin left(0,31cdot x-1,57right)+8;]
[y’=7cdot 0,31cdot cos left(0,31cdot x-1,57right)=2,17cdot cos left(0,31cdot x-1,57right).]
Далее получаем:
[A_{y} =int limits _{6}^{15}left(28cdot sin left(0,31cdot x-1,57right)+8right)cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}28cdot 2,17cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}8cdot 2,17cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=int limits _{6}^{15}60,76cdot sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx +]
[+int limits _{6}^{15}17,36cdot cos left(0,31cdot x-1,57right)cdot dx .]
Вычисляем первый интеграл $I_{1} $:
[I_{1} =60,76cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot cos left(0,31cdot x-1,57right)cdot dx =]
[=60,76cdot frac{1}{0,31} cdot int limits _{6}^{15}sin left(0,31cdot x-1,57right)cdot dleft(sin left(0,31cdot x-1,57right)right) =]
[=196cdot left[frac{sin ^{2} left(0,31cdot x-1,57right)}{2} right]_{6}^{15} =]
[=98cdot left(sin ^{2} left(0,31cdot 15-1,57right)-sin ^{2} left(0,31cdot 6-1,57right)right)approx -7,64.]
Вычисляем второй интеграл $I_{2} $:
[I_{2} =17,36cdot int limits _{6}^{15}cos left(0,31cdot x-1,57right)cdot dx =]
[=17,36cdot frac{1}{0,31} cdot left[sin left(0,31cdot x-1,57right)right]_{6}^{15} =]
[=56cdot left(sin left(0,31cdot 15-1,57right)-sin left(0,31cdot 6-1,57right)right)approx -12,57.]
Работа силы вдоль оси $Oy$:
[A_{y} =I_{1} +I_{2} =-7,64-12,57=-20,21.]
Общая работа силы при перемещении вдоль кривой:
[A=A_{x} +A_{y} =135,15-20,21=114,94.]
п.1. От ускорения к скорости и координате
Рассматривая применение производной в физике и технике (см. §51 данного справочника), мы во второй производной от уравнения прямолинейного равномерного движения (x(t)) пришли к постоянному ускорению (a=const).
С помощью интегрирования можно пройти обратный путь.
Начнем с постоянного ускорения (a=const).
Интеграл от ускорения по времени – это скорость: $$ v(t)=int adt=aint dt=at+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная скорость (v_0). Получаем: $$ v(t)=at+v_0 $$ Интеграл от скорости по времени – это координата: $$ x(t)=int v(t)dt=int (at+v_0)dt=frac{at^2}{2}+v_0 t+C $$ Физический смысл постоянной интегрирования (C) в этом случае – начальная координата (x_0). Получаем: $$ x(t)=frac{at^2}{2}+v_0 t+x_0 $$ Таким образом, если нам известны ускорение (a), начальная скорость (v_0) и начальная координата (x_0), мы всегда сможем получить уравнение движения (x(t)).
п.2. Физические величины как интегралы других величин
Если (v(t)) – скорость некоторого физического процесса, уравнение этого процесса можно найти интегрированием: $$ f(t)=int v(t)dt $$ Такие величины часто встречаются в различных разделах физики и техники.
Исходная величина (скорость)
Уравнение процесса (интеграл по времени)
Ускорение (a(t))
Скорость (v(t)=int a(t)dt)
Скорость (v(t))
Координата (x(t)=int v(t)dt)
Угловое ускорение (beta(t))
Угловая скорость (omega(t)=int beta(t) dt)
Угловая скорость (omega(t))
Угол поворота (varphi(t)=intomega(t)dt)
Скорость расходования горючего (u(t))
Масса горючего ракеты (m(t)=int u(t)dt)
Сила тока (I(t))
Заряд (q(t)=int I(t)dt)
Мощность (N(t))
Работа (A(t)=int N(t)dt)
ЭДС индукции (varepsilon(t))
Магнитный поток (Ф(t)=-intvarepsilon(t)dt)
Скорость радиоактивного распада (I(t))
Число атомов радиоактивного вещества (N(t)=int I(t)dt)
Берутся интегралы и по другим переменным. Например, чтобы найти работу переменной силы (F(x)), нужно взять интеграл по координате: $$ A=int_{x_1}^{x_2}F(x)dx $$ В трехмерном пространстве интегралы могут браться по всем трем координатам.
При решении уравнений в частных производных интегралы берутся и по времени и по координатам.
В современной физике интеграл по времени берётся также и от самого уравнение движения. Полученная скалярная величина называется действием и носит фундаментальный характер. В простейшем случае: $$ S_0=int overrightarrow{p}cdot overrightarrow{v}dt $$ где (overrightarrow{p}cdot overrightarrow{v}) – скалярное произведение векторов импульса и скорости.
п.3. Примеры
Пример 1. Тело движется со скоростью (v(t)) (м/с). Найдите путь, пройденный за промежуток времени от (t_1) до (t_2) (с):
a) (v(t)=3t+2t^2, t_1=0, t_2=6)
Путь: begin{gather*} s(t)=int_{t_1}^{t_2}v(t)dt\ s=int_{0}^{6}(3t+2t^2)dt=left(frac{3t^2}{2}+frac{2t^3}{3}right)|_{0}^{6}=frac{3cdot 36}{2}+frac{2cdot 36cdot 6}{3}-0=\ =3cdot 18+4cdot 36=54+144=198 text{(м)} end{gather*}
б) (v(t)=2(t+2)^{5/2}, t_1=0, t_2=7) begin{gather*} s=int_{0}^{7}2(t+2)^{5/2}dt =2cdotfrac{(t+2)^{frac52+1}}{frac72}|_{0}^{7}=frac47cdot 9^{frac72}-0=frac47cdot 3^7approx 1250 text{(м)} end{gather*}
Пример 2. . Сила тока в проводнике изменяется по закону (I(t)=e^{-t}+2t) (время в секундах, ток в амперах). Какой заряд пройдет через поперечное сечение проводника за время от второй до шестой секунды?
Заряд: begin{gather*} Q(t)=int_{t_1}^{t_2}I(t)dt end{gather*} По условию: begin{gather*} Q=int_{2}^{6}(e^{-t}+2t)dt=(-e^{-t}+t^2)|_{2}^{6}=-e^{-6}+6^2+e^{-2}-2^2=frac{1}{e^2}-frac{1}{e^6}+32=\ =frac{e^4-1}{e^6}+32approx 32,1 text{(Кл)} end{gather*}
Пример 3*. Найдите путь, который пройдет тело от начала движения до возвращения в исходную точку, если его скорость (v(t)=18t-9t^2) (время в секундах, скорость в м/с). Движение тела прямолинейное.
Если тело вернулось в исходную точку, оно меняло направление движения.
В момент разворота скорость равна нулю. Решаем уравнение: $$ 18t-9t^2=0Rightarrow 9t(2-t)=0Rightarrow left[ begin{array}{l} t=0\ t=2 end{array} right. $$ (t=0) – начало движения, (t=2) – разворот.
 |
Уравнение движения: $$ x(t)=int(18t-9t^2)dt=9t^2-3t^3+C $$ В начальный момент времени (x_0=0Rightarrow C=0) $$ x(t)=9t^2-3t^3 $$ В точке C(2;12) кривая (x(t)) имеет максимум. Тело двигалось в течение 2 с в одну сторону и прошло 12 м, а затем за 1 с вернулось обратно. Общий путь: 12+12 = 24 м. |
Ответ: 24 м
Пример 4*. Найдите работу, которую необходимо совершить, чтобы выкачать воду из полусферического котла радиуса R м.
Найдем работу (dA), которую нужно совершить, чтобы выкачать слой воды толщиной (dH) с глубины (H).
Радиус слоя на глубине (H: r^2=R^2-H^2) – по теореме Пифагора.
Объем слоя воды: (dV=pi r^2 dH=pi(R^2-H^2)dH)
Масса слоя воды: (dm=rho dV=pirho(R^2-H^2)dH)
Работа по подъему слоя на высоту (H): $$ dA=dmcdot gH=pirho gH(R^2-H^2)dH $$ Получаем интеграл: begin{gather*} A=int_{0}^{R}dA=int_{0}^{R}pirho gH(R^2-H^2)dH=pirho gint_{0}^{R}(HR^2-H^3)dH=\ =pirho gleft(frac{H^2}{2}R^2-frac{H^4}{4}right)|_{0}^{R}=pirho gleft(frac{R^4}{2}-frac{R^4}{4}-0right)=fracpi 4=rho gR^4 end{gather*} Ответ: (A=fracpi 4=rho gR^4)
Пример 5*. Какую работу выполняют при запуске ракеты массой m кг с поверхности планеты на высоту h м, если радиус планеты равен R м и масса планеты равна M кг?
Сравните работу при запуске ракеты с Земли и Луны на высоту одного радиуса небесного тела, если ускорение свободного падения на поверхности Луны (g_M=1,62) м/с2, радиус Луны (R_M=1737) км; для Земли соответственно (g_E=9,81) м/с2 (R_E=6371) км.
Ускорение свободного падения на поверхности планеты: (g_0=Gfrac{M}{R^2})
Ускорение свободного падения при подъеме на высоту x: begin{gather*} g(x)=Gfrac{M}{(R+x)^2} end{gather*} Работа по преодолению силы тяжести (F(x)=mg(x)) при подъеме ракеты на высоту h: begin{gather*} A=int_{0}^{h}mg(x)dx=mint_{0}^{h}Gfrac{M}{(R+x)^2}dx=GmMint_{0}^{h}frac{dx}{(R+x^2)}=\ =GmMcdotleft(-frac{1}{R+x}right)|_{0}^{h}=GmMcdotleft(-frac{1}{R+h}+frac1Rright)=GmMleft(frac1R-frac{1}{R+g}right)=\ =GmMfrac{R+h-R}{R(R+h)}=GmMfrac{h}{R(R+h)} end{gather*} Также, если выразить работу через ускорение свободного падения на поверхности планеты: $$ A=frac{GM}{R^2}frac{mhR^2}{R(R+h)}=mg_0frac{hR}{R+h} $$ Работа по запуску на высоту одного радиуса небесного тела (h=R): $$ A(R)=mg_0frac{R^2}{2R}=frac{mg_0R}{2} $$ Отношение работ по запуску на один радиус на Земле и Луне: $$ frac{A_E(R_E)}{A_M(R_M)}=frac{mg_ER_E}{mg_MR_M}=frac{g_ER_E}{g_MR_M}, frac{A_E(R_E)}{A_M(R_M)}=frac{9,81cdot 6371}{1,62cdot 1737}approx 22,2 $$ На Земле работа в 22,2 раза больше.
Ответ: (A=GmMfrac{h}{R(R+h)}; frac{A_E(R_E)}{A_M(R_M)}approx 22,2)
Продолжаем предыдущий урок на тему “Применение криволинейных интегралов 2 рода”.
Готовые ответы задач на работу силового поля помогут студентам выучить тему, и научат быстро находить нужные интегралы.
Пример 4.2 Найти работу силы F (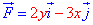
x2/4+y2/9=1 от точки A(- 2;0) к точке B(0;3).
Решение: Запишем уравнение заданного эллипса в параметрическом виде: x=2*cos(t), y=3*sin(t).
Наведем графически траекторию материальной точки вдоль эллипса.
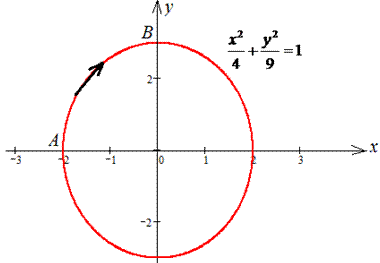
Тогда дифференциал переменных по параметру будет равен dx=-2*sin(t)dt, dy=3*cos(t)dt .
При этом пределы интегрирования ограничатся точками Pi и Pi/2.
Найдем работу силы F по кривой C через криволинейный интеграл ІІ рода : 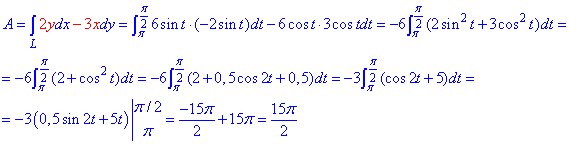
Пересмотрите внимательно формулы интегрирования синуса и косинуса, и понижения степени для таких функций.
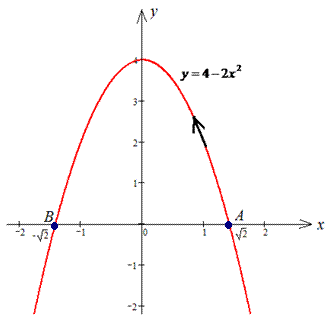
Пример 4.4 Найти работу силы 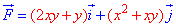
y=4-2x^2 от точки 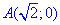
Решение: Построим траекторию движения материальной точки вдоль параболы L: y=4-2x2.
Вычисляем дифференциал дуги y=4-2x2, dy=-4x*dx и из условия выписиваем пределы интегрирования
Работа силы F находим с помощью криволинейного интеграла второго рода
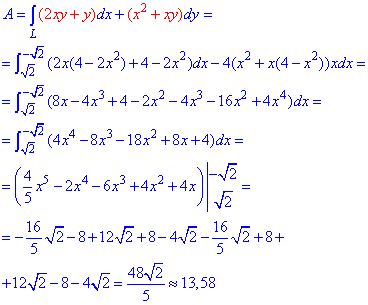
Интегрирование занимает не мало времени и при превращениях можно допустить ошибку, поэтому будьте внимательные в этих местах.
Пример 4.11 Найти работу силы 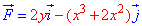
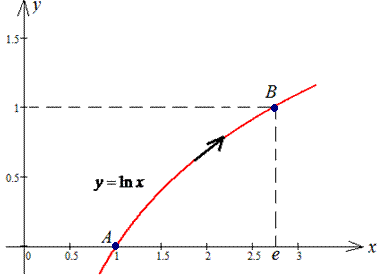
y=ln(x) от точки A(1;0) к точке B(e;1).
Решение: Траектория материальной точки вдоль логарифма имеет вид
Находим дифференциал логарифма y=ln (x), dy=dx/x.
Пределы интегрирования изменяются от единицы к экспоненте.
Работа силы F с помощью криволинейного интеграла ІІ рода примет значение:
Здесь для логарифма применили правило интегрирования частями (u*dv).
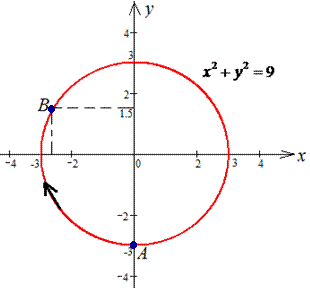
Пример 4.13 Найти работу силы F при перемещении вдоль кривой C:
x2+y2=9 от точки A (0;-3) к точке 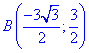
Решение: Построим траекторию движения материальной точки вдоль круга радиусом 3.
Чтобы не выражать две функции (верхняя и нижняя кривая круга) запишем зависимость x(y) и вычислим дифференциал дуги
При этом ордината изменяется от – 3 до 3/2.
Применяя криволинейный интеграл ІІ рода находим роботу силы F при перемещении вдоль круга:
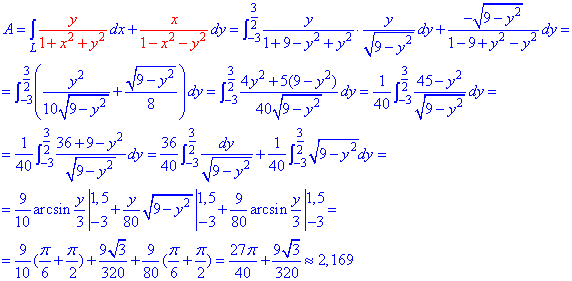
Бороться с корнями во время интегрирования непросто, о чем свидетельствует приведенные вычисления.
Намного проще вычислять интеграл при переходе к полярной системе координат.
Дальше наведем методику интегрирования:
ІІ – способ:
Параметризуэм заданный круг:
Учитывая, что во время движения от точки A(0;-3) к точке 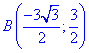
Вычисляем искомый криволинейный интеграл ІІ рода :
В плане вычислений второй метод более легкий, поэтому для круговых и эллиптических форм кривой при симметричном вхождении x, y в уравнение силы рекомендуем переходить к полярной системе координат.
Пример 4.15 Найти работу силы 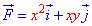
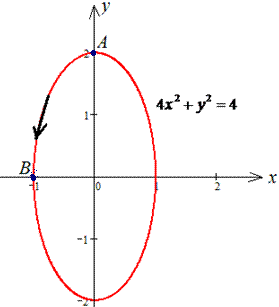
4x2+y2=4 от точки A(0;2) к точке B (-1;0).
Решение: Траектория движения материальной точки по эллипсу приведена ниже
Записываем верхнюю дугу эллипса и ее производную.
Пределы интегрирования изменяются от 0 к -1
Работа силы F через криволинейный интеграл второга рода выражается зависимостью:
Пример 4.18 Найти работу силы 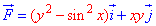
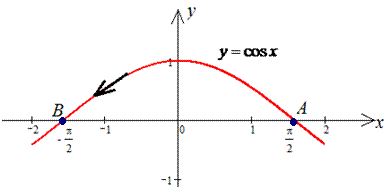
y=cos(x) от точки A(Pi/2;0) к точке B(-Pi/2;0).
Решение: Изобразим траекторию материальной точки вдоль косинуса
Построим дифференциал кривой y=cos(x), dy=-sin(x)*dx.
Он нужен для возведения криволинейного интегралу ІІ рода к определенному.
Находим работу силы F по перемещении вдоль контура интегрированием
Для понижения под интегралом степеней косинуса и синуса применили известные тригонометрические формулы.
Пример 4.21 Найти работу силы 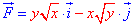
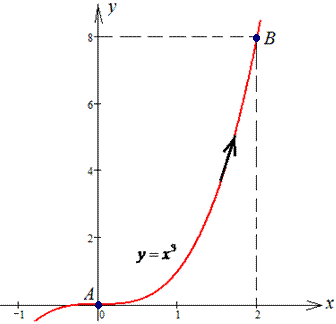
y=x3 от точки A(0;0) к точке B(2;8).
Решение: Построим траекторию материальной точки вдоль кривой y=x3.
Вычисляем дифференциал дуги dy=3x2dx.
Пределы интегрирования приведены на рисунку и в условии.
Работа силы F находим с помощью криволинейного интегралу ІІ рода:
Превращаем все к показательной форме и интегрируем.
Пример 4.23 Найти работу силы 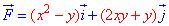
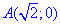
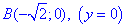
Решение: За инструкцией строим траекторию материальной точки вдоль эллипса: x2+2y2=2.
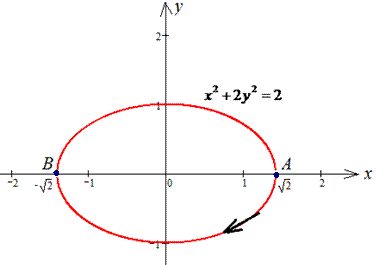
Для простоты вычислений криволинейного интеграла ІІ рода параметризуэм эллипс:
Учитывая, что от точки 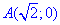
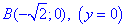
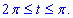
Понижаем степени и интегрируем.
Пример 4.24 Найти работу силы 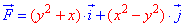
y=1-|x| от точки A(-1;0) к точке B(2;- 1).
Решение: Наведем траекторию материальной точки вдоль модуль функции.
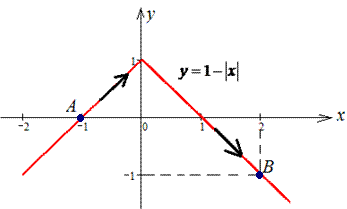
Как ни хотелось встретить задания с разбитием кривой на два интервала, однако одно Пример содержит такое условие. Разделим на две части: y=1+x, тогда пределы равны [-1;0] и дифференциал dy=dx;
На втором участке y=1-x имеем [0;2] и dy=-dx.
Вычисляем работу силы F, потраченную на перемещении точки вдоль модуль функции:
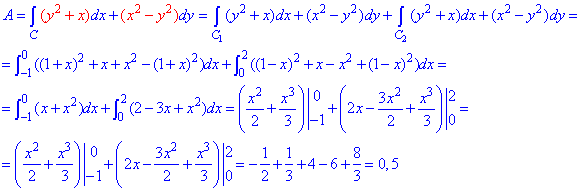
На этом ознакомление из такого сорта примерами завершено.
Больше готовых ответов из курса высшей математики ищите на страницах сайта.
Пусть
материальная точка движется вдоль оси
Ох
от точки х=а,
до х=b
(а<b)
под действием
переменной силы
F=F(x),причём
направление силы совпадает с направлением
движения. Найти работу, произведенную
силой на этом перемещение. Возьмём
элементарное перемещение [x,x+dx].Работа
силы на этом перемещение
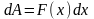
Мы
получим «элемент» работы. Теперь
проинтегрируем по отрезку[a,b]
и получим искомую работу:
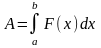
7.2.1. Тело
движется по прямой
из
точки с абсциссой a
до
точки с абсциссой b(a<b)
под
действием переменной
силы
,
являющейся
непрерывной функцией абсциссы х:
=
(х),
причем
сила параллельна прямой
,
а
ее направление совпадает с направлением
движения тела. Найти работу
A,
произведенную
силой
(х)на
этом перемещении.
Решение.
Если бы сила
(х)
была
не переменной, а постоянной, параллельной
прямой Ох,
и
ее направление совпадало с направлением
движения тела, то работа A,
произведенная
ею, была бы равна произведению модуля
силы на пройденный путь, т. е. на длину
отрезка [а,b],
равную
(b—а):
A
= F(b—
а).
Но
сила переменна, а потому этой формулой
для определения работы мы воспользоваться
не можем.
Отрезок
[а,b]
разделим
на п
отрезков
[xk-1
xk]
(k=l,2,3,
…,n).
На
каждом из них выберем произвольную
точку
.
Определим
в этой точке численное значение силы
(х)
Получится
число
(
).
Полагая,
что в пределах каждого частичного
отрезка сила не переменна, а постоянна
и что ее значение на всем частичном
отрезке такое же, как в выбранной точке,
будем считать произведенную этой силой
работу приближенно на каждом частичном
отрезке равной произведению модуля
силы на путь, т. е.
(
)∆xk
Работа
силы
(х)
на
всем отрезке [а,
b]
приближенно
равна сумме работ на всех частичных
участках
Сумма
—
интегральная сумма для функции F(x).
на
отрезке [а,b].
По
формуле (11,4) мы получим не точное значение
работы, а приближенное, потому что на
каждом частичном отрезке мы считали
силу постоянной, в то время как фактически
в пределах каждого частичного отрезка
она непрерывно изменяется.
За
точное значение работы силы
на отрезке [а,b]
мы
примем тот предел, к которому стремится
интегральная сумма (11,4), когда наибольший
из частичных отрезков ∆xk
стремится
к нулю, а число их n
неограниченно
возрастает, т. е.
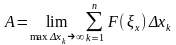
(11.5)
Подынтегральное
выражение F(х)dx
называется
элементарной работой и обозначается
через δА
Работа
А
есть
определенный интеграл от элементарной
работы δА=
F(х)dx.
Таким
образом, для определения работы
переменной силы на прямолинейном
пути надо сначала вычислить элементарную
работу δА,
а после этого интегрированием по формуле
(11,5) найти полную работу.
Приближенное
значение работы, вычисленное по формуле
(11,4), будет тем меньше отличаться от ее
точного значения (11,5), чем меньшими будут
частичные отрезки ∆xk,
на
которые разбит отрезок [а,b]
.
При
определении предела суммы (11,4) наибольший
из отрезков ∆xk→0,
каждое слагаемое
(
)∆xk
— величина бесконечно малая, а количество
их неограниченно возрастает. Поэтому
и здесь определение искомой величины,
как и в задаче 11,1 связано с определением
предела суммы бесконечно малых величин,
когда их количество неограниченно
возрастает.
7.2.2.
Какую работу надо совершить, чтобы
растянуть пружину на 4 см, если известно,
что от нагрузки 1 Н она растягивает на
1 см?
Решение.
Согласно
закону Гука сила F
Н, растягивающая пружину на х
м, равна
.Коэффициент
пропорциональности
найдём из условия :
Если
х=0,01м,
то
F=1Н;
Следовательно,
и
.Тогда
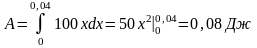
7.2.3.Растяжения
пружины на 0,04 м необходимо совершить
работу 20 Дж. На какую длину модно растянуть
пружину, совершить работу в 80 Дж?
Решение.
По
длине растяжения пружины на 0,04м и
совершенной работе 20 Дж найдём:
k:
,
Откуда
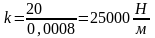
По
и
найдем
:
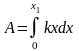
где
-длина,
на которую растянута пружина при
совершенной работе в 80 Дж.
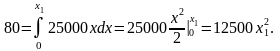
Откуда
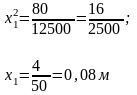
7.2.4.Ккаую
работу нужно затратить, чтобы тело массы
m
поднять с поверхности Земли на высоту
h?Чему
равна эта работа, если тело должно быть
удалено на бесконечность?
Решение.
Величина
сила F
,производящей работу при поднятие тела
с поверхности земли, равна величине
сила притяжения тела Земли, т.е.
,
где
m-масса
тела,M-масса
Земли,r-расстояние
от тела до центра Земли. В этом же
направлении происходит и перемещение
тела из положения
(R-радиус
Земли) в положение
.Работу
силы F(r)
на пути [R,R+h]
вычислим с помощью интеграла
Учитывая,
что на поверхности Земли(при
)
сила притяжения
найдём
коэффициент
:
откуда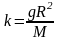
Тогда
и
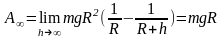
7.2.5.Вычислить
работу, которую надо совершить, чтобы
выкачать воду из резервуара конической
формы с вершиной, обращенной к низу.
Резервуар наполнен доверху водой. Радиус
основания конуса R=1,
высота конуса 2м.
Решение.
На глубине х
выделяем горизонтальный слой высоты
dx
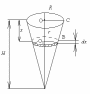
Элементарный
слой принимаем за цилиндр ввиду малости
dx.Тогда
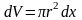
Выразим
r-радиус
слоя через х и постоянные R
и H.
Из подобия треугольников АОС и АО1В
имеем:
откуда
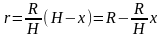
Далее
получим
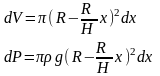
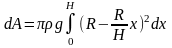
Дж
7.2.6.
Шар лежит на дне бассейна глубиной
Н=14мюОпределить работу, необходимую
для извлечения шара из воды, если его
радиус R=3дм,а
удельный вес
.
Решение.
При
подъеме шара до поверхности воды сила
P1
совершающая
работу, постоянна и равна разносим между
весом шара и весом вытесняемой им воды:
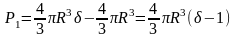
Поэтому
работа Q1,
необходимая для поднятия шара до
поверхности воды, определяется как
произведение силы P1
на высоту
подъема H-2R:
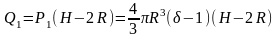
При дальнейшем
подъеме шара сила p,совершающая
работу, будет изменяться в зависимости
от высоты х надводной части шара
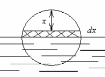
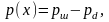
где
-вес
шара ,
вес
воды, вытесняемой подводной частью
шара, численно равный объему шарового
сечения с высотой
;
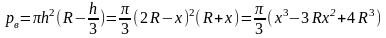
Очевидно,
и работа, совершаемая силой p(x),
некоторой функцией g(x).Допуская,
что при подъёме шара ещё на малую высоту
dx
сила p(x)
остается неизменной, найдем приближенную
величину приращения работы.
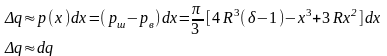
Интегрируя
dq
в пределах от x=0
до x=2R
найдем работу
,которою
надо совершить, чтобы шар, поднятый со
дна бассейна до поверхподнятой воды,
полностью извлечь из воды:
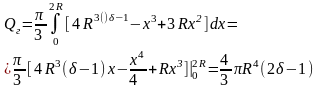
Вся
искомая работа
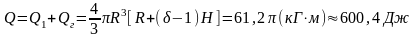
7.2.7.
Какую работу затрачивает подъемный
кран при извлечении железобетонной
надолбы со дна реки глубиной в 5 м, если
надолба имеет форму правильного тетраэдра
с ребром 1м,а плотность железобетона
2500 кг/м3
Решение.
Высота
тетраэдра
объем тетраэдра
м3.Вес
надолбы в воде
Н,
Поэтому
работа на извлечение надолбы до момента
появления на поверхности воды её вершины
Дж
Теперь
найдем работу А1
на извлечение
надолбы из воды. Пусть вершина тетраэдра
вышла на высоту 5+у,
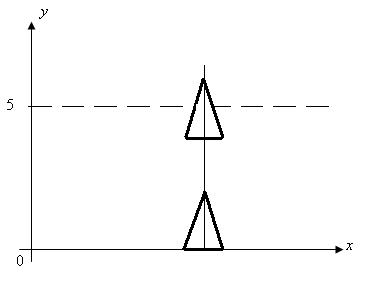
Тогда
объем малого тетраэдра, вышедшего из
воды, равен
а вест тетраэдра
Н
Следовательно
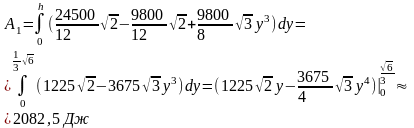
7.2.8. (работа
упругой силы на прямолинейном
перемещении).
К
телу прикреплена пружина, другой конец
которой закреплен неподвижно в точке
О.
Упругая
сила, с которой действует пружина на
тело, подчиняется закону Гука, согласно
которому F=—kx,
где
k—коэффициент
пропорциональности, а
х
—
удлинение пружины. Найти работу
упругой силы на прямолинейном перемещении
по линии действия силы из точки с
абсциссой a
в
точку с абсциссой b.
(Сила
— в килограммах, перемещение — в метрах).
Знак минус в выражении силы показывает,
что упругая сила стремится восстановить
равновесие.
Решение.
Элементарная работа δА
силы
упругости на перемещении dx
равна
dA=—kx
dx,
а
потому полная работа на перемещении из
точки а
в
точку b
определится
по формуле
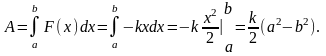
Следует
иметь в виду, что работа упругой силы
положительна, если тело движется в
сторону убывания модуля упругой силы,
и отрицательна, когда движение происходит
в сторону возрастания модуля упругой
силы.
7.2.9.
Тяжелая
цепь длиною L
=
200 м
поднимается,
навиваясь на ворот. Определить работу
силы веса при поднятии цепи, пренебрегая
размерами ворота, если погонный метр
цепи весит 50
кг.
Решение.
Пусть к некоторому моменту времени на
ворот навернулся отрезок цепи длиной
х.
Тогда
свешивается его часть длиной L—х.
Весит
эта часть (L—х)•50кг.
Элементарная
работа силы веса на перемещении dx
будет
равна
δА=—(L—х)∙50dx.
(Знак
минус поставлен потому, что сила веса
направлена противоположно перемещению).
Полную работу найдем по формуле (11,5) как
интеграл от элементарной работы
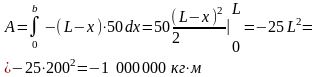
7.2.10.
Вычислить
работу, необходимую для выкачивания
масла из вертикального цилиндрического
резервуара высотой H
= 6м и радиусом основания
R
= 2 м.
Удельный вес масла δ = 0,9.
Решение.
Величина
работы
q,
затрачиваемой на поднятие некоторого
тела, зависит от высоты х
его подъема:
q=Px,
Р— вес
тела.
Допустим,
что работа, затраченная на выкачивание
из резервуара слоя масла толщиною
х,
черт. 1 , есть некоторая функция
q
(x)
и найдем дифференциал этой функции. При
увеличении
х
на величину
dx
объем
v
слоя масла увеличится на величину
∆υ
= π
R2dx,
его вес
р
увеличится на вели-
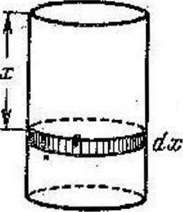
Черт.
I
чину
∆p=πδR2dx,
а затраченная работа
q
увеличится на величин у ∆q
≈ πδR2
х dx
= dq.
Всю
искомую работу Q
получим при изменении х от 0 до H.
Поэтому
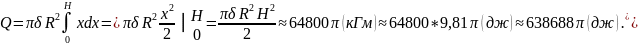
7.2.11.
Цилиндр
высотой Н= 1,5 м и радиусом R
= 0,4м, наполненный газом под атмосферным
давлением (10330кГ/м2),
закрыт поршнем. Определить работу,
затрачиваемую на изотермическое
сжатие газа при перемещении поршня на
расстояние h
= 1,2
м
внутрь цилиндра.
Решение.
При изотермическом изменении состояния
газа, когда его температура остается
неизменной, зависимость между объемом
υ
и давлением
р
газа выражается
формулой
pυ=
с = const.(Закон
Бойля-Мариотта)
Поэтому,
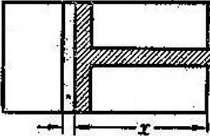
если поршень будет вдвинут на
х м
внутрь
цилиндра (черт: 1 ‘), то давление
р(х)
газа на единицу
площади
поршня будет
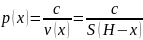
Полагая,
что работа, затрачиваемая при вдвижении
поршня на
х м,
есть некоторая функция
q{x),
.и допуская, что при дальнейшем вдвижении
поршня. на малое расстояние dx
испытываемое им давление
Р(х)
остается неизменным, найдем, приближенную
величину приращения (дифференциал)
функции
q(x):
∆q
≈ Р (х)dx
=
dx
= dq.
Всей
искомой работе Q
соответствует .изменение
х
от 0 до
h, поэтому
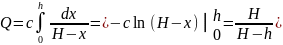
При
H=1,5м,
R = 0,4м,
h ~=
1,2
м,
= 10 330
кГ/м2
найдем
v0
=
πR2H=0,24πм3;
c = p0v0
= 2479,2π;
Q ≈ 12533,3
кГм
≈122951,7
дж.
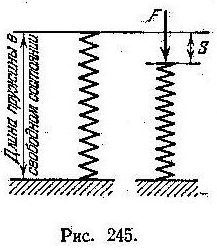
7.2.12.
Сжатие
S
винтовой пружины пропорционально
приложенной силе F.
Вычислить работу силы F
при сжатии пружины на 5
см,
если для сжатия её на 1
см нужна
сила в 1 кг
(Рис. 245).
Р
ешение.
Сила F
и перемещение
S
связаны
по условию зависимостью F
= kS,
где k
– постоянная.
Будем выражать S
в метрах, F
– в килограммах.
При
S
= 0.01 F = 1,
т.
е.
1 = k ·
0.01,
откуда
k
= 100,
F = 100S.
На основе формулы
(1) имеем:
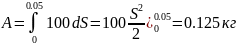
7.2.13. Сила F,
с которой электрический заряд e1
отталкивает
заряд e2
(того же
знака), находящийся от него на расстоянии
r,
выражается формулой
,
где k
– постоянная.
Определить работу
силы F
при перемещении
заряда e2
из точки
A,
отстоящий от заряда e1
на расстоянии r1
в точку
A2,
отстоящую от e1
на расстоянии r2,
полагая, что заряд e1
помещен в точке A0,
принятой за начало отсчета.
Решение.
По формуле
(1) имеем:
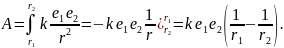
При r2
= ∞
получим:
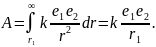
При e2
= 1
.
Последняя величина называется потенциалом
поля,
создаваемого зарядом e1.
Вычисление работы с помощью определенного интеграла
Вычисление
работы с помощью определенного интеграла
Пусть
под действием некоторой силы (данная функция непрерывна на отрезке
) материальная
точка М движется по прямой OS, работа силы по перемещению точки
на отрезке
Пример:
Сила, действующая на материальную точку
меняется по закону , найти работу данной силы при перемещении тела из
координаты x=2
до координаты х=7