Как найти работу сил электрического поля

На заряд q_пр
помещённый в произвольную точку
электростатического поля с напряжённостью
Е, действует сила F=
q_пр
E.
Если заряд не закреплён, то сила заставит
его перемещаться и, значит, будет
совершаться работа. Элементарная работа,
совершаемая силой F
при перемещении точечного электрического
заряда q_пр
из точки а электрического поля в точку
b
на отрезке пути dℓ,
по определению, равна

dA
= Fdℓcosα

(α
– угол между F
и направлением движения) (рис.12.13).

Если работа
совершается внешними силами, то dA<
0 , если силами поля, то dA
> 0. Интегрируя последнее выражение,
получим, что работа против сил поля при
перемещении q_пр
из точки a
в точку b

(12.20)

Рисунок -12.13

(
– кулоновская сила, действующая на
пробный заряд q_пр
в каждой точке поля с напряжённостью
E).

Тогда работа

(12.21)

Перемещение
совершается перпендикулярно вектору
,
следовательно cosα
=1, работа переноса пробного заряда q_пр
от a
к b
равна

(12.22)

Работа сил
электрического поля при перемещении
заряда не зависит от формы пути, а зависит
лишь от взаимного расположения начальной
и конечной точек траектории.

Следовательно,
электростатического поля точечного
заряда является потенциальным
, а электростатические силы –
консервативными.

Это свойство
потенциальных полей. Из него следует,
что работа совершаемая в электрическом
поле по замкнутому контуру, равна нулю:

(12.23)

Интеграл

называется циркуляцией
вектора напряженности.
Из обращения в нуль циркуляции вектора
Е следует, что линии напряжённости
электростатического поля не могут быть
замкнутыми, они начинаются на положительных
и кончаются на отрицательных зарядах.

Как известно,
работа консервативных сил совершается
за счёт убыли потенциальной энергии.
Поэтому, работу сил электростатического
поля можно представить как разность
потенциальных энергий, которыми обладает
точечный заряд q_пр
в начальной и конечной точках поля
заряда q:

(12.24)

откуда следует,
что потенциальная энергия заряда q_пр
в поле заряда q
равна

(12.25)

Для одноименных
зарядов q_прq
>0 и
потенциальная энергия их взаимодействия
(отталкивания) положительна, для
разноимённых зарядов q_прq
< 0 и
потенциальная энергия их взаимодействия
(притяжения) отрицательна.

Если поле
создаётся системой n
точечных зарядов q_1,
q_2,
…. q_n,
то потенциальная энергия U
заряда q_пр,
находящегося в этом поле, равна сумме
его потенциальных энергий U_i,
создаваемых каждым из зарядов в
отдельности:

(12.26)

Отношение

не зависят от заряда q
и является энергетической характеристикой
электростатического поля.

Скалярная
физическая величина, измеряемая
отношением потенциальной энергии
пробного заряда в электростатическом
поле к величине этого заряда, называется
потенциалом электростатического поля.

(12.27)

Потенциал поля,
создаваемый точечным зарядом q,
равен

(12.28)

Единица потенциала
– вольт.

Работа, совершаемая
силами электростатического поля при
перемещении заряда q_пр
из точки 1 в точку 2 может быть представлена
как

(12.29)

т.е. равна произведению
перемещаемого заряда на разность
потенциалов в начальной и конечной
точках.

Разность
потенциалов двух точек электростатического
поля φ₁-φ₂
равна напряжению. Тогда

Отношение работы,
совершаемой электростатическим полем
при перемещении пробного заряда из
одной точки поля в другую, к величине
этого заряда называется напряжением
между этими точками.

(12.30)

Графически
электрическое поле можно изображать
не только с помощью линий напряжённости,
но и с помощью эквипотенциальных
поверхностей.

Эквипотенциальные
поверхности
– совокупность точек, имеющих одинаковый
потенциал.
Из рисунка видно, что линии напряжённости
(радиальные лучи) перпендикулярны
эквипотенциальным линиям.

Эквипотенциальных
поверхностей вокруг каждого заряда и
каждой системы зарядов можно провести
бесчисленное множество
(рис.12.14).
Однако их
проводят так, чтобы разности потенциалов
между любыми двумя соседними
эквипотенциальными поверхностями были
одинаковы. Тогда густота эквипотенциальных
поверхностей наглядно характеризует
напряжённость поля в разных точках.
Там, где эти поверхности расположены
гуще, напряжённость поля больше. Зная
расположение эквипотенциальных линий
(поверхностей), можно построить линии
напряжённости или по известному
расположению линий напряжённости можно
построить эквипотенциальные поверхности.

Соседние файлы в папке Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

Работа по перемещению заряда в электростатическом поле:

В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.

Работа по перемещению заряда в однородном электростатическом поле

Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.

Пусть в однородном электростатическом поле напряженностью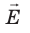

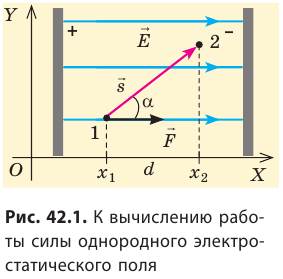
Вычислим работу А, которую совершает сила 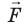, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.

Поле однородное, поэтому сила 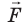постоянна, ее модуль равен: F=qE, а scosα=d=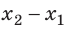является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( 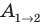) равна:

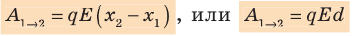
Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.

Обратите внимание! Формула 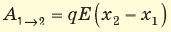будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.

Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:

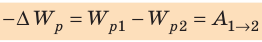
Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:

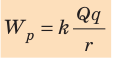
Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( < 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.

Что называют потенциалом электростатического поля

Потенциал 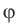электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к значению q этого заряда:

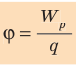
Единица потенциала в Си — вольт: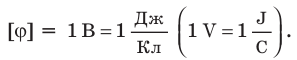

Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле: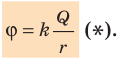

Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.

Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 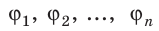полей, созданных каждым зарядом:

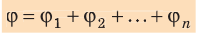
Как определяют разность потенциалов

Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: 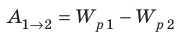. Поскольку 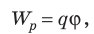то 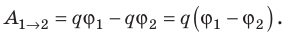Выражение 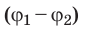называют разностью потенциалов, где 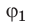— значение потенциала в начальной точке траектории движения заряда, 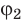— значение потенциала в ее конечной точке.

Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:

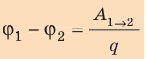
Единица разности потенциалов в Си — вольт: 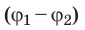= 1 В (V).

Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов 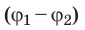− также называют напряжением (U). Важно не путать изменение потенциала 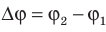и разность потенциалов (напряжение) .

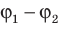Как связаны напряженность однородного электростатического поля и разность потенциалов

Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).

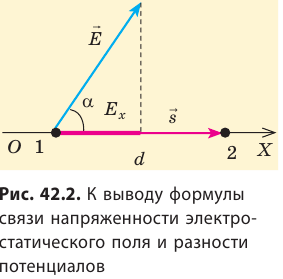
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: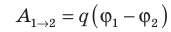; 2) через напряженность поля: 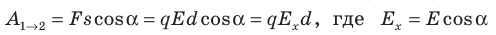— проекция вектора 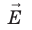на ось Ох, проведенную через точки 1 и 2.

Приравняв оба выражения для работы, получим: 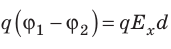, откуда: 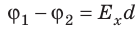, или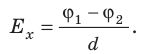

Если заряд перемещается в направлении напряженности электрического поля () , последняя формула примет вид:

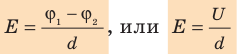
Из последней формулы следует единица напряженности в Си — вольт на метр:

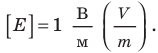
Какие поверхности называют эквипотенциальными

Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.

Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.

Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).

Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( 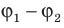), а на эквипотенциальной поверхности .

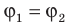Работу электростатического поля также можно представить через силу 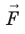, действующую на заряд со стороны поля: A F= scosα , где α — угол между векторам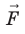и и 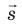. Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы 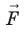, а следовательно, и вектор напряженности 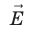поля в любой точке перпендикулярны вектору перемещения .

Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).

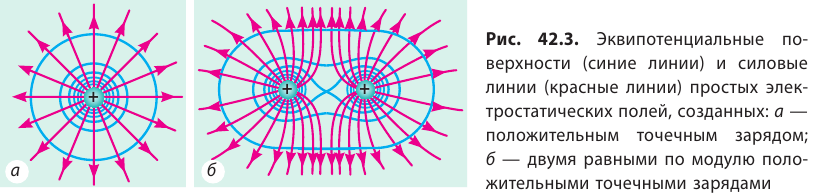
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.

• Заказать решение задач по физике

Пример решения задачи

Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона 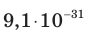кг, заряд 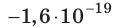Кл.

Заряд электрона — отрицательный, его начальная скорость 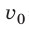= 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.

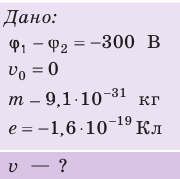
Решение:

Поиск математической модели, решение Согласно теореме о кинетической энергии:

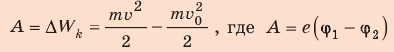— работа сил поля.

Таким образом, 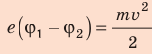, отсюда .

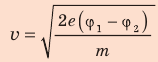Проверим единицу, найдем значение искомой величины:

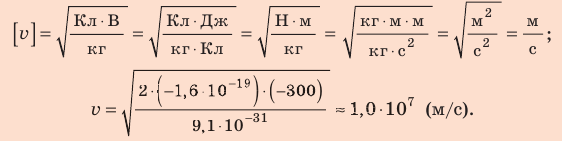
Ответ: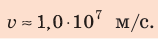

Выводы:

Работа электростатического поля

На электрические заряды в электростатическом поле действуют силы. Поэтому, если заряды перемещаются, то эти силы совершают работу. Рассчитаем работу сил однородного электростатического поля при перемещении положительного заряда q из точки A в точку B (рис. 1).

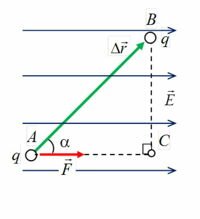
На заряд q, помещенный в однородное электрическое поле с напряженностью E, действует сила (~vec F = q cdot vec E ). Работу поля можно рассчитать по формуле

(~A_{AB} = F cdot Delta r cdot cos alpha,)

где Δr⋅cos α = AC = x₂ – x₁ = Δx — проекция перемещения на силовую линию (рис. 2).

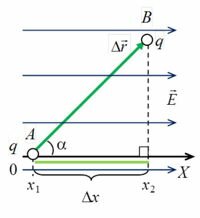
Тогда

(~A_{AB} = q cdot E cdot Delta x. (1))

Рассмотрим теперь перемещение заряда по траектории ACB (см. рис. 1). В этом случае работа однородного поля может быть представлена как сумма работ на участках AC и CB:

(~A_{ACB} = A_{AC} + A_{CB} = q cdot E cdot Delta x + 0 = q cdot E cdot Delta x)

(на участке CB работа равна нулю, т.к. перемещение перпендикулярна силе (~vec F )). Как видно, работа поля такая же, как и при перемещении заряда по отрезку AB.

Не сложно доказать, что работа поля при перемещении заряда между точками AB по любой траектории будет находиться все по той же формуле 1.

Таким образом,

• работа по перемещению заряда в электростатическом поле не зависит от формы траектории, по которой двигался заряд q, а зависит только от начального и конечного положений заряда.
• Это утверждение справедливо и для неоднородного электростатического поля.

Найдем работу на замкнутой траектории ABCA:

(~A_{ABCA} = A_{AB} + A_{BC} + A_{CA} = q cdot E cdot Delta x + 0 – q cdot E cdot Delta x = 0.)

Поле, работа сил которого не зависит от формы траектории и на замкнутой траектории равна нулю, называется потенциальным или консервативным.

Потенциал

Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система “заряд — электростатическое поле” обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:

(~A_{12} = -(W_{2} – W_{1}) = W_{1} – W_{2} . )

Сравнивая полученное выражение с уравнением 1, можно сделать вывод, что

(~W = -q cdot E cdot x, )

где x — координата заряда на ось 0Х, направленную вдоль силовой линии (см. рис. 1). Так как координата заряда зависит от выбора системы отсчета, то и потенциальная энергия заряда так же зависит от выбора системы отсчета.

Если W₂ = 0, то в каждой точке электростатического поля потенциальная энергия заряда q₀ равна работе, которая была бы совершена при перемещении заряда q₀ из данной точки в точку с нулевой энергией.

Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q. Будем помещать в некоторую точку этого поля различные пробные заряды q₀. Потенциальная энергия их различна, но отношение (~dfrac{W}{q_0} = operatorname{const}) для данной точки поля и служит характеристикой поля, называемой потенциалом поля φ в данной точке.

• Потенциал электростатического поля φ в данной точке пространства — скалярная физическая величина, равная отношению потенциальной энергии W, которой обладает точечный заряд q в данной точке пространства, к величине этого заряда:

(~varphi = dfrac{W}{q} .)

Единицей потенциала в СИ является вольт (В): 1 В = 1 Дж/Кл.

• Потенциал — это энергетическая характеристика поля.

Свойства потенциала.

• Потенциал, как и потенциальная энергия заряда, зависит от выбора системы отсчета (нулевого уровня).

  В технике за нулевой потенциал выбирают потенциал поверхности Земли или проводника, соединенного с землей. Такой проводник называют заземленным.

  В физике за начало отсчета (нулевой уровень) потенциала (и потенциальной энергии) принимается любая точка, бесконечно удаленная от зарядов, создающих поле.

• На расстоянии r от точечного заряда q, создающего поле, потенциал определяется формулой

(~varphi = k cdot dfrac{q}{r}.)

• Потенциал в любой точке поля, создаваемого положительным зарядом q, положителен, а поля, создаваемого отрицательным зарядом, отрицателен:

  если q > 0, то φ > 0; если q < 0, то φ < 0.

• Потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R, в точке, находящейся на расстоянии r от центра сферы

  (~varphi = k cdot dfrac{q}{R}) при r ≤ R и (~varphi = k cdot dfrac{q}{r}) при r > R .

• Принцип суперпозиции: потенциал φ поля, созданного системой зарядов, в некоторой точке пространства равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:

(~varphi = varphi_1 + varphi_2 + varphi_3 + … = sum_{i=1}^n varphi_i .)

Зная потенциал φ поля в данной точке, можно рассчитать потенциальную энергию заряда q₀ помещенного в эту точку: W₁ = q₀⋅φ. Если положить, что вторая точка находится в бесконечности, т.е. W₂ = 0, то

(~A_{1infty} = W_{1} = q_0 cdot varphi_1 .)

Потенциальная энергия заряда q₀ в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q₀ из данной точки в бесконечность. Из последней формулы имеем

(~varphi_1 = dfrac{A_{1infty}}{q_0}.)

• Физический смысл потенциала:

  потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в бесконечность.

Потенциальная энергия заряда q₀ помещенного в электростатическое поле точечного заряда q на расстоянии r от него,

(~W = k cdot dfrac{q cdot q_0}{r}.)

• Если q и q₀ — одноименные заряды, то W > 0, если q и q₀ — разные по знаку заряды, то W < 0.

• Отметим, что по этой формуле можно рассчитать потенциальную энергию взаимодействия двух точечных зарядов, если за нулевое значение W выбрано ее значение при r = ∞.

Разность потенциалов. Напряжение

Работа сил электростатического поля по перемещению заряда q₀ из точки 1 в точку 2 поля

(~A_{12} = W_{1} – W_{2} .)

Выразим потенциальную энергию через потенциалы поля в соответствующих точках:

(~W_{1} = q_0 cdot varphi_1 , W_{2} = q_0 cdot varphi_2 .)

Тогда

(~A_{12} = q_0 cdot (varphi_1 – varphi_2) .)

Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.

Из этой формулы разность потенциалов

(~varphi_1 – varphi_2 = dfrac{A_{12}}{q_0} .)

• Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.

В СИ единицей разности потенциалов является вольт (В).

• 1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.

Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ₁ – φ₂ часто называют электрическим напряжением между данными точками поля и обозначают U:

(~U = varphi_1 – varphi_2 .)

• Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую.

Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах.

• 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10^-19 Кл) между двумя точками, напряжение между которыми равно 1 В.

1 эВ = 1,6·10^-19 Кл·1 В = 1,6·10^-19 Дж.

1 МэВ = 10⁶ эВ = 1,6·10^-13 Дж.

Разность потенциалов и напряженность

Рассчитаем работу, совершаемую силами электростатического поля при перемещении электрического заряда q₀ из точки с потенциалом φ₁ в точку с потенциалом φ₂ однородного электрического поля.

С одной стороны работа сил поля (~A = q_0 cdot (varphi_1 – varphi_2)).

С другой стороны работа по перемещению заряда q₀ в однородном электростатическом поле (~A = q_0 cdot E cdot Delta x).

Приравнивая два выражения для работы, получим:

(~q_0 cdot (varphi_1 – varphi_2) = q_0 cdot E cdot Delta x, ;; E = dfrac{varphi_1 – varphi_2}{Delta x},)

где Δx — проекция перемещения на силовую линию.

Эта формула выражает связь между напряженностью и разностью потенциалов однородного электростатического поля. На основании этой формулы можно установить единицу напряженности в СИ: вольт на метр (В/м).

Литература

1. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 228-233.
2. Жилко, В. В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) /В. В. Жилко, Л. Г. Маркович. — 2-е изд., исправленное. — Минск: Нар. асвета, 2008. — С. 86-95.

Часть задач школьного уровня связана с поиском работы и энергии в электростатическом поле.

Работа по перемещению заряда в электростатическом поле.

• Поле однородно

Однородным называется поле, напряжённость которого во всех точках одинакова (). Поместим в данное поле заряд . Тогда, исходя из определения напряжённости электростатического поля, модуль силы, действующей на заряд:

(1)

• где

Вспомним определение механической работы:

(2)

Подставим (1) в (2):

(3)

Соотношение (3) удобно для поиска работы, в случае заряда в однородном электростатическом поле.

Важно: в задачах однородное поле должно быть задано самим выражением «считать поле однородным», также электростатическое поле плоского конденсатора можно считать однородным.

• Поле неоднородно

Неоднородным называется поле, напряжённость которого непостоянно в различных точках пространства. В случае неоднородности поля, воспользуемся выражением (3):

=  =  (4)

Мы воспользовались определением перемещения: разность конечного () и начального () положения тела.

Исходя из определения потенциала:

=  =  (5)

Тогда, если ввести и , получим:

(6)

Т.е. в неоднородном электростатическом поле (а на самом деле, в любом), работа по переносу заряда численно равна переносимому заряду, умноженному на разность потенциалов между точками переноса.

Важно: неоднородное поле в задаче вводится через саму фразу «поле неоднородное» и через источники: точечный заряд, шар, которые также создают неоднородные поля.

Вывод: в задачах на нахождение работы по переносу заряда необходимо выяснить характер поля (однородное или неоднородное) и применить соответствующее выражение (3) или (6).

Энергия взаимодействия зарядов

А теперь обсудим энергию взаимодействия зарядов. Энергия взаимодействие зарядов на школьном уровне даётся без вывода, поэтому мы тоже ещё просто зафиксируем:

(7)

• где