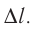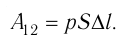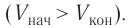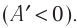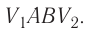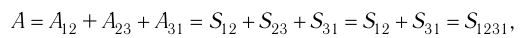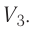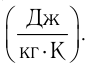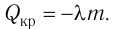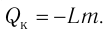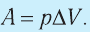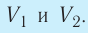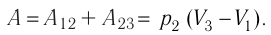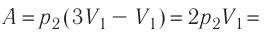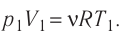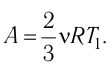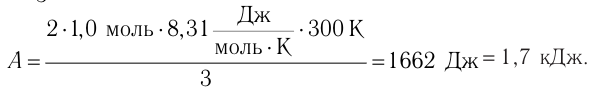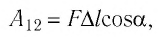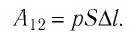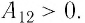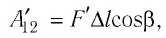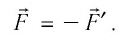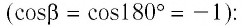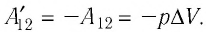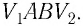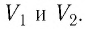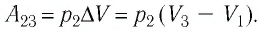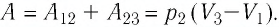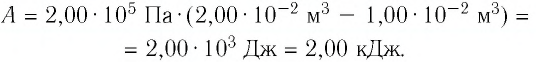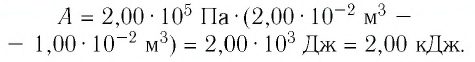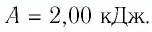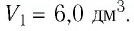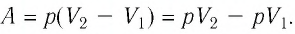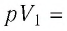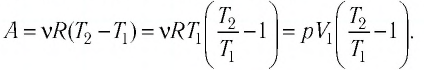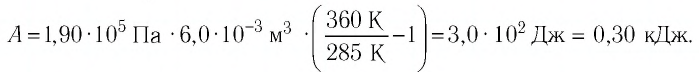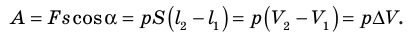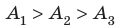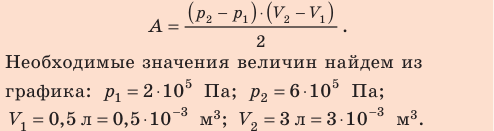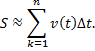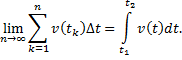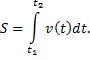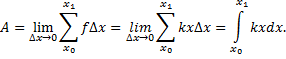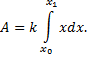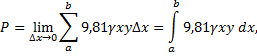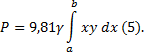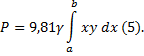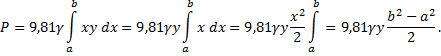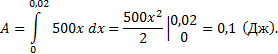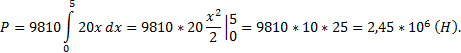Как найти работу силу давления

При изучении физики в восьмом классе мы говорили о том, что
изменить состояние термодинамической системы, то есть её внутреннюю энергию, можно
двумя способами: используя теплопередачу или совершая механическую работу.
Поговорим о последней более подробно.

Итак, когда мы изучали механику, мы с вами говорили о том,
что работа силы (то есть механическая работа) связана с превращением одного
вида энергии в другой, например, механической энергии во внутреннюю. При этом работу
силы мы рассматривали как меру изменения энергии физической системы.

А вот как определить работу в термодинамике, ведь при
рассмотрении термодинамических процессов механическое перемещение макротел в
целом не рассматривается?

Забавно, но работа в термодинамике определяется так же, как и
в механике, но она равна изменению не механической энергии тела, а изменению
его внутренней энергии.

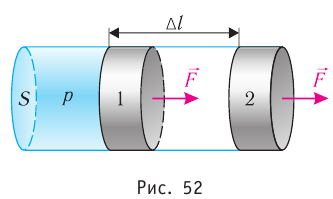
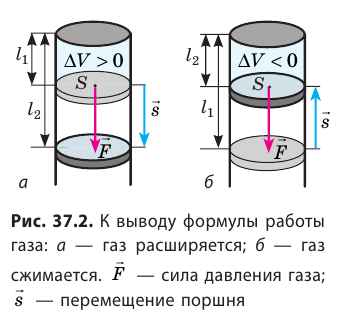
Итак, давайте рассмотрим газ, находящийся в цилиндрическом
сосуде с площадью основания S, и закрытый
подвижным поршнем. Взаимодействие газа с поршнем, а также со стенками сосуда
можно характеризовать давлением, которое газ оказывает на них.

Начнём медленно нагревать газ так, чтобы его давление не
изменялось. Очевидно, что в этом случае газ будет изобарически расширяться, а
поршень начнёт перемещаться за счёт работы силы давления газа над внешними
телами.

Предположим, что поршень переместился на расстояние ∆l.
Так как в процессе расширения давление газа не изменялось, то и сила давления
газа на поршень оставалась неизменной:

F
= pS.

Поэтому работу этой силы мы можем найти как произведение
модуля силы на модуль перемещения и на косинус угла между направлением вектора
силы и вектора перемещения (в нашем примере правда, этот угол равен нулю):

Подставим в записанное уравнение выражение для силы давления:

А теперь давайте подумаем, что определяет произведение площади
основания сосуда (она же площадь основания поршня) и модуля перемещения поршня?..
Да, оно определяет приращение объёма:

Тогда работа газа при его изобарном расширении будет
определяться произведением давления газа на изменение его объёма:

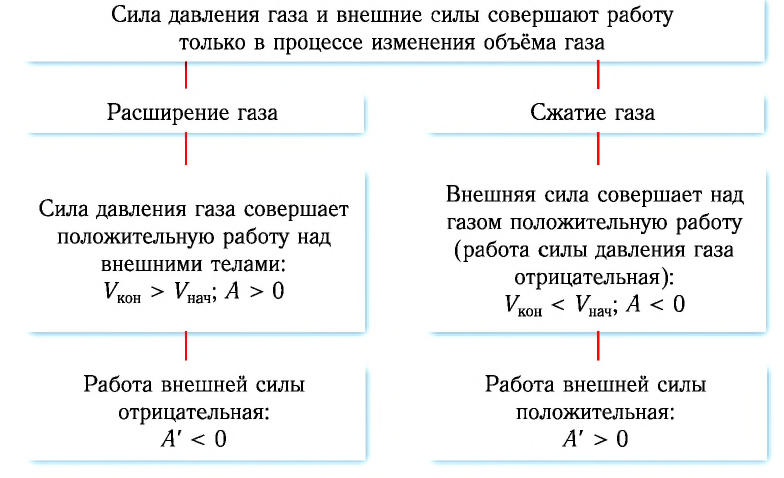
Из этой формулы следует, что сила давления газа совершает
работу только в процессе изменения объёма газа.

А так как давление газа всегда величина положительная, то из
формулы также следует, что при расширении газ совершает положительную работу. При
сжатии же газа сила давления будет совершать отрицательную работу.

Процесс медленного изобарного сжатия газа можно
характеризовать и работой внешних сил над газом, которая отличается от работы
самого газа только знаком:

А теперь давайте запишем уравнение Клайперона — Менделеева
для двух состояний газа в цилиндре:

И вычтем из второго уравнение первое:

В левой части полученного равенства у нас стоит произведение
давления газа на изменение его объёма. А это, как мы с вами нашли ранее, есть не
что иное, как работа газа при изобарном процессе:

Теперь предположим, что в сосуде под поршнем находится один
моль идеального газа и в результате изобарного расширения его температура
изменилась на один кельвин. Тогда получим, что «А равно Эр»:

Отсюда вытекает физический смысл универсальной газовой
постоянной: она численно равна работе, совершаемой одним молем идеального
газа при его изобарном нагревании на один кельвин.

Работе газа при его изобарном расширении или сжатии можно
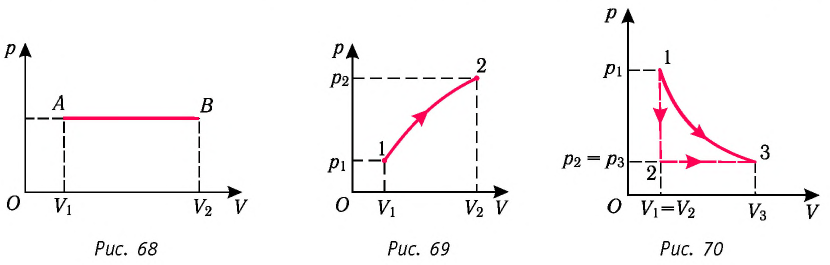
дать простое геометрическое токование. Для этого давайте построим график
зависимости давления газа от занимаемого им объёма. Очевидно, что графиком
является прямая линия, параллельная оси абсцисс.

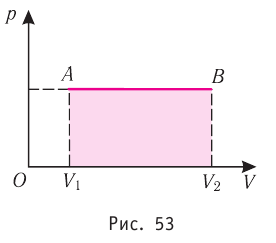
А площадь прямоугольника, ограниченного графиком процесса,
осью V и прямыми, соответствующими значениям объёмов в начальном и
конечном состояниях газа, — это есть ничто иное, как работа газа.

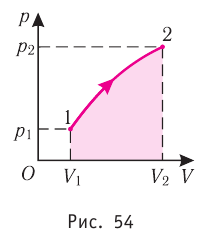
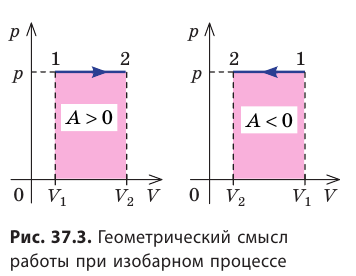
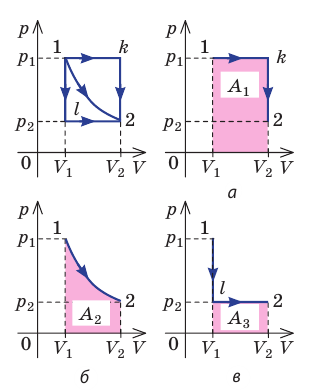
Если процесс перехода газа из начального состояния в конечное
не является изобарным, то кривую зависимости давления газа от занимаемого им
объёма можно представить как ломаную, состоящую из большого числа изохор и
изобар. Работа на изохорных участках равна нулю, а суммарная работа на всех
изобарных участках будет равна площади заштрихованной фигуры.

А теперь для закрепления материала решим с вами несколько
классических задач. В первой задаче нам необходимо будет определить работу, совершаемую
силой давления идеального газа определённой массы при его изобарном нагревании от
290 К до 355 К, если давление газа и его начальный объём соответственно 200 кПа
и 0,1 м³.

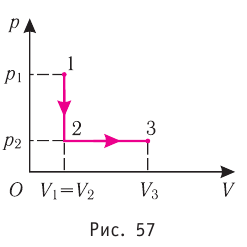
Задача 2. Идеальный газ в количестве 3 молей находится
при температуре 350 К. После изохорного охлаждения, в результате которого
давление уменьшилось в два раза, газ испытывает изобарное расширение, причём в
конечном состоянии температура равна первоначальной. Изобразите графически эти
процессы в осях p, V и вычислите совершённую газом работу.

Термодинамическая
система совершает работу L или воспринимает
теплоприток Q только тогда, когда
совершаеттермодинамический процесс.Процесс состоит из последовательноститермодинамических состояний системы.

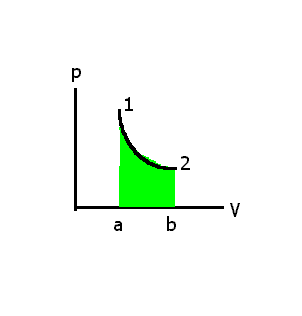
Рис.1-2. Изображение равновесного
процесса 1-2 в рV-диаграмме.
Площадь под кривой процесса выражает
работу сил давления, представленную
формулой (1-5).

2.5.Вычисление работы сил давления

Величина физической работы Lв общем случае определяется черезпроизведение силы напуть. В
нашем частном случае в качестве силы
выступает давление р, в качестве пути
– изменение объема V вследствие перемещения
границы системы. Элементарная работа
при элементарном изменении объема

dL = pdV.
(1-4)

Введем обозначения и единицы измерения:

p – давление системы на поршень или на
другую подвижную часть границы
“система-среда”, измеряется в паскаляхПа = Н/м²;

V₁,V₂– начальный и конечный
объемы термодинамической системы, м³;

L – работа сил давления при изменении
объема, Дж=Па.м³.

Если процесс изменения объема происходит
при постоянном давлении (изобарно), то
в этом частном случае работа

L=p(V₂-V₁).

В общем случае, когда процесс не
обязательно изобарный, работа системы
в процессе, переводящем систему из
состояния 1 в состояние 2, равна

L = p
dV
(1-5)

На рис.1-2 представлена в pV-диаграмме
зависимость 1-2 между давлением р со
стороны системы (газ) на движущийся
поршень и изменяющимся объемом V
системы. Согласно формуле (5) работа L
газа, расширяющегося под поршнем,
положительна и в силу формулы (5) должна
выражаться (с учетом масштаба) площадью
a-1-2-b, расположенной под кривой процесса
1-2.

2.6. Вычисление теплового потока. Энтропия

Как следует из первого закона термодинамики,
внутренняя энергия системы, т.е. энергия
ее внутримолекулярного и межмолекулярного
движения накапливается и расходуется
за счет двух принципиально различных
потоков энергии – работы и теплообмена.
Причем, в количественном отношении обе
формы потока энергии могут даже
компенсировать друг друга. Так, возможен
процесс, когда теплоприток, поступающий
к системе, совпадает по величине с
работой системы, направленной во внешнюю
среду: Q = L. В таком процессе согласно
первому закону внутренняя энергия
системы будет оставаться неизменной,
U₂=U₁, но неизменной только в
количественном отношении. Изменения,
конечно, неизбежны, но уже в отношении
качества внутренней энергии. А именно,
может и должен изменяться характер
внутримолекулярного и межмолекулярного
движения как носителя внутренней
энергии. Что понимается под изменением
качества внутренней энергии, следует
из теоретической физики. Там выясняется,
что наблюдаемое равновесное состояние
термодинамической системы (еемакросостояние) на самом деле есть
непрерывная хаотичная последовательность
огромного множества отличающихся друг
от другамикросостояний – мгновенной
совокупности значений энергии каждой
из множества частиц. Эти микросостояния
(кадры) непрерывно чередуются в пределах
данного макросостояния вследствие
переноса энергии между движущимися
частицами при их столкновениях, вообще
при их взаимодействиях. В силу принципа
квантования энергии численность
микросостояний (отличающихся кадров)
выражается хотя и очень большим, но
конечным числом. Это число микросостояний
напрямуюне связано ни одним из выше
рассмотренных параметров и функций
равновесного состояния системы.Следовательно, оно само является
самостоятельным параметром или функцией
равновесного состояния термодинамической
системы, определяякачествоее
внутренней энергии. При совершении
равновесной работы (адиабатный процесс)
число микросостояний не меняется, при
теплообмене – меняется. Для отображения
этого числа в термодинамике предусмотрена
специальная величина – удельная энтропия.Ее обозначение – s, единица измерения –
кДж/кг/К. Соответственно

S = s.m , кДж/ К

– энтропиясистемы массой m.

В таблицах термодинамических
свойств рабочих тел удельная энтропия
s представлена наряду с энтальпией как
функция каких-либо двух термических
параметров состояния, обычно температуры
и давления.

В курсах физики и в классических
руководствах по термодинамике приводится
несколько способов доказательства, что
удельный тепловой поток dqв случае равновесного процесса связан
с изменением удельной энтропииdsсистемы равенством

dq = T ds, (1-6)

где Т – абсолютная термодинамическая
температура, выраженная вкельвинах,s– удельная энтропия,
кДж/кг/К.

Видно, что энтропия не меняется (ds=0)
в равновесном адиабатном процессе, приdq=0.

Отсюда уравнение первого закона для
одного кг закрытой системы принимает
вид

Tds=du+pdv.
(1-7)

Его
называют основным уравнением термодинамики
для равновесных процессов. Эти уравнения
открывают дорогу к вычислениям в случаях,
когда в закрытой системе задан равновесный
процесс, например, изотермический,
изобарный или др., и известны
термодинамические свойства рабочего
тела в каждом состоянии, через которое
проходит процесс.

Равенство (1-6) позволяет универсальным
способом вычислять тепловые потоки в
любых равновесных процессах, лишь бы
была известна зависимость между
температурой и энтропией процесса.
Действительно, для произвольногоравновесногопроцесса из состояния
1 в состояние 2 удельный теплоприток
определится формулой общего вида

q=Tds.

В частном случае равновесного
изотермического процесса (Т = const) имеем

q=T(s₂-s₁).
(1-8)

Содержание:

Работа в термодинамике:

В 9 классе вы узнали, что работа силы (механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. Работу силы рассматривают как меру изменения энергии физической системы. А как определить работу в термодинамике? Как может быть выражена эта работа через макроскопические параметры — давление и об1

Рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, закрытом подвижным поршнем (рис. 52).

Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением р, которое газ оказывает на них. Допустим, что в результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние

Модуль силы давления газа, действующей на поршень, F = pS. Эта сила совершает работу по перемещению поршня

 (10.1)

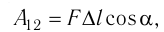
где а — угол между направлениями силы и перемещения. В рассматриваемом примере а = 0, тогда

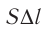
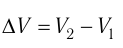
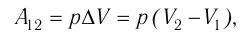
Произведение определяет приращение объёма (см. рис. 52), поэтому работа газа при его изобарном расширении

 (10.2)

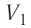
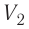
где — начальный объём газа, — объём газа в конечном состоянии.

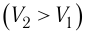
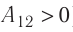
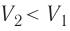
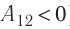
Так как давление р газа всегда величина положительная, из формулы (10.2) следует, что, если газ расширяется , работа, совершённая силой давления газа, положительная (), а в случае сжатия () работа отрицательная ().

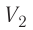
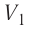
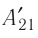
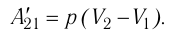
Процесс медленного изобарного сжатия газа из состояния 2 с начальным объёмом в состояние 1 с конечным объёмом можно характеризовать работой внешних сил над газом:
 (10.З)

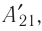
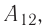
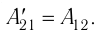
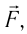
Из сравнения равенств (10.2) и (10.3) вытекает соотношение между работой у совершённой внешними силами, и работой совершённой силой давления газа:Это соотношение согласуется с третьим законом Ньютона (внешняя сила действующая на газ со стороны поршня, имеет
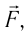
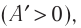
направление, противоположное силе давления действующей на поршень со стороны газа). Из формулы (10.3) видно, что работа, совершённая внешними силами, положительная если происходит сжатие газа
Если газ расширяется 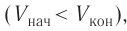), то работа, совершённая внешними силами отрицательная

Геометрическое толкование работы

Построим график зависимости давления газа от его объёма при р = const. Как видно из рисунка 53, при изобарном расширении газа работа, совершённая силой давления газа, численно равна площади прямоугольника

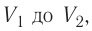
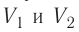
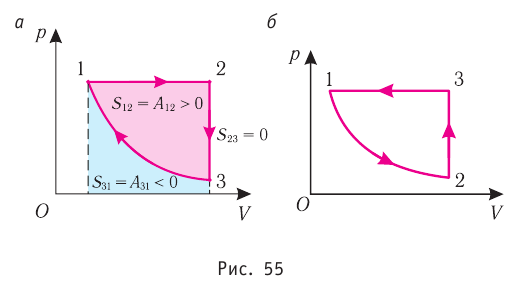
Если процесс перехода газа из начального состояния в конечное не является изобарным, то работа, совершённая силой давления газа при изменении его объёма от численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов (рис. 54).

Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, снова возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 55). Работа, совершаемая системой при циклическом процессе, или работа цикла, равна площади фигуры, ограниченной линиями, которые изображают цикл:

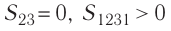
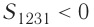
где на рисунке 55, а и на рисунке 55, б.

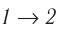
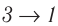
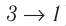
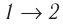
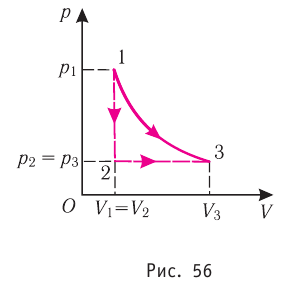
Если «кривая расширения» (изобара) (см. рис. 55, а) расположена выше «кривой сжатия» (изотерма ), то полная работа, совершённая системой за цикл (работа цикла), положительная. Если же, как изображено на рисунке 55, б, «кривая сжатия» (изобара ) расположена выше «кривой расширения» (изотерма), то работа цикла отрицательная.

Из рисунка 56 видно, что численное значение работы цикла определяется не только начальным и конечным состояниями системы, но и видом процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения, либо сначала изохорно понизив его давление до значения а затем изобарно увеличив его объём от значения до значения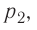

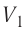
Как видно из рисунка 56, в первом случае работа, совершённая силами давления газа, больше, чем во втором. Следовательно, работа, совершаемая при переходе термодинамической системы из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.

Количество теплоты и удельная теплоёмкость

Итак, существуют два способа передачи энергии от одного тела к другому. Первый характеризуется передачей энергии в процессе механического взаимодействия тел — механическая энергия одного тела переходит в энергию хаотического движения частиц вещества другого тела или, наоборот, убыль энергии хаотического движения частиц вещества одного тела сказывается на увеличении механической энергии другого тела. Такую форму передачи энергии в термодинамике (как и в механике) называют работой. Так, например, в рассмотренной нами ранее термодинамической системе (газ в цилиндрическом сосуде под поршнем) расширение газа приводит к перемещению поршня. При этом убыль внутренней энергии газа равна работе, совершённой силой давления газа, под действием которой поршень переместился.

Второй способ передачи энергии осуществляется при непосредственном обмене энергией между хаотически движущимися частицами взаимодействующих тел. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей энергии частицам более холодного тела. В результате внутренняя энергия первого тела уменьшается, а второго тела увеличивается. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей. Как вы уже знаете, существуют три вида теплопередачи: теплопроводность, конвекция и излучение.

Количественной мерой энергии, переданной телу в процессе теплопередачи, является количество теплоты Q. В СИ единицей количества теплоты является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию (1 кал = 4,19Дж).

Если процесс теплопередачи не сопровождается изменением агрегатного состояния вещества, то
 (10,4)
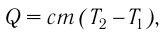
где m — масса тела, 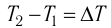— разность температур в конце и в начале процесса теплопередачи, с — удельная теплоёмкость вещества — физическая величина, численно равная количеству теплоты, которое получает или отдаёт вещество массой 1 кг при изменении его температуры на 1 К. Удельную
теплоемкость измеряют в джоулях, деленных на килограмм, кельвин
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкости тела. Обозначают теплоёмкость тела С и измеряют в джоулях на кельвин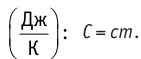Теплоёмкость, в отличие от удельной теплоёмкости, является тепловой характеристикой тела, а не вещества.
 

Удельная теплота плавления

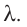
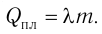
Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления Для плавления тела массой m, предварительно нагретого до температуры плавления, ему необходимо сообщить количество теплоты При кристаллизации тела выделяется количество теплоты

Удельная теплота парообразования

Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Количество теплоты, необходимое для превращения жидкости массой m, предварительно нагретой до температуры кипения, в пар, определяют по формуле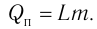Конденсация пара сопровождается выделением количества теплоты

Удельная теплота сгорания топлива

Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания топлива q. Количество теплоты, выделившееся при полном сгорании некоторой массы m топлива, определяют по формуле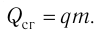Оно передаётся телам, образующим термодинамическую систему, и по отношению к ним является положительной величиной.

Отметим, что в результате теплопередачи могут изменяться как обе составляющие внутренней энергии тела, так и одна из них. При нагревании (охлаждении) изменяются кинетическая энергия хаотического движения частиц, которые составляют тело, и потенциальная энергия их взаимодействия. При плавлении (кристаллизации), кипении (конденсации) изменяется только потенциальная энергия взаимодействия частиц вещества.

При совершении работы также может изменяться как кинетическая, так и потенциальная энергия частиц вещества. Следовательно, как при теплопередаче, так и при совершении работы происходит изменение кинетической и потенциальной энергий частиц вещества, что приводит к изменению внутренней энергии тела.

1. Работу газа при изобарном процессе выражают через макроскопические параметры термодинамической системы:

2.    Работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёмов

3.    Работа, совершаемая при переходе системы из одного состояния в другое, зависит не только от начального и конечного состояний, но и от вида процесса.

4.    Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей.

Пример №1

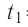
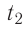
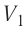
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от = 12 °С до = 87 °С, если давление газа и его начальный объём соответственно p=190кПа и = 6,Одм’5.

Дано:

Пример №2

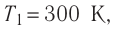
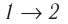
Состояние идеального газа, взятого в количестве v=l,0 моль при температуре изменяется так, как показано на рисунке 57. Определите работу газа в ходе всего процесса, если на изохоре его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.

Дано:

v = 1,0 моль

= 300 к

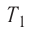
А — ?

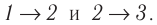
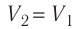
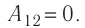
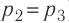
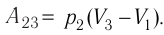
Решение. Работа Л газа в ходе всего процесса равна сумме работ на участках Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный ), то работа газа . Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным ()следовательно, работа газа Тогда
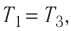
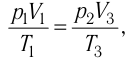
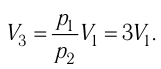
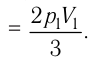
Так как по условию то воспользуемся уравнением Клапейрона (5.2):

откуда  Следовательно,
Согласно уравнению Клапейрона—Менделеева

Тогда

Ответ: А = 1,7 кДж.

Работа в термодинамике

В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.

Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.

Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.

Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.

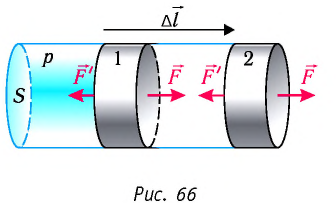
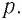
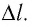
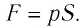
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре В результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние Модуль силы давления газа  на поршень Эта сила совершила работу по перемещению поршня, равную    

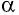
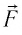
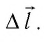
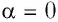
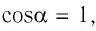
где — угол между направлениями силы  и перемещения поршня Поскольку в рассматриваемом примере и то

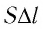
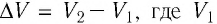
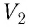
Произведение  определяет изменение объёма  — начальный объём газа; — объём газа в конечном состоянии (см. рис. 66).

Таким образом, работа силы давления газа при его изобарном расширении:

Так как давление р газа — величина положительная, то из формулы (12.1) следует, что

При изобарном расширении газа из состояния 1 в состояние 2 работа силы 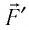(см. рис. 66):

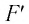
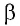
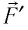
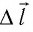
где — модуль силы, действующей на газ со стороны поршня (внешняя сила); — угол между направлениями силы и перемещения поршня.

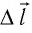
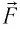
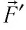
Перемещение поршня одно и то же, а сила давления газа на поршень и сила давления поршня на газ — силы, подчиняющиеся третьему закону Ньютона:

Следовательно, работы 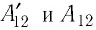отличаются только знаком

Таким образом, можно сделать следующие выводы.

 

Геометрическое толкование работы:

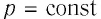
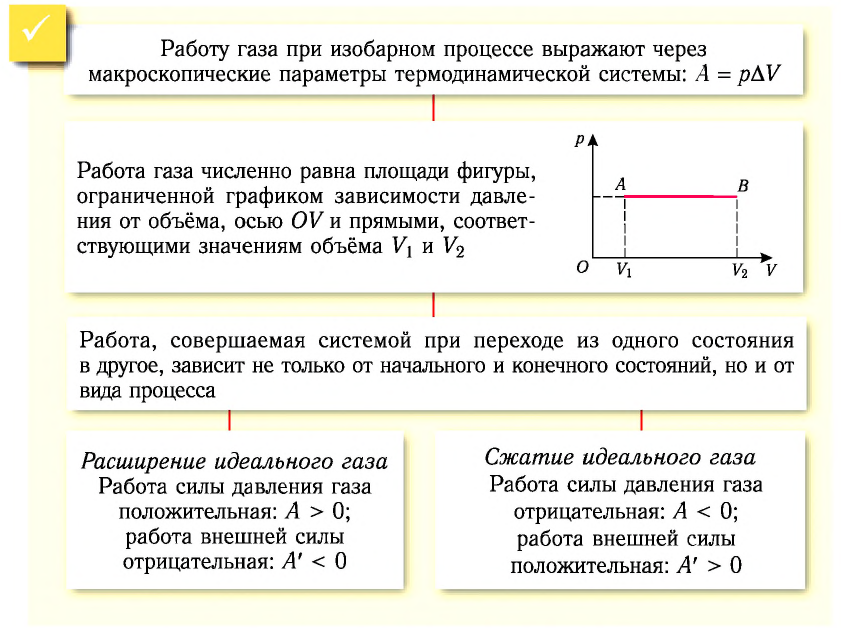
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при (рис. 68). Если процесс перехода газа из начального состояния в конечное является изобарным (АВ — изобара), то работа силы давления газа численно равна площади прямоугольника 

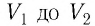
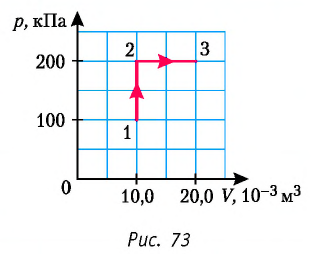
Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от численно равна площади фигуры, ограниченной графиком процесса (кривая 1—2), осью OV и прямыми, соответствующими значениям объёмов 

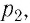
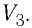
Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения а затем изобарно увеличив его объём до значения В первом случае работа газа больше, чем во втором.

Следовательно, работа, совершаемая термодинамическом системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.

Пример №3

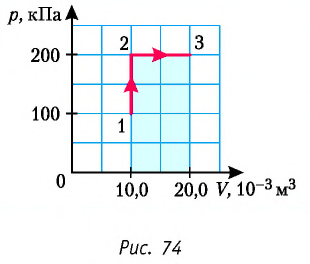
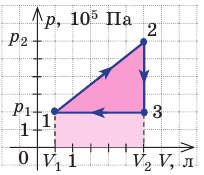
Определите работу, совершаемую силой давления идеального газа определённой 200 массы при переходе из состояния 1 в состояние 3 (рис. 73).   

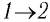
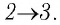
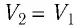
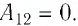
Решение. 1 способ. Работа А газа в ходе всего процесса равна сумме работ на участках и Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс ), то работа, совершаемая силой давления газа, В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу

Тогда при переходе из состояния 1 в состояние 3 работа

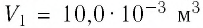
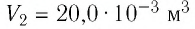
2 способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёма и (закрашенная область на рисунке 74).

Ответ:

Пример №4

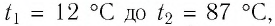
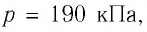
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от если давление газа а его начальный объём

Решение. Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому

Согласно уравнению Клапейрона—Менделеева,
Следовательно,

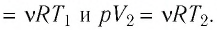
Ответ:

Как определить работу в термодинамике

В конце XVIII в. английский физик Бенджамин Томпсон (граф Румфорд) исследовал тепло, выделяющееся при сверлении бронзовых пушек. Румфорд успевал вскипятить поставленные на пушки котлы с водой за счет тепла, которое выделялось, пока лошади приводили в движение очень тупое сверло. В данном случае энергия механического движения сверла превращалась в энергию хаотического движения молекул бронзы и воды. А можно ли сделать наоборот?

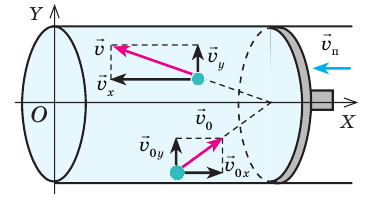
Почему при изменении объема газа изменяется его внутренняя энергия

Внутренняя энергия газа может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ сжимают (газ совершает отрицательную работу) (рис. 37.1) и он при этом не отдает энергию окружающей среде, то скорость движения молекул газа, а соответственно, и внутренняя энергия, и температура газа увеличиваются. И наоборот: если газ расширяется (то есть совершает положительную работу), то скорость движения молекул, температура и внутренняя энергия газа уменьшаются.

Рис. 37.1. При сжатии газа скорость его молекул после столкновения с поршнем увеличивается (v > 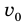) — газ нагревается. (Аналогично увеличивается скорость мяча после удара волейболиста, когда его рука движется навстречу мячу.)

Как вычислить работу газа

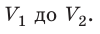
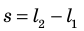
Вычислим работу, которую совершает сила давления газа при изменении его объема от По определению работы: A=Fscosα. Если газ расширяется изобарно, то сила, действующая со стороны газа на поршень, постоянна: F=pS (p — давление газа; S — площадь поршня); модуль перемещения поршня (рис. 37.2, а); α = 0.

Таким образом, работа газа при его изобарном расширении равна:

Работе газа при изобарном расширении (или сжатии) можно дать простое геометрическое толкование: работа газа численно равна площади прямоугольника под графиком зависимости p(V) (рис. 37.3).

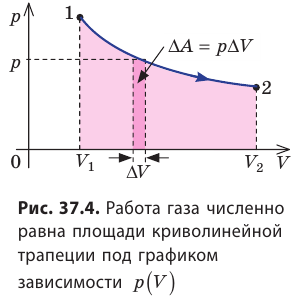
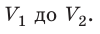
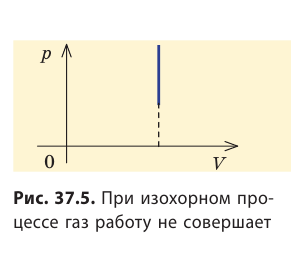
Пусть некоторый газ переходит из состояния 1 в состояние 2 (рис. 37.4). Если изменение объема газа (∆V) достаточно мало, то давление газа можно считать неизменным. Тогда работа газа численно равна площади выделенной на рисунке полосы. Полная работа при изменении объема от будет равна сумме площадей всех полос, то есть площади криволинейной трапеции под графиком зависимости p (V).

Очевидно, что при изохорном процессе (V = const) площадь фигуры под графиком зависимости p (V) равна нулю (рис. 37.5), — газ работу не совершает (A = 0) . Работа газа зависит от того, каким образом происходил переход газа из начального состояния в конечное (рис. 37.6).

Рис. 37.6. три пути перехода газа из состояния 1 в состояние 2: а — газ изобарно расширяется (участок 1k), затем изохорно охла ждается (участок k2); б — газ изотермически расширяется; в — газ изохорно охлаждается (участок 1l), затем изобарно расширяется (участок l2). сравнив площади фигур под графиками, видим, что:

Пример №5

На рисунке графически изображен циклический процесс, совершаемый идеальным газом. Определите работу газа за цикл.

Решение:

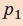
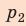
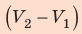
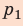
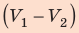
Полная работа за цикл равна сумме работ, совершенных газом в ходе каждого процесса цикла. Работа газа в ходе процесса 1–2 численно равна площади трапеции, основания которой равны и , а высота — ; объем газа увеличивается, поэтому работа газа положительна. Работа газа в ходе процесса 2–3 равна нулю, поскольку этот процесс изохорный. Работа газа в ходе процесса 3–1 численно равна площади прямоугольника со сторонами и ; объем газа уменьшается, поэтому работа отрицательна. Следовательно, для определения работы за весь цикл нужно из площади трапеции вычесть площадь прямоугольника. То есть, как видно из рисунка, работа газа за цикл численно равна площади прямоугольного треугольника 1–2–3:

Выводы:

• При отсутствии теплообмена с окружающей средой, если над газом совершают работу, внутренняя энергия газа увеличивается; если газ сам совершает работу, его внутренняя энергия уменьшается.
• Если объем газа увеличивается, то газ совершает положительную работу. Если объем газа уменьшается, то работа газа отрицательна.
• Работа газа численно равна площади фигуры под графиком зависимости p (V). При изобарном процессе работу газа можно определить по формуле A=p∆V, при изохорном процессе работа газа равна нулю: A = 0.

Цель урока:

• обобщить и закрепить ключевые задачи по теме;
• научиться работать с теоретическими вопросами
  темы;
• научиться применять интеграл к решению
  физических задач.

План урока:

1. Схема решения задач на приложения
определенного интеграла
2. Нахождение пути, пройденного телом при
прямолинейном движении
3. Вычисление работы силы, произведенной при
прямолинейном движении тела
4. Вычисление работы, затраченной на растяжение
или сжатие пружины
5. Определение силы давления жидкости на
вертикально расположенную пластинку

Тип урока: интегрированный.

Воспитательная работа: расширение
кругозора и познавательной деятельности
учащихся, развитие логического мышления и умения
применять свои знания.

Техническое обеспечение:
интерактивная доска. Компьютер и диск.

Приложение: «Рапсодия
природы».

ХОД УРОКА

I. Организационный момент

II. Постановка цели урока

– Урок хотелось бы провести под девизом
Готфрида Вильгельма Лейбница – немецкого философа,
логика,
математика,
физика:
«Общее искусство знаков представляет чудесное
пособие, так как оно разгружает воображение…
Следует заботиться о том, чтобы обозначения были
удобны для открытий. Обозначения коротко
выражают и отображают сущность вещей. Тогда
поразительным образом сокращается работа
мысли».

III. Повторим основные понятия и
ответим на вопросы:

– Скажите основное определение интеграла?
– Что вы знаете о интеграле (свойства, теоремы)?
– Знаете ли вы какие-нибудь примеры задач с
применением интеграла?

IV. Объяснение нового материала
(рассмотрение теории):

1. Схема решения задач на приложения
определенного интеграла

С помощью определенного интеграла можно решать
различные задачи физики, механики и т. д., которые
трудно или невозможно решить методами
элементарной математики.

Так, понятие определенного интеграла
применяется при решении задач на вычисление
работы переменной силы, давления жидкости на
вертикальную поверхность, пути, пройденного
телом, имеющим переменную скорость, и ряд других.

Несмотря на разнообразие этих задач, они
объединяются одной и той же схемой рассуждений
при их решении. Искомая величина (путь, работа,
давление и т. д.) соответствует некоторому
промежутку изменения переменной величины,
которая является переменной интегрирования. Эту
переменную величину обозначают через Х, а
промежуток ее изменения – через [а, b].

Отрезок [a, b] разбивают на n равных частей, в
каждой из которых можно пренебречь изменением
переменной величины. Этого можно добиться при
увеличении числа разбиений отрезка. На каждой
такой части задачу решают по формулам для
постоянных величин.

Далее составляют сумму (интегральную сумму),
выражающую приближенное значение искомой
величины. Переходя к пределу при , находят искомую величину
I в виде интеграла

I = , где f(x)
– данная по условиям задачи функция (сила,
скорость и т. д.).

2. Нахождение пути, пройденного телом при
прямолинейном движении

Как известно, путь, пройденный телом при
равномерном движении за время t, вычисляется по
формуле S = vt.

Если тело движется неравномерно в одном
направлении и скорость его меняется в
зависимости от времени t, т. е. v = f(t), то для
нахождения пути, пройденного телом за время от до , разделим этот
промежуток времени на n равных частей Δt. В каждой
из таких частей скорость можно считать
постоянной и равной значению скорости в конце
этого промежутка. Тогда пройденный телом путь
будет приблизительно равен сумме , т.е.

Если функция v(t) непрерывна, то

Итак,

3. Вычисление работы силы, произведенной
при прямолинейном движении тела

Пусть тело под действием силы F движется по
прямой s, а направление силы совпадает с
направлением движения. Необходимо найти работу,
произведенную силой F при перемещении тела из
положения a в положение b.

Если сила F постоянна, то работа находится по
формуле
(произведение силы на длину пути).

Пусть на тело, движущееся по прямой Ох,
действует сила F, которая изменяется в
зависимости от пройденного пути, т. е. . Для того чтобы найти
работу, совершаемую силой F на отрезке пути от а
до b, разделим этот отрезок на n равных частей
. Предположим,
что на каждой части сила сохраняет постоянное значение

Составим интегральную сумму, которая
приближенно равна значению произведенной
работы:

т.е. работа, совершенная этой силой на участке
от а до b, приближенно мала сумме:

Итак, работа переменной силы вычисляется по
формуле: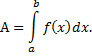

4. Вычисление работы, затраченной на
растяжение или сжатие пружины

Согласно закону Гука, сила F, необходимая для
растяжения или сжатия пружины, пропорциональна
величине растяжения или сжатия.

Пусть х – величина растяжения или сжатия
пружины. Тогда ,
где k – коэффициент пропорциональности,
зависящий от свойства пружины.

Работа на участке выразится формулой , а вся затраченная работа или . Если то погрешность величины
работы стремится к нулю.

Для нахождения истинной величины работы
следует перейти к пределу

Итак,

5. Определение силы давления жидкости на
вертикально расположенную пластинку

Из физики известно, что сила Р давления
жидкости на горизонтально расположенную
площадку S, глубина погружения которой равна h,
определяется по формуле:

, где – плотность жидкости.

Выведем формулу для вычисления силы давления
жидкости на вертикально расположенную пластинку
произвольной формы, если ее верхний край
погружен на глубину a, а нижний – на глубину b.

Так как различные части вертикальной пластинки
находятся на разной глубине, то сила давления
жидкости на них неодинаковa. Для вывода формулы
нужно разделить пластинку на горизонтальных
полос одинаковой высоты . Каждую полосу приближенно
можно считать прямоугольником (рис.199).

По закону Паскаля сила давления жидкости на
такую полосу равна силе движения жидкости на
горизонтально расположенную пластинку той же
площади, погруженной на ту же глубину.

Тогда согласно формуле (4) сила давления на
полосу, находящуюся на расстоянии х от
поверхности, составит , где
– площадь полосы.

Составим интегральную сумму и найдем ее предел,
равный силе давления жидкости на всю пластинку:

т.е.

Если верхний край пластинки совпадает с
поверхностью жидкости, то а=0 и формула (5) примет
вид

Ширина каждой полосы зависит от формы
пластинки и является функцией глубины х
погружения данной полосы.

Для пластинки постоянной ширины формула (5)
упрощается, т.к. эту постоянную можно вынести за
знак интеграла:

V. Разбор задач по теме

1) Скорость движения материальной точки
задается формулой = (4 м/с.
Найти путь, пройденный точкой за первые 4с от
начала движения.

Решение:

2) Скорость движения изменяется по закону м/с . Найти длину
пути, пройденного телом за 3-ю секунду его
движения.

Решение:

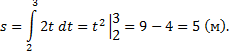
3) Скорость движения тела задана уравнением м/с. Определить
путь, пройденный телом от начала движения до
остановки.

Решение:

Скорость движение тела равна нулю в момент
начала его движения и остановки. Найдем момент
остановки тела, для чего приравняем скорость
нулю и решим уравнение относительно t; получим

Следовательно,

4) Тело брошено вертикально вверх со скоростью,
которая изменяется по закону м/с. Найти наибольшую высоту
подъема.

Решение:

Найдем время, в течении которого тело
поднималось вверх: 29,4–9,8t=0 (в момент наибольшего
подъема скорость равна нулю); t = 3 с. Поэтому

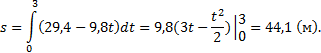
5) Какую работу совершает сила в 10Н при
растяжении пружины на 2 см?

Решение:

По закону Гука сила F, растягивающая пружину,
пропорциональна растяжению пружины , т.е. F = kx.
Используя условие, находим (Н/м), т.е. F = 500x. Получаем

6) Сила в 60Н растягивает пружину на 2 см.
Первоначальная длина пружины равна 14 см. Какую
работу нужно совершить, чтобы растянуть ее до 20
см?

Решение:

Имеем (H/м) и,
следовательно, F=3000x. Так как пружину требуется
растянуть на 0,06 (м), то

7) Определить силу давления воды на стенку
шлюза, длина которого 20 м, а высота 5 м (считая шлюз
доверху заполненным водой).

Здесь y = f(x) = 20, a = 0, b = 5 м, кг/.

Находим

8) В воду опущена прямоугольная пластинка,
расположенная вертикально. Ее горизонтальная
сторона равна 1 м, вертикальная 2 м. Верхняя
сторона находится на глубине 0,5 м. Определить
силу давления воды на пластинку.

Решение:

Здесь y = 1, a = 0,5, b = 2 + 0,5 = 2,5 (м), = 1000 кг/. Следовательно,

9) Скорость прямолинейного движения точки
задана уравнением . Найти уравнение движения точки.

Решение:

Известно, что скорость прямолинейного движения
тела равна производной пути s по времени t, т.е. , откуда ds = v dt.
Тогда имеем

Это искомое уравнение.

10) Скорость тела задана уравнением . Найти уравнение
движения, если за время тело прошло путь .

Решение:

Имеем ds = v dt = (6+ 1) dt; тогда

Подставив в найденное уравнение начальные
условия s = 60 м, t = 3 c, получим

откуда С = 3.

Искомое уравнение примет вид

11) Тело движется со скоростью м/с. Найти закон движения s(t),
если в начальный момент тело находилось на
расстоянии 5 см от начала отсчета.

Решение:

Так как ds = v dt = (, то

Из условия следует, что если t = 0, то s = 5 см = 0,05 м.
подставив эти данные в полученное уравнение,
имеем откуда
0,05 = С.

Тогда искомое уравнение примет вид

12) Вычислить силу давления воды на плотину,
имеющую форму трапеции, у которой верхнее
основание, совпадающее с поверхностью воды,
имеет длину 10 м, нижнее основание 20 м, а высота 3 м.

Решение:

13) Цилиндрический стакан наполнен ртутью.
Вычислить силу давления ртути на боковую
поверхность стакана, если его высота 0,1 м, а
радиус основания 0,04 м. Плотность ртути равна 13600
кг/.

Решение:

Вычислим площадь круглой полоски

Элементарная сила давления составляет

Следовательно

VI. Самостоятельное решение задач на доске,
коллективный разбор решений задач:

1. Скорость движения тела задана уравнением . Найти уравнение
   движения, если в начальный момент времени
2. Найти уравнение движения точки, если к моменту
   начала отсчета она прошла путь , а его скорость задана
   уравнением
3. Скорость движения тела пропорциональна
   квадрату времени. Найти уравнение движения тела,
   если известно, что за 3 с оно прошло 18 м.
4. Тело движется прямолинейно со скоростью м/с. Найти путь,
   пройденный телом за 5 с от начала движения.
5. Скорость движения тела изменяется по закону м/с. Найти путь,
   пройденный телом за 4 с от начала движения.
6. Найти путь пройденный телом за 10-ю секунду, зная,
   что что скорость его прямолинейного движения
   выражается формулой м/с.
7. Найти путь, пройденный точкой от начала
   движения до ее остановки, если скорость ее
   прямолинейного движения изменяется по закону м/с.
8. Какую работу совершает сила в 8 Н при растяжении
   пружины на 6 см?
9. Сила в 40 Н растягивает пружину на 0,04 м. Какую
   работу надо совершить, чтобы растянуть пружину
   на 0,02 м?
10. Вычислить силу давления воды на вертикальную
    прямоугольную пластинку, основание которой 30 м, а
    высота 10 м, причем верхний конец пластинки
    совпадает с уровнем воды.
11. Вычислить силу давления воды на одну из стенок
    аквариума, имеющего длину 30 см и высоту 20 см.

VII. Минутка релаксации

Запуск приложения «Минутка
релаксации»

VIII. Подведение итогов урока:

– Каким вопросам был посвящен урок?
– Чему научились на уроке?
– Какие теоретические факты обобщались на уроке?
– Какие рассмотренные задачи оказались наиболее
сложными? Почему?

Список литературы:

1. Журнал «Потенциал»
2. «Алгебра и начала анализа» 11 класс С.М.
   Никольский, М.К. Потапов и др.
3. «Алгебра и математический анализ» Н.Я. Виленкин
   и др.
4. «Учебник по математическому анализу» Град О.Г.,
   Змеев О.А.
5. «Высшая математика: Учебник для вузов». В 3
   томах. Бугров Я.С. Никольский С.М.
6. «Математический анализ». Е.Б. Боронина

1