Парашютист массой 80 килограмм спрыгнул с неподвижно висящего вертолета и, пройдя до раскрытия парашюта путь 200 метров, приобрел скорость 50 метров в секунду.
Найти работу силы сопротивления воздуха на этом пути.
Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000
Решения задачи
Данные задачи: парашютист пролетел не раскрывая парашюта
| Масса парашютиста | m | 80 | кг |
|---|---|---|---|
| Путь парашютиста | S=h | 200 | м |
| скорость парашютиста | $v_{200}$ | 50 | м |
| Работа силы сопротивления воздуха на этом пути. | $W_{сопр}$ | ? |
Составляем уравнение силы тяжести и силы сопротивления воздух
$W=FS=maS=m(g-b)h$
откуда результируещее ускорение от силы тяжести и от силы сопр.воздуха
$a=g-b$
в то же время
$S=(g-b)t^2=200 м$
и
$v_{200}=(g-b)t=50 м/с$
время падения
$t=frac{S}{v_{200}}=frac{200}{50}=4 с$
Ускорение от силы сопротивления воздуха
$b=frac{v_{200}-gt}{t}=frac{50-9,81×4}{4}=2,69frac{м}{с^2}$
Работа силы сопротивления воздуха
$W_сопр=mbS=4×2,69×200=2152 Дж$
Ответ:
$ Работа силы сопр. воздуха равна 2152 Дж. $
Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь
Работа, проделанная в сопротивление воздуха заключается в смещении или сопротивлении движению объекта. Остановимся подробнее на том, как над объектом совершается работа сопротивлением воздуха.
Работа, совершаемая сопротивлением воздуха, равна сила трения который сопротивляется движению объекта, поскольку он ощущается в направлении, противоположном движению. Сопротивление воздуха в основном отвечает за снижение кинетической энергии объекта; таким образом, совершается работа по увеличению его время полета в воздухе.
Далее мы подробно обсудим работу, совершаемую сопротивлением воздуха, положительную или отрицательную, и как ее вычислить, как она влияет на сопротивление воздуха, влияет ли сопротивление воздуха на силу тяжести и гравитационную силу тел, а также работу за счет сопротивления воздуха при свободном падении.
Какая работа совершается при сопротивлении воздуха?
Сопротивление воздуха – это сила сопротивления, действующая на объект из-за воздуха. Здесь мы более подробно обсудим работу, совершаемую при сопротивлении воздуха.
Работа сопротивления воздуха изменяет скорость тела при прохождении через столб воздуха. Воздух представляет собой текучую среду, состоящую из атомов и молекул. Когда объект протаскивается через эту среду из-за гравитации и кинетической энергии, эти молекулы воздействуют на объект силой, которая сопротивляется скорости объекта.
Работа, совершаемая сопротивлением воздуха, положительна или отрицательна?
Совершенная работа определяет мощность силы сопротивления воздуха, действующую на объект. Давайте обсудим, положительное оно или отрицательное.
Работа, совершаемая сопротивлением воздуха, может быть положительной или отрицательной в зависимости от его скорости и кинетической энергии объекта. Работа, совершаемая над объектом, является следствием его движения, а не объема воздуха. Сила трения о воздух создается частицей истирание.
Влияет ли на работу сопротивление воздуха?
Сопротивление воздуха в основном ощущается всеми объектами, движущимися по воздуху. Обсудим, как сопротивление воздуха влияет на общую работу системы.
На работу влияет сопротивление воздуха, если сила сопротивления воздуха велика и совершенная работа положительна. Работа сопротивления воздуха положительна, если дующий с большой скоростью воздух увлекает тело со своего пути. Сопротивление воздуха приводит к изменению импульса объекта, что влияет на общую работу.
Как рассчитать работу сопротивления воздуха?
Существуют различные параметры, на которые влияет общая работа силы сопротивления воздуха. Научимся рассчитывать работу сил сопротивления воздуха.
Работа, совершаемая сопротивлением воздуха, рассчитывается как произведение силы трения на расстояние, пройденное телом при сопротивлении воздуха, как W = Fd, где F — сила сопротивления воздуха. Это изменение потенциальной энергии объекта, сформулированное как W = ∆E, где ∆E — изменение энергии.

Влияет ли сопротивление воздуха на работу силы тяжести?
Гравитация влияет на сопротивление воздуха. Давайте посмотрим, влияет ли сопротивление воздуха, которое, в свою очередь, на работу силы тяжести или нет, подробно.
Сопротивление воздуха влияет на работу силы тяжести в зависимости от объема и скорости воздуха. Хотя напряженность гравитационного поля постоянна для всех объектов, сопротивление воздуха меняется в зависимости от массы объекта. Объекты, обладающие меньшей гравитационной потенциальной энергией, меньше ощущают силу сопротивления воздуха.
Работа, проделанная сопротивлением воздуха в свободном падении
Объект сразу падает вниз, преобразуя свой потенциал в кинетическую энергию во время свободного падения. Обсудим, как действует сопротивление воздуха на объект при его свободном падении.
Работа сопротивления воздуха при свободном падении равна произведению смещения тела на силу тяжести. Во время свободного падения при максимальной амплитуде объекта гравитационная сила становится равной силе сопротивления воздуха, ощущаемой на объекте, и остается неподвижной в течение нескольких миллисекунд.
Часто задаваемые вопросы
Какова работа сопротивления воздуха, совершаемая волейбольным мячом в воздухе при силе сопротивления воздуха 13 Н на пути 30 м?
Выражение для расчета работы, совершаемой сопротивлением воздуха, имеет вид W= Fd.
Работа, совершаемая на волейбольном мяче сопротивлением воздуха, равна 390 Дж. Принято, что F = 13 Н, а d = 30 м. Отсюда W = 13 Н × 30 м = 390 Дж.
Как зависит сила сопротивления воздуха от площади поверхности тела?
Сопротивление воздуха напрямую зависит от площади поверхности объекта. Сила сопротивления воздуха больше для большой площади поверхности объекта, поскольку она дает больше поверхности для воздействия воздушной силы.
Одинакова ли сила сопротивления воздуха для всех тел?
Сопротивление воздуха не одинаково для всех тел, движущихся в одной и той же среде. Это связано с тем, что площадь поверхности и конфигурация каждого объекта могут различаться, и, следовательно, воздух, оказывающий сопротивление воздуха, различается.
Испытывают ли тяжелые предметы большую силу сопротивления, чем более легкие предметы?
Тяжелые объекты движутся в воздухе быстрее, чем более легкие; следовательно, тяжелые объекты испытывают большую силу сопротивления, чем более легкие объекты.
Может ли сопротивление воздуха для двух тел быть одинаковым?
Сопротивление воздуха для двух объектов может быть одинаковым при условии, что два объекта имеют одинаковую плотность и площадь поверхности.
Заключение
Работа, совершаемая сопротивлением воздуха, отрицательна и может быть положительной, если скорость воздуха против направления движения объекта достаточно высока, чтобы изменить его импульс. Сила сопротивления воздуха зависит от скорости, плотности, массы и гравитации.
Узнайте больше о Потери энергии на сопротивление воздуха.
Узнайте больше о Сопротивление воздуха и гравитация.
Определение силы сопротивления в физике и её формула
Содержание:
-
Что такое сила сопротивления в физике
- От чего зависит в механике и динамике
-
Разновидности сил сопротивления
- Сила сопротивления качению
- Сила сопротивления воздуха
- Как найти трение
- Силы сопротивления при больших скоростях
Что такое сила сопротивления в физике
Сила сопротивления — сила, которая возникает во время движения тела в жидкой или газообразной среде и препятствует этому движению.
Важно уметь отличать силу сопротивления от силы трения. Во втором случае рассматривается характер взаимодействия твердых тел друг с другом. Таким образом, трение можно наблюдать, когда какой-либо предмет перемещается по поверхности другого. Вектор этой силы будет направлен в противоположную сторону направления движения.
Для того чтобы рассчитать силу сопротивления необходимо умножить коэффициент сопротивления материала на силу, провоцирующую перемещение этого предмета.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Примечание
В качестве примера силы сопротивления можно рассмотреть движение поезда. Воздух, окружающий состав, замедляет скорость его перемещения, то есть возникает сила сопротивления.
От чего зависит в механике и динамике
Сила сопротивления зависит от нескольких факторов. На ее величину оказывают влияния следующие характеристики:
- Особенности среды и показатели ее плотности, к примеру, жидкость обладает большей плотностью, чем газообразное вещество.
- Форма тела, так как предметы, обладающие обтекаемыми вытянутыми вдоль направления движения формами подвержены меньшему сопротивлению, чем тела с множеством плоскостей, расположенных перпендикулярно движению.
- Скорость перемещения тела.
Силу сопротивления можно наблюдать опытным путем. К примеру, если предмет переместился на величину пути l , когда на него воздействует сила сопротивления, обозначение которой представлено, как ($$F_{r}$$), затрачивается работа, которую можно рассчитать по формуле:
($$A=F_{r}times l$$)
В случае, когда площадь поперечного сечения движущегося предмета равна S, он будет сталкиваться с частицами, объем которых составляет Sl. Полную массу этих частиц можно представить, как ($$rho_{ a}times Sl$$). Если частицы полностью увлекаются телом, они приобретают скорость V. Кинетическую энергию можно рассчитать по формуле:
($$K=frac{rho_{ a}times Sltimes V^{2}}{2}$$)
Энергию создают внешние силы за счет своей работы с мощностью по определению силы сопротивления. Откуда, A=K. Таким образом,
($$F_{r}=frac{rho_{ a}times Stimes V^{2}}{2}$$)
В этом случае зависимость силы сопротивления от скорости перемещения объекта возрастает и становится пропорциональна ее второй степени. В отличие от силы внутреннего трения ее обозначают, как силу динамического лобового сопротивления.
Следует отметить, что теория, в которой частицы среды полностью увлекаются транспортируемыми телами, преувеличена. В условиях реального времени любой движущийся предмет обтекаем потоком, который снижает воздействие на него сил сопротивления. Поэтому при расчетах нередко используют коэффициент сопротивления С, обозначая силу лобового сопротивления формулой:
($$F_{r}=Ctimes Stimes frac{rho_{ a}times V^{2}}{2}$$)
Разновидности сил сопротивления
Существует несколько типов силы сопротивления, отличающихся по характеру воздействия на движущиеся предметы.
Сила сопротивления качению
Сила сопротивления качению обозначается, как Pf. В данном случае сила определяется несколькими факторами:
- разновидность и состояние опоры, по которой перемещается объект;
- скорость движения тела;
- давление воздуха и другие параметры окружающей среды.
Состояние и тип опорной поверхности определяет величину коэффициента сопротивления качению, который обозначается f. Если в среде повышается температура, и возрастает давление, то данный показатель будет уменьшаться.
Сила сопротивления воздуха
Сила сопротивления воздуха или величина лобового столкновения Pв образуется в результате различных показателей давления. Данная характеристика напрямую зависит от интенсивности вихреобразования спереди и сзади движущегося предмета. Указанные параметры определяются формой перемещающегося тела.
Примечание
Большее влияние на силу сопротивления будет оказывать вихреобразование в передней части объекта. Если плоскостенную фигуру закруглить спереди и сзади, то получится снизить сопротивление до 72%.
Рассчитать силу лобового сопротивления можно по формуле:
($$P=cxtimes ptimes F_{b}$$)
сх — обтекаемость или коэффициент лобового сопротивления; p — плотность воздуха; Fв — площадь лобового сопротивления (миделевого сечения).
Во время поступательного движения масса объекта встречает сопротивление разгону, то есть ускорению. Найти данную силу можно с помощью второго закона Ньютона.
($$Pj=mtimes dVdt$$)
где m выражает массу движущегося объекта, а (dVdt) обозначает ускорение центра масс.
Как найти трение
Определить силу сопротивления можно, если применить третий закон Ньютона. Для того чтобы предмет равномерно перемещался по опоре в горизонтальном направлении, к нему необходимо приложить силу, соизмеримой с силой сопротивления. Корректно рассчитать данные величины можно с помощью динамометра. Сила сопротивления будет прямо пропорциональна массе объекта. Более точные расчеты производятся с учетом u коэффициента, который зависит от следующих факторов:
- материал, из которого изготовлено опорное основание;
- материал, из которого состоит перемещаемое тело.
Рассчитывая силу сопротивления, используют постоянную величину g, равную 9,8 метров на сантиметр в квадрате. При этом если движение тела происходит на определенной высоте, на него оказывает воздействие сила трения воздуха. Данная величина зависит от скорости, с которой движется предмет. Искомая величина определяется с помощью следующей формулы только при условии, что предмет перемещается на небольшой скорости:
($$F=Vtimes a$$)
где V является скоростью перемещения тела, a — коэффициентом сопротивления среды.
Силы сопротивления при больших скоростях
Сила сопротивления, оказывающая воздействие на движущиеся предметы с малой скоростью, зависит от нескольких внешних факторов. К таким условиям относятся:
- вязкость жидкости;
- скорость перемещения тела;
- линейные размеры движущегося предмета.
В условиях больших скоростей характер действия силы сопротивления несколько изменяется. Законы вязкого трения в этом случае не применяются для воздуха и воды. Если скорость предмета составляет 1 сантиметр в секунду, то данные факторы учитываются лишь тогда, когда тела обладают крошечными размерами, измеряемыми в миллиметрах.
Примечание
Если пловец ныряет в воду, то на него будет действовать сила сопротивления. Однако в данном случае закон вязкого трения не будет действовать.
Объект, двигаясь с малой скоростью в водной среде, плавно обтекается жидкостью. Сила сопротивления в данном случае будет рассчитываться, как сила вязкого трения. Если скорость большая, то с задней части перемещающегося тела наблюдается более сложное движение жидкости с образованием необычных по форме фигур, вихрей, колец. Картина таких струек будет постоянно изменяться. Движение такого характера называется турбулентным. Турбулентное сопротивление все еще будет определяться скоростью и размерами тела, но не так, как при вязком сопротивлении. В данном случае сила рассчитывается пропорционально квадрату скорости и линейным размерам предмета. Вязкость водной среды более не имеет решающего значения, определяющая функция переходит к показателю плотности.
Сила турбулентного сопротивления рассчитывается по формуле:
($$F=ptimes V^{2}times L^{2}$$)
где V обозначает показатели скорости движения, L — соответствует линейным размерам тела, p — равна плотности среды.
где Асп — работа сил поля, Астор — работа сторонних сил. Согласно (4.10), работа сил поля равна убыли потенциальной
энергии частицы: A сп U. Подставив это выражение в предыдущее и перенеся U влево, получим
K U (K U) A стор .
Отсюда видно, что работа сторонних сил идет на приращение K + U. Эту величину — сумму кинетической и потенциальной энергий — называют полной механической энергией частицы в поле и обозначают E:
Заметим, что полная механическая энергия E, как и потенциальная U, определяется с точностью до произвольной постоянной.
Итак, из предыдущих двух уравнений следует, что приращение полной механической энергии частицы в стационарном поле консервативных сил при перемещении ее из точки 1 в точку 2 можно записать в виде
т. е. приращение полной механической энергии частицы на некотором пути равно алгебраической сумме работ всех сторонних сил, действующих на частицу на том же пути. Если
A стор 0, то полная механическая энергия частицы увеличивается, если A стор 0, то уменьшается.
Пример. Тело массы m бросили со скоростью v0 с обрыва высотой h над поверхностью воды. Найдем работу, которую совершила сила сопротивления со стороны воздуха, при условии, что тело упало на поверхность воды со скоростью v.
Если рассматривать движение тела в поле сил тяжести, то сила сопротивления со стороны воздуха будет сторонней и, согласно уравнению (4.31), искомая работа Aстор E2 E1mv 2 /2 (mv02 /2 mgh ) или
Aстор m(v 2 v02 )/2 mgh.
Интересно, что полученная величина может оказаться не только отрицательной, но и положительной (это зависит, например, от характера ветра в процессе падения тела).
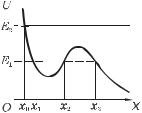
Рис. 4.9
|
Закон сохранения энергии |
111 |
Итак, полная механическая энергия частицы может измениться под действием только сторонних сил. Отсюда непосредственно вытекает закон сохранения механической энергии частицы: если сторонние силы отсутствуют или таковы, что не совершают работы в течение интересующего нас времени, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной за это время:
Уже в такой простейшей форме закон сохранения энергии позволяет достаточно легко получать ответы на ряд важных вопросов без привлечения уравнений движения, что часто сопряжено с проведением громоздких и утомительных расчетов. Именно это обстоятельство и превращает законы сохранения в весьма действенный инструмент исследования.
Проиллюстрируем возможности и преимущества, которые дает применение закона сохранения (4.32), на следующем примере.
Пример. Пусть частица движется в одномерном стационарном поле, где ее потенциальная энергия U(х) 
имеет вид, как на рис. 4.9. Если сторонние силы отсутствуют, то полная механическая энергия час-
тицы в данном поле, т. е. E, не изменяется в процессе движения и можно просто ответить, например, на следующие вопросы.
1. Определить, не решая основного уравнения динамики, скорость частицы в зависимости от ее координаты.
Для этого достаточно знать, согласно уравнению (4.32), конкретный вид потенциальной кривой U(х) и значение полной энергии E.
2. Установить область изменения координаты x частицы, в которой она может находиться при данном значении полной энергии E.
Ясно, что в область, где U>E, частица попасть не может, поскольку потенциальная энергия U частицы не должна превышать ее полную энергию. Отсюда сразу следует, что при E = E1 (рис. 4.9) частица будет двигаться или в области между коор-
динатами x1 и x2 (совершает колебания), или правее координаты x3. Перейти из первой области во вторую (или обратно) частица не может: этому препятствует потенциальный барьер, разделяющий обе области. Заметим, что когда частица движется в ограниченной области поля, то говорят, что она заперта в потенциальной яме (в нашем случае — между x1 и x2).
Иначе ведет себя частица при E = E2 (рис. 4.9): для нее доступна вся область правее координаты x0. Если в начальный момент частица находилась в точке x0, то в дальнейшем она будет двигаться вправо. Полезно самостоятельно проследить, как будет меняться при этом кинетическая энергия частицы
взависимости от ее координаты x.
§4.4. Потенциальная энергия системы
Собственная потенциальная энергия системы
До сих пор мы ограничивались рассмотрением поведения одной частицы с энергетической точки зрения. Теперь перейдем к системе частиц. Это может быть любое тело, газ, какой-то механизм, Солнечная система и т. д. Рассмотрим систему, между частицами которой действуют одни лишь центральные силы,
т.е. силы, зависящие при данном характере взаимодействия только от расстояния между частицами и направленные по прямой, проходящей через эти частицы.
Покажем, что независимо от системы отсчета работа всех этих внутренних сил при переходе системы частиц из одного положения в другое может быть представлена как убыль некоторой функции, зависящей при данном характере взаимодействия только от относительного расположения частиц системы,
т.е. от ее конфигурации. Эту функцию называют собственной потенциальной энергией системы (в отличие от внешней потенциальной энергии, характеризующей взаимодействие данной системы с другими телами).
Сначала возьмем систему из двух частиц 1 и 2. Определим алгебраическую сумму элементарных работ сил F1 и F2, с которыми эти частицы взаимодействуют. Пусть в произвольной
K-системе отсчета за время dt частицы совершили перемещения dr1 и dr2. Тогда соответствующая сумма работ этих сил
A1,2 F1 dr1 F2 dr2 .
|
Закон сохранения энергии |
113 |
Учитывая, что F2 F1 (согласно третьему закону Ньютона), перепишем предыдущее уравнение:
A1,2 F1 (dr1 dr2 ).
Величина, стоящая в скобках, представляет собой не что иное, как перемещение частицы 1 относительно частицы 2, точнее, перемещение частицы 1 в K -системе отсчета, жестко связанной с частицей 2 и перемещающейся вместе с ней поступательно относительно исходной K-системы отсчета. Действительно, перемещение dr1 частицы 1 в K-системе отсчета может быть представлено как перемещение dr2 K -системы отсчета (связанной с частицей 2) плюс перемещение dr1 частицы 1 относительно этой K -системы, т. е. dr1 dr2 dr1 . Отсюда dr1 dr2 dr1 и
A1,2 F1 dr1 .
Полученный таким образом результат весьма замечателен: алгебраическая сумма элементарных работ пары сил взаимодействия в произольной K-системе отсчета оказывается всегда равной элементарной работе, которую совершает сила, действующая на одну частицу, в системе отсчета, где другая частица покоится. Иначе говоря, работа А1,2 не зависит от выбора исходной K-системы отсчета.
Сила F1, действующая на частицу 1 со стороны частицы 2, является центральной, а значит и консервативной. Поэтому работа данной силы на перемещении dr1 может быть представлена, согласно (4.10), как убыль потенциальной энергии частицы 1 в поле частицы 2 или как убыль потенциальной энергии взаимодействия рассматриваемой пары частиц:
A1,2 dU1 2 ,
где U12 — функция, зависящая только от расстояния между этими частицами. При конечном же перемещении
A1,2 U1 2 .
Рассмотрим теперь систему из трех частиц. (Полученный в этом случае результат легко обобщить и на систему из произвольного числа частиц.) Работа, которую совершают все силы
взаимодействия при перемещении всех частиц, может быть представлена как алгебраическая сумма работ всех трех пар сил взаимодействий: A A1,2 A1,3 A2,3 . Но для каждой пары этих сил A ik Uik , поэтому
A (U1 2 U1 3 U2 3 ) Uсоб ,
где Uсоб — собственная потенциальная энергия данной системы частиц:
Uсоб U1 2 U1 3 U2 3 .
Так как каждое слагаемое этой суммы зависит от расстояния между соответствующими частицами, то очевидно, что собственная потенциальная энергия данной системы зависит от относительного расположения частиц (в один и тот же момент), или, другими словами, от конфигурации системы.
Подобные рассуждения справедливы и для системы из любого числа частиц. Поэтому каждой конфигурации системы частиц присуще свое значение собственной потенциальной энергии и работа всех внутренних центральных (консервативных) сил при изменении этой конфигурации равна убыли собственной потенциальной энергии системы:
|
A внутр U1 соб U2 соб Uсоб , |
(4.33) |
где U1 соб и U2 соб — собственная потенциальная энергия системы в начальном и конечном состояниях.
Таким образом, суммарная работа внутренних центральных сил не зависит от того, как конкретно система переходит от конфигурации 1 к конфигурации 2. Данная работа определяется исключительно самими конфигурациями системы. Все это позволяет дать более общее определение консервативных сил:
консервативными называют силы, зависящие только от конфигурации системы и суммарная работа которых не зависит от «пути» перехода, а определяется только начальной и конечной конфигурациями системы.
Собственная потенциальная энергия системы — величина не аддитивная, т. е. она не равна в общем случае сумме собственных потенциальных энергий ее частей. Необходимо учесть еще
|
Закон сохранения энергии |
115 |
потенциальную энергию взаимодействия Uвз отдельных частей системы:
где Un — собственная потенциальная энергия n-й части системы.
Следует также иметь в виду, что собственная потенциальная энергия системы, как и потенциальная энергия взаимодействия каждой пары частиц, определяется с точностью до произвольной постоянной.
В заключение приведем полезные формулы для расчета собственной потенциальной энергии системы. Прежде всего покажем, что эта энергия может быть представлена в виде
где Ui — потенциальная энергия взаимодействия i-й частицы со всеми остальными частицами системы. Здесь сумма берется по всем частицам системы.
Убедимся в справедливости этой формулы сначала для системы из трех частиц. Выше было показано, что собственная потенциальная
энергия данной системы Uсоб U1 2 U1 3 U2 3 . Преобразуем эту сумму следующим образом. Представим каждое слагаемое Uik в симмет-
ричном виде: Uik (Uik Uki )/2, так как ясно, что Uik Uki . Тогда
Uсоб 1/2 (U1 2 U2 1 U1 3 U3 1 U2 3 U3 2 ).
Сгруппируем члены с одинаковым первым индексом:
Uсоб 1/2 [(U1 2 U1 3 ) (U2 1 U2 3 ) (U3 1 U3 2 )] .
Каждая сумма в круглых скобках представляет собой потенциальную энергию Ui взаимодействия i-й частицы с остальными двумя. Поэтому последнее выражение можно переписать так:
3
Uсоб 1/2 (U1 U2 U 3 ) 1/2 .Ui , i 1
что полностью соответствует формуле (4.35).
Обобщение полученного результата на произвольную систему очевидно, так как подобные рассуждения не зависят от числа частиц, составляющих систему.
Для системы, взаимодействие между частицами которой имеет гравитационный или кулоновский характер, формулу (4.35) можно преобразовать и к другому виду, воспользовавшись понятием потенциала. Заменим в (4.35) потенциальную энергию i-й частицы выражением Ui mi i , где mi — масса (заряд) i-й частицы, а i — потенциал, создаваемый всеми остальными частицами системы в точке нахождения i-й частицы. Тогда
Если массы (заряды) распределены в системе непрерывно, то суммирование сводится к интегрированию:
|
Uсоб 1/2 dm 1/2 dV , |
(4.37) |
где — объемная плотность массы (заряда), dV — элемент объема. Здесь интегрирование проводится по всему объему, занимаемому массами (зарядами).
«Внешняя» потенциальная энергия системы
Рассмотрим случай, когда система находится во внешнем стационарном поле консервативных сил. В этом случае каждая частица системы будет характеризоваться своим значением потенциальной энергии Ui в данном поле, а вся система — величиной
Эту величину мы и будем называть «внешней» потенциальной энергией системы в отличие от Uсоб — собственной потенциальной энергии, зависящей только от взаимодействия частиц системы между собой.
Согласно (4.10), убыль потенциальной энергии каждой частицы во внешнем поле равна работе силы данного поля на соответствующем перемещении, поэтому убыль Uвнеш всей системы равна Авнеш — алгебраической сумме работ всех сил внешнего поля, действующих на все частицы системы:
|
Закон сохранения энергии |
117 |
Получим полезную формулу для вычисления внешней потенциальной энергии системы, находящейся в однородном силовом поле. Пусть, например, это поле тяжести, где на i-ю частицу системы действует сила mig. В этом случае потенциальная энергия данной частицы, согласно (4.13), есть migzi, где zi — вертикальная координата частицы, отсчитанная от некоторого произвольного уровня О. Тогда потенциальная энергия всей системы во внешнем однородном поле (собственная потенциальная энергия нас сейчас не интересует) может быть записана так:
Uвнеш .m i gz i .m i z i g.
Сумма, стоящая в скобках, в соответствии с (3.8) есть не что иное, как произведение массы m всей системы на вертикальную координату zC центра масс данной системы, т. е.
.m i z i mz C . Поэтому выражение для Uвнеш можно переписать в окончательном виде:
т. е. потенциальная энергия системы во внешнем однородном поле тяжести равна произведению массы m системы на g и на вертикальную координату zC ее центра масс.
Приращение величины Uвнеш при перемещении системы рав-
но
где z C — приращение вертикальной координаты центра масс данной системы частиц.
§ 4.5. Закон сохранения механической энергии системы
Диссипативные силы
Помимо разделения всех сил на внешние и внутренние (в зависимости от выбора системы частиц), силы, как мы уже знаем, принято подразделять на консервативные и неконсервативные (в зависимости от их природы).
К неконсервативным силам относятся диссипативные силы — это силы трения и сопротивления. Любая диссипативная сила может быть представлена в виде
где v — скорость данного тела относительно другого тела (или среды), с которым оно взаимодействует; k(v) — положительный коэффициент, зависящий в общем случае от скорости v. Сила F всегда направлена противоположно вектору v.
В зависимости от выбора системы отсчета работа этой силы может быть как положительной, так и отрицательной. Однако, как мы сейчас покажем и что будет важно для дальнейшего,
суммарная работа всех внутренних диссипативных сил в системе — величина всегда отрицательная независимо от системы отсчета:
Переходя к доказательству, отметим прежде всего, что внутренние диссипативные силы в данной системе встречаются попарно, причем в каждой паре, согласно третьему закону Ньютона, они одинаковы по модулю и противоположны по направлению. Найдем элементарную работу произвольной пары диссипативных сил взаимодействия между телами 1 и 2 в системе отсчета, где скорости этих тел в данный момент равны v1 и v2:
A дис F1 v1dt F2 v2 dt.
Учтем, что F2 F1 , v1 v2 v — скорость тела 1 относительно тела 2, а также то, что F1 kv. Тогда выражение для работы преобразуется:
A дис F1 (v1 v2 )dt kvvdt kv 2 dt.
Отсюда видно, что работа произвольной пары внутренних диссипативных сил взаимодействия всегда отрицательна, а значит, и суммарная работа всех пар внутренних диссипативных сил также всегда отрицательна, причем в любой системе отсчета.
|
Закон сохранения энергии |
119 |
Кинетическая энергия системы
Согласно (4.28), приращение кинетической энергии каждой частицы равно работе всех сил, действующих на частицу:K i A i . Поэтому работу А, которую совершают все силы, действующие на все частицы системы, при изменении ее состояния, можно записать так: A . A i . K i . K i , или
где K — суммарная кинетическая энергия системы.
Итак, приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы:
Заметим, что кинетическая энергия системы — величина аддитивная: она равна сумме кинетических энергий отдельных частей системы независимо от того, взаимодействуют они между собой или нет.
Уравнение (4.45) справедливо как в инерциальных, так и в неинерциальных системах отсчета. Следует только помнить, что в неинерциальных системах отсчета кроме работ сил взаимодействия необходимо учитывать и работу сил инерции.
Собственная механическая энергия системы
Только что было показано, что приращение K кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы. Разделим эти силы на внешние и внутренние, а внутренние, в свою очередь, на консервативные и диссипативные. Тогда предыдущее утверждение можно записать так:
K A внеш A внутр A внеш A внутрконс A внутрдис .
Учтем, что работа внутренних консервативных сил равна,
согласно (4.33), убыли собственной потенциальной энергии сис-
темы: A внутрконс Uсоб . Тогда
|
K Uсоб K(K Uсоб ) A внеш A внутрдис . |
(4.46) |
Решение.
Для
решения задачи рассмотрим физическую систему «тело – гравитационное поле Земли».
Тело будем считать материальной точкой, а гравитационное поле Земли – однородным. Выделенная физическая система
является незамкнутой, т.к. во время движения тела взаимодействует с воздухом.
Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха,
то изменение полной механической энергии системы равняется работе силы
сопротивления воздуха, т.е.
∆
E
=
A c
.
Нулевой
уровень потенциальной энергии выберем на поверхности Земли. Единственной
внешней силой в отношении системы «тело – Земля» является сила сопротивления
воздуха, направленная вертикально вверх. Начальная энергия системы
E 1
, конечная
E 2
.
Работа
силы сопротивления
A.
Т.к.
угол между силой сопротивления и перемещением равен 180° , то косинус равен -1,
поэтому
A
= –
F c h
. Приравняем
A.
Рассматриваемую
незамкнутую физическую систему можно также описать теоремой от изменении
кинетической энергии системы взаимодействующих между собой объектов, согласно
которой изменение кинетической энергии системы равно работе, совершенной
внешними и внутренними силами при ее переходе из начального состояния в
конечное. Если не учитывать выталкивающую силу, действующую на тело со стороны
воздуха, а внутренней – сила тяжести. Следовательно
∆
E
к
=
A
1
+
A
2
, где
A
1
=
mgh
– работа силы тяжести,
A
2
=
F c hcos
180°
= –
F c h
– работа силы сопротивления;
∆
E
=
E
2
–
E
1
.
Это творческое задание для мастер-класса по информатике для школьников при ДВФУ.
Цель задания – выяснить, как изменится траектория тела, если учитывать сопротивление воздуха. Также необходимо ответить на вопрос, будет ли дальность полёта по-прежнему достигать максимального значения при угле бросания в 45°, если учитывать сопротивление воздуха.
В разделе “Аналитическое исследование” изложена теория. Этот раздел можно пропустить, но он должен быть, в основном, понятным для вас, потому что бо
льшую часть из этого вы проходили в школе.
В разделе “Численное исследование” содержится описание алгоритма, который необходимо реализовать на компьютере. Алгоритм простой и краткий, поэтому все должны справиться.
Аналитическое исследование
Введём прямоугольную систему координат так, как показано на рисунке. В начальный момент времени тело массой m
находится в начале координат. Вектор ускорения свободного падения направлен вертикально вниз и имеет координаты (0, –g
).
– вектор начальной скорости. Разложим этот вектор по базису: ![]() . Здесь , где
. Здесь , где
– модуль вектора скорости, – угол бросания.
Запишем второй закон Ньютона: .
Ускорение в каждый момент времени есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени: .
Следовательно, 2-й закон Ньютона можно переписать в следующем виде:
, где – это равнодействующая всех сил, действующая на тело.
Так как на тело действуют сила тяжести и сила сопротивления воздуха, то  .
.
Мы будем рассматривать три случая:
1) Сила сопротивления воздуха равна 0:
.
2) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна скорости: ![]() .
.
3) Сила сопротивления воздуха противоположно направлена с вектором скорости, и её величина пропорциональна квадрату скорости: ![]() .
.

Проанализируем полученные формулы.
Найдём время полёта
тела. Приравняв y
к нулю, получим

Дальность полёта
равна значению координаты x
в момент времени t
0:

Из этой формулы следует, что максимальная дальность полёта достигается при .
Теперь найдём уравнение трактории тела
. Для этого выразим t
через x

И подставим полученное выражение для t
в равенство для y
.

Полученная функция y
(x
) — квадратичная функция, её графиком является парабола, ветви которой направлены вниз.
Про движение тела, брошенного под углом к горизонту (без учёта сопротивления воздуха), рассказывается в этом видеоролике.
Теперь рассмотрим второй случай: ![]() .
.
Второй закон приобретает вид  ,
,
отсюда  .
.
Запишем это равенство в скалярном виде:

Мы получили два линейных дифференциальных уравнения
.
Первое уравнение имеет решение
![]()
В чём можно убедиться, подставив данную функцию в уравнение для v x
и в начальное условие ![]() .
.
Здесь e = 2,718281828459… — число Эйлера .
Второе уравнение имеет решение
Так как ![]() ,
,
![]() , то при наличии сопротивления воздуха движение тела стремится к равномерному, в отличие от случая 1, когда скорость неограниченно увеличивается.
, то при наличии сопротивления воздуха движение тела стремится к равномерному, в отличие от случая 1, когда скорость неограниченно увеличивается.
В следующем видеоролике говорится, что парашютист сначала движется ускоренно, а потом начинает двигаться равномерно (даже до раскрытия парашюта).
Найдём выражения для x
и y
.
Так как x
(0) = 0, y
(0) = 0, то


Нам осталось рассмотреть случай 3, когда ![]() .
.
Второй закон Ньютона имеет вид , или
, или
 .
.
В скалярном виде это уравнение имеет вид:

Это система нелинейных дифференциальных уравнений
. Данную систему не удаётся решить в явном виде, поэтому необходимо применять численное моделирование.
Численное исследование
В предыдущем разделе мы увидели, что в первых двух случаях закон движения тела можно получить в явном виде. Однако в третьем случае необходимо решать задачу численно. При помощи численных методов мы получим лишь приближённое решение, но нас вполне устроит и небольшая точность. (Число π или квадратный корень из 2, кстати, нельзя записать абсолютно точно, поэтому при расчётах берут какое-то конечное число цифр, и этого вполне хватает.)
Будем рассматривать второй случай, когда сила сопротивления воздуха определяется формулой![]() . Отметим, что при k
. Отметим, что при k
= 0 получаем первый случай.
Скорость тела ![]() подчиняется следующим уравнениям:
подчиняется следующим уравнениям:

В левых частях этих уравнений записаны компоненты ускорения  .
.
Напомним, что ускорение есть (мгновенная) скорость изменения скорости, то есть производная от скорости по времени.
В правых частях уравнений записаны компоненты скорости. Таким образом, данные уравнения показывают, как скорость изменения скорости связана со скоростью.
Попробуем найти решения этих уравнений при помощи численных методов. Для этого введём на временной оси сетку
: выберем число
и будем рассматривать моменты времени вида :
.
Наша задача — приближённо вычислить значения
![]()
в узлах сетки.
Заменим в уравнениях ускорение (мгновенную скорость
изменения скорости) на среднюю скорость
изменения скорости, рассматривая движение тела на промежутке времени :

Теперь подставим полученные аппроксимации в наши уравнения.


Полученные формулы позволяют нам вычислить значения функций ![]() в следующем узле сетки, если известны значения этих функций в предыдущем узле сетки.
в следующем узле сетки, если известны значения этих функций в предыдущем узле сетки.
При помощи описанного метода мы можем получить таблицу приближённых значений компонент скорости.
Как найти закон движения тела, т.е. таблицу приближённых значений координат x
(t
), y
(t
)? Аналогично!
Имеем
Значение vx[j] равняется значению функции , для других массивов аналогично.
Теперь остаётся написать цикл, внутри которого мы будем вычислять vx через уже вычисленное значение vx[j], и с остальными массивами то же самое. Цикл будет по j
от 1 до N
.
Не забудьте инициализировать начальные значения vx, vy, x, y по формулам , x
0 = 0, y
0 = 0.
В Паскале и Си для вычисления синуса и косинуса имеются функции sin(x)
, cos(x)
. Обратите внимание, что эти функции принимают аргумент в радианах.
Вам необходимо построить график движения тела при k
= 0 и k
> 0 и сравнить полученные графики. Графики можно построить в Excel.
Отметим, что расчётные формулы настолько просты, что для вычислений можно использовать один только Excel и даже не использовать язык программирования.
Однако в дальнейшем вам нужно будет решить задачу в CATS, в которой нужно вычислить время и дальность полёта тела, где без языка программирования не обойтись.
Обратите внимание, что вы можете протестировать
вашу программу и проверить ваши графики, сравнив результаты вычислений при k
= 0 с точными формулами, приведёнными в разделе “Аналитическое исследование”.
Поэкспериментируйте со своей программой. Убедитесь в том, что при отсутствии сопротивления воздуха (k
= 0) максимальная дальность полёта при фиксированной начальной скорости достигается при угле в 45°.
А с учётом сопротивления воздуха? При каком угле достигается максимальная дальность полёта?
На рисунке представлены траектории тела при v
0 = 10 м/с, α = 45°, g
= 9,8 м/с 2 , m
= 1 кг, k
= 0 и 1, полученные при помощи численного моделирования при Δt
= 0,01.

Вы можете ознакомиться с замечательной работой 10-классников из г. Троицка, представленной на конференции “Старт в науку” в 2011 г. Работа посвящена моделированию движения теннисного шарика, брошенного под углом к горизонту (с учетом сопротивления воздуха). Применяется как численное моделирование, так и натурный эксперимент.
Таким образом, данное творческое задание позволяет познакомиться с методами математического и численного моделирования, которые активно используются на практике, но мало изучаются в школе. К примеру, данные методы использовались при реализации атомного и космического проектов в СССР в середине XX века.
Все составляющие
сопротивления воздуха трудно определяются
аналитически. Поэтому в практике нашла
применение эмпирическая формула, имеющая
для диапазона скоростей движения,
характерного для реального автомобиля,
следующий вид:
где с
х
– безразмерный
коэффициент
обтекаемости воздухом
,
зависящий от формы тела; ρ в
– плотность воздуха ρ в =
1,202…1,225 кг/м 3 ;
А
– площадь миделева сечения (площадь
поперечной проекции) автомобиля, м 2 ;
V
– скорость автомобиля, м/с.
В литературе
встречается коэффициент
сопротивления воздуха
k
в
:
F
в
=
k
в
А
V
2
,
где k
в
=с
х
ρ
в
/2
,
–коэффициент сопротивления воздуха,
Нс 2 /м 4 .
…и фактор
обтекаемости
q
в
:
q
в
=
k
в
· А.
Если вместо с
х
подставить с
z
,
то получим аэродинамическую подъемную
силу.
Площадь миделева
сечения для авто:
А=0,9 · В
max
· Н
,
где В
max
– наибольшая колея автомобиля, м; Н
– высота автомобиля, м.
Сила приложена в
метацентре, при этом создаются моменты.
Скорость сопротивления
потока воздуха с учетом ветра:
 ,
,
где β
– угол между направлениями движения
автомобиля и ветра.
С
х
некоторых автомобилей
|
ВАЗ 2101…07 |
Оpel |
|||
|
ВАЗ 2108…15 |
||||
|
Land |
||||
|
ВАЗ 2102…04 |
||||
|
ВАЗ 2121…214 |
||||
|
грузовик |
||||
|
грузовик с |
-
Сила сопротивления подъему
F
п
=
G
а
sin
α.
В дорожной практике
величину уклона обычно оценивают
величиной подъема полотна дороги,
отнесенную к величине горизонтальной
проекции дороги, т.е. тангенсом угла, и
обозначают i
, выражая полученное значение в процентах.
При относительно небольшой величине
уклона допустимо в расчетных формулах
при определении силы сопротивления
подъему использовать не sin
α., а величину i
в относительных
значениях. При больших значениях
величины уклона замена sin
α величиной тангенса (i
/100)
недопустима.
-
Сила сопротивления разгону
При разгоне
автомобиля происходит разгон поступательно
движущейся массы авто и разгон вращающихся
масс, увеличивающих сопротивление
разгону. Это увеличение можно учесть в
расчетах, если считать, что массы
автомобиля движутся поступательно, но
использовать некую эквивалентную массу
m
э,
несколько большей m
a
(в классической
механике это выражается уравнением
Кенига)
Используем метод
Н.Е. Жуковского, приравняв кинетическую
энергии поступательно движущейся
эквивалентной массы сумме энергий:
 ,
,
где J
д
– момент инерции маховика двигателя и
связанных с ним деталей, Н·с 2 ·м
(кг·м 2);
ω д
– угловая скорость двигателя, рад/с; J
к
–момент инерции одного колеса.
Так как ω к
= V
а
/
r
k
,
ω д
= V
а
·
i
кп
·
i
o
/
r
k
,
r
k
=
r
k
0
,
то получим
 .
.
Момент инерции
J
узлов трансмиссии автомобилей, кг· м
2
|
Автомобиль |
Маховик |
Ведомые колеса (2 колеса с |
Ведущие колеса (2 колеса с |
Произведем замену:
m
э
=
m
а
·
δ,
Если автомобиль
загружен не полностью:
 .
.
Если автомобиль
идет накатом: δ
= 1 + δ 2
Сила сопротивления
разгону автомобиля (инерции): F
и
=
m
э
· а
а
=
δ
·
m
а
· а
а
.
В первом приближении
можно принять: δ
= 1,04+0,04
i
кп
2
Дорожная эксплуатационная мощность, затрачиваемая на преодоление сопротивлений, весьма велика (см. рис.). Например, для поддержания равномерного движения (190 км/ч
) четырех дверного седана, массой 1670 кг
, площадью миделя 2,05 м 2
, С х = 0,45 требуется около 120 кВт
мощности, причем 75 % мощности затрачивается на аэродинамическое сопротивление. Мощности, затрачиваемые на преодоление аэродинамического и дорожного (качения) сопротивления приблизительно равны на скорости 90 км/ч, и в сумме составляют 20 – 25 кВт
.
Примечание к рисунку
: сплошная линия – аэродинамическое сопротивление; пунктирная линия – сопротивление качению.
Сила сопротивления воздуха Р w
обусловлена трением в прилегающих к поверхности автомобиля слоях воздуха, сжатием воздуха движущейся машиной, разрежением за машиной и вихреобразованием в окружающих автомобиль слоях воздуха. На величину аэродинамического сопротивления автомобиля влияет ряд и других факторов, главным из которых является его форма. В качестве упрощенного примера влияния формы автомобиля на его аэродинамическое сопротивление проиллюстрировано на схеме, приведенной ниже.
Направление движения автомобиля
Значительная часть всей силы сопротивления воздуха составляет лобовое сопротивление, которое зависит от лобовой площади (наибольшей площади поперечного сечения автомобиля).
Для определения силы сопротивления воздуха используют зависимость:
Р w
= 0,5·с х ·ρ·F·v n
,
где с х
– коэффициент, характеризующий форму тела и аэродинамическое качество машины (коэффициент аэродинамического сопротивления
);
F
– лобовая площадь автомобиля (площадь проекции на плоскость, перпендикулярную продольной оси), м 2
;
v
– скорость движения машины, м/с
;
n
– показатель степени (для реальных скоростей движения автомобилей принимается равным 2).
ρ
– плотность воздуха:
, кг/м 3
,
где ρ 0
= 1,189 кг/м
3 , р 0
= 0,1 МПа
, Т 0
= 293К
– плотность, давление и температура воздуха при нормальных условиях;
ρ
, р
, Т
– плотность, давление и температура воздуха при расчетных условиях.
При расчетах лобовую площадь F
легковых автомобилей со стандартным кузовом определяют по приближенной формуле:
F
= 0,8В г Н г
,
где В г
– габаритная ширина автомобиля, м
;
Н г
– габаритная высота автомобиля, м
.
Для автобусов и грузовых автомобилей с кузовом в виде фургона или с тентом:
F
= 0,9В Г Н Г
.
Для условий работы автомобиля плотность воздуха изменяется мало (ρ
= 1,24…1,26 кг/м 3
). Заменив произведение (0,5·с х ·ρ
) , через к w
, получим:
Р w
= к w ·F·v 2
,
где к w
– коэффициент обтекаемости
; по определению он представляет собой удельную силу в Н
, необходимую для движения со скоростью 1 м/с
в воздушной среде тела данной формы с лобовой площадью 1 м
2:
, Н·с 2 /м 4
.
Произведение (к w ·F
)называют фактором сопротивления воздушной среды
или фактором обтекаемости
, характеризующим размеры и форму автомобиля в отношении свойств обтекаемости (его аэродинамические качества).
Средние значения коэффициентов с х
, k w
и лобовых площадей F
для различных типов автомобилей приведены в табл. 2.1.
Таблица 2.1.
Параметры, характеризующие аэродинамические качества автомобилей
:
Известные значения аэродинамических коэффициентов c x
и k w
и площади габаритного поперечного (миделевого) сечения F
для некоторых серийно выпускаемых автомобилей (по данным заводов-изготовителей) приведены в табл. 2.1.-а
.
Таблица 2.1-а.
Аэродинамические коэффициенты и лобовая площадь автомобилей:
| № | Автомобиль | с х |
к w |
F |
| ВАЗ-2121 | 0,56 | 0,35 | 1,8 | |
| ВАЗ-2110 | 0,334 | 0,208 | 2,04 | |
| М-2141 | 0,38 | 0,24 | 1,89 | |
| ГАЗ-2410 | 0,34 | 0,3 | 2,28 | |
| ГАЗ-3105 | 0,32 | 0,22 | 2,1 | |
| ГАЗ-3110 | 0,56 | 0,348 | 2,28 | |
| ГАЗ-3111 | 0,453 | 0,282 | 2,3 | |
| «Ока» | 0,409 | 0,255 | 1,69 | |
| УАЗ-3160 (jeep) | 0,527 | 0,328 | 3,31 | |
| ГАЗ-3302 бортовой | 0,59 | 0,37 | 3,6 | |
| ГАЗ-3302 фургон | 0,54 | 0,34 | 5,0 | |
| ЗИЛ-130 бортовой | 0,87 | 0,54 | 5,05 | |
| КамАЗ-5320 бортовой | 0,728 | 0,453 | 6,0 | |
| КамАЗ-5320 тентовый | 0,68 | 0,43 | 7,6 | |
| МАЗ-500А тентовый | 0,72 | 0,45 | 8,5 | |
| МАЗ-5336 тентовый | 0,79 | 0,52 | 8,3 | |
| ЗИЛ-4331 тентовый | 0,66 | 0,41 | 7,5 | |
| ЗИЛ-5301 | 0,642 | 0,34 | 5,8 | |
| Урал-4320 (military) | 0,836 | 0,52 | 5,6 | |
| КрАЗ (military) | 0,551 | 0,343 | 8,5 | |
| ЛиАЗ bus (city) | 0,816 | 0,508 | 7,3 | |
| ПАЗ-3205 bus (city) | 0,70 | 0,436 | 6,8 | |
| Ikarus bus (city) | 0,794 | 0,494 | 7,5 | |
| Mercedes-Е | 0,322 | 0,2 | 2,28 | |
| Mercedes-А (kombi) | 0,332 | 0,206 | 2,31 | |
| Mercedes -ML (jeep) | 0,438 | 0,27 | 2,77 | |
| Audi A-2 | 0,313 | 0,195 | 2,21 | |
| Audi A-3 | 0,329 | 0,205 | 2,12 | |
| Audi S 3 | 0,336 | 0,209 | 2,12 | |
| Audi A-4 | 0,319 | 0,199 | 2,1 | |
| BMW 525i | 0,289 | 0,18 | 2,1 | |
| BMW- 3 | 0,293 | 0,182 | 2,19 | |
| Citroen X sara | 0,332 | 0,207 | 2,02 | |
| DAF 95 trailer | 0,626 | 0,39 | 8,5 | |
| Ferrari 360 | 0,364 | 0,227 | 1,99 | |
| Ferrari 550 | 0,313 | 0,195 | 2,11 | |
| Fiat Punto 60 | 0,341 | 0,21 | 2,09 | |
| Ford Escort | 0,362 | 0,225 | 2,11 | |
| Ford Mondeo | 0,352 | 0,219 | 2,66 | |
| Honda Civic | 0,355 | 0,221 | 2,16 | |
| Jaguar S | 0,385 | 0,24 | 2,24 | |
| Jaguar XK | 0,418 | 0,26 | 2,01 | |
| Jeep Cherokes | 0,475 | 0,296 | 2,48 | |
| McLaren F1 Sport | 0,319 | 0,198 | 1,80 | |
| Mazda 626 | 0,322 | 0,20 | 2,08 | |
| Mitsubishi Colt | 0,337 | 0,21 | 2,02 | |
| Mitsubishi Space Star | 0,341 | 0,212 | 2,28 | |
| Nissan Almera | 0,38 | 0,236 | 1,99 | |
| Nissan Maxima | 0,351 | 0,218 | 2,18 | |
| Opel Astra | 0,34 | 0,21 | 2,06 | |
| Peugeot 206 | 0,339 | 0,21 | 2,01 | |
| Peugeot 307 | 0,326 | 0,203 | 2,22 | |
| Peugeot 607 | 0,311 | 0,19 | 2,28 | |
| Porsche 911 | 0,332 | 0,206 | 1,95 | |
| Renault Clio | 0,349 | 0,217 | 1,98 | |
| Renault Laguna | 0,318 | 0,198 | 2,14 | |
| Skoda Felicia | 0,339 | 0,21 | 2,1 | |
| Subaru Impreza | 0,371 | 0,23 | 2,12 | |
| Suzuki Alto | 0,384 | 0,239 | 1,8 | |
| Toyota Corolla | 0,327 | 0,20 | 2,08 | |
| Toyota Avensis | 0,327 | 0,203 | 2,08 | |
| VW Lupo | 0,316 | 0,197 | 2,02 | |
| VW Beetl | 0,387 | 0,24 | 2,2 | |
| VW Bora | 0,328 | 0,204 | 2,14 | |
| Volvo S 40 | 0,348 | 0,217 | 2,06 | |
| Volvo S 60 | 0,321 | 0,20 | 2,19 | |
| Volvo S 80 | 0,325 | 0,203 | 2,26 | |
| Volvo B12 bus (tourist) | 0,493 | 0,307 | 8,2 | |
| MAN FRH422 bus (city) | 0,511 | 0,318 | 8,0 | |
| Mercedes 0404(inter city) | 0,50 | 0,311 | 10,0 |
Примечание:
c x
, Н·с 2 /м·кг; к w
, Н·с 2 /м 4
– аэродинамические коэффициенты;
F
, м 2
– лобовая площадь автомобиля.
Для автомобилей, имеющих высокие скорости движения, сила Р w
имеет доминирующее значение. Сопротивление воздушной среды определяется относительной скоростью автомобиля и воздуха, поэтому при её определении следует учитывать влияние ветра.
Точка приложения результирующей силы сопротивления воздуха Р w
(центр парусности) лежит в поперечной (лобовой) плоскости симметрии автомобиля. Высота расположения этого центра над опорной поверхностью дороги h w
оказывает значительное влияние на устойчивость автомобиля при движении его с высокими скоростями.
Увеличение Р w
может привести к тому, что продольный опрокидывающий момент Р w
·h w
настолько разгрузит передние колеса машины, что последняя потеряет управляемость вследствие плохого контакта управляемых колес с дорогой. Боковой ветер может вызвать занос автомобиля, который будет тем более вероятен, чем выше расположен центр парусности.
Попадающий в пространство между нижней части автомобиля и дорогой воздух создает дополнительное сопротивление движению за счет эффекта интенсивного образования вихрей. Для снижения этого сопротивления желательно передней части автомобиля придавать конфигурацию, которая препятствовала бы попадание встречного воздуха под его нижнюю часть.
По сравнению с одиночным автомобилем коэффициент сопротивления воздуха автопоезда с обычным прицепом выше на 20…30%, а с седельным прицепом – примерно на 10%. Антенна, зеркало внешнего вида, багажник над крышей, дополнительные фары и другие выступающие детали или открытые окна увеличивают сопротивление воздуха.
При скорости движения автомобиля до 40 км/ч
сила Р w
меньше силы сопротивления качению Р f
на асфальтированной дороге. При скоростях свыше 100 км/ч
сила сопротивления воздуха представляет собой основную составляющую тягового баланса автомобиля.
Грузовые автомобили имеют плохо обтекаемые формы с резкими углами и большим числом выступающих частей. Чтобы снизить Р w
, на грузовиках устанавливают над кабиной обтекатели и другие приспособления.
Подъемная аэродинамическая сила
. Появление подъемной аэродинамической силы обусловлено перепадом давлений воздуха на автомобиль снизу и сверху (по аналогии подъемной силы крыла самолета). Преобладание давления воздуха снизу над давлением сверху объясняется тем, что скорость воздушного потока, обтекающего автомобиль снизу, гораздо меньше, чем сверху. Значение подъемной аэродинамической силы не превышает 1,5% от веса самого автомобиля. Например, для легкового автомобиля ГАЗ-3102 «Волга» подъемная аэродинамическая сила при скорости движения 100 км/ч
составляет около 1,3% от собственного веса автомобиля.
Спортивным автомобилям, движущимся с большими скоростями, придают такую форму, при которой подъемная сила направлена вниз, которая прижимает автомобиль к дороге. Иногда с этой же целью такие автомобили оснащают специальными аэродинамическими плоскостями.
Решение.
Для
решения задачи рассмотрим физическую систему «тело – гравитационное поле Земли».
Тело будем считать материальной точкой, а гравитационное поле Земли – однородным. Выделенная физическая система
является незамкнутой, т.к. во время движения тела взаимодействует с воздухом.
Если не учитывать выталкивающую силу, действующую на тело со стороны воздуха,
то изменение полной механической энергии системы равняется работе силы
сопротивления воздуха, т.е.
∆
E
=
A c
.
Нулевой
уровень потенциальной энергии выберем на поверхности Земли. Единственной
внешней силой в отношении системы «тело – Земля» является сила сопротивления
воздуха, направленная вертикально вверх. Начальная энергия системы
E 1
, конечная
E 2
.
Работа
силы сопротивления
A.
Т.к.
угол между силой сопротивления и перемещением равен 180° , то косинус равен -1,
поэтому
A
= –
F c h
. Приравняем
A.
Рассматриваемую
незамкнутую физическую систему можно также описать теоремой от изменении
кинетической энергии системы взаимодействующих между собой объектов, согласно
которой изменение кинетической энергии системы равно работе, совершенной
внешними и внутренними силами при ее переходе из начального состояния в
конечное. Если не учитывать выталкивающую силу, действующую на тело со стороны
воздуха, а внутренней – сила тяжести. Следовательно
∆
E
к
=
A
1
+
A
2
, где
A
1
=
mgh
– работа силы тяжести,
A
2
=
F c hcos
180°
= –
F c h
– работа силы сопротивления;
∆
E
=
E
2
–
E
1
.
