Как найти работу силы тяги поезда

Что такое сила тяги

Сила тяги — сила, прикладываемая к телу для поддержания его в постоянном движении.

Действие силы тяги

Множество сил, действующих на движущийся объект, для упрощения вычислений делят на две группы: силу тяги и силы сопротивления.

Её прекращение

Когда действие силы тяги прекращается, движущееся тело замедляется и постепенно останавливается, так как на него воздействуют силы, мешающие продолжать двигаться, например, трение.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

1 закон Ньютона о действии

Согласно этому закону в формулировке самого Ньютона, любое тело остается в покое или равномерно движется по прямой, пока на него не воздействуют силы, заставляющие его изменить это состояние.

В современной физике в формулировку внесены уточнения:

• закон применим только в системах отсчета, называемых инерциальными;
• тело может вращаться на месте, не находясь под воздействием внешних сил, поэтому вместо термина «тело» следует использовать термин «материальная точка».

Чтобы переместить неподвижный предмет, на него должна воздействовать некая сила. Чтобы изменить скорость движения предмета, также необходимо воздействие силы, замедляющей его или ускоряющей. Так как предметы обладают разной массой и соответственно разной инертностью, силы, достаточные для эффективного воздействия, тоже будут различаться.

Состояние ускорения после воздействия силы тяги

Когда движение равномерное, сила тяги и сила трения совершают одинаковую работу, уравновешивая друг друга. Воздействие силы на тело в направлении движения придает ему ускорение. Если направить ту же силу в противоположном направлении, она замедлит движение тела, что можно назвать отрицательным ускорением.

Формулы для определения силы тяги

Согласно второму закону Ньютона, сумма сил, воздействующих на движущееся тело, равна массе (m), умноженной на ускорение (a). Универсальной формулы, подходящей для любого сочетания сил, не существует. Чаще всего силу тяги находят с помощью общей формулы( F_т-;F_{с}=m;times;a), где (F_т) — сила тяги, (F_{с}) — силы сопротивления.
При решении конкретной задачи силы, воздействующие на тело, схематически изображают в виде векторов. На схеме:

• сила тяжести mg;
• сила реакции опоры (N);
• сила трения( F_{тр});
• сила тяги (F). 

При нахождении тела на горизонтальной поверхности сила тяжести и сила реакции опоры уравновесят друг друга. Но если транспортное средство движется в гору или под гору, придется учесть влияние уклона. Тогда формула может выглядеть так: (F_т-;F_с-;mg;times;sinalpha=m;times;a.)

Работа A, которую должна совершить сила тяги, сдвигая тело, связана с ней соотношением (A;=;F;times;s). (s) здесь — расстояние, на которое тело переместилось.

Какое условие должно соблюдаться

Сила тяги всегда должна быть больше противодействующих ей сил.

Формула через мощность

Полезную механическую мощность (N) можно вычислить по формуле (N=F_т;times;v), где (v) — скорость. Для определения силы тяги нужно разделить мощность на скорость: (F_т;=;frac N v.)

Измерение и обозначение силы тяги

Силу тяги обозначают (F_т) или (F). Единица измерения — ньютон ((Н)).
Для решения задач недостаточно измерить усилие, приложенное к объекту, и выразить его конкретным числом, так как сила обладает еще и направлением. Чтобы подчеркнуть, что сила — векторная величина, к буквенному обозначению добавляют стрелку.

Как определить силу тяги двигателя. Примеры решения задач

Задача 1

Автомобиль может разгоняться до 216 км/ч. Максимальная мощность двигателя равна 96 кВт. Определите максимальную силу тяги двигателя.

Решение

Переведем киловатты в ватты, а километры в час — в метры в секунду:

(96;times;1000=96000;Вт)

(frac{216times1000}{3600}=60frac мс)

(F_т;=;frac N v = frac{96000}{60} = 1600 Н)

Задача 2

Троллейбус весом 12 тонн за 5 секунд проезжает по горизонтальной дороге 10 метров. Сила трения равна 2,4 кН. Определите силу тяги, которую развивает двигатель.

Решение

Переведем тонны в килограммы, а килоньютоны в ньютоны:

(12;times;1000=12000;кг)

(2,4;times;1000=2400;Н)

(F_т-;F_{тр}=m;times;a), следовательно, (F_т=mtimes a;+;F_{тр})

Чтобы определить ускорение а, воспользуемся формулой (s;=;frac{at^2}2)

Подставив численные значения величин, получаем:

(a;=;frac{2s}{t^2}^{}=frac{20}{25};=;0,8)

(F_т=;12000times0,8;+;2400;=;12000;Н;=;12;кН)

Задача 3

Транспорт, весящий 4 тонны, едет в гору. Уклон — 1 метр на каждые 25 метров пути. (mu) — 0,1 от силы тяжести, (а = 0). Определите силу тяги.

Решение

Начертим схему:

(mtimes g;+;N;+;F_{тр;}+;F_т;=;mtimes a)

Сделаем проекции на координатные оси:

(OX: -;mg;times;sinalpha;-;F_{тр;}+;F_т;=;0)

(OY: N;-;mg;times;cosalpha;=;0 => N;=;mg;times;cosalpha;)

(F_{тр};=;mu N;=;mu mg;times;cosalpha)

Подставим значение (F_{тр}) в уравнение (OX) и определим (F_т):

(-mg;times;sinalpha;-;mu)

(mg;times;cosalpha;+;F_т;=;0)

(=> F;=;mg;left(sinalpha;+;mu;times;cosalpharight))

Найдем синус и косинус (alpha), подставим их в общую формулу:

(sinalpha;=;frac hl;=;frac1{25})

(cosalpha;=;frac{sqrt{l^{2;}-;h^2}}l;)

(F;=;frac{4;times;10^{3;};times;9,8;timesleft(1;+;0,1;sqrt{l^{2;}-;h^2}right)}{25};=;5,5;times;10^3;Н;=;5,5;кН)

Движение поезда

Если мы представим поезд в виде системы связанных между собой тел — локомотива и вагонов (рис. 2), то увидим у каждого тела наличие тех же двух групп сил. Каждую единицу подвижного состава собственная сила тяжести q_i прижимает к рельсам. Силы трения (о них мы далее поговорим подробнее) оказывают сопротивление движению каждой единицы подвижного состава. В сумме эти силы представляют собой сопротивление движению поезда W₀. А движущая сила F у поезда одна — ее должен создать локомотив, который тянет поезд.

Так как локомотив и вагоны в составе поезда движутся в среднем с одной и той же скоростью, т.е. проходят одно и то же расстояние (от одной станции до другой) за одно и то же время, весь поезд можно считать одним телом с суммарным весом (Р + Q), где Q — вес состава. Тогда схема его движения под действием сил на горизонтальном пути будет аналогична рис. 1,б.

Подведем первые итоги. Движение поезда определяется величиной движущей силы F. Это та сила, с которой локомотив тянет состав. Поэтому в железнодорожной практике движущая сила, развиваемая локомотивом, называется силой тяги^*. В некоторых других видах транспорта, например, е авиации или ракетной технике, ее называют просто «тягой» (говорят, что двигатель самолета развивает тягу в столько-то килоньютон и т.п.).

* Слово «тяга» как железнодорожный термин было очень распространено в России. Раньше на железных дорогах страны службы локомотивного хозяйства назывались службами тяги, инженеры и техники по локомотивам были «тяговики» по специальности. Были общероссийские съезды инженеров тяги и т.д. Сейчас это слово используется реже, например, говорят «электрическая тяга» Тем не менее, и сейчас это емкое и чисто русское понятие сохранилось в названии железнодорожной науки “Теория локомотивной тяги».

Движению всегда препятствуют силы сопротивления W, физическая природа которых связана с трением. Рассмотрим несколько подробней эти силы применительно к железнодорожному транспорту. Начнем с сил сопротивления.

Сила сопротивления движению в простейшем случае движения тела по горизонтальной плоскости (см. рис, 1,б) — это сила трения скольжения W₀. Из физики известно, что она пропорциональна весу тела , где  — коэффициент пропорциональности, называемый коэффициентом трения. Его величина зависит от многих факторов: материала и состояния (шероховатости) трущихся поверхностей, наличия и вязкости смазки, скорости перемещения и т.д.

Для трения дерева по дереву , металла по металлу , для скольжения твердых поверхностей со смазкой . Таким образом, для перемещения тела «волоком» по горизонтальной поверхности необходимо тянуть его с силой, равной по величине не менее 20 % его веса. Однако и такое сопротивление при скольжении слишком велико, если говорить о массовой транспортировке грузов. В таких условиях, например, тепловоз 2ТЭ10М, который развивает силу тяги примерно 500 кН (50 тс), смог бы тянуть состав по горизонтальному пути массой всего 250 т, т.е. в самом лучшем случае самого себя, так как масса тепловоза 2ТЭ10М составляет 271 т.

Рекомендуемые материалы

Рис. 2. Силы, действующие на поезд

Весь путь развития средств транспорта за историю человечества — это борьба с трением. Громадным достижением на этом пути было изобретение колеса. Сопротивление движению при качении существенно меньше, чем при скольжении. Сила трения качения может быть в десятки и даже в сотни раз меньше, чем при скольжении. Его величина тем меньше, чем тверже колесо и путь и чем больше диаметр колеса.

Вот почему дорога стала железной, ведь трение качения стального колеса по стальному рельсу минимально.

Правда, помимо сопротивления качению по рельсу движению препятствует трение между шейками осей колесных пар и подшипниками букс. Однако работа трения скольжения в подшипниках уменьшается в отношении диаметра колеса к диаметру шейки.

Сила тяги. Механическая работа, которую совершает сила тяги при движении поезда, является одной из форм энергии. В соответствии с законом сохранения энергии — энергия не возникает и не исчезает, а только переходит из одной формы в другую. Поэтому, чтобы совершить работу движения поезда, локомотив должен преобразовать в нее какое-то количество энергии другого вида, например, внутреннюю химическую энергию топлива, Такое преобразование на тепловозе происходит в двигателе внутреннего сгорания, на паровозе — в топке и т.д.

Чтобы вызвать движение, сила должна быть приложена к телу, т.е. быть внешней по отношению к телу. Но сила, создаваемая двигателем внутреннего сгорания вследствие давления газов в цилиндрах на поршни, — это сипа внутренняя. Она не может вызвать движение поезда, как не могут привести к поступательному движению «шаги» человека, висящего на гимнастической перекладине.

Рис. 3. Создание силы тяги при взаимодействии колеса с рельсом

Внешняя движущая сила создается локомотивом во взаимодействии с рельсами (рис. 3). В результате преобразования электрической энергии в механическую работу тяговый электродвигатель через зубчатую передачу редуктора сообщает оси колесной пары вращающий момент М. Если пренебречь потерями на трение в моторно-осевых и буксовых подшипниках, можно посчитать, что вся величина этого момента используется для вращении колесной пары с частотой n_k (об/мин).

Момент в соответствии с правилами физики можно представить в виде пары сил F₁ и , действующих на плече, равном радиусу колеса . Эта пара сил сама по себе является внутренней по отношению к локомотиву и, следовательно, не может вызвать его движения.

В этом нетрудно убедиться, если представить локомотив поднятым над рельсами, например, на домкратах. Его двигатели могут работать, колесные пары вращаться под действием момента М, но поступательного движения не будет — локомотив в этом случае не имеет точки опоры. Так же и человек, когда теряет эту опору, оказавшись, например, на скользком льду, может перемещаться лишь с большим трудом и медленно. Однако, когда локомотив не поднят и находится на рельсах, вращение его колесных пар приводит к поступательному движению. Значит, есть сила, преодолевающая сопротивление движению, т.е. трение.

Что же это за сила? Самое удивительное в том, что по природе своей это тоже сила трения. Когда колесо прижато к рельсу силой тяжести Р, действие силы  на рельс в точке касания колеса 0 при отсутствии его проскальзывания (т.е. при достаточном трении) приводит к появлению равной по величине реакции F, действующей от рельса на колесо в направлении его поступательного движения. Сила F — пассивная, она появляется только тогда, когда колесо упирается в рельс под действием приложенного к нему момента М. Но, тем не менее, именно эта сила и является причиной движения, т.е. внешней движущей силой.

Вместе с этой лекцией читают “7.1 Многопараметрические линейные модели – описание модели”.

Силу сопротивления проскальзыванию колеса относительно рельса называют силой сцепления. Физическая природа процесса сцепления колес локомотива с рельсами представляется очень сложной и во многом неясной до настоящего времени. Дело в том, что движение колеса локомотива по рельсу связано одновременно с трением качения и трением скольжения, в том числе и упругого (крипа). На величину силы сцепления колес с рельсами оказывают существенное влияние скорость движения локомотива, состояние колес и рельсов, а также степень их износа, атмосферные условия (снег, дождь и т.д.), конструкция экипажной части, вес локомотива и целый ряд других случайных факторов.

В первом приближении силу сцепления F_сц определяют как силу трения, т.е, . Здесь коэффициент пропорциональности  по аналогии с формулой для определения силы трения можно назвать коэффициентом сцепления. Сила тяги F (см. рис. 3) не может быть больше предела, устанавливаемого условиями сцепления . В этом, как говорят, состоит ограничение силы тяги по сцеплению.

Объясним это ограничение на примере: шестиосный локомотив весом 1200 кН (массой 120 т) при идеальных условиях реализации максимального расчетного значения коэффициента сцепления  сможет создать силу тяги 40 кН независимо от его мощности, т.е. даже в этом случае сила тяги может быть равной лишь трети веса локомотива .

Таким образом, трение, с которым люди борются, чтобы облегчить работу любой машины или уменьшить затраты энергии на транспорт, в данном случае выполняет полезную службу. Чем больше трение (сцепление) между колесом и рельсом, тем больше может быть сила тяги локомотива. Потеря сцепления, например, при наличии жидкости (воды, масла и т.д.) между колесом и рельсом ведет к проскальзыванию (пробоксовыванию) колес и к потере (частичной или полной) силы тяги. Так буксуют, например, колеса автомобиля в гололед или на грязной дороге.

При проектировании локомотивов расчетные значения силы тяги F_кр, по которым рассчитывают возможный для локомотива вес поезда, устанавливают не по пределу сцепления, а с некоторым запасом, считая , где  — так называемый коэффициент тяги ‹)

Величина коэффициента тяги, например, для большинства серийных грузовых тепловозов находится в пределах 0,18 — 0,19 при расчетной величине коэффициента сцепления примерно 0,26.

3.2
Определение ограничения скоростей

      При
построении кривой V(S)
необходимо нанести следующие ограничения скоростей движению:

● по
стрелочным переводам (V = 40
км/ч):

,

где      – длина стрелки;

      – длина поезда;

● по
спускам (из тормозной задачи);

● по
кривым:

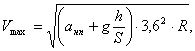
 где     – радиус кривой.

4 
ОПРЕДЕЛЕНИЕ
ВРЕМЕНИ ХОДА ПОЕЗДА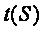

Время
хода поезда определяем с помощью треугольника Дегтярёва.

5  
ПОСТРОЕНИЕ КРИВОЙ

Кривая
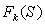на участках движения в режиме
тягистроится на основаниикривой скорости 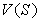и тяговой характеристики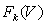. При построении кривой 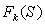величины 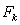определяются по тяговой
характеристике в зависимости от скорости, соответствующей данной точке перелома
кривой 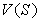, и откладываются в качестве ординаты
по месту расположения этой точки перелома.

5.1 Установление
режимов работы локомотива

В
режиме ЧF сила тяги определяется по
формуле:

,

где      – сопротивление,
соответствующее движению с частичным использованием тяги.

Для :

Туда
(кгс).

         
(кгс).

                  Обратно  (кгс).

                                  (кгс).

6 ОПРЕДЕЛЕНИЕ
РАСХОДА ТОПЛИВА ТЕПЛОВОЗА

Расход
топлива за время движения поезда по участку пути, кг, определяется о формуле:

,

где             – время работы дизеля,
в пределах которого скорость движения поезда принята постоянной, мин;

              – расход топлива,
соответствующий средней скорости движения поезда в интервале времени Δt при
используемой позиции контролера();

      – расход топлива силовыми установками
тепловоза на холостом ходу  (.

Для
 туда:

.

Для
 обратно:

.

7 ОПРЕДЕЛЕНИЕ
МЕХАНИЧЕСКОЙ РАБОТЫ СИЛЫ ТЯГИ ЛОКОМОТИВА

Механическая
работа силы тяги локомотива на участке пути от 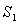 до
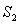 выражается интегралом:

.

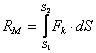Так
как определённый интеграл есть площадь, ограниченная функцией  в интервале от  до ,
то для определения  необходимо подсчитать
площадь , заключённую между этой кривой и
осью пути.

Эта
площадь с учётом выбранного масштаба и будет представлять механическую работу
силы тяги локомотива, ткм:

,

где      – площадь, ограниченная кривой  и осью пути, ;

– цена единицы площади, .

,

где      – масштаб 1км пути, мм;

– масштаб 1000 кгс силы тяги, мм.

Для
 туда:                                                        Для
 обратно:

                                                                        

                            

8 ОПРЕДЕЛЕНИЕ
МЕХАНИЧЕСКОЙ РАБОТЫ СИЛ СОПРОТИВЛЕНИЯ

Механическая работа сил сопротивления, ткм, определяется
через механическую работу силы тяги локомотива по формуле:

,

где      – разность конечной и начальной
проектных отметок рассматриваемого участка пути, м;

– скорости соответственно в начале и
конце участка пути, км/ч.

Так
как работа сил сопротивления подчитывается на участке пути, ограниченном
раздельными пунктами, т.е. , последнее
слагаемое формулы обращается в нуль, и уравнение примет вид:   

Для
 туда:

 ткм.

Для
 обратно:

 ткм.

литература

1.Правила тяговых расчетов
для поездной работы. – М.: Транспорт, 1985 г.

2. Тяговые расчеты при
проектировании железных  дорог.- учебное пособие под

редакцией Е.С. Свинцова  –
СПб , 2004 г.

3. Технико – экономическое
сравнение вариантов трассы при проектировании новых железных дорог. – учебное
пособие под редакцией В.М. Петров, Н.С. Бушуев – Ленинград, 1987 г

Цитировать:

Аблялимов О.С. О методике расчёта механической работы локомотива и поезда // Universum: технические науки : электрон. научн. журн. 2020. № 8(77). URL: https://7universum.com/ru/tech/archive/item/10614 (дата обращения: 23.05.2023).

АННОТАЦИЯ

Предложен алгоритм графического и аналитического (табличного) способов расчёта механической работы внешних сил, действующих на поезд. Могут использоваться при оценке тягово – энергетической эффективности  локомотивов дизельной и электрической тяги в условиях эксплуатации.

ABSTRACT

An algorithm for graphical and analytical (tabular) methods for calculating the mechanical operation of external forces acting on a train is proposed. They can be used to assess the traction and energy efficiency of diesel and electric traction locomotives under operating conditions.

Ключевые слова: локомотив, поезд, скорость, расчёт, график, режим.

Keywords: locomotive, train, speed, calculation, schedule, mode.

Высокоэффективное использование энергетических ресурсов для тяги поездов непосредственно определяет количество и качество работы железных дорог, а энергосберегающая технология перевозочного процесса имеет первостепенное значение, где режим работы силовых энергетических систем локомотивов, обусловленный режимом тяги, является главным фактором их энергетической эффективности.

Для корректного обоснования сказанного необходимо уметь рассчитывать механическую работу сил тяги, сопротивления движению и тормозных на различных режимах ведения поезда – тяги, холостого хода и торможения.

Механическая работа локомотива, затрачиваемая на перемещение поезда, напрямую зависит от тягового качества профиля пути и трассы железной дороги, которые, в свою очередь, характеризуются крутизной, протяжённостью и расположением уклонов элементов профиля, а также кривизной пути.

Эти характеристики профиля пути оказывают существенное влияние на режимы движения поезда и работу силовых энергетических систем локомотива, расход электрической энергии и дизельного топлива локомотивами на тягу поездов, пропускную и провозную способности железных дорог, а также стоимость железнодорожных грузовых и пассажирских перевозок.

Опираясь на рекомендации [4,5], автором были разработаны и предложены соответствующие методики расчёта механической работы локомотива в режиме тяги [1] и поезда в целом [2], основу которых составляет графоаналитический метод расчёта.

Ниже предлагаем алгоритм вычисления (расчёта) механической работы сил основного сопротивления движению поезда в режиме тяги, для реализации которого поступаем следующим образом.

Предварительно строится и располагается рядом с кривой скорости V = f(S)

диаграмма W_О = f(V) сил основного сопротивления движению поезда в режиме тяги так, чтобы оси их скоростей совпали между собой (рис. 1).

Исходной информацией для реализации этих целей являются данные таблицы удельных равнодействующих сил поезда в режиме тяги и интегральная кривая скорости V = f(S), ранее построенная в результате тягового расчёта, а также заданный, спрямлённый профиль железнодорожного пути.

Рисунок 1. Алгоритм графического расчёта механической работы сил

основного сопротивления движению поезда в режиме тяги

По изломам интегральной кривой скорости V(S) намечаются (выбираются) интервалы скоростей движения поезда в пределах, не превышающих изменение скорости в 10 км/ч и с учётом упомянутой диаграммы W_О = f(V) строится графическая зависимость W_О = f(S) (рис. 1). По ней можно будет определять средние значения сил основного сопротивления движению поезда в каждом принятом для расчёта i – м интервале скоростей движения последнего.

Методика аналитического (табличного) расчёта механической работы А_С сил основного сопротивления движению поезда в режиме тяги приведена в табл. 1, где обозначено: V_Н, V_К – соответственно, скорости в начале и конце каждого i – го интервала скорости движения поезда, определяемого по зависимости V = f(S) при условии изменения интервала скорости ΔV ≤ 10 км/ч; W_ОН, W_ОК – соответствующие им силы основного сопротивления движению поезда, которые находим по диаграммам W_О = f(V) или W_О = f(S); W_Оср – среднее значение силы основного сопротивления движению поезда в каждом i – м интервале; ΔS_i – путь, проходимый поездом при изменении скорости движения в каждом i – м интервале.

Таблица 1.

Пример аналитического расчёта механической работы сил

основного сопротивления движению поезда в режиме тяги

Известные путь ΔS_i (км) и среднее значение сил W_Оср (кН) основного сопротивления движению поезда, которые он будет иметь при изменении скорости движения в каждом i – м интервале, позволят аналитическим путём определить механическую работу А_С упомянутых выше сил по такой формуле

МДж                                                       (1)

Для реализации методики расчёта механической работы А_С сил основного сопротивления движению поезда в режиме тяги определяем её значение в диапазоне изменения скоростей движения поезда от V₁=90 км∕ч до V₅=60 км∕ч (см. рис. 1) по исходным данным [3] – величина механической работы составляет А_С = 1186,61 МДж (табл. 1).

Исследованиями [1,3] установлено, что увеличение механической работы сил основного сопротивления движению однозначно связано с увеличением времени работы силовой энергетической установки (системы) локомотива под нагрузкой, то есть на режимах тяги, что приводит к увеличению расхода топливно – энергетических ресурсов, затрачиваемых на перемещение поезда.

Внешние управляемые машинистом силы, искусственно создаваемые тормозными средствами поезда во взаимодействии с рельсами и приложенные к ободам колёс в направлении, противоположном движению, называют тормозными силами поезда, а режим ведения поезда – тормозным.

При тормозном режиме кинетическая энергия движущегося поезда за весьма короткий промежуток времени преобразуется в работу тормозных средств, мощность которых в отличие от касательной мощности (силы тяги) локомотива, реализуемой при взаимодействии колес с рельсами, теоретически не имеет ограничений по величине.

Поэтому механическая работа тормозных сил поезда является важной и весомой составляющей при проведении теоретических и экспериментальных исследований по обоснованию эффективности использования тягового подвижного состава в условиях эксплуатации.

На рис. 2 изображён предложенный автором алгоритм графического расчёта механической работы А_Т тормозных сил поезда.

Рисунок 2. Графическая интерпретация расчёта механической работы

тормозных сил поезда

Пример аналитического расчёта механической работы А_Т тормозных сил поезда по исходным данным [3] показан в табл. 2, где обозначено: V_Н, V_К – скорости в начале и конце каждого i – го интервала скорости движения поезда, определяемого по зависимости V = f(S) при условии изменения интервала скорости ΔV ≤ 10 км/ч; В_ТН, В_ТК – соответствующие им тормозные силы поезда, которые находим по диаграммам В_Т = f(V) или В_Т = f(S); В_Тср – среднее значение тормозной силы поезда в каждом i – м интервале; ΔS_i – путь, проходимый поездом при изменении скорости движения в каждом i – м интервале.

Аналогично [1,4], исходной информацией для реализации этих целей являются данные таблицы удельных равнодействующих сил поезда и интегральная кривая скорости V = f(S) на режимах торможения, а также заданный, спрямлённый профиль железнодорожного пути.

Интервалы скоростей движения поезда намечаются (выбираются), в пределах не превышающих изменение скорости в 10 км/ч, по изломам интегральной кривой скорости V(S) в режиме торможения и с учётом упомянутой диаграммы В_Т = f(V) строится графическая зависимость В_Т = f(S) (рис. 2), по которым можно будет определять средние значения тормозных сил поезда в каждом принятом для расчёта i – м интервале его скоростей движения.

Последовательность расчёта механической работы А_Т тормозных сил поезда в режиме торможения приведена в табл. 2.

Таблица 2.

Пример расчёта механической работы тормозных сил поезда

в режиме торможения 

Результирующее значение величины механической работы тормозных сил поезда на рассматриваемом участке счёта будем вычислять, используя данные табл. 2, по следующей формуле:

                    МДж                                             (2)

Таким образом, величина механической работы А_Т тормозных сил поезда на участке счёта составит

А_Т = 6034,68 + 5519,36 + 7426,00 + 7269,52 + 8024,74= 34274,3 МДж

Торможение производится для остановки поезда или регулирования его скорости уменьшением кинетической энергии движения и увеличение механической работы тормозных сил поезда, однозначно, будет происходить с увеличением длины тормозного пути.

Разработанные методики расчёта рекомендуется использовать при оценке тягово – энергетической эффективности локомотивов в условиях эксплуатации.

Список литературы:

1. Аблялимов О. С. Основы управления локомотивов [Текст] / О. С. Аблялимов, Э. С. Ушаков // Учебник для профессиональных колледжей железнодорожного транспорта. – Ташкент: «Davr», 2012. – 392 с.
2. Аблялимов О. С. Графоаналитический метод расчёта механической работы поезда [Текст] / О. С. Аблялимов, Х. К. Кабинов // Журнал «Вестник ТашИИТ» / Ташкентский ин-т. инж. ж.д. транспорта. – Ташкент, 2014. № 1. – С. 57 – 61.
3. Аблялимов О.С. Исследование эффективности использования тепловозной тяги на холмистом участке железнодорожного пути [Текст] / О. С. Аблялимов, Ж. Х. Атахажаев // Журнал «Вестник ТашИИТ» / Ташкентский ин-т. инж. ж.д. транспорта. – Ташкент, 2013. № 3/4. – С. 22 – 26.
4. Деев В. В. Тяга поездов [Текст] / В. В. Деев, Г. А. Ильин, Г. С. Афонин // Учебное пособие для вузов. – М.: Транспорт, 1987. – 264 с.
5. Подвижной состав и тяга поездов. [Текст] / Третьяков А. П. и др. Под ред. В. В. Деева, Н. А. Фуфрянского // Учебник для студентов вузов железнодорожного транспорта. – М.: Транспорт, 1979. – 368 с.